Психологическая наука и образование
2003. Том 8. № 4
ISSN: 1814-2052 / 2311-7273 (online)
Развивающие эффекты системы Д.Б. Эльконина – В.В. Давыдова
Аннотация
Статья посвящена разработке в системе Д.Б. Эльконина — В.В. Давыдова диагностических средств для определения учебных достижений подростков. Раскрывается понятие компетентности как базового понятия для тестов на компетентность. Приводятся результаты эксперимента на определение математической компетентности учащихся. Приведены факторы, влияющие на успешность решения тестовых задач, —интеллектуальный уровень, выраженность поисковой активности, житейский опыт учащихся.
Общая информация
Ключевые слова: компетентность, тест PISA, диагностика, Д.Б. Эльконин, подростковый возраст, умение учиться, предметность знания
Рубрика издания: Психология образования
Для цитаты: Цукерман Г.А., Ермакова И.В. Развивающие эффекты системы Д.Б. Эльконина – В.В. Давыдова // Психологическая наука и образование. 2003. Том 8. № 4.
Полный текст
Образовательная система Д. Б. Эльконина — В. В. Давыдова претендует на ряд нетрадиционных развивающих эффектов обучения [2]. Есть десятки доказательств того, что такие эффекты достигаются. Однако эти доказательства получены в основном с помощью диагностических методик, разработанных с теоретических позиций В. В. Давыдова для решения исследовательских задач и недостаточно валидизированных для превращения в тестовые измерители. Кроме того, по большей части исследования развивающих эффектов системы Д. Б. Эльконина — В. В. Давыдова были проведены в начальной школе.
В рамках компетентностного подхода разработана система надежных измерителей, с помощью которых можно ликвидировать некоторый дефицит наших знаний о качестве знаний и умений подростков, обучавшихся по системе Д. Б. Эльконина — В. В. Давыдова. В этой статье речь идет о диагностике таких учебных достижений подростков, как предметность знаний (ориентация на существенные отношения задачи), умение учиться.
Компетентность как метафора
В западной педагогике компетентностные педагогические цели, ценности и соответствующие технологии обучения и тестирования органично выросли из размышлений и/или действий, направленных на преодоление недостатков образования. При этом определение того, что в образовании дурно, делалось с позиции потребителей образовательных продуктов. Расчетливые хозяева рынка труда сформулировали запрос на качества, которыми должен обладать выпускник образовательного учреждения. При переводе этого запроса на язык образовательных реалий и возникло понятие «компетентность», ассоциированное с успешным поведением в нестандартных ситуациях, предполагающих неформализованное взаимодействие с партнерами, с решением недоопределенных или запутанных задач, с оперированием противоречивой информацией, с динамичными и сложно интегрированными процессами, управление которыми требует теоретического знания [10].
В тех странах, где идеология и технологии компетентностного подхода к образованию зародились и укореняются, отношение к нему неоднозначно. Одни считают его самым
удачным ответом образования на вызовы современной социально-экономической действительности [9], другие более скептичны. Голландский исследователь Вим Вестера утверждает, что термин «компетентность» в нынешнем его употреблении — это не более чем неточная этикетка, плохо отличимая от привычного термина «умелость» и ничего не прибавляющая к нашему пониманию природы обучения действенному мышлению и умному действию [16]. Английский специалист по проблемам высшего образования Рональд Барнетт мудро предлагает понять ограниченность компетентностного подхода прежде, чем преисполниться энтузиазмом и присягнуть ему на верность [8]. Анализируя то, что может и чего принципиально не может достигнуть образование, взявшее на вооружение компетентностный подход, Р. Барнетт показывает, что во имя результативности, предприимчивости, социальной мобильности выпускников образование (во всяком случае университетское) может утратить традиционную установку на воспитание понимания, критичности и рефлексивности.
В российское психолого-педагогическое сообщество слово «competence» залетело как новая мода. И судьба у компетентностного подхода к отечественному образованию может сложиться такая же, как и у любой моды: поносят 1—2 сезона и сменят на более модное. Сейчас «модники» от педагогики бойко обновляют гардероб: переименовывают все свои педагогические результаты в компетентности. Раньше говорили «первоклассник научился вести себя на уроке», теперь говорят «стал компетентным школьником». Раньше говорили «выучился читать», теперь — «приобрел читательскую компетентность»... Слова, слова, слова...
Чтобы не влезать в терминологическую распрю, рассмотрим только то определение компетентности, которое легло в основу тестов компетентности, в частности теста PISA, о котором пойдет речь в данной статье. Это определение выработано программой DeSeCo (Definition and Selection of Competencies: Theoretical and Conceptual Foundations), созданной в 1997 г. под эгидой OECD[12].
Термины «умение» и «компетентность» не используются здесь как синонимы. Умения обеспечивают возможность выполнять сложные двигательные и/или умственные действия легко, точно, четко, аккуратно, приспосабливаясь к меняющимся условиям действования. Термин «компетентность» описывает сложную систему действий, включающую и умения, и другие компоненты действия, обеспечивающие возможность достигать желаемого результата и соответствовать требованиям общества и отдельных людей.
Для компетентности, согласно DeSeCo, характерно следующее:
она обнаруживается только в реальном действии (на которое влияют мотивы, цели и намерения действующего), совершаемом в определенной ситуации. Внешние требования — социальный контекст ситуации входит в компетентность наряду с индивидуальными способностями и склонностями;
компетентность включает когнитивные и некогнитивные компоненты (двигательные и умственные навыки, знания (в том числе и «смутные» знания), мотивацию, ценностные и этические ориентации, установки и прочие социальные и поведенческие компоненты), т. е. все то, что может быть мобилизовано для эффективного действия;
компетентности приобретаются и развиваются пожизненно через действия и взаимодействия в самых разных формальных и неформальных образовательных ситуациях и институтах;
ключевые компетентности существенны для успеха в самых разных сферах жизни любого человека и общества. Поэтому они нужны каждому человеку и всему социуму. Выделение ключевых компетентностей зависит от ценностей данного социума, от того, что делает человека успешным социально, экономически и личностно именно в данном социуме. Предметно-специфичные компетентности (например, компетентности пианиста) не обязательны для каждого человека и не обеспечивают успех во всех сферах жизни (работа, семья, здоровье...) и/или не повышают качество жизни человека и общества;
чтобы справляться со сложными требованиями современной жизни, человеку необходимо достичь определенного уровня когнитивной сложности, основанного на критическом мышлении, рефлексии и целостном видении жизни. Компетентному человеку присущ авторский (self-authoring) уровень когнитивной сложности, при котором он может быть независимым от множества ожиданий и претензий своего окружения, способным контролировать свои действия на основе собственных чувств, мыслей и ценностей, действовать самостоятельно, а не являться орудием чьих-то действий, быть автором собственной жизни, а не играть роль в чужом сценарии.
При характерной для психологии и педагогики размытости почти каждого термина ком- петентностный подход может оказаться полезным по крайней мере в одном отношении: как прием поэтического отстранения, как неожиданная метафора, которая помогает стереть пыль с затертых слов и по-новому увидеть привычные реалии. Эти реалии давно обжиты в психолого-педагогическом обиходе. С одной стороны, это умения (неотличимые от навыков), с другой — способности (неотличимые от одаренности).
Можно представить себе умения и способности как два полюса единого образовательного континуума факторов, влияющих на успешность решения задач. Компетентность претендует на место в широкой пограничной полосе недоопределенности. Мы не знаем, где кончается умелость (то, чему человек может научиться, упражняясь в использовании существующих в культуре средств и способов достижения анонимных целей) и начинается способность (то, что позволяет человеку самостоятельно изобретать средства и способы достижения его собственных целей). Эту зону неопределенности стали называть компетентно- стью. Мы не знаем, где кончается формирование (один из механизмов передачи знаний, умений, навыков) и начинается поддержка детской инициативы (один из механизмов фасилитации способностей). Эту зону неопределенности стали называть компетентностно ориентированным образованием.
Таким образом, компетентностная мода попала в самое яблочко извечных педагогических поисков и мечтаний о работе в зазоре между навыком и способностью. Постулированный, но всерьез не доказанный «формальный эффект обучения» (когда учат, например, математике, а выучивают дисциплине ума) схватывает педагогическую интуицию взаимозависимости обучения и развития. Издревле педагогика искала возможности обучать тому, что психология называет способностями. Например, создавались формальные предметы: учили решать творческие задачи (ТРИЗ), рассуждать непротиворечиво (логика), разбираться в противоречиях (дебаты). В то же время, формируя навыки, даже самый традиционный педагог надеется подготовить своих учеников не только к экзаменам, но и к жизни, где эти навыки (знания, умения) пригодятся в самых неожиданных, непохожих на школьные, обстоятельствах. Раньше это называлось «перенос навыка» [3]. (Воистину, новое — это хорошо забытое старое.) На языке теории поэтапного формирования действий речь идет об обобщенности действия . В. В. Давыдов назвал это же качество действия и/или мысли системностью и обобщенностью знания . На языке «педагогики здравого смысла» это называется функциональной грамотностью .
Не стоит продолжать список названий чрезвычайно близких психологических реалий. Важно не как они называются, а поможет ли новое именование застарелых проблем их продуктивному разрешению. Для того чтобы оценить инструментальность компетентностного подхода, рассмотрим его собственный инструментарий.
В отличие от тестов IQ, тесты компетентности не претендуют на «свободу от культуры и научения», они откровенно строятся на школьном материале и предполагают его усвоение. Чем же тогда отличаются задачи тестов компетентности от привычных контрольных работ и экзаменов, проверяющих усвоение школьной премудрости? Тесты компетентности претендуют на измерение того «сухого остатка» школьного обучения, который будет реально применен в жизни и сделает ее успешной.
Однако «не все, что существенно для жизни, поддается измерению. Не все, что поддается измерению, существенно» — с таким смиренным самоограничением подходят создатели теоретических определений и тестовых измерителей компетентности к диагностике готовности школьников к жизни в современном обществе [12]. Легче всего поддаются измерению умения. Именно их измеряют в тестах компетентности, но с одной чрезвычайно существенной оговоркой. Эти тесты опираются на содержание школьного образования, но не предполагают использования всего объема знаний и умений школьников. Более того, они предполагают использование очень незначительного объема школьных знаний, но применять эти знания приходится в ситуациях, не похожих на те, где эти знания приобретались и контролировались.
Условия эксперимента.
Тестовый материал. На успешность выполнения теста влияет множество факторов, многие из которых не имеют никакого отношения к проблеме широкого переноса умений. В качестве материала для анализа этой проблемы были выбраны две задачи из математического субтеста теста PISA (см. Приложение). Выбор задач был обусловлен следующими причинами:
эти задачи (по замыслу авторов) выявляют не только усвоение математических зна- ний/умений, но и умение учиться, самостоятельно приобретать эти знания. Такие задачи в тесте PISA называются структурированными. Они «включают несколько вопросов относительно одной и той же ситуации, которые располагаются по возрастающей сложности... Вопросы составлены таким образом, чтобы в процессе последовательных ответов на них учащиеся получали некоторые «подсказки», необходимые для решения расположенных на последнем месте наиболее сложных вопросов» [4, c. 15];
данные задачи предполагают работу со знаковыми системами (формулы, графики, схемы) и переходами от одного знакового отображения к другому. Решение этих задач показывает, владеет ли ученик знаковым опосредствованием собственных действий с реальными ситуациями, описанными на языке математики;
эти задачи являются провокационными: они позволяют различить натуральное и понятийное отношения к математической задаче, или (на языке В. В. Давыдова) предметность математического знания;
анализируемые задачи не предполагают одного, единственно верного способа решения. Их можно решать по-разному:
и эмпирически, и теоретически, и в умственном, и в предметном плане, и с помощью рисунков, и с помощью формул. Иными словами, для успешного решения этих задач не обязательно обладать каким-то определенным учебным стилем, типом мышления или другими индивидуальными особенностями, не имеющими отношения к загадочным компетентностям, измеряемым тестами;
эти задачи не перегружены ни текстовой информацией, ни техническими навыками, в частности навыками вычисления. Следовательно, трудности ребенка при решении выбранных задач не будут «зашумлены» побочными факторами.
Иначе говоря, выбранные для микроанализа задачи позволяют увидеть и то, чему ребенка можно научить впрямую, традиционными методами трансляции готовых знаний, и то, чему традиционными репродуктивными методами научить крайне сложно (умение учиться, предметность знания, знаковое опосредствование). Эти задачи, действительно, расположены в зазоре между навыком и способностью. В переводе на язык компетентност- ного подхода — они позволяют измерить функциональную математическую грамотность школьников .
Кроме того, выбор этих двух задач обусловлен и их социальной значимостью: обе задачи решены в российской выборке рекордно плохо, они диагностируют самые болевые точки отечественного образования (если смотреть на него с позиций компетентностного подхода).
Процедура тестирования. Тексты двух отобранных задач предъявлялись ученикам письменно: каждый получал ксерокопию соответствующих страниц стандартных тетрадей PISA-2000. Свои ответы они писали на чистых листах (в клеточку). На доске были записаны дополнительные вопросы, которые позволили нам судить о способе размышлений ученика. Инструкция о форме записи давалась устно и была чрезвычайно подробной. Тестирование проводилось во время урока и занимало ровно урок. Практически не было детей, которые не ответили бы на какой-то вопрос из-за недостатка времени.
Экспериментальные выборки. Сравниваемые выборки отвечали следующим тре- бованиям:1) относительно уравненные по возрастному, половому, национальному и социальному составам выборки различались по базисным характеристикам учебного процесса; 2) лишь одна из выборок принадлежала к образовательной системе, претендующей на такие образовательные результаты, как умение учиться, предметность знания, знаковое опосредствование; 3) ни в одной из выборок не практиковался компетентностно ориентированный подход к образованию.
Эксперимент проводился с восьмиклассниками (13—14 лет) из московских школ, известных высоким качеством образования.
Первая выборка (45 учеников — 22 девочки, 23 мальчика): школа № 91, работающая по системе Д. Б. Эльконина — В. В. Давыдова. В обследованной параллели эта система была воплощена в той полноте, на которую сегодня способна практика (т. е., разумеется, со многими оплошностями). В начальной школе в форме учебной деятельности преподавались математика, русский язык, литература, изо, естествознание. В средней школе добавились химия, физика, биология. С I по VII класс практиковалось безотметочное обучение. Образовательная среда, обрамляющая урок как административно закрепленную единицу учебной деятельности, в школе практически отсутствует. Однако семейная образовательная среда учеников этой школы чрезвычайно насыщена.
Вторая выборка (50 учеников — 29 девочек, 21 мальчик): школа № 458, вошедшая в первую пятерку российских школ по предыдущим исследованиям с помощью тестов компетентности. Классы обучались по традиционной системе, при этом в школе создавалась насыщенная образовательная среда, обрамляющая и восполняющая учебный процесс, развертывающийся на уроке. Для тестирования были выбраны два гимназических класса. Отбор и конкурс в гимназические классы позволяют хотя бы отчасти уравнять две выборки по социальному составу.
Результаты решения двух структурированных задач теста PISA.
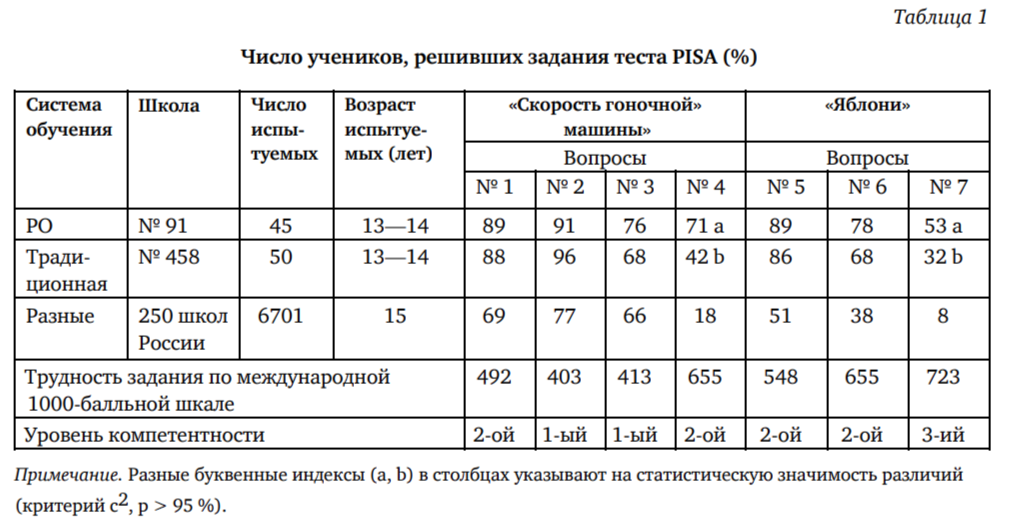
В табл. 1 приведены результаты решения двух задач в каждой выборке. Сравниваемые выборки отличаются лишь в двух вопросах (№ 4, 7). Для того чтобы понять, о чем говорят эти отличия, проведем психологический анализ каждого вопроса.
Из семи тестовых вопросов, на которые отвечали школьники, два вопроса (№ 2, 3) принадлежат к первому уровню математической компетентности, предполагающему воспроизведение математических фактов и методов (в данном случае — умения читать график скорости) и проверяемому с помощью традиционных заданий [4, с. 15). Иными словами, эти вопросы показывают, как школа справляется с традиционной задачей трансляции знаний, умений, навыков.
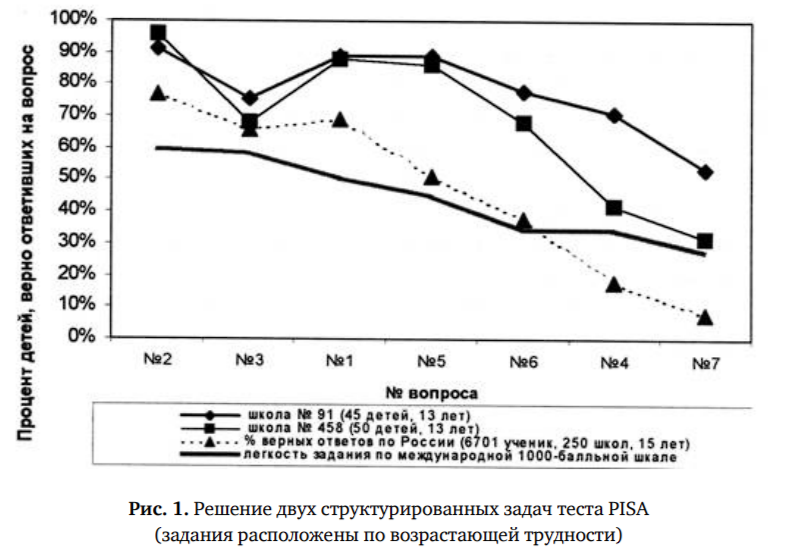
Четыре вопроса (№ 1, 4, 5, 6) относятся ко второму уровню компетентности, что предполагает установление связей и интеграцию материала из разных тем курса математики и проверяется с помощью несложных жизненных задач (там же). Качественный анализ ответов на эти вопросы показывает, что они в высшей степени неравнозначны по требованиям, предъявляемым к ученику. Вопросы № 1, 5, 6 можно рассматривать как изолированные, самостоятельные задачи. Вопрос № 4 предполагает опору на знания о задачной ситуации, которые были добыты при ответе на предыдущие вопросы — № 1—3. Именно этот вопрос и показывает, может ли ученик учиться самостоятельно, в данном случае на основе своего собственного опыта. Трудность вопроса № 4 (по 1000-балльной международной шкале) совпадает с трудностью вопроса № 6 (655 баллов). Однако на вопрос № 6 школьники отвечают значимо лучше во всех выборках, кроме выборки школы № 91 (в которой установка на то, чтобы учить детей учиться, наиболее четко сформулирована и, как мы видим, реализована). Это расхождение ответов на вопросы № 4 и 6, трудность которых оценена одинаково, и указывает на то, что при ответе на данные вопросы школьники опираются на разные умения и способности.
Особняком стоит вопрос № 7, принадлежащий к третьему уровню компетентности, который предполагает математические размышления, требующие обобщения и интуиции. Для проверки достижений третьего уровня используются задания, в которых необходимо самостоятельно «математизировать» предложенную жизненную ситуацию: выделить в ней проблему, которая решается средствами математики, и разработать математическую модель ситуации (там же). С помощью этой модели несложно решить ту проблему, которая не решается или решается чрезвычайно громоздко при обращении к самой жизненной ситуации. Вопрос № 7, так же как и вопрос № 4, предполагает опору на знание о ситуации задачи, добытое собственными силами при ответе на вопросы № 5, 6. Не случайно вопросы № 4 и 7 оказались самыми трудными во всех сравниваемых выборках.
О том, что вопросы № 4 и 7 существенно отличаются от остальных пяти вопросов, выразительно говорят кривые на рисунке. Именно в вопросах № 4 и 7 кривые двух «хороших» школ и кривая общероссийской выборки оказываются по разные стороны «баррикады» — международной 1000-балльной шкалы трудности, построенной на основе результатов тестирования во всех 32 странах, включая Россию . Иначе говоря, характер трудности вопросов № 4 и 7 — особый. Эти вопросы составляют отдельный кластер и будут далее рассматриваться как критические для диагностики умения учиться.
Критические задания теста компетентности (вопросы № 4 и 7).
Вопросы № 4 и 7 завершают серии вопросов, относящихся к определенной задачной ситуации. Вопросу № 4 предшествуют три вопроса, заставляющих ученика разбираться в графике скорости. Вопрос № 4 касается того же самого графика, в котором ученик, казалось бы, разобрался. Однако ответ на вопрос № 4 может быть для ребенка либо продолжением действия с графиком скорости и ситуацией гонки, либо совершенно отдельным действием, не связанным с предыдущими. Аналогично и вопрос № 7 может быть либо продолжением размышления о соотношении двух величин (числа яблонь и числа хвойных деревьев), либо совершенно новым вопросом, не связанным с предыдущими. Что нужно ученику, чтобы успешно справиться с критическими вопросами?
Умение учиться. Вопросы № 4 и 7 были бы невероятно сложны, если бы не подсказки, содержащиеся в предыдущих вопросах.
Известно, что подсказки помогают тем ученикам, которые умеют извлекать урок из самых разных источников опыта, в частности из опыта собственных действий. Связность, цельность опыта собственных действий — одно из существенных условий умения учиться. О том, что «подсказки» работают и «самообучение» происходит, говорят сами дети («Яблони», вопрос № 7):
«Как было замечено, количество хвойных деревьев = 8n, а количество яблонь = n2» (Юра В.).
«Не надо забывать, что число яблонь = n2, а число хвойных деревьев = 8n» (Марина Д.).
«Из прошлых двух заданий следует, что при увеличении размера сада количество яблонь, бывшее сначала в 8 раз меньше количества хвойных деревьев, со временем догонит количество хвойных деревьев, а далее будет становиться еще больше и больше, чем количество хвойных деревьев, так как (далее — формулы)» (Маша Л.).
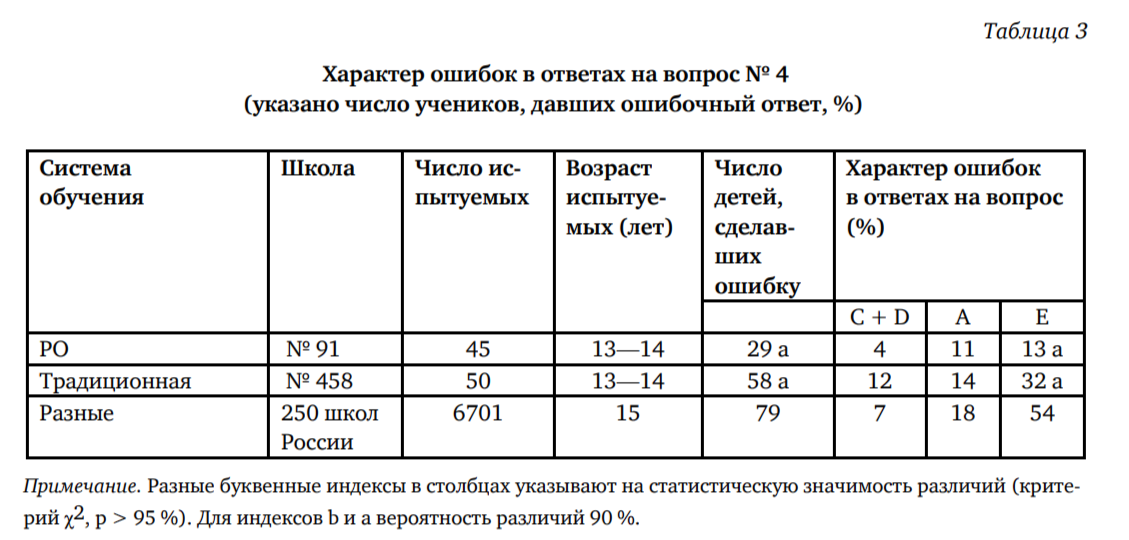
Данные, приведенные в табл. 2, позволяют утверждать, что хорошее традиционное обучение (школа № 458) хуже справляется с задачей научить детей учиться, чем хорошее обучение по системе Д. Б. Эльконина — В. В. Давыдова. О том, что в обеих школах детей обучают хорошо, говорит отсутствие различий между нашими выборками во всех заданиях, кроме критических (табл. 1).
Предметность знания. Термин «предметность (или предметная отнесенность) знания» был введен В. В. Давыдовым для выделения важнейшей характеристики понятия: «содержательной абстракции, позволяющей адекватно ориентироваться в существенных отношениях усвоенного материала» [2, с. 230]. Сотрудники В. В. Давыдова (Г. Г. Микулина, О. В. Савельева, М. А. Семенова, А. М. Аверин, А. Л. Малеев, А. А. Либерман) разработали диагностические задачи, позволяющие определять, обладает ли понятие, которым пользуется ученик, достоинством предметной отнесенности. Принцип построения этих диагностических задач состоял в том, чтобы исключить возможность ориентации на не существенные для данной задачи условия и сделать заметным, явно наблюдаемым способ ориентации в задаче.
Наиболее грубо отсутствие предметности знания (понятия) обнаруживается в тех случаях, когда ребенок, решая, к примеру, математическую задачу, ориентируется не на математические, а на житейские отношения, содержащиеся в условиях задачи. Знаменитым проявлением такого житейского, натурального рассуждения стал тезис Буратино о яблоках из жизни и яблоках из задачи.
Оба критических вопроса задач теста PISA содержат провокацию натурализма — рассуждения, выходящего за рамки задачи и основанного не на понятийной, а на житейской логике.
Вопрос № 7 «Яблони» содержит два типа провокаций натурализма:
Провокация житейской ситуацией. Рассуждение с позиции фермера.
«Будет увеличиваться количество хвойных деревьев, загораживающих яблони от ветра, — это практически. Но, учитывая, что яблони более быстро развиваются, то на некоторый момент времени яблонь будет больше, а хвойные деревья будут еще саженцами» (Александра М.).
«Чтобы ветер не проходил через хвойные деревья туда, где растут яблони
(а фермер этого не хочет), ему надо плотнее сажать хвойные деревья» (Дима Ф.).
«Хвойные деревья. Потому что от них зависит рост яблонь» (Диана Э.).
Провокация рисунком/схемой и таблицей из вопроса № 5. Рассуждение с точки зрения ученика, не умеющего пользоваться подсказками и извлекать уроки из собственных действий.
«Количество хвойных деревьев, потому что по рисунку из пятого вопроса видно, что рядом и вокруг одного дерева находятся 2—3 хвойных дерева» (Саша Ш.).
«Когда яблоня была одна, хвойных деревьев было уже восемь» (Нисо А.).
«Быстрее будет увеличиваться количество хвойных деревьев, так как мы составили таблицу» (Вячеслав К.).
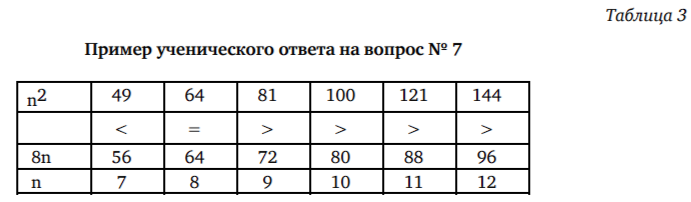
Когда вчитываешься в эти и подобные ответы учеников, кажется, что они заворожены данностью и никак не могут сделать следующий шаг в математическом рассуждении. Этот шаг предполагает выход за данные рисунка, где максимальное значение 4 = n (условия задачи), за пределы таблицы, где максимальное значение 5 = n (вопрос № 5), за пределы формулы, где максимальное значение 8 = n (вопрос № 6). Одна из сильных подсказок, которой не воспользовались ученики, чьи ответы процитированы выше, содержится в самом тексте задания: «Ниже на рисунке изображены схемы посадки яблонь и хвойных деревьев для нескольких значений n, где n — количество рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа n».
О необходимости выхода за пределы условий задачи впрямую говорят ученики, верно ответившие на вопрос № 7. Приведенные ниже примеры демонстрируют разные способы решения задачи.
«Количество яблонь будет увеличиваться быстрее. Количество яблонь — это n2. Количество хвойных деревьев — это 8n. Если просто подставлять числа в порядке возрастания на место n, то это будет заметно. Потому что, к примеру, квадрат числа 9 будет больше, чем 8 • 9.
«Сначала быстрее будет увеличиваться число хвойных деревьев, пока n < 8, так как n2 < 8 n (12 < 8 • 1, 22 < 8 • 2, 32 < 8 • 3 и т. д.). Затем при n=8 они один раз одинаково увеличиваются по количеству (8 n=n, так как 8*8=82). Затем при n > 8 быстрее будет расти число яблонь: n2 > 8 n (92 > 8*9,102 > 8*10 и т. д.)»» (Оля П.).
«Количество яблонь будет увеличиваться быстрее, у = n2 — зависимость увеличения количества яблонь, у = 8n — зависимость увеличения хвойных деревьев» (Гриша Ж.).
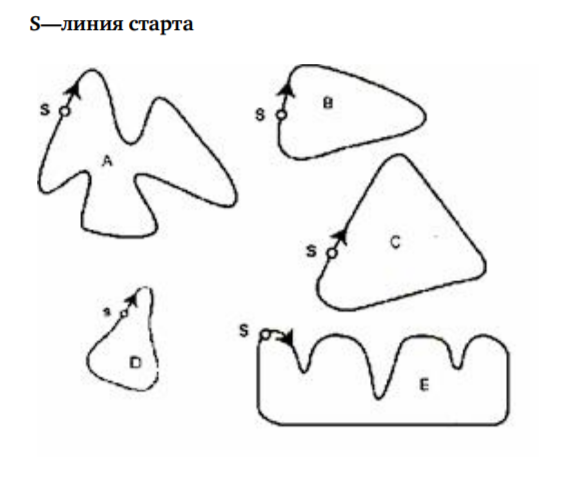
Вопрос № 4 «Скорость гоночной машины» содержит сильную зрительную провокацию натурализма — соотнесение двух графических форм отображения реальной ситуации (гонки) по внешнему сходству (выбор Е). Ответы некоторых учеников прямо указывают на то, что они ориентируются на внешнее сходство графика скорости и схемы трассы, а не на математический смысл графика.
«Е. График очень похож на часть трассы Е. Как и на графике, здесь есть три резких поворота» (Ира Л.).
«А. Трассы В, С и D почти прямые, а трасса Е сначала похожа на данную трассу, но потом идет полкруга прямо, а это не указано на данном графике» (Нисо А.).
«Е. Я сверила с графиком и увидела, что из этих пяти трасс похожа (вернее, является графиком, приведенным ранее) только Е» (Ира К.).
Для того чтобы отвергнуть другие схемы гоночных трасс, от ученика требовался достаточно тонкий анализ графика и схемы. Приведем образец такого анализа.
«Остальные трассы не соответствуют графику скорости. На поворотах машина тормозит. Судя по графику, машина тормозила 3 разаЮ на трассе 3 поворота Ю ответы А и Е не подходят. На прямом участке трассы машина сохраняет и повышает скорость. После старта машина уменьшила скорость (поворачивала) Ю ответ С не подходит. На первом повороте торможение было меньше, чем на втором повороте,
Ю угол первого поворота был меньше, чем угол второго поворота, Ю D не подходит. Остается В» (Соня Ж.)
Анализ характера детских ошибок (табл. 3) свидетельствует о том, что обучение по системе Д. Б. Эльконина — В. В. Давыдова существенно сокращает число учеников, страдающих «крутым» натурализмом в понимании графиков (выбор Е). Ошеломляющее число таких выборов в российской выборке указывает на отсутствие предметности математических понятий, выраженных в знаковой (графической) форме.
Поиск факторов, влияющих на успешность решения тестовых задач.
Компетентность и IQ. IQ, а точнее — фактор g, казалось бы, должен напрямую влиять на успешность выполнения теста компетентности, ибо g и определяется как фактор, обусловливающий успешность любой деятельности. В то же время известно, что g не является достаточно надежным предиктором эффективности обучения и результативности многих практических видов деятельности, определяя 20—25 % разброса результатов [13].
Чтобы определить, как связана успешность решения задач теста PISA, существенно обусловленного обучением, и теста IQ, считающегося «свободным от культурных воздействий» (culture free), мы провели дополнительную серию экспериментов с учениками школы № 91.
Был использован интеллектуальный тест Кеттелла, шкала 2 CFT20 в адаптации Р. Вайса [15]. Результаты 43 восьмиклассников, выполнивших оба теста (ICFT20 и PISA), были подвергнуты статистическому анализу.
Непараметрический корреляционный анализ (коэффициент корреляции Спирмена) выявил наличие существенных связей между значениями IQ и результатами решения задач теста PISA. При этом связь с показателем IQ обнаружена как для навыковых, так и для критических задач. Означает ли наличие этой связи то, что между детьми, решившими разное число задач теста PISA, существуют значимые различия по IQ?
Дисперсионный анализ (ANOVA) выявил эти различия только для последнего критического вопроса (№ 7). Можно предположить, что для данной выборки фактор обучения нивелировал различия между детьми по IQ: их компетентность в целом не зависит от интеллектуальных показателей, измеряемых с помощью теста Кеттелла.
Компетентность и поисковая активность. Высокая поисковая активность предполагает устремление к новому, в частности к новым задачам, для решения которых у человека еще нет средств. Такая устремленность на поиск средств решения новых задач еще не обеспечивает успешности в их решении. Компетентность предполагает успешность в решении задач, но задачи теста компетентности для школьников новые, они отличаются от тех задач из учебника, которые помогли школьнику усвоить то или иное знание и умение.
Вопрос об отношении компетентности и поисковой активности решался на выборке школы № 91. Поисковая активность учеников двух обследованных восьмых классов измерялась систематически, раз в семестр на протяжении всех 7 лет школьного обучения. Измерение поисковой активности осуществлялось экспертным методом [7].
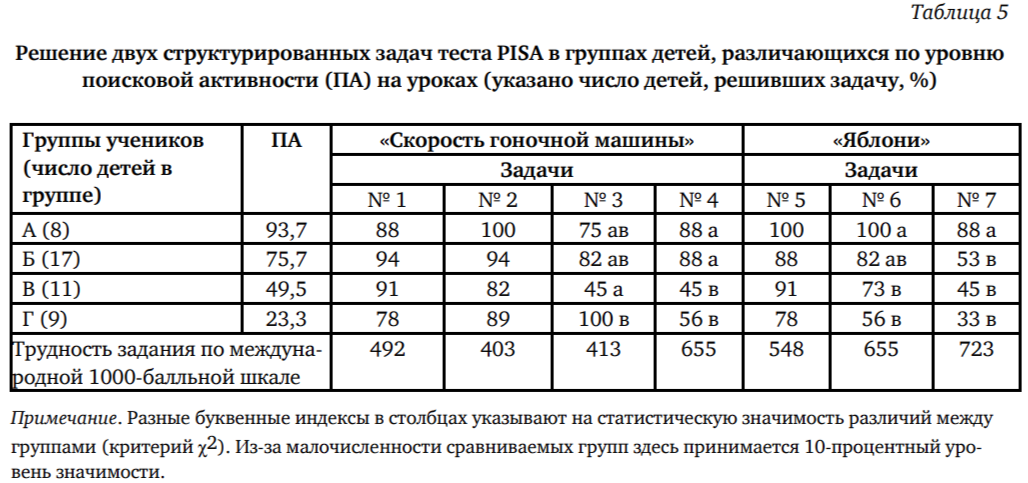
В табл. 4 приведены усредненные показатели поисковой активности каждого школьника, оцененные девятью экспертами-учителями за два месяца до проведения теста PISA. Выделенные группы значимо различаются именно по поисковой активности.
В группу А входят ученики, поисковая активность которых превышает средний показатель по классу плюс стандартное отклонение от среднего. В группу Б входят ученики, чья поисковая активность выше средней по классу, но в пределах стандартного отклонения. В группу В входят ученики, чья поисковая активность ниже средней по классу, но в пределах стандартного отклонения. В группу Г входят те ученики, чья поисковая активность ниже среднего по классу минус стандартное отклонение от среднего.
Данные, приведенные в табл. 4, свидетельствуют о существовании связи между показателями «поисковая активность в ситуации новой задачи» и «успешность в задачах теста компетентности». Наиболее отчетливо эта связь прослеживается в двух «критических» задачах. В «подготовительных» задачах (кроме № 6) эта связь не обнаруживается. О том же говорят и коэффициенты корреляции уровня поисковой активности на уроках на успешность в тесте PISA: 0,429 — для двух «критических» вопросов (значимость не ниже 99 %), 0,231 — для пяти «подготовительных» вопросов (не значимо).
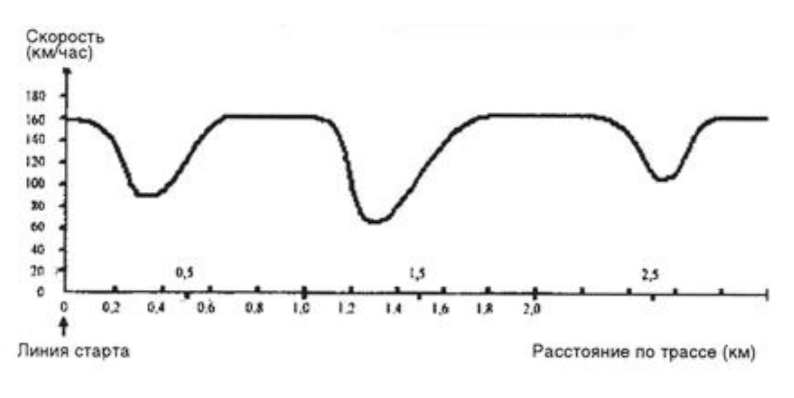
Математическая компетентность и житейский опыт. Нужно ли ясное понимание физических реалий, описываемых графиком, для правильных манипуляций с этим графиком? Для ответа на этот вопрос были сопоставлены детские ответы на два вопроса задачи «Скорость гоночной машины». Вопрос № 1 из этой задачи: «Чему примерно равно расстояние от линии старта до начала самого длинного прямолинейного участка трассы? — А. 0,5 км, В. 1,5 км, С. 2,3 км, D. 2,6 км» — требует манипуляций с графиком. Дополнительный вопрос
№ 1а: «Отметь на графике самый длинный прямолинейный участок трассы» — позволяет определить, имеет ли ученик, правильно выполнивший эти манипуляции, представление о том, как гонщик наращивает скорость, выходя из поворота на прямолинейный участок трассы, и замедляет скорость, приближаясь к следующему повороту.
На оба вопроса ответили 36 восьмиклассников одной из обследованных выборок. Правильные манипуляции с графиком (вопрос № 1) совершили 89 % школьников. Из них правильно (с учетом тормозного пути) отметить на графике самый длинный прямолинейный участок трассы смогли 22 % школьников. Иными словами, чтобы ответить на вопрос по графику, совсем необязательно в деталях понимать те физические реалии, которые описывает этот график. 24 ученика (67 %) справились с вопросом по графику и не сумели описать реалии, стоящие за графиком. Корреляция между «физической» и «математической» частями вопроса о прямолинейном участке трассы незначима (r = 0,189).
Нужен ли личный опыт действия для понимания физических реалий? Личный опыт езды на велосипеде, которым обладают 95 % опрошенных подростков, не влияет на знание о действиях гонщика. Об этом свидетельствует низкая корреляция (r = - 0,081) между ответами на два дополнительных вопроса: «На графике видно, что гонщик три раза снижал скорость. Почему он снижал скорость?» и «Ездишь ли ты на велосипеде?» Не помогает ответить на вопрос о причинах снижения скорости даже небольшой опыт вождения машины (о нем сообщили 63 % восьмиклассников): коэффициент корреляции этих двух вопросов тоже не достигает уровня значимости (r = 0,271).
Почему такие мелочи важны? «Державники», испытывающие жгучую обиду из-за плохих результатов России в международных исследованиях компетентности, ищут и находят массу таких объяснений неудач России, которые мешают прийти к простому и главному выводу: обнаруженная тестом PISA-2000 некомпетентность наших школьников объясняется тем, что в отечественном образовании отсутствует направленность на становление умений, входящих в понятие «компетентность». К примеру, нельзя объяснить тот факт, что российские школьники существенно (не менее чем на 10 %) хуже ответили на вопрос № 4 в задаче «Скорость гоночной машины», тем, что среднее число машин в российских семьях значимо ниже, чем в «развитых» странах. Наши ученики не умеют работать со знаковыми преобразованиями, потому что они не умеют работать со знаковыми преобразованиями. Это не тавтология, а запрет на поиск причин некомпетентности российских школьников за пределами образовательной ситуации в России. Не увеличение числа машин в российских семьях, а изменение характера математического образования в российских школах может привести к улучшению показателей математической компетентности наших учеников.
Какие уроки преподают нам тесты компетентности?
Урок 1. Что помогает детям выходить за пределы заданного? Компетентностный подход (по крайней мере его воплощение в инструментах для измерения компетентности школьников) обнаруживает свою действенность (валидность) именно потому, что помогает удерживать различие между умелостями, жестко привязанными к ситуации их освоения, и умением выходить за пределы этих ситуаций (умение учиться). Загрубляя проведенный анализ двух задач теста PISA, можно говорить о двух составляющих компетентности, измеряемых тестом PISA. Во-первых, это умелость в обращении с культурными орудиями, в частности с понятиями, знаковыми средствами, текстами. Этому можно научить. Умелый (учитель) может передать соответствующие знания и навыки неумелому (ученику). Вторая составляющая компетентности — это умение результативно действовать в новых ситуациях, не встречавшихся в прошлом опыте. Ресурсом такого действия является и уже накопленный арсенал культурных орудий, и умение извлекать из прошлого опыта (своего и общечеловеческого) новое знание. Этому впрямую научить нельзя, но можно научиться там, где ученики получают опыт выхода за пределы выученного, переживают такой опыт как ценность, уважают себя за способность самостоятельно расширять границы своих знаний и умений, проявляют инициативу в новых ситуациях.
Описанные выше эксперименты показали, что возможность выхода за пределы наличной ситуации более выражена при обучении на основании содержательного обобщения, когда ученикам помогают ориентироваться на общий способ решения класса задач, но никогда не дают эти способы в готовом виде. Поиск общих способов действия — вот ключевые слова для описания системы Д. Б. Эльконина — В. В. Давыдова. Эту формулу следует прочитать трижды, с тремя разными акцента ми: на слове «поиск», на словах «общий способ» и на слове «действие». «Поиск» и «действие», несомненно, являются ключевыми словами и для описания компетентностного подхода к образованию. Что касается давыдовской идеи общего способа как основы решения широкого класса конкретно-практических задач — это лишь одно из возможных решений проблемы умения, обладающего достоинством широкого переноса за пределы ситуации освоения этого умения. Структура мысли школьников, имевших значительный опыт поиска общих способов решения новых учебных задач, действительно, меняется, но проблема их самостоятельности, инициативности и ответственности остается открытой.
Проектный метод, межпредметные связи или интеграция учебного содержания, особый школьный уклад, обеспечивающий богатство познавательно-созидательной жизни школьников вне урока, — вот ключевые слова для укоренения компетентностного подхода в образовании [6]. Однако данные тестов компетентности показывают весьма посредственные результаты в школе, где все эти новые педагогические реалии построены, но разрушена традиционная урочная форма обучения, а предметное содержание школьных дисциплин отодвинуто на периферию.
Урок 2. Что поможет нашему образованию выйти за пределы наличной ситуации? Не существует единственно верного или самого лучшего способа обучения, делающего человека компетентным. Но никакие частности, никакие заплаты на традиционную школьную форму не помогут оформить новый социальный заказ: воспитание продуктивных работников, способных к постоянному самообучению. Можно заниматься частностями: обучить российских школьников основам статистики, «подтянуть» работы с графиками, сделать тренинги по тестированию, можно даже усилить линию развития пространственного мышления. Но это не решит задачу переноса навыков за пределы ситуации приобретения и предъявления этих навыков.
Диагностика — это средство САМОконтроля и САМОоценки, которые ценны не сами по себе, а лишь как основание для следующего действия. Результатом педагогической диагностики является решение образовательной системы о САМОизменении (или об отказе от изменений). Для того чтобы принять такое решение, надо обладать способностью выхода за пределы наличной ситуации. Обучение по системе Д. Б. Эльконина — В. В. Давыдова дает такой результат. Но его можно добиться и другими путями.
ПРИЛОЖЕНИЕ
«Скорость гоночной машины»
На графике показано, как изменялась скорость гоночной машины, когда она проходила второй круг по трехкилометровой круговой трассе без подъемов и спусков.
Скорость гоночной машины на трассе длиной 3 км (при прохождении второго круга)
Вопрос № 1.
Чему примерно равно расстояние от линии старта до начала самого длинного прямолинейного участка трассы?
А. 0,5 км
1,5 км
2,3 км
2,6 км
Вопрос № 2.
В каком месте трассы скорость машины была наименьшей при прохождении второго круга?
На линии старта.
Примерно на отметке 0,8 км.
Примерно на отметке 1,3 км.
Примерно посередине трассы.
Вопрос № 3.
Что можно сказать о скорости машины при прохождении трассы между отметками 2,6 км и 2,8 км?
Скорость машины увеличивалась.
Скорость машины уменьшалась.
По данному графику невозможно определить изменение скорости машины.
Вопрос № 4.
Ниже изображены пять различных по форме гоночных трасс.
По какой из этих трасс ехала гоночная машина, график скорости которой приведен ранее? Обведите букву, которой обозначена эта трасса.
«Яблони»
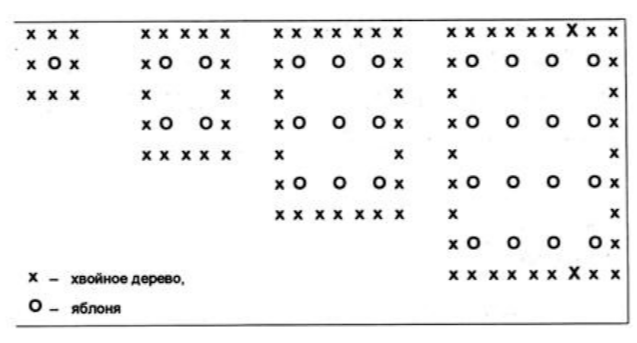
Фермер на садовом участке посадил яблони в форме квадрата, как показано на рисунке. Для защиты яблонь от ветра по краям участка он посадил хвойные деревья.
Ниже на рисунке даны схемы посадки яблонь и хвойных деревьев для нескольких значений n, где n — число рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа n.
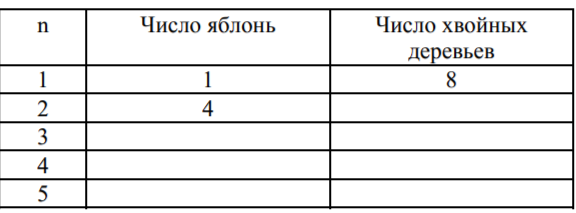
«Вопрос № 5.
Заполните таблицу:
Вопрос № 6.
В рассмотренной выше последовательности число посаженных яблонь и хвойных деревьев подсчитывается следующим образом:
число яблонь = n2,
число хвойных деревьев = 8 n.
Для какого значения n число яблонь будет равно числу посаженных вокруг них хвойных деревьев? Запишите решение.
Вопрос № 7.
Предположим, что фермер решил постепенно увеличивать число рядов яблонь на своем участке. Что при этом будет увеличиваться быстрее: число высаживаемых яблонь или число хвойных деревьев? Запишите объяснение своего ответа.
Литература
- Гальперин П. Я. Лекции по психологии. М., 2002.
- Давыдов В. В. Теория развивающего обучения. М., 1996.
- Кабанова-Меллер Е. Н. Психология формирования знаний и умений у школьников. М., 1962.
- Ковалева Г. С. и др. Основные результаты международного исследования образовательных достижений учащихся PISA — 2000: Краткий отчет. М., 2002.
- Леонтьев А. А. (ред.). Образовательная система «Школа 2100». Педагогика здравого смысла. М., 2003.
- Образовательный процесс в начальной, основной и старшей школе. М., 2001.
- Цукерман Г. А. Опыт типологического анализа младших школьников как субъектов учебной деятельности // Вопросы психологии. 1999. № 6.
- Barnett R. (1994). The Limits of Competence. Knowledge, Higher Education and Society. Buckingham, UK: Open University Press.
- Evers F. T., Rush J. C., Berdrow I. (1998). The Bases of Competence. Skills for Lifelong Learning and Employability. San Francisco, Jossey-Bass Publishers.
- Kirschner P., Vilsteren P. V., Hummel H., Wigman M. (1997). The Desighn of a Study Environment for Acquiring Academic and Professional Competence // Studies in Higher Education. № 22 (2).
-
Reinikainen P. (2003). Brief Presentation of Science in TIMSS and PISA. —
www.pisa.oecd.org - Rychen D. S., Salganik L. H. Definition and Selection of Competencies (DeSeCo): Theoretical and Conceptual Foundations. Strategy Paper: an Overarching Frame of Reference for a Coherent Assessment and Research Program on Key Competencies. — www.deseco.admin.ch.
- Sternberg R. J., Grigorenko E. Practical intelligence and the principle // Spotlight on Student Success. № 603. — www.temple.edu/LSS.
- Sundburg L. (2001). A holistic approach to competence development // Systems Research and Behavioral Science. 18, 103—114.
- Wei R. H. (1987). Grundintelligenztest Skala 2 CFT 20. Verlag fur Psychologie Dr. C. J. Hogrefe. Gottingen.
- Westera W. (2001). Competence in education // J. Curriculum Studies. Vol. 33. № 1.
Информация об авторах
Метрики
Просмотров
Всего: 3477
В прошлом месяце: 17
В текущем месяце: 17
Скачиваний
Всего: 1338
В прошлом месяце: 2
В текущем месяце: 3