Введение
Задача быстродействия известна достаточно давно как задача оптимального управления с естественным функционалом качества – времени, затрачиваемого системой на достижение некоторого заданного терминального состояния [2, 10, 11]. При рассмотрении систем с непрерывным временем данная задача не обладает какими-либо существенными особенностями, выделяющими ее из общей проблематики теории оптимального управления. Решение, полученное на основе принципа максимума Понтрягина [Понтрягин, 1969], гарантирует релейный характер управления для линейных систем.
В то же время системы с дискретным временем имеют ряд фундаментальных отличий от непрерывных систем при построении оптимального управления [3, 4, 12]. Тогда как в непрерывном случае оптимизационная задача является задачей вариационного исчисления, в дискретном времени она представляет собой задачу выпуклого программирования. Данный факт определяет принципиально иной набор средств для построения оптимальных процессов в дискретном случае. Но, несмотря на то, что посредством дискретного принципа максимума [12, 15] и метода динамического программирования [Беллман, 1960] удается решить большую часть задач теории оптимального управления дискретными системами, для задачи быстродействия они оказываются неприменимыми в силу нерегулярности экстремума почти для всех начальных состояний, неединственности оптимальной траектории и дискретного характера критерия качества управления – числа шагов, необходимого для достижения фиксированного терминального состояния из заданного начального [6, 7]. Например, использование известных современных результатов по оптимальному управлению дискретными системами [17, 18, 20, 22] по отношению к задаче быстродействия оказывается некорректным.
В связи с этим приобретает актуальность поиск альтернативных подходов для решения поставленной задачи. На данный момент продемонстрировал свою эффективность метод, базирующийся на использовании множеств 0-управляемости – множеств тех начальных состояний, из которых за конечное число шагов можно перевести систему в начало координат посредством выбора допустимого управления [5, 6, 8, 14]. При этом доказано, что метод решения во многом зависит от ограничений, накладываемых на управление. В случае строго выпуклых ограничений для построения оптимального по быстродействию управления удается модифицировать известный принцип максимума [6, 7]. Если множество допустимых значений управлений представляет собой многогранник, на основе метода динамического программирования решение исходной задачи может быть сведено к решению ряда задач линейного программирования [5, 8]. Также в [Ибрагимов, 2021] описан метод сведения случая произвольных выпуклых ограничений на управление к случаю линейных ограничений за счет проведения полиэдральной аппроксимации множества допустимых значений управления.
Существенным недостатком результатов статей [5, 6, 8] является отсутствие оценок сложности представленных там алгоритмов. Более того, сложность данных методов напрямую зависит от числа множеств 0-управляемости, которые будет необходимо построить для заданного начального состояния, которое совпадает с оптимальным значение критериальной функции в задаче быстродействия. Т.е. для вычисления сложности исследуемой задачи необходимо ее решить.
Целью данной статьи является построение оценок времени быстродействия в виде функций от начального состояния и параметров системы. Полученное решение базируется на аппроксимации множества допустимых значений управлений собственными множествами матрицы системы – такими множествами, образы которых оказываются конгруэнтными прообразу для заданного линейного преобразования [16, 19]. Успешное проведение аппроксимации позволяет свести задачу построения каждого множества 0-управляемости к вычислению суммы геометрической прогрессии, количество слагаемых в которой и является оценкой времени быстродействия.
Постановка задачи
Рассматривается линейная стационарная система управления с дискретным временем и геометрическими ограничениями на управление :
где – вектор состояния, – управляющее воздействие на -м шаге, – матрица системы, – множество допустимых значений управлений. Предполагается, что – выпуклый компакт, , .
Для системы изучается задача быстродействия, т.е. требуется посредством выбора допустимых управляющих воздействий перевести систему из начального состояния в начало координат за минимальное число шагов :
Предполагается, что выполнено условие . Вопросы разрешимости задачи быстродействия для каждого начального состояния подробно обсуждаются в [Сиротин, 2003].
Решение данной задачи состоит из двух этапов: вычисление величины и построения оптимального процесса , удовлетворяющего условию . В данной работе рассматривается только первый этап.
Известный метод вычисления , изложенный в [6, 8], базируется на использовании класса множеств 0-управляемости где – множество тех начальных состояний, из которых систему можно перевести в начало координат за шагов посредством выбора допустимого управления:
2
Тогда задача вычисления может быть сведена к последовательному построению множеств :
33
Однако такой подход является весьма трудоемкой процедурой, что обусловлено следующим представлением множеств 0-управляемости.
Лемма 1 ([лемма 1; 6]). Пусть последовательность определяется соотношениями , . Тогда для всех верно представление
Операция сложения множеств по Минковскому зачастую труднореализуема с вычислительной точки зрения. Например, когда представляет собой многогранник, а следовательно, каждый также является многогранником [следствие 19.3.2; 13], может быть вычислена средствами линейного программирования. На данном свойстве базируется метод вычисления времени быстродействия посредством проведения предварительной полиэдральной аппроксимации множества [Ибрагимов, 2021]. Но описательная сложность (т.е. число вершин) множеств 0-управляемости и, как следствие, размерность соответствующих задач линейного программирования при этом растет экспоненциально по [теорема 4.1.2; 21].
По этой причине оказывается актуальной задача явного построения зависимости
44
либо построения оценок
5
5
Собственные множества линейного преобразования
Для описания
4 и
5 введем понятие собственного множества линейного оператора
. По определению вектор
называется собственным вектором квадратной матрицы
, соответствующим собственному значению
, если справедливо равенство
. Обобщим данное определение на случай множеств.
Через для произвольного множества обозначим образ множества :
В таком случае можно рассмотреть в качестве отображения в пространстве компактов , где
Компакт будем называть собственным множеством отображения , соответствующим собственному значению , если и . Фактически определение собственного множества предполагает, что и являются конгруэнтными.
Лемма 2. Пусть , . Тогда множество является собственным по отношению к отображению , соответствующим собственному значению , тогда и только тогда, когда является собственным множеством по отношению к отображению , соответствующим собственному значению .
Доказательство. Пусть – собственное множество отображения , соответствующее собственному значению . Тогда
Поскольку в силу невырожденности верно, что и ограничено, то – собственное множество отображения , соответствующее собственному значению .
Пусть – собственное множество отображения , соответствующее собственному значению . Тогда
Поскольку в силу невырожденности верно, что и ограничено, то – собственное множество отображения , соответствующее собственному значению .
Лемма 2 доказана.
Требования ограниченности собственных множеств обусловлены тем, что в случае рассмотрения множеств неограниченных возможно, что будет удовлетворять определению собственного множества для непрерывного набора значений . Т.е. собственное значение для собственного множества может определяться неоднозначно.
Пример 1. Пусть
Тогда равенство верно для любого . С другой стороны, ограниченность собственного множества не гарантирует единственность собственного значения. Пусть – симметричное компактное множество. Тогда . Однако далее будет показано, что собственные значения, соответствующие собственным множествам единственны с точностью до знака.
Важным классом множеств, которые рассматриваются на роль собственных, является класс выпуклых тел. Собственное множество преобразования будем называть нетривиальным, если является выпуклым телом и . Интерес представляет поиск именно нетривиальных собственных множеств, которые можно использовать для различных аппроксимаций выпуклых тел.
Лемма 3. Пусть , – нетривиальное собственное множество преобразования , соответствующее собственному значению . Тогда либо и , либо и .
Доказательство. Обозначим через и образ и ядро линейного преобразования . Поскольку , то для верны соотношения
Тогда , и .
Для верны соотношения
Тогда и .
Лемма 3 доказана.
Лемма 4. Пусть обладает собственными значениями такими, что . Тогда у отображения не существует нетривиального собственного множества.
Доказательство. Предположим обратное, и – нетривиальное собственное множество отображения , соответствующее собственному значению . Поскольку и различные и не комплексно-сопряжённые, то существуют соответствующие им собственные векторы . Причём линейно независимые. В силу нетривиальности найдутся такие, что
Поскольку матрица обладает двумя различными собственными значениями, то . Следовательно, в силу леммы 3 обратима и , что с учётом определения собственного множества приводит для любого к равенствам
При этом по построению
Поскольку ограничено, то для любого последовательности и также ограничены. Это возможно только в том случае, когда
Получили противоречие. Следовательно, не существует нетривиального собственного множества отображения .
Лемма 4 доказана.
Лемма 5. Пусть недиагонализируема. Тогда у отображения не существует нетривиального собственного множества.
Доказательство. Предположим обратное, и – нетривиальное собственное множество отображения , соответствующее собственному значению . Поскольку матрица недиагонализируема, то . Следовательно, в силу леммы 3, обратима и . Согласно лемме 2 допустимо полагать, что совпадает со своей вещественной жордановой формой, которая в силу недиагонализируемости содержит по крайней мере одну из следующих двух жордановых клеток:
Тогда в силу нетривиальности существует , такой что
66
Для этого достаточно положить все координаты равными 0, кроме координаты, соответствующей второй строке вещественной жордановой клетки или третьей строке комплексной жордановой клетки.
Также для всех должны быть справедливы соотношения
Поскольку
ограничено, то с учётом
6 последовательности
и
должны быть ограничены одновременно, что невозможно. Получили противоречие. Следовательно, не существует нетривиального собственного множества отображения
.
Лемма 5 доказана.
Лемма 6. Пусть , отображение обладает нетривиальным собственным множеством , соответствующим собственному значению . Тогда по модулю совпадает со всем собственными значениями матрицы .
Доказательство. Равенство всех собственных значений по модулю матрицы следует из лемм 3 и 4. Их равенство по модулю также следует из доказательства леммы 4.
Лемма 7. Пусть , отображение обладает нетривиальным собственным множеством , соответствующим собственному значению . Тогда – собственное множество отображения , соответствующее собственному числу для всех .
Доказательство. Доказательство следует из определения нетривиального собственного множества и леммы 3.
Сформулируем окончательный результат в виде следующей теоремы.
Теорема 1. Пусть обладает нетривиальным собственным множеством , соответствующим собственному значению .
Тогда либо и любое компактное множество будет собственным, . Либо и выполняются следующие условия:
-
1. обратима;
-
2. диагонализируема, т.е. обладает линейно независимыми собственными векторами;
-
3.все собственные значения матрицы равны по модулю ;
-
4. является нетривиальным собственным множеством тогда и только тогда, когда является нетривиальным собственным множеством , где
77
Доказательство. Доказательство следует непосредственно из лемм 2–7.
Теорема 1 определяет основные принципы, которыми следует пользоваться при построении нетривиальных собственных множеств для линейного преобрзования
. В общем случае данная задача либо не имеет решения, либо может быть сведена к аналогичной для матрицы вида
7.
Оценка времени быстродействия на основе аппарата собственных множеств
Если в системе множество является собственным множеством отображения , то в силу леммы 1 построение множества 0-управляемости оказывается тривиальным и сводится к вычислению суммы геометрической прогрессии. Однако, как следует из теоремы 1, такое возможно только тогда, когда все собственные значения равны по модулю, что является весьма частным случаем. Тем не менее к данному условию можно свести любую систему посредством декомпозиции.
Лемма 8. Пусть , , , . Тогда
Доказательство. Пусть , . Т.е. для всех верны включения , . Следовательно, . Тогда
Пусть . Т.е. для всех верны включения . Следовательно, найдутся , такие, что . Тогда
Лемма 8 доказана.
Введем функцию :
Здесь предполагается, что – выпуклый компакт, содержащий в качестве своей внутренней точки, а через для обозначен функционал Минковского [разд. 3.2, Гл. III; 9]:
Также для произвольного под будем понимать минимальное целое число не меньшее, чем :
Получим представление 4 для важного частного случая системы .
Теорема 2. Пусть , , – нетривиальное собственное множество матрицы , соответствующее собственному числу , , справедливы представления
Тогда
-
1.для всех верно представление
-
2.для произвольного , удовлетворяющего условию , включение верно тогда и только тогда, когда
где , , ;
-
3. при этом верно равенство
Доказательство. Поскольку для каждого матрица обладает нетривиальным собственным множеством, соответствующим собственному числу , то согласно теореме 1. Следовательно, . Тогда для любого справедливо представление
Отсюда в силу лемм 1 и 8 следует пункт 1 теоремы 2.
Из определения декартова произведения включение равносильно тому, что для всех будет выполнено условие
что с учетом определения функционала Минковского эквивалентно неравенствам
Отсюда следует пункт 2 теоремы 2. А в совокупности с 3 и пункт 3.
Теорема 2 доказана.
Результаты теоремы 2 имеют весьма частный характер. Однако их можно обобщить на случай произвольного выпуклого
посредством следующей леммы, перейдя от равенства
4 к оценкам
5.
Лемма 9. Пусть справедливо включение , где – выпуклые и компактные множества, содержащие , задача быстродействия для разрешима для систем , , , а величины , , – оптимальные значения критерия в задаче быстродействия для данных систем соответственно.
Тогда
Доказательство. Из определения следует, что для любого верно включение
где
– множества 0-управляемости за
шагов для систем
,
,
, соответственно. Тогда доказательство леммы 9 следует непосредственно из представления
3.
Теорема 3. Пусть в системе матрица
диагонализируема,
,
– невырожденная матрица перехода в вещественный жорданов базис
, выбранная так, чтобы для некоторых
вида
7 и
было верно представление
Тогда для любого , удовлетворяющего условию , справедливы оценки
где , для всех верно, что , , – нетривиальные собственные множества отображения , соответствующие собственному числу и удовлетворяющие включению
Доказательство. Обозначим через класс множеств 0-управляемости системы . Согласно лемме 1 верно представление
Отсюда следует, что включение
верно тогда и только тогда, когда справедливо условие
. Т.е. с учетом
3 оптимальное значение критерия в задаче быстродействия для систем
и
совпадает для начальных состояний
и
соответственно.
Для краткости введем обозначения:
В силу пункта 3 теоремы 2 оптимальное значение критерия в задаче быстродействия для системы и начального состояния имеет вид
Аналогично, оптимальное значение критерия в задаче быстродействия для системы и начального состояния имеет вид
Тогда в силу леммы 9 теорема 3 полностью доказана.
Теорема 3 позволяет получить априорные оценки величины для начального состояния только в случае, когда у матрицы системы существует линейно независимых собственных векторов. Данный факт существенен, так как в силу леммы 5 у недиагонализируемой матрицы не существует нетривиальных собственных множеств.
Вообще говоря из условия для исходной системы не следует аналогичное условие для вспомогательной системы , если система не является устойчивой, а предельное множество 0-управляемости ограничено. В этом случае можно положить значение равным бесконечности, что сохранит формальную корректность теоремы 3, но сделает полученные оценки менее конструктивными.
Также применение теоремы 3 на практике предполагает знание нетривиальных собственных множеств
,
,
. Однако формулировка теоремы не дает конкретных указаний на их вычисление, хотя из леммы 1 и соотношения
3 следует, что лучшая точность оценок будет достигаться при наибольших по включению
и наименьших по включению
. В таком случае, если зафиксировано некоторое нетривиальное собственное множество
, то можно на его основе однозначно построить
в ходе решения задачи выпуклого программирования:
88
При этом множества , как правило, определяются неоднозначно и их линейные размеры во многом зависят от формы выбранных нетривиальных собственных множеств , что может значительно определять точность результирующей оценки.
Численные расчеты времени быстродействия
Рассмотрим системы вида , полагая фазовое пространство трехмерным: . Матрицу перехода в вещественный жорданов базис и набор начальных состояний для всех примеров положим общими:
Пример 2. Рассмотрим систему :
Данная система удовлетворяет условиям теоремы 3 при , , , , . В этом случае все нетривиальные собственные множества , , согласно теореме 1 являются отрезками. С учетом симметрии множества данные отрезки следует выбирать симметричными относительно . Тогда справедливо представление
Значения
,
,
могут быть вычислены из решения задачи
8:
Значения , , определяют вписанный в параллелепипед и могут быть определены неединственным образом. В данном примере были выбраны следующие значения:
Для любого верно представление для функционала Минковского . Отсюда следует, что
Тогда на основе теоремы 3 можно получить следующие оценки времени быстродействия для системы для различных начальных состояний:
Пример 3. Рассмотрим систему :
Данная система удовлетворяет положениям теоремы 3 при , , , , . В этом случае согласно теореме 1 все нетривиальные собственные множества являются некоторыми отрезками, а – двухмерными симметричными выпуклыми компактами.
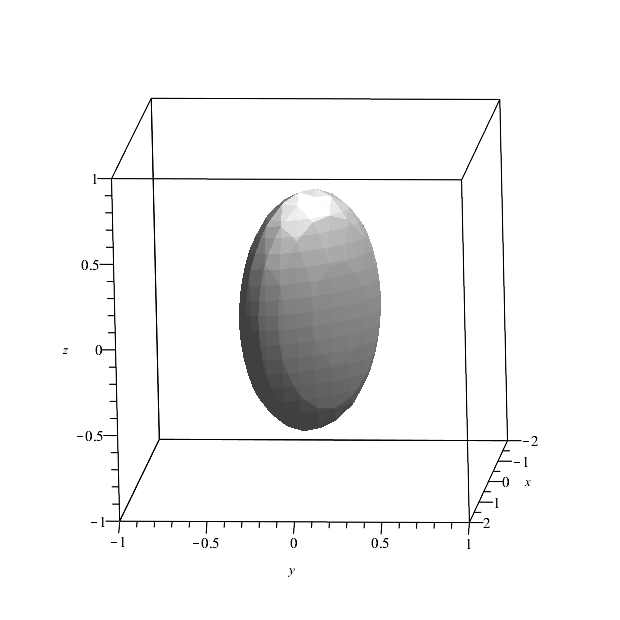
Множество изображено на рис. 1 и является эллипсоидальным множеством, ориентированным вдоль оси третьей координаты:
Тогда в качестве нетривиального собственного множества можно выбрать сечение плоскостью, определяемой условием :
Отрезок
определяется из решения задачи
8.
Аналогично примеру 2 множества и определяются неоднозначно. В данном примере были рассмотрены два варианта:
Различные внутренние аппроксимации множества могут дать различные верхние оценки для , из которых следует выбрать наименьшее значение. Так было получено
Рис. 1. Множество в примере 3
С учетом теоремы 3 можно получить следующие оценки времени быстродействия для системы для различных начальных состояний:
Более точные оценки были получены при выборе в качестве внутренней аппроксимации множества .
Пример 3. Рассмотрим систему :
Данная система удовлетворяет положениям теоремы 3 при , , . С учетом теоремы 1 искомые нетривиальные собственные множества могут быть выбраны в виде замкнутых трехмерных шаров с центром в :
Значения , определены числено. Тогда имеют место соотношения
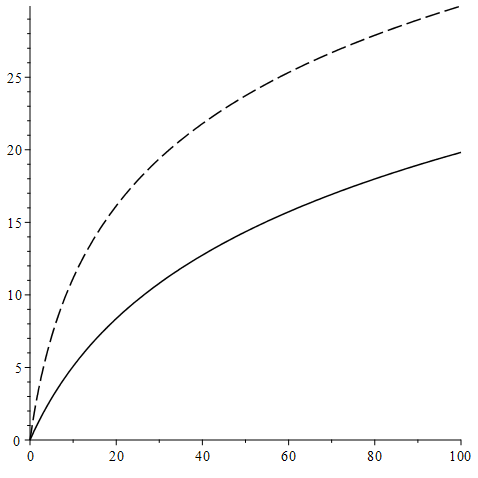
Графически данные зависимости от изображены на рис. 2.
Рис. 2. Зависимости (сплошная линия) и (пунктирная линия) от в примере 4
С учетом теоремы 3 можно получить следующие оценки времени быстродействия для системы для различных начальных состояний:
Из примеров следует, что точность оценок
5 существенно зависит от выбора нетривиальных собственных множеств в теореме 3. Причем неоднозначность выбора внутренней аппроксимации также может быть использована для уточнения верхней оценки
, как это было продемонстрировано в примере 3.
Заключение
В статье рассмотрена задача быстродействия для стационарной линейной дискретной системы с ограниченным управлением. В частности, разработан метод априорного оценивания оптимального времени быстродействия. Для решения поставленной задачи построен аппарат собственных множеств линейного отображения. Доказано, что нетривиальные собственные множества существует только для диагонализируемых матриц, у которых все собственные значения равны по модулю. Также удается свести задачу построения такого множества к аналогичной задаче для вещественной жордановой формы исходной матрицы.
Полученные в разделе 4 оценки времени быстродействия базируется на приведении матрицы системы к ее вещественной жордановой форме. Это позволяет провести декомпозицию исходной системы так, чтобы в каждой подсистеме матрица обладала равными по модулю собственными значениями, а следовательно, и нетривиальными собственными множествами. Данные множества могут быть использованы для построения внутренних и внешних аппроксимаций исходных ограничений на управление, что позволит получить искомые оценки времени быстродействия.
Установлено, что точность полученных методов зависит от большого числа параметров: от собственных значений и устойчивости системы, от формы выбранных для аппроксимации нетривиальных собственных множеств, от начального состояния и выбора внутренней аппроксимации. Варьируя различные параметры, можно добиться более качественных оценок. Дальнейшего изучения требуют методы, позволяющие определить оптимальный набор параметров.