Об условиях ограниченности множеств достижимости и управляемости для линейных систем с дискретным временем и суммарными ограничениями первого порядка на скалярное управление

Ибрагимов Д.Н.; Самонов С.С.

doi:10.17759/mda.2025150104

Моделирование и анализ данных
2025. Том 15. № 1. С. 51–80
doi:10.17759/mda.2025150104
ISSN: 2219-3758 / 2311-9454 (online)

Об условиях ограниченности множеств достижимости и управляемости для линейных систем с дискретным временем и суммарными ограничениями первого порядка на скалярное управление

5

Ибрагимов Д.Н., Самонов С.С.

Аннотация

Рассматриваются линейные системы с дискретным временем и суммарными ограничениями на скалярное управление первого порядка. Для данного класса систем изучаются множества достижимости и 0-управляемости за конечное число шагов и их предельные аналоги. Сформулирован и доказан строгий критерий ограниченности предельных множеств достижимости управляемости в терминах матриц системы. В случае их ограниченности определены условия, при которых исследуемые множества являются многогранниками. Определена структура данных многогранников. Представлены примеры, и проведено численное моделирование множеств достижимости и 0-управляемости различных систем.

Общая информация

Ключевые слова: дискретная линейная система, дискретное время, суммарные ограничения, множества достижимости, множества управляемости, управляемость

Рубрика издания: Методы оптимизации

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2025150104

Получена: 09.01.2025

Принята в печать: 30.01.2025

Для цитаты: Ибрагимов Д.Н., Самонов С.С. Об условиях ограниченности множеств достижимости и управляемости для линейных систем с дискретным временем и суммарными ограничениями первого порядка на скалярное управление // Моделирование и анализ данных. 2025. Том 15. № 1. С. 51–80. DOI: 10.17759/mda.2025150104

Полный текст

Введение

Анализ управляемых динамических систем тесно связан с построением их областей достижимости и управляемости. Так, например, задача с терминальным критерием качества может быть сведена к оптимизационной задаче по терминальному состоянию на множестве достижимости за время функционирования системы [1-4]. При рассмотрении вопросов стабилизации множества управляемости определяют те начальные состояния, для которых данная задача разрешима в принципе [5-6]. Отдельно следует упомянуть задачу быстродействия [7-8], для которой множества 0-управляемости фактически представляют собой множества уровня функции будущих потерь, из-за чего использование метода динамического программирования [Беллман, 1960] неразрывно связан с построением данных множеств.

Наибольшую эффективность аппарат множеств достижимости и управляемости демонстрирует при изучении систем с дискретным временем [2-3]. Во многом это связано с тем, что последовательности этих множеств могут быть построены рекуррентным образом и в ряде случаев данная процедура сводится к стандартным операциям выпуклого анализа [Рокафеллар, 1973]. С другой стороны, на практике работа с непрерывными системами часто осуществляется при помощи дискретизации [Мордухович, 1988], что делает неизбежной аппроксимацию исходных множеств достижимости и управляемости их дискретными аналогами. Однако устремление к нулю шага дискретизации приводит к тому, что конечное непрерывное время начинает описываться бесконечным числом шагов системы дискретной. Это делает актуальным, с одной стороны, исследование вопросов сходимости последовательности множеств дискретной системы к множествам непрерывной системы [Зыков, 2022], с другой стороны, не менее важной оказывается задача построения и исследования свойств предельных множеств дискретной системы непосредственно [13-18].

Известны аналитические представления множеств достижимости и 0-управляемости для линейных систем с дискретным временем и ограничениями на функцию управления в смысле

l_{\infty}

-нормы. В частности, доказано, что в случае линейных ограничений на управление множества достижимости и 0-управляемости за конечное число шагов представляют собой многогранники [Ибрагимов, 2021]. Для их предельных аналогов сформулированы необходимые и достаточные условия ограниченности [19-21].

Случай суммарных ограничений на управление в смысле

l_{p}

-нормы является менее изученным, и основные результаты по данной тематике представлены в [16-18]. В [17-18] подробно рассмотрен случай

p > 1

. В частности, представлены необходимые и достаточные условия ограниченности предельных множеств достижимости и 0-управляемости, явным образом описана структура их опорных гиперплоскостей, а также предложен эффективный метод формирования внешних оценок произвольного порядка точности на основе принципа сжимающих отображений. В то же время случай

p = 1

рассмотрен значительно менее подробно: доказаны только достаточные условия ограниченности, а описание их полиэдральной структуры представлено в весьма общем виде.

Целью данной статьи является расширение и уточнение результатов [Ибрагимов, 2022]. В частности, необходимо сформулировать и доказать строгий критерий ограниченности множеств достижимости и 0-управляемости линейных систем с дискретным временем и суммарными

l_{1}

-ограничениями на управление. Также требуется определить условия, когда исследуемые множества представляют собой многогранники, и построить их явное описание в этом случае. Полученные теоретические результаты предполагается проиллюстрировать различными примерами численного моделирования систем с дискретным временем.

Постановка задачи

Рассматривается автономная линейная система с дискретным временем и суммарными

l_{1}

-ограничениями на скалярное управление:

\begin{matrix} x (k + 1) = Ax (k) + bu (k), k \in N \cup {0}, \\ x (0) = x_{0}, \sum_{k = 1}^{\infty} | u (k) | \leq 1, \end{matrix}

(1)

где

x (k) \in R^{n}

– вектор состояния,

u (k) \in R

– управляющее воздействие на

k

-ом шаге,

A \in R^{n \times n}, b \in R^{n}

– матрицы системы. Заданное ограничение является ограничением на

l_{1}

-норму управления

{u (k)}_{k = 0}^{\infty}

. В ряде случае будет предполагаться, что выполнено ранговое условие Калмана:

rank (b, Ab, ..., A^{n - 1} b) = n .

(2)

Для произвольного

N \in N \cup {0}

обозначим через

Y_{1} (N)

множество достижимости системы (1), т.е. множество тех состояний, в которые можно перевести систему (1) за

N

шагов из 0 посредством выбора допустимого управления:

Y_{1} (N) = {\begin{matrix} {x \in R^{n} : x = \sum_{k = 0}^{N - 1} A^{N - k - 1} bu (k), \sum_{k = 0}^{N - 1} | u (k) | \leq 1}, & N \in N, \\ {0}, & N = 0 \end{matrix}

(3)

Введем также предельное множество достижимости

Y_{1, \infty}

– множество тех состояний, в которые можно перевести систему (1) за конечное число шагов из 0 посредством выбора допустимого управления:

Y_{1, \infty} = ⋃_{N = 0}^{\infty} Y_{1} (N) .

(4)

Аналогично для произвольного

N \in N \cup {0}

обозначим через

X_{1} (N)

множество 0-управляемости системы (1), т.е. множество тех начальных состояний, из которых можно перевести систему (1) за

N

шагов в 0 посредством выбора допустимого управления:

X_{1} (N) = {\begin{matrix} {x_{0} \in R^{n} : - A^{N} x_{0} = \sum_{k = 0}^{N - 1} A^{N - k - 1} bu (k), \sum_{k = 0}^{N - 1} | u (k) | \leq 1}, & N \in N, \\ {0}, & N = 0. \end{matrix}

(5)

И также введем предельное множество 0-управляемости

X_{1, \infty}

– множество тех начальных состояний, из которых можно перевести систему (1) за конечное число шагов в 0 посредством выбора допустимого управления:

X_{1, \infty} = ⋃_{N = 0}^{\infty} X_{1} (N) .

(6)

Обозначим через

σ (A) = {λ_{1}, \dots, λ_{n}}

спектр матрицы

A

, т.е. множество всех собственных значений

A

с учетом кратности, и приведем следующие известные результаты.

Лемма 1 ([16, лемма 1]). Пусть семейства множеств

{Y_{1} (N)}_{N = 0}^{\infty}

и

{X_{1} (N)}_{N = 0}^{\infty}

для системы (1) определяются соотношениями (3) и (5) соответственно,

N \in N

. Тогда

1.множество $Y_{1} (N)$ допускает представление

Y_{1} (N) = conv {b, - b, Ab, - Ab, \dots, A^{N - 1} b, - A^{N - 1} b};

2.если $detA \neq 0$ , то множество $X_{1} (N)$ допускает представление

X_{1} (N) = conv {A^{- 1} b, - A^{- 1} b, \dots, A^{- N} b, - A^{- N} b} .

Теорема 1 ([16, теорема 1]). Пусть множества

Y_{1, \infty}

и

X_{1, \infty}

для системы (1) определяются соотношениями (4) и (6) соответственно. Тогда

если система (1) устойчива, т.е. $\max_{λ \in σ (A)} | λ | < 1$ , то существует такая величина
1. $N_{\max}^{'} \in N$ , что

Y_{1, \infty} = Y_{1} (N_{\max}^{'});

2.если система (1) неустойчива, т.е. $\max_{λ \in σ (A)} | λ | > 1$ , то существует такая величина
1. $N_{\max}^{''} \in N$ , что

X_{1, \infty} = X_{1} (N_{\max}^{''}) .

Можно заметить, что теорема 1 задает исключительно достаточные условия ограниченности множеств (4) и (6), которые являются в действительности довольно жесткими. В [Ибрагимов, 2023] для случая

l_{p}

-ограничений на управление продемонстрировано, что необходимые и достаточные условия ограниченности предельных множеств достижимости и 0-управляемости в действительности зависят от соотношения

A

и

b

, а не только от спектрального радиуса

A

. С другой стороны, теорема 1 в совокупности с леммой 1 гарантируют, что множества (4) и (6) при определенных условиях окажутся многогранниками, однако в [Ибрагимов, 2022] не дается конструктивных указаний на то, как априорно вычислить величины

N_{\max}^{'}

и

N_{\max}^{''}

.

В данной работе требуется определить необходимые и достаточные условия ограниченности предельных множеств достижимости (4) и 0-управляемости (6), а также построить верхние оценки величин

N_{\max}^{'}

и

N_{\max}^{''}

:

N_{\max}^{'} \leq \bar{N_{\max}^{'}} (A, b), N_{\max}^{''} \leq \bar{N_{\max}^{''}} (A, b) .

Априорные оценки $N_{\max}^{'}$ и $N_{\max}^{''}$

На основе утверждений из выпуклого анализ и матричной алгебры предложим способ априорного оценивания величин

N_{\max}^{'}

и

N_{\max}^{''}

из теоремы 1.

Лемма 2. Пусть семейства множеств

{Y_{1} (N)}_{N = 0}^{\infty}

и

{X_{1} (N)}_{N = 0}^{\infty}

для системы (1) определяются соотношениями (3) и (5) соответственно. Тогда

если $A^{N} b \in Y_{1} (N)$ , то для любого $k \in N \cup {0}$ также выполнено включение
$A^{N + k} b \in Y_{1} (N)$ ;
если $\det A \neq 0$ и $A^{- (N + 1)} b \in X_{1} (N)$ , то для любого $k \in N$ также выполнено включение $A^{- (N + k)} b \in X_{1} (N)$ ;

Доказательство. Докажем сначала пункт 1. Пусть

A^{N} b \in Y_{1} (N)

. Тогда в силу пункта 1 леммы 1 найдутся

λ_{0}, \dots, λ_{N - 1}

такие, что

A^{N} b = \sum_{i = 0}^{N - 1} λ_{i} A^{i} b, \sum_{i = 0}^{N - 1} | λ_{i} | = 1 .

Предположим, что для некоторого

k \in N \cup {0}

выполнено включение

A^{N}, \dots, A^{N + k} b \in Y_{1} (N) .

Тогда в силу пункта 1 леммы 1 верно, что

Y_{1} (N) = ... = Y_{1} (N + k + 1) .

Отсюда получаем включение

A^{N + k + 1} b = \sum_{i = 0}^{N - 1} λ_{i} A^{i + k + 1} b \in conv {- A^{k + 1} b, A^{k + 1} b, \dots, - A^{N + k} b, A^{N + k} b} \subset

\subset Y_{1} (N + k + 1) = Y_{1} (N) .

Таким образом, по принципу математической индукции

A^{- (N + k)} b \in Y_{1} (N)

для любого

k \in N

.

Пункт 2 доказывается в силу леммы 1 аналогично при замене

A

на

A^{- 1}

,

b

на

A^{- 1} b

.

Лемма 2 доказана.

∎

Обозначим для произвольного

x \in X

и выпуклого

X \subset R^{n}

, содержащего

0

в качестве внутренней точки, через

μ (x, X)

функционал Минковского [22, разд. 3, §2, Гл. III]:

μ (x, X) \overset{△}{=} ∥ x ∥_{X} = \inf {α > 0 : x \in α X} .

Также для произвольной квадратной матрицы

A \in R^{n \times n}

определим следующую норму:

∥ A ∥_{1} = \max_{i = \bar{1, n}} \sum_{j = 1}^{n} | a_{ij} | .

Данная матричная норма в действительности является операторной нормой для случая, когда в

R^{n}

введена норма

∥ x ∥_{1} = \sum_{i = 1}^{n} | x_{i} | .

Согласно лемме 2 величины

N_{\max}^{'}

и

N_{\max}^{''}

однозначно определяются включениями

A^{N_{\max}^{'}} b \in Y_{1} (N_{\max}^{'}),

A^{- (N_{\max}^{''} + 1)} b \in X_{1} (N_{\max}^{''}) .

С учетом определения функционала Минковкого данные включения эквивалентны неравенствам

μ (A^{N_{\max}^{'}} b, Y_{1} (N_{\max}^{'})) \leq 1,

μ (A^{- (N_{\max}^{''} + 1)} b, X_{1} (N_{\max}^{''})) \leq 1 .

Данные неравенства в общем случае достаточно сложно разрешить из-за неявной зависимости функционала Минковского в левой части от

N_{\max}^{'}

или

N_{\max}^{''}

. Однако для случаев

N_{\max}^{'}, N_{\max}^{''} \geq n

можно получить простые верхние оценки

\bar{N_{\max}^{'}}

и

\bar{N_{\max}^{''}}

, используя более строгие условия

A^{\bar{N_{\max}^{'}}} b \in Y_{1} (n) \subset Y_{1} (N_{\max}^{'}),

A^{- (\bar{N_{\max}^{''}} + 1)} b \in X_{1} (n) \subset X_{1} (N_{\max}^{''}),

которые в свою очередь эквивалентны неравенствам

.

$μ (A^{\bar{N_{\max}^{'}}} b, Y_{1} (n)) \leq 1,$	(7)
$μ (A^{- (\bar{N_{\max}^{''}} + 1)} b, X_{1} (n)) \leq 1 .$	(8)

Представим точное выражение для функционалов Минковского

μ (x, Y_{1} (n))

и

μ (x, X_{1} (n))

для управляемых систем в виде следующей леммы.

Лемма 3. Пусть выполнено условие (2), семейства множеств

{Y_{1} (N)}_{N = 0}^{\infty}

и

{X_{1} (N)}_{N = 0}^{\infty}

для системы (1) определяются соотношениями (3) и (5) соответственно. Тогда

справедливы соотношения

μ (x, Y_{1} (n)) = ∥ A_{n}^{- 1} x ∥_{1} \leq ∥ A_{n}^{- 1} ∥_{1} ∥ x ∥_{1}, A_{n} = (b, \dots, A^{n - 1} b);

2.если $\det A \neq 0$ , то справедливы соотношения

μ (x, X_{1} (n)) = ∥ B_{n}^{- 1} x ∥_{1} \leq ∥ B_{n}^{- 1} ∥_{1} ∥ x ∥_{1}, B_{n} = (A^{- 1} b, \dots, A^{- n} b) .

Доказательство. Докажем сначала пункт 1. Из определения (3), полагая

N = n

, получим цепочку равенств

Y_{1} (n) = {\sum_{k = 0}^{n - 1} A^{n - k - 1} bu (k) : \sum_{k = 0}^{n - 1} | u (k) | \leq 1} =

{(b, \dots, A^{n - 1} b) u : u \in R^{n}, ∥ u ∥_{1} \leq 1} = {A_{n} u : u \in R^{n}, ∥ u ∥_{1} \leq 1} .

Учтем, что из (2) следует обратимость матрицы

A_{n}

, и получим следующие соотношения для функционала Минковского:

μ (x, Y_{1} (n)) = \inf {α > 0 : x \in α Y_{1} (n)} = \inf {α > 0 : x = α A_{n} u, u \in R^{n}, ∥ u ∥_{1} \leq 1} =

\inf {α > 0 : \frac{A_{n}^{- 1} x}{α} = u, u \in R^{n}, ∥ u ∥_{1} \leq 1} = \inf {α > 0 : {‖ \frac{A_{n}^{- 1} x}{α} ‖}_{1} \leq 1} =

\inf {α > 0 : ∥ A_{n}^{- 1} x ∥_{1} \leq α} = ∥ A_{n}^{- 1} x ∥_{1} .

Окончательно, в силу неравенства Гельдера

μ (x, Y_{1} (n)) = ∥ A_{n}^{- 1} x ∥_{1} \leq ∥ A_{n}^{- 1} ∥_{1} ∥ x ∥_{1} .

Пункт 2 доказывается в силу леммы 1 аналогично при замене

A

на

A^{- 1}

,

b

на

A^{- 1} b

и

A_{n}

на

B_{n}

.

Лемма 3 доказана.

∎

Обозначим через

[α]

наименьшее целое, которое не меньше чем

α

:

[α] = \min {k \in Z : k \geq α} .

При помощи леммы 3 построим величины

\bar{N'_{\max}}

и

\bar{N ″_{\max}}

явным образом для случая, когда

A

диагонализируема.

Теорема 2. Пусть верно (2), множества

Y_{1, \infty}

и

X_{1, \infty}

для системы (1) определяются соотношениями (4) и (6) соответственно, матрица

A

диагонализируема, т.е. существуют невырожденная матрица

S \in R^{n \times n}

и числа

λ_{1}, \dots, λ_{n_{1}}

,

r_{1}, \dots, r_{n_{2}} > 0

,

φ_{1}, \dots, φ_{n_{2}} \in R

такие, что

A = SΛ S^{- 1}, Λ = (\begin{matrix} λ_{1} & \dots & 0 \\ ⋱ \end{matrix} ⋮ r_{1} A_{φ_{1}} ⋮ ⋱ 0 \dots r_{n_{2}} A_{φ_{n_{2}}}) \in R^{n \times n},

(9)

A_{φ} = (\begin{matrix} \cos φ & \sin φ \\ - \sin φ & \cos φ \end{matrix}) \in R^{2 \times 2}, n_{1}, n_{2} \geq 0, n_{1} + 2 n_{2} = n .

Тогда для

y = S^{- 1} b

если система (1) устойчива, т.е. $\max_{λ \in σ (A)} | λ | < 1$ , то

N_{\max}^{'} \leq \bar{N_{\max}^{'}} \overset{△}{=} [\frac{- \ln (∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}))}{\ln (\max_{λ \in σ (A)} | λ |)}];

2.если система (1) неустойчива, т.е. $\max_{λ \in σ (A)} | λ | > 1$ , то

N_{\max}^{''} \leq \bar{N_{\max}^{''}} \overset{△}{=} [\frac{\ln (∥ B_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}))}{\ln (\min_{λ \in σ (A)} | λ |)}] - 1 .

Доказательство. Докажем сначала пункт 1. Из спектрального разложения (9) для любого

k \in N

следует представление

A^{k} = S Λ^{k} S^{- 1} = S (\begin{matrix} λ_{1}^{k} & \dots & 0 \\ ⋱ \end{matrix} ⋮ r_{1}^{k} A_{k φ_{1}} ⋮ ⋱ 0 \dots r_{n_{2}}^{k} A_{k φ_{n_{2}}}) S^{- 1} .

A^{k} b = S Λ^{k} y =

Тогда верны соотношения

∥ A^{k} b ∥_{1} = ∥ S Λ^{k} S^{- 1} b ∥_{1} \leq ∥ S ∥_{1} ∥ Λ^{k} S^{- 1} b ∥_{1} = ∥ S ∥_{1} ∥ Λ^{k} y ∥_{1} = ∥ S ∥_{1} \sum_{j = 1}^{n_{1}} | λ_{j}^{k} y_{j} | +

+ ∥ S ∥_{1} \sum_{i = 1}^{n_{2}} r_{i}^{k} (| y_{n_{1} + 2 i - 1} \cos (k φ_{i}) + y_{n_{1} + 2 i} \sin (k φ_{i}) | + | y_{n_{1} + 2 i} \cos (k φ_{i}) - y_{n_{1} + 2 i - 1} \sin (k φ_{i}) |) .

Рассмотрим оптимизационную задачу

a + b \to \max_{\begin{matrix} a^{2} + b^{2} = C^{2} \\ a, b \geq 0 \end{matrix}} .

Применяя метод множителей Лагранжа, можно установить, что

\max_{\begin{matrix} a^{2} + b^{2} = C^{2} \\ a, b \geq 0 \end{matrix}} (a + b) = \sqrt{2} C .

Если положить

C = {| y_{n_{1} + 2 i - 1} \cos (k φ_{i}) + y_{n_{1} + 2 i} \sin (k φ_{i}) |}^{2} + + {| y_{n_{1} + 2 i} \cos (k φ_{i}) - y_{n_{1} + 2 i - 1} \sin (k φ_{i}) |}^{2} =

y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2},

то для всех

i = \bar{1, n_{2}}

верны оценки

| y_{n_{1} + 2 i - 1} \cos (k φ_{i}) + y_{n_{1} + 2 i} \sin (k φ_{i}) | + | y_{n_{1} + 2 i} \cos (k φ_{i}) - y_{n_{1} + 2 i - 1} \sin (k φ_{i}) | \leq

\leq \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})} .

Таким образом, окончательно справедливы оценки

∥ A^{k} b ∥_{1} \leq ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | λ_{j}^{k} y_{j} | + \sum_{i = 1}^{n_{2}} r_{i}^{k} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}) .

С учетом леммы (3)

μ (A^{k} b, Y_{1} (n)) \leq ∥ A_{n}^{- 1} ∥_{1} ∥ A^{k} b ∥ \leq

\leq ∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | λ_{j}^{k} y_{j} | + \sum_{i = 1}^{n_{2}} r_{i}^{k} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}) \leq

\leq ∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} {(\max {\max_{j = \bar{1, n_{1}}} | λ_{j} |; \max_{j = \bar{1, n_{2}}} r_{i}})}^{k} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}) =

∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} {(\max_{λ \in σ (A)} | λ |)}^{k} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}) .

Тогда неравенство

μ (A^{k} b, Y_{1} (n)) \leq 1

будет следователь из условия

∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} {(\max_{λ \in σ (A)} | λ |)}^{k} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}) \leq 1,

{(\max_{λ \in σ (A)} | λ |)}^{k} \leq \frac{1}{∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})})},

k \ln (\max_{λ \in σ (A)} | λ |) \leq - \ln (∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})})),

(10)

Положим

k = \bar{N_{\max}^{'}}

и получим из (7) искомые оценки

\bar{N_{\max}^{'}} \geq - \frac{\ln (∥ A_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}))}{\ln (\max_{λ \in σ (A)} | λ |)} .

Из последнего неравенства следует пункт 1 теоремы 2.

Для доказательства пункта 2 проведем аналогичные рассуждения, заменив в силу леммы 1

A

на

A^{- 1}

,

A_{n}

на

B_{n}

и

Y_{1} (N)

на

X_{1} (N)

. Учтем, что собственные значения

A

и

A^{- 1}

взаимнообратны и выберем

k = \bar{N_{\max}^{''}} + 1

в условии (10):

(\bar{N_{\max}^{''}} + 1) \ln (\max_{λ \in σ (A)} {| λ |}^{- 1}) \leq - \ln (∥ B_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})})) .

Отсюда в силу (8) следуют искомые оценки

\bar{N_{\max}^{''}} + 1 \geq \frac{\ln (∥ B_{n}^{- 1} ∥_{1} ∥ S ∥_{1} (\sum_{j = 1}^{n_{1}} | y_{j} | + \sum_{i = 1}^{n_{2}} \sqrt{2 (y_{n_{1} + 2 i - 1}^{2} + y_{n_{1} + 2 i}^{2})}))}{\ln (\min_{λ \in σ (A)} | λ |)} .

Из последнего неравенства следует пункт 2 теоремы 2.

Теорема 2 полностью доказана.

∎

Заметим, что в теореме 2 возможны ситуации, когда

n_{1} = 0

, т.е. все собственные значения

A

существенно комплексные, и когда

n_{2} = 0

, т.е. все собственные значения

A

действительные. В этих случаях оценки, представленные в теореме 2, несколько упрощаются. Важным является частный случай

n = 2

, так как для него возможно только две ситуации:

n_{1} = 2

,

n_{2} = 0

или

n_{1} = 0

,

n_{2} = 1

. Приведем оценки для двумерных систем в виде следствия.

Следствие 1. Пусть выполнены предположения теоремы 2,

n = 2

. Тогда для

y = S^{- 1} b

если система (1) устойчива, т.е. $\max_{λ \in σ (A)} | λ | < 1$ , то

N_{\max}^{'} \leq \bar{N_{\max}^{'}} \overset{△}{=} {\begin{matrix} [\frac{- \ln (∥ A_{2}^{- 1} ∥_{1} ∥ S ∥_{1} ∥ y ∥_{1})}{\ln (\max {| λ_{1} |; | λ_{2} |})}], & σ (A) = {λ_{1}, λ_{2}} \subset R, \\ [\frac{- \ln (∥ A_{2}^{- 1} ∥_{1} ∥ S ∥_{1} ∥ y ∥_{2} \sqrt{2})}{\ln r_{1}}], & σ (A) = {r_{1} e^{\pm i φ_{1}}} ⊄ R; \end{matrix}

2.если система (1) неустойчива, т.е. $\max_{λ \in σ (A)} | λ | > 1$ , то

N_{\max}^{''} \leq \bar{N_{\max}^{''}} \overset{△}{=}

Доказательство. Доказательство следствия 1 вытекает непосредственно из теоремы 2 при замене

n = 2

.

∎

Необходимые и достаточные условия ограниченности множеств $Y_{1, \infty}$ , $X_{1, \infty}$

В [Ибрагимов, 2023] доказано, что для случая суммарных

l_{p}

-ограничений на управление ограниченность множеств

Y_{1, \infty}

,

X_{1, \infty}

определяется соотношением

A

и

b

. В частности, разложением

b

по вещественному жорданову базису матрицы

A

.

Жордановым базисом матрицы

A

называется набор линейно независимых векторов

h_{1}, \dots, h_{n} \subset R^{n}

, который задает преобразование подобия матрицы

A

в ее вещественную жорданову каноническую форму [23, разд. 3.4, Гл. 3]. Такой базис единственен с точностью до ненулевых сомножителей и порядка векторов

h_{1}, \dots, h_{n}

, и каждый базисный вектор соответствует некоторой жордановой клетке, т.е. некоторому собственному значению матрицы

A

. Если разбить элементы жорданова базиса на три множества по критерию того, соответствуют ли они собственному значению матрицы

A

большему, равному или меньшему 1 по модулю, то получится определить следующие три инвариантных подпространства:

L_{1} = Lin {h_{i} : h_{i} соответствует с . з. λ, | λ | < 1},

L_{1} = Lin {h_{i} : h_{i} – собственный вектор, соответствующий с . з . λ, | λ | = 1},

L_{1} = Lin {h_{i} : h_{i} соответствует с. з. λ, | λ | > 1} .

Заметим, что

L_{1}

не включает в себя присоединенные векторы, соответствующие собственному значению

λ, | λ | = 1

.

Теорема 3. Пусть множества

Y_{1, \infty}

и

X_{1, \infty}

для системы (1) определяются соотношениями (4) и (6) соответственно.

Тогда

множество $Y_{1, \infty}$ ограничено тогда и только тогда, когда

b \in Lin (L_{1} \cup L_{1});

2.множество $X_{1, \infty}$ ограничено тогда и только тогда, когда $\det A \neq 0$ и

b \in Lin (L_{1} \cup L_{1}) .

Доказательство. Докажем сначала пункт 1. Обозначим через

l_{1}

пространство суммируемых числовых последовательностей:

l_{1} = {(u_{1}, u_{2}, \dots) : \sum_{k = 1}^{\infty} | u_{k} | < \infty}, {| u ‖}_{1} = \sum_{k = 1}^{\infty} | u_{k} | .

Предельное множество достижимости

Y_{1, \infty}

в силу определений (3), (4) и [17, лемма 9] с точностью до замыкания является проекцией шара из нормированного пространства

l_{1}

на конечномерное пространство

R^{n}

:

\bar{Y_{1, \infty}} = (b, Ab, A^{2} b, \dots) {u \in l_{1} : ∥ u ∥_{1} \leq 1} .

Отсюда следует, что множество

Y_{1, \infty}

ограничено тогда и только тогда, когда ограничен оператор

B' = (b, Ab, A^{2} b, \dots) = (\begin{matrix} y^{1} \\ ⋮ \\ y^{n} \end{matrix}) .

Оператор

B'

ограничен в свою очередь в том и только в том случае, когда образующие его линейные функционалы

y^{i}

,

i = \bar{1, n}

, являются ограниченными. Это в силу теоремы Рисса [Колмогоров, 1981] эквивалентно ограниченности последовательностей

y^{1}, \dots, y^{n}

. Таким образом, множество

Y_{1, \infty}

ограничено тогда и только тогда, когда последовательность

{A^{k} b}_{k = 0}^{\infty} \subset R^{n}

ограничена.

Рассмотрим ограниченность последовательности

{A^{k} b}_{k = 0}^{\infty}

. Пусть вектор

b

допускает разложение

b = α_{1} h_{1} + \dots + α_{n} h_{n} .

Через

S \in R^{n \times n}

обозначим невырожденную матрицу, задающую преобразование

A

к её вещественной жордановой форме:

S^{- 1} AS = J \overset{△}{=}

(11)

где

J_{i}

соответствует либо вещественному собственному значению

λ_{i} \in R

и имеет вид

J_{i} =

(12)

либо соответствует паре комплексно-сопряженных собственных значений

r e^{\pm i φ} \in C

:

J_{i} =

(13)

Заметим, что в силу (11) справедливы равенства

(b, Ab, A^{2} b, \dots) = (b, SJ S^{- 1} b, S J^{2} S^{- 1} b, \dots) = S (S^{- 1} b, J S^{- 1} b, J^{2} S^{- 1} b, \dots) .

Отсюда следует, что последовательности

{A^{k} b}_{k = 0}^{\infty}

и

{J^{k} S^{- 1} b}_{k = 0}^{\infty}

ограничены одновременно. Сгруппируем координаты вектора

S^{- 1} b

в соответсвии с размерностями и расположением жордановых клеток в разложении (11):

S^{- 1} b = {(α_{1, 1}, \dots, α_{1, n_{1}}, \dots, α_{m, 1}, \dots, α_{m, n_{m}})}^{T},

Аналогично для всех

k \in N

обозначим

J^{- k} S^{- 1} b = {(α_{1, 1} (k), \dots, α_{1, n_{1}} (k), \dots, α_{m, 1} (k), \dots, α_{m, n_{m}} (k))}^{T} .

С учетом (11) для любых

i = \bar{1, m}

верно соотношение

(\begin{matrix} α_{i, 1} (k) \\ ⋮ \\ α_{i, n_{i}} (k) \end{matrix}) = J_{i}^{k} (\begin{matrix} α_{i, 1} \\ ⋮ \\ α_{i, n_{i}} \end{matrix}) .

В случае, определенном соотношением (12), для всех

k \geq n_{i} - 1

справедливо

J_{i}^{k} =

где здесь и везде далее через

C_{k}^{j}

обозначено число сочетаний из

k

по

j

:

C_{k}^{j} = \frac{k!}{(k - j)! j!} .

Получим предсталение

α_{i, j} (k) = \sum_{l = j}^{n_{i}} α_{i, l} C_{k}^{l - j} λ_{i}^{k - l + j}, j = \bar{1, n_{i}} .

Если

| λ_{i} | < 1

и

k > 2 (n_{i} - 1)

, то справедливы оценки:

| α_{i, j} (k) | \leq \sum_{l = j}^{n_{i}} | α_{i, l} | C_{k}^{l - j} {| λ_{i} |}^{k - l + j} \leq C_{k}^{n_{i} - 1} {| λ_{i} |}^{k - n_{i} + 1} \sum_{l = 1}^{n_{i}} | α_{i, l} | \leq

\leq \frac{\sum_{l = 1}^{n_{i}} | α_{i, l} |}{(n_{i} - 1)!} \frac{k!}{(k - n_{i} + 1)!} {| λ_{i} |}^{k - n_{i} + 1} \leq \frac{\sum_{l = 1}^{n_{i}} | α_{i, l} |}{(n_{i} - 1)!} k^{n_{i} - 1} {| λ_{i} |}^{k - n_{i} + 1} \overset{k \to \infty}{⟶} 0 .

Таким образом, последовательность

(α_{i, j}, α_{i, j} (1), α_{i, j} (2), \dots)

сходится, а следовательно, ограничена.

Пусть

| λ_{i} | > 1

и найдется

j = \bar{1, n_{i}}

такой, что

α_{i, j} \neq 0

. Без ограничений общности будем считать, что

j = n_{i}

или

α_{i, j + 1} = \dots = α_{i, n_{i}} = 0

. Тогда

α_{i, j} (k) = α_{i, j} λ_{i}^{k} \overset{k \to \infty}{⟶} \infty .

Следовательно,

(α_{i, j}, α_{i, j} (1), α_{i, j} (2), \dots)

не является ограниченной последовательностью.

Если же

α_{i, 1} = \dots = α_{i, n_{i}} = 0

, то при любом

λ_{i} \in R

и

k \in N

справедливо, что

α_{i, j} (k) = 0

,

j = \bar{1, n_{i}}

, т.е.

(α_{i, j}, α_{i, j} (1), α_{i, j} (2), \dots)

ограничена.

Пусть

| λ_{i} | = 1

и

α_{i, 1} \neq 0

, но

α_{i, j} = 0

для всех остальных

j = \bar{2, n_{i}}

. Тогда

| α_{i, 1} (k) | = | α_{i, 1} λ_{i}^{k} | = | α_{i, 1} |,

α_{i, j} (k) = 0, j = \bar{2, n_{i}} .

Таким образом, для всех

j = \bar{1, n_{i}}

последовательность

(α_{i, 1}, α_{i, 1} (1), α_{i, 1} (2), \dots)

ограничена.

Пусть

| λ_{i} | = 1

и существует такой

α_{i, j^{'}} \neq 0

, где

j' = \bar{2, n_{i}}

. Без ограничения общности будем полагать, что

j = n_{i}

или

α_{i, j + 1} = \dots = α_{i, n_{i}} = 0

. Тогда

α_{i, j - 1} (k) = α_{i, j - 1} λ_{i}^{k} + k α_{i, j} λ_{i}^{k - 1},

т.е. последовательность

(α_{i, j - 1}, α_{i, j - 1} (1), α_{i, j - 1} (2), \dots)

не ограничена.

Получаем, что в случае (12) последовательность

(\begin{matrix} α_{i, 1} & α_{i, 1} (1) & α_{i, 1} (2) & \dots \\ ⋮ & ⋮ & ⋮ \end{matrix} α_{i, n_{i}} (1) α_{i, n_{i}} (2) \dots)

ограничена тогда и только тогда, когда либо

| λ_{i} | < 1

, либо

| λ_{i} | = 1

и

α_{i, j} = 0

для всех

j \neq 1

, либо

α_{i, 1} = \dots = α_{i, n_{i}} = 0

.

Рассмотрим случай (13), и для всех

j = \bar{1, n_{i}}

введем обозначения

{\tilde{α}}_{i, j} = (\begin{matrix} α_{i, 2 j - 1} \\ α_{i, 2 j} \end{matrix}), {\tilde{α}}_{i, j} (k) = (\begin{matrix} α_{i, 2 j - 1} (k) \\ α_{i, 2 j} (k) \end{matrix}) .

Для всех

k \geq n_{i} - 1

справедливо

J_{i}^{k} =

Получим представление

{\tilde{α}}_{i, j} (k) = \sum_{l = j}^{n_{i}} C_{k}^{l - j} r_{i}^{k - l + j} A_{(k - l + j) φ_{i}} {\tilde{α}}_{i, l}, j = \bar{1, n_{i}} .

Если

r_{i} < 1

и

k > 2 (n_{i} - 1)

, то справедливы оценки:

∥ {\tilde{α}}_{i, j} (k) ∥ \leq \sum_{l = j}^{n_{i}} C_{k}^{l - j} r_{i}^{k - l + j} ∥ A_{(k - l + j) φ_{i}} {\tilde{α}}_{i, l} ∥ \leq C_{k}^{n_{i} - 1} r_{i}^{k - n_{i} + 1} \sum_{l = 1}^{n_{i}} ∥ {\tilde{α}}_{i, l} ∥ \leq

\leq \frac{\sum_{l = 1}^{n_{i}} ∥ {\tilde{α}}_{i, l} ∥}{(n_{i} - 1)!} \frac{k!}{(k - n_{i} + 1)!} r_{i}^{k - n_{i} + 1} \leq \frac{\sum_{l = 1}^{n_{i}} ∥ {\tilde{α}}_{i, l} ∥}{(n_{i} - 1)!} k^{n_{i} - 1} r_{i}^{k - n_{i} + 1} \overset{k \to \infty}{⟶} 0 .

Таким образом, последовательность

({\tilde{α}}_{i, j}, {\tilde{α}}_{i, j} (1), {\tilde{α}}_{i, j} (2), \dots)

сходится в

R^{2}

, а следовательно, сходится и покоординатно. Т.е. также сходятся и, как следствие, ограничены последовательности

(α_{i, 2 j - 1}, α_{i, 2 j - 1} (1), α_{i, 2 j - 1} (2), \dots)

и

(α_{i, 2 j}, α_{i, 2 j} (1), α_{i, 2 j} (2), \dots)

.

Пусть

r_{i} > 1

и найдется

j = \bar{1, n_{i}}

такой, что

{\tilde{α}}_{i, j} \neq 0

. Без ограничений общности будем считать, что

j = n_{i}

или

{\tilde{α}}_{i, j + 1} = \dots = {\tilde{α}}_{i, n_{i}} = 0

. Тогда

∥ {\tilde{α}}_{i, j} (k) ∥ = ∥ r_{i}^{k} A_{k φ_{i}} {\tilde{α}}_{i, j} ∥ = r_{i}^{k} ∥ {\tilde{α}}_{i, j} ∥ \overset{k \to \infty}{⟶} \infty .

Таким образом,

({\tilde{α}}_{i, j}, {\tilde{α}}_{i, j} (1), {\tilde{α}}_{i, j} (2), \dots)

не является ограниченной последовательностью в

R^{2}

. Отсюда с учетом неравенства Минковского следует, что хотя бы одна из последовательностей

(α_{i, 2 j - 1}, α_{i, 2 j - 1} (1), α_{i, 2 j - 1} (2), \dots)

или

(α_{i, 2 j}, α_{i, 2 j} (1), α_{i, 2 j} (2), \dots)

также не является ограниченной.

Если же

{\tilde{α}}_{i, 1} = \dots = {\tilde{α}}_{i, n_{i}} = 0

, то при любом

r_{i} \in R

и

k \in N

справедливо, что

{\tilde{α}}_{i, j} (k) = 0

,

j = \bar{1, n_{i}}

, т.е. обе последовательности

(α_{i, 2 j - 1}, α_{i, 2 j - 1} (1), α_{i, 2 j - 1} (2), \dots)

или

(α_{i, 2 j}, α_{i, 2 j} (1), α_{i, 2 j} (2), \dots)

являются тождественно нулевыми и, как следствие, ограничены.

Пусть

r_{i} = 1

и

{\tilde{α}}_{i, 1} \neq 0

, но

{\tilde{α}}_{i, j} = 0

для всех остальных

j = \bar{2, n_{i}}

. Тогда

∥ {\tilde{α}}_{i, 1} (k) ∥ = ∥ r_{i}^{k} A_{k φ_{i}} {\tilde{α}}_{i, 1} ∥ = ∥ {\tilde{α}}_{i, 1} ∥,

{\tilde{α}}_{i, j} (k) = 0, j = \bar{2, n_{i}} .

Таким образом, для всех

j = \bar{1, n_{i}}

последовательности

(α_{i, 2 j - 1}, α_{i, 2 j - 1} (1), α_{i, 2 j - 1} (2), \dots)

и

(α_{i, 2 j}, α_{i, 2 j} (1), α_{i, 2 j} (2), \dots)

ограничены.

Пусть

r_{i} = 1

и существует такой

α_{i, j^{'}} \neq 0

, где

j' = \bar{2, n_{i}}

. Без ограничения общности будем полагать, что

j = n_{i}

или

{\tilde{α}}_{i, j + 1} = \dots = {\tilde{α}}_{i, n_{i}} = 0

. Тогда

∥ {\tilde{α}}_{i, j - 1} (k) ∥ = ∥ r_{i}^{k} A_{k φ_{i}} {\tilde{α}}_{i, j - 1} + k r_{i}^{k - 1} A_{(k - 1) φ_{i}} {\tilde{α}}_{i, j} ∥ \geq

\geq ∥ k r_{i}^{k - 1} A_{(k - 1) φ_{i}} {\tilde{α}}_{i, j} ∥ - ∥ r_{i}^{k} A_{k φ_{i}} {\tilde{α}}_{i, j - 1} ∥ = k ∥ {\tilde{α}}_{i, j} ∥ - ∥ {\tilde{α}}_{i, j - 1} ∥ \overset{k \to \infty}{⟶} \infty .

Таким образом,

({\tilde{α}}_{i, j}, {\tilde{α}}_{i, j} (1), {\tilde{α}}_{i, j} (2), \dots)

не является ограниченной последовательностью в

R^{2}

. Отсюда с учетом неравенства Минковского следует, что хотя бы одна из последовательностей

(α_{i, 2 j - 1}, α_{i, 2 j - 1} (1), α_{i, 2 j - 1} (2), \dots)

или

(α_{i, 2 j}, α_{i, 2 j} (1), α_{i, 2 j} (2), \dots)

также не является ограниченной.

Получаем, что в случае (13) последовательность

(\begin{matrix} α_{i, 1} & α_{i, 1} (1) & α_{i, 1} (2) & \dots \\ ⋮ & ⋮ & ⋮ \end{matrix} α_{i, 2 n_{i}} (1) α_{i, 2 n_{i}} (2) \dots)

ограничена тогда и только тогда, когда либо

r_{i} < 1

, либо

r_{i} = 1

и

{\tilde{α}}_{i, j} = 0

для всех

j \neq 1

, либо

{\tilde{α}}_{i, 1} = \dots = {\tilde{α}}_{i, n_{i}} = 0

. А в свою очередь ограниченность последовательностей

{A^{k} b}_{k = 0}^{\infty}

и

{J^{k} S^{- 1} b}_{k = 0}^{\infty}

равносильна тому, что данные условия будут выполнятся для всех

i = \bar{1, m}

, что эквивалентно включению

b \in Lin (L_{1} \cup L_{1}) .

Рассмотрим вопросы ограниченности

X_{1, \infty}

. Если

\det A = 0

, то у матрицы

A

существует собственный вектор

h \in R^{n}

, соответствующий собственному значению

λ = 0

. Тогда согласно (5) верно включение

Lin {h} \subset X_{1} (1)

, что с учетом (6) приводит к включению

Lin {h} \subset X_{1, \infty}

, откуда следует, что

X_{1, \infty}

неограничено. Если

\det A \neq 0

, то существует матрица

A^{- 1}

, собственные значения которой взаимнообратны собственным значениям

A

[23, Гл. I]. Отсюда ясно, что доказательство пункта 2 теоремы 3 аналогично доказательству пункта 1, если заменить

A

на

A^{- 1}

.

Теорема 3 доказана.

∎

Важно сопоставить результаты теоремы 3 с результатами [Ибрагимов, 2023]. Напомним, что в случае

l_{p}

-ограничений на скалярное управление при

p > 1

предельные множества достижимости (4) и 0-управляемости (6) оказываются ограниченными тогда и только тогда, когда

b \in L_{1}

и

b \in L_{1}

соответственно [17, теоремы 2, 3]. Эти условия исключают возможность одновременной ограниченности этих множеств, за исключением тривиального случая

b = 0

. Для систем с суммарными

l_{1}

-ограничениями, как следует из теоремы 3, такая ситуация возможна. Представим данный факт в виде следствия.

Следствие 2. Пусть множества

Y_{1, \infty}

и

X_{1, \infty}

для системы (1) определяются соотношениями (4) и (6) соответственно. Тогда данные множества ограничены тогда и только тогда, когда

b \in L_{1}

Доказательство. Доказательство следствия 2 следует непосредственно из теоремы 3.

∎

Примеры

На языке Maple была написана программа, которая в соответствии с разработанными методами строит множества достижимости и 0-управляемости. В качестве фазового пространства было выбрано

R^{2}

.

Пример 1. Пусть

A = (\begin{matrix} 0.31 & - 0.11 \\ 0.33 & 0.79 \end{matrix}), b = (\begin{matrix} 1 \\ 1 \end{matrix}) .

(14)

Матрица собственных значений

Λ

и матрица

S

из разложения (9) имеют вид

Λ = (\begin{matrix} 0.4 & 0 \\ 0 & 0.7 \end{matrix}), S = (\begin{matrix} - 0.76 & 0.27 \\ 0.65 & - 0.96 \end{matrix}) .

Собственные значения матрицы

A

по модулю меньше единицы, значит, мы имеем дело с устойчивой системой.

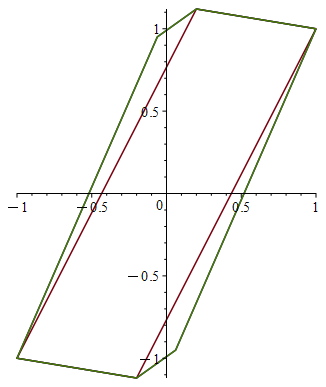
Искомая величина

\bar{N_{\max}^{'}}

, вычисленная в соответствие с пунктом 1 следствия 1, для этой системы равна 3. На рис. 1 изображен многогранник

Y_{1} (3) = Y_{1, \infty}

. Также при помощи леммы 2 вычислено точное значение

N_{\max}^{'} = 2

.

Рис. 1. Множества достижимости для системы (14)

Пример 2. Пусть

A = \frac{3}{4} (\begin{matrix} \frac{\sqrt{3}}{2} & \frac{- 1}{2} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{matrix}), b = (\begin{matrix} 1 \\ 1 \end{matrix}) .

(15)

Матрица

A

имеет только комплексно-сопряженные собственные значения. Матрица собственных значений

Λ

и матрица

S

из разложения (9) имеют вид

Λ = (\begin{matrix} 0.65 & 0.38 \\ - 0.38 & 0.65 \end{matrix}), S = (\begin{matrix} 0.71 & 0 \\ 0 & - 0.71 \end{matrix}) .

Модуль собственных значений матрицы

A

меньше единицы, следовательно, система устойчива.

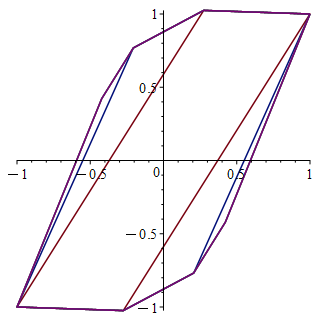
Априорная оценка

\bar{N'_{\max}}

, вычисленная в соответствии с пунктом 1 следствия 1, для этой системы равна 5. На рис. 2 изображен многогранник

Y_{1} (5) = Y_{1, \infty}

. Также при помощи леммы 2 вычислено точное значение

N'_{\max} = 3

.

Пример 3. Пусть

A = \frac{10}{19} (\begin{matrix} - 1 & - 6 \\ 2 & 6 \end{matrix}), b = (\begin{matrix} 1 \\ 1 \end{matrix}) .

(16)

Матрица собственных значений

Λ

и матрица

S

из разложения (9) имеют вид

Λ = (\begin{matrix} 1.05 & 0 \\ 0 & 1.58 \end{matrix}), S = (\begin{matrix} - 0.89 & 0.83 \\ 0.45 & - 0.55 \end{matrix}) .

Собственные значения матрицы

A

оказались больше единицы по модулю, следовательно, система является неустойчивой, а значит, мы можем для нее построить предельные множества 0-управляемости.

Априорная оценка

\bar{N ″_{\max}}

, вычисленная в соответствии с пунктом 2 следствия 1, для этой системы равна 88. На рис. 3 изображен многогранник

X_{1} (88) = X_{1, \infty}

. Также при помощи леммы 2 вычислено точное значение

N ″_{\max} = 7

.

Рис. 2. Множества достижимости для системы (15)

Рис. 3. Множества 0-управляемости для системы (16)

Пример 4. Пусть

A = \frac{6}{5} (\begin{matrix} \frac{\sqrt{2}}{2} & \frac{- \sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{matrix}), b = (\begin{matrix} 1 \\ 1 \end{matrix}) .

(17)

Матрица

A

имеет только комплексно-сопряженные собственные значения. Матрица собственных значений

Λ

и матрица

S

из разложения (9) имеют вид

Λ = (\begin{matrix} 0.85 & 0.85 \\ - 0.85 & 0.85 \end{matrix}), S = (\begin{matrix} 0.71 & 0 \\ 0 & - 0.71 \end{matrix}) .

Модуль комплексно-сопряженных собственных значений матрицы

A

больше единицы, следовательно система неустойчива, поэтому можем построить предельные множества
0-управляемости.

Априорная оценка

\bar{N ″_{\max}}

, вычисленная в соответствии с пунктом 2 следствия 1, для этой системы равна 7. На рис. 4 изображен многоугольник

X_{1} (7) = X_{1, \infty}

. Также при помощи леммы 2 вычислено точное значение

N ″_{\max} = 3

.

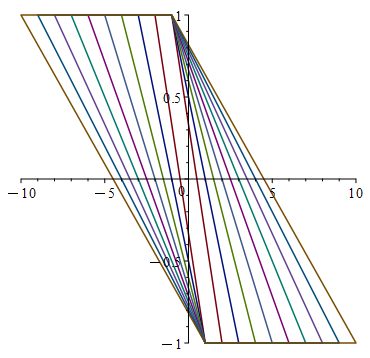
Рис. 4. Множества 0-управляемости для системы (17)

Пример 5. Пусть

A = (\begin{matrix} \cos 1 & - \sin 1 \\ \sin 1 & \cos 1 \end{matrix}), b = (\begin{matrix} 1 \\ 1 \end{matrix}) .

(18)

Матрица

A

совпадает со своей вещественной жордановой формой из разложения (9):

Λ = A, S = I .

В таком случае матрица системы имеет только комплексно-сопряженные собственные значения, равные по модулю единице. По этой причине нельзя воспользоваться результатами теорем 1 и 2 для построения предельных множества достижимости и 0-управляемости, хотя в силу теоремы 3 множества

Y_{1, \infty}

и

X_{1, \infty}

являются ограниченными, и представляют собой круг радиуса 1 с центром в начале координат. Докажем это.

Множество достижимости является выпуклой оболочкой множества точек, полученных путем умножения возведенной в степень

N

матрицы системы

A

на вектор

b

. Последовательность

{\pm A^{N} b}_{N = 0}^{\infty}

является плотной в окружности радиуса 1, поскольку матрица

A

является матрицей поворота на угол, отношение которого к

π

не является рациональным числом. То есть замыкание этого множества точек является окружностью, следовательно, замыкание выпуклой оболочки данной последовательности точек должно совпадать с выпуклой оболочкой окружности, то есть с кругом [10, Теорема 17.2]. Из этого следует, что с точностью до замыкания предельное множество достижимости совпадает с кругом.

Аналогичные рассуждения справедливы также для последовательности

{\pm A^{- N} b}_{N = 1}^{\infty}

и множеств 0-управляемости.

Пример 6. Пусть

A = (\begin{matrix} 1 & 1 \\ 0 & 1 \end{matrix}), b = (\begin{matrix} 0 \\ 1 \end{matrix}) .

(19)

Матрица собственных значений

Λ

и матрица

S

из разложения (9) имеют вид

Λ = (\begin{matrix} 1 & 1 \\ 0 & 1 \end{matrix}), S = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) .

Матрица

A

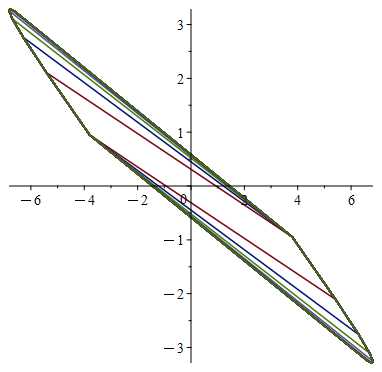
имеет одно собственное значение кратности 2, а вектор

b

– присоединенный вектор, соответствующий этому собственному значению. Согласно теореме 3 предельные множества достижимости и 0-управляемости будут неограниченными. На рис. 6 изображена последовательность множеств 0-управляемости данной системы для

N \in {2, \dots, 10}

, которая неограниченно возрастает.

Рис. 5. Множества достижимости для системы (18)

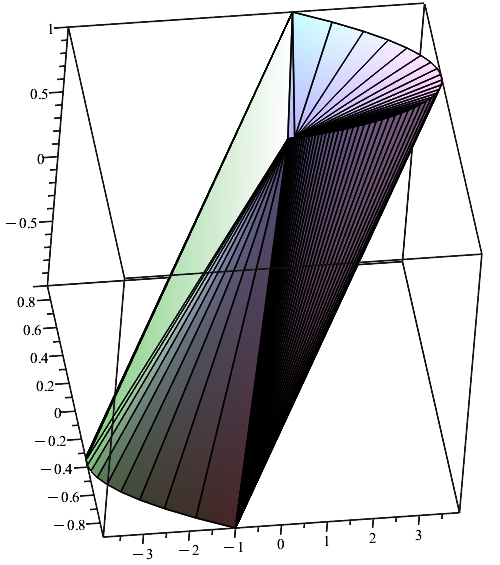
Рис. 6. Множества 0-управляемости для системы (19)

Пример 7. В ранее рассмотренном примере 5 система не имела действительных собственных значений, а лишь комплексно-сопряженные. Выясним, существуют ли такие системы, собственные значения которых будут действительными, а им соответствующие множества достижимости и 0-управляемости будут ограниченными, однако не будут являться многогранниками.

Рассмотрим систему следующего вида для

n = 3

:

A = (\begin{matrix} \frac{1}{α} & \frac{- 1}{α^{2}} & 0 \\ 0 & \frac{1}{α} & 0 \\ 0 & 0 & 1 \end{matrix}), b = (\begin{matrix} 0 \\ 1 \\ 1 \end{matrix}), α \in (0, 1) .

(20)

Вещественная жорданова форма

Λ

и матрица

S

из разложения (9) для данной системы имеют вид

Λ = (\begin{matrix} \frac{1}{α} & 1 & 0 \\ 0 & \frac{1}{α} & 0 \\ 0 & 0 & 1 \end{matrix}), S = (\begin{matrix} - α^{2} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}) .

Согласно теореме 3 предельное множество 0-управляемости

X_{1, \infty}

ограничено, однако оно не удовлетворяет теореме 1 и не является многогранником. Докажем это.

Для матрицы

A

справедливы следующие тождества:

A^{- 1} = (\begin{matrix} α & 1 & 0 \\ 0 & α & 0 \\ 0 & 0 & 1 \end{matrix}), A^{- k} = (\begin{matrix} α^{k} & k α^{k - 1} & 0 \\ 0 & α^{k} & 0 \\ 0 & 0 & 1 \end{matrix}), A^{- k} b = (\begin{matrix} k α^{k - 1} \\ α^{k} \\ 1 \end{matrix}) .

Рассмотрим следующий вектор для произвольного фиксированного

k_{0} \in N

:

p = (\begin{matrix} 1 \\ \frac{- k_{0} \ln α + 1}{α \ln α} \\ k_{0} \end{matrix}) .

Тогда

(p, A^{- k} b) = k α^{k - 1} - \frac{k_{0} \ln α + 1}{\ln α} α^{k + 1} + k_{0} .

Найдем максимум этого функционала по

k \in N

. Для этого введем функцию

f (x) = x α^{x - 1} - \frac{k_{0} \ln α + 1}{\ln α} α^{x + 1} + k_{0} .

Вычислим стационарные точки

f

:

f' (x) = (x - k_{0}) α^{x - 1} \ln α = 0,

x = k_{0} .

Определим характер экстремума в точке

x = k_{0}

, для этого выберем малое

ε > 0

и определим знак производной в

ε

-окрестности точки

k_{0}

.

f' (k_{0} - ε) = (k_{0} - ε - k_{0}) α^{k_{0} + ε - 1} = - ε α^{k_{0} + ε - 1} \ln α > 0,

f' (k_{0} + ε) = (k_{0} + ε - k_{0}) α^{k_{0} + ε - 1} = ε α^{k_{0} + ε - 1} \ln α < 0 .

Таким образом,

(p, A^{- k} b) < (p, A^{- k_{0}} b), k \in N k_{0}} .

Теперь рассмотрим величину

(p, - A^{- k} b) = - k α^{k - 1} + \frac{k_{0} \ln α + 1}{\ln α} α^{k + 1} - k_{0} .

Найдем максимум этого функционала по

k \in N

. Для этого введем функцию:

g (x) = - x α^{x - 1} + \frac{k_{0} \ln α + 1}{\ln α} α^{x + 1} - k_{0} .

Так как

g (x) = - f (x)

, точка

x = k_{0}

является минимумом функции

g (x)

. Тогда

\underset{x \geq 1}{} g (x) = \max {g (1), \lim_{x \to + \infty} g (x)} .

g (1) = - 1 + \frac{k_{0} \ln α + 1}{\ln α} - k_{0} = - 1 + \frac{1}{\ln α},

\lim_{x \to \infty} g (x) = \lim_{x \to \infty} (- x α^{x - 1} + \frac{k_{0} \ln α + 1}{\ln α} α^{x - 1} - k_{0}) =

\lim_{x \to \infty} (- x α^{x - 1}) + \lim_{x \to \infty} (\frac{k_{0} \ln α + 1}{\ln α} α^{x - 1}) - k_{0} = - k_{0},

\underset{x \geq 1}{} g (x) = \max {- 1 + \frac{1}{\ln α}, - k_{0}} < 0 < f (k_{0}) .

Таким образом,

(p, - A^{- k} b) < (p, A^{- k_{0}} b), k \in N .

Рассмотрим также два предельных случая. Пусть

x_{\infty}^{+ = \lim_{N \to \infty} A^{- N} b = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}), x_{\infty}^{- = \lim_{N \to \infty} - A^{- N} b = (\begin{matrix} 0 \\ 0 \\ - 1 \end{matrix}) .}}

Следовательно, в

k_{0}

достигается единственный максимум функционала

(p, \pm A^{- k} b)

по

k \in N

. Т.е.

A^{- k_{0}} b

согласно [10, Следствие 32.3.2] является крайней для замыкания

X_{1, \infty}

. Но поскольку

k_{0} \in N

был выбран произвольно, то множество крайних точек

X_{1, \infty}

не является счетным.

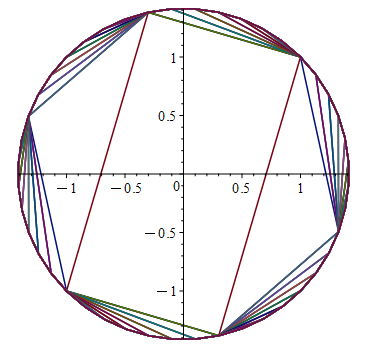
Проиллюстрируем пример на рис.7, выбрав

α = 0.9

.

Рис. 7. Множества 0-управляемости для системы (20)

Заключение

Для решения задач анализа и численного моделирования линейных систем с дискретным времен и геометрическими ограничениями на управление в статье решена задача построения предельных множеств достижимости и 0-управляемости. Определен и доказан строгий критерий ограниченности этих множеств, сводящийся к построению вещественного жорданова базиса матрицы системы. В виде теоремы 2 предложен метод построения априорных оценок предельных множеств достижимости и 0-управляемости. Определены условия, при которых исследуемые множества являются многогранниками.

Эффективность теоретических результатов продемонстрирована на примере построения множеств достижимости и 0-управляемости для различных систем. Отдельно стоит упомянуть примеры, демонстрирующие существование систем, для которых рассматриваемые множества не являются многогранниками, несмотря на то, что они ограничены.

Литература

Моисеев Н.Н. Элементы теории оптимальных систем. М.: Наука, 1975.
Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука, 1973.
Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука, 1973.
Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.:Наука, 2005.
Yang H., Xia Y., Geng Q. Stabilization on Null Controllable Region / In: Analysis and Synthesis of Delta Operator Systems with Actuator Saturation. Studies in Systems, Decision and Control. 2019. V. 193. P. 39–65. DOI: 10.1007/978-981-13-3660-7_3.
Amato F., Cosentino C., Tommasi G. D., Pironti A., Romano M. Input–Output Finite-Time Stabilization of Linear Time-Varying Discrete-Time Systems // IEEE Transactions on Automatic Control. V. 67. No. 9. P. 4438–4450. DOI: 10.1109/TAC.2022.3161374.
Ибрагимов Д.Н. О задаче быстродействия для класса линейных автономных бесконечномерных систем с дискретным временем, ограниченным управлением и вырожденным оператором // АиТ. 2019. № 3. C. 3–25. DOI: 10.1134/S0005231019030012.
Ибрагимов Д.Н., Новожилкин Н.М., Порцева Е.Ю. О достаточных условиях оптимальности гарантирующего управления в задаче быстродействия для линейной нестационарной дискретной системы с ограниченным управлением // АиТ. 2021. № 12. С. 48–72. DOI: 10.31857/S0005231021120047.
Беллман Р. Динамическое программирование. М.: ИИЛ, 1960.
Рокафеллар Р. Выпуклый анализ. М.: Мир, 1973.
Мордухович Б.Ш. Методы аппроксимаций в задачах оптимизации и управления. М.: Наука, 1988.
Зыков И.В. Приближенное вычисление множеств достижимости линейных управляемых систем при разнотипных ограничениях на управление // Известия института математики и информатики Удмуртского государственного университета. 2022. Т. 60 С. 16–33. DOI: 10.35634/2226-3594-2022-60-02
Зайцева М.В., Точилин П.А. Методы построения оценок множеств достижимости в задаче моделирования потоков людей // Журн. вычисл. матем. и матем. физ. 2023. Т. 63. № 8. С. 1381–1394. DOI: 10.31857/S0044466923070190
Kuntsevich V.M., Kurzhanski A.B. Attainability Domains for Linear and Some Classes of Nonlinear Discrete Systems and Their Control // J. Autom. Sci. 2010. V. 42. No. 1. P. 1–18. DOI: 10.1615/JAutomatInfScien.v42.i1.10.
Берендакова А.В., Ибрагимов Д.Н. О методе построения внешних оценок предельного множества управляемости для линейной дискретной системы с ограниченным управлением // АиТ. 2023. № 2. С. 3–34. DOI: 10.31857/S0005231023020010
Ибрагимов Д.Н., Осокин А.В., Сиротин А.Н., Сыпало К.И. О свойствах предельных множеств управляемости для класса неустойчивых линейных систем с дискретным временем и -ограничениями // Известия РАН. Теория и системы управления. 2022. № 4. С. 3–21. DOI: 10.31857/S0002338822040102
Ибрагимов Д.Н., Сиротин А.Н. О некоторых свойствах множеств ограниченной управляемости для стационарных линейных дискретных систем с суммарным ограничением на управление // Известия РАН. Теория и системы управления. 2023. № 6. С. 3–32. DOI: 10.31857/S0002338823050086
Ибрагимов Д.Н. О внешнем оценивании предельных множеств достижимости и 0-управляемости для линейных дискретных систем с суммарным ограничением на скалярное управление // АиТ. 2024. № 4. С. 3–30. DOI: 10.31857/S0005231024040018
Сиротин А.Н., Формальский А.М. Достижимость и управляемость дискретных систем при ограниченных по величине и импульсу управляющих воздействиях // АиТ. 2003. № 12. С. 17–32.
Colonius F., Cossich J.A.N., Santana A.J. Controllability properties and invariance pressure for linear discrete-time systems // J. Dynam. Equat. 2022. Vol. 34. P. 5–22. DOI: 10.1007/s10884-021-09966-4.
Darup M.S., Mönnigmann M. On general relations between null-controllable and controlled invariant sets for linear constrained systems // 53rd IEEE Conference on Decision and Control. Los Angeles. 2014. P. 6323–6328. DOI: 10.1109/CDC.2014.7040380.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1981.
Хорн Р., Джонсон Ч. Матричный анализ. М.:Мир, 1989.

Информация об авторах

Ибрагимов Данис Наилевич, кандидат физико-математических наук, доцент кафедры «Теория вероятностей и компьютерное моделирование», Московский авиационный институт (национальный исследовательский университет) (МАИ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0001-7472-5520, e-mail: rikk.dan@gmail.com

Самонов Степан Сергеевич, студент, кафедра «Теория вероятностей и компьютерное моделирование», Московский авиационный институт (национальный исследовательский университет) (МАИ), Москва, Российская Федерация, ORCID: https://orcid.org/0009-0006-5188-1727, e-mail: stepan.samonov.s@gmail.com

Метрики

Просмотров web

За все время: 17
В прошлом месяце: 0
В текущем месяце: 17

Скачиваний PDF

За все время: 5
В прошлом месяце: 0
В текущем месяце: 5

Всего

За все время: 22
В прошлом месяце: 0
В текущем месяце: 22

PlumX

Метрики публикации

Аннотация

Общая информация

Полный текст

Введение

Постановка задачи

Априорные оценки N max ' и N max ' '

Необходимые и достаточные условия ограниченности множеств Y 1 , ∞ , X 1 , ∞

Примеры

Заключение

Литература

Информация об авторах

Метрики

Просмотров web

Скачиваний PDF

Всего

Априорные оценки $N_{\max}^{'}$ и $N_{\max}^{''}$

Необходимые и достаточные условия ограниченности множеств $Y_{1, \infty}$ , $X_{1, \infty}$