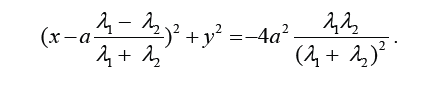Алгебраические кривые низших порядков в преподавании высшей математики

Куланин Е.Д.; Степанов М.Е.

doi:10.17759/mda.2025150110

Моделирование и анализ данных
2025. Том 15. № 1. С. 168–209
doi:10.17759/mda.2025150110
ISSN: 2219-3758 / 2311-9454 (online)

Алгебраические кривые низших порядков в преподавании высшей математики

2

Куланин Е.Д., Степанов М.Е.

Аннотация

Статья продолжает цикл ([1] – [15]) методических разработок авторов. В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Главным объектом обсуждения являются алгебраические кривые. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

Общая информация

Ключевые слова: высшее образование, методика преподавания математики, аналитическая геометрия, математический анализ, переменная, неявная функция, обратная функция, производная, секущая, касательная, полиномы, алгебраическая кривая, кривые второго порядка, семейства кривых, пучки, геометрические преобразования

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2025150110

Получена: 10.12.2024

Принята в печать: 10.01.2025

Для цитаты: Куланин Е.Д., Степанов М.Е. Алгебраические кривые низших порядков в преподавании высшей математики // Моделирование и анализ данных. 2025. Том 15. № 1. С. 168–209. DOI: 10.17759/mda.2025150110

Полный текст

ВВЕДЕНИЕ

Важнейшим понятием курса высшей математики является функциональная зависимость между действительными и комплексными переменными. Следует отметить, что это понятие несёт весьма широкую смысловую нагрузку. Но в курсе математического и комплексного анализа в первую очередь рассматриваются явно выраженные функции одного переменного. Между тем, функции в достаточно продвинутых математических теориях очень часто встречаются неявные функции. При этом студент, как правило, уже сконцентрирован на привычном ему явном выражении функций. По этой причине затрудняется восприятие, например, теории обыкновенных дифференциальных уравнений. Таким образом, желательно более активно знакомить студентов с математическими объектами, описываемыми неявным образом. Алгебраические кривые являются именно такими объектами. При изучении кривых второго порядка в рамках аналитической геометрии очень активно используются неявные описания этих кривых, но с точки зрения авторов этой статьи этого недостаточно. Нужен более широкий спектр объектов такого вида.

Конечно, авторам могут возразить, что в рамках аналитической геометрии проводится достаточно подробное изучение методов работы с неявными функциями. Более того, в математическом анализе специально рассматриваются вопросы, связанные с определением неявных функций и методами работы с ними, например, выводится формула дифференцирования таких функций.

Тем не менее, на взгляд авторов существует определённый разрыв между курсами аналитической геометрии и математического анализа. Например, то же дифференцирование и проведение касательных с его помощью, если и упоминается в курсе аналитической геометрии, то вскользь. Наоборот, в курсе математического анализа работа с коническими сечениями приводится как пример, что в известной степени ослабляет внимание студента к самим кривым второго порядка.

Желательно, предложить учащимся задания, в которых работа с кривой второго порядка проводится так, что их вниманию в равной степени предлагаются вопросы, связанные с формой кривой, её расположению на декартовой плоскости, а также применению методов математического анализа, направленных на работу с неявными функциями. Отметим, что для улучшения образного восприятия кривых будут использоваться компьютерные программы, строящие эти кривые на экране.

При таком подходе естественным образом возникают задания, касающиеся не только кривых второго порядка, но и алгебраических кривых более высоких порядков. При этом чрезвычайно важным моментом является соединение геометрических образов и вычислений. Здесь, кстати, появляется возможность естественного перехода к сложным математическим теориям, таким как теория эллиптических функций и алгебраическая геометрия.

ПОСТРОЕНИЕ КРИВЫХ НА ЭКРАНЕ

Работая с теми или иными кривыми, различным образом описанными формулами, прежде всего желательно составить представление о поведении каждой из них на декартовой плоскости. Образ этой кривой может облегчить решение целого ряда математическими вопросов. Рассмотрим те методы, которые будут использоваться для построения алгебраических кривых на экране компьютера. Программы будут написаны на языке программирования Small Basic. Перечислим несколько вариантов задания кривых. Начнём с явного описания функции.

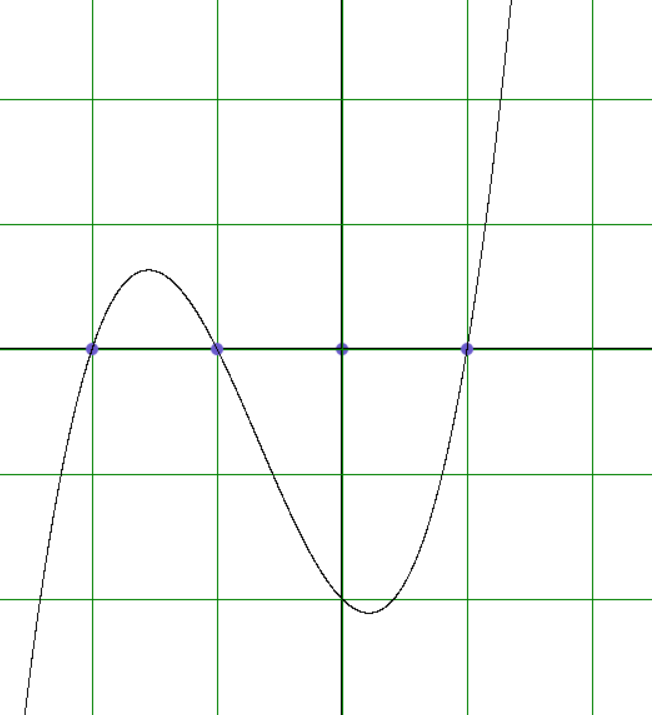
Задание 1. Построить на экране график многочлена от одной переменной.

Решение. Для построения графика любой явно выраженной функции одной действительной переменной следует перенести на экран прямоугольный фрагмент бесконечной декартовой плоскости. Обозначим координаты на декартовой плоскости через

(x; y)

, а экранные координаты через (xe

; y

e). Как правило отображаемая область содержит начало координат. Пусть ему на экране соответствует точка

(x_{0}; y_{0})

.

Кроме того, необходимо задать на экране масштаб. Это делается с помощью указания количества пикселов в единичном отрезке. Пусть этот параметр определяет значение переменной ed. Тогда переход от декартовых координат к экранным осуществляется формулами

xe = x_{0} + ed ∙ x

и

ye = y_{0} + ed ∙ y

.

При построении графика исходные вычисления проводятся с переменными

(x; y)

. После чего полученные координаты переводятся в экранные. Результат работы программы показан на рисунке 1.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Корни многочлена

c1 = -2

c2 = -1

c3 = 1

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Выделение корней

xe = x0 + ed*c1

GraphicsWindow.FillEllipse(xe - 5, y0 - 5, 10, 10)

xe = x0 + ed*c2

GraphicsWindow.FillEllipse(xe - 5, y0 - 5, 10, 10)

xe = x0 + ed*c3

GraphicsWindow.FillEllipse(xe - 5, y0 - 5, 10, 10)

'Построение графика

For x = -3 To 3 Step .001

'Вычисление значений многочлена

y = (x - c1)*(x - c2)*(x - c3)

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndFor

Рисунок 1

Следующим способом описания кривых является их параметрическое задание.

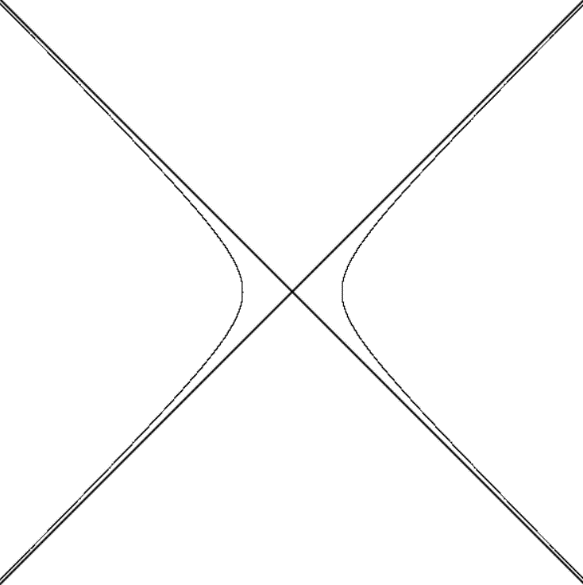
Задание 2. Построить на экране график гиперболы, используя параметрическое задание с помощью гиперболических функций.

Решение. Как известно гиперболические синус и косинус задаются формулами:

s h x = \frac{e^{x} - e^{- x}}{2}

,

c h x = \frac{e^{x} + e^{- x}}{2}

. Параметрические уравнения

x = a ∙ ch t

и

y = b ∙ sh t

описывают гиперболу

\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1

. Отметим, что в языке Small Basic функция

y = e^{x}

задаётся оператором: exp = Math.Power(2.71828, x). Результат работы программы показан на рисунке 2.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 300

y0 = 300

ed = 50

a = 1

b = 1

GraphicsWindow.DrawLine(0,600,600,0)

GraphicsWindow.DrawLine(0,0,600,600)

For x = -6 To 6 Step .001

ex1 = Math.Power(2.71828,x)

ex2 = Math.Power(2.71828,-x)

cn = (ex1 + ex2)/2

sn = (ex1 - ex2)/2

xe = x0 + a*cn*ed

ye = y0 - b*sn*ed

GraphicsWindow.SetPixel(xe,ye,"")

xe = x0 - a*cn*ed

ye = y0 - b*sn*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Рисунок 2

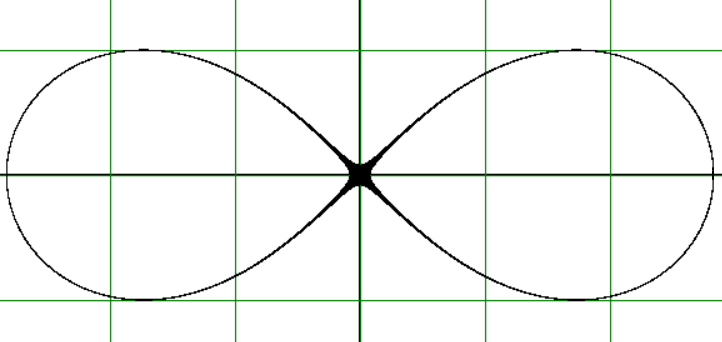
Наконец, рассмотрим метод построения кривых, заданных неявшым уравнением.

Задание 3. Построить на экране кривую четвёртого порядка, описываемую формулой

Решение. Соответствующая кривая называется лемнискатой Бернулли [Савёлов, 1960]. Соответствующей кривой второго порядка является сечение горизонтальной плоскостью

z = 0

поверхности, описываемой функцией от двух переменных

z =

. Будем сканировать прямоугольник на декартовой плоскости и отмечать точки, в которых абсолютное значение переменной z достаточно мало. Кривая, соответствующая значению параметра а = 2, показана на рисунке 3.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Параметр лемнискаты

a = 2

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5, y0-5, 10, 10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Сканирование декартовой плоскости

For x = -3 To 3 Step .001

For y = -3 To 3 Step .001

'Вычисление значений функции z = F(x, y)

z = (x*x + y*y)*(x*x + y*y) - 2*a*a*(x*x - y*y)

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

If z<.05 And z>-.05 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

Рисунок 3

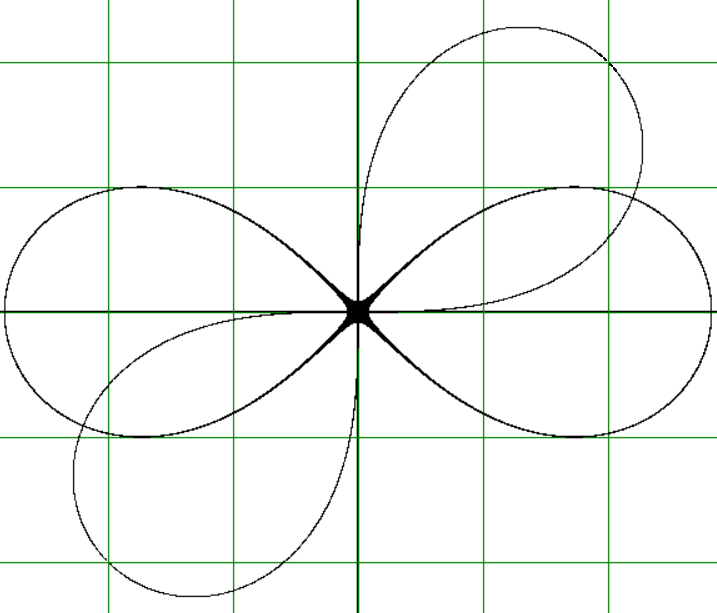
Задание 4. Повернуть лемнискату Бернулли на угол

\frac{π}{4}

.

Решение. Используем формулы поворота декартовой плоскости на угол α:

x_{1} = x ∙ \cos α - y ∙ \sin α

,

y_{1} = x ∙ \sin α + y ∙ \cos α

.

В предыдущую программу добавим следующий цикл.

Pi = Math.Pi

sn = Math.Sin(Pi/4)

cs = Math.Cos(Pi/4)

For x = -3 To 3 Step .001

For y = -3 To 3 Step .001

z = (x*x + y*y)*(x*x + y*y) - 2*a*a*(x*x - y*y)

If Math.Abs(z)<.01 Then

x1 = x*cs - y*sn

y1 = x*sn + y*cs

xe = x0 + ed*x1

ye = y0 - ed*y1

GraphicsWindow.SetPixel(xe,ye,"")

EndIf

EndFor

Результат работы расширенной программы показан на рисунке 4.

Рисунок 4

Перейдём к более подробному рассмотрению различных классов алгебраических кривых.

ПРЯМЫЕ

Прямые и окружности изучаются в школе. По этой причине они наиболее известны студентам. Однако в курсе высшей математики появляются новые возможности описания этих линий. В частности, в отношении прямых кроме явного описания начинают применяться параметрическое и неявное описание. Именно с прямых мы и начнём. Но прежде сделаем пояснение. Статья называется «Алгебраические кривые в преподавании высшей математики». Уместно ли рассматривать в ней прямые? Дело в том, что более правильно было бы говорить об алгебраических линиях, то есть объектах, которые описываются алгебраическими уравнениями. Прямые, естественно, являются именно такими объектами.

Важным обстоятельством является то, что в курсе аналитической геометрии широко используются идеи векторной алгебры. По этой причине задания, связанные с различными способами описания прямых, должны, по возможности, использовать понятие вектора.

Задание 5. На плоскости заданы точка

A (x_{0}; y_{0})

и исходящий из неё вектор

V (a; b) .

Построить египетский прямоугольный треугольник, прямой угол которого расположен в вершине А. При этом катет, перпендикулярный вектору

(a; b)

, следует построить с помощью неявного уравнения прямой, второй катет – с помощью параметрических уравнений прямой, а гипотенуза – с помощью канонического (школьного) уравнения прямой

Решение. Длины катетов египетского треугольника относятся друг к другу как 4 к 3. Уравнение прямой, на которой лежит первый катет, может быть получено с помощью скалярного произведения:

a ∙ (x - x_{0}) + b ∙ (y - y_{0}) = 0

. После раскрытия скобок это уравнение приводится к виду

ax + by + c = 0

, гдесвободный член вычисляется по формуле

c = - a ∙ x_{0} - b ∙ y_{0}

. Параметрическое уравнение прямой, на которой лежит второй катет, можно интерпретировать как вычисление координат концов вектора

λ ∙ V

при всевозможных значениях параметра λ.

Вектор W, перпендикулярный вектору

V (a; b)

, имеет координаты

W (- b; a)

. Этот вектор направлен вдоль первого катета. Пусть первый катет по длине имеет длину в четыре раза большую, чем длина вектора

W

. Таким образом, первый катет проектируется на отрезок

[x_{0}; x_{0} - 4 b]

. Ординату второго конца этого катета y1 можно получить, подставив в уравнение прямой абсциссу

x_{1} = x_{0} - 4 b

.

Параметрические уравнения прямой, на которой лежит второй катет, имеют вид

x = x_{0} + λ ∙ a

и

y = y_{0} + λ ∙ b

. Первый катет по длине имеет длину в три раза большую, чем длина вектора

V

. Координаты

(x_{2}; y_{2})

второго конца этого катета можно получить с помощью параметрических уравнений при

λ = - 3

.

Каноническое уравнение прямой, на которой лежит гипотенуза, можно получить используя тот факт, что эта прямая проходит через точки

(x_{1}; y_{1})

и

(x_{2}; y_{2})

.

Все эти соображения позволяют написать программу. Результат работы программы показан на рисунке 5.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

'Исходные данные

xx0 = -2

yy0 = .5

a = Math.Cos(2*pi/3)

b = Math.Sin(2*pi/3)

xe = x0 + (xx0+a)*ed

ye = y0 - (yy0+b)*ed

GraphicsWindow.FillEllipse(xe-5,ye-5,10,10)

c = - a*xx0 - b*yy0

xx1 = xx0 + 4*b

yy1 = -(a*xx1 + c)/b

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Первый катет

xe = x0 + xx0*ed

ye = y0 - yy0*ed

GraphicsWindow.FillEllipse(xe-5,ye-5,10,10)

xe = x0 + xx1*ed

ye = y0 - yy1*ed

GraphicsWindow.FillEllipse(xe-5,ye-5,10,10)

'Сканирование декартовой плоскости

For x = xx0 To xx1 Step .01

For y = -3 To 3 Step .01

'Вычисление значений функции z = F(x, y)

z = a*x + b*y + c

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

If z<.01 And z>-.01 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

'Второй катет

xx2 = xx0 + a*(-3)

yy2 = yy0 + b*(-3)

xe = x0 + xx2*ed

ye = y0 - yy2*ed

GraphicsWindow.FillEllipse(xe-5,ye-5,10,10)

For lm = 0 To -3 Step -.01

x = xx0 + lm*a

y = yy0 + lm*b

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndFor

'Гипотенуза

k = (yy2 - yy1)/(xx2 - xx1)

bb = yy1 - k*xx1

For x = xx2 To xx1 Step .01

y = k*x + bb

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndFor

Рисунок 5

Рассмотренное задание несколько тяжеловесно из-за того, что используются три различных метода построения прямых. Впрочем, оно показывает, что даже внимательное рассмотрение прямых может представить определённые трудности для студентов.

На практике такое сложное задание обычно разбивают на несколько простых. Как известно, стандартными заданиями, связанными с прямыми, являются следующие.

Даны координаты двух точек на плоскости. Получить уравнение прямой, проходящей через эти точки. (Эта задача включена в предыдущее задание).
Даны уравнения двух прямых. Найти точку пересечения.
Разделить отрезок, соединяющий две заданные точки в данном отношении.

Задание 6. Разделить катеты и гипотенузу египетского треугольника соответственно на 3, 4 и 5 равных отрезков.

Решение. Используем параметрические уравнения катетов и гипотенузы. В предыдущую программу достаточно добавить три цикла.

'Разбиение сторон

For t = 0 To 1 Step 1/4

x = xx0 + (xx1 - xx0)*t

y = yy0 + (yy1 - yy0)*t

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

EndFor

For t = 0 To 1 Step 1/3

x = xx0 + (xx2 - xx0)*t

y = yy0 + (yy2 - yy0)*t

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

EndFor

For t = 0 To 1 Step 1/5

x = xx2 + (xx1 - xx2)*t

y = yy2 + (yy1 - yy2)*t

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

EndFor

Рассмотрим такое новое для студентов понятие как пучок прямых [Четверухин, 1969]. Пучком прямых называется либо множество прямых, проходящих через одну точку (пучок первого типа), либо множество параллельных прямых (пучок второго типа). Отметим, что с точки зрения проективной геометрии параллельные прямые проходят через одну общую бесконечно удалённую точку. Пучок задан, если задана соответствующая точка. Однако возможно и другое определение пучка. Если заданы две прямые пучка, то задан и весь пучок.

Пусть на декартовой плоскости заданы неявные уравнения двух прямых, а именно:

a_{1} x + b_{1} y + c_{1} = 0

и

a_{2} x + b_{2} y + c_{2} = 0

. Координаты точки пересечения неизвестны. Их можно найти, решив соответствующую систему двух линейных уравнений. Но оказывается, что и не зная этих координат, можно найти уравнение любой прямой из этого пучка. Дело в том, что линейная комбинация этих уравнений

λ_{1} ∙ (a_{1} x + b_{1} y + c_{1})

+ λ_{2} ∙ (a_{2} x + b_{2} y + c_{2}) = 0

в центре пучка обращается в ноль, а, значит, описывает некоторую прямую этого пучка.

Задание 7. Найти уравнения вертикальной и горизонтальной прямых пучка.

Решение. Понятно, что в конечном счёте речь идёт о решении системы двух линейных уравнений, но алгебраические преобразования при этом получают геометрический характер. Пусть

λ_{1} = b_{2}

и

λ_{2} = {- b}_{1}

, тогда уравнение принимает вид:

)

∙ x = -

). Следовательно,

x = \frac{- c_{1} ∙ b_{2} - c_{2} ∙ b_{1}}{a_{1} ∙ b_{2} - a_{2} ∙ b_{1}}

. Если положить

λ_{1} = a_{2}

и

λ_{2} = {- a}_{1}

, то получаем, что

y = \frac{c_{1} ∙ a_{2} - c_{2} ∙ a_{1}}{a_{1} ∙ b_{2} - a_{2} ∙ b_{1}}

. Фактически получены формулы Крамера. Ниже приводится программа, которая строит четыре прямых из пучка (рисунок 6).

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Коэффициенты прямых

a1 = 1

b1 = 2

c1 = -2

a2 = -1

b2 = 3

c2 = 1

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Построение пучка

xp = -(c1*b2 - c2*b1)/(a1*b2 - a2*b1)

yp = (c1*a2 - c2*a1)/(a1*b2 - a2*b1)

For x = -3 To 3 Step .01

For y = - 3 To 3 Step .01

z1 = a1*x + b1*y + c1

z2 = a2*x + b2*y + c2

If Math.Abs(z1)<.01 Or Math.Abs(z2)<.01 Then

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"")

EndIf

EndFor

xe=x0 + ed*xp

ye=y0 - ed*yp

GraphicsWindow.DrawLine(xe,0,xe,600)

GraphicsWindow.DrawLine(0,ye,600,ye)

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10,10)

Рисунок 6

ОКРУЖНОСТИ

Уравнение окружности является, по-видимому, наиболее прозрачным, поскольку явственно выражает факт равной удалённости точек окружности от её центра. Это уравнение является основным примером, объясняющим различие между явным и неявным заданием функции. Окружность при этом рассматривается как совокупность двух ветвей, каждая из которых может быть явно описана формулами

y = \pm \sqrt{r^{2} - x^{2}}

. Используя их, окружность можно построить программой, которая строит два графика.

Что касается параметрических уравнений, описывающих окружность, то они связаны с определением на всём множестве действительных чисел таких важнейших функций математического анализа, как синус и косинус. Таким образом, использование окружности как алгебраической кривой даже по этим причинам совершенно обязательно в курсе высшей математики.

Следует отметить, что параметрические уравнения окружности являются источником замечательных образов. Прежде всего следует назвать правильные многоугольники и звёзды. Более того, именно на примере окружностей можно увидеть, как одни алгебраические кривые преобразовываются в другие, и то, как они позволяют создавать новые способы описания любых алгебраических кривых, например, в результате введения новых систем координат.

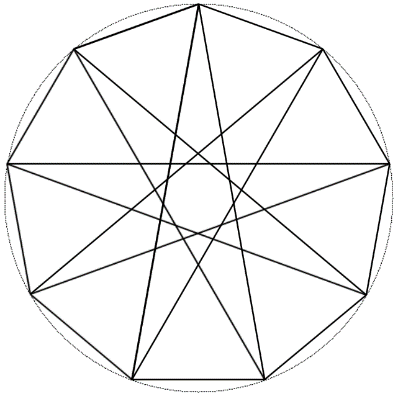
Задание 8. Построить с помощью параметрических уравнений окружности окружность, вписанный в неё девятиугольник, и девятиугольную звезду, у которой вершины девятиугольника соединяются через четыре.

Решение. Все эти образы можно реализовать с помощью соответствующей программы. Результат её работы показан на рисунке 7.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

n = 9

m = 4

x0 = 300

y0 = 300

r = 250

For u = pi/2 To 2*pi + pi/2 Step pi/500

x = x0 + r* Math.Cos(u)

y = y0 - r* Math.Sin(u)

GraphicsWindow.SetPixel(x,y,"")

EndFor

For u = pi/2 To 2*pi + pi/2 Step 2*pi/n

x1 = x0 + r* Math.Cos(u)

y1 = y0 - r* Math.Sin(u)

x2 = x0 + r* Math.Cos(u+2*pi/n)

y2 = y0 - r* Math.Sin(u+2*pi/n)

x3 = x0 + r* Math.Cos(u+m*2*pi/n)

y3 = y0 - r* Math.Sin(u+m*2*pi/n)

GraphicsWindow.DrawLine(x1,y1,x2,y2)

GraphicsWindow.DrawLine(x1,y1,x3,y3)

EndFor

Рисунок 7

Кроме того, окружность порождает такую кривую как эллипс, поскольку эллипс является сжатой окружностью. Сжатие декартовой плоскости мы будем проводить по вертикали. При этом все вертикальные расстояния умножаются на одно и то же число, называемое коэффициентом сжатия, а горизонтальные расстояния сохраняются. На картинах по этой причине круглые предметы имеют эллиптические очертания. В частности, это имеет место при изображении цилиндров, призм и пирамид.

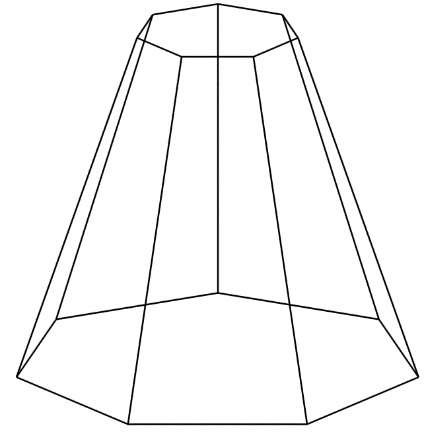
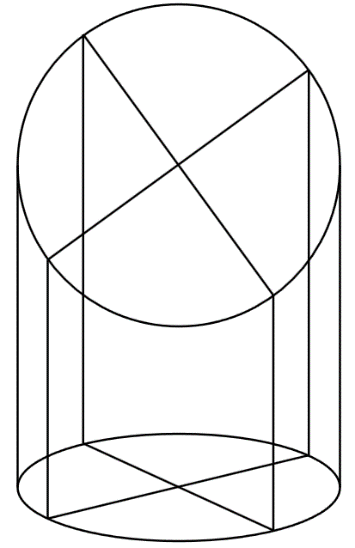
Задание 9. Построить с помощью параметрических уравнений сжатой окружности усечённую пирамиду.

Решение. Результат работы очередной программы показан на рисунке 8.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

u0 = pi/7

k = 1/3

n = 7

x0 = 300

y0 = 450

r1 = 250

r2 = 100

h = 400

For u = pi/2 To 2*pi + pi/2 Step 2*pi/n

x1 = x0 + r1* Math.Cos(u)

y1 = y0 - k*r1* Math.Sin(u)

x2 = x0 + r1* Math.Cos(u+2*pi/n)

y2 = y0 - k*r1* Math.Sin(u+2*pi/n)

x3 = x0 + r2* Math.Cos(u)

y3 = y0 - k*r2* Math.Sin(u) - h

x4 = x0 + r2* Math.Cos(u+2*pi/n)

y4 = y0 - k*r2* Math.Sin(u+2*pi/n) - h

GraphicsWindow.DrawLine(x1,y1,x2,y2)

GraphicsWindow.DrawLine(x3,y3,x4,y4)

GraphicsWindow.DrawLine(x1,y1,x3,y3)

EndFor

Рисунок 8

Задание 10. При сжатии окружности её перпендикулярные диаметры переходят в сопряжённые диаметры эллипса. С помощью программы продемонстрировать этот факт.

Решение. Результат работы программы показан на рисунке 9.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

u0 = pi/5

k = 1/3

x0 = 300

y0 = 470

r = 150

h = 300

y00 = y0 - h

GraphicsWindow.DrawEllipse(x0 - r, y00 - r, 2*r, 2*r)

GraphicsWindow.DrawEllipse(x0 - r, y0 - k*r, 2*r, 2*k*r)

x1 = x0 + r* Math.Cos(u0)

y1 = y00 - r* Math.Sin(u0)

x2 = x0 + r* Math.Cos(u0 + pi)

y2 = y00 - r* Math.Sin(u0 + pi)

GraphicsWindow.DrawLine(x1,y1,x2,y2)

x3 = x0 + r* Math.Cos(u0)

y3 = y0 - k*r* Math.Sin(u0)

x4 = x0 + r* Math.Cos(u0 + pi)

y4 = y0 - k*r* Math.Sin(u0 + pi)

GraphicsWindow.DrawLine(x3,y3,x4,y4)

GraphicsWindow.DrawLine(x1,y1,x3,y3)

GraphicsWindow.DrawLine(x2,y2,x4,y4)

x1 = x0 + r* Math.Cos(u0+pi/2)

y1 = y00 - r* Math.Sin(u0+pi/2)

x2 = x0 + r* Math.Cos(u0+3*pi/2)

y2 = y00 - r* Math.Sin(u0+3*pi/2)

GraphicsWindow.DrawLine(x1,y1,x2,y2)

x3 = x0 + r* Math.Cos(u0+pi/2)

y3 = y0 - k*r* Math.Sin(u0+pi/2)

x4 = x0 + r* Math.Cos(u0+3*pi/2)

y4 = y0 - k*r* Math.Sin(u0+3*pi/2)

GraphicsWindow.DrawLine(x3,y3,x4,y4)

GraphicsWindow.DrawLine(x1,y1,x3,y3)

GraphicsWindow.DrawLine(x2,y2,x4,y4)

GraphicsWindow.DrawLine(x0-r,y00,x0-r,y0)

GraphicsWindow.DrawLine(x0+r,y00,x0+r,y0)

Рисунок 9

Многие стандартные задачи аналитической геометрии связаны с взаимным расположением точек, прямых и окружностей. Рассмотрим некоторые из них.

Прежде всего, вспомним о полярной системе координат. Если декартова система координат возникает на основе рассмотрения двух взаимно перпендикулярных пучков параллельных прямых, то полярная система координат строится с помощью пучка концентрических окружностей [Энциклопедия элементарной математики, 1963] и пучка прямых с центром, совпадающим с центром семейства концентрических окружностей.

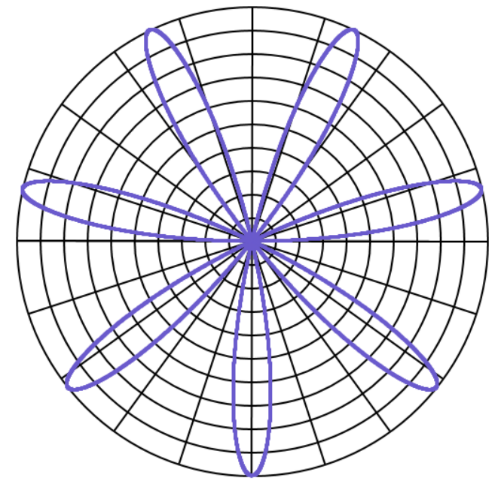
Задание 11. В полярной системе координат построить одну из алгебраических кривых из семейства роз Гвидо Гранди [Савёлов, 1960].

Решение. В декартовой системе координат описание роз Гранди весьма сложно. Зато в полярной системе координат оно является очень простым:

r = \sin (k ∙ α)

. Результат работы программы показан на рисунке 10.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

k = 7

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0 - 5, y0 - 5,10,10)

'Пучок окружностей

For r = 25 To 250 Step 25

GraphicsWindow.DrawEllipse(x0 - r,y0 - r, 2*r,2*r)

EndFor

'Пучок прямых

For al = 0 To pi Step pi/10

x1 = x0 + 250* Math.Cos(al)

y1 = y0 - 250* Math.Sin(al)

x2 = x0 + 250* Math.Cos(al + pi)

y2 = y0 - 250* Math.Sin(al + pi)

GraphicsWindow.DrawLine(x1,y1,x2,y2)

EndFor

'Роза или Цветик-семицветик

For al = 0 To pi Step pi/10000

x = x0 + 250* Math.Cos(al)*Math.Sin(k*al)

y = y0 - 250* Math.Sin(al)*Math.Sin(k*al)

GraphicsWindow.FillEllipse(x-2, y-2, 4, 4)

EndFor

Рисунок 10

Перейдём к рассмотрению пучков окружностей. Определение пучка окружностей с геометрических позиций даётся с помощью понятия радикальной оси [Степанов, а]. Но можно его дать и чисто алгебраически с помощью понятия линейной комбинации, как это было сделано для прямых.

Пусть на декартовой плоскости заданы две окружности

=

r_{1}^{2}

и

=

r_{2}^{2}

. Пучком окружностей называется множество кривых вида

λ_{1} ∙

- r_{1}^{2}

+

λ_{2} ∙

- r_{2}^{2}

.

Задание 12. Доказать, что линейная комбинация двух уравнений окружностей также описывает окружность, центр которой находится на линии центров двух исходных окружностей.

Задание 13. Вывести уравнение радикальной оси.

Решение. Радиус окружностей в связке может быть сколь угодно большим. Окружность с бесконечно большим радиусом превращается в прямую. Возникает вопрос: можно ли с помощью одной из линейных комбинаций получить прямую? Очевидно, что квадраты икса и игрека уничтожаются при

λ_{1} = 1

и

λ_{2} = - 1

. Уравнение соответствующей прямой, называемой радикальной осью, описывает прямую перпендикулярную линии центров двух исходных окружностей.

Задание 14. Написать программу, которая строит пучок окружностей по двум заданным исходным окружностям.

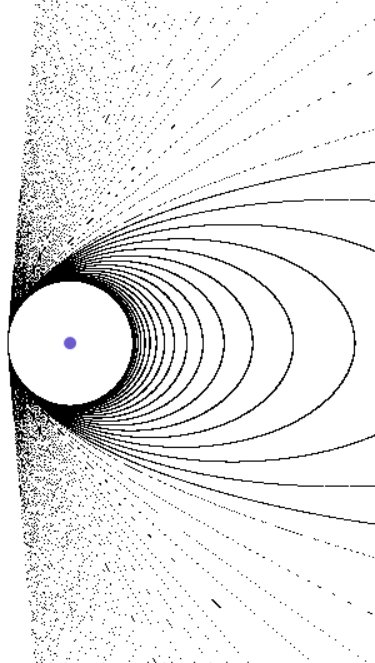
Решение. Пучки окружностей бывают трёх видов в зависимости от того, пресекаются, касаются или не имеют общих точек исходные окружности. Все три варианта показаны на рисунках 11, 12 и 13. Названия этих пучков таковы: пучок пересекающихся окружностей, пучок касающихся окружностей и пучок непересекающихся окружностей. Для простоты вычислений центры исходных окружностей расположены на одной горизонтали и применён метод сканирования плоскости.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 300

y0 = 300

ed = 100

x1 = -1

y1 = 0

r1 = 1.75

x2 = 1.5

y2 = 0

r2 = 1

xrad = (x2*x2 - x1*x1 + y2*y2 - y1*y1 + r1*r1 - r2*r2)/(2*(x2 - x1))

xe = x0 + ed*xrad

GraphicsWindow.DrawLine(xe, 0, xe, 600)

xe = x0 + ed*x1

ye = y0 - ed*y1

re = r1*ed

GraphicsWindow.DrawEllipse(xe - (re - 1), ye - (re - 1), 2*(re - 1), 2*(re - 1))

GraphicsWindow.DrawEllipse(xe - re, ye - re, 2*re, 2*re)

GraphicsWindow.DrawEllipse(xe - (re + 1), ye - (re + 1), 2*(re + 1), 2*(re + 1))

xe = x0 + ed*x2

ye = y0 - ed*y2

re = r2*ed

GraphicsWindow.DrawEllipse(xe - (re - 1), ye - (re - 1), 2*(re - 1), 2*(re - 1))

GraphicsWindow.DrawEllipse(xe - re, ye - re, 2*re, 2*re)

GraphicsWindow.DrawEllipse(xe - (re + 1), ye - (re + 1), 2*(re + 1), 2*(re + 1))

For t = -1 To 2 Step .1

For x = -3 To 3 Step .005

For y = -3 To 3 Step .005

z1 = x*x - 2*x1*x + x1*x1 + y*y - 2*y1*y + y1*y1 - r1*r1

z2 = x*x - 2*x2*x + x2*x2 + y*y - 2*y2*y + y2*y2 - r2*r2

z = z1 + t*(z2 - z1)

If Math.Abs(z)<.01 Then

xe = x0 + ed*x

ye = y0 - ed*y

GraphicsWindow.SetPixel(xe, ye, "")

EndIf

EndFor

Рисунок 11

Рисунок 12

Рисунок 13

Задание 15. Написать программу для построения пучков окружностей при произвольном положении исходных окружностей.

Решение. Программа в целом остаётся прежней. Усложняется только построение радикальной оси.

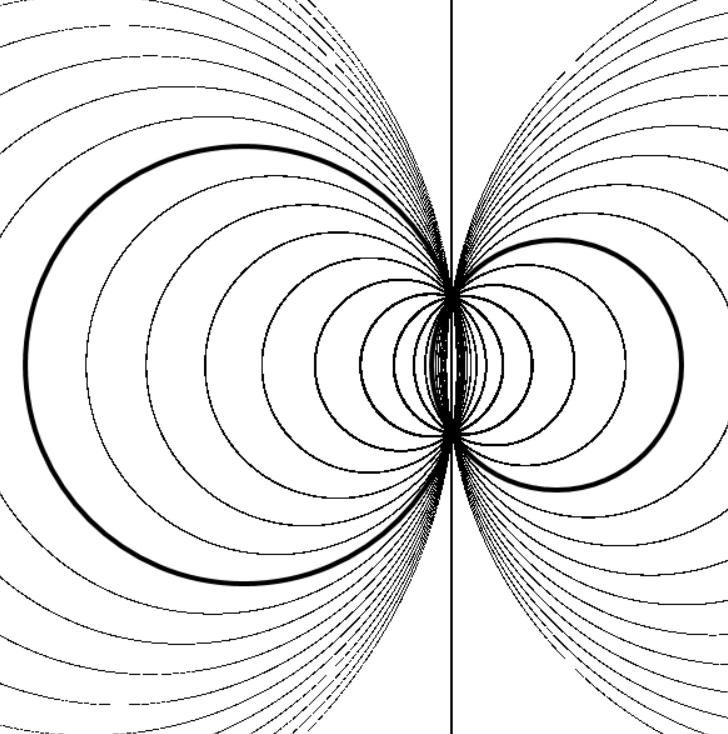
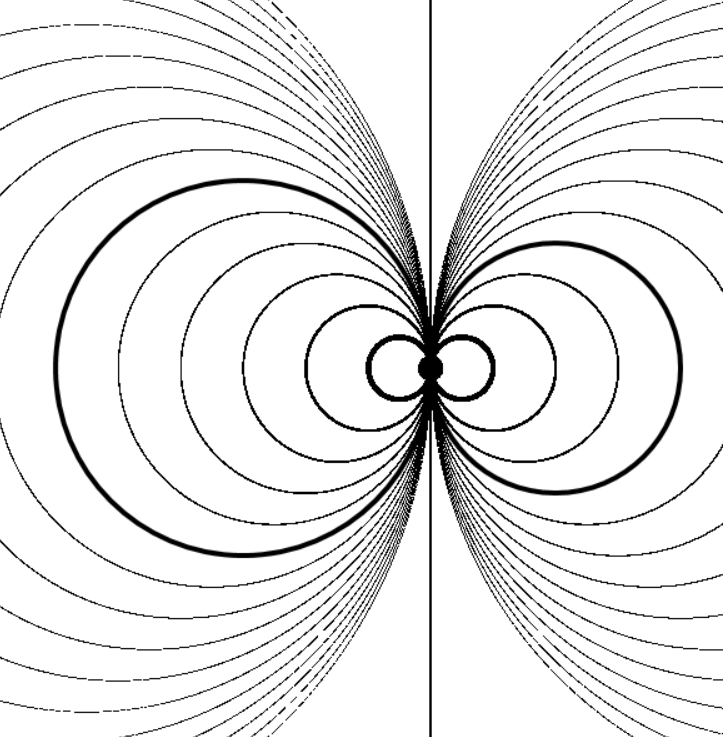
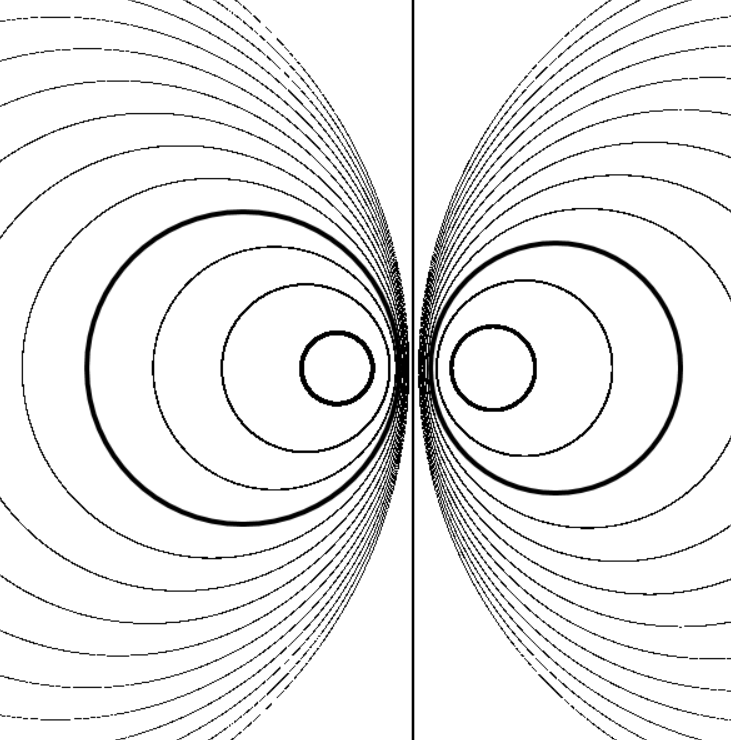
Задание 16. Показать, что в пучке непересекающихся окружностей имеется две предельные точки, в которые стягиваются окружности, убывающего радиуса.

Решение. Предположим, что предельные точки существуют и имеют координаты

(- a; 0)

и

(a; 0)

. Тогда они должны рассматриваться как окружности нулевого радиуса. Их уравнения имеют вид

и

. Любая другая окружность из пучка непересекающихся окружностей может быть получена как линейная комбинация с коэффициентами

λ_{1}

и

λ_{2}

.

Достаточно простые преобразования позволяют получить уравнение, которое имеет вид

x^{2} - 2 ax \frac{λ_{1} - λ_{2}}{λ_{1} + λ_{2}}

+

y^{2} + a^{2} = 0

.

После дополнительных преобразований уравнение примет вид

В правой части уравнения стоит квадрат радиуса соответствующей окружности. Поскольку он должен быть положительным, коэффициенты

λ_{1}

и

λ_{2}

должны иметь разный знак. Теперь можно написать программу, которая построит семейство окружностей, описываемых последним из уравнений. Легко понять, что вертикальная радикальная ось пучка проходит через начало декартовой системы координат. Построение пучка при этом проводится не сканированием, а с помощью команды, которая строит окружность по координатам центра и радиусу. Результат работы программы показан на рисунке 14.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 300

y0 = 300

ed = 100

a = 1

GraphicsWindow.FillEllipse(x0 + a*ed - 5, y0 - 5, 10, 10)

GraphicsWindow.FillEllipse(x0 - a*ed - 5, y0 - 5, 10, 10)

GraphicsWindow.DrawLine(x0, 0, x0, 600)

For l = 0 To 1 Step .045

lm1 = -1

lm2 = l

xe = x0 + ed*a*(lm1 - lm2)/(lm1 + lm2)

q = Math.SquareRoot(-lm1*lm2)

r = 2*a*q/(lm1 + lm2)*ed

GraphicsWindow.DrawEllipse(xe - r, y0 - r, 2*r, 2*r)

lm1 = l

lm2 = -1

xe = x0 + ed*a*(lm1 - lm2)/(lm1 + lm2)

q = Math.SquareRoot(-lm1*lm2)

r = 2*a*q/(lm1 + lm2)*ed

GraphicsWindow.DrawEllipse(xe - r, y0 - r, 2*r, 2*r)

EndFor

Рисунок 14

Задание 17. Предположим, что предельные точки из предыдущего задания с координатами

(- a; 0)

и

(a; 0)

одновременно являются точками пересечения окружностей пучка пересекающихся окружностей. Построить оба пучка одновременно. Эти пучки называются сопряжёнными.

Решение. Получим уравнения окружностей, проходящих через точки

(- a; 0)

и

(a; 0)

. Очевидно, что их центры лежат на оси ординат, то есть имеют координаты

(0; y_{1})

. Квадрат радиуса такой окружности равен

a^{2} + y_{1}^{2}

. Чтобы построить сопряжённые пучки, к предыдущей программе добавим следующий цикл. . Результат работы программы показан на рисунке 15.

GraphicsWindow.DrawLine(0, y0, 600, y0)

For y1 = -3 To 3 Step .25

r2 = a*a + y1*y1

ye = y0 - y1*ed

r = Math.SquareRoot(r2)*ed

GraphicsWindow.DrawEllipse(x0 - r, ye - r, 2*r, 2*r)

EndFor

Рисунок 15

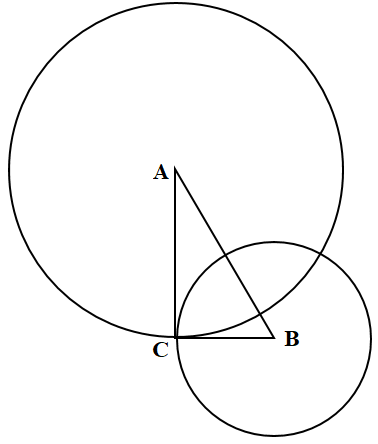
Задание 18. Доказать, что два сопряжённых пучка являются взаимно ортогональными, то есть каждая окружность пересекающегося пучка ортогональна каждой окружности непересекающегося пучка.

Решение. Пусть две ортогональных окружности с центрами А и В пересекаются в точке С. Тогда треугольник АВС является прямоугольным (рисунок 16). Таким образом, квадрат отрезка АВ, соединяющего центры равен сумме квадратов радиусов окружностей.

Рисунок 16

Для нашего скучая это обстоятельство выражается уравнением

+

y_{1}^{2} = - {4 a}^{2} \frac{λ_{1} λ_{2}}{}

.

Доказательство не составляет труда.

Задание 19. Найти пучок, ортогональный пучку касающихся окружностей. Напишите программу для построения ортогональных пучков.

КРИВЫЕ ВТОРОГО ПОРЯДКА. Приступим к изучению любых кривых второго порядка, а не только окружностей.

Задание 20. Построить на экране кривую второго порядка, описываемую формулой

a_{11} x^{2} + 2 a_{12} xy

+

a_{22} y^{2}

+

b_{1} x

+

b_{2} y + c = 0.

Решение. Сечение поверхности, описываемой функцией от двух переменных

z = a_{11} x^{2} + 2 a_{12} xy

+

a_{22} y^{2}

+

2 b_{1} x

+

2 b_{2} y + c = 0,

горизонтальной плоскостью

z = 0

является соответствующей кривой второго порядка. Естественно, в программе будет применёно сканирование декартовой плоскости.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Коэффициенты кривой второго порядка

a11 = 2

a12 = 3

a22 = 1

b1 = .5

b2 = -2

c = 1

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Сканирование декартовой плоскости

For x = -3 To 3 Step .01

For y = -3 To 3 Step .01

'Вычисление значений функции z = F(x, y)

z = a11*x*x + 2*a12*x*y + a22*y*y + 2*b1*x + 2*b2*y + c

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

If z<.05 And z>-.05 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

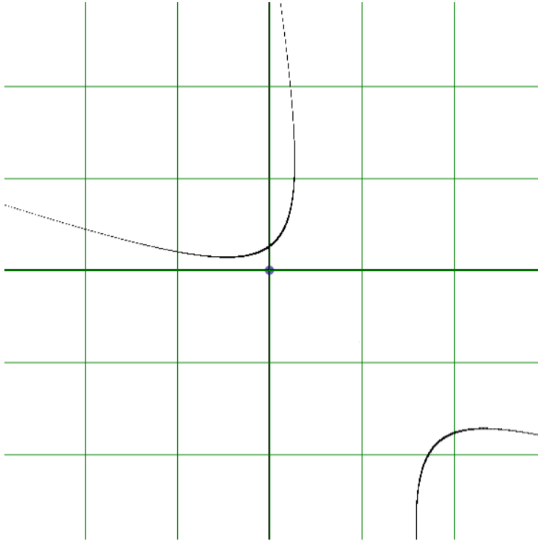
Результат работы программы показан на рисунке 17. В данном конкретном случае кривая оказалась гиперболой. Но эта же программа при смене коэффициентов построит любую кривую второго порядка, в том числе и вырожденную.

Рисунок 17

Задание 21. Найти центр кривой второго порядка, описываемой формулой

a_{11} x^{2} + 2 a_{12} xy

+

a_{22} y^{2}

+

b_{1} x

+

b_{2} y + c = 0.

Решение. В любом курсе аналитической геометрии рассматриваются канонические уравнения кривых второго порядка. Такой раздел аналитической геометрии как «Общая теория кривых второго порядка» рассматривается далеко не во всех курсах аналитической геометрии. Но именно в этом разделе рассматриваются методы работы с общим уравнением соответствующих кривых. Студент, работающий над заданием, подобным данному, должен обратиться к подробному курсу аналитической геометрии, например, [Александров, 1979].

Для нахождения координат центра кривой второго порядка

(x_{c}; y_{c})

нужно решить систему двух линейных уравнений, называемых уравнениями центра:

a_{11} x + a_{12} y + b_{1} = 0

,

a_{12} x + a_{22} y + b_{2} = 0

.

Для построения асимптот используется уравнение

a_{11} ∙ α^{2} + 2 ∙ a_{12} ∙ α ∙ β + a_{22} ∙ β^{2} = 0.

Координаты (α; β) задают вектор, указывающий направление асимптот (в случае эллипса мнимых). Если обозначить отношение

\frac{α}{β}

через λ, то с помощью квадратного уравнения можно получить два вектора (

λ_{1}; 1

и (

λ_{2}; 1

, которые задают направление асимптот, исходящих из центра кривой второго порядка

(x_{c}; y_{c})

. Таким образом, к предыдущей программе следует добавить новые строки. Результат работы расширенной программы показан на рисунке 18.

'Центр кривой второго порядка

xc = -(b1*a22 - b2*a12)/(a11*a22 - a12*a12)

yc = (b1*a12 - b2*a11)/(a11*a22 - a12*a12)

xe = x0 + xc*ed

ye = y0 - yc*ed

GraphicsWindow.FillEllipse(xe - 5, ye - 5, 10,10)

'Асимптоты

d2 = a12*a12 - a11*a22

d = Math.SquareRoot(d2)

lm1 = (-a12 + d)/a11

lm2 = (-a12 - d)/a11

For t = -7 To 7 Step .001

xa = xc - t*lm1

ya = yc - t

xe = x0 + xa*ed

ye = y0 - ya*ed

GraphicsWindow.SetPixel(xe,ye,"")

xa = xc - t*lm2

ya = yc - t

xe = x0 + xa*ed

ye = y0 - ya*ed

GraphicsWindow.SetPixel(xe,ye,"")

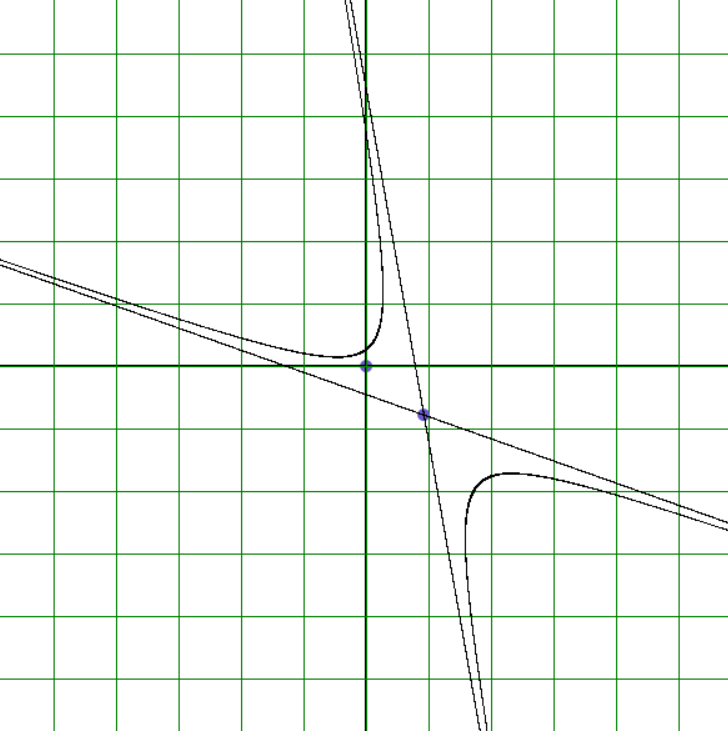
EndFor

Рисунок 18

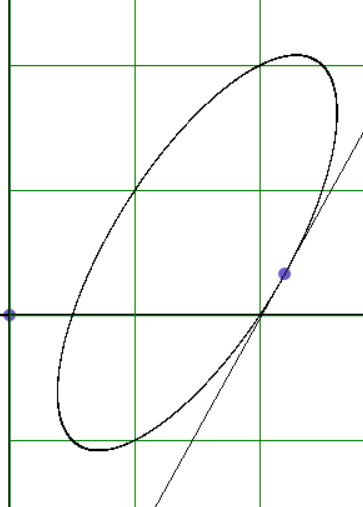
Задание 22. Построить касательную к эллипсу в заданной точке.

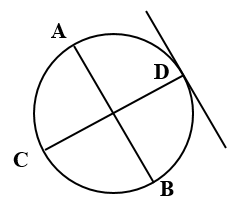
Решение. Проведём два перпендикулярных диаметра окружности АВ и CD (рисунок 19),

Рисунок 19

Тогда касательная к окружности в точке D параллельна диаметру АВ. Если подвергнуть окружность сжатию, то перпендикулярные диаметры окружности перейдут в сопряжённые диаметры эллипса. Таким образом, чтобы провести касательную к эллипсу в точке D, нужно определить направление диаметра, сопряжённого к диаметру, проходящему через D. Касательная к эллипсу будет параллельна сопряжённому диаметру. На основании этих рассуждений можно написать программу. Результат её работы показан на рисунке 20.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

pi = Math.Pi

x0 = 300

y0 = 300

ed = 100

a = 2

b = 1

ug = 2*pi/7

GraphicsWindow.DrawEllipse(x0 - a*ed, y0 - b*ed, 2*a*ed, 2*b*ed)

'Точка на эллипсе

xd = a* Math.Cos(ug)

yd = b* Math.Sin(ug)

xde = x0 + xd*ed

yde = y0 - yd*ed

GraphicsWindow.FillEllipse(xde - 5, yde - 5, 10,10)

'Направление касаеульной

p = ed*a* Math.Cos(ug + pi/2)

q = ed*b* Math.Sin(ug + pi/2)

'Касательная

For t = -3 To 3 Step .001

xe = xde + p*t

ye = yde - q*t

GraphicsWindow.SetPixel(xe,ye,"")

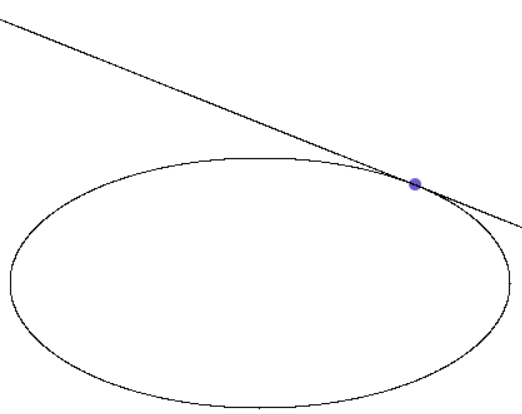
EndFor

Рисунок 20

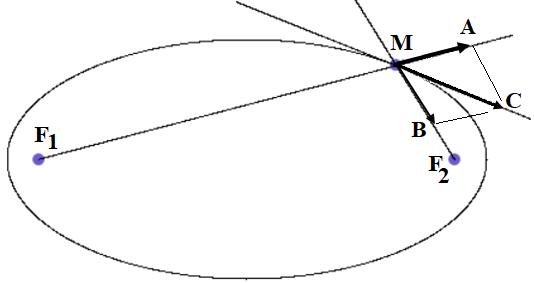
Задание 23. Доказать, что касательная к эллипсу является биссектрисой угла, смежного с углом между фокальными радиусами.

Решение. Для доказательства используем метод Роберваля, основанный на идеях кинематики [Берёзкин, 1974]. Скорость точки, движущейся по кривой, направлена по касательной к этой кривой. В случае эллипса эту скорость MC можно разложить на две составляющие MA и MB, направленные по линиям фокальных радиусов F1M и F2M (рисунок 21).

Рисунок 21

Вектора МА и МВ имеют одинаковую длину, поскольку сумма длин F1M и F2M постоянна. Таким образом, длина фокального радиуса F1M возрастает с такой же скоростью, с которой убывает длина фокального радиуса F2M. Из этого следует, что касательная направлена по биссектрисе угла АMВ.

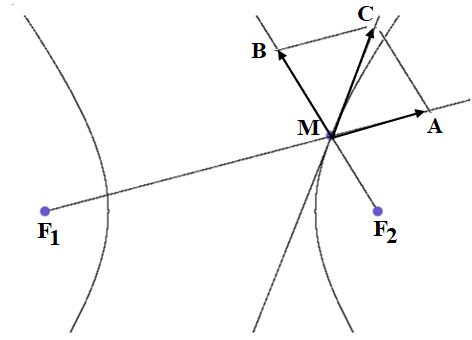
Задание 24. Доказать, что касательные к конфокальным эллипсу и гиперболе перпендикулярны.

Решение. Если эллипс и гипербола имеют общие фокусы, то в точке их пересечения у них совпадают фокальные радиусы. Опять используем метод Роберваля, который помог разобраться с касательной к эллипсу. Снова скорость точки, движущейся по гиперболе, разложим на две составляющие MA и MB, направленные по линиям фокальных радиусов F1M и F2M (рисунок 22). В данном случае вектор МВ имеет прежнюю длину и направлен в противоположном направлении по отношению к случаю эллипса. Дело в том, что постоянным является модуль разности длин отрезков F1M и F2M.

Суммарная скорость, получаемая после сложения векторов MA и MB направлена по биссектрисе угла F1MF2. Легко понять, что касательные к конфокальным эллипсу и гиперболе ортогональны.

Рисунок 22

Задание 25. Построить конфокальные эллипс и гиперболу и провести к ним касательные в точке их пересечения.

Решение. Дополним программу из задания 22. Вычислим параметры a1 и b1, определяющие гиперболу. Пусть f1 и f2 длины фокальных радиусов, общих для эллипса и гиперболы, тогда

a_{1} = \frac{| f_{1} - f_{2} |}{2}

. Далее,

b_{1} = \sqrt{c^{2} - a_{1}^{2}}

. Построение гиперболы описано в задании 2. В программу из задания 22 добавим следующие строки.

'Фокусы

xe1 = x0 - c*ed

xe2 = x0 + c*ed

GraphicsWindow.FillEllipse(xe1 - 5, y0 - 5, 10, 10)

GraphicsWindow.FillEllipse(xe2 - 5, y0 - 5, 10, 10)

'Фокальные радиусы

For t = 0 To 3 Step .001

xe = xe1 + (xde - xe1)*t

ye = y0 + (yde - y0)*t

GraphicsWindow.SetPixel(xe,ye,"")

xe = xe2 + (xde - xe2)*t

ye = y0 + (yde - y0)*t

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

'Гипербола

f1 = Math.SquareRoot((xd + c)*(xd + c) + yd*yd)

f2 = Math.SquareRoot((xd - c)*(xd - c) + yd*yd)

a1 = Math.Abs(f1 - f2)/2

b1 = Math.SquareRoot(c*c - a1*a1)

For x = -3 To 3 Step .001

ex1 = Math.Power(2.71828,x)

ex2 = Math.Power(2.71828,-x)

cn = (ex1 + ex2)/2

sn = (ex1 - ex2)/2

xe = x0 + a1*cn*ed

ye = y0 - b1*sn*ed

GraphicsWindow.SetPixel(xe,ye,"")

xe = x0 - a1*cn*ed

ye = y0 - b1*sn*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

'Касательная к гиперболе

For t = -3 To 3 Step .001

xe = xde + q*t

ye = yde + p*t

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

'Фокусы

xe1 = x0 - c*ed

xe2 = x0 + c*ed

GraphicsWindow.FillEllipse(xe1 - 5, y0 - 5, 10, 10)

GraphicsWindow.FillEllipse(xe2 - 5, y0 - 5, 10, 10)

Результат работы программы показан на рисунке 23.

Рисунок 23

Задание 26. Построить к кривой второго порядка касательную в заданной точке, используя методы математического анализа.

Решение. Кривую второго порядка как обычно построим с помощью сканирования декартовой плоскости. Для нахождения точки на кривой следует задать конкретное значение абсциссы, получить квадратное уравнение и найти два значения ординат и выбрать одно из них.

Для построения касательной нужно найти производную неявной функции по формуле

k = \frac{- \frac{\partial F}{\partial y}}{\frac{\partial F}{\partial x}}

. Повторение вывода соответствующей формулы является очень полезным, поскольку она часто остаётся за пределами внимания студентов. Наконец, построение касательной к кривой второго порядка показывает практическую важность этой формулы. Результат работы программы показан на рисунке 24.

GraphicsWindow.Width = 320

GraphicsWindow.Height = 520

'Коэффициенты кривой второго порядка

a11 = 2

a12 = -1

a22 = 1

b1 = -2.5

b2 = 1

c = 2

'Начало экранных координат

x0 = 10

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=0 To 3 Step .01

For y=-2 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=0 To 3 Step 1

For y=-2 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Сканирование декартовой плоскости

For x = 0 To 3 Step .005

For y = -2 To 3 Step .005

'Вычисление значений функции z = F(x, y)

z = a11*x*x + 2*a12*x*y + a22*y*y + 2*b1*x + 2*b2*y + c

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

If Math.Abs(z)<.01 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

'Точка на кривой

xt = 2.2

p1 = a22

p2 = 2*a12*xt + 2*b2

p3 = a11*xt*xt + 2*b1*xt + c

d2 = p2*p2 - 4*p1*p3

d = Math.SquareRoot(d2)

yt = (-p2 - d)/(2*p1)

xte = x0 + xt*ed

yte = y0 - yt*ed

GraphicsWindow.FillEllipse(xte - 5,yte - 5,10,10)

'Производная в точке

dfdx = 2*a11*xt + 2*a12*yt + 2*b1

dfdy = 2*a22*yt + 2*a12*xt + 2*b2

k = -dfdy/dfdx

'Касательная

For t = -2 To 2 Step .01

xe = xte + t*k*ed

ye = yte - t*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Рисунок 24

СЕМЕЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА

Перейдём к изучению различных семейств кривых второго порядка. Кривые второго порядка на первых взгляд разбиты на несколько совершенно непохожих друг на друга кривых. При этом объединяет их вид общей формулы, используемой для их описания. Понимание геометрической общности кривых второго порядка достигается в рамках проективной геометрии. Но и в рамках аналитической геометрии удаётся объединять воедино канонические формулы соответствующих кривых.

Рассмотрим такие формулы, которые обычно остаются за пределами стандартных курсов аналитической геометрии.

Задание 27. Построить семейства конфокальных эллипсов и гипербол по единой формуле

\frac{x^{2}}{λ^{2}} + \frac{y^{2}}{λ^{2} - c^{2}} = 1

[Делоне, 1968].

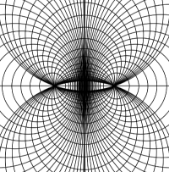
Решение. Хотя формула по достаточно очевидным причинам объединяет эллипсы и гиперболы (параметр λ играет роль полуоси а), в программе построение каждого вида кривых приходится проводить отдельным циклом, поскольку изменение параметра λ для эллипсов и гипербол сильно различается.

Результатом работы программы является построение ортогональной сети (рисунок 25), как доказано в задании 24.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 300

y0 = 300

ed = 50

c = 1

GraphicsWindow.FillEllipse(x0 - c*ed - 5, y0 - 5, 10,10)

GraphicsWindow.FillEllipse(x0 + c*ed - 5, y0 - 5, 10,10)

For x = -6 To 6 Step .01

For y = -6 To 6 Step .01

For lm = 1.25 To 10.25 Step .5

Z = x*x/(lm*lm) + y*y/(lm*lm - c*c) - 1

If Math.Abs(z)<.01 Then

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndIf

EndFor

For x = -6 To 6 Step .005

For y = -6 To 6 Step .005

For lm = .05 To .95 Step .1

Z = x*x/(lm*lm) + y*y/(lm*lm - c*c) - 1

If Math.Abs(z)<.01 Then

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndIf

EndFor

Рисунок 25

Задание 28. Построить семейства кривых второго порядка с общей вершиной в начале координат по единой формуле

y^{2} = 2 px - (1 - ε^{2}) ∙ x^{2}

[Делоне, 1968].

Решение. Поясним значение параметров, используемых в уравнении. Величина p является расстоянием от фокуса до самой близкой к нему вершины кривой второго порядка. Величина ε представляет собой эксцентриситет эллипса (ε < 1) и гиперболы (ε > 1).

Программа практически совпадает с программой из предыдущего задания. Изменения состоят в следующем. Экран сужен, и начало координат перенесено к левому краю. Вместо величины с используется величина р = 1. В циклах меняется параметр eps. Вычисляется величина z формуле

z = y*y - 2*p*x + (1 -eps*eps)*x*x.

Результат работы программы показан на рисунке 26.

Рисунок 26

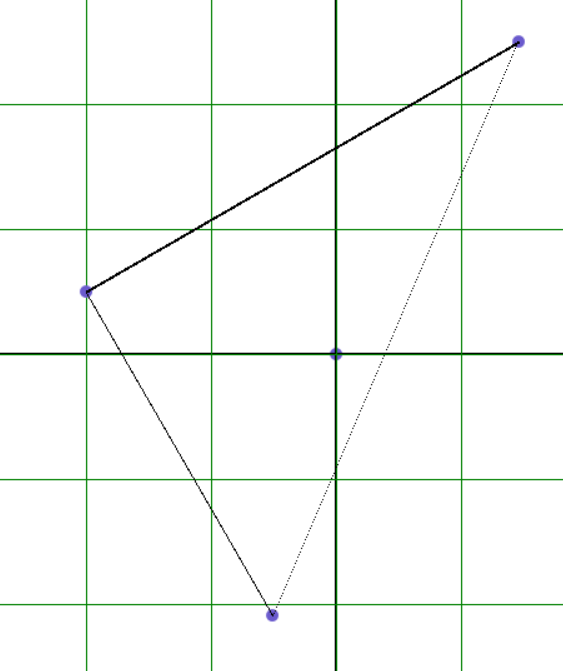
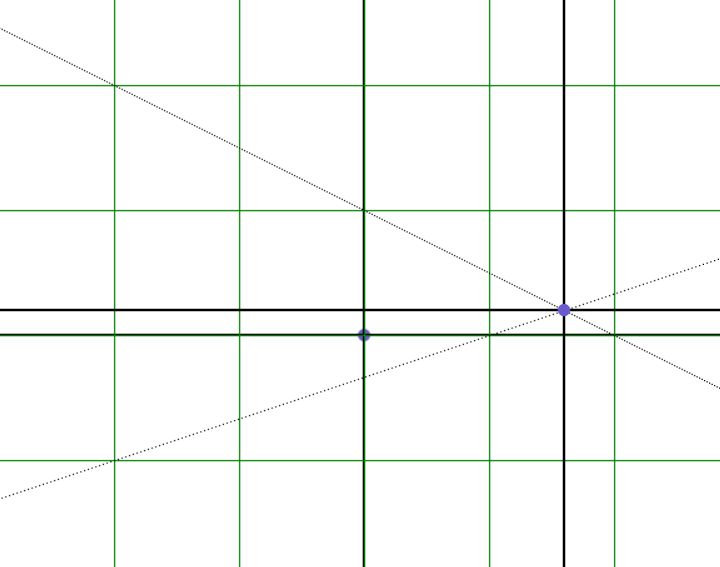
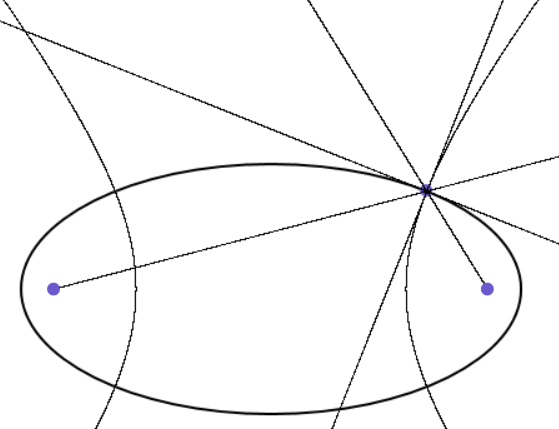
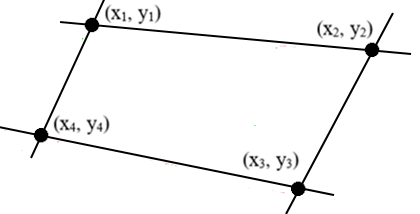
Перейдём к рассмотрению пучков кривых второго порядка [Мусхелишвили, 1947]. Пучком кривых второго порядка на плоскости называется однопараметрическое семейство кривых, проходящих через четыре фиксированных точки этой плоскости с координатами (xi, yi), где i = 1, 2, …, 4. Пусть уравнения F1(x, y) = 0 и F2(x, y) = 0 задают кривые из одного пучка, тогда любая другая кривая этого пучка имеет уравнение F(x, y) = F1(x, y) + λ·F2(x, y) = 0 .

На роль кривых второго порядка F1(x, y) = 0 и F2(x, y) = 0 можно взять уравнения двух вырожденных кривых второго порядка, распадающихся на две пары прямых, являющихся противоположными сторонами соответствующего четырёхугольника (рисунок 27). Пусть, например, А1 х + В1 у + С1 = 0 – уравнение прямой, проходящей через пару точек (x1, y1) и (x2, y2), а А2 х + В2 у + С2 = 0 – уравнение прямой, проходящей через пару точек (x3, y3) и (x4, y4), тогда положим, что F1(x, y) = (А1 х + В1 у + С1)

∙

( А2 х + В2 у + С2). Пусть далее А3 х + В3 у + С3 = 0 – уравнение прямой, проходящей через пару точек (x1, y1) и (x4, y4), а А4 х + В4 у + С4 = 0 – уравнение прямой, проходящей через пару точек (x2, y2) и (x3, y3), тогда положим, что F2(x, y) = (А3 х + В3 у + С3)

∙

( А4 х + В4 у + С4).

Рисунок 27

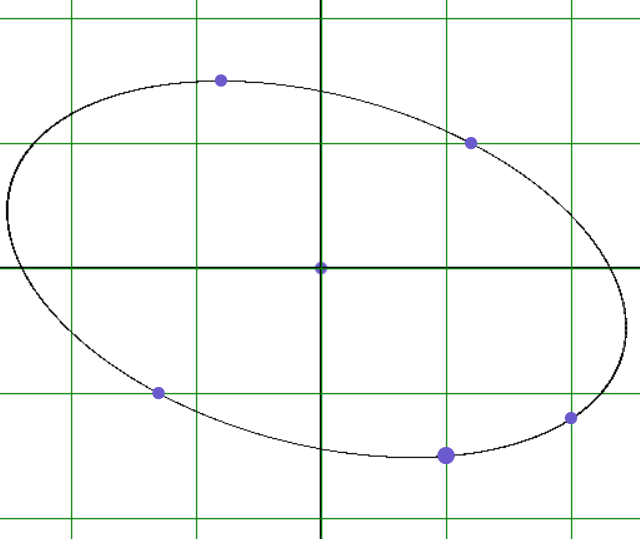
Пусть на плоскости заданы пять точек с координатами (xi ; yi), где i = 1, 2, …5. Тогда уравнение кривой второго порядка, проходящей через все пять точек можно получить при таком значении параметра λ, которое определяется уравнением F1(x5, y5) + λ·F2(x5, y5) = 0.

Выше сказанное позволяет построить либо пучок кривых второго порядка, либо единственную кривую второго порядка, проходящую через пять заданных точек.

Задание 29. Построить пучок кривых второго порядка, проходящих через четыре заданных точки.

Решение. Результат работы программы показан на рисунке 28.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-6 To 6 Step .01

For y=-6 To 6 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-6 To 6 Step 1

For y=-6 To 6 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Точки на плоскости

x1 = -.8

y1 = 1.5

x2 = 1.2

y2 = 1

x3 = -1.3

y3 = -1

x4 = 2

y4 = -1.2

'Уравнения прямых

k1 = (y2 - y1)/(x2 - x1)

b1 = y1 - k1*x1

k2 = (y4 - y3)/(x4 - x3)

b2 = y3 - k2*x3

k3 = (y4 - y1)/(x4 - x1)

b3 = y1 - k3*x1

k4 = (y3 - y2)/(x3 - x2)

b4 = y2 - k4*x2

'Сканирование декартовой плоскости

For lm = -1 To 2 Step .2

For x = -3 To 3 Step .01

For y = -3 To 3 Step .01

'Вычисление значений функции z = F(x, y)

z1 = (y - k1*x - b1)*(y - k2*x - b2)

z2 = (y - k3*x - b3)*(y - k4 *x - b4)

z = z1 + lm*(z2 - z1)

'Переход к экранной системе координат

If Math.Abs(z)<.01 Then

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

xe = x0 + x1*ed

ye = y0 - y1*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

xe = x0 + x2*ed

ye = y0 - y2*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

xe = x0 + x3*ed

ye = y0 - y3*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

xe = x0 + x4*ed

ye = y0 - y4*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10, 10)

Рисунок 28

Задание 30. Построить кривую второго порядка, проходящую через пять заданных точек.

Решение. В предыдущей программе несколько меняется сканирующая часть. Результат работы программы показан на рисунке 29.

'Сканирование декартовой плоскости

x5 = 1

y5 = -1.5

z15 = (y5 - k1*x5 - b1)*(y5 - k2*x5 - b2)

z25 = (y5 - k3*x5 - b3)*(y5 - k4 *x5 - b4)

lm = -z15/z25

For x = -3 To 3 Step .01

For y = -3 To 3 Step .01

'Вычисление значений функции z = F(x, y)

z1 = (y - k1*x - b1)*(y - k2*x - b2)

z2 = (y - k3*x - b3)*(y - k4 *x - b4)

z = z1 + lm*z2

'Переход к экранной системе координат

If Math.Abs(z)<.01 Then

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

Рисунок 29

ЗАКЛЮЧЕНИЕ

В первой части данной статьи рассматриваются вопросы, связанные с углублённым изучением линий не выше второго порядка. Особое внимание уделяется различным семействам алгебраических кривых, в частности пучкам прямых, окружностей и кривых второго порядка.

Обсуждение соответствующих вопросов может помочь молодым преподавателям при изучении различных разделов высшей математики. Кроме того, некоторые рассмотренные темы могут быть предложены в качестве тем курсовых и дипломных работ.

Продолжение статьи будет посвящено рассмотрению алгебраических кривых высших порядков, начиная с кубических кривых.

Литература

Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. № 4. С.127-144.
Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. № 4. С.145-156.
Куланин Е.Д.,Степанов М. Е., Нуркаева И.М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. 2020. Т.10. №2 С.110 - 128.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ данных. 2020. Т.11. №1. С.40 - 60.
Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. №1. С.54-94.
Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения Моделирование и анализ данных. 2022. Т.12. №3. С.58 – 70.
Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. Моделирование и анализ данных. 2022. Т.12. №4. С.67 – 84.
Куланин Е.Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. Моделирование и анализ данных. 2022. Т.12. №4. С.94 - 104.
Куланин Е.Д., Степанов М. Е., Панфилов А.Д., Потонышев И.С. Системный подход к методике тифлопедагогики на примере задач математического анализа. 2022. Т.12. №2. С.34 - 82.
Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики на примере теории чисел. Моделирование и анализ данных. 2024. Т.14. №1. С.170 - 195.
Куланин Е.Д., Степанов М. Е. Использование образов в преподавании высшей математики. Моделирование и анализ данных. Т.14. №2. C.192-225.
Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения. Моделирование и анализ данных. Т.14. №3. C.174-202.
Савёлов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство). М., Гос. изд. физ.-мат. литературы. 1960.
Четверухин Н. Ф. Проективная геометрия. М., Просвещение. 1969.
Энциклопедия элементарной математики. Книга четвёртая. Геометрия. М., Гос. изд. физ.-мат. литературы. 1963.
Степанов М. Е. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – Вып. 3.,
Александров П. С. Курс аналитической геометрии и линейной алгебры. М., Наука. 1979.
Берёзкин Е. Н. Курс теоретической механики. М., Издательство Московского Университета. 1974.
Делоне Б. Н., Райков Д. А. Аналитическая геометрия. Том 1. М. – Л., ОГИЗ. 1968.
Мусхелишвили Н. И. Курс аналитической геометрии. М. – Л., ОГИЗ, 1947.

Информация об авторах

Куланин Евгений Дмитриевич, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Степанов Михаил Евграфович, кандидат педагогических наук, доцент кафедры прикладной математики факультета информационных технологий, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Метрики

Просмотров web

За все время: 21
В прошлом месяце: 0
В текущем месяце: 21

Скачиваний PDF

За все время: 2
В прошлом месяце: 0
В текущем месяце: 2

Всего

За все время: 23
В прошлом месяце: 0
В текущем месяце: 23

PlumX

Метрики публикации