Перейти к основному содержанию

Моделирование и анализ данных
2025. Том 15. № 1. С. 210–251
doi:10.17759/mda.2025150111
ISSN: 2219-3758 / 2311-9454 (online)

Множества точек, находящихся на рациональных расстояниях друг от друга

4

Куланин Е.Д., Степанов М.Е.

PDF (RUS)
GS
Информация
в Google Scholar

Аннотация

Статья продолжает цикл ([1] – [15]) методических разработок авторов. В статье рассматриваются задачи, связанные с множествами точек, расстояния между которыми являются рациональными числами (назовём эти множества рациональными). Изучение подобных множеств, связано с решением диофантовых уравнений. Соответствующие задачи могут использоваться при выборе тем для исследовательской работы студентов. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

Общая информация

Ключевые слова: Расстояние на плоскости, Евклидова геометрия, диофантовы уравнения, целочисленные треугольники, пифагоровы треугольники, пифагоровы тройки

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2025150111

Получена: 31.01.2025

Принята в печать:

Для цитаты: Куланин Е.Д., Степанов М.Е. Множества точек, находящихся на рациональных расстояниях друг от друга // Моделирование и анализ данных. 2025. Том 15. № 1. С. 210–251. DOI: 10.17759/mda.2025150111

Полный текст

ВВЕДЕНИЕ

Одной из целей данной статьи является рассмотрение задач, которые связаны с описанием множеств точек на евклидовой плоскости таких, что расстояние между двумя любыми двумя точками множества является рациональным числом. Уже при изучении множеств, состоящих всего из трёх точек, приходится решать диофантовы уравнения. Для множеств, содержащих более трёх точек, естественно, задача усложняется. При этом могут возникнуть проблемы любой степени сложности. Ниже будут рассмотрены примеры соответствующих множеств, содержащих как любое конечное число точек, так и бесконечное их число.

Отметим, что в данной статье ставятся вопросы, проблемы и задачи, возникновение которых связано с геометрической проблематикой, а решение основывается на идеях теории чисел. В целом круг соответствующих задач иногда называют арифметическими проблемами евклидовой геометрии вообще и планиметрии в частности.

Однако по поводу структуры этих множеств необходимо сделать важное замечание. Если на плоскости заданы точки А, В и С, то с ними связаны три расстояния – длины сторон треугольника АВС. Этот треугольник может являться равносторонним, и при этом длины всех его сторон могут задаваться одинаковыми иррациональными числами. При таком подходе этот конкретный треугольник должен быть исключён из сферы нашего рассмотрения.

Но, конечно, это неправильная точка зрения. На самом деле следует рассматривать этот треугольник, как и все изучаемые множества точек на плоскости, с позиций соизмеримости расстояний, связанных с данной геометрической конфигурацией. Если все расстояния соизмеримы, то все их можно выразить рациональными числами, а если требуется, то и натуральными. Таким образом, соответствующие множества на плоскости нужно рассматривать с точностью до преобразования подобия. При этом существенным является только факт соизмеримости всех расстояний между точками множества.

В статье будут рассмотрены и некоторые другие задачи, связанные с рациональными расстояниями.

ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ

Прямоугольные треугольники, все стороны которых являются натуральными числами, называются пифагоровыми. Натуральные числа, задающие длины сторон пифагорова треугольника, расположенные в порядке возрастания называют пифагоровыми тройками. Подробное рассмотрение вопросов, связанных с пифагоровыми треугольниками и пифагоровыми тройками дано в книге [Серпинский, 1959]. Учитывая предыдущее замечание о роли подобия и несколько отклоняясь от общепринятой терминологии, иногда будем называть прямоугольный треугольник пифагоровым, если все его стороны являются рациональными числами.

Пифагоров треугольник называется основным, если длины его катетов выражаются взаимно простыми числами. Среди подобных пифагоровых треугольников есть наименьший. Наименьший пифагоров треугольник является основным.

Задание 1. Доказать, что прямоугольный треугольник является пифагоровым тогда и только тогда, когда синусы и косинусы его острых углов являются рациональными числами.

Решение. Обозначим катеты прямоугольного треугольника через а и b, а гипотенузу через с. Острый угол противолежащий стороне a, обозначим через α. Коль скоро а, b и с – рациональные числа, то sin α = a c и cos α = b c являются рациональными числами.
Наоборот, пусть синус и косинус острого угла  рациональны. Допустим, что sin α = p q и cos α = s t . Возьмем прямоугольный треугольник с катетами, равными синусу и косинусу угла . Его гипотенуза равна 1. Построим подобный ему треугольник с коэффициентом подобия q t. Сам он, естественно, является прямоугольным, а длина его катетов и гипотенузы выражается целыми числами: р t, s q и q t. Значит, этот прямоугольный треугольник является пифагоровым.

Если найти способ нахождения углов с рациональными синусами и косинусами, то можно описать все пифагоровы треугольники.

Задание 2. Доказать, что синус и косинус угла рациональны тогда и только тогда, когда тангенс половины этого угла является рациональным числом.

Решение. Пусть синус и косинус угла  рациональны. Построим прямоугольный треугольник АВС (рисунок 1) с катетами sin  и cos . Проведем биссектрису АМ угла А =.

 

 

Рисунок 1

По условию ВС = sin  и АС = cos , АВ = 1. Пусть МС = х, тогда по свойству биссектрисы можно записать пропорцию х : АС = ВМ : АВ, или х : ВС = (ВС – х) : АВ. Поскольку длины отрезков ВС, АС и АВ являются рациональными числами, мы получили для х линейное уравнение с рациональными коэффициентами. Из этого следует, что длина отрезка МС рациональна. В треугольнике АМС катеты АС и МС имеют рациональную длину, а угол МАС равен α 2 , значит, tg α 2 является рациональным числом.
Пусть теперь tg α 2 является рациональным числом, то есть tg α 2 = m n . Построим прямоугольный треугольник с катетами m и n. Квадрат его гипотенузы c равен m + n . Тогда sin α = m c и cos α = n c .

Используя формулы для синусов и косинусов суммы углов, получим выражения для синуса и косинуса угла :

sin α = sin α 2 ∙ cos α 2 + cos α 2 ∙ sin α 2 = 2 mn m 2 + n 2 ,
cos α = cos α 2 ∙ cos α 2 − sin α 2 ∙ sin α 2 = m 2 − n 2 m 2 + n 2 .

Это рациональные числа, и, значит, прямоугольный треугольник с углом  пифагоров. Отметим, что в данном доказательстве фактически используется универсальная тригонометрическая подстановка, применяемая при интегрировании.

В результате выполнения задания найдены общие формулы для нахождения сторон любых пифагоровых треугольников. Иными словами, получено решение диофантова уравнения x 2 + y 2 = z 2 :
x = 2 mn m 2 + n 2 , y = m 2 − n 2 m 2 + n 2 , z = 1 .
 
Задание 3. Доказать, что если треугольник является пифагоровым, то прямоугольный треугольник с острым углом, равным половине острого угла исходного треугольника, с точностью до подобия имеет целые катеты n и m. Тогда стороны исходного пифагорова треугольника также с точностью до подобия выражаются через числа n и m по формулам: x = 2mn, y = m – n , z = m + n .

Пояснение. Использовать результаты предыдущего задания.

Итак, мы имеет в своём распоряжении операцию получения из прямоугольного треугольника, вообще говоря не пифагорова, пифагорова треугольника.

Интерпретируем эту операцию несколько иначе. Пусть m больше n. Рассмотрим комплексное число m + i ∙ n . Модуль этого числа равен m 2 + n 2 , а аргумент равен арктангенсу числа n m . Предположим, что этот аргумент равен α. Возведём данное комплексное число в квадрат. Результат равен ( m 2 − n 2 ) + 2 mn ∙ i . Его модуль и аргумент соответственно равны m 2 + n 2 и 2 α .

Французский математик 16-го века Франсуа Виет обобщил данную операцию. Он ввел в математику перемножение прямоугольных треугольников.

Пусть дан прямоугольный треугольник с необязательно имеющими рациональные длины катетами n1 и m1, а также прямоугольный треугольник с катетами n2 и m2. При этом их наименьшие острые углы равны α и β . С первым прямоугольным треугольником свяжем комплексное число m 1 + i ∙ n 1 , а со вторым – комплексное число m 2 + i ∙ n 2 ,

Задание 4. Рассмотреть произведение соответствующих комплексных чисел и связать его с некоторым прямоугольным треугольником. Выяснить, всегда ли этот треугольник является пифагоровым.

Решение. Будем действовать по аналогии с возведением комплексного числа в квадрат. Действительная и мнимая часть комплексного числа, равного произведению, будут задавать катеты соответствующего прямоугольного треугольника. Эти катеты равны m 1 ∙ m 2 − n 1 ∙ n 2 и m 1 ∙ n 2 + n 1 ∙ m 2 . Модуль произведения равен произведению модулей сомножителей и задаёт длину гипотенузы. Аргументом является острый угол итогового прямоугольного треугольника, равный α + β.
Пусть числа m 1 , n 1 , m 2 и n 2 являются натуральными. Тогда катеты итогового треугольника, очевидно, являются целыми. Однако гипотенуза может оказаться иррациональным числом. Например, в случае, когда m 1 = 2 , n 1 = 1 , m 2 = 3 и n 2 = 2 длина гипотенузы равна 2 2 + 1 ∙ 3 2 + 2 2 = 65 , а это иррациональное число.
А вот при перемножении двух пифагоровых треугольников снова получается пифагоров треугольник. Действительно, модули сомножителей с точностью до подобия в этом случае являются натуральными числами. По этой причине гипотенуза итогового треугольника тоже является натуральным числом. Покажем это на примере. Пусть m 1 = 4 , n 1 = 3 , m 2 = 21 и n 2 = 20 . Тогда модули сомножителей равны 5 и 29. Перемножим комплексные числа 4 + 3i и 21 + 20i:

(4 + 3i)(21 + 20i) = 24 + 141i.

 

Модуль этого числа равен

 

24 2 + 143 2 = 576 + 20449 = 21025 = 145 = 5 ∙ 29 .
Естественно, возможны и ситуации, в которых перемножение не пифагоровых треугольников приводит к появлению пифагорова треугольника. В качестве примера приведём возведение в квадрат треугольника с катетами 2 и 1. Его гипотенуза имеет длину 5 . В результате будет получен так называемый египетский треугольник со сторонами 3, 4 и 5. Действительно, (2 + i)2 = 3 + 4i. Отметим, что исходный треугольник можно связать с золотым сечением, поскольку с ним связано число 5 .

Задание 5. Дать геометрическую интерпретацию перемножения прямоугольных треугольников.

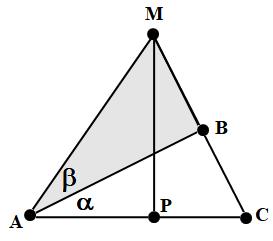
Решение. Напомним, что мы рассматриваем треугольники с точностью до подобия. Возьмем два прямоугольных треугольника с наименьшими острыми углами  и . Подобие позволяет сделать равными прилежащие к этим углам катеты. Сложим треугольники, приложив равные катеты друг к другу (рисунок 2).

 

Рисунок 2

Итак, после того как к треугольнику АВС приложен треугольник АВМ, будет получен треугольник АСМ. В нём можно провести высоту МР. Треугольник АМР является произведением треугольников АВС и АВМ.

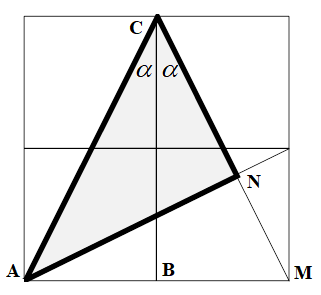
Задание 6. Российский архитектор и исследователь культуры Древнего Египта Игорь Павлович Шмелев на одном из своих рисунков показывает возникновение египетского треугольника ANC в квадрате 2 на 2 (рисунок 3). Доказать, что этим способом действительно построен египетский треугольник.

Рисунок 3

Пояснения. Нужно доказать, что треугольник ANC прямоугольный, а затем использовать то обстоятельство, что он является произведением треугольников АВС и МВС.

Используем некоторые полученные результаты для приближённого вычисления числа .

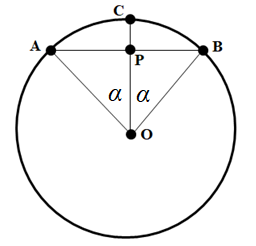
Задание 7. Сформулировать условие того, что хорда окружности единичного радиуса имеет единичную длину.

Решение. Пусть на хорду АВ опирается центральный угол, равный 2α (рисунок 4).

 

Рисунок 4

Половина хорды АВ равна sin α . Это число должно быть рациональным. Как было показано в задании 2, что это требование эквивалентно рациональности числа tg α 2 . Положим, что tg α 2 = m n , тогда sin α = 2 mn m 2 + n 2 , а общая длина хорды равна 4 mn m 2 + n 2 .
Задание 8. Разработать способ приближённого вычисления числа π , основаный на результатах предыдущего задания.
Решение. Выберем числа m и n, задающие tg α 2 таким образом, чтобы угол 2α был достаточно мал. Разобьём четверть окружности единичного радиуса, расположенную в первом квадранте, на дуги с угловой мерой 2α. Естественно, конец последней дуги перейдёт во второй квадрант. Проблема состоит в том, что нужно подсчитать число маленьких дуг. Дело в том, что мы вычисляем число π и не можем его использовать в промежуточных вычислениях.

Начнём с того, что отложим против часовой стрелки от точки (1; 0) первую дугу с угловой мерой 2α (рисунок 5).

 

 

Рисунок 5

Пусть tg α 2 = m n , тогда вектор ОС имеет координаты ( m 2 − n 2 m 2 + n 2 , 2 mn m 2 + n 2 ), где sin α = 2 mn m 2 + n 2 и cos α = m 2 − n 2 m 2 + n 2 . Из этого следует, что tg α = 2 mn m 2 − n 2 = m 1 n 1 . Этот тангенс позволяет получить координаты вектора ОА, наклонённого под углом 2α. В итоге получим, что sin 2 α = 2 m 1 n 1 m 1 2 + n 1 2 и cos 2 α = m 1 2 − n 1 2 m 1 2 + n 1 2
Рассмотрим комплексное число z = cos 2 α + i ∙ sin 2 α , задаваемое вектором OA. Его степеням z k соответствуют концы дуг, имеющих длину 2 ∙ sin α . Когда одна из степеней выйдет за пределы первого квадранта, будет установлено число соответствующих дуг. Четверть круга покрыта k дугами длины 2 ∙ sin α . Добавим ещё непокрытый кусочек дуги, равный последнему положительному косинусу. Таким образом, π ≈ 4 ∙ k ∙ sin α + 2∙ cos 2 k α .

Программа приближённого вычисления числа π не содержит никаких вычислений кроме арифметических операций. Нет даже извлечения квадратных корней.

m = 10000000

n = 1

sa = 2*m*n/(m*m + n*n)

ca = (m*m - n*n)/(m*m + n*n)

m1 = 2*m*n

n1 = m*m - n*n

sd = 2*m1*n1/(m1*m1 + n1*n1)

cd = -(m1*m1 - n1*n1)/(m1*m1 + n1*n1)

sp = sd

cp = cd

k = 1

met:

sb = sd*cp + cd*sp

cb = cd*cp - sd*sp

sp = sb

cp = cb

If cp > 0 Then

del = cp

k = k + 1

Goto met

EndIf

pi = 4*k*sa + 2*del

GraphicsWindow.DrawText(50,100,pi)

После выбора очень маленького угла α удаётся получить достаточно высокую точность: π ≈ 3,1415926535897722945043434304. Видимо, уместно вспомнить по этому поводу мнемонику числа π, связанную с числом букв в словах: «Это я знаю и помню прекрасно. Пи многие знаки мне лишни, напрасны».

Если рассматривать все треугольники с натуральными длинами сторон a, b и c, то единственным ограничением на выбор чисел a, b и c являются неравенства треугольника. Такие треугольники называются целочисленными (целыми) или рациональными. При наложении дополнительных требований на свойства треугольника поиск чисел a, b и c может усложниться. Однако некоторые задачи легко решаются с помощью пифагоровых треугольников.

Целочисленные треугольники с целой площадью называются героновыми.

Задание 9. Описать процедуру получения героновых треугольников с помощью пифагоровых треугольников.

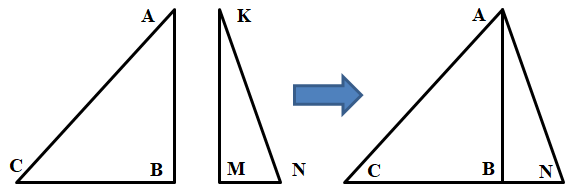
Решение. Как известно, даже такой «хороший» треугольник, как равносторонний c единичной длиной сторон, имеет иррациональную площадь. Чтобы построить треугольник с рациональной площадью следует взять два пифагоровых треугольника АВС и KMN. Подвергнув один из них преобразованию подобия, добьёмся, чтобы катеты АВ и KM имели одинаковую длину. После этого сложим из этих двух треугольников один с высотой АВ (рисунок 6). Очевидно, что полученный треугольник имеет рациональную площадь.

 

 

Рисунок 6

Кроме всего прочего в результате мы получили множество из четырёх точек А, В, С и N, удалённых друг от друга на рациональные расстояния. Правда, три из этих точек лежат на одной прямой, что делает соответствующую конфигурацию менее ценной.

Предложим задачу для самостоятельного решения.

Задание 10. Геронов треугольник разрезан по высоте. Обязательно ли полученные прямоугольные треугольники являются пифагоровыми?

Задание 11. Построить множество из четырёх точек, удалённых на рациональные расстояния. При этом никакие три точки не должны лежать на одной прямой.

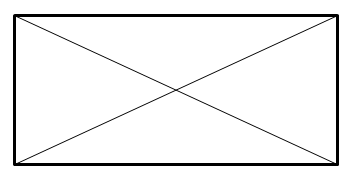
Решение. Одним из вариантов такого множества являются вершины прямоугольника, сложенного из двух равных пифагоровых треугольников (рисунок 7). Центр прямоугольника тоже может быть добавлен к этому множеству в качестве пятой точки.

 

Рисунок 7

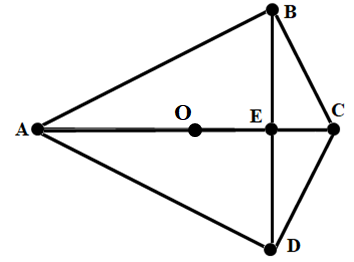
Можно складывать равные пифагоровы треугольники и другими способами. Один из них показан на рисунке 7. Точка О является серединой гипотенуз.

Рисунок 8

Задание 12. Доказать, что точки A, B, C, D, E и О, изображённые на рисунке 7, удалены друг от друга на рациональные расстояния.

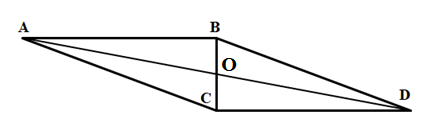
Мы разными способами складывали фигуру из двух равных пифагоровых треугольников. Есть ещё один способ, показанный на рисунке 8.

 

 

Рисунок 9

Возникает вопрос, могут ли вершины полученного параллелограмма быть удалены друг от друга на целые расстояния?

ПРИМЕРЫ РЕШЕНИЯ АРИФМЕТИЧЕСКИХ ПРОБЛЕМ ЕВКЛИДОВОЙ ПЛАНИМЕТРИИ

На примере этой задачи покажем, что она, подобно камню, брошенному в воду, порождает новые проблемы. При этом некоторые из них могут решаться теоретически. В других случаях приходится писать программу, чтобы с помощью компьютерных вычислений искать конкретные решения той же или связанной с ней задачи.

Начнём с того, что треугольники АВС и АВО должны быть пифагоровыми и иметь общий катет АВ. В книге [Серпинский, 1959] рассматриваются задачи поиска пифагоровых треугольников, имеющих общие свойства. В частности, рассматривается и поиск пифагоровых треугольников, имеющих общие катеты.

Задание 13. Показать, что существует бесконечно много рациональных пифагоровых треугольников с общим катетом.

Решение. Как мы знаем пифагоров треугольник имеет катеты целой длины x = 2mn и y = m – n . Подвергнем его преобразованию подобия с коэффициентом 1 2 ∙ m ∙ n , тогда один из катетов получает длину 1, а второй длину m – n 2 ∙ m ∙ n . Множество соответствующих треугольников можно расположить, совместив единичные катеты (рисунок 9).
 

Рисунок 10

В результате будет получено множество точек, состоящее из бесконечного множества точек лежащих на одной прямой, и ещё одной точки. Расстояние между любыми двумя точками соответствующего множества рационально. Можно добавить ещё одну точку, симметрично отразив треугольники относительно прямой.

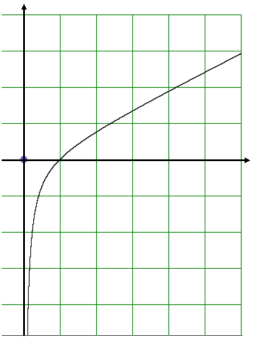
Задание 14. Показать, что множество вершин треугольников из предыдущего задания, лежащих на вертикальной прямой, является всюду плотным множеством.

Решение. Вертикальные катеты треугольников с рисунка 9 имеют длины выражаемые формулой u = m – n 2 ∙ m ∙ n . Введём обозначение дроби m n через t. Тогда длина вертикальных катетов соответствующих треугольников выражается функцией одной переменной u = t 2 − 1 2 t = t 2 − 1 2 t . Форма графика этой функции (ограничимся положительными значениями аргумента) определяется поведением линейной функции и верви гиперболы.

Функция непрерывна и принимает все значения от минус бесконечности до плюс бесконечности (рисунок. 10). К тому же значения функции рациональны при рациональных значениях аргумента.

 

 

Рисунок 11.

Полученный результат мы используем в дальнейшем.

Что же касается конфигурации, изображённой на рисунке 8, мало факта существования двух пифагоровых треугольников с общим катетом. Необходимо, чтобы катет ВС был ровно в два раза длиннее катета ОВ. Итак, возникает новая проблема.

Задание 15. Выразить только что сформулированное условие с помощью диофантова уравнения.

Решение. Длины катетов ВС и ВО пифагоровых треугольников АВС и АВО на рисунке 8 могут быть выражены формулой u = t 2 − 1 2 t с различными значениями параметра. Пусть BC = t 1 2 − 1 2 t 1 и BO = t 2 2 − 1 2 t 2 . Требуется, чтобы t 1 2 − 1 2 t 1 = t 2 2 − 1 t 2 или ( t 1 2 − 1 ) t 2 = 2 ( t 2 2 − 1 ) t 1 . Продолжим преобразования и получим уравнение 2 t 1 t 2 2 + ) t 2 − 2 t 1 = 0 , которое позволяет выразить параметр t 2 через t 1 :
t 2 = − 1 + t 1 2 ± 1 + 14 t 1 2 + t 1 4 4 t 1 .
Поскольку параметр t 2 должен быть рациональным, под корнем должен стоять полный квадрат. Пусть t 1 = m n , тогда это обстоятельство можно записать как диофантово уравнение
m 4 + 14 m 2 n 2 + n 4 = k 2 .
Это уравнение имеет бесконечно много целых решений при m = n . Однако для наших целей нужно найти решение для случая, когда m и n неравны между собой.
Итак, с конфигурацией на рисунке 8 связано диофантово уравнение m 4 + 14 m 2 n 2 + n 4 = k 2 . Вопрос о наличии у него решения с нужными свойствами можно решать, теоретически изучая уравнение. Это, как правило, сложный и творческий процесс. В данном случае предположительно таких решений не существует. Другой путь – поиск решений с помощью компьютерной программы. Он порой приводит к нахождению частных решений.
Задание 16. Написать программу для поиска решений диофантова уравнения m 4 + 14 m 2 n 2 + n 4 = k 2 .

Решение. Программа построена фактически на методе перебора натуральных значений переменных m и n, исключающем возможность совпадения этих значений. Возможен ряд существенных улучшений, которые, однако, усложнили бы программу и затруднили бы понимание её смысла.

 

GraphicsWindow.Clear()

'Число решений

nom = 0

For m = 1 To 1000

For n = m + 1 To 1000

'Вычисление левой части уравнения

k2 = m*m*m*m + 14*m*m*n*n + n*n*n*n

'Извлечение корня

k = Math.SquareRoot(k2)

k0 = Math.Floor(k)

'Проверка того, что корень является натуральным числом

If k = k0 Then

nom = nom + 1

'Печать переменных, дающих решение

GraphicsWindow.DrawText(50,nom*30,m)

GraphicsWindow.DrawText(200,nom*30,n)

GraphicsWindow.DrawText(300,nom*30,k0)

EndIf

EndFor

EndFor

'Итоговое число найденных решений

GraphicsWindow.DrawText(50,nom*30+30,nom)

Данный вариант программы не обнаруживает ни одного решения. Это обстоятельство в известном смысле подтверждает гипотезу о полном отсутствии решений искомого вида. Однако при увеличении интервалов изменения переменных m и n до 10000 вдруг появляются сообщения о наличии решений. Фрагмент с четырьмя сообщениями показан на рисунке 11.

Рисунок 12

 

Неопытного вычислителя это может обрадовать, но знаток сразу предположит, что компьютерные вычисления приводят к потере точности и формированию неверных результатов. Нужна проверка, которая при одном взгляде на первую тройку чисел сразу наводит на мысль об ошибке. Итак, первое сообщение даёт вариант m = 1 , n = 10000 , k = 100000007 . Для проверки будем вычислять последние цифры десятичной записи левой и правой частей диофантова уравнения при заданных значениях. Очевидно, что эти цифры равны 1 и 9, то есть несовпадение налицо.
Если посмотреть, каков компьютерный результат вычисления выражения m 4 + 14 m 2 n 2 + n 4 программой при m = 1 и n = 10000 , то он равен пространному числу 100000000140000000001 (верному!). Но квадратный корень из него без округления является целым числом 10000000007. Так или иначе, речь идёт об ошибке.

Задание 15. Проверить остальные три варианта, предложенных компьютером и, если потребуется, забраковать ошибочные.

Как некоторый итоговый вывод можно утверждать, что как теоретические, так и вычислительные исследования в рассматриваемой сфере требуют значительных интеллектуальных усилий.

Рассмотрим ещё несколько связанных с конфигурацией на рисунке 8 задач. В конечном счёте, данная фигура является параллелограммом особого вида. Таким образом, возникает следующий вопрос, который мы оформим в виде очередного задания.

Задание 16. Выяснить, существует ли параллелограммы с целой длиной сторон, такой, что их диагонали также имеют длину, выражаемую целыми числами.

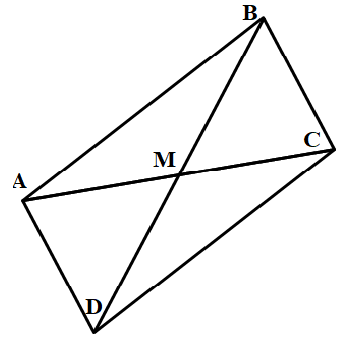
Решение. На рисунке 12 изображён параллелограмм ABCD. Точка М является точкой пересечения диагоналей. Если ограничится рассмотрением треугольника АВС, то медиана АМ должна иметь целую длину. Итак, задание 16 сведено к новому заданию.

 

Рисунок 13

Задание 17. Описать процедуру, позволяющую определённым образом располагать целые треугольники не декартовой плоскости.

Решение. Отметим, прежде всего, что рассматриваемые нами задачи позволяют двояко рассматривать рациональные множества. Поясним это на примере целых треугольников. Такой треугольник определяется тройкой натуральных чисел, являющихся длиной его сторон. Эти числа должны удовлетворять неравенствам треугольника. При этом мы не рассматриваем какое-то конкретное вложение соответствующего треугольника в декартову плоскость. Именно с таким вложением как раз связана вторая точка зрения на целые треугольники.

Назовём треугольник, рассматриваемый как тройка натуральных чисел, абстрактным треугольником. Решим задачу вложения абстрактного треугольника в декартову плоскость. При этом будем иметь ввиду, что треугольники рассматриваются нами с точностью до преобразования подобия.

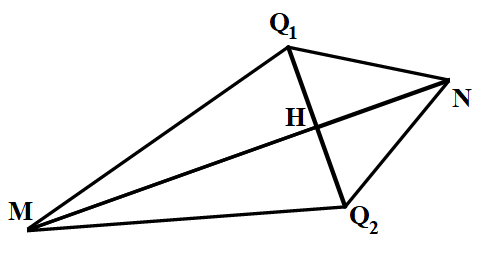
Пусть дан целый абстрактный треугольник ( a ; b ; c ) и отрезок MN на декартовой плоскости, где M ( x 1 ; y 1 ) и N ( x 2 ; y 2 ) . Вершину абстрактного треугольника, из которой исходят стороны a и b через С, а вершину абстрактного треугольника, из которой исходят стороны a и c через В. Третью вершину абстрактного треугольника обозначим через А. Задача состоит в том, чтобы построить на декартовой плоскости точку Q, такую, что треугольники АВС и QMN подобны.

Очевидно, что на роль точки Q могут быть выбраны две точки декартовой плоскости (рисунок 13). Выбор одной из них определяется дополнительными условиями.

 

Рисунок 14

Положим, что MN = c , M Q 1 = a , N Q 1 = b , MH = x , тогда
a 2 − x 2 = b 2 − ( c − x ) 2 .
А, значит, x = a 2 − b 2 + c 2 2 a . Тогда координаты точки Н выражаются по формулам x H = x 1 + x ∙ и y H = y 1 + x ∙ . Положим, что t = a 2 − x 2 . Вычисление координат точки Q 1 можно провести по следующей схеме: вычислить координаты единичного вектора, коллинеарного вектору MN, вычислить координаты ортогонального к вектору MN единичного вектора, умножить этот вектор на t = a 2 − x 2 и получить итоговые координаты точки Q 1 .

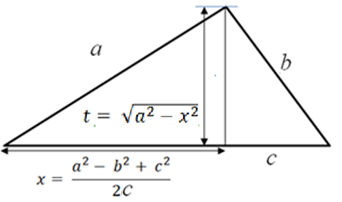
Выведенные выше формулы будут использованы далее неоднократно. По этой причине зафиксируем их на рисунке 14, что позволит достаточно быстро сверяться с ними.

 

Рисунок 15

 

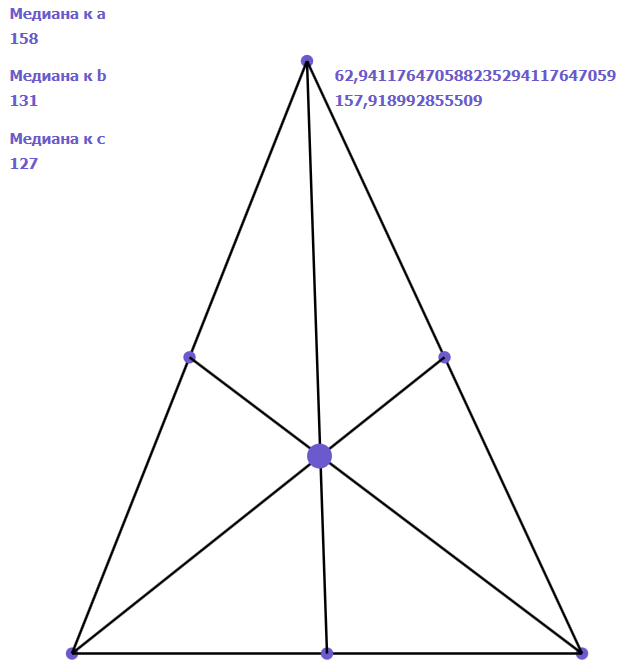
Задание 18. Написать программу, позволяющую выяснить, существует ли целые треугольники, хотя бы одна медиана которых имеет длину, выражаемую целым числом. С её помощью проверить тот факт, что все медианы целого треугольника со сторонами 136, 170 и 174 имеют длину, выражаемую целыми числами. Оценить степень достоверности проверки, осуществляемой компьютерным вычислением.

Решение. Расположим исследуемый треугольник на декартовой плоскости так, чтобы сторона длины a была горизонтальна. Это упростит вычисления. после определения координат вершин треугольника следует вычислить длины медиан и определить, являются ли эти длины целыми числами.

 

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Треугольник

xe1 = 100

ye1 = 550

GraphicsWindow.FillEllipse(xe1 - 5, ye1 - 5, 10, 10)

ed = 3

a = 136

b = 170

c = 174

x1 = 0

y1 = 0

x2 = a

y2 = 0

xe2 = xe1 + x2*ed

ye2 = ye1 - y2*ed

GraphicsWindow.FillEllipse(xe2 - 5, ye2 - 5, 10, 10)

x3 = (a*a + b*b - c*c)/(2*a)

y3 = Math.SquareRoot(b*b - x3*x3)

GraphicsWindow.DrawText(310,80,x3)

GraphicsWindow.DrawText(310,100,y3)

xe3 = xe1 + x3*ed

ye3 = ye1 - y3*ed

GraphicsWindow.FillEllipse(xe3 - 5, ye3 - 5, 10, 10)

GraphicsWindow.DrawLine(xe1,ye1,xe2,ye2)

GraphicsWindow.DrawLine(xe2,ye2,xe3,ye3)

GraphicsWindow.DrawLine(xe3,ye3,xe1,ye1)

'Построение медиан

pa = (x1 + x2)/2

qa = (y1 + y2)/2

mx1 = xe1 + pa*ed

my1 = ye1 - qa*ed

GraphicsWindow.FillEllipse(mx1 - 5, my1 - 5, 10, 10)

GraphicsWindow.DrawLine(mx1,my1,xe3,ye3)

pb = (x1 +x3)/2

qb = (y1 + y3)/2

mx2 = xe1 + pb*ed

my2 = ye1 - qb*ed

GraphicsWindow.FillEllipse(mx2 - 5, my2 - 5, 10, 10)

GraphicsWindow.DrawLine(mx2,my2,xe2,ye2)

pc = (x2 + x3)/2

qc = (y2 + y3)/2

mx3 = xe1 + pc*ed

my3 = ye1 - qc*ed

GraphicsWindow.FillEllipse(mx3 - 5, my3 - 5,10,10)

GraphicsWindow.DrawLine(mx3,my3,xe1,ye1)

xg = (mx1 + mx2 + mx3)/3

yg = (my1 + my2 + my3)/3

GraphicsWindow.FillEllipse(xg - 10, yg - 10,20,20)

median()

'Проверка длины медиан

Sub median

m1 = Math.SquareRoot((x3 - pa)*(x3 - pa) + (y3 - qa)*(y3 - qa))

If m1 = Math.Floor(m1) Then

GraphicsWindow.DrawText(50,30,"Медиана к стороне a")

GraphicsWindow.DrawText(50,50,m1)

EndIf

m2 = Math.SquareRoot((x2 - pb)*(x2 - pb) + (y2 - qb)*(y2 - qb))

If m2 = Math.Floor(m2) Then

GraphicsWindow.DrawText(50,80,"Медиана к стороне b")

GraphicsWindow.DrawText(50,100,m2)

EndIf

m3 = Math.SquareRoot((x1 - pc)*(x1 - pc) + (y1 - qc)*(y1 - qc))

If m3 = Math.Floor(m3) Then

GraphicsWindow.DrawText(50,130,"Медиана к стороне с")

GraphicsWindow.DrawText(50,150,m3)

EndIf

EndSub

 

Результат работы программы показан на рисунке 15.

 

 

Рисунок 16

 

В частности, вычисления показывают, что координаты одной из вершин треугольника являются дробными числами. Значит, тот факт, что исходящая из этой вершины медиана, имеет целую длину, установлен предположительно. Проведём конкретный пример вычислений, который обеспечивает полную уверенность в том, что соответствующая длина является целым числом.

Вычисления будут использовать теорему косинусов (рисунок 16). Прежде всего, запишем равенство 1742 = 1362 + 1702 – 2∙136∙170∙ cos α . Далее получаем, что cos α ∙ 68 ∙ 17 = 428 . Или в итоге cos α = 107 17 2 . Теперь можно вычислить длину x одной из медиан.
Итак, x2 = 1362 + 852 – 2∙136∙85∙ cos α = 136 2 + 85 2 – 2 ∙ 136 ∙ 85 ∙ 107 17 2 = 17161 = 131 2 .
 

Рисунок 17

Основываясь на подобных вычислениях можно переписать программу из задания 18, что, конечно, усложнит её.

Итак, мы познакомились с различными вариантами изучения рациональных множеств. Например, вопрос об описании пифагоровых треугольников был решён теоретически с помощью решения диофантова уравнения, а исследование целых треугольников, обладающих особыми свойствами, проводилось с помощью вычислений.

Здесь мы можем отметить, что подобная ситуация наблюдается и в теории чисел. Это сходство следует обсудить более подробно, поскольку оно проявляется в исследовании рациональных множеств.

ОБ ЭМПИРИЧЕСКИХ ИССЛЕДОВАНИЯХ МНОЖЕСТВ С ЦЕЛЫМИ РАССТОЯНИЯМИ МЕЖДУ ТОЧКАМИ

Что касается эмпирических исследований в математике, то речь, конечно, идёт о вычислениях. Такие математики как Архимед, Эйлер, Гаусс и Рамануджан нередко делали великие теоретические открытия, основываясь на результатах сложнейших вычислений. В книге [Зюзьков, 2019] автор ссылается на мнение Ю. Манина, который так характеризует роль компьютерных технологий в современной математике: «То, что умели Эйлер и Гаусс, может делать любой математик за своим письменным столом». Сам автор этой книги отмечает, что «компьютеры иногда позволяют получить неформальные аргументы в пользу того или иного предположения, а иногда, наоборот, опровергнуть казавшиеся правдоподобными гипотезы».

И, конечно, основной областью исследований, основанных на вычислениях, является теория чисел. Причины этого легко понять. Натуральные числа вполне упорядочены. Именно на этом основаны эмпирические исследования в теории чисел. Речь может идти, например, о последовательном вычислении простых чисел или чисел близнецов. Поиск решения диофантовых уравнений может производиться перебором. Долгое время проводились вычисления, связанные с великой теоремой Ферма. Это лишь немногие примеры популярных исследовательских тем в сфере теории чисел. Авторы в своей статье [Куланин, 2024] дают примеры программ, используемых в подобных вычислениях.

Задачи, связанные с арифметическими проблемами евклидовой геометрии, также могут решаться с помощью вычислительных экспериментов. Не в последнюю очередь это связано с тем, что рациональные множества перечислимы. Более подробно поясним это утверждение.

Каждое рациональное множество чисто формально можно связать с полным графом [Оре, 1980], с каждым ребром которого связывают число, равное расстоянию между этими точками в рациональном множестве. Описание является формальным, поскольку расстояние между вершинами графа может быть произвольным. Не менее наглядно, чем полным графом, рациональное множество можно представить симплексом. Симплекс – аналог треугольника или тетраэдра в многомерном пространстве. У симплекса с n вершинами каждую пару вершин соединяет ребро. Таким образом, число рёбер равно c n 2 = n ∙ ( n − 1 ) 2 . Представление тоже является формальным.
Но пока для нас важно только то, что с каждым реально существующим рациональным множеством из n точек можно связать набор из n ∙ ( n − 1 ) 2 целых чисел. Поскольку согласно [Александров, 1948] множество всех рациональных точек n-мерного пространства счётно, можно утверждать, что число различных рациональных множеств из n точек либо конечно, либо счётно. Следовательно, эти множества перечислимы.

Итак, мы показали, что число рациональных множеств из n точек при любом n не более чем счётно. А поскольку объединение счётного множества счётных множеств является счётным множеством, то множество рациональных множеств с конечным множеством точек является счётным. Конечным оно быть не может, поскольку целых треугольников бесконечно много.

Перечисление элементов этого множества и различных его подмножеств может производиться многими способами. Для проведения вычислительных экспериментов, связанных с поиском и построением рациональных множеств, наиболее перспективным является генетический подход. Его суть в том, чтобы отправившись от целого треугольника постепенно переходить к рациональным множествам с большим числом точек.

Такой переход напоминает построение симплициального комплекса [Прасолов, 2004], хотя имеются и некоторые отличия. Напомним, что симплициальный комплекс — топологическое пространство, представленное как объединение множеств, гомеоморфных симплексу и образующих триангуляцию этого пространства. В нашем случае речь идёт о триангуляции части плоскости.

Если рассмотреть процедуру построения рациональных множеств с увеличивающимся числом точек без углубления в детали, то будет получена следующая схема (рисунок 17).

 

Рисунок 18

К стороне исходного целого треугольника прикладываем один за другим новые целые треугольники и проверяем то расстояние, которое может оказаться иррациональным. Затем к стороне или диагонали целого четырёхугольника прикладываем очередные треугольники и делаем соответствующие проверки. Процедура может продолжаться сколь угодно долго.

На практике при реализации этой схемы, конечно, возникнет много проблем. Основной исследовательской ситуацией можно считать следующую. Уже построено рациональное множество из n точек. Выбрав из их числа две точки А и В, к ним следует прилагать различные рациональные треугольники АВС. Далее производится определение расстояний до остальных точек исходного множества и оценка их рациональности. На самом деле это достаточно сложная проблема.

При одном из подходов нужно расположить исходное рациональное множество из n точек на декартовой плоскости и работать с ним. Далее необходимо использовать метод прикладывания к отрезку треугольника, описанный в задании 17. И как было показано выше, могут возникнуть проблемы с определением факта рациональности расстояний.

При втором подходе описание рациональное множество из n точек должно иметь следующий вид. Вершины занумерованы и для каждой пары вершин указано расстояние между ними.

Хотя в целом картина исследования остаётся одной и той же, но любое изменение предполагает получение новых результатов. Таким образом, открывается возможность организации независимых самостоятельных исследований для нескольких студентов. При этом возможно получение нового результата, что повышает значимость исследования и интерес к нему.

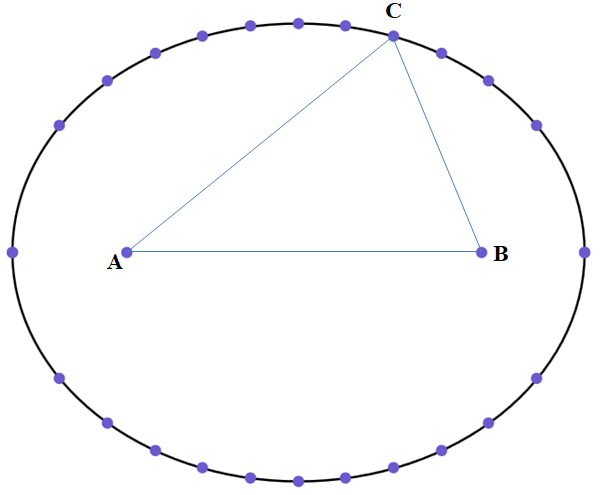
Процедура добавления новой точки требует того или иного способа перечисления целых треугольников. Естественно, что таких способов очень много. рассмотрим один из них. Этот способ перечисления является многоуровневым. На каждом уровне рассматриваются целые треугольники АВС с заданным периметром. Если длину одной из сторон, например, АВ, фиксировать, то вершины соответствующих треугольников лежат на эллипсе с фокусами в точках А и В. В целом треугольники упорядочиваются по возрастанию периметра, а также по длине стороны АВ.

Задание 19. Написать программу, которая строит вершины С целых треугольников АВС с заданным периметром и фиксированной длиной стороны АВ.

Решение. Очевидно, что соответствующие точки лежат на эллипсе. В программе используются формулы, выведенные в задании 17 и зафиксированные на рисунке 14. Результат работы программы показан на рисунке 18.

 

GraphicsWindow.Width = 700

GraphicsWindow.Height = 700

x0 = 350

y0 = 350

ed = 25

'Полусумма двух негоризонтальных сторон – большая полуось эллипса

a = 10

'Половина длины горизонтальной стороны

'Расстояние от фокуса до центра эллипса

c = 6

Малая полуось эллипса

b = Math.SquareRoot(a*a - c*c)

xc1 = x0 - ed*c

xc2 = x0 + ed*c

yc = y0

GraphicsWindow.FillEllipse(xc1 - 5, y0 - 5, 10,10)

GraphicsWindow.FillEllipse(xc2 + 5, y0 - 5, 10,10)

GraphicsWindow.DrawEllipse(x0 - a*ed, y0 - b*ed, 2*a*ed,2*b*ed)

p = 2*c

'При zn = 1 вершины на верхней дуге эллипса

zn = 1

For q = a - c To a + c

ver()

EndFor

'При zn = –1 вершины на нижней дуге эллипса

zn = -1

For q = a - c To a + c

ver()

EndFor

'Вычисление координат вершины, лежащей на эллипсе

Sub ver

r = 2*a - q

s = (p*p + q*q - r*r)/(2*p)

t = Math.SquareRoot(q*q - s*s)

xe = x0 - c*ed + s*ed

ye = y0 - zn*t*ed

GraphicsWindow.FillEllipse(xe - 5, ye - 5, 10,10)

EndSub

 

 

Рисунок 19

Подобная визуализация наводит на следующую мысль. Множество вершин, лежащих на эллипсе, может содержать пары точек, удалённых на расстояние, выражаемое целым числом. Естественно желание найти такие пары.

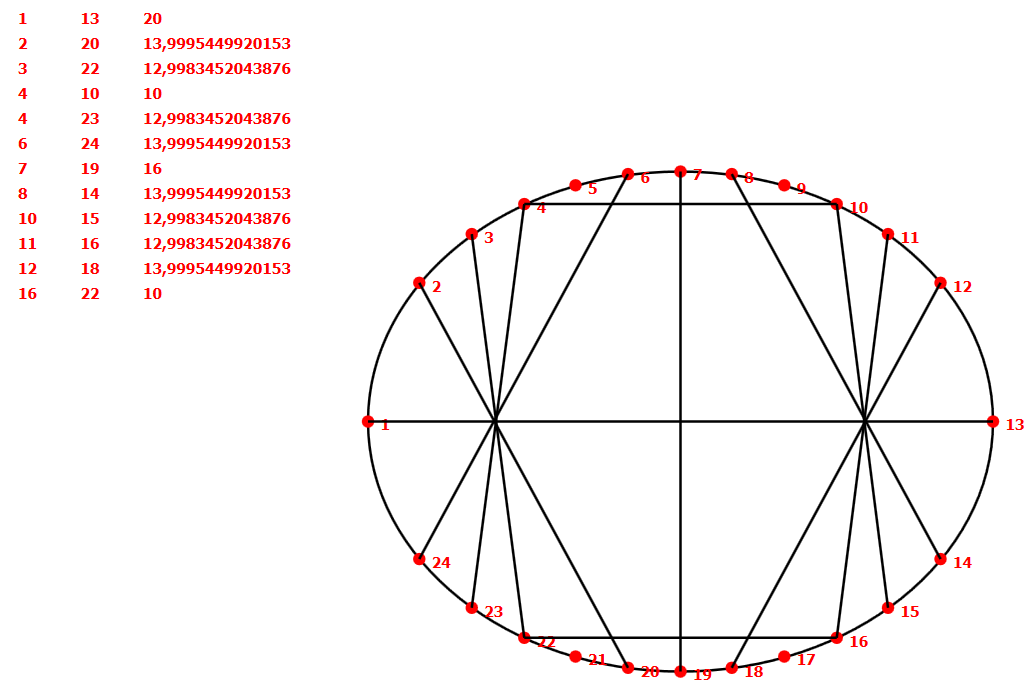
Задание 20. Точки на эллипсе получены с помощью программы из задания 19. Написать программу, которая предположительно проверяет, является ли целым расстояние между двумя различными точками на эллипсе (рисунок 19).

 

 

Рисунок 20

Решение. Вопрос состоит в заведомом определении того, что вершины С и D удалены друг от друга на расстояние, которое не является целым. Перебирая пары точек на эллипсе, будем находить расстояния между ними и отбрасывать те, которые заведомо не могут быть целыми.

 

GraphicsWindow.Width = 900

GraphicsWindow.Height = 700

i = 1

m = 0

a = 10

c = 6

b = Math.SquareRoot(a*a - c*c)

p = 2*c

zn = 1

For q = a - c To a + c

ver()

EndFor

zn = -1

For q = a + c - 1 To a - c + 1 Step -1

ver()

EndFor

x0 = 550

y0 = 350

ed = 25

GraphicsWindow.DrawEllipse(x0 - a*ed, y0 - b*ed, 2*a*ed, 2*b*ed)

GraphicsWindow.BrushColor = "red"

For i=1 To m

xe = x0 + x[i]*ed

ye = y0 - y[i]*ed

GraphicsWindow.FillEllipse(xe - 5,ye - 5, 10,10)

GraphicsWindow.DrawText(xe+10, ye - 5, i)

EndFor

n = 1

For i = 1 To m - 1

For j = i + 1 To m

kw1 = (x[j] - x[i])*(x[j] - x[i])

kw2 = (y[j] - y[i])*(y[j] - y[i])

l = Math.SquareRoot(kw1 + kw2)

lo = Math.Round(l)

If Math.Abs(l - lo) < .01 Then

GraphicsWindow.DrawText(20, n*20, i)

GraphicsWindow.DrawText(70, n*20, j)

GraphicsWindow.DrawText(120, n*20, l)

GraphicsWindow.DrawLine(x0 + x[i]*ed, y0 - y[i]*ed,x0 + x[j]*ed, y0 - y[j]*ed)

n = n + 1

EndIf

EndFor

EndFor

Sub ver

r = 2*a - q

s = (p*p + q*q - r*r)/(2*p)

t = Math.SquareRoot(q*q - s*s)

x[i] = -c + s

y[i] = zn*t

i = i + 1

m = m + 1

EndSub

 

На рисунке 20 показан вариант с большим количеством точек на эллипсе (для случая a = 20 и c = 12.

 

 

Рисунок 21

 

Проверка того, являются ли выбранные расстояния целыми, а не близкими к целым, должна производиться специальными ручными вычислениями. Мы поговорим о них немного позже. Что касается конкретного эллипса с рисунка 19, то здесь практически решается следующий вопрос: существуют ли фокальные хорды эллипса, имеющие целую длину.

Сейчас же отметим, что процедура расширения рационального множества {Ai} с n элементами ещё на один элемент An+1 требует аналогичных вычислений. В простейшем случае речь идёт о переходе от целого треугольника к целому четырёхугольнику. Это делается с помощью прикладывания к исходному целому треугольнику АВС целого треугольника DВС и проверкой длины AD (рисунок 21). Добавляется при этом точка D.

 

Рисунок 22

В общем же случае элемент An+1 должен проверяться для всех таких конфигураций (четырёхугольников), образованных всевозможными тройками точек исходного множества и точкой An+1. Очевидно, что работа очень большая, а достижение благоприятного результата маловероятно. Таким образом, поиск достаточно представительных целых множеств точек весьма трудоёмок.

Отметим только, что выбор исходной точки An+1 можно связать с эллипсом, фокусами которого являются две точки исходного множества.

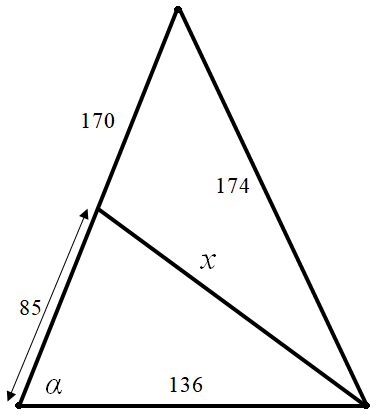
Так или иначе, нами описан путь поиска целых множеств с растущим числом элементов. Остаётся подробно описать те ручные вычисления, которые позволяют определить, является ли расстояние AD целым (рисунок 21). Использоваться будут формулы, зафиксированные на рисунке 14.

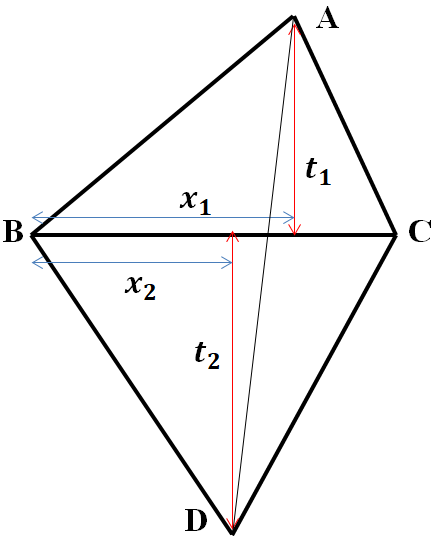
Отметим, что при различных вариантах взаимного расположения треугольников АВС и DВС вычисления приобретают свою специфику. Мы рассмотрим только один конкретный вариант вычислений (рисунок 22), поскольку другие отличаются только тем, что суммы длин заменяются на разности и наоборот.

 

 

Рисунок 23

Пусть ВС = a, AB = c, AC = b, BD = p и CD = q. Тогда x 1 = b 2 − c 2 + a 2 2 a и t 1 = b 2 − x 1 2 , кроме того, x 2 = p 2 − q 2 + a 2 2 a и t 2 = p 2 − x 2 2 . Теперь можно вычислить квадрат отрезка AD:
AD 2 = =
+ 2 b 2 − x 1 2 ∙ p 2 − x 2 2 .

Чтобы расстояние AD выражалось рациональным числом, необходимо, чтобы число AD 2 было рациональным. Для этого рациональным должно быть слагаемое 2 b 2 − x 1 2 ∙ p 2 − x 2 2 . Именно с проверки этого обстоятельства и следует начать проверку рациональности расстояния AD. Если AD 2 рационально, то этого мало. Это число должно быть квадратом. Так или иначе, но проверка соответствующих обстоятельств может быть произведена без особых усилий.

Кроме того, исходя из выше сказанного, поиск рациональных четырёхугольников следует вести для случаев, когда t1 и t2 рациональны. Это условие выполняется, когда искомый четырёхугольник составлен из четырёх пифагоровых треугольников. Но, конечно, для успешного поиска необходимо разработать алгоритм перебора пифагоровых треугольников.

ПОСТРОЕНИЕ БЕСКОНЕЧНОГО РАЦИОНАЛЬНОГО МНОЖЕСТВА

В задании 13 (рисунок 9) построено бесконечное рациональное множество точек, основная часть которых лежит на одной прямой. Далее будет построено бесконечное рациональное множество, точки которого уже не расположены на одной прямой.

Начнём с того, что укажем геометрические преобразования плоскости, которое переводят рациональные множества в рациональные. Речь идёт об инверсии [Бакельман, 1966]. Напомним некоторые факты, связанные с инверсией.

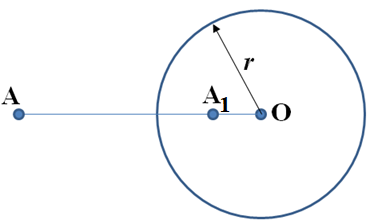
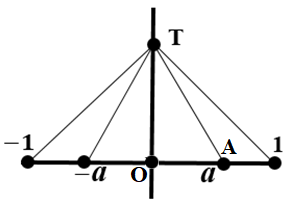
Инверсией плоскости относительно окружности ω, с центром в точке О (центр инверсии) и радиусом r называется отображение, которое точке А ставит в соответствие точку А1, лежащую на луче ОА (рисунок 23). При этом выполняется условие ОА∙А1 = r2.

 

Рисунок 24

 

Для нас особенно важен тот факт, что инверсия переводит прямую, не проходящую через точку О, в окружность, проходящую через точку О.

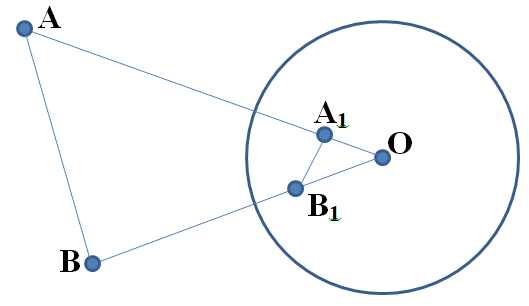
Покажем, что инверсия относительно окружности рационального радиуса r действительно переводит точки, которые отстоят друг от друга на рациональные расстояния, в точки, которые также отстоят друг от друга на рациональные расстояния. Пусть треугольник АВО является рациональным. Инверсия переводит точку А в точку А1, а точку В в точку В1. Рассмотрим треугольник А1В1О (рисунок 24).

 

Рисунок 25

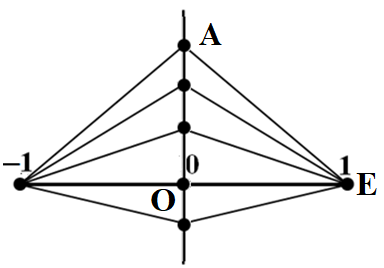
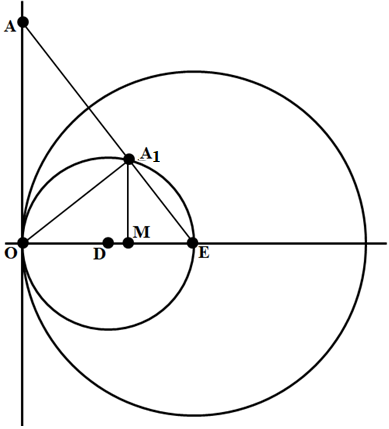
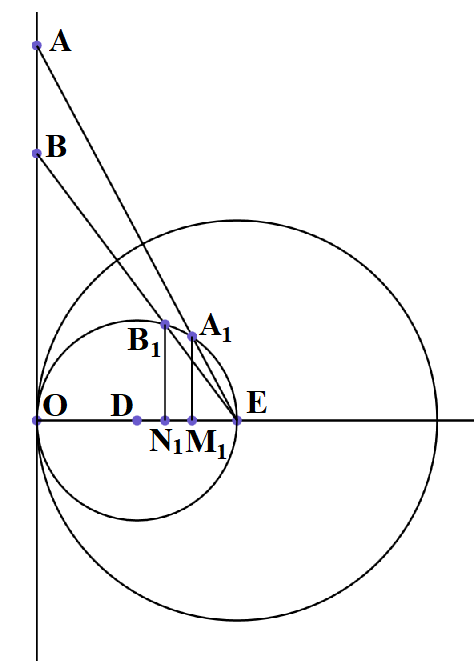
Поскольку АО∙А1О = r2 и ВО∙В1О = r2, то отрезки А1О и В1О имеют рациональную длину. Кроме того, AO BO = B 1 O A 1 O , то есть треугольники АОВ и В1ОА1 подобны. Из этого следует, что отрезок А1В1 имеет рациональную длину. Более того, можно без труда вывести формулу для вычисления расстояния А1В1.
Из подобия треугольников АВО и В1А1О следует, что A 1 B 1 AB = B 1 O AO . Следовательно, A 1 B 1 = AB ∙ B 1 O AO .

Задание 21. Подвергнуть множество точек из задания 13 (рисунок 9) инверсии относительно окружности единичного радиуса с центром в точке Е. Найти координаты точек, полученных в результате преобразования.

Решение. Точки с рациональными координатами, лежащими на прямой АО, после инверсии перейдут в точки, лежащие на окружности радиуса 1 2 с центром в точке D (рисунок 25). Пусть точка А переходит в точку А1.
 

Рисунок 26

Рассмотрим пифагоров треугольник АОЕ. Он имеет стороны следующей длины: OE = 1 , AO = t 2 − 1 2 t , AE = t 2 + 1 2 t . Поскольку точка А1 является инверсным образом точки А, получаем, что A 1 E = 1 AE = 2 t t 2 + 1 . Если рассмотреть систему координат с началом точке Е и с осью абсцисс, направленной влево, то координаты точки А1 равны длинам отрезков ЕМ (абсцисса) и А1М (ордината). Найдём соответствующие величины.
Из подобия треугольников ЕМА1 и ЕОА следует, что ME OE = A 1 E AE и A 1 M OA = A 1 E AE . Значит, x = EM = A 1 E AE = 4 t 2 и y = A 1 M = AO ∙ A 1 E AE = t 2 − 1 2 t ∙ 4 t 2 . Итак, окончательно x = 4 t 2 и y = 2 t ∙ ( t 2 − 1 ) .
Задание 22. Найти расстояние между двумя образами А1 и В1, подвергнутых инверсии точек А и В, положение которых определяется параметрами t 1 и t 2 (рисунок 26).
 

Рисунок 27

Решение. Пусть точки А и В удалены от точки О соответственно на расстояния AO = t 1 2 − 1 2 t 1 и BO = t 2 2 − 1 2 t 2 . Расстояние между ними равно AB = t 2 2 − 1 2 t 2 − t 1 2 − 1 2 t 1 = ( t 2 − t 1 ) ∙ ( t 1 ∙ t 2 + 1 ) 2 ∙ t 1 ∙ t 2 .
Расстояние же между точками А1 и В1 по ранее доказанному в несколько иных обозначениях, соответствующих рисунку 25, равно A 1 B 1 = AB ∙ B 1 E AE , или A 1 B 1 = ( t 2 − t 1 ) ∙ ( t 1 ∙ t 2 + 1 ) 2 ∙ t 1 ∙ t 2 ∙ 2 t 2 t 2 2 + 1 t 1 2 + 1 2 t 1 = 2 ( t 2 − t 1 ) ∙ ( t 1 ∙ t 2 + 1 ) ( t 1 2 + 1 ) ∙ ( t 2 2 + 1 ) .

Визуализация рисунка 26 может быть выполнена следующей программой.

GraphicsWindow.Width = 620

GraphicsWindow.Height = 820

x0 = 110

y0 = 410

ed = 200

GraphicsWindow.FillEllipse(x0 - 5,y0 - 5, 10,10)

GraphicsWindow.DrawLine(x0, 0, x0, 800)

GraphicsWindow.DrawLine(x0, y0, 610, y0)

xe = x0+ed

GraphicsWindow.FillEllipse(xe-5,y0-5,10,10)

GraphicsWindow.DrawEllipse(xe - ed,y0-ed,2*ed,2*ed)

xd = x0+ed/2

GraphicsWindow.FillEllipse(xd-5,y0-5,10,10)

GraphicsWindow.DrawEllipse(x0,y0-ed/2,ed,ed)

t1 = 4

oa = (t1*t1 - 1)/(2*t1)

ae = 1/oa

ya = y0 - ed*oa

GraphicsWindow.FillEllipse(x0-5,ya-5,10,10)

GraphicsWindow.DrawLine(x0,ya, xe,y0)

t2 = 3

ob = (t2*t2 - 1)/(2*t2)

yb = y0 - ed*ob

GraphicsWindow.FillEllipse(x0-5,yb-5,10,10)

GraphicsWindow.DrawLine(x0,yb, xe,y0)

dxa1 = 4*t1*t1/((t1*t1 + 1)*(t1*t1 + 1))

xm1 = xe - dxa1*ed

GraphicsWindow.FillEllipse(xm1-5,y0-5,10,10)

dya1 = 2*t1*(t1*t1 - 1)/((t1*t1 + 1)*(t1*t1 + 1))

xa1 = xe - dxa1*ed

ya1 = y0 - dya1*ed

GraphicsWindow.FillEllipse(xa1-5,ya1-5,10,10)

GraphicsWindow.DrawLine(xm1,y0,xa1,ya1)

dxa2 = 4*t2*t2/((t2*t2 + 1)*(t2*t2 + 1))

xm2 = xe - dxa2*ed

GraphicsWindow.FillEllipse(xm2-5,y0-5,10,10)

dya2 = 2*t2*(t2*t2 - 1)/((t2*t2 + 1)*(t2*t2 + 1))

xa2 = xe - dxa2*ed

ya2 = y0 - dya2*ed

GraphicsWindow.FillEllipse(xa2-5,ya2-5,10,10)

GraphicsWindow.DrawLine(xm2,y0,xa2,ya2)

В итоге нами построено бесконечное рациональное множество точек, основная часть которых лежит на одной окружности. В задании 14 показано, что исходное множество точек на прямой всюду плотно. Из этого следует, что и рациональное множество точек на окружности также всюду плотно. Из этого в частности следует, что любой вписанный в окружность многоугольник можно сколь угодно малым сдвигом вершин в рациональный.

Задание 23. Получить тождество, которое основано на полученных выше формулах, связанных с инверсией, и доказать его с помощью алгебраических преобразований.

Решение. Отметим, что в ряде случаев ранее известные тождества позволяют доказывать новые теоремы. В качестве примера можно привести теорему Лагранжа о том, что каждое натуральное число можно представить как сумму не более четырёх квадратов натуральных чисел. Для её доказательства используется замысловатое тождество Эйлера, согласно которому произведение двух сумм четырёх квадратов также является суммой четырёх квадратов [Михелович, 1962].

Таким образом, искомое тождество в принципе может оказаться полезным. Кроме того, доказательство этого тождества позволяет чисто алгебраически получить формулы для инвертирования точек.

Тождество строится на основе двух различных выражений длины отрезка А1В1 (рисунок 25). При этом используется пять величин: координаты (х1; у1) точки А1, координаты (х2; у2) точки А2 и длина отрезка А1В1. Тождество имеет вид

или

Конкретные значения этих пяти величин таковы.

 

x 1 = 4 t 1 2
y 1 = 2 t 1 ( t 1 2 − 1 )
x 2 = 4 t 2 2
y 2 = 2 t 2 ( t 2 2 − 1 )
A 1 B 1 = 2 ( t 2 − t 1 ) ∙ ( t 1 ∙ t 2 + 1 ) ( t 1 2 + 1 ) ∙ ( t 2 2 + 1 )
Преобразуем разность: x 2 − x 1 = 4 t 2 2 . Тождество примет вид
.

Разделим обе части уравнения на 4 и получим уравнение

 

.

Его можно считать соответствующим тождеством. Его доказательство может быть проведено с помощью достаточно кропотливых преобразований.

Мы же получим из этого уравнения довольно интересное задание. Для этого сначала избавимся от дробей, умножив обе части уравнения на . Тогда в правой части будет стоять выражение
.

В левой части уравнения стоит квадрат, значит, квадратом должна быть и правая часть. На основе этого можно сформулировать задание.

Задание 24. Доказать, что выражение

 

является квадратом.

Решение. Соответствующее выражение является разностью квадратов. По этой причине оно разлагается на два множителя

 

( t 1 2 + 1 ) ∙ ( t 2 2 + 1 ) − 2 ∙ ( t 1 + t 2 ) ∙ ( 1 − t 1 ∙ t 2 ) и
( t 1 2 + 1 ) ∙ ( t 2 2 + 1 ) + 2 ∙ ( t 1 + t 2 ) ∙ ( 1 − t 1 ∙ t 2 ) .
Докажем, что каждый из сомножителей также является квадратом. Произведение 2 ∙ ( t 1 + t 2 ) ∙ ( 1 − t 1 ∙ t 2 ) наводит на мысль о квадрате суммы (или разности) многочленов ( t 1 + t 2 ) и ( 1 − t 1 ∙ t 2 ) . Если это верно. То должно выполняться равенство ( t 1 2 + 1 ) ∙ ( t 2 2 + 1 ) = . Его доказательство не представляет труда.

Как уже отмечалось, построенное рациональное множество точек на окружности является всюду плотным.

Задание 25. Продемонстрировать это обстоятельство с помощью программы.

Решение. Соответствующая программа заполняет небольшими кружочками большую окружность на экране.

 

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 550

y0 = 300

r = 250

For t = -100 To 100 Step .001

x = 4*t*t/((t*t + 1)*(t*t + 1))

y = 2*t*(t*t - 1)/((t*t + 1)*(t*t + 1))

xe = x0 - 2*r*x

ye = y0 - 2*r*y

GraphicsWindow.FillEllipse(xe- 2, ye- 2, 4,4)

EndFor

Отметим, что величина x = 4 t 2 , характеризующая положение инвертированной точки на окружности, не является абсциссой, хотя она задаёт некоторое горизонтальное расстояние (рисунок 25). В связи с этим выведем формулы, которые будут определять положение аналогов инвертированных точек на единичной окружности. Легко понять, что абсцисса будет равна удвоенному расстоянию DM с рисунка 25. Ордината точки на единичной окружности соответствует удвоенной величине y = 2 t ∙ ( t 2 − 1 ) .
Итак, положение точки на единичной окружности определяется координатами x = 1 − 8 t 2 и y = 4 t ∙ ( t 2 − 1 ) .

Задание 27. Доказать алгебраически, что определяемая этими координатами точка удалена от начала координат на единичное расстояние.

Решение. Нужно доказать тождество

 

+ ( 4 t ∙ ( t 2 − 1 ) .

Избавимся от дробей в равенстве и получим

 

+ 16 ∙ t 2 ∙ .

Доказательство этого тождества не представляет труда.

Задание 29. Найти бесконечное множество решений в целых числах диофантова уравнения x 2 + y 2 = z 4 .

Решение. Тождество из предыдущего задания

 

+ 16 ∙ t 2 ∙
позволяет получить набор соответствующих решений. Например при t = 9 , получаем решение, для которого x = 6076 , y = 2880 , z = 82 .

Задание 30. Указать способ выбора инвертированной точки, сколь угодно близкой к некоторой фиксированной точки на единичной окружности.

Решение. Положение точки на единичной окружности определяется углом наклона α радиуса вектора, направленного из начала координат в эту точку. Сама точка имеет координаты . Инвертированная точка на единичной окружности определяется координатами x = 1 − 8 t 2 и y = 4 t ∙ ( t 2 − 1 ) .

Таким образом, для того, чтобы фиксированная и инвертированная точки совпадали следует решить уравнение

1 − 8 t 2 .

Для нахождения инвертированной точки, близкой к фиксированной, это уравнение нужно решить приближённо. Преобразуем уравнение,

 

( 1 − cos α ) ∙
Обозначив 1 − cos α через c, а ( t 2 + 1 ) через z , получаем квадратное уравнение
c ∙ z 2 − 8 z + 8 = 0

Его решения выражаются по формуле

 

z 1 ,2 = 8 ± 64 − 32 ∙ c 2 ∙ c = 4 ± 2 ∙ 4 − 2 ∙ c c .
Величина c меняется в пределах от нуля до двух. Следующая программа показывает, что функция z 4 + 2 ∙ 4 − 2 ∙ c c на соответствующем интервале имеет значение больше двух (рисунок 27).

GraphicsWindow.Width = 450

GraphicsWindow.Height = 610

x0 = 100

y0 = 600

GraphicsWindow.FillEllipse(x0 - 5, y0 - 5, 10,10)

ed1 = 100 'Декартова плоскость сжата для наглядности

ed2 = 25

For t=-1 To 5 Step .01

For u=-1 To 30 Step 1

x=x0 + ed1*t

y=y0 - ed2*u

GraphicsWindow.SetPixel(x,y,"green")

EndFor

EndFor

For t=-1 To 5 Step 1

For u=-1 To 30 Step .01

x=x0 + ed1*t'

y=y0 - ed2*u

GraphicsWindow.SetPixel(x,y,"green")

EndFor

EndFor

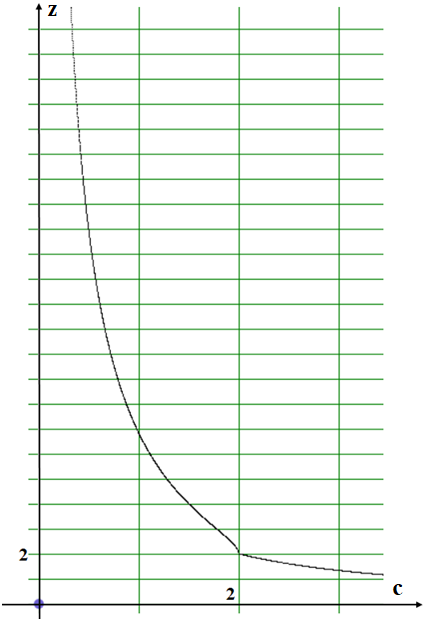
For c = .1 To 5 Step .001

z = (4 + Math.SquareRoot(4 - 2*c))/c

xe = x0 + ed1*c

ye = y0 - ed2*z

GraphicsWindow.SetPixel(xe,ye,"black")

EndFor

 

Таким образом, t 2 из уравнения z = ( t 2 + 1 ) при любом фиксированном z является неотрицательным числом. Следовательно, t имеет два действительных значения. Положительное значение определяет точку на верхней полуокружности, а отрицательное – на нижней. Итак, имеет место формула
t = ± z − 1 .

В принципе значение t может быть иррациональным. Приближённое значение корня квадратного как раз и позволяет найти нужную точку.

 

 

Рисунок 28

Задание 31. Строго доказать, что z ( c ) > 2 на интервале [0; Куланин, 2020].

Задание 32. Построить рациональный треугольник, близкий к равнобедренному прямоугольному треугольнику.

Решение. Рассмотрим равнобедренный прямоугольный треугольник с вершинами A ( − 1 ; 0 , C ( 1 ; 0 ) и B ( 0 ; 1 ) . Вершина прямого угла находится в последней из точек B. Тогда в соответствии с результатами задания 30, полагаем, что α = π 2 . Следовательно, с = 1, а t = 3 + 2 ∙ 2 = 2,4142135623731 … Далее нужно округлить t и вычислить координаты инвертированной точке, которая заменит вершину B ( 0 ; 1 ) точкой с координатами ( x ; y ) .
Начнём с грубого округления t = 2 , которое облегчит вычисления. По формулам x = 1 − 8 t 2 и y = 4 t ∙ ( t 2 − 1 ) получаем, что x = − 7 25 и y = 24 25 . Перейдём к подобному треугольнику с целыми сторонами и вычислим длину сторон треугольника, подобного треугольнику АВС. В итоге получаем, что АВ = 30, ВС = 40 и АС = 50. Таким образом, получен египетский треугольник.
Сделаем более точное округление: t = 2 ,5 = 5 2 . Прежде чем проводить вычисления, займёмся преобразованием формул без лишних подробностей. Пусть t = p q , тогда x = 1 − 8 t 2 и y = 4 t ∙ ( t 2 − 1 ) . Вершины целочисленного треугольника АВС в этом случае имеют следующие координаты:
А ( − ; 0), С ( ; 0), В (х ∙ ; у ∙ ).
Проведём вычисления для случая p = 5 и q = 2 . Вершины имеют следующие координаты: А ( − 841 ; 0 , С ( 841 ; 0 ) , В (41; 840). Длины сторон таковы: АС = 1682, АВ = 1218 и ВС = 1160.
Наконец, проведём ещё одно округление: t = 2 ,4 = 12 5 . Вершины будут иметь следующие координаты: А ( − 28561 ; 0 , С ( 28561 ; 0 ) , В ( − 239; 28560). Вычисление длины сторон АС и ВС, однако, может вызвать затруднения. Координаты стали выражаться слишком большими числами. Использование калькулятора и Small Basic приводит к потере точности. Но Excel и в данном случае позволяет получить нужные результаты: АС = 57122, АВ = 40222 и ВС = 40560 .
Дальнейшее уточнение величины t приведёт к ещё большему росту координат. Тем не менее, можно считать, что последнее приближение даёт хороший результат – треугольник близок к равнобедренному.

Как известно, чёрный квадрат Казимира Малевича не является квадратом. Наши вычисления позволяют получить целое приближение чёрного квадрата (рисунок 7) и, тем самым, соединить математику и искусство.

Когда мы говорили о конечных рациональных множествах. Речь шла о возможном увеличении числа точек, хотя бы на одну. Что касается бесконечных рациональных множеств, то попытка добавления новой точки может привести к тому, что новое множество останется бесконечным, но из него при этом может выпасть бесконечное подмножество точек. Приведём пример.

Рассмотрим бесконечное рациональное множество точек, основная часть которых лежит на одной прямой из задания 13 (рисунок 9). Кроме того, в него входят две точки, на этой прямой не лежащие. Попытаемся найти ещё две дополнительные точки на горизонтали (рисунок 28).

 

 

Рисунок 29

Пусть одна из новых точек имеет координаты (а; 0). Точка Т, как мы знаем имеет координаты (0; t 2 − 1 2 t . Мы хотим, чтобы треугольник ТОА при этом являлся пифагоровым для бесконечного множества точек Т, задаваемых параметром t. Таким образом, ( t 2 − 1 2 t 2 + a 2 = z 2 или ( t 2 − 1 2 + 4 ∙ t 2 a 2 = 4 ∙ t 2 z 2 . В итоге получим диофантово уравнение t 4 + 2 ∙ ( 1 − 2 ∙ a 2 ) t 2 + 1 = 4 ∙ t 2 z 2 . Нужно найти число a , при котором уравнение имеет бесконечное количество рациональных решений, или доказать, что такого числа не существует.
Немного упростим уравнение, чтобы предварительно решить более обозримое диофантово уравнение. Положим, что t = p q , 1 − 2 ∙ a 2 = c и 2 pq z = u , тогда, избавившись от дробей, мы получаем своеобразное биквадратное диофантово уравнение, которое следует решать в целых числах
p 4 + 2 c p 2 q 2 + q 4 = u 2
Отметим, что задача упростилась не слишком, поскольку нужно искать ещё и число c .

Наконец, кратко, поскольку размеры статьи не позволяют подробно обсуждать столь сложную тематику, коснёмся вопроса о преобразованиях рациональных множеств.

РАЦИОНАЛЬНЫЕ МНОЖЕСТВА И ПРЕОБРАЗОВАНИЯ

Преобразования рациональных множеств как минимум могут быть двух видов. Примером преобразования первого типа является описанное выше преобразование Виета, которое один пифагоров треугольник переводит в другой. При этом преобразование имеет следующий характер. Исходный треугольник задан, а его образ строится по некоторому алгоритму на основе вершин исходного треугольника.

Обобщая, можно определить преобразования первого типа следующим образом: рациональное множество из n точек конструктивно преобразуется в рациональное же множество из n точек с иными расстояниями между точками.

Примером преобразования второго типа является инверсия. Это преобразование, которое затрагивает не только рациональное множество, но и все точки плоскости.

Возникает вопрос: существуют ли другие преобразования первого и второго типа, сохраняющие рациональные расстояния.

При этом, конечно, преобразования второго должны существенно и непропорционально расстояния между точками рационального множества. Движения и подобия плоскости этому условию не удовлетворяют.

Возможен случай, что кроме инверсии других преобразований второго рода не существует. Тогда это нужно доказать.

Ещё один круг вопросов, связанных со структурой рациональных множеств, направлен на изучение симметрий рациональных множеств, которые, естественно, эти множества не меняют. Таким образом, речь идёт о группах преобразований рациональных множеств.

Сформулируем две конкретных задачи.

Задача 1. Имеет ли бесконечное рациональное множество точек, основная часть которых лежит на одной прямой из задания 13 (рисунок 9) подмножества, которые являются арифметическими прогрессиями значительной длины или даже бесконечными. Речь и идёт о возможности сдвигов.

Задача 2. Изучить симметрии рационального множества точек на окружности. В частности, речь идёт и о возможности поворотов.

Отметим, что симметрия относительно оси абсцисс уже отмечалась.

Более подробное обсуждение этих вопросов требует новой статьи.

ЗАКЛЮЧЕНИЕ

При защите дипломных работ, как у бакалавров, так и у магистров, комиссия, оценивая работу, в первую очередь смотрит на уровень освоения идей и методов высшей математики, а также новизну полученных результатов. Научный руководитель в свою очередь должен кроме этих требований должен учитывать посильность выбранной темы для бакалавра или магистра. Оценим с этих позиций темы выпускных работ, связанные с тематикой данной статьи.

  • Решение вопросов, связанных с решением диофантовых уравнений и работой с целыми и рациональными числами с помощью компьютерных программ, требует высокого уровня подготовки студента.

  • Новизна результатов практически обеспечена, даже в случае, когда результаты отрицательные. Поясним это утверждение примером из области теории чисел. Долгое время компьютерная проверка великой теоремы Ферма состояла в том, что устанавливалось отсутствие решений меньших некоторой границы.

  • Посильность задач, выбранных руководителем, должна продумываться очень внимательно. Слишком много здесь может возникнуть затруднений.

Укажем две темы, которые можно считать приемлемыми по всем параметрам. В книге [Серпинский, 1959] есть параграф, который называется «Пифагоровы треугольники со сторонами, меньшими 100». Темой достаточно простой работы может стать поиск и перечисление пифагоровых треугольников, некоторые стороны которых больше 100.

Более сложной темой является поиск рациональных четырёхугольников, не вписанных в окружность.

Но в целом круг задач по соответствующей тематике необозрим. По этой причине авторы надеются, что обсуждение вопросов, связанных с рациональными множествами, может оказаться полезным для преподавателей математики.

Литература

  1. Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
  2. Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
  3. Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. № 4. С.127-144.
  4. Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. № 4.  С.145-156.
  5. Куланин Е.Д.,Степанов М. Е., Нуркаева И.М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. 2020. Т.10. №2 С.110 - 128.
  6. Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ данных. 2020. Т.11. №1. С.40 - 60.
  7. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
  8. Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. №1. С.54-94.
  9. Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения Моделирование и анализ данных. 2022. Т.12. №3.  С.58 – 70.
  10. Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. Моделирование и анализ данных. 2022. Т.12. №4.

С.67 – 84.

  1. Куланин Е.Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. Моделирование и анализ данных. 2022. Т.12. №4. С.94 - 104.
  2. Куланин Е.Д., Степанов М. Е., Панфилов А.Д., Потонышев И.С. Системный подход к методике тифлопедагогики на примере задач математического анализа. 2022. Т.12. №2. С.34 - 82.
  3. Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики на примере теории чисел. Моделирование и анализ данных. 2024. Т.14. №1. С.170 - 195.
  4. Куланин Е.Д., Степанов М. Е. Использование образов в преподавании высшей математики. Моделирование и анализ данных. Т.14. №2. C.192-225.
  5. Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения. Моделирование и анализ данных. Т.14. №3. C.174-202.
  6. Серпинский В. Пифагоровы треугольники. М., Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959.
  7. Зюзьков В. М. Эксперименты в теории чисел. Томск Издательство НТЛ, 2019.
  8. Оре О. Теория графов. М., Наука, 1980.
  9. Александров П. С. Введение в общую теорию множеств и функций. М. – Л. Гос. изд. технико-теоретической литературы. 1948.
  10. Прасолов В. В. Элементы комбинаторной и дифференциальной топологии. М., МЦНМО, 2004.
  11. Бакельман Н. Я. Инверсия. М., Наука, 1966.
  12. Михелович Ш. Х. Теория чисел. М., Высшая школа, 1962.

Информация об авторах

Куланин Евгений Дмитриевич, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Степанов Михаил Евграфович, кандидат педагогических наук, доцент кафедры прикладной математики факультета информационных технологий, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Метрики

 Просмотров web

За все время: 20
В прошлом месяце: 0
В текущем месяце: 20

 Скачиваний PDF

За все время: 4
В прошлом месяце: 0
В текущем месяце: 4

 Всего

За все время: 24
В прошлом месяце: 0
В текущем месяце: 24

!
Портрет читателя
Пройти опрос