Моделирование и анализ данных
2022. Том 12. № 2. С. 34–82
doi:10.17759/mda.2022120203
ISSN: 2219-3758 / 2311-9454 (online)
Системный подход к методике тифлопедагогики на примере задач математического анализа
Аннотация
Общая информация
Ключевые слова: высшее образование, система знаний, тифлопедагогика, Евклидова геометрия, уровень развития
Рубрика издания: Методика преподавания
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2022120203
Получена: 18.04.2022
Принята в печать:
Для цитаты: Куланин Е.Д., Степанов М.Е., Панфилов А.Д., Потонышев И.С. Системный подход к методике тифлопедагогики на примере задач математического анализа // Моделирование и анализ данных. 2022. Том 12. № 2. С. 34–82. DOI: 10.17759/mda.2022120203
Полный текст
Авторы исходят из следующей точки зрения. Глубокое освоение математических знаний предполагает овладение целым рядом понятий и навыков. Прежде всего, необходимо понимать соответствующий материал, а, по мнению авторов статьи, понимание основывается на образном мышлении [Куланин, 2020]. В то же время, как правило, освоение математических знаний связано с получением вычислительных навыков в широком смысле. Наконец, студент должен уметь свободно выражать свои мысли вне зависимости от того, основываются ли они на образах или на алгоритмических и вычислительных навыках. На самом деле, конечно, процесс обучения значительно более сложен, однако, общая идея, из которой авторы исходят, может быть выражена именно так.
В области тифлопедагогики особенно затрудняется обучение, направленное на развитие образного мышления. Одним из путей решения этой проблемы является использование осязательной предметности [Куланин, 2019]. Но одной замены визуальных учебных пособий на осязаемые пособия, конечно, недостаточно. Необходим системный подход, позволяющий соединить воедино различные направления и идеи, используемые при обучении математике. Авторы предполагают, что для эффективного осуществления такого системного подхода необходимо основываться на системах заданий, позволяющих студентам с дефектами зрения успешно осваивать различные разделы математики.
Основной педагогической целью разработки системы заданий является создание атмосферы целенаправленного размышления по вопросам, связанным с изучаемой темой.
Отметим, в связи с вышесказанным, что использование термина «система» в данной статье имеет два аспекта. Первый из них состоит в том, что рассматриваемые ниже задания должны соединять в себе различные аспекты математической деятельности, например, такие как образное манипулирование геометрическими объектами и проведение, связанных с этими объектами вычислений. Второй аспект связан с созданием набора заданий, который мы будем называть «системой заданий».
2. ВОПРОСЫ, СВЯЗАННЫЕ ОСВОЕНИЕМ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Как своеобразный полигон реализации системного подхода к изучению различных разделов высшей математики авторы выбрали интегральное исчисление, а точнее совокупность задач, которые направлены на получение с помощью интегралов площадей и объёмов геометрических фигур и тел.
Важно отметить, что поскольку решение подобных задач связано с предварительным развитием пространственного воображения, в обширную систему заданий будут включены и задачи, относящиеся к различным разделам геометрии, в том числе и геометрии элементарной. При этом необходимо ясно понимать, что в рамках тифлопедагогики некоторые элементарные, а порой и просто тривиальные на первый взгляд задачи и вопросы исключительно важны и даже незаменимы. В дальнейшем это следует иметь в виду.
Кроме того, по мнению авторов, достижение достаточно глубокого уровня понимания изучаемых студентами математических вопросов возможно с помощью получения одних и тех же результатов различными способами, начиная от элементарных решений и кончая методами, основанными на использовании сложных математических теорий.
Таким образом, использование системного подхода к разработке соответствующих комплексов заданий предполагает обращение к достаточно разнородной, на первый взгляд, совокупности математических идей и теорий.
Рассматриваемый нами ниже круг вопросов затрагивает
1. Задания, непосредственно направленные на развитие пространственного воображения у студентов с дефектами зрения. Они могут использоваться как начальная база для освоения самых разных разделов математики. При решении соответствующих задач могут использоваться различные подходы, включая осязательные эксперименты с материальными моделями геометрических объектов.
2. Вопросы планиметрии, связанные с вычислением площадей.
3. Вопросы стереометрии, связанные с вычислением объёмов.
4. Геометрические образы, изучаемые в аналитической геометрии (кривые и поверхности второго порядка) и математическом анализе (графики функций одной и двух переменных).
5. Понятие определённого интеграла, которое также весьма тесно связано с геометрическими образами.
6. Понятие неопределённого интеграла и первообразной и рассмотрение методов интегрирования.
7. Формула Ньютона – Лейбница.
8. Рассмотрение важного аналитического навыка, на котором во многом основано прикладное использование определённого интеграла. Речь идёт об умении эффективно использовать символику Лейбница, что позволяет осознанно рассматривать соответствующие интегралы как пределы естественно формируемых сумм.
9. В данной статье особое значение будут иметь и широко использоваться идеи, связанные с принципом Кавальери. Дело в том, что при практическом применении этого принципа образное мышление часто важнее вычислительных навыков. При этом принцип Кавальери, будет предварительно доказан с помощью понятий интегрального исчисления.
10. Основные понятия теории геометрических преобразований плоскости и трёхмерного пространства. Этот пункт (как и следующий) связан с эффективным использованием принципа Кавальери. Важным примером является преобразование сжатия к прямой, которое позволяет получить формулу площади эллипса.
11. Элементарные понятия, связанные с топологическими преобразованиями геометрических объектов на плоскости и в трёхмерном пространстве. Эти преобразования также будут использоваться при решении задач, относящихся к принципу Кавальери. Примером одного из таких преобразований является преобразование пирамиды в конус, не меняющего площади поперечных сечений и объёма преобразуемых объектов.
12. Развитие понятия интеграла (кратные и криволинейные интегралы).
Перечисленные выше двенадцать пунктов можно рассматривать как те базовые области, системно соединив которые, можно научить студента с дефектами зрения осознанно и свободно работать с интегралами. В данной статье мы затронем только часть перечисленных вопросов, в первую очередь те, которые наиболее тесно связаны с принципом Кавальери, имеющим наглядный геометрический характер.
Дело в том, что при рассмотрении этой тематики речь идёт скорее не о разработке одной целостной системы заданий, а о целом ряде систем заданий, естественным образом дополняющих друг друга. Например, пункт 12 содержит очень большой круг весьма сложных вопросов, которые нужно рассматривать, так сказать, обособленно от более элементарных тем, связанных с остальными одиннадцатью пунктами.
Ниже авторы статьи демонстрируют не столько конечные результаты в виде готовых и чётко зафиксированных систем заданий, сколько особенности работы в этом направлении.
Важной особенностью предлагаемой методики является то обстоятельство, что при решении многих из соответствующих задач перед студентом в полной мере раскрывается смысл слов, Андрея Николаевича Колмогорова, давшего известное определение математики: «Математика — наука о количественных отношениях и пространственных формах действительного мира». Задачи, предлагаемые студенту, заставляют его одновременно размышлять о геометрических формах, характеризуемых численными (точнее функциональными) соотношениями, и о топологических преобразованиях исходных форм в новые формы, подчинённые всё тем же числовым и функциональным отношениям.
Добавим, что некоторые из предлагаемых заданий можно с успехом предлагать и студентам, которые полноценно могут работать с чертежами, рисунками и прочей графической информацией. По этой причине некоторые задания будут дублироваться в графической форме (иногда по типу комиксов).
3. ЗАДАНИЯ, НАПРАВЛЕННЫЕ НА НЕПОСРЕДСТВЕННОЕ РАЗВИТИЕ ПРОСТРАНСТВЕННОГО ВООБРАЖЕНИЯ
Круг используемых в данных темах заданий, прежде всего, связан с простейшими плоскими фигурами, трёхмерными телами и их поверхностями. При этом необходимо сделать следующее уточнение. В принципе почти любая задача геометрического характера в известном смысле связана с развитием пространственного воображения. Однако в рамках тифлопедагогики восприятие стандартной геометрической задачи может вызывать значительные затруднения. По этой причине ниже мы будем рассматривать вопросы, которые подготавливают учащихся с дефектами зрения к тому, чтобы они научились вербальную формулировку задачи разворачивать в полноценный чувственный образ, позволяющий понять условие задачи настолько, чтобы приступить к её решению.
Перейдём к рассмотрению некоторых типов задач, которые направлены на мысленное воспроизведение некоторых геометрических реалий. Именно решение таких, пусть и достаточно простых, задач позволяет дать начальный толчок к достаточно свободному мысленному манипулированию пространственными образами.
Первый рассматриваемый нами блок задач, связан с разрезанием плоских фигур. Вопросы в каждом случае имеют одинаковый характер – сколько существует различных вариантов, возникающих после разрезания исходной фигуры; сколько фигур получается в каждом из вариантов; какие фигуры при этом могут возникнуть. В этой связи вместо подробной формулировки задачи ограничимся только указанием вида фигуры и характера разреза. Приведём примеры вопросов и ответов, имея в виду, что форма ответов будет в дальнейшем учитываться при обсуждении реализации тестирующей программы, которую можно использовать при изучении соответствующих вопросов.
1. Треугольник разрезан по прямой, проходящей через его вершину.
Ответ: вариант один; в результате разрезания получится два треугольника.
2. Треугольник разрезан по произвольной прямой.
Ответ имеет вид: варианта два; в результате разрезания получится либо два треугольника, либо треугольник и четырёх угольник.
Приведём несколько примеров подобных задач, но уже в основном без ответов. При этом напомним, что в тифлопедагогике не следует бояться даже самых элементарных задач.
3. Треугольник разрезан по прямой, перпендикулярной стороне.
4. Треугольник разрезан по прямой, параллельной стороне.
5. По какой прямой можно отрезать от треугольника подобный ему треугольник?
Ответ: по прямой, параллельной одной из сторон треугольника.
6. Прямоугольник разрезан по прямой, проходящей через его центр.
7. Четырёхугольник разрезан по произвольной прямой.
8. Квадрат разрезан по двум его диагоналям.
9. Выпуклый многоугольник разрезан по двум диагоналям
Следующий блок задач, связан со складыванием плоских фигур из других фигур.
1. Какие фигуры можно получить при складывании двух равных равнобедренных прямоугольных треугольников.
2. Какие фигуры можно получить при складывании двух равных равнобедренных треугольников.
3. Какие фигуры можно получить при складывании двух равных прямоугольных треугольников.
4. Какие фигуры можно получить при складывании двух прямоугольных треугольников, имеющих по одному равному катету.
5. Какие фигуры можно получить при складывании двух равных треугольников.
6. Какие фигуры можно получить при складывании двух треугольников, имеющих по одной равной стороне.
Рассмотрим блок задач, связанный с разрезанием исходной фигуры и последующим складыванием новой фигуры. Этот блок особенно важен по той причине, что тесно связан с вычислением площадей плоских фигур.
1. Разрезать квадрат и из частей сложить два равных квадрата.
2. Разрезать два равных квадрата и из частей сложить один квадрат.
Отметим, что данная задача напрямую связана с задачей, которую Платон обсуждает в диалоге «Менон», а затем делает далеко идущие философские выводы [Платон. Собрание сочинений, 1990].
Отметим здесь и ещё одну параллель с античной математикой. Речь идёт о задаче построения куба, имеющего объём в два раза больший, чем у исходного куба [Прасолов, 1992]. В дальнейшем мы вновь соприкоснёмся с двумя этими задачами.
3. Разрезать параллелограмм и сложить прямоугольник.
4. Разрезать трапецию и сложить прямоугольник.
5. Разрезать треугольник и сложить параллелограмм.
Блок задач, связанный с изгибанием плоских фигур и рассмотрением выпуклых оболочек изогнутых фигур.
Блоку задач должно предшествовать определение выпуклого множества, как множества М точек плоскости или трёхмерного пространства, обладающего тем свойством, что в случае, когда точки А и В принадлежат М, то и весь отрезок АВ принадлежит множеству М.
Следующее определение выпуклой оболочки множества точек Т состоит в том, что соответствующей выпуклой оболочкой является наименьшее из выпуклых множеств, содержащих все точки из Т.
Первые задания по данной теме направлены на то, чтобы хорошо понять исходные определения.
1. Какова выпуклая оболочка двух точек А и В?
2. Какова выпуклая оболочка трёх точек А, В и С?
3. Какова выпуклая оболочка четырёх точек в пространстве?
4. Какова выпуклая оболочка четырёх точек на плоскости?
5. Какова выпуклая оболочка пяти точек в пространстве?
Далее можно предлагать задания, связанные с изгибанием плоских фигур.
6. Треугольник изогнут по прямой, проходящей через вершину. Какова выпуклая оболочка изогнутой фигуры.
7. Треугольник изогнут по произвольной прямой. Какова выпуклая оболочка изогнутой фигуры.
Важную роль играют задания, позволяющие понять общие методы построения выпуклых оболочек.
8. Какова выпуклая оболочка нескольких точек на плоскости?
9. Как построить выпуклая оболочка нескольких точек на плоскости?
10. Заданы плоский выпуклый многоугольник А1А2…Аn и точка A0, не лежащая в его плоскости. Что является выпуклой оболочкой точек А0, А1, … Аn?
11. Какова выпуклая оболочка нескольких точек в пространстве?
12. Как построить выпуклая оболочка нескольких точек в пространстве?
Блок заданий, связанный с развёртками многогранников и линейчатых поверхностей.
1. Какую поверхность можно склеить из плоского прямоугольника?
2. Какую поверхность можно склеить из сектора круга?
3. Как найти кратчайший путь по поверхности куба между точками, лежащими на соседних гранях этого куба.
4. Как найти кратчайший путь по поверхности цилиндра между точками, лежащими на этом цилиндре?
5. Как найти кратчайший путь по поверхности конуса между точками, лежащими на этом конусе?
Блок заданий, связанный с получением тел вращения.
1. Плоский прямоугольник АВСD вращается вокруг стороны АВ. Какую кривую описывает центр этого прямоугольника?
2. Плоский прямоугольник АВСD вращается вокруг стороны АВ. Какую поверхность заметёт сторона СD?
3. При тех же условиях какую поверхность заметёт сторона ВС?
4. В плоском прямоугольнике АВСD проведена диагональ АС. Какая поверхность будет заметена этой диагональю при вращении прямоугольника вокруг стороны АВ?
5. Внутри плоского прямоугольника со стороной АВ, серединой которой является точка О, построена полуокружность с центром О и радиусом ОА. Какая поверхность будет заметена полуокружностью при вращении прямоугольника вокруг стороны АВ?
Блок заданий, связанный с разрезанием трёхмерных тел.
1. Как разрезать выпуклую многогранную призму на несколько трехгранных призм.
2. Как разрезать куб на несколько пирамид?
3. Как разрезать выпуклый многогранник на несколько пирамид?
Блок заданий, связанный со сгибанием плоских фигур без разрезания и склейкой рёбер.
1. Лист бумаги L с прямолинейным граничным отрезком АВ согнут по сгибу ОМ, проходящему через внутреннюю точку О этого отрезка. Какую поверхность заметает отрезок ОМ при изменении угла сгиба?
Ответ. Конус с образующей ОА.
2. Каково пересечение этого конуса с листом бумаги L?
Ответ. Кроме линии ОА ещё и линия, симметричная ОА относительно линии сгиба ОМ.
3. Сделаны два сгиба ОМ и ОN, проходящие через точку О. При каких условиях соответствующие конусы соприкасаются по одной образующей?
Ответ. Угол МОN является прямым.
4. Когда соответствующие конусы имеют только общую вершину?
Ответ. Угол МОN является тупым.
5. Когда соответствующие конусы пересекаются по образующим, лежащим вне листа бумаги L?
Ответ. Угол МОN является острым.
6. Сделаны два сгиба ОМ и ОN, проходящие через точку О. При каких условиях возможно возникновение трёхгранного угла после склейки ОА и ОВ?
7. Задан плоский выпуклый многоугольник. Какие сгибы нужно сделать в надежде на склейку пирамиды?
Ответ. По линиям, соединяющим середины соседних сторон.
Назовём склейку рёбер, приводящую к возникновению подобия плоского конверта, вырожденной.
8. Из какого треугольника можно склеить невырожденную пирамиду?
9. Из какого треугольника можно склеить плоскую вырожденную пирамиду-конверт?
10. Из какого треугольника нельзя склеить пирамиду?
11. Каковы результаты склейки квадрата?
12. Каковы результаты склейки произвольного выпуклого четырёхугольника?
13. Склейка каких выпуклых четырёхугольников приводит к появлению «конвертов»?
14. Можно ли получить пирамиду из выпуклого многоугольника с числом углов более четырёх?
Блок заданий, связанный с плоскими сечениями объёмных тел.
В этом блоке следует максимально широко использовать материальные модели, с помощью которых можно осязательно изучать тела, как целостные объекты, так и плоские сечения соответствующих тел. В число соответствующих объектов следует включить призмы, пирамиды, цилиндры, конусы, параллелепипеды, антипризмы, правильные многогранники. Что касается плоских сечений, то соответствующие модели могут иметь различную степень сложности.
Простейшими являются модели, в которых исходное тело распадается на меньшие тела, например, большая пирамида должна быть составлена из малой пирамиды и пирамиды усечённой. В качестве модели высокой сложности (она ещё не разработана) можно рассмотреть стержневую модель с наклонным плоским сечением цилиндра и шарами Данделена.

Рис.1
Что касается правильных многогранников, то для осознанного понимания их структуры, следует использовать модели, которые показывают, как эти многогранники можно разлагать на пирамиды и антипризмы (рис. 1). В частности такой подход позволяет несколько иначе взглянуть на правильный тетраэдр (вырожденная антипризма, рис. 2), куб (две трёхгранных пирамиды и антипризма, рис. 3) и октаэдр (антипризма, рис. 4).

Рис. 2, 3,4
рис. 5
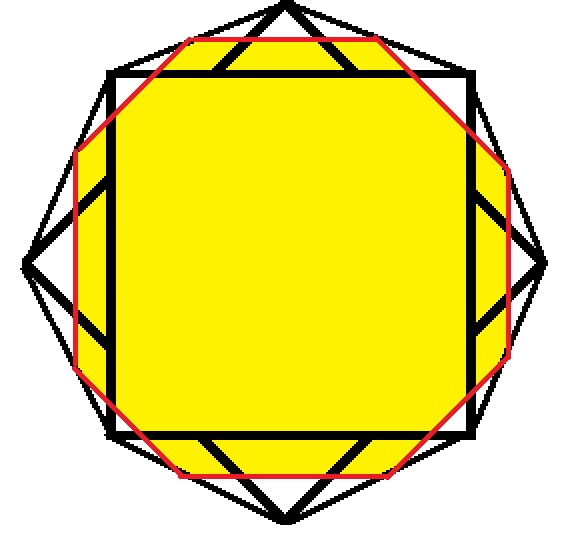
В дальнейшем будут рассматриваться задания, связанные с определением объёма антипризм. По этой причине нужно рассмотреть вопрос о форме горизонтального сечения антипризм (рис. 5), используя осязательные модели.
Соответствующая тематика в значительной мере может быть привязана к вопросам тестирования уровня развития пространственного воображения у студентов с дефектами зрения.
Как известно, в настоящее время тестирование является распространённым методом оценки тех или иных аспектов качества учебного процесса. При этом обычно результаты тестирования являются отчуждёнными от самого учебного процесса. Тестирование рассматривается как технология, позволяющая оценить знания учащегося вне рамок полноценного общения учащегося и преподавателя.
Столь же часто по результатам тестирования определённые инстанции оценивают эффективность работы преподавателя. Эта оценка также является отчуждённой от человеческого содержания обучения, состоящего в передаче не только знаний, но и в формировании ряда психологических структур, определяющих характер развивающейся личности.
В нашем же случае предполагается, что цели тестирования таковы. Прежде всего, речь идёт о самооценке студента в плане развития у него пространственного воображения. Следующим шагом должно стать устранение пробелов, выявленных в ходе тестирования. Самостоятельная работа студента может успешно дополняться совместной работой нескольких студентов. Возможно и участие преподавателя.
Время тестирования неограниченно по той причине, что цель работы состоит в саморазвитии учащегося. Основой для создания интерфейса тестирующей программы должен стать своеобразный тезаурус, что позволяет пользователю давать многоуровневые ответы на каждый из вопросов, входящих в данную систему заданий.
Например, выше приведен вопрос: «По какой прямой можно отрезать от треугольника подобный ему треугольник?» и ответ на него: «По прямой, параллельной одной из сторон треугольника». Чтобы пользователь мог успешно ответить на соответствующий вопрос, в тезаурус необходимо включить термин, связанный с параллельностью.
Естественно, что детальная проработка принципов, положенных в основу соответствующей диалоговой программы, потребует значительных усилий.
4. ПОСЛЕДОВАТЕЛЬНЫЕ ЗАДАНИЯ, ПРИВОДЯЩИЕ К ПОЛУЧЕНИЮ ДОСТАТОЧНО СЛОЖНЫХ РЕЗУЛЬТАТОВ
Точно также как и при рассмотрении задач, связанных со сгибанием плоских фигур без разрезания и склейкой рёбер, где выстроена последовательность вопросов, помогающая разобраться в соответствующей проблематике, можно выстраивать последовательные системы заданий, приводящие к решению геометрических задач и доказательству теорем.
Начнём с рассмотрения теоремы Пифагора.
1. Дан квадрат со стороной a + b. Какова его площадь?
2. Дан прямоугольный треугольник с катетами a и b. Какова его площадь?
3. В квадрат со стороной a + b вложены без наложения друг на друга четыре прямоугольных треугольника с катетами a и b. Какова не покрытая ими площадь?
4. Можно ли в квадрат со стороной a + b вложить без наложения друг на друга четыре прямоугольных треугольников с катетами a и b так, чтобы их катеты полностью покрыли периметр этого квадрата?
Ответ. В каждый угол квадрата по кругу вкладываются треугольник за треугольником. При этом длина катетов при движении по периметру образует последовательность a, b, a, b, a, b, a, b.
5. Какова при этом форма непокрытой треугольниками области.
6. На основе этого факта сформулируйте теорему Пифагора.
Теорема Пифагора является важнейшим базовым фактом, позволяющим вводить метрику в многомерных евклидовых пространствах. По этой причине естественным продолжением соответствующей тематики могут стать соответствующие задания. Есть, однако, и иные варианты.
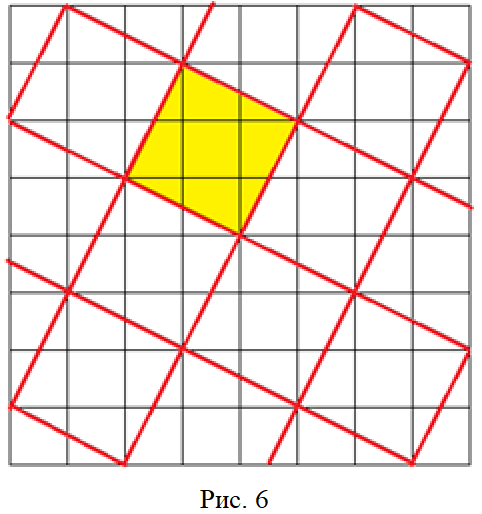
Задача. На плоскости построена сетка из единичных квадратов. Построить сетку из квадратов площади 5 (рис. 6).
1. Примем один из узлов сетки единичных квадратов за начало системы координат О. Найти узловую точку А такую, что длина вектора ОА равна , используя тот факт, что 5 = 12 + 22.
2. Найти узловую точку С такую, что длина вектора ОС равна , а сам этот вектор перпендикулярен вектору ОА.
3. Найти координаты точки В такой, что ОАВС является квадратом.
4. Описать алгоритм, который позволяет проводить прямые, образующие искомую сетку.
Отметим, что столь простое построение сетки для квадратов площади, задаваемой натуральными числами иногда возможно, а иногда это построение является более сложным. Этот факт связан с тем, что не все натуральные числа представимы в виде суммы двух квадратов [Бухштаб, 1966]. Такое представление возможно только в том случае, когда разложение этого числа на множители не содержит простых сомножителей вида . Это обстоятельство необходимо иметь в виду по той причине, что оно для некоторых студентов, пусть и немногих, открывает путь к изучению новых разделов математики.
Рассмотрим задачу, сформулированную по мотивам вопроса из книги Кордемского [Кордемский, 1956]. Вопрос таков. В комнате обычной формы большой злой мяч хочет раздавить шарик от пинг-понга (рис. 7). Куда спрятаться малышу? Ответ ясен – прятаться нужно в угол. Перейдём к аналогичной геометрической задаче с более чёткой формулировкой.

рис.7
Развернём решение задачи в последовательность вопросов.
1. Каково положение центра большой окружности О?
2.

3. Как следует расположить малую окружность относительно большой, чтобы радиус r малой окружности имел максимальное значение?
4. Каковы расстояния между различными комбинациями точек А, В (концы диагонали), М и N (точки пересечения большой окружности с диагональю АВ)?
5. Есть ли у малой окружности отрезок, аналогичный одному из отрезков предыдущего вопроса?
Ответ. Речь идёт об отрезках МВ и NВ, которые рассматривались ранее. Их длины таковы: NB = , МВ = .
6. Каково отношение радиусов малой и большой окружности, получаемое из соображений подобия?
Ответ. .
Можно аналогичным образом рассмотреть и трёхмерный вариант задачи Кордемского.
Отметим, что подобный подход не только можно, но и нужно развивать при создании систем заданий, направленных на самый широкий круг математических теорий.
В частности, рассматриваемые далее задания, связанные с вычислением площадей и объёмов желательно разворачивать в последовательность вопросов, позволяющую постепенно прийти к результату, например, несколько раз используя теорему Пифагора. Конечно, важную поддержку студентам с дефектами зрения должны оказывать осязательные модели.
5. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ И ОБЪЁМОВ
С этого момента мы приступаем к рассмотрению основной тематики данной статьи, то есть к вопросам, связанным с вычислением площадей и объёмов. Что касается вопросов, связанных с простейшими формулами нахождения площадей и объёмов, то здесь нужно подразумевать как минимум два аспекта. Один из них связан со свободным освоением элементарных методов вычисления площадей, а второй должен быть направлен на овладение базовыми понятиями, лежащими в основании интегрального исчисления. Но и в том, и в другом случае все формулы, позволяющие вычислять площади и объёмы, можно свести к вычислению площадей прямоугольников и прямоугольных параллелепипедов.
При этом, как это делается уже в школьном курсе геометрии, формула вычисления площади произвольного прямоугольника изначально обосновывается на примере прямоугольников с натуральной длиной сторон. Здесь фактически даётся и исходное определение площади, как числа единичных квадратов, из которых сложена фигура. Формулу вычисления площади прямоугольника с натуральными длинами сторон вначале можно без доказательства на образном уровне перенести на любые прямоугольники и свободно ею пользоваться.
Имея это в виду, начнём обзор возможных заданий с рассмотрения вопросов, относящихся к первому аспекту, то есть с вывода формул планиметрии, направленных на вычисление площадей многоугольников. Как показывает опыт преподавания высшей математики, в современных условиях, начинать рассмотрение вопросов, связанных с вычислением площадей различных фигур, следует именно с простейших случаев, относящихся к планиметрии. С одной стороны это связано с определёнными пробелами в школьном математическом образовании. С другой стороны, если сконцентрировать внимание на проблемах тифлопедагогики, именно работа с плоскими геометрическими фигурами (как, впрочем, и с объёмными телами) позволяет развивать пространственное воображение и геометрическую интуицию студентов с дефектами зрения. С точки зрения авторов статьи здесь заключён один из важнейших моментов изучения математики соответствующей группой учащихся.
Вывод формул для вычисления площадей многоугольников основывается на ранее рассмотренных заданиях, направленных на разрезание фигур и комбинирование новых фигур из полученных частей.
1. С помощью минимального числа разрезов параллелограмма склеить из полученных частей прямоугольник. Получить формулу для вычисления площади параллелограмма.
Аналогичные задания можно сформулировать для треугольников и трапеций. При этом можно рассматривать задания о вычислении площадей особых фигур.
2. Вычислить площадь правильного треугольника со стороной, имеющей длину а.
3. Вычислить площадь равнобедренного треугольника с основанием, имеющим длину а, и боковыми сторонами длины b.
Поскольку в ряде случаев необходимо вычислять площади, отправляясь не только от длин отрезков, но и от углов, следует рассмотреть и вопросы связанные с тригонометрическими функциями. Для этого нужно разработать соответствующий блок заданий, что выходит за рамки данной статьи. Здесь кстати проявляется одна из сложностей создания всеобъемлющих методических систем. Количество затрагиваемых вопросов нарастает подобно снежной лавине. При современном же состоянии образования необходимо начинать с элементарных вопросов, что мы и вынуждены отметить в очередной раз.
Не рассматривая заданий чисто тригонометрического характера, ограничимся несколькими задачами, связанными с использованием тригонометрии для вычисления площадей.
4. Вычислить площадь треугольника по длинам сторон а и b и углу α между ними.
5. Вычислить площадь правильного n-угольника, вписанного в окружность радиуса r.
6. Вычислить площадь правильного n-угольника, описанного вокруг окружности радиуса r.
В случае, когда вычисления проводятся с помощью теоремы Пифагора, используемые осязательные модели, должны быть дополнены хорошо осязаемыми отрезками, связанными с соответствующими вычислениями. Например, высота равнобедренного треугольника в такой модели, должна быть выполнена либо в виде стержня, либо в виде желобка. Аналогичные соображения применимы и к моделям, поясняющим тригонометрические вычисления.
Отметим при этом, что использование характерных для планиметрии методов получения формул вычисления площадей, основанных на преобразованиях исследуемых фигур в изученные уже фигуры той же площади (имеется в виду разрезание плоских фигур и составлении из них прямоугольников), преследует ещё одну цель. Речь идёт о подготовке к использованию значительно более сложных преобразований, в том числе и топологического характера. При этом на соответствующие преобразования наложено следующее ограничение: площади исходной и конечной фигуры равны между собой.
В дальнейшем подобные преобразования будут нами применяться и для трёхмерных тел. Интересно, что Леонардо да Винчи во фрагменте «Книга, озаглавленная О преобразовании, т. е. о преобразовании одного тела в другое без убавления пли возрастания материи» рассматривает этот вопрос [Зубов, 2008].
Мы уже активно пользовались формулой площади прямоугольника при выводе формул прочих фигур, обосновав её правильность на примере прямоугольников с натуральной длиной сторон. Но для подготовки рассуждений, связанных с введением понятия определённого интеграла, следует более подробно рассмотреть ситуации, относящиеся к вычислению площадей прямоугольников с любыми длинами сторон. В дальнейшем будет осуществлён переход к вычислению объёмов цилиндрических и призматических «блинчиков», в основании которых лежат криволинейные трапеции.
А сейчас вернёмся к вычислению площадей прямоугольников. Уже многократно отмечалось, что исходным видом фигур, на рассмотрении свойств которых основывается понятие площади, являются прямоугольники с длиной сторон, выражаемой натуральными числами. При кажущейся очевидности того факта, что прямоугольник с шириной и высотой имеет площадь , в сфере тифлопедагогики полезно иметь соответствующие осязательные модели.
Обобщение соответствующей формулы на случай, когда длины сторон прямоугольника являются рациональными числами, требует определённых усилий, но может быть безупречно обосновано логически на элементарном уровне. Использование модели осязаемого квадрата позволяет с помощью осязания рассмотреть вычисление площадей прямоугольников, имеющих рациональную длину сторон. При этом предполагается, что длина стороны квадрата равна единице, а, значит, эта сторона разбита на отрезки длины . Здесь, кстати, можно отметить тот факт, что одна и та же осязаемая модель может интерпретироваться различным образом.
Конечно, и здесь осязательные модели играют вспомогательную роль, но, в очередной раз повторим, что в тифлопедагогике не следует пренебрегать возможностью чувственной проверки даже самых простых понятий и формул.
Что касается перехода от натуральных длин к дробным – это путь к работе со сколь угодно узкими прямоугольниками, что необходимо при переходе к успешному определению операции интегрирования.
1. Доказать, что площадь многоугольника с длиной сторон и равна .
2. Доказать, что площадь многоугольника с длиной сторон и равна .
Важным моментом, связанным с образным восприятием площади, является чёткое понимание характера зависимости площади подобных фигур от
1. Сторона квадрата увеличена в два раза. Как изменится его площадь? Объяснить причины характера соответствующего изменения.
2. Сторона квадрата уменьшена в два раза. Как изменится его площадь?
3. Сторона квадрата увеличена в n раз (n – натуральное число). Как изменится его площадь?
4. Сторона квадрата уменьшена в n раз (n – натуральное число). Как изменится его площадь?
5. Сторона квадрата изменена в λ раз (λ – рациональное число). Как изменится его площадь? Объяснить причины характера соответствующего изменения.
Следует рассмотреть аналогичные задания, связанные с вычислением объёмов параллелепипедов. В качестве осязательных моделей можно использовать кубики и коробочки, в которые эти кубики можно вкладывать. При этом интерпретация этих моделей и в данном случае может быть различной, что позволяет от натуральных длин перейти к длинам рациональным.
6. КРИВОЛИНЕЙНЫЕ ТРАПЕЦИИ И МЕТОД ИСЧЕРПЫВАНИЯ Перейдём к обсуждению второго аспекта, направленного на овладение понятиями, лежащими в основании интегрального исчисления. Это уместно по той причине, что подавляющее большинство формул (за исключением площадей многоугольников и объёмов прямоугольных параллелепипедов и призм) выводятся методами интегрального исчисления. Речь, например, идёт о площади кругов, секторов и сегментов. В случае же объёмов, как показывает третья проблема Гильберта, интегрирование необходимо практически повсеместно.
Поскольку целью рассматриваемых здесь заданий является подготовка к осознанной работе с интегралами, рассматриваемые фигуры и тела имеют такие формы, которые, в конечном счёте, можно интерпретировать как криволинейные трапеции. С геометрической точки зрения соответствующие плоские фигуры можно разрезать на сколь угодно узкие полоски, площадь которых можно приближать площадями прямоугольников. Рассматриваемые тела можно разрезать на цилиндрические или призматические «блинчики». Описание соответствующих форм можно дать также в рамках терминологии принципа Кавальери, что и будет в дальнейшем сделано.
В рамках данной тематики ярко проявляется одна из методических проблем, характерных именно для математики. Речь идёт о компромиссе между строгостью доказательств, которая может создать значительные сложности при восприятии учащимся того или иного раздела математики, и опорой на интуицию и образы, что облегчает освоение предмета, но нарушает логическое совершенство его последовательного построения.
Вывод формулы площади прямоугольника с вещественной длиной сторон в полной мере демонстрирует эту ситуацию. По всей видимости, необходимо разрабатывать методике разного характера, которые в крайних вариантах ориентируются на логику и интуицию. Нужны и методики, которые можно трактовать как промежуточные. В данном разделе мы будем обсуждать именно такую методику, основанную на методе исчерпывания.
Метод исчерпывания мы будем трактовать следующим образом. При вычислении площади фигуры F строится последовательность вложенных в F фигур V1, V2, … Vn, … площади которых вычислимы и возрастают, а также последовательность объемлющих F фигур W1, W2, … Wn, … площади которых вычислимы и убывают. При этом разность площадей Wn – Vn может быть сделана сколь угодно малой. При рассмотрении конкретных ситуаций это позволяет получить формулу, предназначенную для вычисления площади фигуры F.
В качестве примера рассмотрим вывод формулы площади прямоугольника с вещественной длиной сторон α и β.
1. Вещественное число трактуется как десятичная дробь (конечная, бесконечная периодическая или бесконечная непериодическая). Данная дробь может быть получена с помощью процедуры измерения отрезков α и β с использованием единичного отрезка и его долей длины .
2. Рассмотрим прямоугольник Р с вещественными сторонами α и β.
3. Для любых чисел α и β могут быть построены последовательности приближений с недостатком и избытком (γm < α < δm, λm < β < μm).
4. Прямоугольник со сторонами γm и δm может рассматриваться как прямоугольник, вложенный в Р, а прямоугольник со сторонами λm и μm может рассматриваться как прямоугольник, объемлющий исходный прямоугольник Р.
5. Площади вложенных (γmδm) и объемлющих (λmμm) прямоугольников сколь угодно близко к произведению αβ.
6. Таким образом, площадь прямоугольника Р с вещественными сторонами α и β равна αβ.
Можно рассмотреть конкретный пример вычисления площади квадрата со стороной . Уже на примере рассуждений из платоновского диалога «Менон» известно, что эта площадь равна 2, однако вычисления показывают, каков характер постепенного приближения площадей, например вложенных квадратов.
Поскольку = 1,414213562, может быть получена возрастающая последовательность площадей: 12 = 1; 1,42 = 1,96; 1,412 = 1,9881; 1,4122 = 1,99996164; 1,41212 = 1,999989924; 1,412132 = 1,999998409; 1,4121352 = 1,999999824 …
Необходимость проведения подобных расчётов может быть подвергнута сомнению, поскольку речь идёт о «малонаучном мероприятии», но, видимо, принятие решения об использовании соответствующих вычислений следует предоставить преподавателю. Желательно при этом иметь в виду переформулированные слова Паскаля: «Предмет математики настолько сложен, что нельзя упускать случая сделать его немного более понятным, дополнив абстрактные рассуждения конкретными вычислениями».
Важнейший геометрический объект, связанный с операцией интегрирования – это криволинейная трапеция. Криволинейная трапеция в рамках математического анализа – это плоская фигура, ограниченная сверху графиком функции f(x), снизу – осью абсцисс, слева – прямой x = а и, наконец, справа – прямой x = b. По поводу использования слова «сверху» поясним, что нацеливаясь на задачи вычисления площадей и объёмов, мы будем рассматривать только функции с неотрицательными значениями.
Приведём и следующую образную трактовку криволинейной трапеции, когда она рассматривается как одна из двух частей прямоугольника, разрезанного особым образом. График функции при этом воспринимается как пластический образ континуума или отрезок, деформируемый в кривую.
Фактически при этом даётся наглядное объяснение причин, по которым график функции является кривой. Само объяснение таково. Представим себе, что на оси абсцисс в декартовой плоскости расположен пластичный, легко деформируемый стержень. Ординаты всех его точек равны нулю. Стержень можно параллельно оси абсцисс переместить вверх на некоторую величину с. При этом ординаты всех его точек примут одинаковые значения с, уже неравные нулю. С помощью этой процедуры построен график функции у = с. Пусть далее нам дана функция y = f(x). Теперь мы будем перемещать по вертикали не весь стержень целиком, а каждую его точку х сдвинем на своё особое расстояние y = f(x). При этом стержень деформируется и предстанет в виде кривой.
Теперь попытаемся непосредственно определить криволинейную трапецию как разрезанный прямоугольник. Пусть нижней горизонтальной стороной разрезаемого прямоугольника является отрезок [a; b]. От некоторой точки прямой x = а начинаем резать прямоугольник до прямой x = b.
1. Каким свойством должен обладать характер разреза, чтобы в итоге получилась криволинейная трапеция.
Ответ. Если расстояние режущей точки от прямой x = а в момент времени t равно s = x(t), то это строго возрастающая функция.
2. Доказать, что при любой зависимости y = y(t), формулы s = x(t) и y = y(t) являются параметрическими уравнениями некоторой функции y = f(x).
3. Любая система вертикальных разрезов исходного прямоугольника может послужить основой для вычисления площади криволинейной трапеции методом исчерпывания.
Ответ. Для каждой вертикальной полосы криволинейной трапеции может быть построен вложенный и объемлющий прямоугольник.
Авторы статьи отдают себе отчёт в том, что для ряда преподавателей подобные рассуждения могут представляться не только ненужными, но и неуместными. Однако они считают, что обсуждение, пусть и простых, математических образов в тифлопедагогике приближает учащегося к пониманию вопроса.
7. ПРИНЦИП КАВАЛЬЕРИ
Можно сказать, что криволинейная трапеция – это множество вертикальных отрезков длины f(x), исходящих из каждой точки x горизонтального отрезка [a; b]. Это означает, что при таком определении легко усмотреть самую тесную связь с геометрическими структурами, рассматриваемыми в принципе Кавальери. К рассмотрению этого принципа мы и переходим.
При этом мы оставим без обсуждения пункты 4 – 7 исходной для нас программы. Речь идёт о следующих темах «Геометрические образы, изучаемые в аналитической геометрии (кривые и поверхности второго порядка) и математическом анализе (графики функций одной и двух переменных)»; «Понятие определённого интеграла, которое также весьма тесно связано с геометрическими образами»; «Понятие неопределённого интеграла и первообразной и рассмотрение методов интегрирования»; «Формула Ньютона – Лейбница».
Мы не будем останавливаться на этом круге вопросов не по той причине, что здесь не требуется разработки соответствующих заданий с уклоном на тифлопедагогику. Такая работа до сих пор необходима в рамках любой математической темы. Дело в том, что перечисленные выше вопросы носят вполне традиционный характер. Таким образом, здесь хотя бы ясно, о чём говорить. Вопрос только в том, как говорить об этом, чтобы сделать материал максимально доступным для студентов с дефектами зрения.
Использование же принципа Кавальери для современного этапа преподавания интегрального исчисления к числу обязательных тем не относится. В то же время здесь заключены интересные методические возможности. При этом мы будем использовать математические методы, которые следовало бы обсудить в пунктах 4 – 7.
В книге [Никифировский, 1985] приводятся сведения о итальянском математике Бонавентуре Кавальери (1598 – 1647). Будучи монахом, Кавальери активно занимался математикой. Им написаны книги «Геометрия, изложенная новым способом с помощью неделимых непрерывного» и «Шесть геометрических опытов».
В первой книге Кавальери описал общие методы вычисления объёмов тел, которые до него не рассматривались. Основным понятием геометрии Кавальери служат неделимые. Таковыми для плоской фигуры являются параллельные между собой отрезки, на которые разбивается данная фигура. Для тела в трёхмерном пространстве неделимыми являются плоские сечения тела, параллельные между собой.
В легендарном школьном учебнике геометрии А. П. Киселёва (1852 – 1940) принцип Кавальери формулируется следующим образом: «Объёмы двух тел или площади двух плоских фигур будут равны, когда равны между собой площади или длины всех соответствующих сечений, параллельных одной и той же плоскости или прямой». В терминологии Кавальери плоскость или прямая, задающая направление всех сечений, называется регулой. Любую прямую, перпендикулярную регуле, назовём осью сравниваемых тел Кавальери (рис. 9).

Фактически при современном понимании сравнения двух площадей или объёмов по методу Кавальери каждой точке h числовой оси соответствуют функции и , задающая площади или длины «неделимых» (и то и другое можно назвать мерой) на высоте h.
Использование определённого интеграла позволяет доказать принцип Кавальери независимо от того, вычисляется ли площадь или объём. Итак, функции и , задают площади или длины «неделимых» (и то и другое можно назвать мерой) на высоте h (0 < h < H). Для случая длин произведения вида f(x)dx являются площадями, а для случая площадей эти произведения являются объёмами. Но и в том, и в другом случае , что и доказывает утверждения, которые называются принципом Кавальери.
Важной особенностью принципа Кавальери является то обстоятельство, что общим вычислительным приёмом можно вычислить площади и объёмы различных геометрических объектов, например, объёмы пирамид и конусов. По этой причине связь между формой соответствующих объектов носит не геометрический, а топологический характер. При этом на топологические преобразования наложены ограничения, связанные с сохраняющимися числовыми соотношениями. Речь, естественно, идёт о неизменности меры «неделимых». Таким образом, рассматривая те или иные плоские фигуры и объёмные тела, можно предварительно с помощью топологических преобразований перейти к некоторым каноническим формам (как мы упоминали, в духе Леонардо да Винчи).
Как мы уже отмечали, при рассмотрении задач, решаемых с помощью принципа Кавальери, перед студентом в полной мере раскрывается связь, существующая между количественными отношениями и пространственными формами.
Итак, задачи на принцип Кавальери, предлагаемые студентам, должны заставить его одновременно размышлять о геометрических формах, характеризуемых функциональными соотношениями, и о топологических преобразованиях исходных форм в новые формы, подчинённые тем же числовым и функциональным отношениям.
Что касается вида канонических форм, то для плоских фигур речь может идти о традиционной форме криволинейной трапеции, описанной ранее. Для объёмных тел речь может идти о телах, получаемых вращением графика функции вокруг оси абсцисс. Задачи на вычисление объёмов таких тел входят в курс математического анализа. Применительно к принципу Кавальери тело вращения образуется вращением вокруг соответствующей оси. «Неделимые» при этом являются кругами с соответствующими площадями. Так, например, усечённые пирамиды при таких преобразованиях должны переходить в усечённые конусы, а призмы – в цилиндры. Будем называть подобные тела функциональными телами вращения (ФТВ). Слово «функциональные» указывает на неизменную функциональную зависимость площадей неделимых от координат точек оси.
На образном уровне можно уподобить преобразование объёмных геометрических структур Кавальери, характеризуемых осью и регулой, манипуляциями с пластилиновыми объектами. Прежде всего, речь идёт об упомянутом переходе от произвольных форм к телам вращения.
Ещё одним из видов задач, основанных на работе с каноническими формами, являются задания, связанные с делением плоских фигур и объёмных тел на части. Деление должно быть выполнено таким образом, чтобы полученные в результате составляющие исходного геометрического объекта имели заданные соотношения мер (площадей или объёмов).
Деление может производиться как вдоль оси канонического тела Кавальери (назовём такое деление продольным), так и параллельно регуле этого тела (назовём такое деление поперечным). Простейшим, фактически тривиальным, является поперечное деление цилиндра на n равных по объёму частей. В результате возникнет несколько цилиндров того же сечения, что и исходный цилиндр, а высоты которых равны высоте исходного цилиндра, делёной на n. Несмотря на простоту данной операции, она хорошо объясняет смысл более сложных задач на ту же тему, особенно студентам с дефектами зрения.

Рис.10

Если все неделимые ФТВ имеют площадь строго большую нуля, то из данного ФТВ можно вырезать цилиндр, такой что останется либо веретёнообразное тело, либо два веретёнообразных тела с остриями внутри оси. Примером такого разбиения ФТВ является продольное разбиение усечённого конуса на цилиндр и веретёнообразное тело (рис. 11).
Далее мы рассмотрим три блока задач, связанных с принципом Кавальери. Речь идёт о непосредственном вычислении площадей и объёмов с помощью операции интегрирования. При этом объём одного и того же тела можно вычислять различными способами в зависимости от выбора оси и регулы. Ещё два блока задач будут связаны с поперечным и продольным делением геометрических объектов.
8. ОБ ЭФФЕКТИВНОМ ИСПОЛЬЗОВАНИИ СИМВОЛИКИ ЛЕЙБНИЦА, СВЯЗАННОЙ С ОПРЕДЕЛЁННЫМ ИНТЕГРАЛОМ Решение задач, в которых требуется находить площади и объёмы, требует свободного владения операцией интегрирования. Чрезвычайно удачная символика Лейбница помогает студенту успешно освоить круг соответствующих вопросов. Перечислим несколько базовых положений, связанных с использованием интегрального исчисления.
1. Площадь криволинейной трапеции равна пределу суммы площадей f(x)∆х полосок ширины ∆х при ∆х стремящемся к нулю.
2. Предел суммы величин f(x)∆х на отрезке [a; b] при ∆х стремящемся к нулю называется определённым интегралом и согласно обозначениям Лейбница обозначается через . Смысл этого обозначения прост: знак ∫ – стилизованная буква S, символизирующая сумму. Буквы a и b указывают отрезок, на котором задана величина f(x). Они называются пределами интегрирования. Произведение f(x)dx выражает бесконечно малые суммируемые порции вычисляемой величины – длины, площади, объёма и т. д.
3. Первообразной функции f(x) называется такая функция F(x), для которой производная F′(x) равна исходной функции f(x). Первообразная имеет ещё одно название – неопределённый интеграл и обозначается через .
4. Первообразной функции f(x) является определённый интеграл с переменным верхним пределом интегрирования (то есть площадь криволинейной трапеции на отрезке [a; х]).
5. Если известна хотя бы одна первообразная F1(x) функции f(x), то любая другая её первообразная F2(x) отличается от F1(x) на постоянную величину, то есть F1(x) – F2(x) = С.
6. Если F(x) является первообразной функции f(x), верна формула Ньютона – Лейбница: .
Итак, интуитивно интеграл является пределом суммы бесконечно малых величин f(x)dx. При этом его можно использовать для вычисления не только площадей, но и других геометрических величин.
Отметим, что величина f(x) в ряде задач может быть непосредственно задана аналитически, но при решении задач, имеющих чисто геометрическую постановку, необходимо получить соответствующее выражение для величины f(x) самостоятельно.

Пример. Вычислить объём прямого кругового конуса с высотой Н и радиусом основания R.
Решение. Конус можно разбить на бесконечно тонкие блинчики, которые можно рассматривать как цилиндры радиуса r, находящиеся на расстоянии h от вершины конуса. Из подобия треугольников получаем, что (рис. 12). Тогда объём блинчика равен .
Весь объём конуса есть сумма блинчиков по всей высоте, то есть от 0 до Н. Итак,
Основываясь на принципе Кавальери, можно сделать следующий вывод: полученная формула верна и для наклонного кругового конуса.
На основе подобных соображений, сутью которых является зависимость величины r от h можно получить целый ряд формул для вычисления площадей и объёмов. При этом величина r может интерпретироваться различным образом.
Если считать, что рисунок 12 изображает равнобедренный треугольник с высотой H и основанием , то площадь треугольника можно вычислить по формуле
Основываясь на принципе Кавальери, можно сделать вывод, что полученная формула верна и для любых треугольников, а не только для равнобедренных.
Вычислив объём прямого кругового конуса, можно аналогичным образом вычислять также и объёмы любых конусов. При этом конусом мы будем называть следующую геометрическую конструкцию. Пусть в трёхмерном пространстве заданы плоская область F (основание конуса) и точка V вне этой плоскости (вершина конуса). Конусом называется выпуклая оболочка плоской области F и точки V. В частности в случае, когда область F является многоугольником, конус представляет собой пирамиду. Расстояние от вершины конуса до плоскости основания называется высотой конуса.
1. Вычислить объём конуса в случае, когда площадь основания равна S, а высота конуса равна H.
Решение. Если высоту конуса рассматривать как ось конструкции Кавальери, а основание как регулу, то конус состоит из гомотетичных неделимых, площадь которых зависит от высоты сечения по формуле . Объём конуса равен = .
Рассмотренные задания показывают, что главной задачей при вычислении площадей и объёмов является определение функциональной зависимости между высотой и мерой неделимых, которая позволяет записать соответствующий интеграл, а затем и вычислить его. В ряде случаев эта функциональная зависимость дана непосредственно.
2. На отрезке [a; b] задана функция . Определить объём тела вращения, заметаемого соответствующей криволинейной трапецией при вращении вокруг отрезка [a; b].
Решение. Данная задача включается в набор обязательных заданий в рамках изучения интегрального исчисления. Она проста, но связана с достаточно эффектной геометрической конструкцией: .
3. Тело Кавальери, площади неделимых которого выражаются через значения их высот функциями преобразовано в функциональное тело вращения. Каков вид функции ?
Ответ. Функция задаётся формулой .
В более сложных случаях можно использовать выражение используемых в задаче геометрических величин через параметр.
4. Выразить значение некоторой величины Р через значения параметра t так, чтобы зависимость была линейной, а при t = 0 значение и при t = 1 значение .
Решение. Условия задачи позволяют определить параметры соответствующей линейной зависимости: .
5. Рассмотрим конструкцию Кавальери с высотой H и мерой неделимых . Пусть высота неделимых h выражена как функция от параметра t ( . С учётом этого представления величин через параметр выразить меру конструкции Кавальери .

И на этом этапе, когда уже используются методы интегрирования, желательно сочетать задания разного характера, а именно, те, где непосредственно используются уже выведенные формулы с теми, где результат достигается с помощью интегрирования.
6. Вычислить основные линейные параметры правильного тетраэдра, длина стороны которого равна a. Речь идёт о величинах, которые позволяют определить объём тетраэдра.
Решение. Используя рис. 13, легко провести все вычисления. Весьма полезна была бы соответствующая рисунку 13 стержневая осязательная модель. Перейдём к расчётам. , , ,
7. Найти объём правильного тетраэдра, длина стороны которого равна a.
Решение. Используя результаты предыдущей задачи и формулу объёма пирамиды, получаем: .
Перейдём ко второму варианту вычисления объёма правильного тетраэдра.
8.

Решение. Проведём расчёты, ориентируясь на рис. 14. И здесь была бы полезна соответствующая рисунку 14 стержневая осязательная модель. ,
9.

Решение. Рассмотрим следующую динамическую модель. Сечение тетраэдра движется за время t (от 0 до 1) по всей высоте конструкции. Пусть . Тогда длина одной из сторон прямоугольного сечения, параллельной ребру АВ, линейно зависит от t и имеет длину . Длина перпендикулярной стороны прямоугольного сечения, параллельной ребру CD, линейно зависит от 1 – t и имеет длину .
По формуле из задачи 5 (замена переменной) получаем:
.
Без решения приведём сходные по характеру задачи. Напомним при этом, что цель решения соответствующих заданий состоит не только в освоении вычислительной техники, связанной с интегрированием, но и в развитии пространственного воображения студентов и их геометрической интуиции.
10. Вычислить объём антипризмы по схеме, которая была использована в задаче 9.
11. Найти объём октаэдра, рассматривая его как комбинацию двух четырёхугольных пирамид.
12. Найти объём октаэдра, рассматривая его как антипризму (рис. 4).
13. Найти объём куба, рассматривая его как комбинацию двух треугольных пирамид и антипризмы (рис. 3).
Теперь рассмотрим задачи иного характера, связанные с формулами вычисления площади равнобедренных прямоугольных треугольников, с объёмом четырёхугольных пирамид и интерпретацией площади некоторых криволинейных трапеций.
1. Существует пирамиды специального вида, объёмы которых определяются без интегрирования. Речь идёт о равных четырёхугольных пирамидах, на которые можно разбить куб. Описать характер этого разбиения.
Решение. Рассмотрим разбиение куба со стороной а на шесть четырёхугольных пирамид. Их основаниями являются грани куба, а вершиной – центр куба. Объём каждой из полученных пирамид равен одной шестой объёма куба.
Определение. Пусть в пространстве выбрана некоторая плоскость L и число λ > 0. Введём следующее преобразование, которое называется сжатием / растяжением к плоскости L.
Рассмотрим в пространстве точку М. Пусть точка N – основание перпендикуляра МN, опущенного на плоскость L. При сжатии / растяжении точка М переходит в точку М1 такую, что М и М1 лежат в одном полупространстве относительно L и длина отрезка М1N равна длине отрезка МN, умноженной на λ.
При λ > 1 речь идёт о растяжении, а при λ < 1 речь идёт о сжатии.
Кратко говоря, при сжатии / растяжении все расстояния на прямых, перпендикулярных плоскости L умножаются на λ.
2. Дать определение сжатия / растяжения к прямой на плоскости.
3. Пирамида из задания 1 подвергнута растяжению в два раза от плоскости основания. Определить объём полученной пирамиды.
Решение. Исходная пирамида имеет высоту . После растяжения пирамиды высота увеличится в два раза. Толщина блинчиков, составляющих пирамиду, также увеличивается в два раза. Таким образом, речь идёт об объёме четырёхугольной пирамиды высотой a с площадью основания . Объём итоговой пирамиды равен .
Практически результат получен без использования операции интегрирования. Тем самым намечен подход для пропедевтики операции интегрирования по отношению к линейным и квадратичным функциям с образной опорой на формулы вычисления площадей и объёмов.
Площадь криволинейной трапеции (треугольника) под графиком линейной функции может отныне интерпретироваться как интеграл .
Можно рассмотреть разбиение куба на шесть равных пирамид для достижения ещё одной цели. Речь идёт о выводе формулы объёма усечённой пирамиды с помощью разности кубов. Данная тема рассматривалась в статье Н. Я. Виленкина «О вычисления объёма усечённой пирамиды в Древнем Египте» [Историко-математические исследования. М, 1985].
Данная тема имеет не только историко-математический интерес, но и интерес методический, поскольку позволяет студенту хорошо разобраться в структуре довольно сложной формулы.
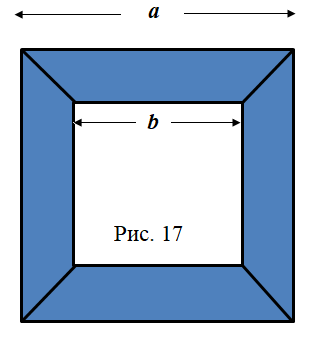
Заметив, что выражение соответствует высоте трапеции, можно считать, что формула площади трапеции может быть получена с помощью формулы «разность квадратов».
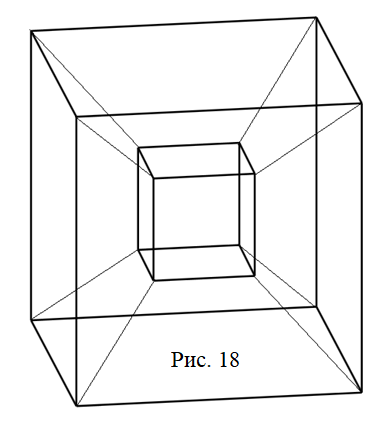
.
Заметив, что выражение соответствует высоте усечённой пирамиды, получаем формулу вычисления объёма усечённой пирамиды: «Объем усеченной пирамиды равен одной трети произведения высоты пирамиды на сумму площадей верхнего и нижнего оснований и среднего геометрического из произведения оснований усеченной пирамиды».
Формула разности кубов хорошо объясняет причины появления такого необычного слагаемого как среднее геометрическое из произведения оснований усеченной пирамиды. Кроме того, она же помогает запомнить соответствующую формулу, опираясь на знание фактов алгебраического характера. Наконец, принцип Кавальери позволяет перенести эту формулу на общий случай усечённого конуса.
Продемонстрируем вывод этой формулы с помощью методов интегрального исчисления. В основу этого вывода положим формулу линейной зависимости радиуса усечённого конуса от высоты сечения h: .
В итоге получен тот же самый результат, но относительная сложность вывода затемняет причины, по которым получена именно такая формула.
9. ПЛОЩАДИ И ОБЪЁМЫ КРИВОЛИНЕЙНЫХ ТЕЛ
Выше уже рассматривались вопросы, связанные с вычислением площадей и объёмов подобных тел. Тем не менее, желательно обратиться к той же тематике более систематическим образом. В частности это вызвано тем, что в дальнейшем будут рассматриваться упомянутые ранее функциональные тела вращения.
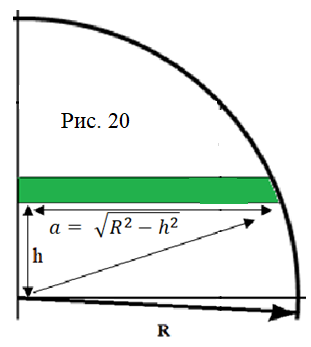
Кроме того, определение площадей и объёмов криволинейных фигур предоставляет весьма широкие возможности рассмотрения вычислений самого разного уровня сложности. Несомненно, проведение таких вычислений должно помочь в развитии геометрической интуиции студента. Начнём с подхода, который был характерен для древней индусской математики времён Бхаскары (рис. 19), и вычислим площадь круга, разбитого на бесконечно узкие треугольные сектора с основаниями и высотой R.
Вычисление таково: .


Это особенно важно по той причине, что до сих пор далёк от решения вопрос о соотношении искусственного интеллекта и интеллекта естественного, присущего человеку с древнейших времён. Сколь угодно сложный аналог машины Тьюринга, лишён эмоциональной составляющей. Он даже обманывать людей в духе теста Тьюринга будет совершенно бесстрастно. В то же время психика человека вырастает из тонких ощущений и нюансов, о которых В. Я. Брюсов однажды сказал: «Есть тонкие властительные связи меж контуром и запахом цветка».
Можно вспомнить, что весьма немолодой Томас Гоббс, впервые познакомившись с теоремой Пифагора, воскликнул: «Этого не может быть!» Такое удивление является мощным стимулом, заставляющим увлечься предметом. Кроме того, вопреки мнению некоторых маститых математиков, здесь можно почувствовать непреходящую культурную важность математических фактов, которые известны тысячелетиями. Так или иначе, педагог должен максимально использовать аналогии и связи между различными фактами. Это может повысить интерес к изучению математики.

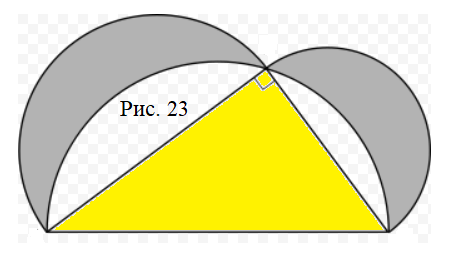
Следует выделить и ещё одну дополнительную тему. Речь идёт о луночках Гиппократа (рис. 23). По всей видимости, использование соответствующих задач особенно уместно в рамках тифлопедагогики, поскольку в них соединяются наглядность и логическая стройность рассуждений, связанных с равенством площадей.
Переходя к вопросам вычисления объёмов, отметим, что вычисление объёма шара может быть обосновано тем же чертежом (рис. 20), который используется при вычислении площади круга. При этом сам процесс вычисления объёма шара оказывается более простом, чем процесс вычисления площади круга.
.
Рассмотрев разбиение шара на бесконечно тонкие конусы с высотой и основаниями площади , покрывающими в совокупности поверхность шара, можно вычислить объём шара в духе Бхаскары: = . Это позволяет вычислить поверхность шара: .
Использование сжатия к прямой в двумерном случае и сжатия к плоскости в пространстве позволяет получить формулы для вычисления площадей эллипсов и объёмов эллипсоидов. Естественным продолжением этого круга вопросов могут стать системы заданий, связанные с вычислением площадей и объёмов фигур и тел, возникающих при рассмотрении кривых и поверхностей второго порядка. Подобные задачи во многом имеют стандартный характер. По этой причине мы ограничиваемся только упоминанием о них.
В книге [Фихтенгольц, 1966] рассматривается задача о нахождении объёма цилиндрического отрезка (рис.24). Особенно интересно то, что соответствующие вычисления производятся в двух вариантах, что в полной мере соответствует целям развития пространственного воображения студентов.
Наконец, отметим ещё одну интересную линию получения объёмов и поверхностей, которая может быть рассмотрена при изучении более продвинутых методов вычисления. Речь идёт об использовании понятия центра тяжести. Отправляясь от дискретной системы материальных точек, для каждой из которых известна её масса и её координаты, с помощью использования интегралов можно перейти к вычислению координат центров тяжести кривых и поверхностей. В итоге можно получить первую и вторую теоремы Паппа – Гюльдена, которая, в частности, позволяет получить формулы вычисления поверхности и объёма тора. Подробное изложение темы дано в книге [Балк, 1987].
10. ПОПЕРЕЧНОЕ ДЕЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЁМОВ В СИСТЕМЕ КАВАЛЬЕРИ
Рассмотрим задания указанного вида различного уровня сложности. Как всегда будем отмечать темы, изучение которые может стать новым направлением изучения математических вопросов.
1. Разделить треугольник линией, параллельной основанию, на равные по площади части. Элементарное решение и решение с помощью интеграла.
Элементарное решение. Пусть в треугольнике АВС с высотой АН проведена линия МN, параллельная основанию ВС. Таким образом, треугольник АВС разделен на две части, а именно на треугольник АМN с высотой АР и трапецию МNСВ. Предположим, что эти части имеют равные площади. Из этого следует, что треугольник АВС имеет площадь в два раза больше, чем треугольник АМN. Поскольку треугольники АВС и АМN подобны, верна пропорция АР : АН = МN : ВС = λ. Поскольку площадь треугольника АВС равна произведению АН на ВС, а площадь треугольника АМN равна произведению АР на МN, получается, что отношение этих площадей с одной стороны равно одной второй, а с другой стороны оно равно λ2. Таким образом, λ = .
Этот результат можно истолковать так. Чтобы получить из исходного треугольника подобный ему с площадью в два раза больше, нужно увеличить высоту в раз.
2. Разделить треугольник линиями, параллельными основанию, на несколько равных по площади частей.
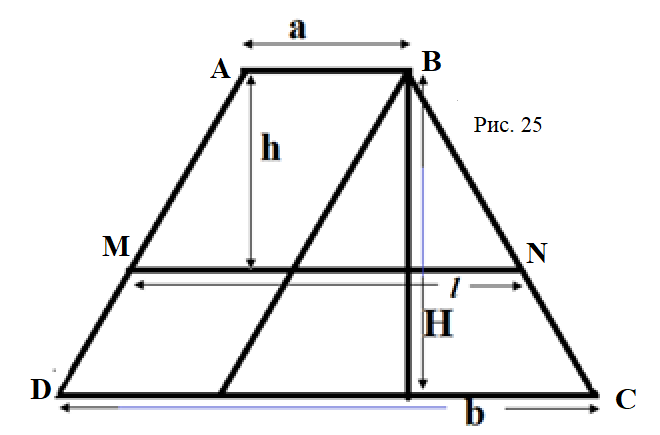
3. Вывести с полным геометрическим обоснованием формулу функциональной зависимости длины линии, параллельной основанию трапеции, от высоты этой линии.
Решение. Пусть в трапеции АВСD с высотой 1 проведена линия МN, параллельная основанию СD на расстоянии h от основания АВ. Кроме того, пусть АВ = а и СD = b (рис. 25).
Тогда длина l отрезка МN линейно зависит от h и меняется от значения а до значения b. Формула, выражающая эту зависимость, имеет вид
Если же высота трапеции АВСD равна H, то формула приобретает вид
4. Разделить трапецию линией, параллельной основанию, на равные по площади части.
Решение. Используя предыдущий результат, запишем площади трапеций АВNМ и АВСD.
Поскольку первая из площадей в два раза меньше второй, получаем равенство
которое переходит в квадратное уравнение
Дискриминант данного уравнения равен , а положительное значение высоты вычисляется по формуле
Длина отрезка МN выражается по формуле
Достаточно простая проверка показывает, что задача решена верно. Отметим также, что здесь можно найти, пусть и отдалённое, сходство с задачей, рассмотренной в диалоге «Менон».
5. Разделить трапецию линиями, параллельными основанию, на несколько равных по площади частей.
Решение. Используя аналогичные расчёты, приводящие к квадратному уравнению, можно разделить трапецию на две части, имеющие заданное отношение площадей. Это открывает путь к решению задачи 5. Например, при делении трапеции на три части линиями, параллельными основаниям, сначала следует разделить трапецию на части с отношением площадей 2 : 1 или 1 : 2. Затем большую из полученных частей нужно разделить на две равные части.
Тесно с данными задачами связана ещё одна задача: пристроить к нижней части трапеции расширяющую её часть той же площади. При этом заданы величины и , и нужно найти величину .
6. Построить трапецию, поперечное деление которой на равные площади можно описать с помощью рациональных параметров.
Решение. При рассмотрении данной задачи следует использовать простейшие методы решения диофантовых уравнений [Башмакова, 1972]. Эта тематика, несомненно, может рассматриваться, как одно из новых направлений работы заинтересованного студента.
Формула требует нахождения таких рациональных параметров a и b, для которых величина l также является рациональным. Таким образом, речь идёт о решении диофантова уравнения . Данное уравнение имеет решение . Можно перейти к более простому уравнению , где .
На кривой лежит точка (1; 1). Проведём через эту точку прямую с рациональным тангенсом угла наклона k. Уравнение этой прямой имеет вид . Найдём координаты второй точки пересечения этой прямой с окружностью . Исключив переменную y из этих двух уравнений и используя, что квадратное уравнение уже имеет корень, равный единице, получим, что
Положив, например, k = 3, получим x = 1,4 и y = . Умножив величины на 10 и перейдя к положительному значению величины y, получим конкретный пример соответствующей трапеции (рис. 26). Этот пример позволяет построить осязаемую модель, позволяющую ощутить основные моменты, связанные с соответствующей задачей.
7. Разделить конус плоскостью, параллельной основанию, на равные по объёму части.
Решение. По аналогии с первой задачей данного блока можно установить, что объём конуса растёт как куб какого-либо из линейных размеров, например высоты конуса. Таким образом, для увеличения объёма конуса в два раза его высоту следует увеличить в . Исходя из этих соображений, можно провести и деление конуса на две равные по объёму части.
8. Разделить конус плоскостями, параллельными основанию, на несколько равных по объёму частей.
Решение. Высоты конусов с объёмами 1, 2, 3, … образуют последовательность длин, относящихся друг к другу как
9. Разделить усечённую четырёхгранную пирамиду плоскостью, параллельной основанию, на две равные по объёму части.
Решение. Рассмотрим рис. 25, несколько иначе интерпретируя его, а именно, считая, что на чертеже изображена усечённая пирамида в вертикальном разрезе. Используя те же самые обозначения, которые приведены на рис. 25, можно провести достаточно простые вычисления.
Поскольку , уравнение, определяющее деление усечённой пирамиды пополам, то есть можно заменить на уравнение . В итоге получаем уравнение . Здесь просматривается аналогия с задачей удвоения кубического жертвенника в Дельфах. К сожалению, рациональных решений, кроме случая , у этого диофантова уравнения нет [Серпинский, 1961].

10. Вывести кубическое уравнение, предназначенное для поперечного деления усечённого конуса в заданном отношении.

Решение. Рассмотрим рис. 27. Радиус r сечения линейно зависит от высоты сечения h по формуле . Объём верхней части усечённого конуса, возникающей при поперечном делении на высоте H равен

Объём неразделённого усечённого конуса равен
Если нужно отсечь от этого объёма долю, определяемую параметром λ, высота H отсекаемой части определяется уравнением
λ = 0.
11. Сформулировать и решить конкретную задачу деления усечённого конуса плоскостью, параллельными основанию, на две части, имеющие заданные отношения объёмов.
Решение. Будем исходить из простых геометрических соображений. Пусть усечённый конус состоит из трёх уровней одинаковой высоты. Тогда верхний уровень гомотетичен двум нижним как единому целому (рис. 28).

Положим, что , тогда = 63 , а кубическое уравнение принимает вид
Итак, к решению этого уравнения сводится следующая задача: отсечь сверху от усечённого конуса с параметрами часть, составляющую по объёму одну девятую от общего объёма конуса.
Исходные данные при решении соответствующего уравнения подобраны так, что корень является целым числом ( ). По этой причине поиск корня сводится к перебору делителей свободного члена.
12. Разделить полушарие плоскостью, параллельной основанию, на равные по объёму части
Решение. Будем рассматривать полушарие радиуса единица. Оно имеет объём равный . Полушарие нужно разделить на шаровой сегмент и шаровой пояс, объёмы которых равны . При этом объём шарового пояса высоты H равен
В итоге для нахождения высоты шарового пояса получено кубическое уравнение . Для его решения нужно использовать формулу Кардано [Курош, 1968]. Под знаком квадратного корня стоит выражение ( ). Значение этой величины является отрицательным. Это означает, что кубическое уравнение является неприводимым (этот термин не связан с неприводимостью многочленов) [Курош, 1968]. В этом случае применение формулы Кардано затруднено. Тем не менее, в данном случае возможно получение обозримого результата.
Итак, формула Кардано для нахождения корней имеет вид
Поскольку кубические корни нужно извлекать из комплексных чисел в тригонометрической форме, это можно сделать без проблем. В результате корни кубического уравнения равны , , . Таким образом, корни выражены с помощью тригонометрических функций. По смыслу задачи .
11. ПРОДОЛЬНОЕ ДЕЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЁМОВ В СИСТЕМЕ КАВАЛЬЕРИ
Задания указанного вида также обладают различным уровнем сложности от тривиальных до очень сложных. О простейших заданиях уже говорилось выше. Речь идёт о своеобразной задаче, похожей на бытовую деятельность, связанную с колкой дров, то есть о продольном делении цилиндра на части, равные по объёму. Однако, как отмечалось, задача дополняется топологическим преобразованием «поленьев» в прямые круговые цилиндры.
Прежде чем рассматривать конкретные задачи на продольное деление, очертим некоторые особенности этих заданий, на которые следует обратить особое внимание. Вычисление площади и объёма структуры Кавальери с заданным направлением оси сводится к вычислению интеграла, и после такого сведения, в известном смысле, обезличивается. Благодаря этому задачи на продольное деление могут рассматриваться двояко: и как деление криволинейных трапеций и как деление объёмных тел. Однако постановка исходной задачи обязательно связана с рассмотрением геометрических и топологических аспектов вопроса. Таким образом, при решении соответствующих заданий возможен попеременный переход то к более абстрактной точке зрения (вычислительной), то к более конкретной (геометрической). Это очень удачно сочетается с исходной методической позицией, в равной степени направленной на освоение вычислительных навыков и на развитие геометрической интуиции.
Из вышесказанного следует, что один из видов задач имеет одну из следующих стандартных формулировок.
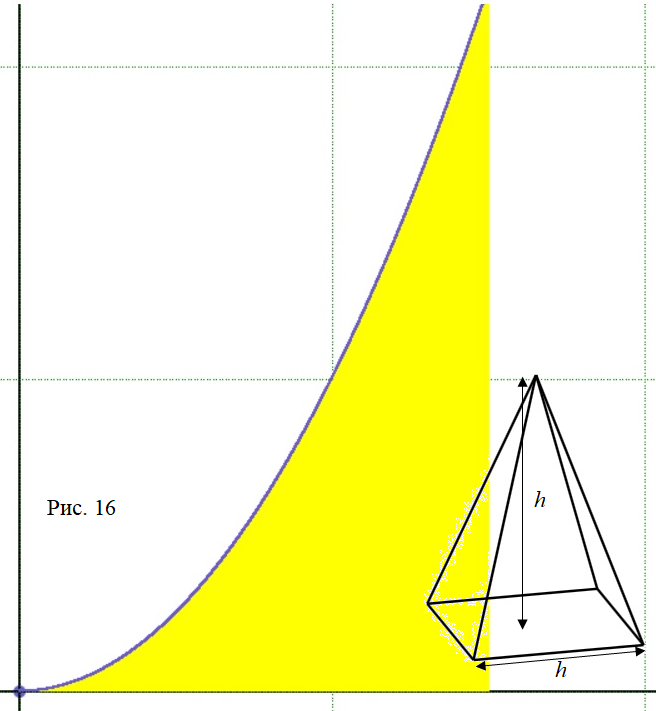
1. Структура Кавальери характеризуется заданной некоторой функцией меры, зависящей от положения неделимой относительно оси. Дать геометрическую интерпретацию этой структуры для случая площади и случая объёма. (В качестве примера можно рассмотреть вопрос, проиллюстрированный рисунком 16, о связи площади криволинейной трапеции, ограниченной параболой, и объёмом пирамиды).
2. Структуру Кавальери, связанную определением площади интерпретировать как структуру вычисления объёма.
3. Структуру Кавальери, связанную определением объёма интерпретировать как структуру вычисления площади.
Исходной структурой при рассмотрении той или иной задачи, как правило, удобнее брать криволинейную трапецию. Таким образом, начнём с рассмотрения задач, связанных с продольным делением криволинейных трапеций.
Отметим тот факт, что в отличие от задач поперечного деления, постановка которых однозначна, задачи продольного деления в целом неопределённы. Продемонстрируем это на примере. В качестве криволинейной трапеции используем прямоугольник (в этом случае функция, определяющая меру, является постоянной ).
Общая постановка задачи. Провести продольное деление прямоугольника на две части равной площади.
Решение задачи может быть проведено бесконечным количеством способов. При этом для каждого решения должно выполняться только одно услови
Итак, задачу следует конкретизировать. Рассмотрим пример.
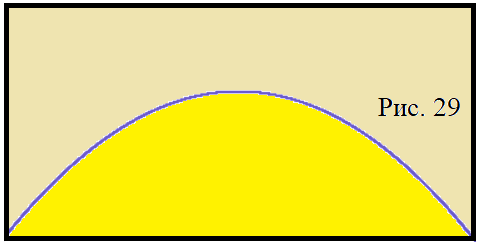
Решение. Прямоугольник является областью на декартовой плоскости, определяемой неравенствами . Функция, определяющая сегмент параболы, определяется уравнением .
Площадь сегмента равна . В итоге получаем, что . Например, для случая квадрата, определяемого параметрами коэффициент равен .
Ещё одна поясняющая задача. Отсечь от прямоугольника с параметрами параболический сегмент, площадь которого равна двум третям площади прямоугольника. Дать интерпретацию, связанную с вычислением объёма.

Таким образом, в трёхмерном случае производится отсечение от цилиндра вписанного в него шара, то есть рассматривается знаменитый результат Архимеда, связанный с вычислением объёма шара. Более того, чертёж, иллюстрирующий данный результат, как известно, был размещён на могиле величайшего математика всех времён и народов (рис. 30).
После рассмотрения поясняющих задач перейдём к рассмотрению ряда заданий, начиная с весьма простых и постепенно переходя к более сложным. В очередной раз напомним, что в рамках тифлопедагогики уместны даже очень простые задачи.
1. Выполнить продольное деление треугольника на заданное количество равных по площади треугольников.
2. Выполнить продольное деление треугольника на заданное количество треугольников с заданным отношением площадей.
3. Выполнить продольное деление трапеции на заданное количество равных по площади трапеций.
4. Выполнить продольное деление трапеции на заданное количество трапеций с заданным отношением площадей.
Пояснение. Эти задачи следует решать методами элементарной геометрии, которые указывают, что нужно делить основания треугольников и трапеций в соответствующих отношениях. Ещё один возможный вариант подхода к этим задачам – использование криволинейных трапеций, ограниченных графиком линейной функции.
Аналогичные задачи могут быть рассмотрены в отношении трёхмерных структур.
5. Выполнить продольное деление конуса на заданное количество конусов с заданным отношением объёмов.
6. Выполнить продольное деление усечённого конуса на заданное количество конусов с заданным отношением объёмов.
Пояснение. В этих задачах студент должен начать с рассмотрения площадей оснований конусов, имеющих заданные отношения, а затем перейти к определению радиусов этих оснований.
Рассмотрим более сложные задачи, имеющие к тому же более общую постановку.
7. Выполнить продольное деление криволинейной трапеции на заданное количество криволинейных трапеций с заданным отношением площадей.
Решение. Задачу деления криволинейной трапеции на несколько областей можно последовательно свести к задаче деления криволинейной трапеции на две части с заданным отношением площадей. Пусть криволинейная трапеция ограничена сверху графиком функции . Нужно выполнить её продольное деление, при котором площади частей будут относится друг к другу как m к n. Очевидно, что график функции решает эту задачу.
8. Плоская область ограничена графиками двух функций. Выполнить продольное деление области на заданное количество областей с заданным отношением площадей.
Решение. Используем криволинейную трапецию, ограниченную графиком разности соответствующих функций. Согласно принципу Кавальери топологическое преобразование исходной области в криволинейную трапецию сохраняет площадь, а, следовательно, позволяет перейти к условиям предыдущей задачи.

9. Выполнить продольное деление прямоугольника на два криволинейных треугольника равной площади с помощью нелинейной функции.
Пояснение. Расположив прямоугольник так, чтобы его стороны были параллельны осям координат, а его центр совпадал с началом координат можно использовать для деления любую подходящую нечётную функцию (рис. 31). Подходящей же является функция, график которой проходит через противоположные углы прямоугольника и расположен внутри этого прямоугольника.

10. Выполнить продольное деление прямоугольника на несколько криволинейных треугольников произвольной площади с помощью нелинейных функций.
Пояснение. Можно построить нижний график (функция , который удовлетворяет условиям, налагаемым на функции. Затем над ним следует построить следующий график (функция и так далее. Следует отметить, что в такой форме построение выглядит довольно кустарным. При этом требуется следить за правильным поведением функций, что требует определённых усилий в случае, когда функции задаются аналитически. Зато нарисовать графики от руки не представляет труда.

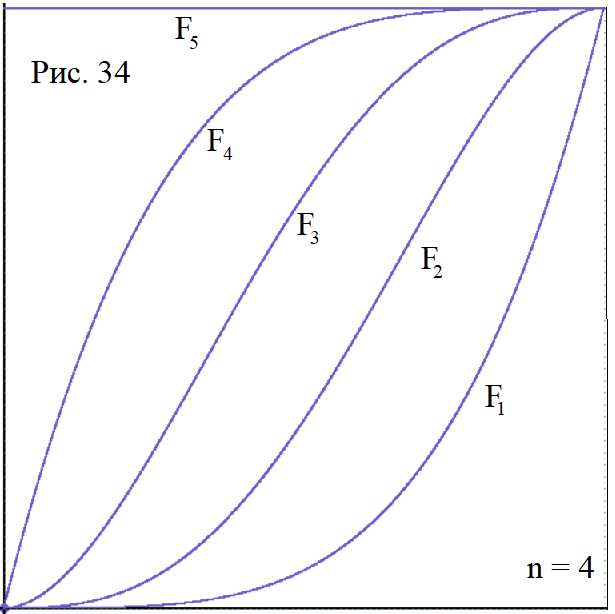
Для деления прямоугольника на несколько областей можно использовать и многочлены степени n, имеющие вид , где – число сочетаний из n по k.
11. Выполнить продольное деление прямоугольника с помощью соответствующих многочленов. Доказать, что области, полученные в результате деления, имеют равные площади (рис. 34).
Решение. Положим, что . Очевидно, что = 1. Выбранные таким образом графики функций как раз и производят искомое деление прямоугольника. Более того, это деление выполнено вполне корректно, то есть графики проходят через угловые точки и не пересекаются во внутренних точках прямоугольника.
Доказательство равенства площади соответствующих областей выполняется с помощью следующей цепочки вычислений. Площадь области между графиками и равна (выбор отрезка [0; Степанов, 2017] не приводит к потере общности). Будем вычислять интеграл по частям. Положим, что и . Тогда и .
Таким образом, доказано равенство площадей двух соседних областей, а, значит, и площадей всех областей, на которые разделён прямоугольник. Следовательно, площадь каждой из областей равна .
Соответствующая геометрическая конструкция позволяет обратиться к задачам теории вероятностей, поскольку область, разделённая на части, наводит на мысли о связи с геометрическими вероятностями [Кендалл, 1972]. Только что рассмотренная задача непосредственно приводит к следующему заданию.
12. Проводится серия из n испытаний по схеме Бернулли. Вероятность успешного исхода испытания выбирается перед проведением серии испытаний наугад. Найти вероятность того, что в результате испытаний выпадет ровно k успехов.
Продольное деление криволинейных трапеций более сложно, чем деление прямоугольников и позволяет рассмотреть большое количество соответствующих задач. При этом следует учитывать тот факт, что диагональная линия, с помощью которой разделена трапеция, должна находиться внутри трапеции. Это накладывает ограничения и на эту линию и на график функции, ограничивающий трапецию. По этой причине прежде чем ставить задачу деления трапеции, нужно предварительно эту трапецию построить.
13.

Решение. Будем опираться на некоторые методы вычислительной математики [21. Демидович, 1966]. Использоваться будет интерполяционный многочлен Лагранжа и формула Симпсона, позволяющая определить площадь криволинейной трапеции. При этом в случае, когда криволинейная трапеция ограничена квадратичной функцией, формула Симпсона даёт точное значение площади.
Сначала построим интерполяционный многочлен, проходящий через точки ( . Тогда площадь криволинейной трапеции по формуле Симпсона .
Разделим её на две части прямолинейной диагональю с уравнением . После деления криволинейная трапеция будет разбита на две части, имеющие площади 4 и 3. Нужно искривить линию деления так, чтобы уравнять площади.

Теперь можно заменить прямую на параболу . Эта замена решает задачу (рис. 36).

С топологической точки зрения в рамках принципа Кавальери нет разницы между параллелепипедом и прямым круговым цилиндром, имеющими одинаковую высоту и обладающими горизонтальными сечениями равной площади. Однако изучение результатов продольного деления этих геометрических тел даже при внешнем сходстве способа деления показывает, что требуются разные подходы.


Выполним продольное деление цилиндра на два равных по объёму веретёнообразных тела. При этом рассмотрим два варианта: сечение цилиндра плоскостью и деление, при котором горизонтальные сечения являются секторами с линейно растущими по мере изменения высоты сечений площадями (рис. 39).
14. Рассмотрим сечение цилиндра плоскостью и вычислим площади неделимых.
Решение. Как мы говорили выше, в этом случае горизонтальные сечения являются сегментами (рис. 40).
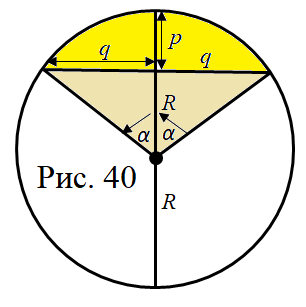
.
Здесь можно ощутить, как простой геометрический способ деления цилиндра приводит весьма сложным формулам, выражающим зависимость площадей неделимых от высоты.
15. Преобразовать две дольки цилиндра, рассечённого плоскостью в функциональные тела вращения (ФТВ).

Полученное разбиение можно представить в виде в графической форме (рис. 41). Студентам с дефектами зрения желательно представить соответствующие осязательные модели.
Результатом разбиения цилиндра, проведённого в предыдущем задании, стали два тела, очень похожие на конусы, но, образно говоря, «более полные», чем конусы. Возможно, это обстоятельство может противоречить чьей-то геометрической, интуиции.
16. Вычесть из цилиндра два разнонаправленных конуса (рис. 42) и установить, какое тело получается в результате.
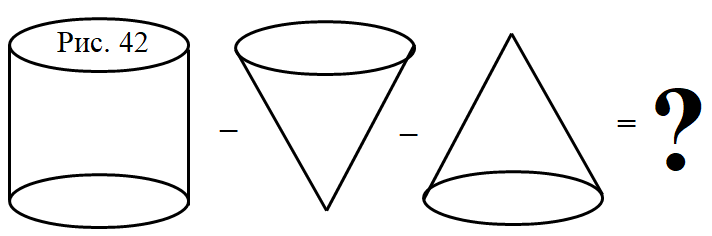
Решение. Задание можно записать в форме математического комикса. При этом следует учесть, что в соответствующих заданиях основания изображённых на схемах объектов одинаковы. Решение задания в данном случае не требует вычислений. Объём конуса равен трети объёма цилиндра. По этой причине после вычитания из цилиндра двух разнонаправленных конусов будет получено обоюдоострое «веретено» с таким же объёмом. Это тело, распределённое, при делении на две части и привело к «утолщению» конусов.
Изменив геометрическое условие задачи, можно получить интересный результат, позволяющий разделить исходный объект на вычислимые объёмы.
17. Вычесть из правильной четырёхгранной призмы две разнонаправленных пирамиды и установить, какое тело получается в результате.
Решение. Чертёж для призмы и двух пирамид, по сути, должен повторять рис. 42. По этой причине мы его не приводим. Площади сечений пирамид, проведённые на высоте h, пропорциональны для одной пирамиды и для противоположно направленной пирамиды. Таким образом, с вычислительной точки зрения речь идёт о разбиении прямоугольника многочленами (см. рис 34) для случая n = 2.
Тело, которое останется после удаления пирамид, соответствует многочлену . Речь идёт о тетраэдре, который расположен особым образом по отношению к оси системы Кавальери (см. рис. 15).
Итак, нами получено разбиение параллелепипеда на две четырёхгранных пирамиды и тетраэдр. Все три объекта имеют одинаковые объёмы.
Вернёмся к рассмотрению клина, получаемого рассечением параллелепипеда диагональной плоскостью (см. рис. 37).
18. Преобразовать клин в ФТВ.
Решение. Как мы уже говорили, площади неделимых для клина линейно зависят от высоты. При преобразовании клина в ФТВ, как и ранее, используется корень квадратный из этой функции. Легко понять, что ФТВ является параболоидом вращения.
Рассмотрим теперь вместо параллелепипеда цилиндр. Если придумать способ, с помощью которого цилиндр будет разрезан на две равных по объёму части так, чтобы их неделимые линейно зависели от высоты, то цилиндр будет разбит на два противоположно расположенных параболоида вращения.
19. Придумать способ деления цилиндра, обеспечивающий линейный рост площадей сечения.
Решение. Фактически этот способ уже описан ранее. Деление цилиндра производится так, чтобы горизонтальные сечения являлись секторами с линейно растущими по мере изменения высоты сечений площадями (см. рис. 39).
Очевидно, что линейно расти должен угол сектора. Возможны различные варианты взаимного расположения секторов. Мы выберем вариант, при котором биссектрисы всех секторов образуют плоскость, проходящую через ось цилиндра.
Конструкция рассечения цилиндра на две равные дольки в целом понятна, но представить себе рассекающую цилиндр поверхность не так уж просто. Естественно, что желательно наличие осязательной модели. Здесь же мы ограничимся рисунком, который даёт объёмное изображение сечения, а также его изображения в двух ракурсах (рис. 43).
Вернёмся к задаче Архимеда, связанной с вычислением объёма шара. На её примере сформулируем задание, которое, в конечном счёте, связано с продольным делением трёхмерных объектов. Задание кратко формулируется одной фразой или предлагается в виде рисунка (рис. 44). То же самое можно сказать и об ответе – либо фраза, либо рисунок (рис. 45).


20. Вычесть из цилиндра конус.
Ответ. Будет получена полусфера.
Если отказаться от условия равенства высоты цилиндра радиусу, то задача может быть переформулирована.
21. Вычесть из цилиндра половину эллипсоида вращения.
Сформулируем ещё несколько заданий подобного рода.
22. Вычесть из цилиндра усечённый конус.
23. Вычесть из усечённого конуса цилиндр того же радиуса, которое имеет малое основание конуса.
24. Вычесть из усечённого конус того же радиуса, которое имеет малое основание конуса.
25. Разделить параболоид вращения на три веретёнообразных тела равного объёма.
Пояснение. Вычесть из параболоида конус. Полученное обоюдоострое веретено имеет объём равный трети параболоида, а конус – две трети.
12. ВЫВОДЫ
Рассматривая в данной статье вопросы, связанные с изучением математики студентами с дефектами зрения, авторы исходили из того, что понимание учебного материала в значительной степени основывается на образном мышлении. Однако именно в области тифлопедагогики особенно затруднены пути развития этого вида мышления.
Одним из способов решения этой проблемы является использование осязательной предметности, но это только один из путей достижения поставленной педагогической задачи и притом не самый важный. Необходим системный подход, позволяющий соединить воедино различные направления и идеи, используемые при обучении математике. Авторы предполагают, что для эффективного осуществления такого системного подхода необходимо основываться на системах заданий, позволяющих студентам с дефектами зрения успешно осваивать различные разделы математики. Авторы считают, что основной педагогической целью разработки таких систем заданий является создание атмосферы целенаправленного размышления по вопросам, связанным с изучаемой темой.
Авторы демонстрируют в статье, сколь сложна и объёмна задача построения системы заданий даже в рамках одной достаточно конкретной темы. В статье как пример рассматриваются вопросы, относящиеся к интегральному исчислению. Кроме всего прочего следует отметить, что разработка заданий, связанных с тифлопедагогикой, нередко приводит к созданию задач с оригинальным содержанием, представляющих общий интерес, например, при изучении математического анализа.
Основной вывод, вытекающий из статьи, состоит в том, что в области тифлопедагогике заинтересованные педагоги могут увидеть перед собой непочатый край интересной и важной работы. Авторы надеются, что их статья послужит стимулом для включения в эту работу, хотя бы нескольких новых энтузиастов.
Литература
- Степанов М. Е. Из опыта работы в области тифлопедагогики. Моделирование и анализ данных. Научный журнал. – №1, 2017.
- Куланин Е. Д., Степанов М. Е., Нгуен Ву Куанг. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. – №4, 2019.
- Степанов М. Е. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – Вып. 3., 2007.
- Степанов М. Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. Научный журнал. – №1, 2017.
- Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. Научный журнал. №4, 2019.
- Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. Том 10. № 2., 2020.
- Платон. Собрание сочинений в 4 томах. Том 1. М.: Мысль, 1990.
- Прасолов В. В. Три классические задачи на построение. М. Наука, 1992.
- Бухштаб А. А. Теория чисел. М.: Просвещение, 1966.
- Кордемский Б. А. Математическая смекалка. М.: Гос. изд. Технико-теоретической лит., 1956.
- Зубов В. П. Леонардо да Винчи. 1452 – 1519. М., Наука, 2008.
- Никифировский В. А. Путь к интегралу. М., Наука, 1985.
- Историко-математические исследования. М.: Наука, 1985, Вып. 28.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Том 2. М.: Наука, 1966.
- Балк М. Б., Болтянский В. Г. Геометрия масс. М.: Наука, 1987.
- Башмакова И. Г. Диофант и диофантовы уравнения. М.: Наука, 1972.
- Серпинский В. О решении уравнений в целых числах. М.: Гос. изд. физ.-мат. лит. 1961.
- Курош А. Г. Курс высшей алгебры. М.: Наука, 1968.
- Степанов М. Е. Некоторые вопросы, связанные с интерполяционным многочленом Эрмита. Моделирование и анализ данных. Научный журнал. – №1, 2014.
- Кендалл М., Моран П. Геометрические вероятности. М.: Наука. 1972.
- 21. Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1966.
Информация об авторах
Метрики
Просмотров web
За все время: 540
В прошлом месяце: 14
В текущем месяце: 10
Скачиваний PDF
За все время: 155
В прошлом месяце: 5
В текущем месяце: 8
Всего
За все время: 695
В прошлом месяце: 19
В текущем месяце: 18