Моделирование и анализ данных
2023. Том 13. № 2. С. 151–179
doi:10.17759/mda.2023130209
ISSN: 2219-3758 / 2311-9454 (online)
Суперэллипсоидальные аппроксимации в задаче быстродействия для двумерной линейной дискретной системы с ограниченным управлением
Аннотация
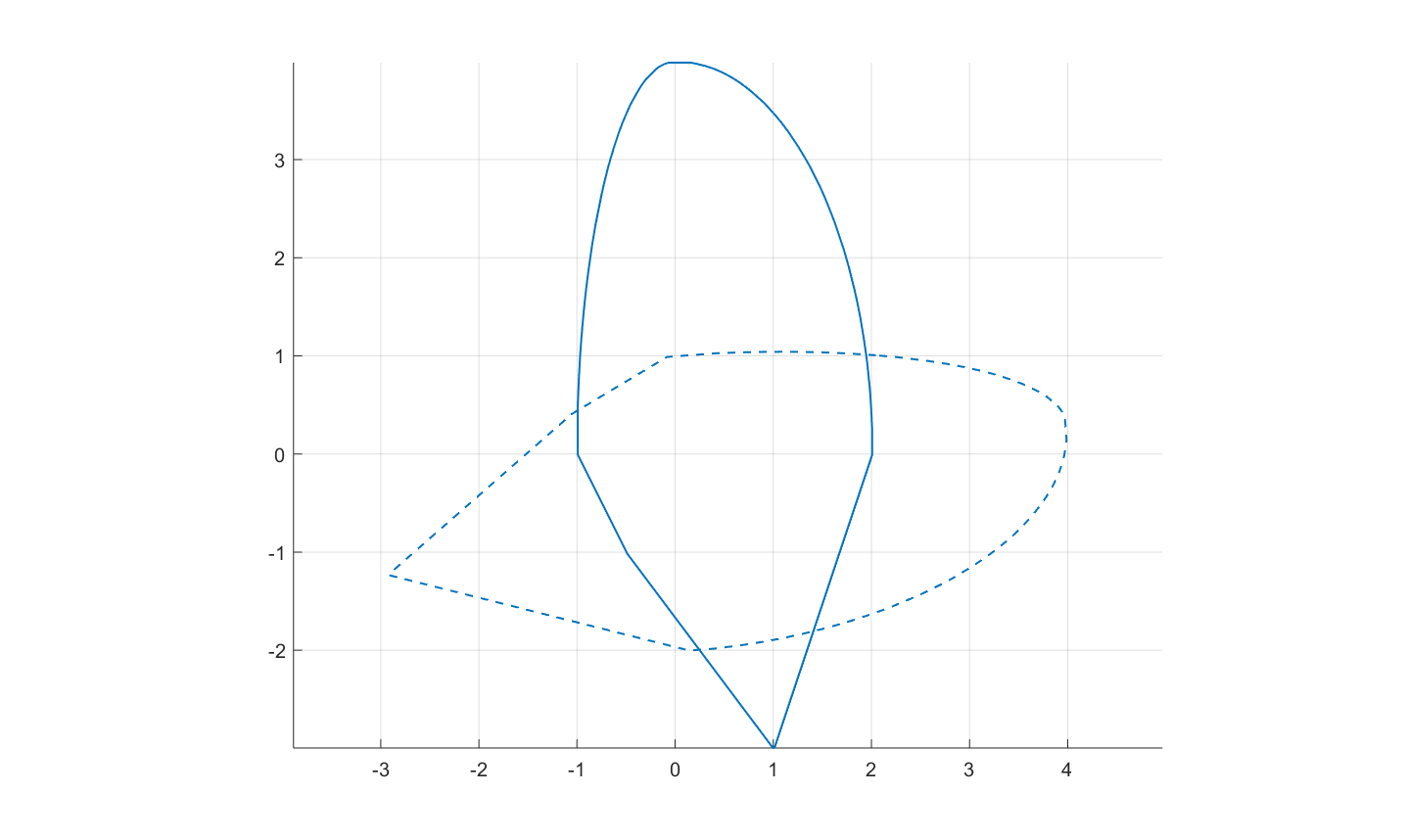
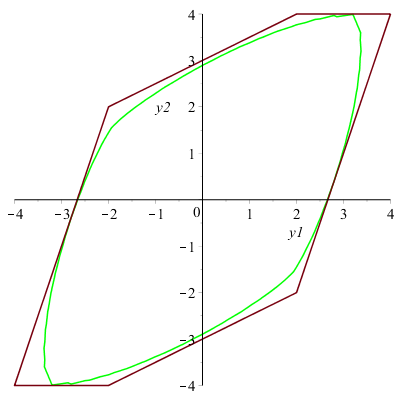
В статье рассматривается двумерная линейная дискретная система с ограниченным управлением. Для системы решается задача быстродействия, то есть построение процесса управления, который переводит систему из начального состояния в начало координат за минимальное число шагов. Если множество допустимых значений управления имеет структуру суперэллипса, то задача вычисления оптимального управления может быть сведена к решению системы алгебраических уравнений. Для множеств произвольной структуры разработан метод суперэллипсоидальной аппроксимации. Приведены примеры.
Общая информация
Ключевые слова: система управления, задача быстродействия, принцип максимума, суперэллипс
Рубрика издания: Методы оптимизации
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130209
Получена: 25.04.2023
Принята в печать:
Для цитаты: Ибрагимов Д.Н., Подгорная В.М. Суперэллипсоидальные аппроксимации в задаче быстродействия для двумерной линейной дискретной системы с ограниченным управлением // Моделирование и анализ данных. 2023. Том 13. № 2. С. 151–179. DOI: 10.17759/mda.2023130209
Полный текст
Введение
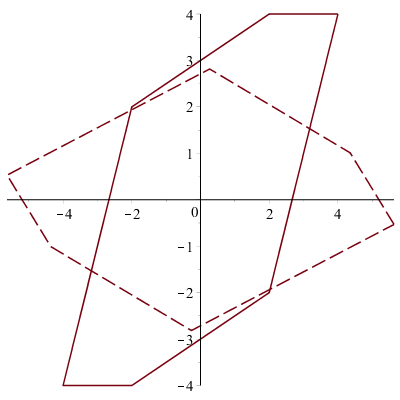
Заключение
Литература
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа // М.: Физматлит. 2012.
- Ашманов С.А., Тимохов С.В. Теория оптимизации в задачах и упражнениях // М.: Наука. 1991.
- Рокафеллар Р. Выпуклый анализ // М.: Мир. 1973.
- Ибрагимов Д.Н., Сиротин А.Н. О задаче быстродействия для класса линейных автономных бесконечномерных систем с дискретным временем и ограниченным управлением // АиТ. 2017. № 10. C. 3–32.
- Ибрагимов Д.Н. О задаче быстродействия для класса линейных автономных бесконечномерных систем с дискретным временем, ограниченным управлением и вырожденным оператором // АиТ. 2019. № 3. C. 3–25.
- Ибрагимов Д.Н., Новожилкин Н.М., Порцева Е.Ю. О достаточных условиях оптимальности гарантирующего управления в задаче быстродействия для линейной нестационарной дискретной системы с ограниченным управлением // АиТ. 2021. № 12. С. 48–72.
- Ибрагимов Д.Н. Оптимальная по быстродействию коррекция орбиты спутника [Электронный ресурс] // Тр. МАИ. 2017. № 94. Доступ в журн. http://trudymai.ru/published.php
- Беллман Р. Динамическое программирование // М.: ИИЛ. 1960.
- Каменев Г.К. Численное исследование эффективности методов полиэдральной аппроксимации выпуклых тел // М.: Вычислительный центр РАН. 2010.
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Б.Ф. Математическая теория оптимальных процессов // М.: Наука. 1969.
- Болтянский В.Г. Оптимальное управление дискретными системами // М.: Наука. 1973.
- Пропой А.И. Элементы теории оптимальных дискретных процессов // М.: Наука. 1973.
- Kurzhanskiy A., Varaiya P. Ellipsoidal Techniques for Reachability Analysis of Discrete-Time Linear Systems // IEEE Transactions on Automatic Control. 2007. Vol. 52, №.1. P. 26–38. DOI: 10.1109/TAC.2006.887900
- Tobler W. R. Superquadrics and Angle-Preserving Transformations // IEEECGA. 1981. Vol. 1. №. 1. P. 11–23.
- Tobler W.R. The Hyperelliptical and Other New Pseudo Cylindrical Equal Area Map Projections // Journal of Geophysical Research. 1973. Vol. 78. №. 11. P. 1753–1759.
- Desoer C.A., Wing J. The Minimal Time Regulator Problem for Linear Sampled-Data Systems: General Theory // J. Franklin Inst. 1961. Vol. 272. №. 3. P. 208–228.
- Lin W.-S. Time-Optimal Control Strategy for Saturating Linear Discrete Systems // Int. J. Control. 1986. Vol. 43. №. 5. P. 1343–1351.
- Мороз А.И. Синтез оптимального по быстродействию управления для линейного дискретного объекта третьего порядка // АиТ. 1965. № 2. С. 193–207.
- Черноусько Ф.Л. Оценивание фазового состояния динамических систем. Метод эллипсоидов // М.: Наукa. 1988.
- Хорн Р., Джонсон И. Матричный анализ // М.: Мир. 1989.
- Ибрагимов Д.Н., Берендакова А.В. Метод построения и оценивания асимптотических множеств управляемости двумерных линейных дискретных систем с ограниченным управлением // Труды МАИ. 2022. № 126. DOI: 10.34759/trd-2022-126-17
Информация об авторах
Метрики
Просмотров web
За все время: 187
В прошлом месяце: 22
В текущем месяце: 5
Скачиваний PDF
За все время: 63
В прошлом месяце: 7
В текущем месяце: 7
Всего
За все время: 250
В прошлом месяце: 29
В текущем месяце: 12