Моделирование и анализ данных
2023. Том 13. № 4. С. 84–110
doi:10.17759/mda.2023130405
ISSN: 2219-3758 / 2311-9454 (online)
Методы численного моделирования множеств 0-управляемости линейной дискретной динамической системы с ограниченным управлением на основе алгоритмов полиэдральной аппроксимации
Аннотация
В статье рассматривается задача построения полиэдральной аппроксимации множеств 0-управляемости линейной дискретной системы с линейными ограничениями на управление. Для проведения аппроксимации предлагается использование двух эвристических алгоритмов, нацеленных на уменьшение числа вершин произвольного многогранника при сохранении точности описания в смысле расстояния Хаусдорфа. Продемонстрировано сведение задачи вычисления расстояния между вложенными многогранниками к задаче выпуклого программирования. Исследованы вопросы оптимальности полученных аппроксимаций. Приведены примеры.
Общая информация
Ключевые слова: система управления, множество управляемости, выпуклый многогранник, полиэдральная аппроксимация, линейное программирование
Рубрика издания: Методы оптимизации
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130405
Финансирование. Работа выполнена при финансовой поддержке Российского научного фонда (грант № 23-21-00293).
Получена: 01.11.2023
Принята в печать:
Для цитаты: Мохначева А.А., Герасимова К.В., Ибрагимов Д.Н. Методы численного моделирования множеств 0-управляемости линейной дискретной динамической системы с ограниченным управлением на основе алгоритмов полиэдральной аппроксимации // Моделирование и анализ данных. 2023. Том 13. № 4. С. 84–110. DOI: 10.17759/mda.2023130405
Полный текст
Введение
Использование множеств достижимости и управляемости в теории управления является довольно широкой практикой, начиная с фундаментальных монографий [1, 2, 9] и заканчивая современными работами в данной тематике [3, 4, 11, 13–21]. Они могут быть использованы как для анализа заданной системы на управляемость [11, 14, 17, 18, 21], так и для формирования оптимального позиционного управления [3, 4, 16] в различных задачах синтеза. В последнем случае множества управляемости и достижимости определяют набор ограничений в задачах выпуклого программирования, к которым сводится решение задачи оптимального управления.
В большинстве работ рассматриваются вопросы построения точного описания множеств управляемости [3, 4, 13, 18] либо исследования их общих свойств [11, 14, 15, 17, 19]. При этом построение точного описания в случае наличия ограничений на управление может быть весьма трудоемкой задачей с вычислительной точки зрения. Так при наличии исключительно линейных ограничений на управление все множества управляемости линейной дискретной системы представляют собой выпуклые многогранники [Ибрагимов, 2021], число вершин которых растет с экспоненциальной скоростью в зависимости от рассматриваемого временного горизонта [Heemels W.P, 2008]. В свою очередь, например, при решении задачи быстродействия для линейной дискретной системы вычисление оптимального позиционного управления в случае линейных ограничений сводится к решению ряда задач линейного программирования, размерность которых совпадает с числом крайних точек множества 0-управляемости [Ибрагимов, 2021], представляющего собой многогранник. Этот факт делает процедуру решения соответствующей задачи оптимального управления фактически нереализуемой стандартными средствами.
Известен подход, направленный на проведение аппроксимации множеств управляемости в случае их сложной структуры. Для этих целей используются, как правило, полиэдральные [Fucheng, 2019] и эллипсоидальные оценки [Ge, 2001]. Недостаток последних связан с недостаточным порядком точности и сложностью их применения для решения задач оптимального управления. Известные методы полиэдральной аппроксимации [Ибрагимов, 2017], наоборот, нацелены на достижение произвольной заранее заданной точности без учета сложности результирующей оценки.
В связи с этим оказывается актуальной адаптация методов полиэдральной аппроксимации множеств управляемости многогранниками с меньшим числом вершин при сохранении заданного порядка точности. Подробно методы полиэдральной аппроксимации выпуклых компактных тел с критерием качества в форме расстояния Хаусдорфа рассмотрены в [Ибрагимов, 2017]. Однако в отличие от классического подхода, нацеленного на построение аппроксимирующего многогранника за минимальное время, в данной статье предлагается минимизировать число вершин результирующего многогранника при фиксированном ограничении на погрешность аппроксимации, что позволит значительно снизить временные затраты на решение различных задач оптимального управления.
Целью данной работы является применение адаптивных методов полиэдральной ап- проксимации для построения минимальной в смысле описания внутренней оценки множества 0-управляемости линейной дискретной системы с заданной точностью в смысле расстояния Хаусдорфа. Существенным является сохранение полиномиальной сложности рассматриваемых алгоритмов, что во многом базируется на их адаптивном характере [Ибрагимов, 2017] и сведении вычисления расстояния Хаусдорфа между вложенными многогранниками к задачам квадратичного программирования [Ibragimov, 2017].
Обозначения
Для произвольного X ⊂ R n обозначим через conv X выпуклую оболочку множества X – наименьшее по включению выпуклое множество, содержащее X в качестве подмножества. Через int X обозначим множество внутренних точек X , через Ext X – множество крайних точек, которое для многогранника совпадает с множеством его вершин. Под card X будем подразумевать мощность множества X , что в случае конечного X является числом его элементов.
Пространство R n будем рассматривать в качестве евклидового со скалярным произведением, определяемым соотношением
( x , y ) = ∑ i = 1 n x i y i , x , y ∈ R n .
Под нормой вектора x ∈ R n , если не оговорено иное, будем понимать норму, ассоциированную со скалярным произведением: ‖ x ‖ = ( x , x ) . Диаметр множества X – расстояние между наиболее удаленными друг от друга его элементами – обозначим, через diam X .
Для произвольных X , U ⊂ R n и A ϵ R n × n введем сумму по Минковскому и образ множества следующим образом:
X + U = \{ x + u : x ∈ X , u ∈ U } , A U = \{ A u : u ∈ U } .
Постановка задачи
Рассматривается линейная дискретная система управления (A, U ):
x ( k + 1 ) = Ax ( k ) + u ( k ) ,
x ( 0 ) = x 0 , u ( k ) ∈ U , k ∈ N ∪ { 0 } , ( 1 )
где x ( k ) ∈ R n – вектор состояния, u ( k ) ∈ R n – управляющее воздействие, A ϵ R n × n – матрица системы, U ⊂ R n – множество допустимых значений управлений. Предполагается, что U – выпуклый многогранник, содержащий 0 в качестве относительно внутренней точки:
U = conv \{ u 1 , … , u M \} . ( 2 )
Без ограничения общности будем далее полагать, что \{ u 1 , … , u M \} ⊂ R n совпадает с множеством вершин многогранника:
Ext U = \{ u 1 , … , u M \} .
Рассматривается задача построения класса множеств 0-управляемости { X ( N ) } N = 0 ∞ системы (1), где каждое X ( N ) состоит из тех начальных состояний, из которых систему (1) возможно перевести в начало координат за N шагов посредством выбора допустимого управления:
X ( N ) = { { x 0 ∈ R n : ∃ u ( 0 ) , … , u ( N − 1 ) ∈ U : x ( N ) = 0 } , N ϵ N , 0 , N = 0. ( 3 )
Как продемонстрировано в [4, лемма 1], в случае невырожденной матрицы системы множества 0-управляемости допускают следующее описание.
Лемма 1 ([4, лемма 1]). Пусть det A ≠ 0 , класс множеств { X ( N ) } N = 0 ∞ определяется соотношениями (3). Тогда для всех N ϵ N справедливо представление
X ( N ) = − ∑ i = 1 N A − i U ,
X ( N ) = A − 1 X ( N − 1 ) + ( − A − 1 U ) .
Согласно лемме 1 построение множеств 0-управляемости в случае (2) сводится к вычислению суммы по Минковскому линейных преобразований многогранника U . Согласно [Кроновер, 2000] верхняя оценка множества вершин многогранника X ( N ) может быть получена явно:
Ext X ( N ) ⊂ { ∑ i = 1 N A − i u j i , j 1 , … , j N = 1 , M ¯ } , N ϵ N . ( 4 )
Однако использование оценки (4) зачастую неприемлемо для описания множества, так как число ее элементов растет экспоненциально в зависимости от номера шага N :
card { ∑ i = 1 N A − i u j i , j 1 , … , j N = 1 , M ¯ } = M N , N ϵ N .
В общем случае для построения точного описания Ext X ( N ) к оценке (4) применяются соответствующие алгоритмы, например, алгоритм быстрой оболочки [Пропой, 1973]. Явное выражение для вычисления card Ext X ( N ) при произвольном n ϵ N неизвестно, как правило, используются экспоненциальные оценки [22, теорема 4.1.2].
Тем не менее, даже в случае построения точного множества вершин Ext X ( N ) сложность его описания может быть неприемлемой с точки зрения решения последующих оптимизационных задач. По этой причине оказывается актуальной задача построения внутренней полиэдральной аппроксимации X ^ ( N ) множества X ( N ) , обладающей наиболее простым описанием при сохранении заданного порядка точности. В качестве критерия точности описания рассматривается расстояние Хаусдорфа [7, 10].
Формально данная задача может быть представлена следующим образом:
card Ext X ^ ( N ) → min
ρ H , X ( N ) ≤ ε , (5)
Ext X ^ ( N ) ⊂ Ext X ( N ) ,
где ε > 0 – заданная допустимая погрешность аппроксимации, через ρ H ( X , Y ) обозначено расстояние Хаусдорфа между компактными множествами X , Y ⊂ R n :
ρ H ( X , Y ) = max { xϵ X inf yϵ Y ‖ x − y ‖ ; yϵ Y inf xϵ X ‖ x − y ‖ } .
3.
Расстояние Хаусдорфа между многогранниками
Как следует из постановки, для решения задачи ( 5 ) необходимо вычислить расстояние Хаусдорфа ρ H ( X ^ ( N ) , X ( N ) ) . При этом в случае ( 2 ) множества X ^ ( N ) и X ( N ) представляют собой вложенные многогранники. Сведем задачу вычисления расстояния Хаусдорфа между вложенными многогранниками к задаче квадратичного программирования.
Везде далее в разделе 3 будем полагать, что
X = conv \{ x 1 , … , x N \} , Ext X = \{ x 1 , … , x N \} , Y = conv \{ y 1 , … , y M \} , Ext Y = \{ y 1 , … , y M \} .
Лемма 2. Пусть X ⊂ Y . Тогда
ρ H ( X , Y ) = y ∈ Y inf x ∈ X | x − y ∨ = y ∈ Y inf x ∈ X | x − y | ∨ .
Доказательство. Поскольку для каждого x ∈ X ⊂ Y верно
inf y ∈ Y ‖ x − y ‖ ≤ ‖ x − x ‖ = 0 ,
то
x ∈ X inf y ∈ Y ‖ x − y ‖ = 0.
Отсюда следует утверждение леммы 2.
Лемма 3. Пусть функция d X : R n → R определяется соотношением
d X ( y ) = inf x ∈ X ‖ x − y ‖ .
Тогда d X - выпуклая на R n функция.
Доказательство. Пусть для произвольного y ∈ R n
x ( y ) = arg min x ∈ X ‖ x − y ‖ .
Выберем произвольные y ' , y ' ' ∈ R n , λ ∈ [ 0 ; 1 ] . В силу выпуклости X верно включение
λ x ( y ' ) + ( 1 − λ ) x ( y ' ' ) ∈ X .
Тогда
d X ( λ y ' + ( 1 − λ ) y ' ' ) = inf x ∈ X | ∨ x − λ y ' − ( 1 − λ ) y ' ' ∨ | ≤
≤ | | λ x ( y ' ) + ( 1 − λ ) x ( y ' ' ) − λ y ' + ( 1 − λ ) y ' ' | | ≤
≤ λ ∨ | x ( y ' ) − y ' ∨ | + ( 1 − λ ) | x ( y ' ' ) − y ' ' ∨ | = λ d X ( y ' ) + ( 1 − λ ) d X ( y ' ' ) .
Теорема 1. Пусть X ⊂ Y . Тогда
ρ H ( X , Y ) = max j = 1 , M ¯ inf x ∈ X ‖ x − y j ‖ .
Доказательство. В силу леммы 2
ρ H ( X , Y ) = y ∈ Y inf x ∈ X ‖ x − y ‖ = y ∈ Y d X ( y ) .
Так как в силу леммы 3 d X выпукла и определена на R n , то согласно [10, Следствие 32.3.4] d X достигает своего максимума на выпуклом компактном множестве Y в одной из его крайних точек:
y ∈ Y d X ( y ) = y ∈ Ext Y d X ( y ) = max j = 1 , M ¯ d X ( y j ) = max j = 1 , M ¯ inf x ∈ X ‖ x − y j ‖ .
□
Следствие 1. Пусть X ⊂ Y , X = ( x 1 … x N ) ∈ R n × N , λ = ( λ 1 , … λ N ) T ∈ R N . Тогда
ρ H ( X , Y ) = max j = 1 , M ¯ ( ‖ y j ‖ 2 + min λ 1 + ... + λ n = 1 λ i ≥ 0 , i = 1 , N ¯ ( λ T X T X λ − 2 λ T X T y j ) ) .
Доказательство. В силу теоремы 1
ρ H ( X , Y ) = max j = 1 , M ¯ inf x ∈ X ‖ x − y j ‖ = max j = 1 , M ¯ inf x ∈ X ‖ x − y j ‖ 2 =
max j = 1 , M ¯ min λ 1 + ... + λ n = 1 λ i ≥ 0 , i = 1 , N ¯ ‖ ∑ i = 1 N λ i x i − y j ‖ 2 = max j = 1 , M ¯ min λ 1 + ... + λ n = 1 λ i ≥ 0 , i = 1 , N ¯ ‖ X λ − y j ‖ 2 =
max j = 1 , M ¯ min λ 1 + ... + λ n = 1 λ i ≥ 0 , i = 1 , N ¯ ( X λ − y j ) T ( X λ − y j ) ,
что эквивалентно утверждению следствия 1.
□
Согласно теореме 1 и следствию 1 вычисление расстояния Хаусдорфа между двумя вложенными многогранниками сводится к решению M задач квадратичного программирования с N неотрицательными переменными и одним ограничением вида равенство, M и N – число вершин большего и меньшего по включению многогранников соответственно.
Алгоритмы полиэдральной аппроксимации многогранника
Очевидный способ решения задачи (5) заключается в полном переборе всех возможных подмножеств Ext X ( N ) . Данный подход позволяет вычислить точное решение поставленной задачи с экспоненциальной временной сложностью, что для множеств X ( N ) с большим числом вершин неприемлемо в силу значительных вычислительных затрат. В разделе 4 рассмотрим два эвристических алгоритма, обладающих полиномиальной временной сложностью, которые позволяют строить множество X ^ ( N ) достаточно близкое к оптимальному.
Везде далее в разделе 4 будем полагать, что 0 ∈ X ⊂ R n и верно представление
X = conv \{ x 1 , … , x N \} , Ext X = \{ x 1 , … , x N \} .
Введём обозначения для произвольного I ⊂ { 1 , … , N } :
X ^ ( I ) = { conv { x ⅈ : i ∈ I } , I ≠ ∅ , 0 , I = ∅ .
Тогда задача (5) может быть преобразована в эквивалентный вид:
card I → min I ⊂ { 1 , … , N } , ε ( I ) ≤ ε ( 6 )
Будем называть набор индексов I ⊂ { 1 , … , N } : оптимальным, если он является точкой минимума задачи (6). Сложность решения задачи (6) заключается в том, что оптимальный набор индексов, вообще говоря, может быть не единственным.
Пример 1. Пусть X = conv { x ⅈ = ( cos 2 π ⅈ N , sin 2 π ⅈ N ) T : ⅈ = 1 , N ¯ } ⊂ R 2 , N > 2 . Рассмотрим в качестве ε расстояние от вершины X до отрезка, соединяющего две смежные вершины:
ε = ρ ( x ⅈ , conv { x ⅈ − 1 , x ⅈ + 1 } ) = inf x ∈ conv { x ⅈ − 1 , x ⅈ + 1 } ‖ x ⅈ − x ‖ , i = 1 , N ¯ .
Здесь предполагается, что x 0 = x N .
Поскольку X представляет собой правильный многогранник, вписанный в окружность радиуса 1, то для всех i = 1 , N ¯
ε = inf x ∈ conv { x ⅈ − 1 , x ⅈ + 1 } ‖ x ⅈ − x ‖ = ‖ x ⅈ − x ⅈ + 1 + x ⅈ − 1 2 ‖ =
( ( cos 2 π ⅈ N − 1 2 cos 2 π ( ⅈ − 1 ) N − 1 2 cos 2 π ( ⅈ + 1 ) N ) 2 + ( sin 2 π ⅈ N − 1 2 sin 2 π ( ⅈ − 1 ) N − 1 2 sin 2 π ( ⅈ + 1 ) N ) 2 ) 1 2 = 1 − cos 2 π N .
Положим N = 8. Тогда для любого I ⊂ \{ 1 , … , 8 } , card I = 3 верно неравенство ε ( I ) > ε . При этом ε ( \{ 1 , 3 , 5 , 7 \} ) = ε ( \{ 2 , 4 , 6 , 8 \} ) = 1 − cos 2 π N = ε . Откуда следует оптимальность наборов {1, 3, 5, 7} и {2, 4, 6, 8}.
Лемма 4. Пусть I 1 ⊂ I 2 ⊂ \{ 1 , … , N \} . Тогда ε ( I 1 ) ≥ ε ( I 2 ) .
Доказательство. Доказательство леммы 4 следует непосредственно из определения расстояния Хаусдорфа и включения X ^ ( I 1 ) ⊂ X ^ ( I 2 ) ⊂ X .
Допустимым набором индексов I ' ⊂ \{ 1 , … , N \} будем называть такой набор индексов, что выполнены следующие два условия:
1.
ε ( I ' ) ≤ ε ;
2.
ε ( I ' ) > ε , для всех I ⊂ I ' , I ≠ I ' .
Из определения следует, что любой оптимальный набор индексов I также является допустимым. Построение оптимального набора I в общем случае затруднительно и сводится к полному перебору. Приведем два алгоритма, нацеленных на построение допустимых наборов индексов, которые могут служить оценкой оптимальных наборов.
Алгоритм 1.
1.
Положить I N ' = \{ 1 , … , N \} и k = N .
2.
Если k = 0 , то завершить алгоритм.
3.
На основе следствия 1 вычислить
j k = arg min j ∈ I k ' ε ( I k ' ∖ \{ j \} ) = arg min j ∈ I k ' ρ H ( X , X ^ ( I k ' ∖ \{ j \} ) ) .
4.
Если ε ( I k ' ∖ \{ j k \} ) > ε , то завершить алгоритм.
5.
Иначе положить I k − 1 ' = I k ' ∖ \{ j k \} , уменьшить k на 1 и перейти к шагу 2.
Алгоритм 2.
1.
Положить I 0 ' ' = ∅ и k = 0 .
2.
На основе следствия 1 вычислить ε ( I k ' ' ) . Если ε ( I k ' ' ) ≤ ε , то положить I k ' = I k ' ' и перейти к шагу 2 алгоритма 1.
3.
Исходя из расчетов, проведенных в пункте 2, вычислить
i k = arg max i ∈ \{ 1 , … , N \} ∖ I k ' ' ( inf x ∈ X ^ ( I k ' ' ) ‖ x − x i ‖ ) .
4.
Положить I k + 1 ' ' = I k ' ' ∪ \{ i k \} , увеличить k на 1 и перейти к шагу 2.
Обозначим через k значение индекса k, на котором завершаются алгоритмы 1 и 2. Согласно определению алгоритм 1 возвращает в ходе работы допустимый набор индексов I k ' . При этом величина N − k является числом итераций алгоритма 1, а k является числом вершин аппроксимирующего многогранника:
k = card Ext X ^ ( I k ) .
С учетом того, что алгоритм 2 завершается вызовом алгоритма 1, то полученный в результате набор индексов I k ' также будет допустимым. При этом для алгоритма 2 переход в пункте 2 к алгоритму 1 является существенным, так как без данного перехода окончательный набор индексов может оказаться недопустимым. Для демонстрации данного факта рассмотрим следующий пример.
Пример 2. Пусть y = ( 0.9 , 0 ) T , рассмотрим следующий набор точек \{ x i \} i = 1 6 ⊂ R 2 :
x 1 = ( − 1 0 ) − y , x 2 = ( 1 0 ) − y , x 3 = ( 0 1 ) − y ,
x 4 = ( 0 − 1 ) − y , x 5 = ( cos 7 π 8 sin 7 π 8 ) − y , x 6 = ( cos 7 π 8 − sin 7 π 8 ) − y .
Пусть X = conv \{ x 1 , … , x 6 \} . Тогда также верно, что Ext X = \{ x 1 , … , x 6 \} , 0 ∈ ∫ X . Выберем ε = 0.1 и применим алгоритм 2 к многограннику X .
Получим следующие результаты, проиллюстрированные на рисунке 1:
I 0 ' ' = ∅ , i 0 = 1 , inf x ∈ X ^ ( I 0 ' ' ) ‖ x − x i 0 ‖ = 1.9 , ε ( I 0 ' ' ∪ \{ i 0 \} ) = 2 ,
I 1 ' ' = { 1 } , i 1 = 2 , inf x ∈ X ^ ( I 1 ' ' ) ‖ x − x i 1 ‖ = 2 , ε ( I 1 ' ' ∪ \{ i 1 \} ) = 1 ,
I 2 ' ' = { 1 , 2 } , i 2 = 3 , inf x ∈ X ^ ( I 2 ' ' ) ‖ x − x i 2 ‖ = 1 , ε ( I 2 ' ' ∪ \{ i 2 \} ) = 1 ,
I 3 ' ' = { 1 , 2 , 3 } , i 3 = 4 , inf x ∈ X ^ ( I 3 ' ' ) ‖ x − x i 3 ‖ = 1 ,
ε ( I 3 ' ' ∪ \{ i 3 \} ) = sin 7 π 8 − cos 7 π 8 − 1 2 ≈ 0.2168 ,
I 4 ' ' = \{ 1 , 2 , 3 , 4 \} , i 4 = 5 , inf x ∈ X ^ ( I 4 ' ' ) ‖ x − x i 4 ‖ = sin 7 π 8 − cos 7 π 8 − 1 2 ≈ 0.2168 ,
ε ( I 4 ' ' ∪ \{ i 4 \} ) = sin 7 π 8 − cos 7 π 8 − 1 2 ≈ 0.2168 ,
I 5 ' ' = \{ 1 , 2 , 3 , 4 , 5 \} , i 5 = 6 , inf x ∈ X ^ ( I 5 ' ' ) ‖ x − x i 5 ‖ = sin 7 π 8 − cos 7 π 8 − 1 2 ≈ 0.2168 ,
ε ( I 5 ' ' ∪ \{ i 5 \} ) = 0 , I 6 ' ' = \{ 1 , … , 6 \} .
Построенный набор I 6 ' ' не является допустимым, так как
\{ 2 , 3 , 4 , 5 , 6 \} ⊂ I 6 ' ' , ε ( \{ 2 , 3 , 4 , 5 , 6 \} ) = 1 + cos 7 π 8 ≈ 0.0761 < ε .
Замечание 1. Алгоритм 2 представляет собой модификацию алгоритма уточнения оценок, рассмотренного в [5, Гл. 4 раздел 4.1]. Отличие заключается в исходном описании многогранника X : в данной работе многогранник рассматривается как выпуклая оболочка конечного числа вершин, в то время как в [Ибрагимов, 2017] используется описание многогранников через систему линейных неравенств. Также в общем случае алгоритм уточнения оценок используется для полиэдральной аппроксимации произвольного выпуклого компакта и не предполагает сходимость за конечное число итераций.
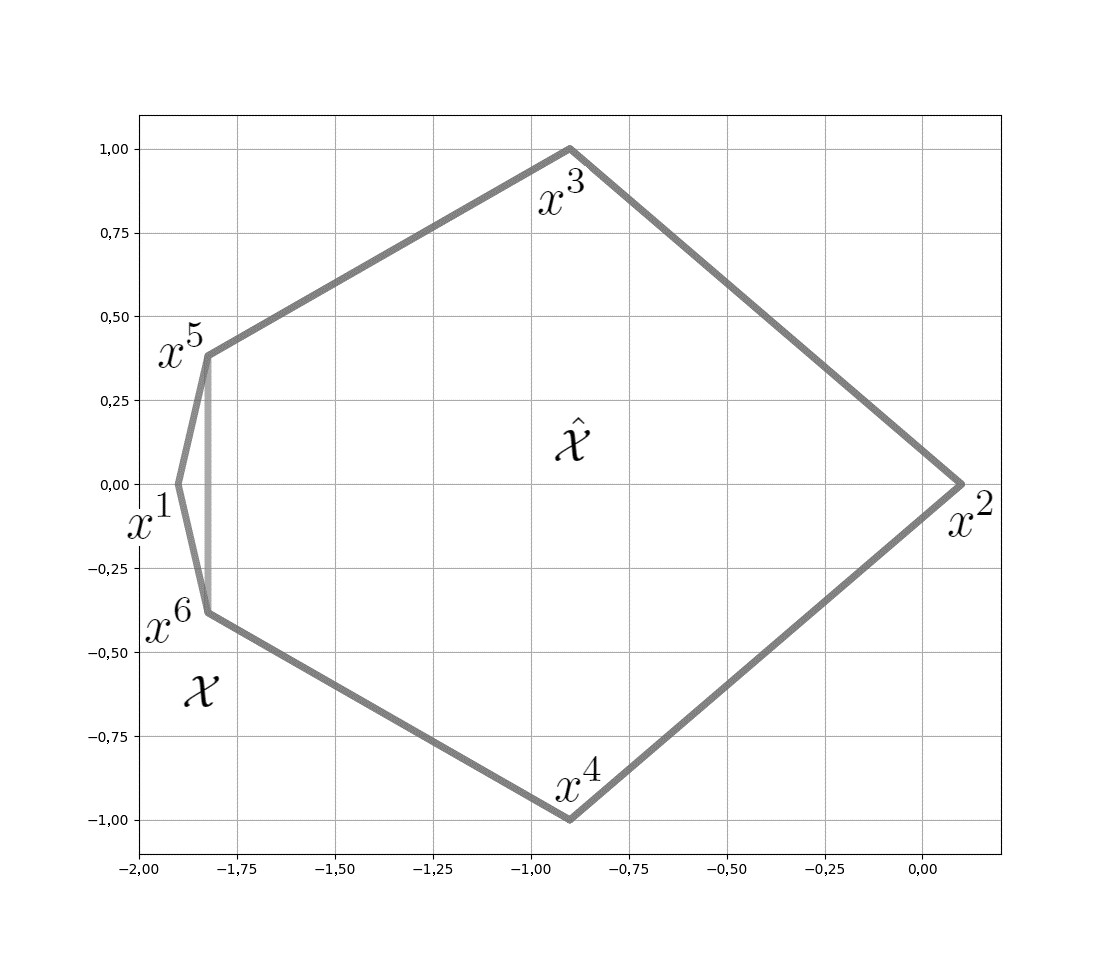
Рис. 1: Аппроксимация X ^ двухмерного многогранника X на основе алгоритма 2, рассмотренного в примере 2.
Вычислительная сложность алгоритмов 1 и 2 сводится к числу решаемых задач квадратичного программирования вида
λ T X T X λ − 2 λ T X T y → min
∑ i = 1 N λ i = 1 , ( 7 )
λ i ≥ 0 , i = 1 , N ¯ ,
к которым сводится вычисление величины ε ( I ) согласно следствию 1 и теореме 1. Обозначим
через QP ( N ) временную сложность решения задачи (7). Поскольку матрица Гессе 2 X T X критериальной функции является симметрической и положительно определенной, то согласно [Ibragimov, 2017] задача (7) может быть решена за полиномиальное время, например, методом эллипсоидов. Сложность алгоритмов 1 и 2 определим в терминах функции QP ( N ) .
Теорема 2. Пусть k – значение индекса k, при котором завершится алгоритм 1 для многогранника X и заданного ε > 0 .
Тогда применение алгоритма 1 потребует решение следующего числа задач вида (7) сложности не более QP ( N − 1 ) :
C 1 ( N ) = ( N + 2 k ) ( N − k + 2 ) ( N − k + 1 ) 6 ≤ N ( N + 1 ) ( N + 2 ) 6 .
Доказательство. Для каждого k = k , N ¯ на шаге 3 происходит перебор по card I k ' = k числу различных индексов для вычисления j k . При этом для каждого j ∈ I k ' происходит вычисление величины ρ H ( X , X ^ ( I k ' ∖ \{ j \} ) ) , что согласно следствию 1 сводится к проектированию card ( \{ 1 , … , N \} ∖ ( I k ' ∖ \{ j \} ) ) = N − k + 1 различных точек на многогранник X ^ ( I k ' ∖ \{ j \} ) c k − 1 вершиной. Таким образом на k-м шаге алгоритма 1 решается k ( N − k + 1 ) задач квадратичного программирования сложности QP ( k − 1 ) .
Тогда
C 1 ( N ) = ∑ k = k N k ( N − k + 1 ) = ( N + 2 k ) ( N − k + 2 ) ( N − k + 1 ) 6 . ( 8 )
Наихудший в смысле сложности случай получается при k = 0 . Однако с учетом шага 2 алгоритма 1 вычисления при данном значении индекса k не проводятся, то есть наибольшее число решенных задач вида (7) определяется значением k = 1 :
C 1 ( N ) ≤ ( N + 2 ⋅ 1 ) ( N − 1 + 2 ) ( N − 1 + 1 ) 6 = N ( N + 1 ) ( N + 2 ) 6 .
□
Теорема 3. Пусть k ∗ - значение индекса k, при котором в алгоритме 2 происходит переход к шагу 2 алгоритма 1 для многогранника X и заданного ε > 0 , k - значение индекса k, при котором завершится вызванный алгоритм 1.
Тогда применение алгоритма 2 потребует решение следующего числа задач вида (7) сложности не более QP :
C 2 ( N ) = N
+ k ( k 2 − 3 k + 2 ) 3 ≤ N ( N + 1 ) ( N + 5 ) 6 .
Доказательство. Для каждого k = 0 , k ∗ ¯ на шагах 2 и 3 происходит перебор по card ( \{ 1 , … , N \} ∖ I k ' ) = N − k числу различных индексов для вычисления i k . При этом для каждого i ∈ \{ 1 , … , N \} ∖ I k ' происходит проектирование вершины x i на многогранник X ^ ( I k ' ' ) c k вершинами. Таким образом на k-м шаге алгоритма 1 решается ( N − k ) задач квадратичного программирования сложности QP ( k ) . В алгоритме 1 индекс k меняется от k ∗ до k , что аналогично соотношению (8) приводит к следующему результату:
C 2 ( N ) = ∑ k = 0 k ∗ ( N − k ) + ∑ k = k k ∗ k ( N − k + 1 ) =
N
Наихудший в смысле сложности случай получается при k = 0 и k ∗ = N .
C 2 ( N ) ≤ N ( N + 1 ) ( N + 5 ) 6 .
□
Следствие 2. Алгоритмы 1 и 2 принадлежат классу сложности P , то есть имеют полиномиальную сложность по N .
Доказательство. Из теорем 2 и 3 следует, что временная сложность алгоритмов 1 и 2 составляет O ( N 3 QP ( N − 1 ) ) . При этом согласно [Ibragimov, 2017] QP ( N − 1 ) - полиномиальная функция. Отсюда следует полиномиальность алгоритмов 1 и 2.
□
Замечание 2. Алгоритм 2 имеет в худшем случае большую сложность, чем алгоритм 1, что связано вызовом алгоритма 1 на шаге 2 алгоритма 2. Однако в предположении, что полиэдральная аппроксимация исходного многогранника X целесообразна, величина k ∗ ожидается значительно меньше N, а величина k ∗ − k оценивается близкой к 0. При этом сложность решаемых задач вида (7) будет ограничена сверху QP , что сделает сложность алгоритма 2 ниже сложности алгоритма 1. Напротив, если число k предполагается достаточно большим, то алгоритм 1 потребует меньшего числа итераций и расчетов, чем алгоритм 2.
Результаты численного моделирования и исследование оптимальности
Продемонстрируем эффективность алгоритмов 1 и 2 на примере полиэдральной аппроксимации различных многогранников.
Пример 3. Рассмотрим следующий многогранник X ⊂ R 2 :
X = { ( − 1.5 0 ) , ( − 1 1 ) , ( 0 1 ) , ( 2 0 ) , ( 1 − 2 ) , ( 0 − 3 ) , ( − 1 − 1.75 ) } .
Пример работы алгоритмов 1 и 2 для ε = 0.32 представлен на рисунке 2, где через x 1 , x 2 , x 3 обозначены вершины X , исключенные алгоритмом 1 в порядке их исключения, через y 1 , y 2 , y 3 , y 4 обозначены вершины X , добавленные алгоритмом 2 в порядке их добавления.
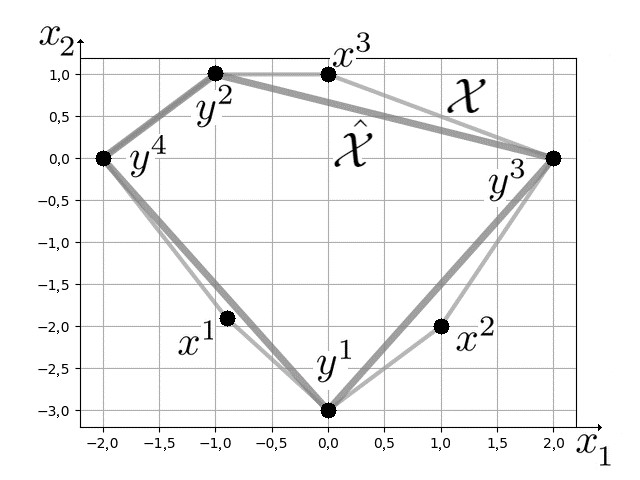
Рис. 2: Результаты примера 3
Можно заметить, что оба алгоритма построили единственный оптимальный набор индексов.
Также проведем сопоставление результатов данной статьи с теоретической оценкой оптимальной погрешности при приближении произвольных выпуклых тел многогранниками, полученной в [Kaba, 2015]. Для различных двумерных многогранников, сгенерированных случайным образом, представим результаты работы алгоритмов 1 и 2 в таблице 1.
Таблица 1.
|
|
120 |
109 |
100 |
100 |
94 |
90 |
80 |
65 |
22 |
17 |
|
|
0.05 |
0.02 |
0.02 |
0.02 |
0.02 |
0.2 |
0.2 |
0.2 |
0.01 |
0.3 |
|
|
11 |
18 |
21 |
18 |
20 |
5 |
6 |
6 |
7 |
6 |
|
|
11 |
18 |
17 |
17 |
17 |
5 |
6 |
5 |
6 |
6 |
Можно заметить, что алгоритм 2 на тестовых примерах демонстрирует результаты не хуже, чем алгоритм 1. Также на рисунках 3, 4 представлены зависимости величин погрешности аппроксимации ε ( I k ' ' ) в алгоритме 2 от числа включенных в аппроксимацию вершин исходного многогранника k в сравнении с теоретической оценкой оптимальной погрешности [Kaba, 2015]. Для достаточно точного описания множества требуется сравнительно небольшое число его вершин. При этом порядок погрешности соответствует оптимальному значению.
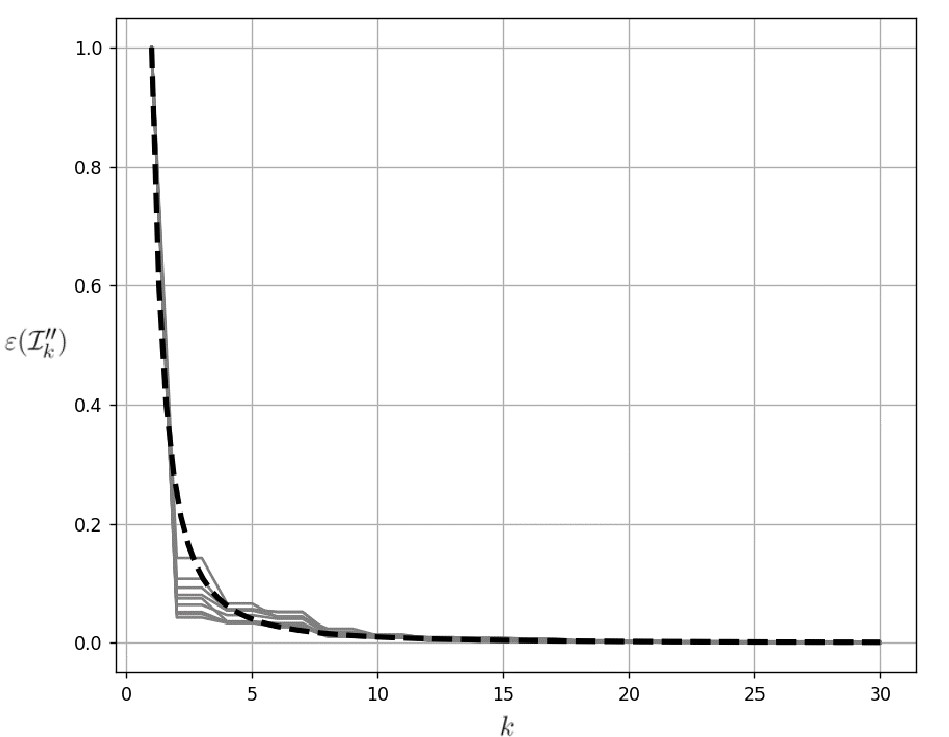
Рис. 3: Зависимость величины погрешности аппроксимации ε ( I k ' ' ) двухмерного многогранника в алгоритме 2 от числа включенных в аппроксимацию вершин k. Пунктирной линией обозначена теоретическая оценка оптимальной погрешности.
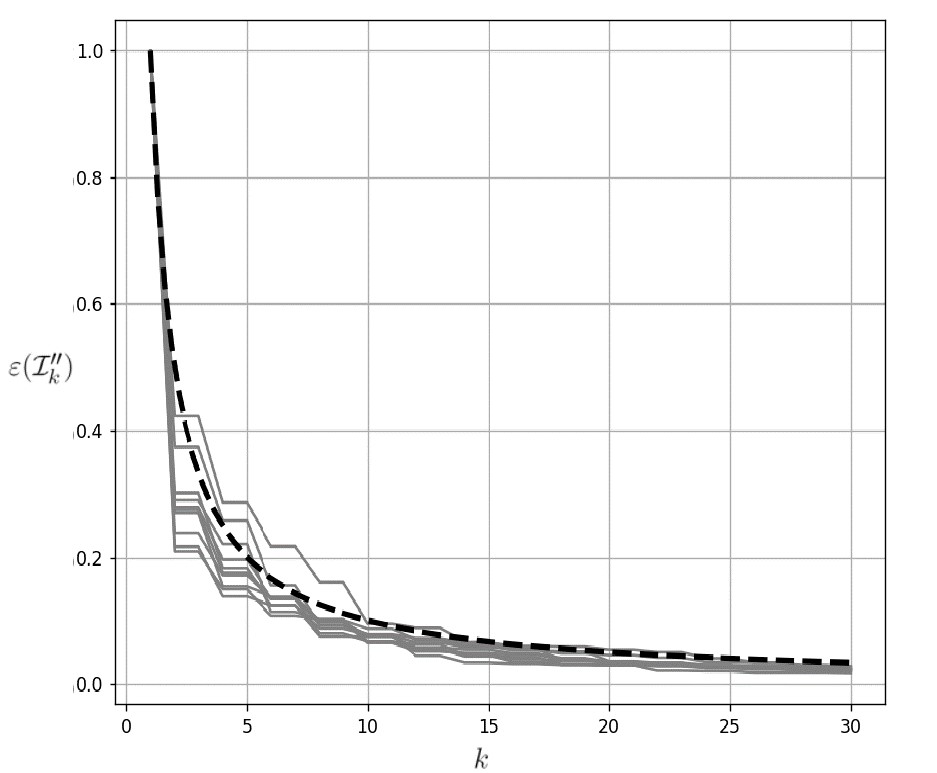
Рис. 4: Зависимость величины погрешности аппроксимации ε ( I k ' ' ) трехмерного многогранника в алгоритме 2 от числа включенных в аппроксимацию вершин k. Пунктирной линией обозначена теоретическая оценка оптимальной погрешности.
Оценки погрешности при последовательной аппроксимации множеств 0-управляемости
Алгоритмы 1 и 2 позволяют при допущениях ( 2 ) произвести аппроксимацию произвольного множества 0-управляемости системы ( 1 ) . Однако в общем случае этого может быть недостаточно. Построение множеств 0-управляемости, как правило, производится рекуррентно в соответствии с леммой 1. При достаточно больших значениях N ∈ N этот процесс может оказаться чересчур трудозатратным с вычислительной точки зрения. В таком случае предлагается производить аппроксимацию многократно на различных шагах по мере того, как число вершин текущего многогранника становится неприемлемо большим.
Через ( X , ε ) обозначим результат аппроксимации многогранника X ⊂ R n , произведенный с точностью ε > 0 . Т.е. ( X , ε ) определяется из условий
ρ H ( ( X , ε ) , X ) ≤ ε , Ext ≈ ( X , ε ) ⊂ Ext X .
Для некоторого m ∈ N выберем 1 < N 1 < … < N m - номера шагов, на которых производится аппроксимация множества 0-управляемости в соответствии с алгоритмами 1 или 2. Точность каждой аппроксимации при этом составляет ε 1 , … , ε m > 0 соответственно. Определим аппроксимирующую последовательность рекуррентно:
X ^ N 1 , … , N m ( N ) = { X ( N ) , ∧ N < N 1 , ( X ( N 1 ) , ε 1 ) , ∧ N = N 1 , X ^ N 1 , … , N m − 1 ( N ) , ∧ N 1 < N < N m , ( 9 ) ( X ^ N 1 , … , N m − 1 ( N m ) , ε m ) , ∧ N = N m , A − 1 X ^ N 1 , … , N m ( N − 1 ) + ( − A − 1 U ) , ∧ N > N m .
При этом в ходе последовательной аппроксимации итоговая погрешность ρ H ( X ^ N 1 , … , N m ( N ) , X ( N ) ) может накапливаться. Рассмотрим задачу вычисления ее априорной оценки. Для этого в дальнейших рассуждениях под нормой матрицы A ∈ R n × n будем понимать ее операторную норму:
| ∨ A ∨ | = | ∨ x ∨ | ≤ 1 | ∨ Ax ∨ | .
Лемма 5. Пусть A ∈ R n × n , U , X , Y ⊂ R n - компактные множества. Тогда
ρ H ( A X + U , A Y + U ) ≤ | ∨ A ∨ | ρ H ( X , Y ) .
Доказательство.Верны соотношения
ρ H ( A X + U , A Y + U ) = max
max { x ∈ X u 1 ∈ U inf y ∈ Y u 2 ∈ U | ∨ Ax + u 1 − Ay − u 2 ∨ | ; y ∈ Y u 2 ∈ U inf x ∈ X u 1 ∈ U | ∨ Ax + u 1 − Ay − u 2 ∨ | } ≤
≤ max { x ∈ X u 1 ∈ U inf y ∈ Y u 2 ∈ U | ∨ A ( x − y ) ∨ + ∨ u 1 − u 2 ∨ | ; y ∈ Y u 2 ∈ U inf x ∈ X u 1 ∈ U | ∨ A ( x − y ) ∨ + ∨ u 1 − u 2 ∨ | } =
max
≤ max
| ∨ A | ∨ max
Лемма 5 доказана. □
Лемма 6. Пусть ε 1 , … , ε m > 0 и 1 < N 1 < … < N m , для системы (1) верно, что det A ≠ 0 , α = | A − 1 | ∨ . Тогда для любых N ≥ N m верна оценка
ρ H ( X ^ N 1 , … , N m ( N ) , X ( N ) ) ≤ ∑ k = 1 m α N − N k ε k .
Доказательство. При m = 1 лемма 6 следует непосредственно из лемм 1 и 5.
Пусть m ≥ 2. Согласно лемме 1 для всех k = 2 , m ¯ верно представление
X ( N k ) = A − ( N k − N k − 1 ) X ( N k − 1 ) + X ( N k − N k − 1 ) .
Также из (9) следует, что
X ^ N 1 , … , N k − 1 ( N k ) = A − ( N k − N k − 1 ) X ^ N 1 , … , N k − 1 ( N k − 1 ) + X ( N k − N k − 1 ) .
Тогда в силу леммы 5 справедлива оценка
ρ H ( X ^ N 1 , … , N k − 1 ( N k ) , X ( N k ) ) ≤ | ∨ A − ( N k − N k − 1 ) | ∨ ρ H ( X ^ N 1 , … , N k − 1 ( N k − 1 ) , X ( N k − 1 ) ) ≤
≤ α N k − N k − 1 ρ H ( X ^ N 1 , … , N k − 1 ( N k − 1 ) , X ( N k − 1 ) ) .
Учтем неравенство треугольника и получим цепочку неравенств
ρ H ( X ^ N 1 , … , N m ( N ) , X ( N ) ) =
ρ H ( A − ( N − N m ) X ^ N 1 , … , N m ( N m ) + X ( N − N m ) , A − ( N − N m ) X ( N ) + X ( N − N m ) ) ≤
≤ | ∨ A − ( N − N m ) | ∨ ρ H ( X ^ N 1 , … , N m ( N m ) , X ( N m ) ) ≤ α N − N m ρ H ( X ^ N 1 , … , N m ( N m ) , X ( N m ) ) ≤
≤ α N − N m ( ρ H ( X ^ N 1 , … , N m ( N m ) , X ^ N 1 , … , N m − 1 ( N m ) ) + ρ H ( X ^ N 1 , … , N m − 1 ( N m ) , X ( N m ) ) ) ≤
≤ α N − N m ( ε m + ρ H ( X ^ N 1 , … , N m − 1 ( N m ) , X ( N m ) ) ) ≤
≤ α N − N m ε m + α N − N m α N m − N m − 1 ρ H ( X ^ N 1 , … , N m − 1 ( N m − 1 ) , X ( N m − 1 ) ) ≤
≤ α N − N m ε m + α N − N m − 1
+ ρ H ( X ^ N 1 , … , N m − 2 ( N m − 1 ) , X ( N m − 1 ) ) ) ≤
≤ α N − N m ε m + α N − N m − 1 ε m − 1 + α N − N m − 1 ρ H ( X ^ N 1 , … , N m − 2 ( N m − 1 ) , X ( N m − 1 ) ) ≤ … ≤
≤ α N − N m ε m + α N − N m − 1 ε m − 1 + … + α N − N 1 ρ H ( X ^ N 1 ( N 1 ) , X ( N 1 ) ) ≤
≤ α N − N m ε m + α N − N m − 1 ε m − 1 + … + α N − N 1 ε 1 .
Лемма 6 доказана. □
Следствие 3. Пусть в условиях леммы 6 верно, что ε 1 = … = ε m = ε . Тогда для любых N ≥ N m верна оценка
ρ H ( X ^ N 1 , … , N m ( N ) , X ( N ) ) ≤ ε α N ∑ k = 1 m α − N k .
Доказательство. В силу леммы 6 верны соотношения
ρ H ( X ^ N 1 , … , N m ( N ) , X ( N ) ) ≤ ∑ k = 1 m α N − N k ε k = ε ∑ k = 1 m α N − N k = ε α N ∑ k = 1 m α − N k .
Следствие 3 доказано. □
Основными результатами леммы 6 и следствия 3 является тот факт, что для фиксированного m ∈ N погрешность при последовательной аппроксимации составляет O ( α N ) . При этом согласно леммам 1 и 5 справедлива оценка
ρ H ( X ( N + 1 ) , X ( N ) ) = ρ H ( A − 1 X ( N ) + ( − A − 1 U ) , A − 1 X ( N − 1 ) + ( − A − 1 U ) ) ≤ ≤ α ρ H ( X ( N ) , X ( N − 1 ) ) ≤ … ≤ α N ρ H ( X ( 1 ) , \{ 0 \} ) = α N diam X ( 1 ) .
Т.е. ρ H ( X ( N + 1 ) , X ( N ) ) = O ( α N ) .
Таким образом порядок погрешности аппроксимации на шаге N совпадает с порядком увеличения размера множества 0-управляемости при переходе на шаг N + 1 .
Это гарантирует, что если требуется для некоторого x 0 ∈ R n определить наименьшее N ∈ N , удовлетворяющее включению x 0 ∈ X ( N ) , то погрешность при использовании аппроксимирующей последовательности (9) может быть ограничена сверху некоторой константой. Разрешение подобного условия представляет интерес, например, при решении задачи быстродействия [3, 4].
Аппроксимация множеств 0-управляемости системы управления движением спутника
Проведем численное моделирование множеств 0-управляемости системы управления движением спутника, расположенного в окрестности круговой орбиты. Предполагается, что коррекция движения осуществляется посредством двигателей импульсной тяги, корректирующие импульсы исполняются без ошибок через равные промежутки времени Δ t > 0 . Свободное движение спутника описывается системой дифференциальных уравнений [Козлов, 1980]:
r ˙ = v R ,
θ ˙ = v T r ,
v ˙ R = v R 2 r − 1 r 2 ,
v ˙ T = − v R v T r ,
где r - расстояние от начала координат до спутника, θ - угол поворота в полярной системе координат, v R и v T - радиальная и трансверсальная составляющие скорости спутника, рассматриваемого как материальная точка.
Круговая орбита описывается значениями переменных r 0 , v R 0 , v T 0 . При рассмотрении задачи коррекции - перевода траектории движения спутника на круговую орбиту - значение переменной θ не представляет интереса, что позволяет перейти к линеаризованной трехмерной системе, записанной относительно малых отклонений от параметров круговой орбиты [Козлов, 1980]:
ξ 1 = r − r 0 ,
ξ 2 = v R − v R 0 ,
ξ 3 = v T − v T 0 , ( 10 )
ξ ˙ 1 = ξ 2 ,
ξ ˙ 2 = ξ 1 + 2 ξ 3 ,
ξ ˙ 3 = − ξ 2 .
Предположение об импульсном характере управления позволяет перейти от рассмотрения непрерывной траектории ξ ( t ) к ее значениям в моменты времени k Δ t , непосредственно предшествующие k -й коррекции:
x ( k ) = ξ ( k Δ t ) , k ∈ N ∪ \{ 0 \} .
Тогда на основе построения аналитического решения системы линейных дифференциальных уравнений (10) можно перейти к рекуррентным соотношениям:
x ( k + 1 ) = Φ ( Δ t ) Φ − 1 ( 0 ) ( x ( k ) + ( 0 , v 1 ( k ) , v 2 ( k ) ) T ) , ( 11 )
x ( 0 ) = x 0 , v 1 ( k ) , v 2 ( k ) ∈ [ − α max ; α max ] , k ∈ N ∪ \{ 0 \} ,
где v 1 ( k ) , v 2 ( k ) - корректирующие импульсы, направленные вдоль радиальной и трансверсальной составляющих вектора скорости соответственно, α max > 0 - величина, ограничивающая максимальную тягу импульсного двигателя, Φ ( t ) ∈ R 3 × 3 - матрица фундаментальной системы решений системы (10):
Φ ( t ) = ( − cos t − sin t − 2 sin t − cos t 0 cos t sin t 1 ) .
Положим
A = Φ ( Δ t ) Φ − 1 ( 0 ) = ( − cos ( Δ t ) + 2 sin ( Δ t ) − 2 cos ( Δ t ) + 2 sin ( Δ t ) cos ( Δ t ) 2 sin ( Δ t ) cos ( Δ t ) − 1 − sin ( Δ t ) 2 cos ( Δ t ) − 1 ) ,
U = Φ ( Δ t ) Φ − 1 ( 0 ) ( 0 0 1 0 0 1 ) [ − α max ; α max ] 2 =
α max conv { ( sin ( Δ t ) − 2 cos ( Δ t ) + 2 cos ( Δ t ) + 2 sin ( Δ t ) − sin ( Δ t ) + 2 cos ( Δ t ) − 1 ) , ( − sin ( Δ t ) + 2 cos ( Δ t ) − 2 − cos ( Δ t ) − 2 sin ( Δ t ) sin ( Δ t ) − 2 cos ( Δ t ) + 1 ) ,
( sin ( Δ t ) + 2 cos ( Δ t ) − 2 cos ( Δ t ) − 2 sin ( Δ t ) − sin ( Δ t ) − 2 cos ( Δ t ) + 1 ) , ( − sin ( Δ t ) − 2 cos ( Δ t ) + 2 − cos ( Δ t ) + 2 sin ( Δ t ) sin ( Δ t ) + 2 cos ( Δ t ) − 1 ) } ,
u ( k ) = Φ ( Δ t ) Φ − 1 ( 0 ) + ( 0 , v 1 ( k ) , v 2 ( k ) ) T .
Тогда дискретные соотношения (11) примут эквивалентный вид (1), что позволяет провести численное моделирование множеств 0-управляемости системы управления движением спутника на основе леммы 1. Без ограничения общности можно положить α max = 1 , как множество допустимых значений управлений U и множества 0-управляемости \{ X ( N ) \} N = 0 ∞ пропорциональны величине α max . Примем Δ t = 0.25 .
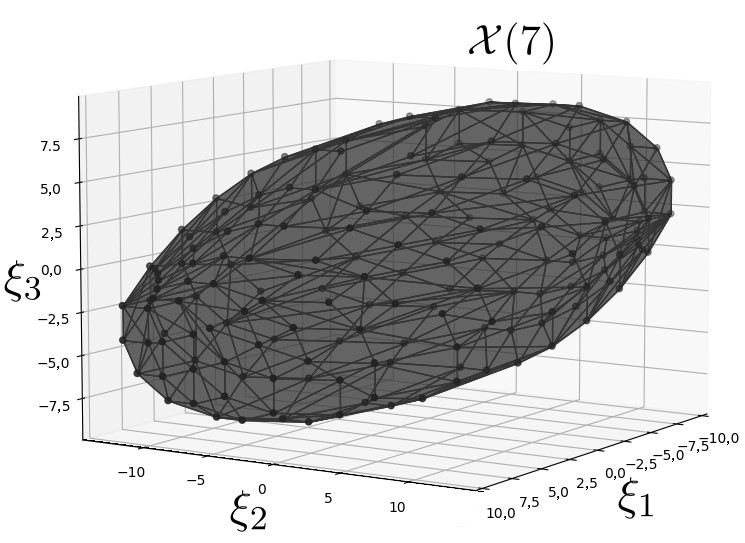
Поскольку M = card Ext U = 4 , для любого N ∈ N ∪ \{ 0 \} множество 0-управляемости X ( N ) представляет собой многогранник с числом вершин, не превосходящим 4 N . Точное значение числа вершин, определенное при помощи алгоритма быстрой оболочки [Пропой, 1973], для N = 1 ,7 ¯ представлено в таблице 2, множество X ( 7 ) изображено на рисунке 4.
Таблица 2.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
4 |
14 |
32 |
58 |
92 |
134 |
184 |
Рис.5: Множество 0-управляемости за 7 шагов X ( 7 ) дискретной системы управления движением спутника, расположенного на околокруговой орбите.
Проведем аппроксимацию множества X ( 7 ) . Выберем ε = 0.05 ⋅ diam X ( 7 ) = 1.638 . Внутренние оценки X ^ 1 ( 7 ) и X ^ 2 ( 7 ) , полученные при помощи алгоритмов 1 и 2 соответственно, имеют следующий вид:
X ^ 1 ( 7 ) = conv { ( − 7.7337 7.2044 0.7337 ) , ( − 8.5733 − 9.9901 − 7.5733 ) , ( 5.1665 0.0402 − 8.1665 ) , ( − 2.2481 9.5813 − 4.7519 ) ,
( − 9.1873 12.8974 2.1873 ) , ( 7.7337 − 7.2044 − 0.7337 ) , ( 8.5733 9.9901 7.5733 ) , ( − 5.1665 − 0.0402 8.1665 ) , ( 2.2481 − 9.5813 4.7519 ) , ( 9.1873 − 12.8974 − 2.1873 ) } ,
X ^ 2 ( 7 ) = conv { ( 9.1873 − 12.8974 − 4.1873 ) , ( − 2.4278 − 3.8361 7.4278 ) , ( − 7.5001 7.2635 8.5001 ) , ( 3.6114 − 11.0447 3.3886 ) ,
( − 6.3704 5.7410 − 0.6296 ) , ( − 9.1873 12.8974 4.1873 ) , ( 2.4278 3.8361 − 7.4278 ) , ( 7.5001 − 7.2635 − 8.5001 ) , ( − 3.6114 11.0447 − 3.3886 ) , ( 6.3704 − 5.7410 0.6296 ) } .
Графически множества X ^ 1 ( 7 ) и X ^ 2 ( 7 ) представлены на рисунках 5 и 6.
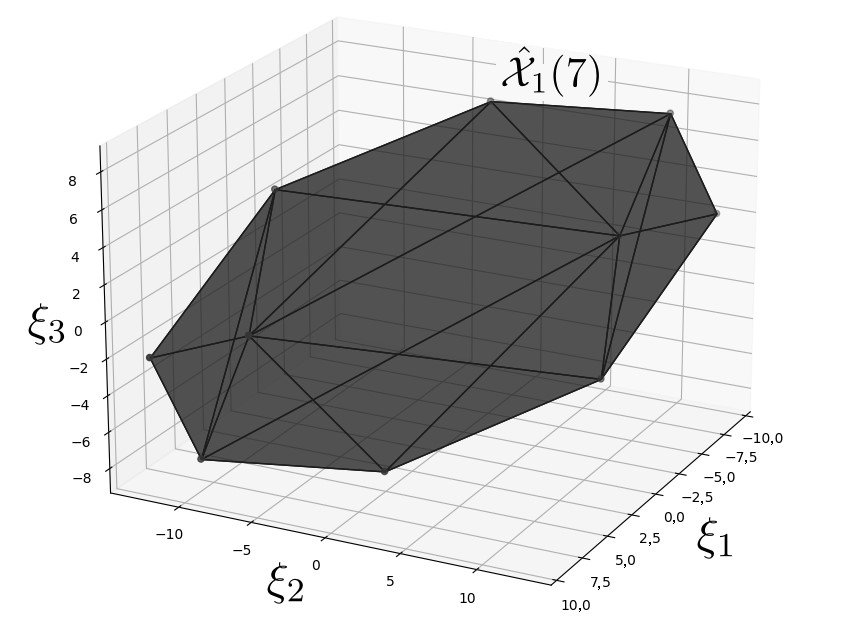
Рис. 6: Оценка X ^ 1 ( 7 ) , построенная на основе алгоритма 1
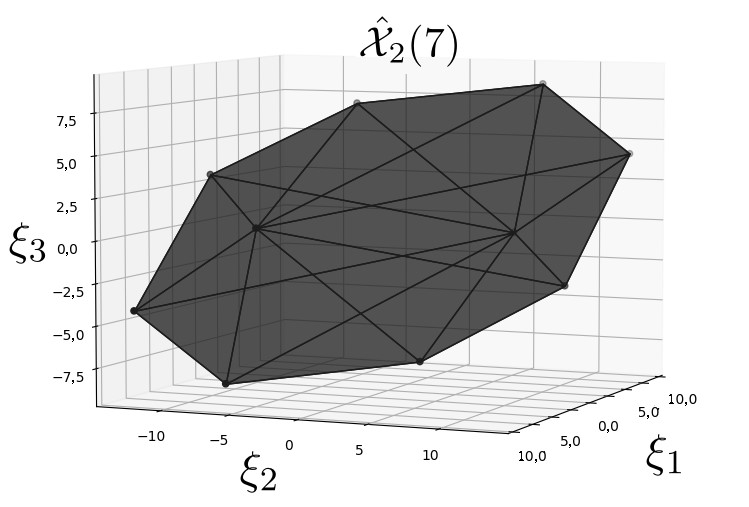
Рис.7: Оценка X ^ 2 ( 7 ) , построенная на основе алгоритма 2
Заключение
Предложены два алгоритма, позволяющих снизить описательную сложность данных множеств на основе проведения полиэдральной аппроксимации. Особенностью данных алгоритмов является то, что они гарантируют заданную точность аппроксимации в смысле расстояния Хаусдорфа. При этом полученные оценки являются субоптимальными, то есть не допускают дальнейшего упрощения при сохранении текущей точности.
В виде теоремы 1 и следствия 1 доказано, что вычисление расстояния Хаусдорфа между вложенными многогранниками сводится к решению ряда задач квадратичного программирования с неотрицательно определенной матрицей квадратичной формы. В виде теорем 2 и 3 сформулированы оценки сложности разработанных алгоритмов. В форме следствия 2 доказано, что данные алгоритмы обладают полиномиальной временной сложностью.
Проведены численные эксперименты работы алгоритмов для двумерных многогранников. На основе полученных результатов проведена аппроксимация множества 0-управляемости системы управления движением спутника, расположенного в окрестности круговой орбиты.
Разработанные алгоритмы могут быть использованы при анализе различных линейных дискретных моделей на предмет управляемость и достижимости. Также в силу полиномиальной временной сложности при помощи их можно проводить численное моделирование областей достижимости различных дискретных объектов.
Литература
- Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит. 2005. 391 с.
- Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука. 1973. 448 с.
- Ибрагимов Д.Н., Новожилкин Н.М., Порцева Е.Ю. О достаточных условиях оптимальности гарантирующего управления в задаче быстродействия для линейной нестационарной дискретной системы с ограниченным управлением // АиТ. 2021. № 12. С. 48–72. DOI: 10.31857/S0005231021120047
- Ibragimov D.N., Novozhilin N.M., Portseva E.Yu. On Sufficient Optimality Conditions for a Guaranteed Control in the Speed Problem for a Linear Time-Varying Discrete- Time System with Bounded Control // Autom. Remote Control. 2021. V. 82. No. 12. P. 2076–2096. DOI: 10.1134/S000511792112002X
- Ибрагимов Д.Н., Сиротин А.Н. О задаче быстродействия для класса линейных автономных бесконечномерных систем с дискретным временем и ограниченным управлением // АиТ. 2017. № 10. C. 3–32. DOI: 10.1134/S0005117917100010
- Ibragimov D.N., Sirotin A.N. On the Problem of Operation Speed for the Class of Linear Infinite-Dimensional Discrete-Time Systems with Bounded Control // Autom. Remote Control. 2017. V. 78. No. 10. P. 1731–1756. DOI: 10.1134/S0005117917100010
- Каменев Г.К. Численное исследование эффективности методов полиэдральной аппроксимации выпуклых тел. М.: Вычислительный центр РАН. 2010. 119 с.
- Козлов М.К., Тарасов С.П., Хачиян Л.Г. Полиномиальная разрешимость выпуклого квадратичного программирования // Ж. вычисл. матем. и матем. физ. 1980. Т. 20. № 5. C. 1319–1323.
- Kozlov M.K., Tarasov S.P., Khachiyan L.G. The polynomial solvability of convex quadratic programming // USSR Computational Mathematics and Mathematical Physics. 1980. Vol. 20. No. 5. P. 223–228. DOI: 10.1016/0041-5553(80)90098-1.
- Кроновер Р.М. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет. 2000. 352 с.
- Малышев В.В., Красильщиков М.Н., Бобронников В.Т., Нестеренко О.П., Федоров А.В. Спутниковые системы мониторинга. Анализ, синтез и управление. М.: МАИ. 2000. 568 с.
- Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука. 1973. 256 с.
- Рокафеллар Р. Выпуклый анализ. М.: Мир. 1973. 471 с.
- Сиротин А.Н. Управляемость линейных дискретных систем с ограниченным управлением и (почти) периодическими возмущениями // АиТ. 2001. № 5. C. 53–64.
- Sirotin A.N. Controllability of linear discrete systems with bounded control and (almost) periodic disturbances // Autom. Remote Control. 2001. Vol. 62. No. 5. P. 724–734. DOI: 10.1023/A:1010266622197.
- Barber C.B., Dobkin D.P., Huhdanpaa H. The quickhull algorithm for convex hulls // ACM Transactions on Mathematical Software. 1996. Vol. 4. No. 22. P. 469–483. DOI: 10.1145/235815.235821.
- Benvenuti L., Farina L. The geometry of the reachability set for linear discrete-time systems with positive controls // SIAM Journal on Matrix Analysis and Applications. 2006. Vol. 28. No. 2. P. 306–325. DOI: 10.1137/040612531.
- Colonius F., Cossich J.A.N., Santana A.J. Controllability properties and invariance pressure for linear discrete-time systems // Journal of Dynamics and Differential Equations. 2022. Vol. 34. P. 5–22. DOI: 10.1007/s10884-021-09966-4.
- Darup M.S., Mönnigmann M. On general relations between null-controllable and controlled invariant sets for linear constrained systems // 53rd IEEE Conference on Decision and Control. Los Angeles. 2014. P. 6323–6328. DOI: 10.1109/CDC.2014.7040380.
- Fucheng L., Mengyuan S., Usman Optimal preview control for linear discrete-time periodic systems // Mathematical Problems in Engineering. 2019. P. 1–11. DOI: 10.1155/2019/8434293.
- Ge S.S., Zhendong S., Lee T.H. Reachability and controllability of switched linear discrete-time systems // IEEE Transactions on Automatic Control. 2001. Vol. 46. No. 9. P. 1437–1441. DOI: 10.1109/9.948473.
- Heemels W.P.M.H., Camlibel M.K. Null controllability of discrete-time linear systems with input and state constraints // 47th IEEE Conference on Decision and Control. Cancun. 2008. P. 3487–3492. DOI: 10.1109/CDC.2008.4739333.
- Kaba M.D., Camlibel M.K. A spectral characterization of controllability for linear discrete-time systems with conic constraints // SIAM Journal on Control and Optimization. 2015. Vol. 53. No. 4. P. 2350–2372. DOI: 10.1137/140960967.
- Kostousova E.K. External polyhedral estimates of reachable sets of discrete-time systems with integral bounds on additive terms // Mathematical Control and Related Fields. 2021. Vol. 11. No. 3. P. 625–641. DOI: 10.3934/mcrf.2021015.
- Kurzhanskiy A., Varaiya P. Ellipsoidal Techniques for Reachability Analysis of Discrete- Time Linear Systems // IEEE Transactions on Automatic Control. 2007. Vol. 52. No. 1. P. 26–38. DOI: 10.1109/TAC.2006.887900.
- Weibel C. Minkowski sums of polytopes: combinatorics and computation. Lausanne: EPFL. 2007. 114 p. DOI: 10.5075/epfl-thesis-3883.
- Бронштейн Е.М., Иванов Л.Д. Приближение выпуклых множеств многогранниками // Сиб. мат. ж. 1975. № 16. C. 1110-1112
Информация об авторах
Метрики
Просмотров web
За все время: 166
В прошлом месяце: 24
В текущем месяце: 11
Скачиваний PDF
За все время: 66
В прошлом месяце: 7
В текущем месяце: 2
Всего
За все время: 232
В прошлом месяце: 31
В текущем месяце: 13