Культурно-историческая психология
2022. Том 18. № 4. С. 4–14
doi:10.17759/chp.2022180401
ISSN: 1816-5435 / 2224-8935 (online)
Развитие формально-логического и диалектического мышления у детей 5-8 лет
Аннотация
В статье представлены данные лонгитюдного исследования, направленного на оценку развития формально-логического и диалектического мышления у детей старшего дошкольного (5—6, затем 6—7 лет) и младшего (7—8 лет) школьного возраста. В исследовании формально-логического мышления приняли участие 58 детей. Были использованы пробы Ж. Пиаже: «Вероятность», «Весы» и «Цилиндр». В исследовании диалектического мышления приняли участие 92 ребенка. Для диагностики были применены три методики: «Рисунок необычного дерева», «Что может быть одновременно?» и «Циклы». Для корреляционного анализа были использованы данные 52 детей, которые были продиагностированы в 5—6 и 7—8 лет. Полученные результаты показывают, что дошкольный возраст сенситивен для развития формальных операций и диалектических мыслительных действий. Была установлена положительная связь между способностью детей 5—6 и 7—8 лет координировать два разнонаправленных движения для создания единого образа и преодолением противоречий. При переходе к обучению в школе снижаются показатели по решению творческой задачи, которая предполагает самостоятельное конструирование противоположных объектов
Общая информация
Ключевые слова: вербально-логическое мышление, диалектическое мышление, логические операции, автоматизированная информационная система, противоречия, дошкольный возраст, адаптация к информационно-ком- муникационным технологиям (ИКТ), младший школьный возраст
Рубрика издания: Возрастная психология
Тип материала: научная статья
DOI: https://doi.org/10.17759/chp.2022180401
Финансирование. Исследование выполнено при финансовой поддержке Российского научного фонда (РНФ) в рамках научного проекта №19-18-00521-П
Получена: 26.07.2022
Принята в печать:
Для цитаты: Веракса Н.Е., Айрапетян З.В., Алмазова О.В., Тарасова К.С. Развитие формально-логического и диалектического мышления у детей 5-8 лет // Культурно-историческая психология. 2022. Том 18. № 4. С. 4–14. DOI: 10.17759/chp.2022180401
Полный текст
Введение
Развитие детской когнитивной психологии ХХ века подготовило основания для изучения двух самостоятельных форм мышления: формально-логического и диалектического. Анализ работ зарубежных [Пиаже, 2004; Piaget; Riegel, 1973; Veraksa N, Basseches, 2022] и отечественных [Веракса, 2019; Запорожец, 2007; Золотарева, 2021; Ильенков, 1979; Копнин, 1962; Ржанова, 2020; Sidneva, 2022; Valeeva, 2021] ученых позволил сформулировать основные отличительные особенности этих форм мышления. В «качестве отличительной черты формальной логики выступило оперирование мыслительными формами, абстрагированными от содержания, а под диалектической логикой стали понимать логику разворачивания противоречия развивающегося содержания» [2, с. 5.]. Диалектика интерпретировалась в качестве несамостоятельного процесса, поддерживающего формирование формальных структур [Piaget]. В нашей статье мы рассмотрим различия с точки зрения парадигмы ассимиляции и аккомодации Ж. Пиаже, для того чтобы удержать перспективу целостности когнитивного развития.
Развитие формально-логического мышления представляет собой длительный процесс, который сопровождается сменами стадий. Каждый этап является результатом качественных изменений в когнитивном развитии ребенка и характеризуется достижением нового уровня подвижного равновесия интеллектуальных процессов. Становление логических операций в парадигме ассимиляции («канва действий, способных активно воспроизводиться») и аккомодации («влияние среды, которое оказывает обратное действие, меняющее ассимилятивный цикл») характеризуется как достижение равновесия между этими процессами. Ж. Пиаже подчеркивал, что «…равновесие операционального мышления отнюдь не представляет собой некоего состояния покоя, а является системой уравновешивающихся обменов и трансформаций, бесконечно компенсирующих друг друга» [Пиаже, 2004, с. 19]. Процесс развития мышления сопровождается изменениями форм равновесия. Так, равновесие перцептивных структур характеризуется «перемещением равновесия», когда каждое изменение значения одного из действующих отношений влечет за собой трансформацию целого, вплоть до образования нового равновесия, отличного от того, которое характеризовало предыдущее состояние. Равновесие операциональных структур одновременно и мобильно, и постоянно; трансформации, внутренне присущие таким системам, не изменяют этого равновесия, потому что они всегда точно компенсируются обратными — реальными или потенциальными — операциями (обратимость).
По мнению Ж. Пиаже, диалектика имеет непосредственное отношение к формированию равновесия: «…в любом познавательном развитии происходит чередование диалектической и дискурсивной фаз» [Piaget, с. 188]. «Диалектика составляет генетический аспект всякого равновесия» [14, 10], т. е. приводит к построению структур. В дискурсивной фазе устойчивые структуры порождают новые взаимозависимости, и опять возникает диалектика, поскольку формируется новая общность, требующая новых уравновешивающих процессов.
Диалектика ведет к построению взаимодействий и связей, которые, по мнению Ж. Пиаже, организованы по модели спирали [Piaget]. В качестве основного конфликта, запускающего процессы взаимодействия, Ж. Пиаже выделял напряженность между «возможным» и «необходимым»: «приобретение знания R (reales) влечет за собой несколько новых возможностей P (posibles). Между некоторыми из этих необходимых отношений N (necesarias) устанавливаются такие, которые затем охватывают исходный объект R, но в дополненной форме R2. Из R2 немедленно вытекают новые возможности P2, а затем новые потребности приведут к R3 и т. д.» [Piaget, с. 193]. Таким образом, в рамках теории Пиаже диалектика является вспомогательным процессом становления новой когнитивной стадии.
Ж. Пиаже отрицает наличие противоречий между двумя объектами. По его мнению, «…как только качества элементов абстрагируются, чтобы рассматривать их как единицы, эквивалентные друг другу, включения могут поддерживаться только расположением, что порождает новую, гораздо более сложную общность, которая является последовательностью в пределах» [Piaget, с. 187]. «Ребенок не способен мыслить отношениями до тех пор, пока он не научился проводить сериации. Сериация является первичной реальностью, любое асимметричное отношение которой есть лишь временно абстрагированный элемент» [Пиаже, 2004, с. 17]. Таким образом, рассуждая о равновесии структур в рамках операционной модели, Ж. Пиаже исключает противоречия за счет применения операции сериации.
Полемизируя с Ж. Пиаже, К. Ригель уделил внимание проблеме понимания детьми противоречий и предложил описания диалектических проявлений на каждой стадии когнитивного развития. В частности, на дооперациональной стадии, по его мнению, ребенок воспринимает два понятия одновременно и способен сортировать предметы по цвету на красные и зеленые, т. е. на те, которые показывают наличие атрибута, например, красного цвета, и те, которые показывают его отсутствие (не красные). К. Ригель отмечал: «Пиаже систематически ищет противоречия в суждениях ребенка и тем самым подрывает свои собственные диалектические интерпретации, а также недооценивает диалектичность ребенка» [Riegel, 1973, с. 11], так как противоречия решаются формально. По мнению Ригеля, это приводит к «отчуждению» мышления, а для того, чтобы достичь зрелости, «отчужденный» ребенок должен будет вернуться к диалектической основе мышления [Riegel, 1973, с. 11]. Развитие идей К. Ригеля о возвращении к диалектическим основам мышления послужило основанием для интерпретации диалектических операций в качестве постформальных [Veraksa N, Basseches, 2022]. Так М. Бессечес, выделил 24 диалектические схемы, которые взрослый человек использует для решения субъективно сложных задач [Veraksa N, Basseches, 2022, с. 7]. Однако рассмотрение диалектического мышления как постформального приводит к тому, что исключается возможность изучения этой формы мышления в детском возрасте.
В исследовании О. Шиян и коллег [Шиян, 2021] была выдвинута гипотеза о том, что в детском возрасте формальные структуры связаны с диалектическим мышлением, если «…формальный интеллект понимается в традиции Ж. Пиаже, как становление обратимости» [Шиян, 2021, с. 21]. Авторы использовали пробы, которые диагностируют представления о сохранении (множеств, длины, массы) и понимания соотношения «часть—целое». В исследовании была показана значимая связь между успешностью решения детьми задачи на сохранение и их способностью к преодолению противоречия.
В отечественной психологии сложилась концепция структурно-диалектической психологии. Это направление сформировалось в контексте культурно-исторической теории и подкреплено работами А.В. Запорожца, в которых были получены данные о чувствительности дошкольников к противоречиям [Запорожец, 2007]. Диалектическое мышление определяется Н.Е Вераксой в качестве самостоятельной ветви когнитивного развития и представляет собой систему мыслительных действий, направленных на оперирование отношениями противоположностей в процессе решения диалектических задач [Веракса, 2006].
Основу модели диалектического мышления составляют отношения противоположности, позволяющие выстроить динамичную структуру мыслительных действий. Диалектическое действие превращения представляет собой мысленную трансформацию объекта А в свою противоположность В (например, утро—вечер). Диалектическое опосредствование объединяет противоположности А и В в единый объект АВ (оранжевый цвет, как желтый и красный одновременно). Диалектическая сериация представляет собой мысленное воспроизведение постепенной трансформации объекта от исходного состояния А к своему противоположному состоянию В через промежуточное состояние АВ. Понимание структуры этого действия связано с построением циклического представления, которое отражает процесс изменения объекта из исходного состояния в противоположное, а затем обратно — из противоположного в исходное (например, утро—день—вечер—ночь—утро) [Веракса, 2006]. Были определены 3 основные задачи, на решение которых направлено диалектическое мышление: 1) создание творческого продукта [Копнин, 1962], 2) понимание процессов развития [Давыдов], 3) преодоление противоречий [Копнин, 1962].
Как показали результаты исследования, проведенного на детях дошкольного возраста [Веракса], процесс развития диалектического мышления носит гетерохронный характер. Предпосылки развития диалектического мышления возникают уже в младшем дошкольном возрасте [Веракса, 2021]. К 4 годам ребенок понимает процессы превращения, хотя в полной мере такая задача, как «Рисунок необычного дерева», остается сложной для детей и количество диалектических рисунков увеличивается к подготовительной группе. В старшем дошкольном возрасте ребенок успешно справляется с сериациями, у него возникает понимание процессов превращения и обращения. На протяжении дошкольного возраста у ребенка совершенствуется способность преодолевать противоречия, применяя мыслительное действие опосредствования. В проведенном ранее исследовании [Веракса] были получены данные о положительной корреляционной связи результатов выполнения детьми 5—6 лет пробы «Вероятность» и результатов выполнения методики «Циклы». Мы предположили, что такой результат может отражать циклическую структуру диалектического мышления у детей старшего дошкольного возраста.
Методы и методики
В нашей работе были поставлены две задачи: 1) проанализировать развитие формально-логического и диалектического мышления у детей с 5 до 8 лет; 2) изучить взаимосвязи этих форм мышления.
Мы выдвинули следующие гипотезы. Гипотеза 1: у детей младшего школьного возраста сохранится обнаруженная ранее в старшем дошкольном возрасте связь развития способности координировать два процесса и оценивать вероятность результата с пониманием процессов развития. Гипотеза 2: понимание пространственных мультипликативных отношений связано с развитием опосредствования. Гипотеза 3: по сравнению с детьми 5—6-летнего возраста у детей младшего школьного возраста, обнаружится снижение успешности решения диалектических задач при повышении успешности выполнения формально-логических операций.
В лонгитюдном исследовании развития формально-логического мышления приняли участие 58 детей, которые выполнили 3 пробы: «Вероятность», «Весы» и «Цилиндр» в старшей группе детского сада и в первом классе школы (разница между выполнением — 2 года). Среди них 27 (46,6%) мальчиков и 31 (53,4%) девочка. В исследовании развития диалектического мышления приняли участие 92 ребенка, у которых диагностика была проведена 3 раза — в старшей группе детского сада, в подготовительной группе детского сада и в первом классе. Среди них 44 (47,8%) мальчика и 48 (52,2%) девочек. Все дети выполнили 3 методики: «Рисунок необычного дерева», «Циклы», «Что может быть одновременно?». Для анализа данных о связи двух форм мышления были использованы данные 52 детей, участвовавших в обоих срезах (в 5—6, а затем в 7—8 лет). Все дети на момент диагностики посещали образовательные учреждения в г. Москве. Исследование проводилось с 2019 по 2021 год.
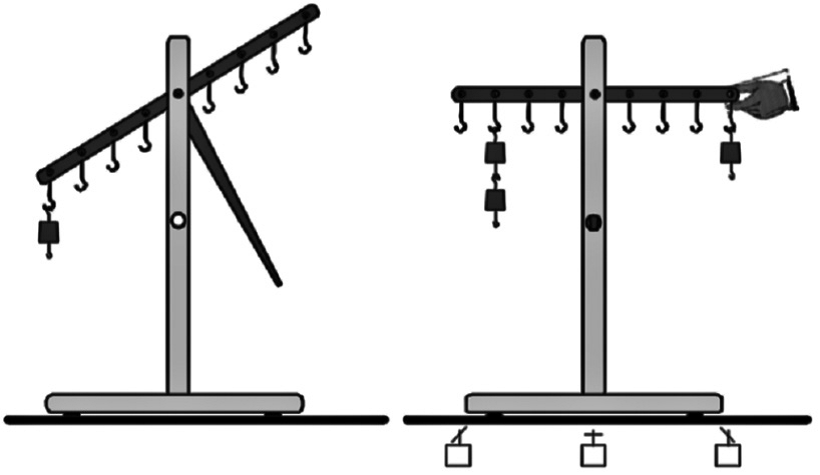
Проба «Весы» [Piaget, 1951; Веракса] была направлена на оценку операций, позволяющих координировать и количественно определять переменные веса и расстояния. Ребенку предлагалась наглядная задача с использованием рычажных весов с 12 равноудаленными от точки опоры отверстиями с каждой стороны и 16 металлическими грузиками весом по 32 гр. (рис. 1). На протяжении всей процедуры проведения плечи весов были зафиксированы в горизонтальном положении. Каждый раз после размещения грузиков экспериментатор задавал ребенку вопрос: «Что произойдет с весами, когда я разблокирую затвор? Они останутся в таком же положении или наклонятся в эту сторону или в эту? В какую? Как ты это понял (а)?». Всего в пробе было пять заданий, из них 2 ознакомительных и 3 тестовых.
Рис. 1. Устройство для проведения пробы «Весы»
Проба «Вероятность» [Piaget, 1951; Веракса] была направлена на оценку операций, позволяющих оценивать вероятность достижения определенного результата, исходя из разных соотношений белых и черных фишек. Инструкция звучала следующим образом: «Представь, что мы положили фишки в мешочки и потрясли. А теперь представь, что мы достаем отсюда (показываем на левую кучку фишек) и отсюда (показываем на правую кучку) по одной фишке. С какой стороны шанс достать белую фишку будет выше? Как ты это понял(а)?». Всего в пробе было пять заданий, из них 2 ознакомительных и 3 тестовых.
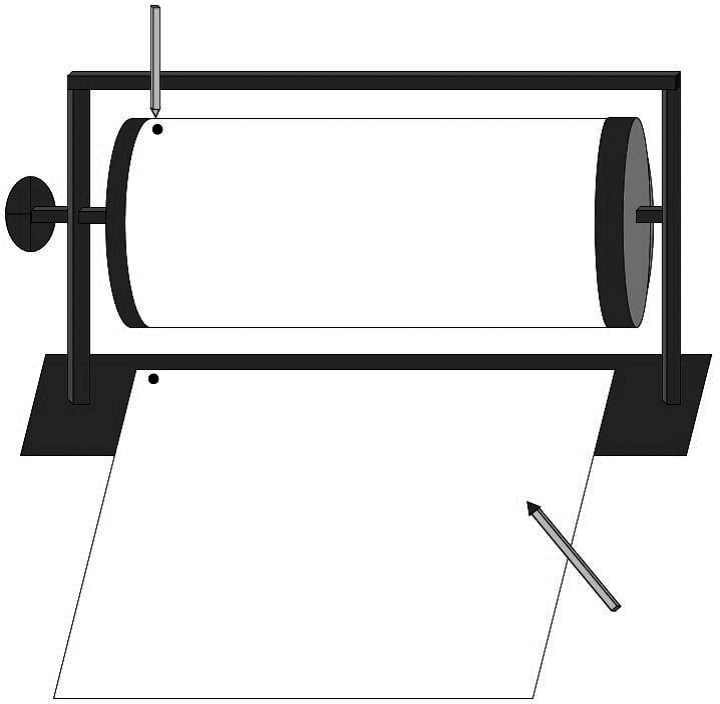
Проба «Цилиндр» [Piaget, 1948; Веракса] оценивала способность координировать два разнонаправленных процесса. Перед ребенком на столе располагали специальную установку, состоящую из цилиндра, который можно вращать с помощью ручки и закрепленной сверху планки. На цилиндр закрепляли лист бумаги со стартовой точкой. На планке устанавливали карандаш, что позволяло перемещать его вдоль цилиндра (рис. 2).
Рис. 2. Устройство для проведения пробы «Цилиндр» и расположение листа для выполнения задания, фронтальный вид со стороны ребенка
Экспериментатор объяснял значение стартовой точки и демонстрировал принципы работы элементов установки. Для выполнения каждого задания ребенку предъявляли лист бумаги со стартовой точкой. Инструкция звучала следующим образом: «Нарисуй, какой получится след, если…». В ознакомительных заданиях экспериментатор демонстрировал ребенку движения карандаша и цилиндра, а в тестовых пробах тестер только озвучивал условия задачи. Всего в пробе было пять заданий, из них 2 ознакомительных и 3 тестовых.
Таким образом, в пробах Пиаже присутствовала координация двух параметров: количества и цвета фишек; количества грузиков и расстояния, на которых они висят; движения цилиндра по вертикали и карандаша по горизонтали. Во всех трех пробах Пиаже каждый ответ ребенка оценивался по стандартизированной 4-балльной системе [Piaget, 1951; Piaget, 1948]: если ребенок не понимал задание, ему ставили 0 баллов; если ребенок в своем ответе учитывал только один параметр, ему ставили 1 балл; если ребенок в ответе упоминал оба параметра, но при прогнозе опирался только на один из них, ему ставили 2 балла; если ребенок пытался соотнести два параметра, ему ставили 3 балла.
Методика «Рисунок необычного дерева» [Веракса, 2021] позволяла оценить успешность решения ребенком творческой задачи по созданию нового графического образа. Для выполнения рисунка дети использовали бланк (лист формата А4) и простой карандаш. Ребенку предлагалась инструкция: «Нарисуй, пожалуйста, необычное дерево». После завершения рисунка, ребенка просили подробно рассказать, в чем заключается необычность изображенного дерева. В результате мы оценивали тип деревьев: нормативное, символическое и диалектическое (0—2 балла) и трансформаций (0—7 баллов) в соответствии со стандартной процедурой оценки [Веракса, 2021]. Среди «нормативных» рисунков были выделены 4 вида деревьев по степени трансформации: 0 — трансформация отсутствовала; 1 —частичная трансформация затрагивает одну часть дерева; 2 — комплексная трансформация — на дереве растут разные плоды растительного происхождения, не свойственные дереву (грибное дерево); 3 — попытка полной трансформации, но дерево существует (кактус). В «символических» рисунках изменения обусловлены волшебством и темой исполнения желаний детей: 4 — в рисунке присутствует тема волшебства и необычности, есть элементы оживления и отражения темы желаний; 5 — комплексная трансформация, при которой отражено многообразие объектов и создание нового образа с помощью скрещивания с иными объектами; 6 — попытка полной трансформации, при которой наблюдаются структурные изменения, но есть и символизм (дерево-фонтан). 7 баллов начислялись за «диалектические» деревья, в которых отразилась структурная трансформация (перевернутые деревья, растущие вниз кроной).
Методика «Циклы» [Веракса, 2021] оценивала способность ребенка решать задачи, отражающие процессы развития. Ребенку предлагались три задания с пятью карточками. Всего было использовано три сюжета: «Растворение кусков сахара в чае», «Приготовление кипятка в чайнике», «Наступление грозы». Инструкция звучала следующим образом: «Разложи карточки так, чтобы получилась история». В зависимости от того, как ребенок выполнял задание, за каждую пробу он получал от 0 до 5 баллов, максимально 15 баллов за 3 задания.
Методика «Что бывает одновременно?» [Веракса, 2021] была направлена на оценку способности преодолевать противоречия. Методика включала пять вопросов, содержащих противоречивую пару признаков. Детям предлагалось ответить на вопрос: «Что бывает сразу, одновременно: и черным, и белым; и легким, и тяжелым; и большим, и маленьким; и живым, и неживым; и тем же самым, и другим?». За каждое задание начислялось от 0 до 4 баллов, итоговая оценка, полученная ребенком при выполнении методики, могла варьироваться от 0 до 20 баллов.
Результаты
Анализ полученных данных производился в 3 этапа. На первом этапе были сформированы описательные статистики выполнения детьми методик, направленных на оценку формально-логического и диалектического мышления. Далее с помощью критерия Вилкоксона для пар связанных выборок была проверена значимость различий в оценках в старшей, подготовительной группах и в первом классе по рассматриваемым параметрам. На третьем этапе был проведен корреляционный анализ связей показателей двух форм мышления. Подсчеты производились в программе IBM SPSS statistics v. 26.
Формально-логическое мышление
В табл. 1 представлена статистика для каждого вида проб Ж. Пиаже. Для всех проб средние значения от старшей группы к первому классу возрастают, а разброс данных уменьшается. При помощи критерия Вилкоксона для пар связанных выборок была проверена значимость различий в оценках в старшей группе и первом классе по рассматриваемым параметрам.
Таблица 1
Статистика выполнения проб Пиаже в старшей группе детского сада и первом классе школы (N=58)
|
Параметр: |
M (SD) |
Med |
M (SD) |
Med |
M (SD) |
Med |
|
Максимум |
Медиана |
Суммарный балл |
||||
|
«Вероятность», диапазон значений в одной пробе: 0—9 баллов |
||||||
|
Старшая группа |
1,03 (0,56) |
1 |
0,90 (0,48) |
1 |
2,81 (1,42) |
3 |
|
Первый класс |
1,32 (0,57) |
1 |
1,12 (0,426) |
1 |
3,41 (1,06) |
3 |
|
Разность |
||||||
|
W |
-2,446 |
-2,457 |
-2,748 |
|||
|
p |
0,014 |
0,014 |
0,006 |
|||
|
«Весы», диапазон значений в одной пробе: 0—9 баллов |
||||||
|
Старшая группа |
1,17 (0,65) |
1,00 |
1,10 (0,51) |
1,00 |
5,34 (2,32) |
5,00 |
|
Первый класс |
2,36 (0,91) |
3,00 |
1,29 (0,56) |
1,00 |
7,97 (2,42) |
8,00 |
|
Разность |
||||||
|
W |
-5,107 |
-1,826 |
-4,549 |
|||
|
p |
<0,001 |
0,068 |
<0,001 |
|||
|
«Цилиндр», диапазон значений в одной пробе:0—9 баллов |
||||||
|
Старшая группа |
1,78 (0,87) |
2,00 |
1,66 (0,84) |
2,00 |
4,95 (2,42) |
6,00 |
|
Первый класс |
2,09 (0,70) |
2,00 |
1,90 (0,64) |
2,00 |
5,69 (1,78) |
6,00 |
|
Разность |
||||||
|
W |
-2,253 |
-2,150 |
-2,236 |
|||
|
p |
0,024 |
0,032 |
0,025 |
|||
По всем рассматриваемым оценкам, кроме «Весы, медиана» оценки в первом классе значимо выше, чем в старшей группе; это указывает на то, что 5—7-летний возраст, сенситивен для развития способностей, лежащих в основе успешного выполнения проб Ж. Пиаже. Чем старше становятся дети, тем лучше они справляются с мультипликативными задачами на координацию двух параметров и оценку вероятностей. В целом, это соответствует развитию формальных операций в детском возрасте и, в свою очередь, указывает на сенситивный период — 5—7 лет для развития способностей, лежащих в основе успешного выполнения проб Ж. Пиаже.
Диалектическое мышление
В старшей группе детского сада, выполняя методику «Рисунок необычного дерева», 47 детей (51,1%) нарисовали нормативное дерево, 36 (39,1%) — символическое и 9 (9,8%) — диалектическое. В подготовительной группе детского сада (через год после первого рисунка) 22 (23,9%) ребенка нарисовали нормативное дерево, 53 (57,6%) — символическое и 17 (18,5%) — диалектическое. В первом классе школы (через два года после первого рисунка) 20 детей (21,7%) нарисовали нормативное дерево, 63 (68,5%) — символическое и 9 (9,8%) — диалектическое. Число «нормативных» деревьев резко сокращается от старшей группы к подготовительной (с 36 до 22) и остается примерно на этом же уровне (с 22 до 20) в первом классе. Число «диалектических» деревьев возрастает от старшей к подготовительной группе (с 9 до 17) и снова падает в первом классе (с 17 до 9). Таким образом, анализируя соотношение типов изображения деревьев, мы видим, что с возрастом дети лучше справляются с творческой задачей (снижение количества нормативных деревьев), при этом к концу дошкольного возраста дети активнее используют диалектическое мыслительное действие превращения, т. е. рисуют перевернутые деревья, деревья, на которых растут деревья и т. д., т. е., сохраняя идею дерева, трансформируют структуру. При этом можно отметить снижение частоты этих действий при переходе к школьному обучению. Такое снижение в решении творческих задач характерно для младшего школьного возраста. Для оценки статистической значимости этого скачка мы использовали критерий Вилкоксона для связных выборок, в котором оценили еще и подуровни трансформаций, которые можно рассматривать, как ранговую шкалу. В табл. 2 приведены основные психометрические характеристики подуровней детей, как результата выполнения методики «Необычное дерево» в разном возрасте.
Таблица 2
Статистика выполнения методик, направленных на оценку диалектического мышления в старшей и подготовительной группах детского сада и первом классе школы (N=92)
|
Группа |
Среднее |
Медиана |
Станд, отк, |
Минимум |
Максимум |
|
«Необычное дерево», подуровни |
|||||
|
Старшая группа |
2,78 |
4,00 |
2,454 |
0 |
7 |
|
Подготовительная группа |
4,12 |
4,00 |
2,220 |
0 |
7 |
|
Первый класс |
3,98 |
4,00 |
1,816 |
0 |
7 |
|
«Циклы», общий балл |
|||||
|
Старшая группа |
5,30 |
5,00 |
3,441 |
0 |
13 |
|
Подготовительная группа |
9,65 |
9,00 |
2,658 |
3 |
15 |
|
Первый класс |
11,45 |
12,00 |
3,072 |
0 |
14 |
|
«Что может быть одновременно?», общий балл |
|||||
|
Старшая группа |
3,66 |
2,00 |
3,433 |
0 |
14 |
|
Подготовительная группа |
7,20 |
7,00 |
4,277 |
0 |
17 |
|
Первый класс |
9,82 |
10,00 |
4,098 |
0 |
18 |
Полученные ранее нормы выполнения детьми старшего дошкольного возраста [Веракса, 2021] указывают на то, что средние показатели выполнения методики «Циклы» лежат в диапазоне от 3 до 9 баллов, а для методики «Что может быть одновременно?» высокий уровень выполнения отсчитывается от 7 баллов. Показатель подуровня в диапазоне от 4—6 баллов указывает на изображение «символических» деревьев различной степени трансформации, 7 баллов означают, что дети изображали «диалектические» деревья, что является показателем применения диалектического мыслительного действия превращения.
При помощи критерия Фридмана для нескольких связных выборок было установлено, что есть значимые различия в оценках детей разных групп по параметрам: «Необычное дерево», подуровни (Chi-square=14,445; p=0,001), «Циклы», общий балл (Chi-square=98,646; p<0,001) и «Что может быть одновременно?», общий балл (Chi-square=73,576; p<0,001). Далее, при помощи попарного сравнения критерием Вилкоксона для двух связных выборок, было выявлено, между какими конкретно возрастами есть различия.
Анализ результатов выполнения детьми методики «Рисунок необычного дерева» с применением критерия Вилкоксона для связных выборок показал:
- подуровень выполнения методики в старшей группе значимо ниже, чем в подготовительной группе (W=-3,981; p<0,001) и в первом классе (W=-3,966; p<0,001);
- подуровни выполнения методики в подготовительной группе и в первом классе значимо не различаются (W=-0,114; p=0,909). Можно заключить, что в конце дошкольного детства в выполнении этой методики наблюдается значимый прирост, который при начале обучения в школе несколько нивелируется.
В ходе сравнительного анализа результатов выполнения детьми заданий методики «Циклы», проведенного с помощью t-критерия для связных выборок было установлено:
- оценки детей в старшей группе оказались значимо ниже, чем в подготовительной группе (W=-6,983; p<0,001) и в первом классе (W=-7,655; p<0,001);
- оценки детей в подготовительной группе значимо ниже, чем в первом классе (W=-5,394; p<0,001). Дети стали лучше решать задачи о процессах развития, используя действие диалектической сериации.
Анализ результатов выполнения детьми методики «Что может быть одновременно?» показал:
- оценки детей в старшей группе значимо ниже, чем в подготовительной группе (W=-5,712; p<0,001) и в первом классе (W=-7,478; p<0,001);
- оценки детей в подготовительной группе значимо ниже, чем в первом классе (W=-4,461; p<0,001). Дети стали успешнее преодолевать противоречия, оперируя действием опосредствования. Полученные результаты позволяют нам сделать вывод, что старший дошкольный и младший школьный возраст сенситивны для развития диалектического мыслительного опосредствования.
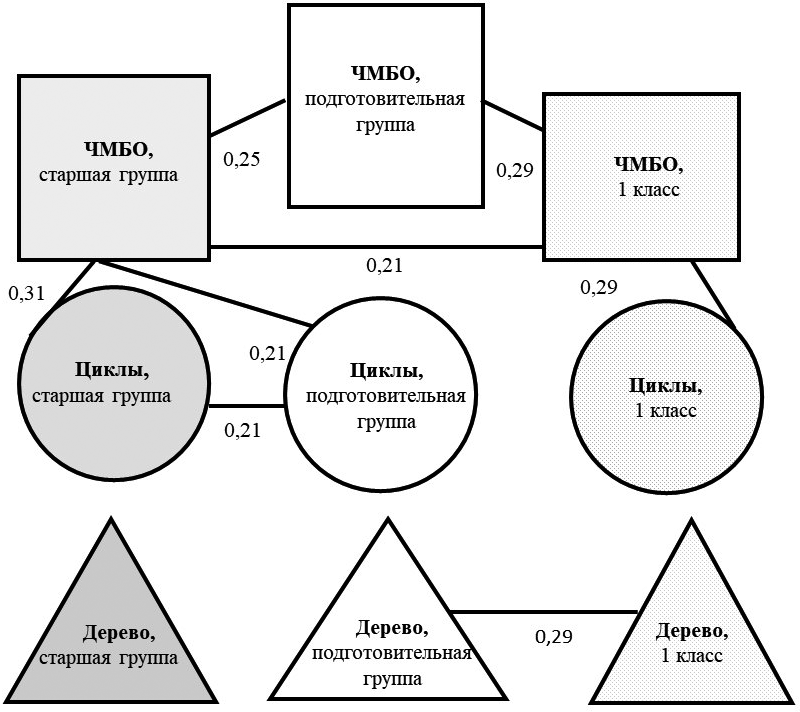
Корреляционная плеяда оценок выполнения детьми трех методик на протяжении трех лет (r>0,2; p<0,05) была подсчитана с помощью коэффициента корреляции Спирмена и приведена на рис. 3.
Как видно из рисунка, результаты выполнения детьми методики «Что может быть одновременно?» оказались связаны попарно во всех возрастных группах. Оценки дошкольников старшей и подготовительной групп по методике «Циклы» также оказались связаны между собой.
Результаты выполнения методики «Рисунок необычного дерева» не связаны с результатами выполнения по другим методикам. Внутри же методики оказались связанными оценки, полученные детьми в подготовительной группе и первом классе. Результаты детей данной выборки показывают наличие устойчивой положительной связи оценок способности находить единый объект, обладающий двумя заданными противоположными свойствами. Полученные данные говорят, что диалектическое опосредствование представляет устойчивую линию развития диалектического мышления на протяжении дошкольного и начала младшего школьного возраста. При этом успешность решения задач на преодоление противоречий связана со способностью дошкольников понимать процессы развития.
Рис. 3. Корреляционная плеяда оценок выполнения методик на выявление уровня развития диалектического мышления у детей в трех диагностиках (в старшей группе детского сада, в подготовительной группе детского сада и в первом классе школы): ЧМБО — «Что может быть одновременно?»; темно-серый цвет — старшая группа; светло-серый — первый класс
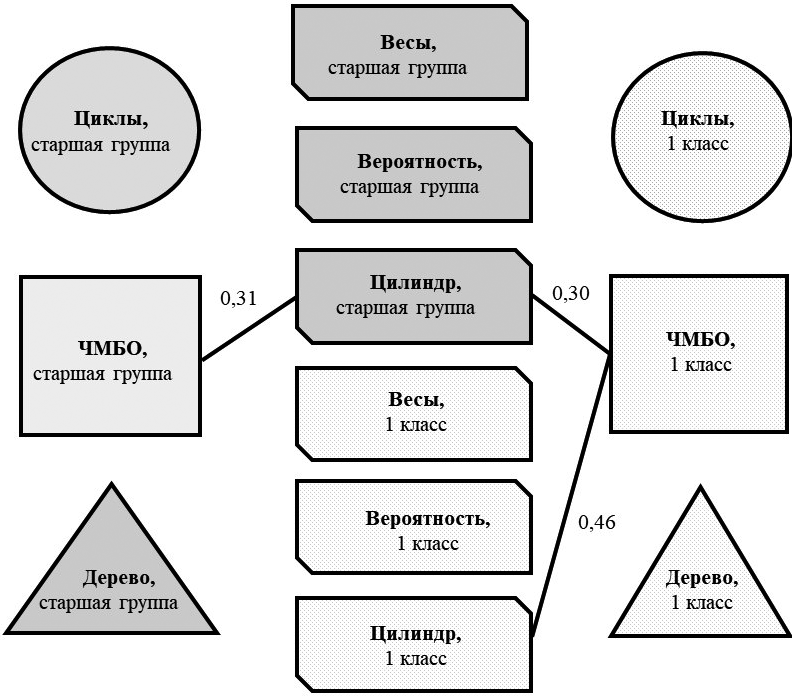
Корреляционная плеяда оценок параметров диалектических и формально-логических операций в старшей группе детского сада и в первом классе(r>0,2; p<0,05) представлена на рис. 4.
В результате корреляционного анализа было выявлено:
1) общий балл по методике «Что может быть одновременно?» в старшей группе детского сада связан с суммарным баллом пробы «Цилиндр» в старшей группе (r=0,31; p<0,05);
2) общий балл по методике «Что может быть одновременно?» в первом классе связан с суммарным баллом пробы «Цилиндр» в старшей группе (r=0,30; p<0,05) и в первом классе (r=0,46; p<0,05).
3) была обнаружена положительная связь между способностью одновременно координировать два процесса и преодолевать противоречие. При этом, чем лучше ребенок способен совершать формальное действие в старшей группе, тем лучше у него получается преодолевать противоречия в старшей группе и в дальнейшем в первом классе. В первом классе связь этих двух действий также сохраняется.
Рис. 4. Корреляционная плеяда оценок диалектического мышления и проб Пиаже в старшей группе детского сада и в первом классе (r>0,2; p<0,05) (n=52): ЧМБО — «Что может быть одновременно?»; темно-серый цвет — старшая группа; светло-серый — первый класс.
Обсуждение результатов
В проведенном ранее исследовании [Веракса] были получены данные о положительной корреляционной связи способности у детей 5—6 лет координировать два процесса и оценивать вероятность результата с пониманием процессов развития, определять вероятность наступления определенного события и понимания процессов развития. Мы предположили в гипотезе 1, что связи будут проявляться и в последующих замерах. Однако в нашем исследовании связь не была обнаружена. Вместе с тем подтвердилась гипотеза 2 и была обнаружена корреляционная зависимость между способностью ребенка решать задачу на преодоление противоречия («Что может быть одновременно?») и пониманием мультипликативных пространственных отношений (см. рис. 4). Существование подобной связи может быть объяснено тем, что в пробе «Цилиндр», успешность решения, т. е. правильное представление о предполагаемом рисунке, возможно только в том случае, если ребенок будет учитывать, что карандаш движется одновременно и по вертикали, и по горизонтали. Это означает, что движение карандаша есть опосредствование двух противоположных движений. Следовательно, и в пробе «Цилиндр», и в методике «Что может быть одновременно?» решение опирается на использование сходных диалектических мыслительных операций, а именно — операции опосредствования. Результаты диагностики показали, что подтвердилась не гипотеза 1, а гипотеза 2 о том, что понимание пространственных мультипликативных отношений связано с развитием опосредствования. При этом мы можем уточнить, что действие опосредствования, направленное на преодоление противоречия, наиболее тесно связано с координацией двух разнонаправленных действий в едином продукте (см. рис. 4). Другими словами, мы можем сказать, что диалектическое мышление связано с формально-логическими операциями мультипликации. Подчеркнем еще раз: существенный момент здесь заключается в том, что мультипликативные действия рассматриваются нами не только как результат развития формального мышления, но и как следствие развития диалектического мышления. Развитие же диалектического мышления мы связываем в дошкольном возрасте с развитием игровой деятельности, имеющей довольно сложную диалектическую структуру. Мы предполагаем, что обнаруженные корреляционные зависимости во многом основаны на переходе диалектического мышления дошкольников в процессе своего развития на новый более высокий уровень. Вероятно, к началу стадии конкретных операций (т. е. ближе к 7 годам) дети начинают активно использовать диалектическую операцию опосредствования, что позволяет им решать мультипликативные задачи. Данные о положительной связи успешности выполнения действия опосредствования с результатами диагностики формальных операций представлены в публикации О.А. Шиян и коллег [Шиян, 2021].
Вместе с тем нами была выдвинута гипотеза о возможности регресса показателей диалектического мышления в конце дошкольного возраста. В проведенном ранее исследовании под руководством Н.Е. Вераксы были получены данные о снижении показателей диалектического мышления у детей в начальной школе [Веракса, 2006]. Эти данные частично подтвердились: мы не обнаружили корреляционные связи результатов выполнения методик «Что может быть одновременно?» и «Рисунок необычного дерева», однако способность преодолевать противоречия в течении 3 лет возросла, а показатели способности создавать новый образ с опорой на диалектические преобразования, после роста в подготовительной группе, снова снизились у первоклассников до показателей детей 5—6-летнего возраста. В большинстве рисунков детей 7—8 лет преобладают символические изображения, т. е. «необычное дерево» отражает чаще эмоциональную составляющую изменений образа дерева, нежели структурные трансформации. Опираясь на культурно-историческую теорию Л.С. Выготского, мы можем предположить, что диалектическое мышление подвергается качественному изменению. Вероятно, при переходе к обучению в школе возникает новая социальная ситуация развития, в которой развитие диалектического мышления реализуется в контексте доминирования знакового отражения объектов в системе понятий.
Выводы
- Проведенное экспериментальное исследование показало, что старший дошкольный возраст сенситивен для развития диалектического мышления. В первом классе дети, принявшие участие в нашем лонгитюдном исследовании, успешнее справляются с заданиями на преодоление противоречий и понимание процессов развития, чем в дошкольном возрасте. В то же время у детей младшего школьного возраста наблюдается снижение использования диалектического мыслительного действия превращения при выполнении творческих графических заданий.
Эти результаты частично подтверждают предположение о том, что у детей младшего школьного возраста, обнаруживается снижение успешности решения диалектических задач при повышении успешности выполнения формально-логических операций. Вероятно, это изменение связано со сменой ведущей игровой деятельности на учебную. В этом случае снижается возможность действия ребенка в мнимой ситуации, позволяющей снять противоречие между желаемым и возможным.
В дальнейшем мы планируем изучить связи двух форм мышления в 8—9-летнем возрасте, для того чтобы проанализировать динамику когнитивного развития в младшем школьном возрасте и сравнить показатели двух форм мышления у детей 5—6, 7—8 и 8—9 лет данной лонгитюдной выборки.
- С возрастом дети успешнее справляются с решением формально-логических задач, направленных на координацию двух условий. Результаты корреляционного анализа показывают, что в 5- и 7-летнем возрасте успехи в преодолении детьми противоречий положительно связаны с пониманием мультипликативных пространственных отношений, когда движения двух разнонаправленных объектов создают единый образ, что свидетельствует в пользу предположения о том, что понимание пространственных мультипликативных отношений связано с развитием диалектического опосредствования.
Литература
- Веракса Н.Е. Диалектическое мышление. Уфа: Вагант, 2006. 212 c.
- Веракса Н.Е. Диалектическое мышление: логика и психология // Культурно-историческая психология. 2019.Том 15. № 3. С. 4—12. DOI:10.17759/chp. 2019150301
- Веракса Н.Е., Алмазова О.В., Айрапетян З.В., Тарасова К.С. Гетерохронность развития диалектического мышления у детей старшего дошкольного возраста // Психологический журнал. 2021. Том 42. № 4.С. 59—73
- Веракса Н.Е., Алмазова О.В., Тарасова К.С. Диалектическое и формально-логическое мышление старших дошкольников // Российский психологический журнал. 2022 (в печати)
- Давыдов В.В. Виды обобщений в обучении. М.: Педагогика,1972. 424с.
- Запорожец А.В., Луков Г.Д. О развитии рассуждения у ребенка младшего возраста // Культурно-историческая психология. 2007. Том 3. № 1. С. 101—108
- Золотарева А.А., Аверина П.А., Тимошина А.Л. Психологические предикторы апатии в средней и поздней взрослости // Национальный психологический журнал. 2021. № 2(42). С. 88—97. DOI:10.11621/npj.2021.0208
- Ильенков Э.В. Проблема противоречия в логике // Диалектическое противоречие. М.: Политиздат, 1979. С. 122—143.
- Копнин П. В. Диалектическая логика и ее отношение к формальной логике / Б.М. Кедров (ред.), Диалектика и логика. М.: АН СССР, 1962. С. 33—62.
- Пиаже Ж. Психология интеллекта. СПб.: Питер, 2004. 192 с.
- Ржанова И.Е., Алексеева О.С., Фоминых А.Я. Половые различия по показателям когнитивной сферы у детей дошкольного и младшего школьного возраста // Вестник Московского университета. Серия 14. Психология. 2020. № 2. С. 141— DOI:10.11621/vsp.2020.02.07
- Шиян О.А., Белолуцкая А.К., Ле-Ван Т.Н., Зададаев С.А. Когнитивное развитие дошкольников: взаимосвязь нормативных, преобразующих и символических способностей // Современное дошкольное образование. 2021. № 6(108). С. 14—25. DOI:10.24412/1997-9657-2021-6108-14-25
- Inhelder B., Piaget J. De la logique de l'enfant à la logique de l'adolescent. Paris: PUF, 1955.
- Piaget J. Les Formes Élémentaires de la Dialectique. Paris: Gallimard,1980. 249 p.
- Piaget J., Inhelder B. La genese de l'idee de hasard chez l'enfant. Paris: PFU, 1951. 257 p.
- Piaget J., Inhelder. B., Sieminska. A. La géométrie spontanée de l'enfant. Paris: PFU, 1948. 239 p.
- Riegel K.F. Dialectic operations: The final period of cognitive development // Human Development. 1973. Vol. 16(5). 346—370. DOI:10.1159/000271287
- Sidneva A.N., Vysotskaya E.V., Korotaeva I.V., Mozharovsky I.L., Shinelis V.A. How Do Primary Schoolchildren Use Concept Defnitions in Recognition Tasks? // Psychology in Russia: State of the Art. 2022. Vol. 13(2), P. 29—46. DOI:10.11621/pir.2020.0203
- Valeeva R., Kalimullin A. Adapting or changing: The covid-19 pandemic and teacher education in Russia // Education Sciences. 2021. Vol. , P. 1—12.
- Veraksa N, Basseches M Brandão A.Dialectical Thinking: A Proposed Foundation for a Post-modern Psychology // Front. Psychol. 2022.Vol. 13: 710815, P. 1— DOI:10.3389/fpsyg.2022.710815
Информация об авторах
Метрики
Просмотров web
За все время: 1216
В прошлом месяце: 59
В текущем месяце: 32
Скачиваний PDF
За все время: 285
В прошлом месяце: 12
В текущем месяце: 4
Всего
За все время: 1501
В прошлом месяце: 71
В текущем месяце: 36