Development of Formal-logical and Dialectical Thinking in Children of 5-8 Years Old

This article presents the longitudinal study results dedicated to evaluation of formal-logical and dialectical thinking development in senior preschool children (5—6 and then 6—7 years old) as well as in elementary school children (7—8 years old). The formal—logical thinking study included 58 children. We used Piaget tests: “Probability”, “Scales” and “Cylinder”. The dialectical thinking study included 92 children. We evaluated three techniques: “Drawing an unusual tree”, “What can be both at the same time?” and “Cycles”. Data of 52 children who participated in the study at the age of 5—6 years old and 7—8 years old were used for the correlation analysis. The research results showed that the preschool age is sensitive for the development of formal operations as well as dialectical thought activities. A positive correlation was identified between the ability of 5—6 and 7—8 years old children to coordinate two differently directed movements to create a holistic image and overcome contradictions. It was also found that during the transition to learning at school, indicators for solving a creative problem (which involved the independent construction of opposite objects) decreased

Introduction

Сhild cognitive psychology development in the 20th century set up a foundation for the research of the two independent forms of thinking: formal-logical and dialectical thinking. Based on the analysis of international [10; 14; 17; 20] and Russian [2; 6; 7; 8; 9; 11; 18; 19] studies, the main distinguishing features of these forms of thinking were formulated. As “a distinctive feature of formal logic the manipulation of mental forms abstracted from the content was used, and dialectical logic began to be understood as the logic of unfolding the contradiction of the developing content” [2, p.5]. Dialectical thinking was interpreted as a non-independent process supporting the formal structures formation [14]. In this article, we will consider the differences from the J. Piaget’s point of view in terms of assimilation and accommodation paradigm in order to maintain the perspective of cognitive development integrity.

The formal logical thinking development is a long process that consists of various subsequent stages. Each stage is the result of qualitative changes in a child’s cognitive development and is characterized by a new level of achievement of dynamic balance of intellectual processes. The logical operations formation in the paradigm of assimilation (“the canvas of actions that can be actively reproduced”) and accommodation (“the influence of the environment, which has the opposite effect, that changes the assimilative cycle”) is described as an achievement of  a balance between these processes. J. Piaget emphasized that “the operational thinking balance does not at all represent a certain state of rest, but is a system of balanced exchanges and transformations, infinitely compensating each other” [10, p. 19]. The thinking development process is accompanied by changes in the forms of equilibrium. Thus, the perceptual structures equilibrium is characterized by a "displacement of equilibrium", when each change of one of the existing relations meaning entails the transformation of the whole, up to the formation of a new equilibrium, that is different from the one that characterized the previous state. The equilibrium of operational structures is both dynamic and permanent at the same time. The transformations inherent in such systems do not change this balance, because they are always accurately compensated by the reverse – real or potential – operations (reversibility).

According to J. Piaget, dialectic is directly linked to the equilibrium formation: “in any cognitive development, there is an alternation of dialectical and discursive phases” [14, p.188]. “Dialectic constitutes the genetic aspect of any equilibrium” [14, p. 10], i.e. leads to the structures’ formation. In the discursive phase, stable structures generate new interdependencies, and once again dialectic arises, since a new commonality is formed, requiring new balancing processes.

Dialectic leads to interactions and connections formation, which, according to J. Piaget, are organized in a spiral model [14]. As the main conflict that triggers the interaction processes J. Piaget described the tension between “possible” and “necessary”: “the acquisition of knowledge R (reals) entails several new possibilities P (possible). Between some of these necessary relations N (necessaries) such relations are established which then cover the original object R, but in the augmented form R2. From R2 new possibilities P2 immediately follow, and then new needs will lead to R3, etc.” [14, p.193]. Thus, based on Piaget’s theory, dialectic is an auxiliary process in the new cognitive stage formation.

1. Piaget denies the existence of contradictions between the two objects. In his opinion, “once the qualities of the elements are abstracted in order to consider them as units equivalent to each other, the inclusions can only be supported by the arrangement, which generates new, much more complex commonality, which is a sequence within” [14, p.187]. “A child is not able to think in terms of relationships until he/she has learned to conduct seriations. Seriation is the primary reality, any asymmetric relationship of which is only a temporarily abstracted element” [10, p.17]. Therefore, when discussing the equilibrium of structures within the operational model, J. Piaget excludes contradictions by using the seriation.

Arguing with J. Piaget, K. Riegel highlighted the problem of understanding the contradictions by children and offered descriptions of dialectical manifestations at each cognitive development stage. In particular, at the preoperational stage, in his opinion, a child perceives two concepts simultaneously and is able to sort objects by color into red and green, i.e., into those that show the presence of an attribute, for example, red, and those that demonstrate its absence (non-red). K. Riegel also pointed out: “Piaget systematically searches for contradictions in the child’s judgments and thereby undermines his own dialectical interpretations, and also underestimates the child’s dialectic” [17, p.11], since contradictions are sorted out formally. According to Rigel, this leads to “alienation” of thinking, and in order to reach maturity, the “alienated” child will have to return to the dialectical basis of thinking [17, p.11]. The development of K. Rigel's ideas about returning to the dialectical foundations of thinking served as the basis for interpreting dialectical operations as post-formal [20]. M. Basseches identified 24 dialectical schemes that an adult uses to solve subjectively complex problems [20, p. 7]. However, considering dialectical thinking as post-formal leads to the fact that the possibility of studying this form of thinking in childhood is excluded.

1. Shiyan et al. [12] hypothesized that in childhood formal structures are associated with dialectical thinking, if “formal intelligence is understood in the J. Piaget tradition as the formation of reversibility” [12, p. 21]. The authors used tests that assessed ideas of preservation (of sets, length, mass) and understanding of the “part-whole” relationship. The research demonstrated that there is a significant relationship between children's success in solving the preservation task and their ability to overcome contradictions.

In Russian psychology, the concept of structural-dialectical psychology has been developed. This research direction was formed in the context of cultural-historical theory. It was supported by the works of A. Zaporozhets, in which data were obtained on the preschoolers’ sensitivity to contradictions [6]. Dialectical thinking is defined by N. Veraksa as an independent branch of cognitive development and it represents a system of mental actions aimed at operating with the relations of opposites while solving dialectical problems [1].

The basis of the dialectical thinking model are the relationships of the opposites, that allow to build a dynamic structure of mental actions. The dialectical action of transformation is the mental transformation of an object A into its opposite – an object B (for example, morning-evening). Dialectical action mediation combines the opposites A and B into a single object AB (orange color, as well as yellow and red at the same time). Dialectical action seriation is a mental reproduction of an object’s gradual transformation from the initial state A to its opposite state B via the intermediate state AB (for example, morning-afternoon-evening-night-morning). Understanding the structure of this action is associated with the construction of a cyclic representation that reflects the process of changing the object from the initial state to the opposite, and then back, from the opposite to the initial one [1]. Dialectical thinking is substantively related to the solution of three problem types: 1) making a creative product [9]; 2) understanding developmental processes [5]; 3) overcoming contradictions [9].

The study conducted on preschool children [4], showed that the dialectical thinking development process is heterochronous. The prerequisites for the dialectical thinking development originate already in the early preschool years [3]. By the age of 4, a child understands the processes of transformation, although such a task as “Drawing an unusual tree” remains difficult for him/her, and the number of dialectical drawings increases by the time of entering a preparatory group. At senior preschool age a child successfully copes with seriations, he/she develops an understanding such processes as transformation and conversion. During preschool age, a child improves the ability to overcome contradictions by applying the mental action of mediation. In a previously conducted study [4] a positive correlation between the “Probability” test results and the “Cycles” test results performed by children of 5-6 years old was discovered. We assumed that such a result may reflect the cyclic structure of dialectical thinking in senior preschool age children.

Research Methods

In this research, there were two tasks: 1) to analyze the formal-logical and dialectical thinking development in children from 5 to 8 years old 2) to explore the interrelations of these thinking forms.

We formulated the following hypotheses. Hypothesis 1: a correlation between the development of the ability to coordinate two processes and evaluate the probability of a result as well as the developmental processes understanding previously discovered in senior preschool children also takes place in elementary school age children. Hypothesis 2: spatial multiplicative relations understanding is connected with the mediation development. Hypothesis 3: elementary school age children show a decrease in the success of dialectical problems solving with an increase in the success of formal logical operations implementation compared with children of 5-6 years old.

A longitudinal study of the formal logical thinking development involved 58 children (31 girls and 27 boys), who completed 3 tests: “Probability”, “Balance” and “Mechanical curve” in the senior kindergarten group and then in 2 years in the 1^st year of elementary school. The study of dialectical thinking development included 92 children (44 boys and 48 girls), who performed the test tasks 3 times –  in the senior kindergarten group, in the preparatory kindergarten group, and in the 1^st year of elementary school. These children completed 3 tests: “Drawing an unusual tree”, “Cycles”, “What can be at the same time?”. To analyze the correlation between the two thinking forms, the data of 52 children were used. All children at the time of the research attended educational institutions in Moscow. The study was conducted from 2019 to 2021.

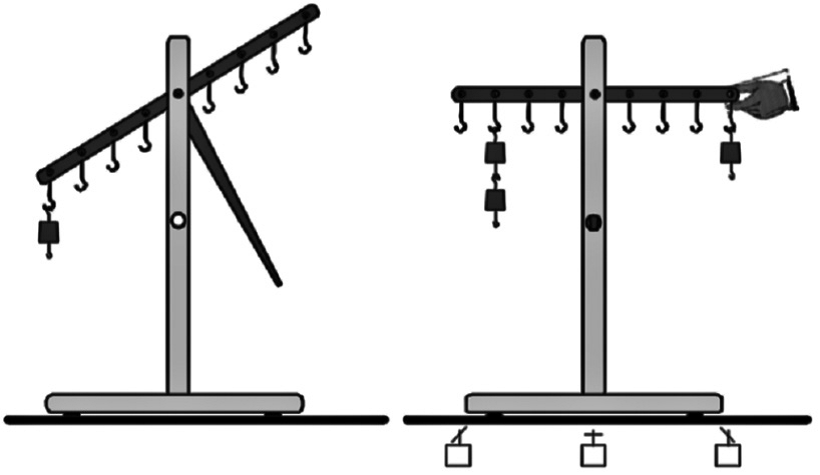
The “Balance” [4; 15] evaluated operations that allow to coordinate and quantify such variables as weight and distance. A child was presented with a visual task using balance scales with 12 holes equidistant from the fulcrum on each side and with 16 metal weights weighing 32 grams each. (Fig. 1). Throughout the test, the arems of the scales were fixed in a horizontal position. Each time the weights were placed, the tester asked a child the question: “What will happen to the scales when I unlock the shutter? Will they stay in the same position or lean to this side or to that one? In which direction? How did you understand this?”. There were 5 tasks in total (2 introductory and 3 actual ones).

Fig. 1. Device for carrying out the “Balance” test

The “Probability” [4; 15] evaluated operations that allow estimating the probability of achieving a certain result based on different ratios of white and black dibs. The instruction was as follows: “Imagine that we have put the dibs in the bags and shook them. Now imagine that we take 1 dib from here (pointing to the left pile of dibs) and 1 dib from here (pointing to the right pile of dibs). Which side will have a higher chance of getting a white chip? How did you understand this?" There were 5 tasks in total (2 introductory and 3 actual ones).

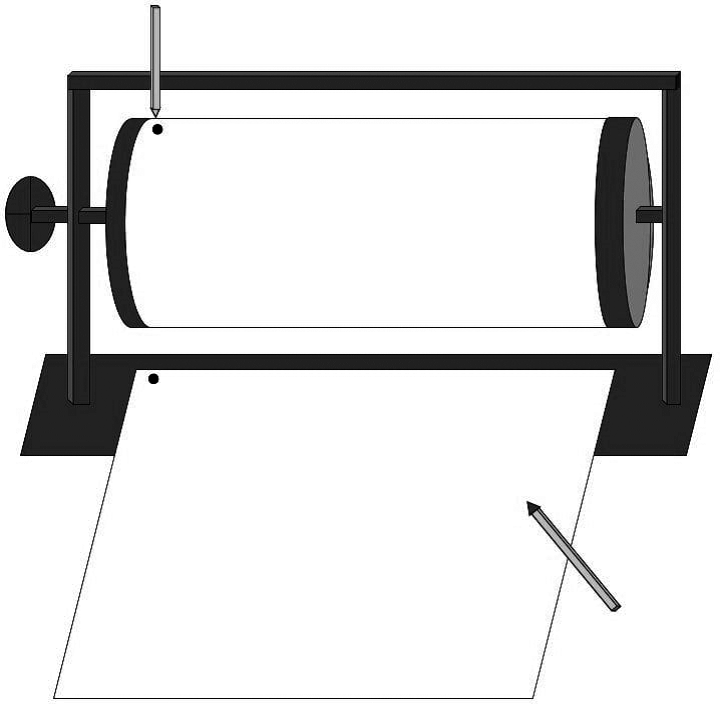
The “Mechanical curve” [16; 4] assessed the ability to coordinate two differently directed processes. A special installation consisting of a cylinder that could be rotated with a handle and a cleat fixed on top of it was placed on the table in front of a child. A sheet of paper with a starting point was fixed on the cylinder. A pencil could be moved along the cylinder (Fig. 2).

Fig. 2. Device for carrying out the “Mechanical curve” test, frontal view from the side of a child.

The tester explained the significance of the starting point and demonstrated the principles of installation elements operation. For each task, a child was presented with a sheet of paper with a starting point. The instruction was as follows: “Draw what the trace will be if ...”. In the introductory tasks, the tester showed a child the movements of the pencil and cylinder, and in the actual test tasks, the tester only voiced the conditions of the task. There were 5 tasks in total (2 introductory and 3 actual ones).

Therefore, the Piaget test contains a coordination of two parameters: amount and color of chips; numberof weights and the distance at which they are hanging; vertical movements of a cylinder and horizontal – of a pencil. In all of the three Piaget tests, each child’s answer was evaluated on standardized 4-point scale [15; 16]: 0 points – a child did not understand the task; 1 point –  a child took into account only one parameter in his/her answer; 2 points –  a child mentioned both parameters in the answer, but relied on only one of them in the forecast; 3 points –  a child tried to correlate two parameters. As a result, we have rated types of trees: normative, symbolic and dialectical (0-2 points) and transformations (0-7 points) in accordance with a standard rating procedure [3]. 4 kinds of trees have been allocated among “normative” drawings according to the degree of transformation: 0 – no transformation; 1 – partial transformation affects one part of a tree; 2 – complex transformation – various plant fruits grow on a tree which aren’t typical for it (mushroom tree); 3 – an attempt of a complete transformation, but a tree still remains (cactus). In “symbolic” drawings modifications are caused by magic and an idea of fulfillment of children’s wishes; 4 – the drawing contains an idea of magic and unusualness, elements of animation and a reflection of theme of desires are present; 5 – complex transformation, which reflects a variety of objects and creation of a new image using a combination with other objects; 6 – an attempt of a full transformation which demonstrates structural changes, but there’s also some symbolism (a fountain tree). 7 points are added for “dialectic” trees which reflect structural transformation (reversed trees which grow upside down).

The “Drawing an unusual tree” [4] made it possible to evaluate the success of a child solving a creative task to generate a new graphic image. To complete the drawing, the children used an A-4 sheet and a pencil. A child was given the following instruction: "Please draw an unusual tree." After completing the drawing, a child told in detail what was unusual about the depicted tree. As a result, we evaluated the type of transformation from 0 to 2 points, as well as the type of transformation in the sublevel from 0 to 7 points.

The “Cycles” [4] assessed a child’s ability to solve problems that reflect developmental processes. A child was given three tasks with five cards. In total, three plots were used such as: “Dissolving lumps of sugar in tea”, “Preparing boiling water in a teapot”, “The beginning of a thunderstorm”. The instruction was as follows: “Lay out the cards so that you get a story”. For each task child received from 0 to 5 points, with a maximum of 15 points in total for 3 tasks.

The “What can be both at the same time?” [4] evaluated the ability to overcome contradictions. The test included five questions containing an inconsistent pair of features. The children were asked to answer the question: “What can be at the same time: both black and white; both light and heavy; both big and small; both living and non-living; both the same and different?” For each task child received from 0 to 4 points, with a maximum of 20 points in total for all 5 tasks.

Results

The obtained data analysis was carried out in 3 stages. At the first stage, descriptive statistics were formed on the children’s performance in tests aimed at assessing formal logical and dialectical thinking. Then, using Wilcoxon signed-rank test, the significance of grades’ differences in the senior kindergarten group, preparatory kindergarten group and in the 1^st year of elementary school was assessed for the parameters under consideration. At the third stage, a correlation analysis of the interrelations between the indicators of the two thinking forms was carried out. The IBM SPSS statistics program v. 26 was used for data analysis.

Formal logical thinking

Table 1 presents the statistics for each type of J. Piaget tests. For all tests, the average values increase from the senior group to the 1^st year of elementary school, while the variation of data decreases.

Table 1

Statistics on the Piaget tests performance in the senior kindergarten group and in the 1^st year of elementary school (N=58)

Using Wilcoxon signed-rank test, the significance of grades’ differences in the senior kindergarten group and in the 1^st year of elementary school was assessed for the parameters under consideration (Table 2).

According to all the considered parameters (except for the “Balance, median”), the scores in the 1^st year of elementary school are significantly higher than in the senior kindergarten group. The older children get, the better they cope with multiplicative tasks of coordinating two parameters and estimating probabilities. In general, this corresponds to the formal operations development in childhood and, in its turn, points to a sensitive period – 5 to 7 years old for the development of abilities that underlie the Piaget tests’ successful completion.

Dialectical thinking

In the senior kindergarten group, while performing the “Drawing an unusual tree” test, 47 children (51.1%) drew a normal tree, 36 (39.1%) –  a symbolic one and 9 (9.8%) – a dialectical one. In the preparatory kindergarten group (one year after the first drawing), 22 (23.9%) children drew a normal tree, 53 (57.6%) – a symbolic one, and 17 (18.5%) – a dialectical one. In the first year of elementary school (two years after the first drawing), 20 children (21.7%) drew a normal tree, 63 (68.5%) – a symbolic tree, and 9 (9.8%) – a dialectical one. The number of “normal” trees sharply decreased from the senior group to the preparatory one (from 36 to 22) and remained approximately at the same level (from 22 to 20) in the first year of elementary school. The number of “dialectical” trees increased from the senior to the preparatory group (from 9 to 17) and fell again in the first year of elementary school (from 17 to 9). Thus, analyzing the ratio of the images of tree types, we see that with age, children better cope with creative task (reducing the number of normal trees). At the same time by the end of preschool age, children more actively use the dialectical mental action of transformation, i.e., draw inverted trees, trees on which grow other trees, etc., i.e., while preserving the idea of a tree, they transform the structure. Moreover, a decrease in the frequency of these actions during the transition to schooling can be noted. Such a decrease in solving creative problems is typical for elementary school age. To assess the statistical significance of this shift, Wilcoxon signed-rank test was used, in which we also evaluated sublevels that could be considered as a rank scale. Table 2 shows the main psychometric characteristics of children’s sublevels, as a result of the “Drawing an unusual tree” test completion at different ages.

Table 2

Statistics on the performance in tests aimed at assessing dialectical thinking in the senior and preparatory kindergarten groups and the 1^st year of elementary school (N=92)

The previously obtained standards of performance by older preschool children [3] indicate that average ratings of completion of the “Cycles” methodology are within the range from 3 to 9 points, and for the “What can happen at the same time?” methodology a high level of performance is measured from 7 points. A figure of the sublevel in the range of 4-6 points indicates a depiction of “symbolic” trees with various degrees of transformation, 7 points mean that children have drawn “dialectic” trees which is an indicator of implementation of a dialectic mental action of transformation.

It has been determined using Friedman test for multiple related samples that there’re significant distinctions in evaluation of children from different groups on “Unusual tree, sublevels” (Chi-square=14.445; p=0.001), “Cycles, overall score” (Chi-square=98.646; p<0.001) and “What can happen at the same time” (overall score) (Chi-square=73.576; p<0.001). Then, using a pairwise comparison via Wilcoxon signed-rank test, it has been determined which exact ages have differences.

An analysis of the children’s results in the “Drawing an unusual tree” test performance using Wilcoxon signed-rank test showed that:

• the sublevel of test implementation in the senior group was significantly lower than in the preparatory group (W=-3.981; p<0.001) and in the first year of elementary school (W=-3.966; p<0.001);
• the sublevels of test implementation in the preparatory group and in the first year of elementary school did not differ significantly (W=-0.114; p=0.909). It can be concluded that at the end of preschool childhood there is a significant increase in children’s results in this test, which is somewhat leveled at the beginning of schooling.

A comparative analysis of the children’s results in the “Cycles” test, carried out using the t-test for linked samples, it was found that:

• the children’s scores in the senior group were significantly lower than in the preparatory group (W=-6.983; p<0.001) and in the first year of elementary school (t=-7.056; p<0.001);
• the children’s scores in the preparatory group were significantly lower than in the first year of elementary school (W=-7.655; p<0.001). Children began to solve the problems of developmental processes better using the dialectical seriation.

Analysis of the children's results in the “What can be both at the same time?” test showed that:

• the children’s scores in the senior group were significantly lower than in the preparatory group (W=-5.712; p<0.001) and in the first year of elementary school (W=-7.478; p<0.001);
• the children’s scores in the preparatory group were significantly lower than in the first year of elementary school (W=-4.461; p<0,001). Children began to overcome contradictions more successfully, using the action of mediation. The obtained results allow us to conclude that senior preschool and elementary school age are sensitive for the dialectical action of mediation development.

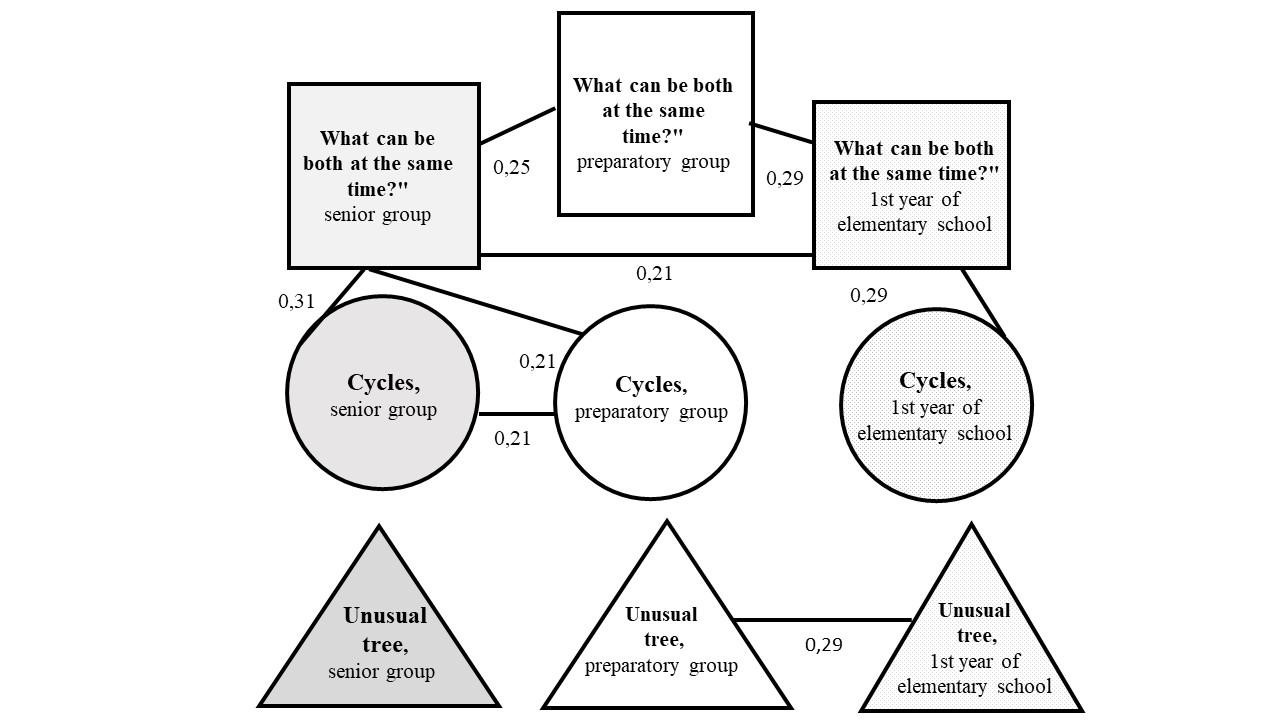
The correlation pleiad (Spearman’s coefficient) of the children’s performance scores in all three tests over the course of three years (r>0.2; p<0.05) is shown in Figure 3.

The children’s results in the “What can be both at the same time?” test were associated in pairs across all age groups. The scores of the senior and preparatory preschoolers according to the “Cycles” test also turned out to be interconnected.

The results of the “Drawing an unusual tree” test were not related to the results of other tests. Within the test itself, the scores obtained by children in the preparatory group and the first year of elementary school turned out to be related. The children’s results in all 3 age groups showed positive correlation of the ability to find a single object that has two given opposite properties. The obtained data demonstrated that dialectical mediation represents a stable line of dialectical thinking development throughout the preschool age and beginning of elementary school age. At the same time, the success of solving problems to overcome contradictions was associated with the ability of preschoolers to understand developmental processes.

Fig. 3. The correlation pleiad of the children’s performance scores of all three tests over the course of three years.

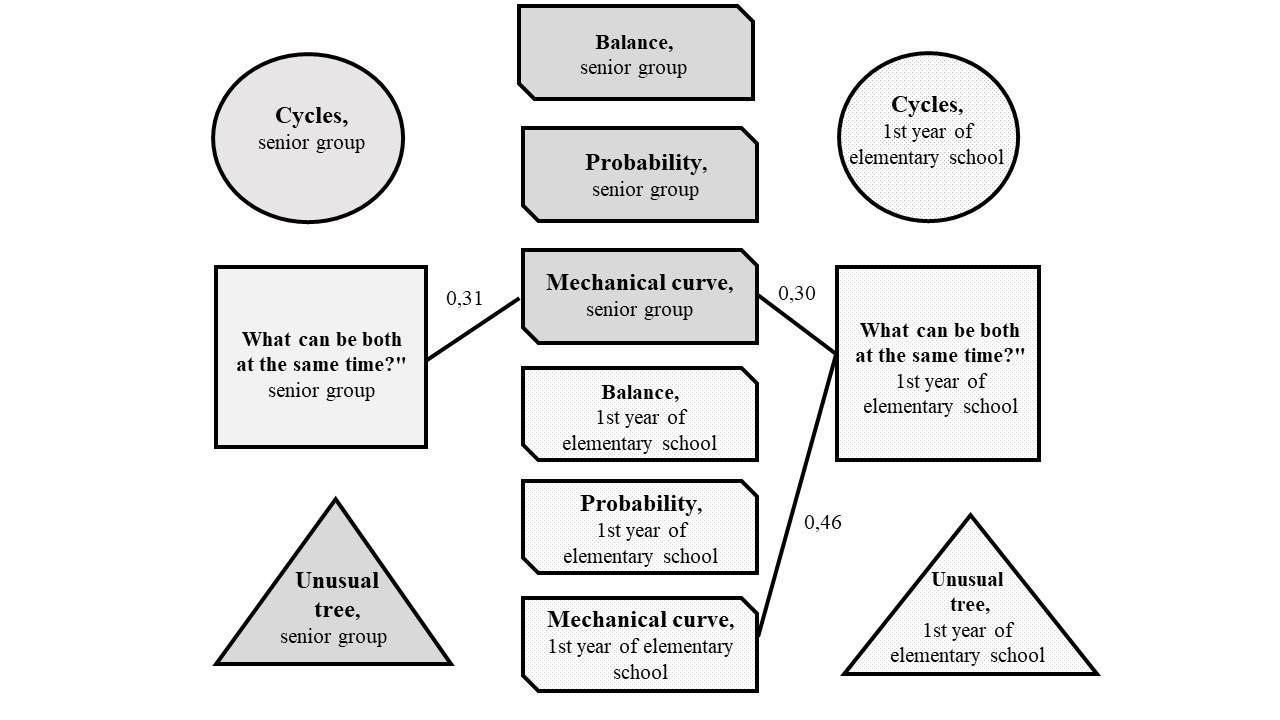
The correlation pleiad of the children’s performance scores in tests for dialectical and formal-logical operations in the senior kindergarten group and in the 1^st year of elementary school is shown in Figure 4.

As a result of the correlation analysis, it was revealed that:

• the total score in the “What can be at the same time?” test in the senior kindergarten group was associated with the total score in the “Mechanical curve” test in the senior kindergarten group (r=0.30; p<0.05);

2)    the total score in the “What can be at the same time?” test in the 1^st year of elementary school was associated with the total score in the “Mechanical curve” test in the senior kindergarten group (r=0.30; p<0.05) and 1^st year of elementary school (r=0.46; p<0.05).

3) a positive correlation was found between the ability to simultaneously coordinate two processes and overcome contradictions. At the same time, the better a child was able to perform a formal action in the senior kindergarten group, the better he/she was able to overcome contradictions in the senior kindergarten group and later in the 1st year of elementary school. The correlation of these two actions was also preserved in the 1st year of elementary school.

Fig. 4. The correlative pleiad of scores in dialectical thinking and Piaget tests in the senior kindergarten group and in the 1^st year of elementary school (r>0.2; p<0.05) (N=52).

Discussion

In a previously conducted study [4], data was obtained on a positive correlation between the ability of children of 5–6 years old to coordinate two processes and evaluate a result’s probability with an understanding of developmental processes. In hypothesis 1 it was assumed that this correlation would also appear in subsequent measurements. However, no such association was found in our study. At the same time, hypothesis 2 was confirmed and a correlation was found between a child’s ability to solve the overcoming the contradiction problem (“What can be both at the same time?”) and understanding of multiplicative spatial relations (see Figure 4). The existence of such a correlation can be explained by the fact that in the “Mechanical curve”, the solution success, i.e., a correct idea of the intended drawing was possible only if a child took into account that the pencil moved both vertically and horizontally at the same time. This meant that the movement of the pencil was the mediation of two opposite movements. Therefore, both in the “Mechanical curve” as well as in the “What can be at the same time?”, the solution was based on the use of similar dialectical mental operations, namely, the operation of mediation. So, the diagnostic results showed that hypothesis 1 was not confirmed, while hypothesis 2 was (that the understanding of multiplicative spatial relations is associated with the mediation development). Moreover, we clarified that the action of mediation, aimed at overcoming the contradiction, was most closely related to the coordination of two differently directed actions in a single object (see Figure 4). In other words, the dialectical thinking was connected with the formal-logical operations of multiplication. Once again it is crucial to emphasize that essentially, we consider multiplicative actions not only as a result of the formal thinking development, but also as a consequence of the dialectical thinking development. The dialectical thinking development in preschool age we associate with the play activity development, which has a rather complex dialectical structure. We assume that the discovered correlations are largely based on the preschoolers’ dialectical thinking transition to a new higher level in the developmental process. Probably, by the beginning of the concrete operational stage (i.e., closer to the age of 7 years), children begin to actively use the dialectical operation of mediation, which allows them to solve multiplicative problems. The data on the positive relationship between the mediation action successful implementation and the tests for formal operations results were presented in the publication by O. Shiyan et al. [12].

At the same time, we also hypothesized about the possibility of a dialectical thinking indicators’ regression at the end of preschool age. In a previously conducted research led by N. Veraksa the data was received on a decrease in the dialectical thinking indicators in children of elementary school [1]. These data were partially confirmed: we did not find correlations between the performance results in the “What can be both at the same time?” and performance results in the “Drawing an unusual tree”. However, the ability to overcome contradictions increased within 3 years, and the indicators of the ability to create a new image based on dialectical transformations, after growth in the preparatory group, again decreased among first graders to the indicators of children of 5-6 years old. In the majority of the drawings done by children of 7-8 years old , symbolic images predominate, i.e., “unusual tree” reflects more often an emotional component of modification of an image of a tree rather than structural transformations. Based on L. Vygotsky cultural-historical theory, we can assume that dialectical thinking is undergoing a qualitative change. Likely, during the transition to schooling a new social situation of development appears. In this situation, dialectical thinking development is going on in the context of the objects’ symbolic reflection dominance in the system of concepts.

Conclusion

1. The conducted experimental study showed that the senior preschool age is sensitive for dialectical thinking development. In the first year of elementary school, the children who took part in our longitudinal study were more successful in coping with tasks to overcome contradictions and understand developmental processes than in preschool age. Moreover, in children of elementary-school age, there was a decrease in the use of the dialectical mental action of transformation when performing creative drawing tasks.

These results partially confirm the assumption that elementary-school age children would show a decrease in the successful dialectical problems solving with an increase in the successful formal logical operations performance. Probably, this change is connected with the leading activity change from the playing one to the educational one. In this case, the possibility of a child’s action in an imaginary situation is reduced, while this imaginary situation made it possible to remove the contradiction between the desired and possible.

In the future on the samples of this longitudinal study, we plan to study the interrelations between the two thinking forms at the age of 8–9 years old in order to analyze the cognitive development dynamics at elementary-school age and compare the two thinking forms’ indicators in children at the ages of 5–6 years old, 7–8 years old and 8–9 years old.

2. With age children are able to cope more successfully with the solution of formal logical problems aimed at coordination of two conditions. The correlation analysis results show that at the age of 5 and 7 years old, the successful overcoming of contradictions by children is positively associated with the multiplicative spatial relations understanding: when the movements of two differently directed objects create a single image. It confirms the assumption that the multiplicative spatial relations understanding is associated with the dialectical mediation development.

1. Veraksa N.E. Dialekticheskoe myshlenie [Dialectical thinking]. Ufa: Vagant, 2006. 212 p. (In Russ.). 
2. Veraksa N.E. Dialekticheskoe myshlenie: logika i psikhologiya [Dialectical thinking: logic and psychology]. Kul'turno-istoricheskaya psikhologiya = Cultural-historical psychology, 2019. Vol. 15, no. 3, pp. 4—12. DOI:10.17759/chp. 2019150301(In Russ.).
3. Veraksa N.E., Almazova O.V., Airapetyan Z.V., Tarasova K.S Geterokhronnost' razvitiya dialekticheskogo myshleniya u detei starshego doshkol'nogo vozrasta [Heterochronism of the development of dialectical thinking in children of senior preschool age]. Psikhologicheskii zhurnal [Psychological Journal], 2021. Vol. 42, no. 4, pp. 59—73. (In Russ.).
4. Veraksa N.E., Almazova O.V., Tarasova K.S. Dialectical and formal-logical thinking of older preschoolers // Russian psychological journal (accepted for publication). (In Russ.).
5. Davydov V.V. Vidy obobshchenii v obuchenii [Types of generalizations in teaching] Moscow: Pedagogika,1972. 424 p. (In Russ.).
6. Zaporozhets A.V., Lukov G.D. O razvitii rassuzhdeniya u rebenka mladshego vozrasta [On the Development of Reasoning in Preschool Children]. Kul'turno-istoricheskaya psikhologiya = Cultural-Historical Psychology, 2007. Vol.3, pp. 101—108 (In Russ.).
7. Zolotareva A.A. Measurement of boredom proneness: Russian adaptation of the BPS-SR. National Psychological Journal [Natsional’nyy psikhologicheskiy zhurnal], 2020. Vol.13, pp. 40—49. DOI:10.11621/npj.2020.0104 (In Russ.).
8. Il'enkov E.V. Problema protivorechiya v logike. [The problem of contradiction in logic] Dialekticheskoe protivorechie [Dialectical contradiction]. Moscow: Politizdat, 1979. pp. 122—143. (In Russ.).
9. Kopnin P.V. Dialekticheskaya logika i ee otnoshenie k formal'noi logike [Dialectical logic and its relation to formal logic]. In Kedrov В.М. (ed.), [Dialektika i logika. Zakony myshleniya]. Moscow: AN SSSR., 1962, pp. 33—62. (In Russ.).
10. Piazhe J. Psikhologiya intellekta [Psychology of intelligence]. Saint-Petersburg: Piter, 2004. 192 p. (In Russ.).
11. Rzhanova I.E., Alekseeva O.S., Fominykh A.Ya. Gender differences in cognitive indicators in preschool and primary school age children. Vestnik Moskovskogo Universiteta. Seriya 14. Psikhologiya [Moscow University Psychology Bulletin], 2020. Vol. 2, pp. 141—157. DOI:10.11621/vsp.2020.02.07 (In Russ.). 12.              Shiyan O.A., Belolutskaya A.K., Le-Van T.N., Zadadaev S.A. Kognitivnoe razvitie doshkol'nikov: vzaimosvyaz' normativnykh, preobrazuyushchikh i simvolicheskikh sposobnostei [Cognitive development of preschoolers: the relationship of normative, transformative and symbolic abilities]. Sovremennoe doshkol'noe obrazovanie [Modern preschool education], 2021. Vol. 6(108). pp. 14—25. DOI:10.24412/1997-9657-2021-6108-14-25 (In Russ.).
12. Inhelder B., Piaget J. De la logique de l'enfant à la logique de l'adolescent, Paris: PFU, 1955.
13. Piaget J. Les Formes Élémentailes de la Dialectique. Gallimard, 1980. 249 p.
14. Piaget J., Inhelder B. La genese de l'idee de hasard chez l'enfant. Paris: PFU, 1951. 257 p.
15. Piaget J., Inhelder. B., Szeminska. A. La géométrie spontanée de l'enfant. Paris: PFU, 239p.
16. Riegel K.F. Dialectic operations: The final period of cognitive development. Human Development, 1973. Vol. 16(5), pp. 346—370. DOI:10.1159/000271287
17. Sidneva A.N., Vysotskaya E.V., Korotaeva I.V., Mozharovsky I.L., Shinelis V.A. How Do Primary Schoolchildren Use Concept Defnitions in Recognition Tasks? Psychology in Russia: State of the Art, Vol. 13(2), pp. 29—46. DOI:10.11621/pir.2020.0203
18. Valeeva R., Kalimullin A., Adapting or changing: The covid-19 pandemic and teacher education in Russia. Education Sciences, 2021. Vol.11, pp. 1—
19. Veraksa N, Basseches M Brandão A Dialectical Thinking: A Proposed Foundation for a Post-modern Psychology. Psychol., 2022. Vol. 13:710815, P. 1—15. DOI:10.3389/fpsyg.2022.710815