О расширении элементарной теории вероятности для моделирования психологических явлений

На основе рассмотрения достижений квантовой механики и психологии восприятия рассмотрены некоторые их возможностей расширения классической теории вероятностей на область представления психологических событий, для которых объединение исходов может иметь вероятность большую, чем вероятность одиночных событий из их общего множества. Отмечено, что модель, опирающаяся на общее пространство элементарных непересекающихся элементов недостаточна для описания психологии поведения, связанного с порождающими процессами и сопредставленными явлениями. Для расширения элементарной теории вероятностей могут быть использованы результаты квантовой теории, относящиеся к представлениям о тестовых пространствах, и возможности объединения отдельных событий в тесте. Предлагаемые модели могут включать как системы отдельных тестов с совмещением событий в дополнительных тестах, так и возможность объединения самих отдельных тестовых событий комбинаторными и геометрическими (проекционными) способами. Простые примеры расширения классических вероятностных моделей показывают, что «ошибку объединения» в психологии эвристического поведения следует считать не столько ошибкой испытуемых, сколько научной иллюзией исследователей, когда поведение более сложной системы пытаются уложить в прокрустово ложе слишком простой модели.

Введение

Известно, что у теории вероятностей не было античных или средневековых предшественников, она целиком — создание Нового времени [9]. Несмотря на относительно простой формальный характер и практическую полезность, появление элементарной теории вероятностей в середине 17 века встретило большое сопротивление и недостаток понимания тогда, когда она была впервые внедрена. Трудности понимания были скорее философскими, чем математическими. В частности, даже великие гении того времени (Джероламо Кардано, Пьер Ферма, Блез Паскаль, Христиан Гюйгенс, Якоб Бернулли и др.) испытывали трудности, «ломая» головы в отношении двух понятий: что можно (и на самом деле нужно) считать предположения, т.е. возможности, которые никогда реально не существовали; что порядок может быть получен из случайности.

В настоящее время в классической теории понятие вероятности в основном включает представление о количественной мере «осуществимости некоторого события при наличии неопределённости, то есть в ситуации, когда это событие характеризуется как возможное (которое может как произойти, так и не произойти)» [18, с. 1]. При этом множество событий в современных учебниках по классической теории вероятностей изначально актуализируется и представляет собой дискретное или континуальные пространства элементарных исходов (событий) [10, 20, 31].

Вместе с тем в философской литературе существует ряд концепций вероятности. В частности, упоминается вероятность как степень следования, вероятность как степень рациональной веры, вероятность как предрасположенность (диспозиция) и др. [11, 12, 29, 41, 43, 53]. В целом о вероятности можно говорить как о промежуточной категории, которая осуществляет «постепенный или плавный переход от необходимости к случайности и от случайности к необходимости. Меньшая вероятность стоит ближе к случайности. Большая вероятность стоит ближе к необходимости. Одним своим «концом» вероятность упирается в случайность, переходит в нее, а другим «концом» переходит в необходимость» [6, с. 593]. Понятие вероятности в качестве недостаточной уверенности в собственном поведении представляет интерес и для более глубокого понимания информации и системной сложности.  Например, согласно У. Матурана понятие «информации относится к степени неуверенности наблюдателя в своем поведении в области определенных им самим альтернатив, … генетическая и нервная системы порождают информацию посредством самоспецификации, которая воспринимается наблюдателем как самодекодирование генетической и нервной систем в процессах роста и поведения» [22, с. 137].

В эпистемологическом смысле можно также видеть, что «само понятие вероятности выполняет роль «мостовой» функции между объектами математики и объектами конкретных приложений» [28, с. 303]. Эти же авторы далее, на наш взгляд, вполне правомерно утверждают, что «выделение эмпирического понятия в качестве самостоятельного обнаруживает его сравнительную узость и ограниченность. Вне контекста теории о нем можно сказать разве только то, что оно может выражаться относительной частотой появляемости события. Т.е. фактически математическая теория вероятностей накладывает свою структуру на, так сказать, безличный случай, диктуя соответствующие схемы и законы безотносительно конкретной природы случайных явлений ...» [28, с. 308-309].

Вместе с тем классическая теория вероятностей показала свою результативность во многих важных областях науки и, фактически, произошел перенос «этой теории на весьма широкий класс массовых явлений, характеризующихся с помощью относительной частоты, ... и притом без достаточно детального обоснования адекватности этого переноса» [28, с. 309]. В особой мере недостатки этого «безоглядного» переноса проявляются в области рассмотрения психологических процессов и явлений. На примере рассмотрения процессов восприятия и принятия человеком решений ранее было показано, что использование стандартных схем расчета вероятностей для соответствующих психологических событий не является валидным и, по нашему мнению, приводит к научным иллюзиям, т.е. речь может идти не об иллюзиях испытуемых, а об иллюзиях ученых исследователей [3, 33, 35].

Научные эксперименты в психологии показали, что у людей есть «ложная» вера в то, что два случайных события имеют большую вероятность взаимного осуществления, чем каждое из событий в отдельности. Естественно, это противоречит одному из правил элементарной теории вероятностей. Явление, связанное с такой «ложной» верой, обычно рассматривается, как когнитивная иллюзия, и было продемонстрировано в большом наборе разных контекстов, включая: оценку частоты встречаемости слов, личностные суждения, медицинские прогнозы, принятие решений в условиях рисков, подозрения в совершении преступлений и политические прогнозы [13].

Вместе с тем вполне можно утверждать и обратное. Своеобразной научной иллюзией является подход, связанный с принятием правил специальной и явно упрощенной модели объединения вероятности случайных событий в качестве нормы для оценки психологических процессов. Это не соответствует действительности, в которой имеется большая вариативность поведения и сосуществование различных тенденций оценки вероятностей появления событий. Т.е. имеет место использование нормы объединения вероятностей независимых случайных событий вне реальных границ ее применимости и принятие этой нормы в качестве универсального стандарта, относящегося к реальности любых случайных событий.

Известно, что в психологии мы встречаемся с такого рода событиями, которые можно считать совместными и объединенными в том числе в силу особого порождающего характера психологических процессов и явлений. Становясь психологически действительными, внешне случайные вещи во многих случаях являются более вероятными в силу имеющихся психологических механизмов восприятия и осмысления. Психология восприятия (в частности, гештальтпсихология) говорит нам о такой целостности психических образов, которая больше, чем сумма своих частей, а память человека вполне естественно может хранить целостные картины взаимосвязанных представлений, что поддерживается на уровне нейрофизиологии сетевым строением мозговых систем [5, 8].

Однако в равно или разно вероятном континууме элементарных событий классической теории вероятностей все случайные события являются несовместными: вероятность их объединения оказывается всегда меньше, чем вероятность появления любого из этих событий по отдельности. Попытка создания субъективной теории вероятности на этом основании также не решает имеющиеся противоречия с психологической действительностью [1].

В особом виде расширение теории вероятностей стало необходимом для квантовой механики, которая в операциональных терминах представляется именно как некоторое исчисление вероятностей. Квантовые высказывания являются ограниченной формой классических высказываний. Вероятности присваиваются только тестируемым высказываниям, но не всем произвольным высказываниям. Квантово-логические свойства являются просто тестируемыми свойствами (с точки зрения прежней концепции измерений). При этом квантовую механику можно понимать как неклассическую теорию вероятностей [54]. Более точное определение представляет квантовую механику не как новую теорию вероятностей, а как конкретную вероятностную теорию, выбранную из класса вероятностных моделей, удовлетворяющих гораздо более общей схеме, которая заслуживает того, чтобы считаться «неклассической» теорией вероятностей [61]. Полученные в этом направлении результаты в значительной мере разбросаны по различным источникам и остаются менее известными, чем следовало бы.

В связи с этим целью настоящей статьи является описание некоторых возможностей расширения теории вероятностей для осуществления применимости ее к более широкому классу явлений и, в частности, к совместным психологическим явлениям. Для этого предлагается ввести изменения в аксиоматику классической теории и расширить множество так называемых элементарных событий на случаи, как несовместности проведения испытаний, так и совместного появления событий первичного дискретного множества или континуума.

Два понятия вероятности в науке 20 века

В естественных науках и математике в 20 веке были выработаны два основных научных понятия, которые позволяют работать с событиями в непрерывных многомерных и бесконечномерных пространствах. В 1919 г. австрийский математик и философ Р. фон Мизес выдвинул понятие вероятности как относительной частоты (частотное или, как его еще называют, эмпирическое понятие вероятности). При помощи этого понятия он изложил основы теории вероятностей, понимаемой как раздел прикладной математики. Строгое изложение теории вероятности дано им в 1931 г. Вероятность события – это предел последовательности частот его появления, предел, возникающий, когда число испытаний (коллектив) стремится к бесконечности [23].

Коллектив, по Мизесу есть некоторая безграничная последовательность экспериментов (испытаний), в которой каждый ее элемент (эксперимент) либо наделен, либо не наделен каким-то определенным признаком, например, таким признаком может быть выпадение фиксированной грани игрального кубика. Причем, каждый признак должен иметь в коллективе определенную долю, которая и есть его вероятность.

Важные свойства коллектива - существование пределов относительных частот определенных признаков и иррегулярность (Regellosigkeit) коллектива. Последовательность результатов испытаний должна быть сходящейся, т.е. постепенно стабилизироваться вокруг того значения, которое будет пределом этой последовательности при гипотетическом продолжении числа испытаний до бесконечности. Иррегулярность вводится для сохранения собственно вероятностного смысла данной концепции. Испытания должны проводиться случайным образом без подгонки к какой-либо (закономерной) тенденции, касающейся результата этих испытаний.

Согласно критикам концепции, из которой исходил фон Мизес, требование иррегулярности ограничивает вероятность чисто случайными явлениями (в частности, отсутствие стратегии игры) и наталкивается на непреодолимые математические трудности, поскольку требование иррегулярности оказывается плохо совместимым с требованием существования предела [30]. Некоторые замечания по этой концепции можно также увидеть в курсе теории вероятностей Б.В. Гнеденко, который следует идеям А.Н. Колмогорова [9].

В 1929 г. советский математик А.Н. Колмогоров опубликовал статью, в которой предложил использовать аксиоматическое понятие вероятности на базе теории множеств и теории меры. В 1933 г. им была написана небольшая книга, в которой были изложены доказанные на базе этого понятия основные теоремы теории вероятностей (книга была издана на немецком языке, в 1936 г. появилась ее русская версия). Согласно концепции Колмогорова, задается множество элементарных событий Ω, множество подмножеств этого множества называется множеством случайных событий. Пустое множество Ø символизирует невозможное событие. Мера множества подчиняется трем естественным аксиомам: P(Ω) = 1, P(Ø) = 0, P(A U B) = P(A) + P(B), если А и B не пересекаются. В современной математике теория вероятностей погружается в контекст представлений об абстрактных многомерных и бесконечномерных функциональных пространствах. Однако сохраняются основные представления теории Колмогорова [14].

В основе всякой теоретико-вероятностной схемы лежит так называемое пространство элементарных событий (Ω, U, P) – измеримое пространство элементов ω, называемых элементарными событиями или элементарными исходами с заданной на σ- алгебре U вероятностной мерой P = P (A): P(Ω) = 1. Множества пространства Ω называются событиями; мера P(A) множества А € U называется вероятностью события А [26].

Хотя формальная аксиоматическая теория вероятностей явилась продуктивной с математической точки зрения, однако она не имеет непосредственного физического осмысления. Конкретный смысл понятия вероятности остается произвольным. Во всех приложениях понятие вероятности события отождествляется с относительной частотой его появления при тех или иных условиях. При этом в приложениях, в частности, в статистической физике, можно идти двумя путями. При каждом применении определить смысл ряда понятий: вероятности, условной вероятности и статистической независимости. Такой путь мыслим для ограниченного круга вопросов. Гораздо более общее и плодотворное решение вопроса получается на пути, систематически проведенном Р. Мизесом, который состоит в том, что уже в рамках математической теории понятие вероятности события связывается с относительной частотой появления данного события в целой их последовательности. Иначе в формальной теории вероятностей, как было отмечено выше, конкретный смысл понятия вероятности остается произвольным [19]. Вместе с этим математические теоретические определения (например, метрики пространства посредством трех аксиом, приведенных выше) предстают как более объективные, а операциональные частотные определения несут по выражению А.А. Печенкина «печать антропоморфизма»: они «включают в содержание определяемого термина не только предметы природы, но и действия человека, оперирующего этими предметами» [25, с. 215].

Вероятность в квантовой механике

В квантовой механике первоначально использовалась частотная интерпретация вероятности, интерпретация в духе идей фон Мизеса [17]. Однако развитие математического аппарата этой теории привело к интерпретации вероятности в духе идей А.Н. Колмогорова. Здесь оказалось возможным обобщить дискретную классическую теорию вероятностей путем допущения множественности наборов исходов, каждый из которых представляет отдельный «эксперимент». В Квантовой механике пространство состояний S является сферой – множество единичных векторов гильбертова пространства H. Не всякое подмножество считается свойством – только получаемые путем пересечения прямых, плоскостей и т.д., проходящих через центр сферы. В результате логика физических свойств является изоморфной решетке множества L(H) подпространств H. прямых, плоскостей и т.д., проходящих через центр координат.

При построении квантовой физики, в частности, выяснилось, что классическая логика не совсем верна. На это указывали рассмотрения квантовых опытов [59]. По сравнению с обычной логикой квантовая – расширяется понятием «одновременной разрешимости», что является характеристикой квантовой механики, т.е. квантовая механика – это классическая логика плюс новая идея (одновременная разрешимость состояний). Физически важные утверждения в квантовой механике образуют некоторую проекционную геометрию, в то время как в классической динамике состояния, имеющие отношение к заданной системе, образуют Булеву алгебру, причем ее можно рассматривать как раздел математической логики, изучающий высказывания и операции над ними.

В частности, было показано, что в квантовой механике плохо обстоит дело дистрибутивным законом [37, 56]. Дистрибутивный закон классической логики, который нарушается в квантовой механике, имеет вид: p & (q or r) = (p & q) or (p & r). Определения логики высказываний: сочетание: p & q (& = и); объединение: p or q (or = или). Классически этот закон очевидно верен: обе стороны равенства «правда», если p «правда» и хотя бы один из q, r «правда».

Х.У. Патнэм (1968) поставил вопрос: может ли «необходимая правда» логики быть неистинной по причине эмпирических факторов? Он утверждал, что ответ на этот вопрос является утвердительным и логика в определенном смысле является естественной наукой. Логика столь же эмпирична, как и геометрия. Вполне можно говорить о «физической логике» также как о «физической геометрии» [56]. Якобы таким образом, квантовая механика представляет собой наиболее глубокую революцию в истории науки, поскольку она изменяет элементарные правила логики. В результате именно такая трактовка квантовой механики представлена, например, в одном из современных курсов математики для студентов-физиков [7].

Чтобы пояснить ситуацию с нарушением дистрибутивного закона, рассмотрим пример. Пусть H является n-размерным евклидовым пространством (например, n = 3). Пусть L(H) является множеством подпространств пространства H: линии, плоскости и др., проходимые через начало координат, включая эту точку начала координат и все пространство. Упорядочим L(H) по вложению элементов множеств, т.е. создадим решетку, которую можно рассмотреть, как неклассическую логику. Решетка дистрибутивна, если пересечение дистрибутивно относительно объединения и объединение дистрибутивно относительно пересечения: a ˅ (b ˄ c) = (a ˅ b) ˄ (a ˅ c) и a ˄ (b ˅ c) = (a ˄ b) ˅ (a ˄ c). Это верно как для множеств (˅=U, ˄=∩), так и для высказываний (˅ = or, ˄ = &). Но это не всегда «правда».

В частности, для L(H): если a, b – отдельные линии, тогда (a ˄ b) = 0, (a ˅ b) – это плоскость; если a, b – отдельные плоскости, тогда (a ˅ b) = 1, (a ˄ b) – это линия. Если a, c – прямые, не лежащие в плоскости b, тогда a ˅ b, b ˅ c = 1, a ˄ b = b ˄ c = a ˄ c = 0. Имеем не дистрибутивный пример, как и ранее. Это и есть квантовая логика фон Неймана в геометрической интерпретации. Если L дистрибутивная решетка, тогда каждый элемент a в ней имеет не более одного дополнения (если имеет дополнение, то оно единственное). В не дистрибутивном случае один элемент может иметь много дополнений. Один из вариантов введения Булевой алгебры, являющейся основой классической логики, как раз и состоит в представлении ее в качестве дополненной дистрибутивной решетки. В квантовой механике решетка подпространств L(H) не является однозначно дополненной и таким образом не является дистрибутивной, т.е. классическую (булеву) логику оказалось надо «спасать».

Один из путей «спасения» классической логики заключается в представлении, что L(H) находится внутри большой булевой алгебры всех подмножеств сферы S. Другими словами, надо позволить произвольным высказываниям о состояниях системы считаться осмысленными. Однако ни одна из вероятностных мер на L(H) не расширяется любым последовательным образом в вероятностную меру на этой большой булевой алгебре. Т.е. по факту не существует такое встраивание L(H) в булеву алгебру, которое сохраняет вероятности. Другими словами, L(H) содержит много маленьких булевых сублогик. Получается, что квантовая логика более общая, чем классическая логика.

Вместе с тем квантово-логические свойства являются всеми теми свойствами, которые действительно существуют в мире. Если это так, то классическая логика является специальным случаем квантовой логики – и надо действительно исправлять представления о том, как работает логика. Однако, современные представления и научные факты говорят о том, что квантовая логика является специализацией классической логики, а не заменой для нее. Но для понимания этого приходится немного расширить наше понимание теории вероятностей [60].

Квантовая механика операционально – это теория возможных статистических распределений результатов определенных измерений, и ее неклассическая «логика» отражает тот фундаментальный факт, что не все наблюдаемые явления можно наблюдать одновременно. Из-за этого существования несовместимых (дополнительных) наблюдаемых, множество вероятностных событий (или суждений) менее богато, чем это было бы в классической теории вероятностей, а множество возможных статистических распределений, соответственно, менее жестко ограничено. То, что некоторые «неклассические» распределения вероятностей, допускаемые этой теорией, на самом деле проявляются в природе, возможно, удивительно, но похоже никоим образом не требует какого-либо глубокого сдвига в нашем понимании логики. Собственно, в сложных системах и, в частности, в биологии такого рода дополнительность также наблюдается, когда речь идет о том, что у системы не существует наибольшей модели, а «формальные системы, как модели, необходимые для описания каждого отдельного аспекта явлений в естественных системах, оказываются невыводимыми одна из другой» [2, с. 54]. Эпистемологические вопросы моделирования сложных систем рассмотрены в работе [4].

Известно, что идея дополнительности была первоначально развита в психологии сознания Уильяма Джеймса, который писал, что у некоторых людей оно может быть разделено на части, которые сосуществуют, взаимно игнорируя и дополняя друг друга [47]. В современной психопатологии имеется большое разнообразие описаний деперсонализации и расщепления сознания личности [21].

В квантовых измерениях состояния являются единичными векторами (векторами длинны 1). Определим измерения в виде максимального набора взаимно ортогональных (перпендикулярных) единичных векторов. Вероятность получения x в состоянии v – квадрат проекции компонента v в направлении x: Pr(x|v) = |(v, x)|2. Это работает и в пространствах большей размерности.

Заимствуя термины из теории вероятностей, событием можно назвать любое подмножество измерений – это любое множество взаимно ортогональных единичных векторов. Любой вектор состояния присваивает вероятность любому событию (просто добавляет). Если посмотреть на квантовую механику под этим углом, то тестируемое свойство можно определить как множество состояний, которые исключаются наблюдением. Это будет множество A векторов состояний ортогональных ко всем (выходным) векторам в событии A. Если A является событием с вероятностью p, тогда вероятность A┴ равна 1-p (если A┴ = B┴, то A и B имеют одинаковую вероятность во всех состояниях).

Формальная структура квантовой механики может быть однозначно определена небольшим числом разумных предположений вместе, возможно, с некоторыми очевидными закономерностями в наблюдаемых явлениях. Эта возможность уже рассматривалась фон Нейманом (в его поздних работах по непрерывной геометрии), но впервые стала явной и программной в работах Джорджа Макки [42]. Он представил последовательность из шести аксиом (определяющих очень консервативную обобщенную теорию вероятностей), которые лежат в основе построения «логики» экспериментальных утверждений, или, в его терминологии, «вопросов», имеющих структуру сигма-ортомодулярного частично упорядоченного множества [51, 52].

Очень естественным направлением для обобщения дискретной классической теории вероятностей является допущение множественности наборов исходов, каждый из которых представляет отдельный «эксперимент». Общим для всех них является Тестовое пространство — это непустая коллекция A непустых множеств E, F, … , каждое из которых понимается как дискретное исходное множество, как в классической теории вероятностей. Каждое множество E ∈ A называется тестом. Множество X = ∪A всех результатов всех тестов, принадлежащих A, называется пространством результатов A. Здесь важно, что различные тесты могут перекрываться, т.е. иметь общие результаты. Было показано, что эта структура может сочетаться как с обычным формализмом теории меры полномасштабной классической теории вероятностей, так и с формализмом гильбертова пространства квантовой теории вероятностей [60].

Факт того, что квантовые структуры являются обобщением традиционных вероятностных конструкций и поэтому они лучше отвечают имеющимся результатам наблюдений, позволил в настоящее время разработать технологию свѐртки прикладных марковских моделей в квантовые представления для моделирования поведения марковских процессов при решении диагностических задач. В результате квантовые представления становятся применимыми к самым разным макропроцессам и, в частности, к задачам психодиагностики [48, 49]. При этом каждое квантовое представление соответствует одному из кластеров, выявленных в результате проведенного кластерного анализа случайных процессов, а кластеры состояний, фактически, являются результатами отдельных тестов в общем тестовом пространстве [15, 16].

Тестовое пространство

Понятие тестового пространства является особенно простой и гибкой математической основой для изучения теории вероятностей — классической, квантовой и других. Тестовое пространство предполагает набор (возможно, перекрывающихся) дискретных выборочных пространств. Первичная идея была подробно разработана в 1970-х и 80-х годах [39, 40, 57]. «Квантовая логика» вполне естественно возникает как инвариант тестовых пространств; однако последние гораздо легче интерпретировать и манипулировать ими.

Тестовое пространство является обобщением понятия дискретного выборочного пространства в классической теории вероятностей. Это пара (X; A), где X — непустое множество, а A — покрытие X непустыми подмножествами, называемыми тестами. Предполагаемая интерпретация состоит в том, что каждое множество E ∈ A представляет множество всех возможных результатов некоторого эксперимента, решения или физического процесса. Соответственно, подмножество теста называется опытом или событием, а элементы теста x ϵ X называются результатами или исходами. Вес вероятности или состояние на (X; A) является функцией w: X -> [0; 1] суммируя до 1 по каждому тесту. (Простая) случайная величина на (X; A) — это отображение f: E -> R, определяемое по тесту E ∈ A.

Как было отмечено выше в общем случае различные тесты могут перекрывать друг друга.  Тестовое пространство, состоящее только из одного теста, является классическим. Тестовое пространство, в котором различные тесты не пересекаются, называется полуклассическим. Однако, как показывают приведенные ниже примеры, не полуклассические тестовые пространства возникают вполне естественно. Следует также отметить то, что вероятность исхода по отношению к данному событию не зависит от теста. Если результат является общим для двух или более тестов, его вероятность в данном опыте не зависит от того, какой тест используется для его получения. Другими словами, вероятности, которые состояния присваивают исходам, не зависят от контекста [60].

В качестве простейшего примера можно взять две (неидентичные) монеты, одна с гранями H и T, другая с гранями h и t. Пусть E — опыт подбрасывания первой монеты, так что E = {H; Т}. Пусть F — опыт подбрасывания второй монеты, так что F = {h; t}. Тогда у нас есть очень простое полуклассическое тестовое пространство с X = {H; Т; h; t} и А = {Е; F} = {{Н; Т}; {h; t}}. Теперь можно рассмотреть последовательные эксперименты: (a) подбросить монету E два раза подряд или (b) подбросить монету E: если результат H, подбросить ее еще раз; если нет, подбросить монету F. Здесь наборы исходов равны {HH; HT; ТH; TT} и {HH; НТ; Тh; Тt}. Они имеют два общих результата, а именно HH и HT. Можно также представить своеобразную квантовую ситуацию, когда монеты E и F «сцеплены» друг с другом и их поведение взаимосвязано: при выпадении H выпадает и h, а при выпадении T получается t. Тогда второй набор исходов имеет вид {HH; НТ; Тt; Tt}.

Дискретная классическая теория вероятностей — это теория тестовых пространств вида (E; {E}), имеющая только один тест. В более общем смысле пусть S — множество, а Ʃ — поле подмножеств S. Пусть B = B(S; Ʃ) — набор (скажем, счетных) разбиений S на непустые Ʃ-измеримые множества. Каждое разбиение E ∈ B можно представить как исходное множество для «крупнозернистого» измерения значения в S. Соответственно, получаем тестовое пространство (Ʃ*; B(S; Ʃ)), где Ʃ* — множество непустых элементов Ʃ. Это называется тестовым пространством Бореля, связанным с (S; Ʃ). Состояния на (Ʃ*; B(S; Ʃ)) соответствуют σ-аддитивным вероятностным мерам на (S; Ʃ), а простые случайные величины на (Ʃ*; B(S; Ʃ)) соответствуют простым случайным величинам (в обычном смысле) на (S; Ʃ); более общие случайные величины могут быть восстановлены как их пределы. Таким образом, Колмогоровская теория вероятностей по существу является теорией Борелевских тестовых пространств [60].

Одно из достоинств тестовых пространств – это простота, с которой можно создавать простые и поучительные специальные примеры. Рассмотрим так называемый треугольник Рона Райта [62], представляющий собой запечатанный треугольный ящик с непрозрачными верхом и дном, и полупрозрачными боковыми стенками. Интерьер ящика разделен на три сообщающиеся камеры (a, b, c), каждая из которых занимает один угол. Внутри коробки в случайном месте находится светлячок, видимый через конкретную стенку тогда и только тогда, когда светлячок занимает одну из двух камер за ней и мигает.

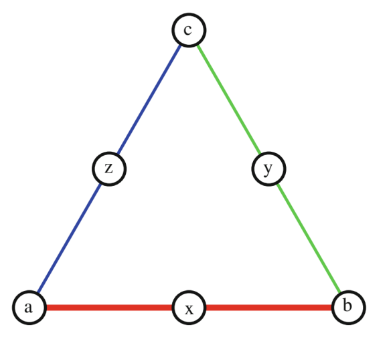
Каждая стенка ящика соответствует эксперименту.  Глядя через одну из стенок, можно увидеть свет в камере (а), свет в камере (b) или вообще не увидеть света. Представляя этот последний результат через x, мы можем представить эксперимент по просмотру этой стенки через {a; x; b}. Аналогично представив эксперименты, связанные с двумя другими стенками, через {b; у; с} и {с; z; a}, получим тестовое пространство M = {{a; x; b}; {b; у; c}; {с; z; а}}, которое удобно представить графически (рисунок 1).

Рис. 1. «Диаграмма Гричи» треугольника Райта, в которой результаты, принадлежащие обычному тесту, лежат вдоль сторон треугольника.

На рисунке 1 показана «Диаграмма Гричи» [44] треугольника Райта, в которой результаты, принадлежащие обычному тесту, лежат вдоль сторон треугольника (в общем случае вдоль прямой линии или гладкой кривой). Каждый узел (a, b, c) представляет результат наблюдения, причем результаты, соответствующие каждому эксперименту, лежат на общей линии, соответствующей трем тестам (x, y, z). Тесты при этом принимают только два состояния, события которых не смешиваются - не могут быть одновременно. В этом случае такие состояния в тестах называются дисперсионно свободными. Пространство Pr(M) всех вероятностных весов на M трехмерно, поскольку такой вес однозначно определяется тройкой (a, b, c), причем для M есть исходы, которые являются не дисперсионно свободными p(a) = p(b) = p(c) = 1/2; p(x) = p(y) = p(z) = 0 [61].

В более общем виде задачу можно усложнить, если представить, что количество светлячков в треугольнике Райта может быть больше одного, а их перемещения внутри ящика являются случайными. В этом случае события смогут происходить одновременно, и система вероятности таких событий будет сложнее. Таким образом, можно предложить дальнейшее расширение понятия тестового пространства. Покажем далее, что такое расширение оказывается важным для расчета вероятностей в ряде психологических задач.

Когнитивная иллюзия, связанная с «ошибкой объединения»

Согласно теории вероятностей вероятность объединения двух и более случайных событий всегда меньше вероятности одного события. Но многочисленные эксперименты показывают, что психологически люди склонны ошибаться и считать, что вероятность двух событий выше вероятности появления одного события [46].

Классический эксперимент Тверски и Канемана посвящен исследованию ситуации с банковской служащей. Испытуемым сообщаются следующие сведения: Линда, возраст 31 год, одинокая, искренняя и привлекательная, специализировалась в философии. Когда была студенткой, была очень обеспокоена вопросами дискриминации и социальной справедливости, а также участвовала в антиядерных демонстрациях.

Затем спрашивается: Какая из следующих альтернатив более вероятна?

1. A) Линда – кассир банка.
2. B) Линда – кассир банка и активно участвует в феминистском движении.

Большинство людей выбирают – B) и эти люди являются «жертвами ошибки объединения». Теоретически, для двух независимых событий не может быть, чтобы они вместе были более вероятны, чем каждое из событий в отдельности [58].

Нарушения правила объединения носят систематический характер. Причины, почему столь неадекватное поведение имеет место и столь часто встречается, оказываются в целом неясными и слабо объяснимыми. В соответствии с общепризнанными нормативными взглядами это поднимает ряд вполне обоснованных вопросов. Почему люди столь часто не принимают во внимание правильную логическую форму утверждений при оценке вероятностей? Почему они столь не расположены координировать оценку вероятности с общепринятой теорией и ее логической структурой?

Много раз отмечалось, что понятие вероятности здесь очень нечетко определено и эти вероятности скорее всего, связаны, например, с суждениями о правдоподобности [45] и вопросом того, насколько хорошие предсказания согласуются с некоторой общей моделью предполагаемой реальности, включающей сосуществование различных (бессознательных и сознательных) тенденций [33].

 Попытки обосновать ответы на представленные выше вопросы привели также к представлениям о том, что когнитивные процессы сродни квантовым явлениям. Ситуацию предпочтения вероятности двух событий можно описать, используя квантовые вероятности. В частности, можно провести анализ с использованием простейшей структуры, возможной в квантовой теории: двумерного векторного пространства [38, 55].

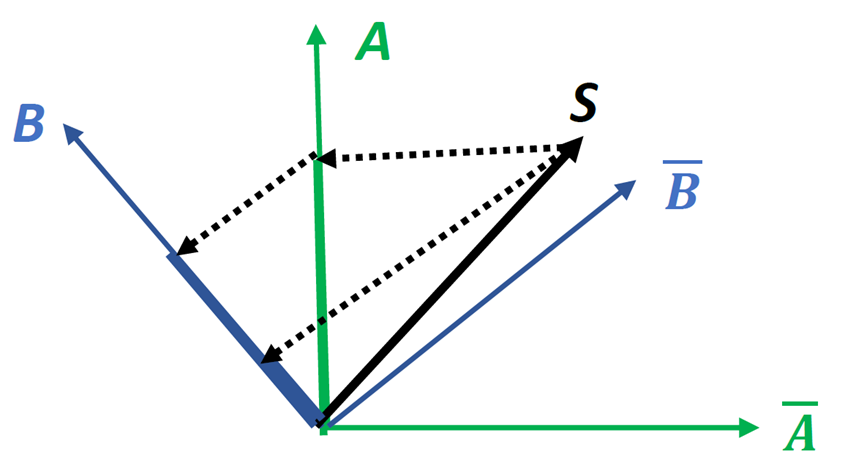
В квантовом объяснении одномерные подпространства (представленные единичными векторами) реализуют предложения A и B и их ортогональные аналоги ????┴ и ????┴.  Кроме того, соответствующие знания о системе (данные с описанием Линды) могут быть представлены простым вектором S, называемым вектором состояния. В основном предполагается, что длины проекций векторов состояния на векторы, представляющие обсуждаемые события, представляют (квантовые) вероятности событий (так называемое правило Борна).

Согласно [38] рассмотрим ситуацию сравнения двух утверждений: (A) «Линда - активно участвует в феминистском движении» с обычной вероятностью 0,61 и (B) «Линда - кассир банка» с вероятностью 0,38. Покажем, что (совместное) утверждение (A & затем B) «Линда - феминистка и кассир банка» вполне может иметь вероятность 0,51. Как представлено на рисунке 2 базовое предположение для обработки объединения состоит в том, что сначала вектор состояния S проецируется в состояние A, а затем результирующий вектор проецируется в состояние B (правило Людерса) [50]. Согласно рисунку 2, результатом этой операции является вектор длины 0,51. Очевидно, что эта операция не соответствует пересечению двух векторных пространств. Чтобы отличить ее от операции пересечения A ∩ B, ее определили как «A & затем B».

Рис. 2. Векторное объяснение ошибки объединения (адаптировано из [55]).

Рисунок 2 иллюстрирует, что обычного двумерного векторного пространства достаточно, чтобы решить проблему объединения вероятностей в психологии. Комплексные числа (как это требуется для охвата истинного гильбертова пространства) в данном случае не нужны. Обычных проекций достаточно, чтобы показать возможность возникновения «ошибки объединения».

Однако нам представляется, что квантовое рассмотрение обладает недостаточной объяснительной силой и при этом привлекает слишком сложные квантовые представления, далекие от психологических явлений. При векторном объяснении ошибки объединения трудно пояснить как могут образоваться еще более большие вероятности объединения событий, что наблюдается на практике. Кроме того, векторное объяснение ошибки объединения трудно соединить с существующими представлениями о механизмах психологических процессов.

Сопредставленная модель объединения вероятностей

В целом, как было отмечено ранее, можно утверждать, что в случае «ошибки объединения» ошибаются не люди, а психологи, принимая более сложные психологические события за простейшие случайные события (бросания монеты или кости), с которыми изначально имеет дело элементарная теория вероятностей. На практике можно понять, что возможность появления многих разных свойств у объекта восприятия часто легче представить, чем остаться только с одним из этих свойств и без всех других (опустим здесь вопрос о развитости сознания или категориальной системы). Рассматривая эти возможности как вероятность в виде частоты появления соответствующих свойств, вполне можно говорить о том, что вероятность появления множества разных свойств в продуктах восприятия обычно больше вероятности появления только одного свойства.

Таким образом, согласно реальности восприятия, для любого объекта более валидно иметь множество определенных и связанных характеристик, чем только одну особенность. Иначе говоря, перцептивные процессы (в отличие от упрощенных процессов мышления) показывают, что объект восприятия с множеством одновременных и связанных с ним (сопредставленных) свойств на самом деле более действителен и актуален, чем абстрактный объект с несколькими случайными признаками. Сопредставленные свойства событий восприятия имеют общее происхождение и оказываются совместно порожденными. Это предполагает, что природа такого познания весьма сложна, что не учитывается в упрощенных абстрактных научных представлениях, например, в модели равновероятностного континуума случайных событий [3].

Разработанный ранее в нашей стране подход трансцендентальной психологии [24, 27, 34] позволяет обосновать сопредставленную математическую вероятностную модель, которая согласуется с психологией восприятия человека и эвристическими суждениями людей в условиях неопределенности [3, 32, 33, 35]. Согласно трансцендентальному подходу, процессы восприятия имеют полифункциональный характер с со-существованием различных альтернатив и обладают функциональной гибкостью, необходимой для эффективного действия перцептивных и когнитивных систем в постоянно изменяющихся условиях [27].

Для моделирования сопредставленности, фактически, не нужно отказываться от теории вероятностей в том числе в ее элементарной форме. Необходимо обратиться к созданию более сложных моделей теории вероятностей и, в первую очередь, представить как элементарные объекты теории вероятностей (монета или игральная кость) могут получить более широкое тестовое пространство с возможностью объединения событий. В принципе эта возможность предполагается и в указанной выше теории тестовых пространств, хотя специально не актуализируется в ней.

Простым примером модели с появлением объединения событий (в качестве отдельного дополнительного события по отношению к известным единичным исходам) является эксперимент с паданием монеты-медальона, которая кроме выпадения двух сторон H и T может вдруг раскрыться и показать одну из частей развернутого медальона, в котором снаружи есть, а внутри нет изображений «орла» и «решки». Для монеты-медальона возможны (и могут быть равновероятны) все четыре варианта событий: два варианта, когда монета-медальон падает как обычная монета, не раскрываясь, и два других варианта, когда монета-медальон падает, раскрываясь как медальон. Тестовое пространство медальона имеет только один возможный тест, состоящий из четырех исходов с возможным появлением двух событий H и T одновременно {H, T, HT, O}.

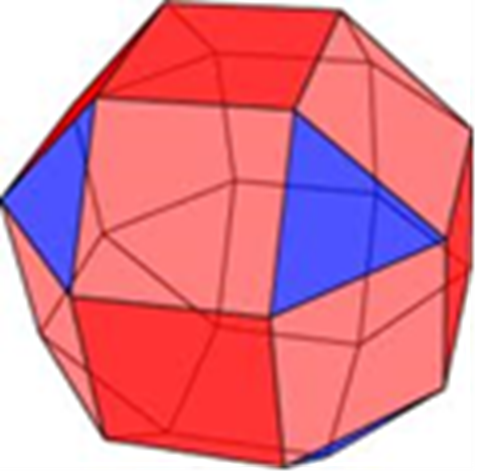
Более сложной моделью, в которой вероятность объединения событий может превысить вероятность одиночных событий, является модель игральной кости, превращенной в более сложную объемную фигуру, например, в ромбокубооктаэдр. Он представляет собой объемную фигуру, которую можно образовать из первичного куба путем превращения его ребер и вершин в отдельные грани и состоящую из 8 треугольников и 18 квадратов. Рассмотрим его как вариант особой «кости», т.е. при бросках будем интересоваться только выпадением всех шести граней, которые в ромбокубооктаэдре являются гранями первичного куба (игральной кости) с учетом проективной возможности наблюдения соответствующих граней куба, находясь в отдалении на линии, перпендикулярной плоскости любой реально выпавшей грани. На рисунке 3, где представлено изображение ромбокубооктаэдра, эти грани первичного куба показаны темно красным цветом.

Рис. 3. Изображение ромбокубооктаэдра (рассматриваемые в качестве исходных событий грани первичного куба выделены темно красным цветом).

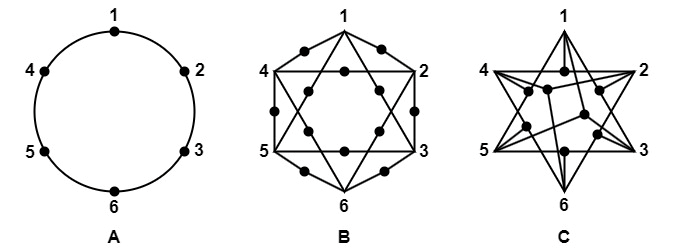
На рисунке 4 представлено тестовое пространство наблюдаемых одновременно (темно красных) граней первичного куба в ромбокубооктаэдре. Это пространство можно представить в виде трех тестов и включает: (A) – 6  состояний выпадения граней первичного куба – игральной кости; (B) - 12 состояний возможности одновременного видения двух граней первичного куба; (C) - 8 состояний возможности одновременного видения трех граней первичного куба).

Рис. 4. Тестовое пространство для ромбокубооктаэдра (A - 6 состояний выпадения граней исходного куба – обычной «кости»; B - 12 состояний возможности видения двух граней исходного куба; C - 8 состояний возможности видения трех граней исходного куба).

Можно видеть, что в ромбокубооктаэдре вероятность увидеть определенную комбинацию из нескольких первичных граней в целом существенно больше вероятности увидеть только одну из этих граней. На любую их первичных граней 1-6 на рисунке 4A приходится 4 состояния из двух граней (рис. 4B) и 4 состояния из трех граней (рис. 4C). Можно видеть, что в данной модели различные объединенные исходы, включающие 2 и 3 отдельных первичных состояний кубической игральной кости, включаются в общее дискретное пространство элементарных исходов Ω, в котором отдельные первичные исходы в результате могут объединяться. При этом важно, что вероятность объединения первичных случайных событий может превышать вероятность любого из этих событий по отдельности, что согласуется с результатами психологических экспериментов. В частности, кросс-культурный эксперимент по восприятию вероятности совместных событий показал возможность влиять на принятие человеком решения в предсказуемом направлении, варьируя воспринимаемые и смысловые параметры ситуации в соответствии с теоретическими предположениями, связанными с новой моделью оценки вероятности [36].

Для ромбокубооктаэдра вероятности выпадения квадратных и треугольных граней не должны быть равны друг другу и предпочтение в величине вероятности, по-видимому, надо отдать квадратной грани, что согласуется с результатами частотных экспериментов.

Примерный расчет вероятностей для пространства исходов ромбокубооктаэдра проведем с учетом того, что вероятность выпасть треугольной грани q равна ¾ от вероятности выпадения любой квадратной грани p. Имеем общую формулу: 18p + 8 (¾)p =1; откуда p = 1/24; q = ¾ p = 1/32. Вероятность получения любой одной исходной (темно красной на рисунке 3) квадратной грани d = 6/24 = ¼. Вероятность получения любых двух квадратных граней с учетом появления этих граней в составе выпадения двух или трех (темно красных) граней e = 1 - d = 3/4. Соответственно вероятность получения любых двух (но не трех) квадратных граней p2 = 12/24 = ½. Вероятность получения любых трех квадратных граней p3 = 8/32 = ¼. Таким образом в тестовой модели ромбокубооктаэдра вероятность объединения событий (совместного появления двух граней первичной игральной кости) может существенно превысить вероятность одного события (выпадения только одной грани первичной игральной кости). В общем случае вероятности объединенных событий могут быть как меньше, так и больше вероятностей отдельных исходов в зависимости от конкретики используемой модели и решаемой задачи.

Рассмотренные примеры показывают, что при создании более сложных вероятностных моделей, с одной стороны, пространство событий может выступать в виде системы отдельных тестов с совмещением событий в разных тестах, а с другой стороны в этих тестах события тоже могут совмещаться в том иди ином виде. В более общем виде этому, например, могут соответствовать: наборы различных проективных геометрий или сетевых иерархических структур, типа различных деревьев.

Заключение

Одной из важных разработок теории квантовой механики является создание представления о тестовых пространствах, что позволяет расширить классическую теорию вероятности. Введение понятия тестовых пространств в состав общей теории вероятностей является, на наш взгляд, важной вехой в развитии этой теории. В целом аксиоматика классической теории вероятностей в этом случае расширяется с множества несовместных элементарных событий на случаи, как повторяемости событий в несовместных тестовых испытаниях, так и случаи совместного появления событий в отдельных тестах. Это обеспечивает новые возможности применения теории вероятностей к более широкому классу явлений и, в частности, к моделированию сопредставленных психологических явлений, в том числе без привлечения к объяснению психологии поведения человека векторных аналогий из квантовой механики.

На этой основе в работе представлены простые математические модели, позволяющие более адекватно объяснить эвристическое поведение человека при оценке вероятностей случайных событий. Фактически, при применении научных норм теории вероятностей в психологии и других науках о живом необходимо строить новые модели, учитывающие относительно более сложный характер рассматриваемых явлений и процессов. В частности, на основе разработанной модели сопредставленных событий удается преодолеть «ошибку объединения» вероятностей [13, 58] и показать, что эвристическое поведение человека при оценке вероятностей случайных событий не должно считаться ошибочным [3, 35].

В результате можно утверждать, что «ошибка объединения» – это скорее научная иллюзия. Когда результаты применения нормативных научных концепций серьезно отличаются от наблюдаемого поведения живых существ, разумно проверить пределы применимости научной модели, которая используется в качестве правильной и валидной нормы. Простая модель, использованная для образования этой нормы, может не соответствовать более сложной системе, которую пытаются уложить в прокрустово ложе более простой модели.

Таким образом, предлагаемое расширение элементарной теории вероятностей для моделирования психологических явлений основано на использовании результатов квантовой теории, относящихся к представлениям о тестовых пространствах (в виде системы отдельных дополнительных полно вероятностных тестов с совмещением событий в разных тестах), и рассмотрения вероятностных моделей с возможностями совмещения (объединения) отдельных случайных событий (с учетом сетевых иерархических структур, типа деревьев, или множества различных проективных геометрий).

1. Абрамов В.Е., Маслов О.Н., Шаталов И.С., Юкласов К.А. Леонард Джимми Сэвидж и его субъективная теория вероятностей. Часть I. Условия возникновения, предпосылки и перспективы. Информационные технологии. Т. 18. № 1. 2020, С. 89-105.
2. Артеменков С.Л. Аспекты моделирования и особые свойства сложных систем // Моделирование и анализ данных. 2016. № 1. С. 47–59. doi:10.17759/mda.04.
3. Артеменков С.Л. Модель сопредставленности для оценки вероятности объединения событий // Моделирование и анализ данных. 2014. №1. С. 43–54.
4. Артеменков С.Л. Онтологический и эпистемологический аспекты моделирования: модельное отношение и адиафорные системы. Моделирование и анализ данных. 2022. № 4. С. 5–24. DOI: 10.17759/mda.2022120401.
5. Аткинсон Р., Шифрин Р. Человеческая память: система памяти и процессы управления // Психология памяти / Под ред. Ю. Б. Гиппенрейтер, В. Я. Романова. 3-е изд. М.: Астрель, 2008. С. 387—407.
6. Балашов Л.Е. Новая метафизика. Категориальная картина мира или основы категориальной логики / Л. Е. Балашов. М.: РГИУ, 2003. 868 с.
7. Бамберг П., Стернберг Ш. Курс математики для студентов-физиков. Фазис. 2006. Т. 1, Т. 2. 1256 с.
8. Вертгеймер М. Продуктивное мышление. М.: Прогресс, 1987. 336 c.
9. Гнеденко Б.В. Курс теории вероятностей / Учебное пособие для высшего и среднего образования гос. ун-тов / Б. В. Гнеденко. 5-е изд. стереотипное. М.: Наука, 1969. 400 с.
10. Горяйнов В.В. Лекции по теории вероятностей / М.: МФТИ, 2019. 59 с.
11. Закон. Необходимость. Вероятность: сборник статей. М.: Прогресс, 1967. 367 с.
12. Кайберг Г. Вероятность и индуктивная логика. М.: Прогресс, 1978. 374 с.
13. Канеман Д., Словик П., Тверски А. Принятие решений в неопределенности: Правила и предубеждения. Харьков: Гуманитарный центр, 2005. 632 с.
14. Колмогоров А.Н. Основные понятия теории вероятности. Москва, Наука, 1974, 120 с.
15. Куравский Л.С., Козырев А.Д., Грешников И.И. Математическая модель сопутствующей деятельности пилота и ее применение для объективной оценки его состояния и профессиональной подготовки // Экспериментальная психология. 2024. Том 17. № 1. С. 161–180. DOI: 10.17759/exppsy.2024170111
16. Куравский Л.С., Юрьев Г.А., Юрьева Н.Е., Исаков С.С., Несимова А.О., Николаев И.А. Адаптивная технология психологической диагностики на основе марковских и квантовых представлений процесса выполнения заданий // Моделирование и анализ данных. 2022. Том 12. № 4. С. 36–55. DOI: 10.17759/mda.2022120403
17. Ландау Л.Д., Лифшиц Е.М. Квантовая механика (нерелятивистская теория) // Теоретическая физика. М.; Л.: ОГИЗ, 1948. Т. 5. Ч. 1. 570 с.
18. Леонов H.H., Сачков Ю.В., Рузавин Г.И. Вероятность / Гуманитарный портал: Концепты [Электронный ресурс] // Центр гуманитарных технологий, 2002–2023 (последняя редакция: 29.11.2023). URL: https://gtmarket.ru/concepts/7069
19. Леонтович М.А. Статистическая физика. М.; Л.: ОГИЗ, 1944. 256 c.
20. Лотов В.И. Лекции по теории вероятностей / учебное пособие для студентов механико-математического факультета НГУ. Новосибирск: НГУ, 2019. 115 с.
21. Лэйнг Р.Д. Расколотое «Я». М.: АСТ, 2021. 288 с.
22. Матурана У. Биология познания. В книге Язык и интеллект. Сб./Пер. с анг. и нем. / Сост. и вступ. Ст. В.В. Петрова. М.: Прогресс, 1995. 95-142.
23. Мизес Р. Вероятность и статистика: Пер. с нем. / Под ред. и с предисл. А.Я. Хинчина. М.: Книжный дом «ЛИБРОКОМ», 2009. 264 с.
24. Миракян А.И. Контуры трансцендентальной психологии (книга 2). М.: Изд-во «Институт психологии РАН, 2004. 384 с.
25. Печенкин А.А. Понятие вероятности в математике и физике (дискуссии 1920–1930-х гг. в СССР). Эпистемология и философия науки. 2019. Т. 56. № 3. С. 202–218.
26. Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. Основные понятия, предельные теоремы, случайные процессы, М.: Наука, 1973. 494 с.
27. Психология восприятия: трансцендентальный вектор развития / под ред. Г. В. Шуковой. М.; СПб.: Нестор-История, 2020. 284 c.
28. Пятницын Б.Н., Григорьян Э.Р. Обоснование и проблема выбора теории вероятностей. Философия науки. Вып. 1. Проблемы рациональности. М.: ИФ РАН, 1995. 302-318.
29. Рузавин Г.И. Логическая вероятность и индуктивный вывод // Вопросы философии. № 4. С. 102-110.
30. Хинчин А.Я. Частотная теория Р. Мизеса и современные идеи теории вероятности // Вопросы философии. 1961. №. 1. С. 91-102. №. 2. С. 77-89.
31. Чернова Н.И. Теория вероятностей: Учебное пособие / СибГУТИ. Новосибирск, 2009. 128 с.
32. ArtemenkovL. Сorepresentation of the features of objects in the processes of perception and assessment of the chances of joint events / 42nd European Conference on Visual Perception (ECVP) 2019 Leuven. Perception. 2019. 48(S2). P. 141. https://journals.sagepub.com/doi/full/10.1177/0301006619863862
33. Artemenkov S.L. Kansei Versus Extensional Reasoning: The Scientific Illusion of the Conjunction Fallacy in Probability Judgments // Proceedings of the First International Workshop on Kansei. 2006. 8-11. Available at: https://www.psycho.hes.kyushu-u.ac.jp/~lab_miura/Kansei/Workshop/proceedings/Opening_talk.pdf
34. Artemenkov S.L. Metaphysics and Fundamentals of Transcendental Psychology Approach. Open Journal of Philosophy, 2021. 11. 125-147. https://doi.org/10.4236/ojpp.2021.111010
35. Artemenkov S.L. Prerequisites of Regulatory Scientific Models in Education and Social Practice: Transcendental Approach to Conjunction Fallacy. Advances in Social Science, Education and Humanities Research (ASSEHR), volume 315. Proceedings of the 2019 International Conference on Pedagogy, Communication and Sociology (ICPCS 2019). 313-317. https://doi.org/10.2991/icpcs-19.2019.69
36. Artemenkov S.L. Scientific conceptions and heuristics in cross-cultural communication and education in terms of a joint probability decision making. Riga: ISMA. Information Technologies, Management and Society, 2013, Vol. 6, No. 1. P. 20–30.
37. Birkhoff G. & von Neumann J. “The Logic of Quantum Mechanics”, Annals of Mathematics, 1936, 37(4): 823–843. doi:10.2307/1968621
38. Blutner R. Complementarity and Quantum Cognition. In S. Satsangi, A.M. Horatschek, A. Srivastav (eds) Consciousness Studies in Sciences and Humanities. 2021. 27-45.
39. Foulis D.J., & Randall C.H. Operational statistics. I. Basic concepts. Journal of Mathematical Physics. 1972, 13. 1667-1675.
40. Foulis, D.J., & Randall, C.H. Manuals, Morphisms and Quantum Mechanics, in A. Marlow, ed., Mathematical Foundations of Quantum Theory, Academic Press, New York. 1978. 105–126.
41. Galavotti M.C. Philosophical introduction to probabilities. Stanford, 2005.
42. George Mackey (1916–2006), Notices of the American Mathematical Society. 2007. 54(7). 824-850.
43. Gillies D. Philosophical theories of probability. L., 2000.
44. GreechieJ. Orthomodular lattices admitting no states, Journal of Combinatorial Theory, Series A. 1971. 10(2). 119-132. https://doi.org/10.1016/0097-3165(71)90015-X
45. Hertwig R., & Gigerenzer G. The ‘conjunction fallacy' revisited: how intelligent inferences look like reasoning errors. Journal of Behavioral Decision Making, 1999. 12, 275-305.
46. Heuristics & Biases: the psychology of intuitive judgement / edited by T. Gilovich, D. Griffin, D. Kahneman. Cambridge University Press. 2002. 857 p.
47. James W. The Principles of Psychology. New York/London: Holt and Macmillan. 1890. V. 1.
48. Kuravsky L.S. Modeling dynamical behavior of stochastic systems: spectral analysis of qubit representations vs the mutual markovian model likelihood estimations. Lobachevskii Journal of Mathematics. 2021. 42 (10). 2364-2376.
49. Kuravsky L.S. Simplification of Solving Diagnostics Problems by Convolution of Applied Markovian Models into the Quantum Representations. Lobachevskii Journal of Mathematics. 2022. 43 (7). 1669–1682.
50. Lüders Über die Zustandsänderung durch den Meßprozeß, Annalen der Physik. 1951. 8, 322–328; English translation by K.A. Kirkpatrick, at arXiv:quant-ph/0403007.
51. Mackey G.W. “Quantum Mechanics and Hilbert Space”, The American Mathematical Monthly, 1957, 64(8): 45–57. doi:10.2307/2308516
52. Mackey G.W. The Mathematical Foundations of Quantum Mechanics: A Lecture-note Volume, New York: W.A. Benjamin. 1963.
53. Mellor D.H. Probability: A philosophical introduction. L., 2005.
54. Pitowsky I. Quantum Mechanics as a Theory of Probability. In W. Demopoulos, I. Pitowsky (eds) Physical Theory and its Interpretation. The Western Ontario Series in Philosophy of Science, vol 72. Springer, Dordrecht. 2006. 213-240. https://doi.org/10.1007/1-4020-4876-9_10
55. Pothos E., & Busemeyer J.R. Formalizing heuristics in decision-making: a quantum probability perspective. Frontiers in psychology, 2011. 2. 289. https://doi.org/10.3389/fpsyg.2011.00289
56. Putnam H. 1968, “Is Logic Empirical?” in R. Cohen and M.P. Wartofski (eds), Boston Studies in the Philosophy of Science (Volume 5), Dordrecht: D. Reidel; reprinted as “The Logic of Quantum Mechanics” in Hilary Putnam, Mathematics, Matter and Method, Cambridge University Press, 1976, second edition 1979, pp. 174–197. doi:10.1017/CBO9780511625268.012
57. Randall C.H., & Foulis D.J. Operational statistics. II. Manuals of operations and their logics. J. Math. Phys. 14 (1973), 1472-1480.
58. Tversky A., Kahneman D. Extensional vs. intuitive reasoning: The conjunction fallacy in probability judgment. Psychological Review, 1983. 90(4). 293-3l5. https://doi.org/10.1037/0033-295X.90.4.293
59. von Neumann J. 1932, Mathematische Grundlagen der Quantenmechanik, Berlin: Springer-Verlag; English translation: Mathematical Foundations of Quantum Mechanics, Princeton: Princeton University Press, 1955.
60. Wilce A. Test Spaces. in K. Engesser, D. Gabbay and D. Lehman (eds), The Handbook of Quantum Structures: Quantum Logic, North Holland, 2009, pp. 443-549.
61. Wilce A. Dynamical states and the conventionality of (non-) classicality. In M. Hemmo, O. Shenker (eds) Quantum, probability, logic. The work and influence of Itamar Pitowsky. Springer Cham. 2020. 585-627. https://doi.org/10.1007/978-3-030-34316-3
62. Wright Generalized urn models. Foundations of Physics. 1990. 20. 881-903.