Экспериментальная психология
2024. Том 17. № 2. С. 154–177
doi:10.17759/exppsy.2024170210
ISSN: 2072-7593 / 2311-7036 (online)
Формирование навыков командной деятельности и их объективная количественная оценка на основе квантовых представлений
Аннотация
Представлены математические и программные средства, обеспечивающие формирование и объективную количественную оценку навыков командной деятельности на основе квантовых представлений. Они опираются на формальные представления деятельности испытуемых посредством матриц вероятностей переходов между выполняемыми ими элементарными операциями. Анализ деятельности испытуемых строится на сравнениях этих матриц для исследуемого паттерна действий с релевантными матрицами для паттернов эмпирических данных, представляющих различные варианты работы испытуемых. При оценке навыков командной деятельности эти сравнения выполняются по «схеме треугольника», предполагающей сопоставление согласованных действий испытуемых, выполненных в паре и индивидуально. Для этого применяется квантовый спектральный анализ, обеспечивающий эффективные количественные сопоставления скрытых периодичностей выполнения типовых элементарных операций и их количеств в спектральной метрике. Инструментальные средства для формирования и оценки навыков командной деятельности реализованы в виде летного тренажера с разделением между пилотами каналов управления и модифицированной компьютерной игры «Морской бой», позволяющей оценивать динамику коммуникации и кооперации партнеров, анализируя их ходы, а также передаваемые друг другу подсказки. Представленный подход к формированию и оценке навыков командной работы достаточно универсален и может быть использован в различных прикладных областях, в том числе при оценке и подготовке летных экипажей, операторов сложных технических систем, обучающихся различных уровней и других целевых групп.
Общая информация
Ключевые слова: психологическая диагностика, навыки командной работы, квантовые представления, марковские процессы, квантовая фильтрация
Рубрика издания: Инструментарий
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2024170210
Финансирование. Исследование выполнено при финансовой поддержке Министерства просвещения Российской Федерации, государственное задание № 073-00037-24-02 от 09.04.2024 г. «Разработка программно-аппаратного реабилитационного комплекса для формирования навыков командной работы на основе современных методов математической психологии».
Получена: 07.04.2024
Принята в печать:
Для цитаты: Куравский Л.С., Юрьев Г.А., Михайловский М.А., Несимова А.О., Юрьева Н.Е., Поляков Б.Ю. Формирование навыков командной деятельности и их объективная количественная оценка на основе квантовых представлений // Экспериментальная психология. 2024. Том 17. № 2. С. 154–177. DOI: 10.17759/exppsy.2024170210
Полный текст
Введение
В последние годы значительно возрос интерес к изучению процесса формирования и объективной количественной оценки навыков командной деятельности при подготовке операторов сложных технических систем, включая экипажи воздушных судов и боевых машин, а также в сфере образования и реабилитации лиц с ограниченными возможностями здоровья. Это обусловлено тем, что уровень подготовки, а также степень сформированности навыков индивидуальной и командной работы специалистов способны оказывать существенное влияние на качество исполнения ими своих обязанностей. Все большее значение приобретают психологические методы, применяемые для профессионального отбора и подготовки.
Если для прикладных областей, предполагающих совместную работу людей, навыки профессионального взаимодействия являются желательными и входят как подмножество в категорию надпрофессиональных, или «мягких», навыков, то для летных экипажей они попадают в категорию основных профессиональных навыков, что обусловлено требованиями безопасности полетов [Якимович, 2013]. В частности, пилоты воздушных судов должны приобрести опыт координации действий членов экипажа, что отражено в Федеральных авиационных правилах [Приказ Минтранса России, 2008].
Длительное время диагностический инструментарий, оценивающий уровень подготовки, опирался на подход [Rasch, 1980], называемый современной теорией тестирования (в оригинале — Item Response Theory, или IRT), и модель Г. Раша, предполагающую простую нелинейную зависимость между вероятностью выполнить полученное задание и разностью между уровнем сформированности профессиональных способностей и трудностью заданий, представленных в безразмерных шкалах. Однако этот подход, ориентированный на работу с психологическими опросниками традиционного типа, плохо вписывается в современный контекст.
Проблемами, ограничивающими применение современной теорией тестирования, являются: игнорирование усталости и других влияющих на оценки факторов, которые могут существенно изменяться со временем; отсутствие при построении расчетных оценок учета времени, затрачиваемого на решение задач; необходимость выполнения значительного числа заданий для получения оценок с приемлемой точностью; сложная для практической реализации процедура оценки точности результата, связанная с применением метода максимального правдоподобия и расчетом доверительных интервалов. Поэтому был разработан новый подход [Куравский, 2010; Марковские модели в, 2017], предполагающий представление диагностических процедур посредством идентифицируемых марковских случайных процессов, определяющих последовательность предъявления заданий и позволяющих вычислять байесовские оценки уровня подготовки испытуемых.
Новый подход позволяет: реализовывать адаптивные процедуры тестирования; выявлять и использовать при построении оценок временную динамику изменения способностей справляться с заданиями; учитывать при построении оценок время, затрачиваемое на решение задач; предъявлять существенно меньшее по сравнению с другими подходами число заданий, обеспечивая заданную точность; используя фильтр Калмана, устранять артефакты, обусловленные подсказками, угадыванием и другими формами некорректного целенаправленного вмешательства в процедуру тестирования.
Однако остались проблемы, связанные с формализацией профессиональной деятельности в форме, доступной для количественного анализа, и недоступностью при решении реальных практических задач достаточно большого объема эмпирических данных, предназначенных для «настройки» диагностического инструментария, что требует сложившаяся парадигма анализа результатов наблюдений. Это позволило говорить о необходимости разработки новых математических подходов, позволяющих извлечь из эмпирических данных существенно больший объем полезной информации, чем классические методы, а также об актуальности появления адаптивных диагностических процедур и разработки профессиональных тренажеров.
В 2022—2023 гг. удалось существенно продвинуться в части указанных направлений: разработан и программно реализован прототип адаптивной системы с функцией интеллектуального помощника, которая обеспечивает не только диагностику, но и обучение, существенно повышая его эффективность [Куравский, 2023]; разработан новый подход к решению задач диагностики путем свертки прикладных марковских моделей в квантовые представления [5; 11—14]. Очевидным преимуществом данного подхода является то, что число представляющих кубитов определяется числом кластеров состояний модели и поэтому в несколько раз меньше числа состояний в исходном марковском процессе, благодаря чему при формировании диагностического решения используется только существенная информация, включая выявляемые квантовым спектральным анализом скрытые периодичности обхода кластеров, которые являются чисто квантовым эффектом и не могут быть выявлены другими методами. Таким образом, квантовые представления позволяют оценивать внутреннюю структуру наблюдаемого процесса деятельности в частотной области, что не охватывают традиционные методы диагностики. Для экспериментов по исследованию эффективности применения квантовых представлений для решения диагностических задач на выборках испытуемых разработан и использован специальный инструмент — информационная система для адаптивной психологической диагностики с использованием прогрессивных матриц Равена [Куравский, 2023], выявившая значительные качественные преимущества нового подхода, включая кратное уменьшение количества эмпирических данных, необходимых для качественной «настройки» диагностических средств (это достигается за счет извлечения большего объема полезной диагностической информации из имеющихся экспериментальных данных).
В области авиации поиском решений рассматриваемых задач занимаются ведущие производители авиационной техники различного назначения. По данным последних лет, на каждый час полета гражданского воздушного судна приходится всего 5 минут ручного пилотирования (взлет, посадка и т.д.), однако за это время происходит 67% летных происшествий и катастроф. Авиационные приложения для задачи оценки навыков командной деятельности являются, очевидно, далеко не единственными, но приоритетными, поскольку цена одной ошибки экипажа — сотни человеческих жизней. В настоящее время для оценки указанных навыков и в России, и за рубежом используется технология «Crew Resource Management», когда навыки командной работы экипажа оцениваются группой экспертов-психологов по видеозаписи. Это дорого, субъективно и ненадежно. Применяемые психологические методики уязвимы для критики. Часто делаются ошибочные заключения, особенно в условиях дефицита пилотов, последствия чего всем известны. Известны масштабные попытки научно-исследовательских подразделений зарубежных авиастроительных компаний перейти к объективной количественной оценке навыков командной работы с использованием современных технологий. Однако они не увенчались успехом, поскольку не удалось формализовать деятельность пилота, построив пригодную для количественного анализа математическую модель. Существовавшие до настоящего времени подходы к оценке указанных навыков, основанные на методах наблюдения, опроса и тестирования, дают лишь субъективную качественную оценку.
Не менее актуальным направлением является разработка средств формирования навыков командной деятельности, а также методов оценки сформированности совместной деятельности и командного взаимодействия людей с ограниченными возможностями здоровья, в частности у лиц с сохранным интеллектом при расстройствах аутистического спектра, как интегративного качества личности, позволяющего социализироваться в трудовом коллективе [Пяткина, 2018].
В настоящее время автоматизированные методы показывают сопоставимую или более высокую точность по сравнению с экспертными оценками. Соответствующие программные средства могут обеспечить автоматизацию процедур тестирования и формирования навыков, что даст возможность регулярно отслеживать прогресс в их развитии. Таким образом, разработка подобных инструментов для формирования и оценки навыков, необходимых для эффективной и согласованной работы в группах, предоставит новые возможности для объективной количественной оценки степени их сформированности.
В работах [5; 11—14] представлен новый подход к анализу и диагностике деятельности, позволяющий оценивать профессиональную подготовку. Применяемый подход показал существенные преимущества по сравнению с альтернативными способами оценок. Он опирается на свертку прикладных марковских процессов, построенных на базе протоколов деятельности пилотов, в квантовые представления, что позволяет выявлять структуру и особенности этих процессов с помощью квантового спектрального анализа. Применение квантовой фильтрации [5; 13—14], представленной в указанных выше публикациях, позволяет получать количественные диагностические оценки деятельности пилотов. Фактически, это первая удачная попытка создания достаточно универсальной математической модели деятельности операторов сложных технических систем, позволяющая количественно сравнивать содержание результатов их работы и опирающаяся на новый и доказавший свою эффективность математический аппарат. Необходимость применения квантовых представлений обусловлена тем, что они, в отличие от классической теории вероятностей, обеспечивают исследование наблюдений в процессе эволюции, а не всей выборки сразу, что критически важно при анализе содержания исследуемой деятельности «во временной развертке» [Куравский; Kuravsky, 2024]. Применяемые квантовые представления программно реализуются на классическом компьютере и не требуют для своей реализации специальных вычислительных инструментов, обеспечивающих квантовые вычисления в привычном понимании, что в данный момент является новым и перспективным решением для охватываемых прикладных областей. Возможность реализации рассматриваемых квантовых методов на обычном компьютере обоснована известной теоремой Готтесмана—Книлла (об эффективном моделировании квантовых вычислений на классическом компьютере) [Nielsen Michael, 2010].
Анализ деятельности операторов на основе формальных протоколов деятельности строится на сравнениях матриц вероятностей переходов для исследуемых паттернов действий или поведения [Куравский], которые опираются на количественные сопоставления степени близости характеристик периодичностей выполнения типовых элементарных операций и их количеств в спектральной метрике, детально и содержательно представляя последовательности действий испытуемых. Основанием для применения такого аппарата является существенно большая эффективность в части извлечения полезной диагностической информации из эмпирических данных по сравнению с классическими методами анализа данных: он позволяет получать диагностические выводы на эмпирических данных гораздо меньшего объема, извлекая из этих данных больше полезной информации [Куравский, 2023]. Новизна рассмотренного аппарата и полученных с его помощью результатов обусловлена тем, что он опирается на новый удобный и достаточно универсальный способ формализации профессиональной деятельности, пригодный для количественного анализа.
В этой статье представлены результаты разработки программно-аппаратного средств для формирования навыков командной деятельности и количественных методов оценки степени их сформированности для подготовки операторов сложных технических систем, а также социальной интеграции лиц с ограниченными возможностями здоровья. Полученные результаты опираются на указанное выше представление профессиональной деятельности, пригодное для анализа математическими средствами, и метод анализа квантовых представлений, позволяющий эффективно решать диагностические задачи.
Высокая научная значимость этих результатов с точки зрения современной психологии обусловлена тем, что, в отличие от существующих процедур, фиксирующих наличный уровень сформированности диагностируемых психологических характеристик, разрабатываемые средства позволяют реализовать новый подход — диагностику и мониторинг самого процесса становления значимых для данной деятельности характеристик, обеспечивающих развитие самой профессиональной деятельности, что является отечественным и мировым приоритетом в разработке нового поколения психологического инструментария. Рассмотренный далее подход достаточно универсален и может быть использован в различных прикладных областях, в том числе при оценке и подготовке летных экипажей, операторов сложных технических систем, обучающихся различных уровней и других целевых групп.
Принцип построения программно-аппаратных средств для формирования навыков командной деятельности
Принцип построения разработанных программно-аппаратных средств опирается на модель совместной интерактивной обучающей среды, предложенную советским психологом Ф.Д. Горбовым [Горбов, 1975; Ермаков, 2024]. Эта модель, названная «Два душа» («The Two-Shower Model»), предполагает разделение управления между несколькими операторами, стремящимися достичь нужной температуры в нескольких душевых лейках, имеющих один и тот же ресурс горячей воды. Анализ, проведенный в работе М. Висте [Viste], показал, что, несмотря на простое описание, данная модель является сложной и трудноуправляемой нелинейной системой, при работе с которой испытуемые должны понять закономерности ее работы, чтобы научиться согласованной деятельности. На основе полученных результатов Ф.Д. Горбов разработал концепцию о взаимосвязанных влияниях между индивидами в группе, где характер решения частной задачи одним участником непосредственно воздействует на общий процесс деятельности, иллюстрируя тем самым важность координации действий в коллективе.
Представленные далее средства для формирования и оценки навыков командной деятельности опираются на современные технические возможности и представляют собой компьютерные игры-тренажеры, управляемые командой (в частности, парой) операторов (игроков) с разделением между ними каналов управления или игровых действий, которые в обычной ситуации контролирует один оператор. Команда операторов (игроков) должна обеспечить корректное управление тренажером или участие в игре путем согласованных действий, получая в реальном времени в удобной, понятной и доступной форме информацию о результатах своей деятельности. Игры-тренажеры должны быть доступны людям, не имеющим специальной подготовки, и допускать настройку параметров, регулирующих трудность управления или участия в игре, обеспечивая таким образом адаптацию к различным уровням профессиональной подготовки и психофизиологическим состояниям операторов (игроков). В результате обеспечивается комплексный подход к обучению, при котором технические и коммуникативные навыки развиваются одновременно, предоставляя операторам (игрокам) возможность наработать опыт согласованного взаимодействия в команде и стимулируя развитие ключевых навыков командной работы.
Инструментальные средства для формирования и оценки навыков командной деятельности реализованы в двух вариантах:
-
в виде тренажера, имитирующего полет воздушного судна и управляемого экипажем с разделением между пилотами каналов управления (работа с этим тренажером предполагает подключение специальных устройств, обеспечивающих управляющие воздействия);
-
в виде модифицированной компьютерной игры «Морской бой», взаимодействующие участники которой сталкиваются с ботом, автоматически размещающим свои корабли на игровом поле: игровой процесс позволяет оценивать динамику коммуникации и кооперации партнеров, анализируя их ходы, а также передаваемые друг другу подсказки (данная игра не предполагает подключения специальных устройств).
Математическая модель согласованной деятельности испытуемых
Следуя работам [Kuravsky, 2021; Kuravsky, 2022], формализованная согласованная деятельность испытуемых представляется посредством матриц вероятностей переходов между выполняемыми ими элементарными операциями. Рассматриваемая типовая модель, названная математической моделью сопутствующей деятельности, представляет вероятностную динамику выполнения рассматриваемых типов элементарных операций как марковский процесс с дискретными состояниями и дискретным временем (цепь Маркова):
Эффективность решения прикладных задач регулируется степенью детализации учитываемых элементарных операций, представляющих и конкретизирующих адаптацию модели к предметной области. Выбор указанной формы математической модели при решении задач классификации обусловлен высокой эффективностью квантового спектрального анализа матриц вероятностей переходов в сочетании с квантовой фильтрацией [Куравский; Kuravsky, 2024; Kuravsky, 2023].
Альтернативный подход, который опирается на оценки взаимных правдоподобий, построенные с использованием матриц вероятностей переходов, при решении данной задачи допустим, однако, как показано в работах [Куравский; Kuravsky, 2024], этот способ решения существенно уступает по полноте, эффективности и качеству получаемых результатов методу, построенному на основе квантовых представлений.
В работах [2; 15—17] демонстрируется возможность создания эффективных диагностических методик, основанных на сопоставлении исследуемых образцов (паттернов) действий или поведения с типовыми паттернами эмпирических данных, накопленными в результате экспериментов. В зависимости от выбора применяемых измеримых характеристик и типа диагностической задачи, в качестве таких паттернов могут использоваться воздействия на ручки управления воздушным судном (ВС), параметры состояния ВС, траектории движения взгляда, временные ряды показателей кардио- и пульсометрии, параметры электроэнцефалограмм и т.д.
Подходы, не использующие сравнения с эмпирическими данными, в контексте диагностической задачи не имеют перспективы из-за отсутствия на сегодняшний день достаточно полной и адекватной наблюдениям формализованной модели действий или поведения оператора, опирающейся на выявленные в результате научных исследований количественные психологические и психофизиологические закономерности. В свою очередь, методы, опирающиеся на сравнение с эмпирическими данными, позволяют формализовать деятельность испытуемого как последовательность дескрипторов разнотипных элементарных операций, регистрируемых с помощью измерительных систем.
Зарегистрированный в результате наблюдений протокол деятельности испытуемого, представляющий собой последовательность дескрипторов, преобразуется в матрицу вероятностей переходов (точнее, в матрицу выборочных оценок вероятностей переходов) между типами выполняемых им элементарных операций, размер которой определяется числом учитываемых типов операций. Полученная выборочная оценка матрицы вероятностей переходов, в свою очередь, дает возможность рассматривать динамику действий оператора как марковский процесс с дискретными состояниями и дискретным временем (или марковскую цепь), состояниями которого являются учитываемые в протоколе типы элементарных операций. В общем случае, данный марковский процесс допускает полную систему связей между состояниями. Имеющая место разнотипность операций несущественна, поскольку используются только их вероятностные связи.
Представление деятельности испытуемых с помощью матриц вероятностей переходов между элементарными операциями имеет существенные преимущества перед другими подходами к построению модели их поведения, включая простоту построения представления деятельности по результатам наблюдений, доступность и разумный объем измерений, необходимых для создания модели поведения, и возможность проведения эффективного анализа данных. Распознаваемые типы испытуемых определяются прикладной задачей, в интересах которой проводится анализ.
Рассмотренный подход применялся для формирования навыков командной деятельности и оценок степени сформированности таких навыков с помощью специального летного тренажера, оснащенного необходимым периферийным оборудованием, а также с помощью специализированной компьютерной игры (см. разделы 5—7).
Математическое представление поведения испытуемых с помощью матриц вероятностей переходов между состояниями марковского процесса
Согласно одному из основных постулатов квантовой механики, наблюдаемые значения являются собственными значениями некоторого эрмитова оператора в гильбертовом пространстве. Если этот оператор рассматривать как гамильтониан формальной квантовой системы, то его можно представить как , где — диагональная матрица, на диагонали которой стоят наблюдаемые («измеряемые») вещественные значения; — комплекснозначная квадратная матрица, столбцами которой являются векторы, образующие ортонормированный базис; — матрица, эрмитово сопряженная к . Выбор указанного ортонормированного базиса является свободным. Столбцы матрицы являются собственными векторами гамильтониана , задающими допустимые варианты этого оператора. Они определяются удобством проведения «измерений» с точки зрения решения прикладной задачи, причем их выбор является прерогативой «наблюдателя» квантовой системы. Таким образом, измеряемые значения, представляемые матрицей , и характеристики «наблюдателя», представляемые матрицей , определяют гамильтониан наблюдаемой квантовой системы. В прикладных задачах число измеряемых значений может быть произвольным, но конечным, что позволяет говорить о квантовых представлениях наблюдаемой системы с помощью кудитов, имеющих более двух наблюдаемых состояний.
В свою очередь, если установлен гамильтониан , то унитарный оператор эволюции квантовой системы определяется как решение уравнения Шредингера , записанного для этого оператора:
Присутствующая в этом выражении экспонента может быть приближенно вычислена как конечная сумма, сходящаяся к пределу суммы известного ряда:
Соответственно, эволюция данной формальной квантовой системы описывается следующим образом:
Однако в вычислительном отношении такой способ описания эволюции системы не является удобным, поскольку требует суммирования медленно сходящегося ряда. Более удобно, хотя и избыточно, рассмотренное в работах [Kuravsky, 2021; Kuravsky, 2022] квантовое представление, где каждое наблюдаемое значение описывается одним кубитом, «чистые» состояния которого выражают факт появления данного значения при наблюдениях или его отсутствия. При этом для обеспечения нормировки выполняется «запутывание по измерениям» (entangled by measuring — EM).
Наблюдаемой величиной является пребывание марковского процесса в определенном кластере состояний. «Измеряемые» значения определяются следующим образом:
-
марковский процесс находится внутри заданного кластера состояний: 1,
-
марковский процесс находится вне заданного кластера состояний: –1.
Структура, представляемая кубитами, описывает динамику пребывания в нескольких кластерах состояний, причем рассматриваемый процесс в каждый момент времени находится в одном и только одном из M рассматриваемых кластеров.
Совокупность таких кубитов называется EM-квантовой системой.
Указанный вариант унитарного оператора не является единственным: в работе [Kuravsky, 2022] рассмотрен общий вид этих операторов для случая биполярных собственных значений, однако оператор вращения является наиболее удобным с точки зрения практических вычислений и интерпретации их результатов. Как правило, выбор унитарного преобразования в конкретных прикладных задачах обусловлен достаточной степенью соответствия эмпирическим данным и возможностью эффективной программной реализации сопутствующих вычислений.
Путем имитационного моделирования в соответствии с вероятностями переходов между состояниями марковского процесса, для каждого распознаваемого класса объектов генерируются выборки траекторий прохождения кластеров состояний. Эти выборки и идентифицированные параметры представлений кубитов используются для вычисления элементов матриц взаимных расстояний в спектральной метрике [Kuravsky, 2021; Kuravsky, 2022]:
Последующее многомерное шкалирование, получив на входе вычисленную матрицу взаимных расстояний, формирует для траекторий прохождения кластеров состояний диаграмму рассеяния в пространстве заданной размерности, на основе которой дискриминантный и кластерный анализ вычисляют решение диагностической задачи.
Искажения, возникающие вследствие разброса выборочных оценок элементов матриц вероятностей переходов между состояниями исходной марковской цепи, устраняются, насколько это возможно, с помощью квантовой фильтрации. Возможность такой фильтрации обусловлена:
-
учетом выявляемой квантовым спектральным анализом [Kuravsky, 2021; Kuravsky, 2022; Kuravsky, 2023] дополнительной скрытой информации о поведении испытуемых;
-
взаимной компенсацией разнонаправленных сдвигов точек диаграммы рассеяния в пространстве шкалирования, что приводит к значительному снижению уровня «шума», связанного с ошибками выборочных оценок.
Квантовая фильтрация обеспечивается выполнением вычислительной процедуры, рассмотренной в [Kuravsky, 2023]. Эта процедура включает:
- свертку марковских процессов, описывающих процессы обхода состояний марковской цепи, в квантовые представления;
- генерацию выборок траекторий прохождения кластеров состояний, формирующих указанные квантовые представления, в соответствии с матрицами вероятностей переходов (для каждого испытуемого создается свое множество траекторий прохождения кластеров состояний фиксированного объема);
- вычисление элементов матриц взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике с выполнением следующих условий:
- каждой паре рассматриваемых испытуемых соответствует своя пара указанных сгенерированных множеств;
- эти матрицы вычисляются для одного и того же разбиения на кластеры, полученного, используя матрицу вероятностей переходов первого элемента пары, для всех траекторий, входящих в указанную пару множеств;
- представление указанных траекторий в виде точек в пространстве шкалирования;
- вычисление статистик Уилкса для пар сгенерированных множеств точек, представляющих траектории обхода кластеров в пространстве шкалирования;
- решение задачи классификации испытуемых, используя в качестве меры близости вычисленные попарные статистики Уилкса.
Применение математической модели сопутствующей деятельности для количественной оценки степени сформированности навыков командной работы
Рассмотренный выше подход представляет собой новый гибкий способ анализа и интерпретации сложного поведения испытуемых, пригодный для решения диагностических задач. Он может быть применен к анализу человеко-машинных систем, где оказываются неэффективными традиционные методы.
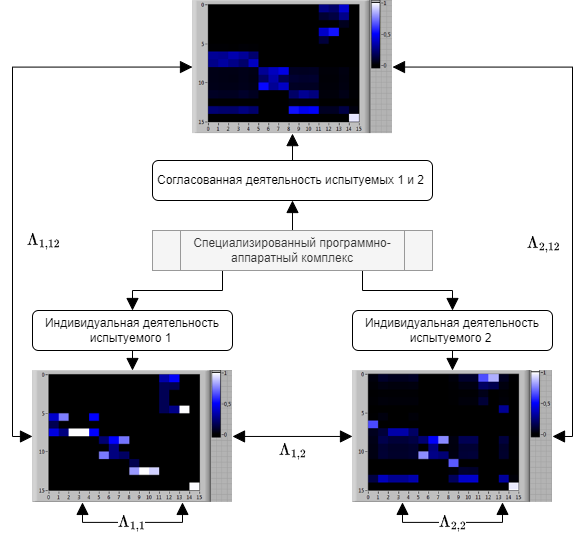
В приложении к оценке навыков командной деятельности целесообразно использовать «схему треугольника», согласно которой пара испытуемых выполняет вместе и индивидуально определенную согласованную и сопоставляемую деятельность, такую как совместное пилотирование воздушного судна или командную игру (рис. 1). Работа должна быть направлена на достижение заданной конкретной цели, понятной испытуемым. Для реализации такой деятельности следует использовать специализированный программно-аппаратный комплекс, позволяющий регистрировать протоколы деятельности испытуемых и формировать матрицы вероятностей переходов между типами выполняемых элементарных операций.
Валидность оценки степени сформированности навыков командной работы обусловлена структурой сравнений по «схеме треугольника» (рис. 1), согласно которой согласованная деятельность испытуемых сопоставляется с их индивидуальной деятельностью, рассматриваемой как эталон выполнения согласованных командных действий. Представление деятельности посредством матриц вероятностей переходов между выполняемыми элементарными операциями в сочетании с построенными на их основе квантовыми представлениями обеспечивает возможность количественных сравнений различных вариантов действий испытуемых с учетом конкретного содержания выполняемой работы в необходимом объёме.
Приведенные выше статистики Уилкса, вычисленные по парам полученных матриц вероятностей переходов, которые реализуются в случае индивидуальной и командной деятельности испытуемых, используются в качестве количественных оценок согласованности их работы. В качестве базы для сравнений целесообразно использовать один из вариантов индивидуальной деятельности. Относительное изменение статистики Уилкса при переходе от индивидуальной к командной деятельности служит удобной и легко интерпретируемой количественной мерой степени сформированности навыков командной деятельности.
Примеры, иллюстрирующие использование специализированных программно-аппаратных средств указанного типа, рассмотрены в разделе 7. В случае неоднократного применения по релевантной методике, эти же комплексы могут служить тренажерами для формирования и совершенствования навыков командной работы у испытуемых.
Рис. 1. Оценка навыков командной деятельности по «схеме треугольника», предполагающей сопоставление согласованных действий испытуемых, выполненных в паре и индивидуально
Тренажер, имитирующий полет воздушного судна (летный тренажер)
Этот тренажер представляет собой программно-аппаратный комплекс, имитирующий для работающих на нем испытуемых полет воздушного судна (рис. 2). Он управляется экипажем с разделением между пилотами каналов управления, которые в реальном полете контролирует один человек. Экипаж в составе двух находящихся рядом пилотов должен обеспечить корректное управление воздушным судном путем согласованных действий, получая в реальном времени в удобной, понятной и доступной форме информацию о результатах своей деятельности, включая отображение положения воздушного судна относительно земной поверхности.
Рис. 2. Управление воздушным судном с разделением каналов управления между пилотами
Работа с этим тренажером предполагает подключение специальных устройств (боковой ручки управления, педалей и рычага управления двигателем), обеспечивающих управляющие воздействия.
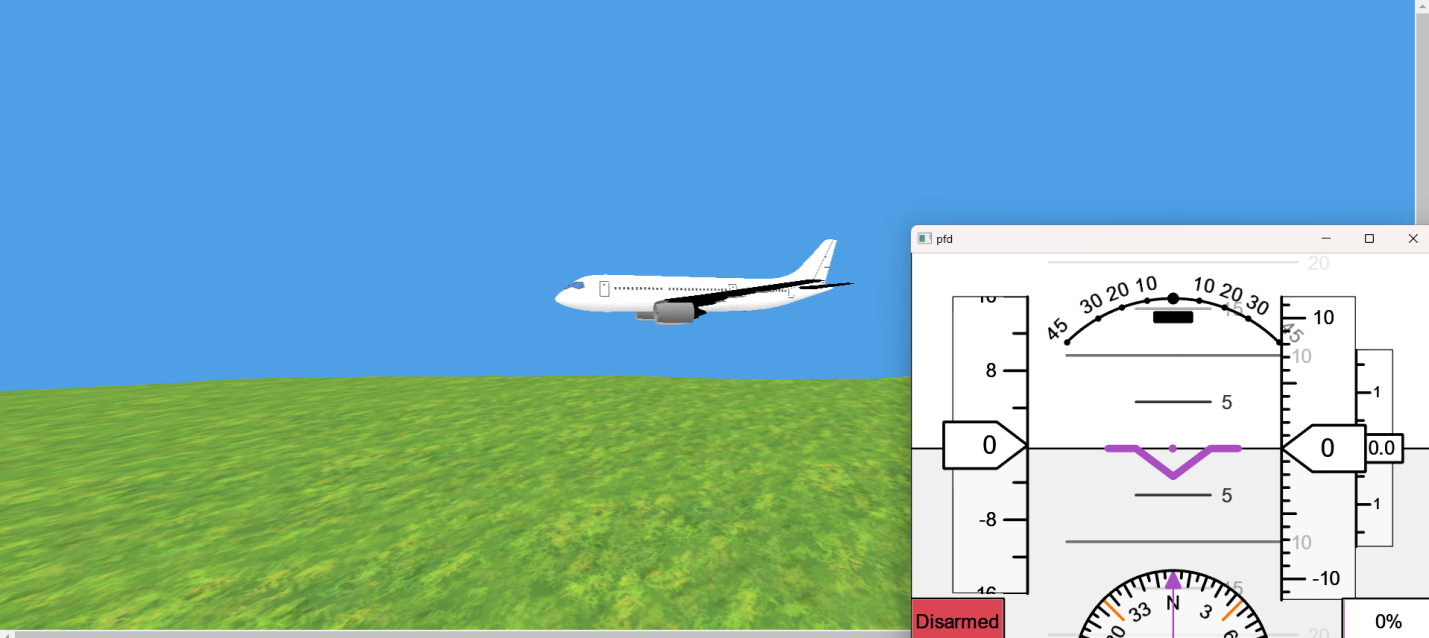
Целью управления является поддержание устойчивого положения воздушного судна, при котором его нос направлен в сторону движения параллельно земной поверхности, а именно: пилоты должны удерживать самолет в определенной ориентации в пространстве, сохраняя движение в заданном направлении в течение установленного периода времени. Экипаж работает с органами управления, получая информацию о геометрическом положении и параметрах полета, отображаемых на основном пилотажном дисплее (рис. 3).
Рис. 3. Информация о геометрическом положении воздушного судна на экране монитора и параметрах полета на основном пилотажном дисплее (Primary Flight Display). На основном пилотажном дисплее отображаются: высота полета, скорость, вертикальная скорость и положение самолета относительно земной поверхности и заданного маршрута
Реализовано следующее разделение каналов управления: первый пилот управляет боковой ручкой управления по каналу крена, рычагом управления двигателем и педалями (т.е. курсом), а второй пилот — ручкой управления по каналу тангажа и рычагом управления двигателем. Кроме того, для получения оценок, представленных в разделе 5, возможно управление воздушным судном только одним пилотом, воздействующим на все имеющиеся органы управления.
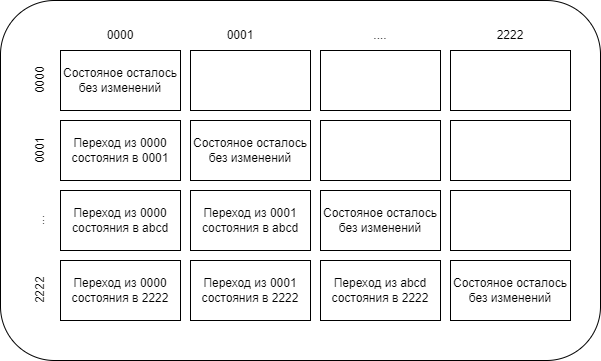
При количественной оценке степени сформированности навыков командной работы, в качестве выполняемых пилотами типов элементарных операций, используются воздействия на боковую ручку управления (по каналам крена и тангажа), педали и рычаг управления двигателем, а именно: воздействия в сторону увеличения значений каждого управляемого параметра, воздействия в сторону их уменьшения, а также отсутствие подобных изменений. Соответственно, матрица вероятностей переходов между типами выполняемых элементарных операций имеет размер, равный 34 (рис. 4).
Рис. 4. Структура матрицы вероятностей переходов между 34типами выполняемых элементарных операций: 4 органа управления (боковая ручка управления по каналу крена,боковая ручка управления по каналу тангажа, педали и рычаг управления двигателем) и 3 варианта управления («0» соответствует отсутствию изменений, «1» соответствует изменению в большую сторону, «2» соответствует изменению в меньшую сторону)
Тренажер доступен людям, не имеющим специальной летной подготовки, и допускает настройку параметров, регулирующих трудность управления воздушным судном, обеспечивая адаптацию к различным уровням профессиональной подготовки и психофизиологическим состояниям операторов (от курсантов летных учебных заведений до лиц с ограниченными возможностями здоровья различных нозологий).
Модифицированная компьютерная игра «Морской бой»
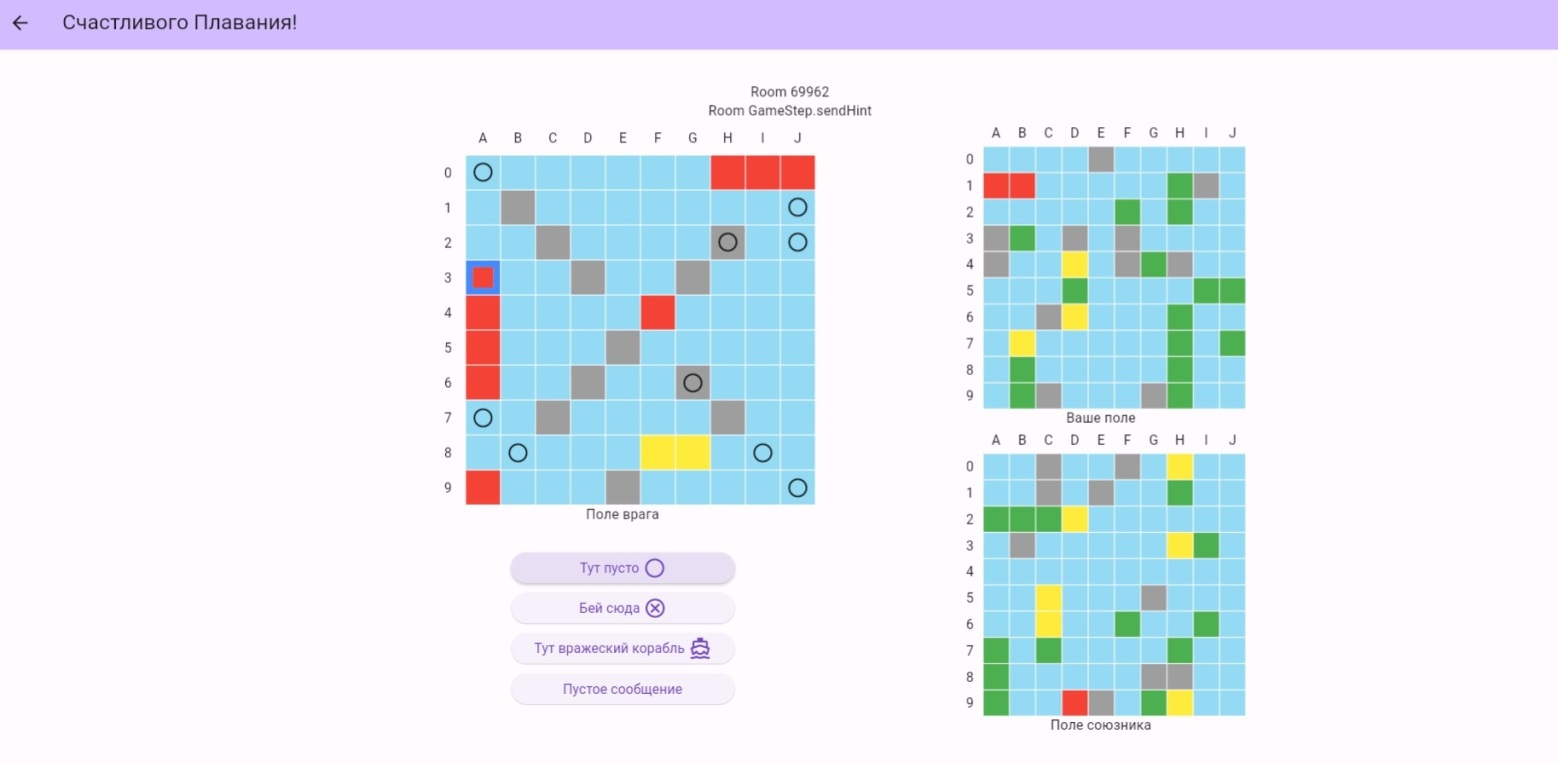
В игре участвуют два игрока, располагающих общим полем боя размером 10х10 клеток. Игроки сталкиваются с ботом, который автоматически размещает свои корабли на поле. Размещение кораблей игроков также происходит автоматически. Участникам доступны три поля: главное поле, на котором отображаются подсказки союзника и нанесенные удары, и два дополнительных поля, содержащих информацию о состоянии собственного флота и флота союзника, что обеспечивает дополнительную мотивацию для игроков (рис. 5).
Ход каждого игрока состоит из выстрела по клетке и последующей подсказки. Подсказки обеспечивают взаимодействие между игроками. Игроки могут следовать подсказкам партнеров или игнорировать их. Например, участник может довериться партнеру и не проверять «пустую» клетку, либо проверить достоверность полученной информации, нанеся удар в клетку, где было заявлено отсутствие корабля.
Игроки побеждают, когда полностью разрушают все корабли виртуального соперника (бота). При этом один из игроков выигрывает при нанесении более значительного урона, в сравнении с союзником.
Анализ взаимодействия игроков опирается на информацию о сделанных ими ходах и реакциях на полученные подсказки. В процессе игры выполняются 30 типов элементарных операций, определяющих размер матриц вероятностей переходов, позволяющих исследовать динамику коммуникаций и кооперации между игроками, анализируя их ходы, а также передаваемые друг другу подсказки и их влияние на действия партнеров.
Рис. 5. Модифицированная компьютерная игра «Морской бой»: иллюстрация
Количественная оценка степени сформированности навыков командной деятельности: иллюстрирующие примеры
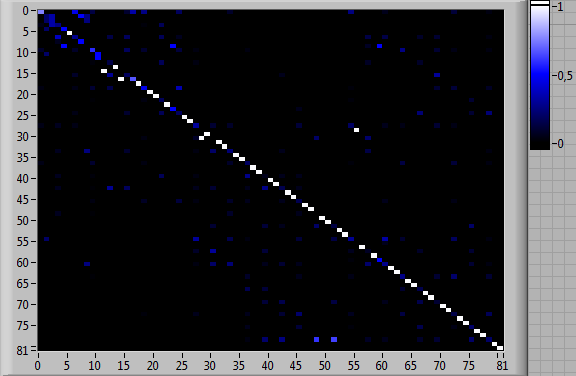
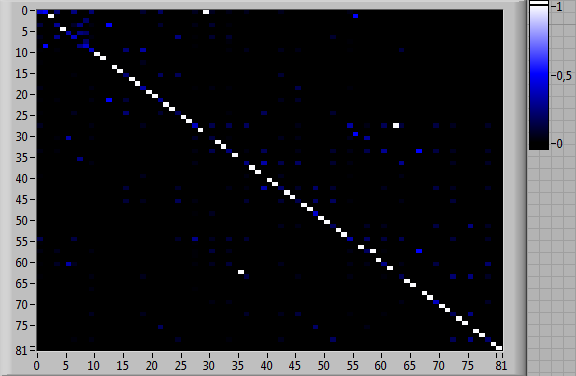
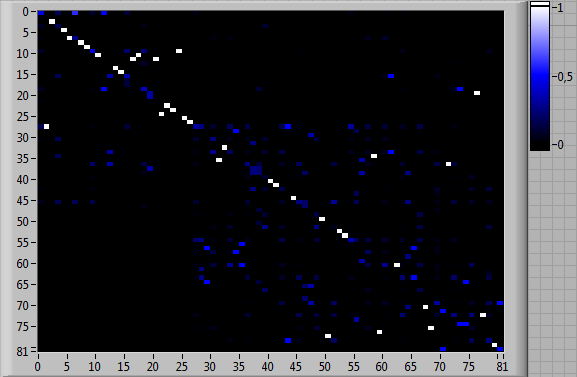
Рассмотрим результаты применения «схемы треугольника» для оценки навыков командной деятельности с помощью представленных выше инструментальных средств: летного тренажера и модифицированной компьютерной игры «Морской бой». Данные средства позволили зарегистрировать протоколы индивидуальной и командной деятельности испытуемых и сформировать на их основе оценки матриц вероятностей переходов между типами выполняемых элементарных операций, представленные нарис.6-7. В качестве вычислительного инструмента для сравнения результатов деятельности, представленных этими матрицами, использована Интеллектуальная система квантового моделирования (The Intelligent System for Quantum Modeling, ISQM) [Куравский; Kuravsky, 2024; Kuravsky, 2023].
Рис. 6. Оценки матриц вероятностей переходов между 81 типом выполняемых элементарных операций для тренажера, имитирующего полет воздушного судна: (а) индивидуальная деятельность испытуемого 1; (б) индивидуальная деятельность испытуемого 2; (в) согласованная деятельность испытуемых 1 и 2
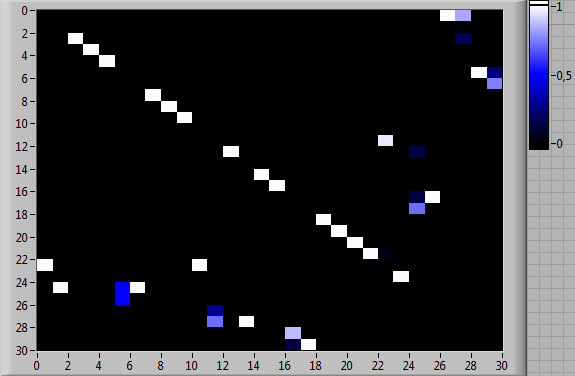
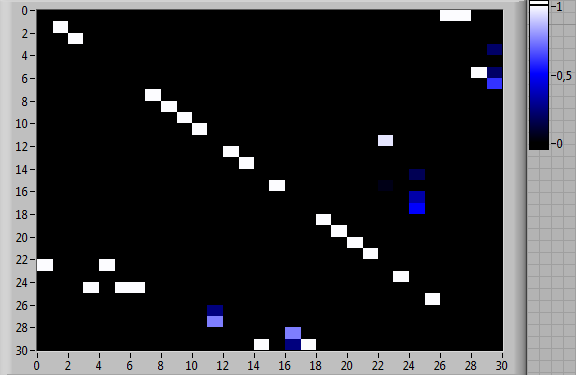
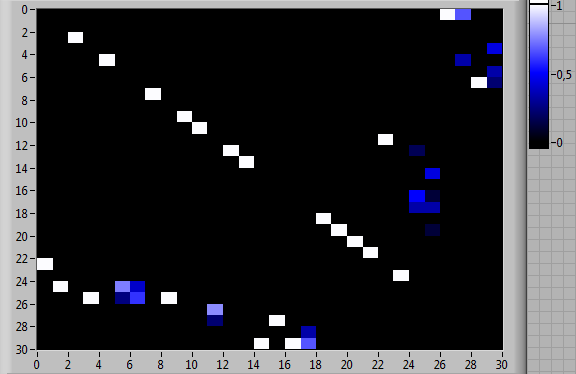
Рис. 7. Оценки матриц вероятностей переходов между 30 типами выполняемых элементарных операций для модифицированной компьютерной игры «Морской бой»: (а) индивидуальная деятельность испытуемого 1; (б) индивидуальная деятельность испытуемого 2; (в) согласованная деятельность испытуемых 1 и 2
Сравнение согласованности командной деятельности испытуемых 1 и 2 с результатом сравнения индивидуальной деятельности испытуемых 1 и 2 позволяет судить о том, насколько согласованность командной деятельности отличается от наблюдаемой вариативности индивидуальной работы испытуемых.
Проведенные сравнения позволяют говорить о том, что эффективность действий испытуемых на летном тренажере более чувствительна к наличию навыков командной деятельности, чем соответствующая характеристика в случае игры «Морской бой». Поэтому различные средства оценки этих навыков могут демонстрировать разную чувствительность к их проявлению.
Очевидно, что, по мере накопления опыта согласованной деятельности, полученного в результате тренировок, оценки согласованности командной деятельности должны эволюционировать в сторону показателя согласованной индивидуальной деятельности, позволяя проводить количественный мониторинг динамики формирования и совершенствования оцениваемых навыков.
Основные результаты и выводы
- Разработаны математические и программные средства, обеспечивающие формирование и объективную количественную оценку навыков командной деятельности на основе квантовых представлений. Эти средства опираются на формальные представления деятельности испытуемых посредством матриц вероятностей переходов между выполняемыми ими элементарными операциями. Анализ деятельности испытуемых строится на сравнениях этих матриц для исследуемого паттерна действий с релевантными матрицами для паттернов эмпирических данных, представляющих различные варианты работы испытуемых. При оценке навыков командной деятельности указанные сравнения выполняются по «схеме треугольника», предполагающей сопоставление согласованных действий испытуемых, выполненных в паре и индивидуально. Для этого применяется квантовый спектральный анализ, обеспечивающий эффективные количественные сопоставления скрытых периодичностей выполнения типовых элементарных операций и их количеств в спектральной метрике. Необходимые вычисления выполняются с помощью специально разработанного программного обеспечения.
- Разработан программно-аппаратный комплекс для формирования и оценки навыков командной деятельности в виде тренажера, имитирующего полет воздушного судна и управляемого командой операторов с разделением между ними каналов управления, которые в реальном полете контролирует один пилот. Команда операторов должна обеспечить корректное управление воздушным судном путем согласованных действий, получая в реальном времени в удобной, понятной и доступной форме информацию о результатах своей деятельности, включая отображение положения воздушного судна. Тренажер доступен людям, не имеющим специальной летной подготовки, и допускает настройку параметров, регулирующих трудность управления воздушным судном, обеспечивая адаптацию к различным уровням профессиональной подготовки и психофизиологическим состояниям операторов.
- Разработана модифицированная компьютерная игра «Морской бой» для оценки и формирования навыков командной деятельности, позволяющая оценивать динамику коммуникации и кооперации партнеров, анализируя их ходы, а также передаваемые друг другу подсказки.
- По мере накопления опыта согласованной деятельности, полученного в результате тренировок, оценки согласованности командной деятельности должны эволюционировать в сторону показателя согласованной индивидуальной деятельности, позволяя проводить количественный мониторинг динамики формирования и совершенствования оцениваемых навыков.
- Предложенный математический аппарат, применяемый для количественной оценки степени сформированности навыков командной деятельности, обеспечивает более высокую эффективность по сравнению с другими подходами, позволяя получать диагностические выводы на эмпирических данных гораздо меньшего объема и извлекая из этих данных больше полезной информации.
- Применение квантовых представлений обусловлено тем, что они обеспечивают исследование наблюдений в процессе эволюции, а не всей выборки сразу, что критически важно при анализе содержания исследуемой деятельности «во временной развертке».
- Доказано, что при достаточно больших объемах эмпирических данных даже разовое проявление некоторой общей закономерности (например, нахождения множеств точек, представляющих траектории прохождения кластеров состояний, в определенных областях пространства шкалирования) фактически свидетельствует о ее наличии.
- Различные средства оценки навыков командной деятельности могут демонстрировать разную чувствительность к их проявлению.
- Представленный подход к формированию и оценке навыков командной деятельности достаточно универсален и может быть использован в различных прикладных областях, в том числе при оценке и подготовке летных экипажей, операторов сложных технических систем, обучающихся различных уровней и других целевых групп.
Литература
- Горбов Ф.Д., Лебедев В.И. Психоневрологические аспекты труда операторов. Медицина, 1975. 206 с.
- Грешников И.И., Куравский Л.С., Юрьев Г.А. Принципы построения программно-аппаратного комплекса для интеллектуальной поддержки экипажа и оценки уровня его подготовки // Моделирование и анализ данных. 2021. Том 11. № 2. C. 5—30. DOI:17759/mda.2021110201
- Ермаков С.С., Быстрова Ю.А. Роль компьютерных тренажеров в формировании, измерении и совершенствовании навыков командной работы // Экспериментальная психология. 2024. Том 17. (В печати).
- Куравский Л.С., Баранов С.Н., Юрьев Г.А. Синтез и идентификация скрытых марковских моделей для диагностики усталостного разрушения. Нейрокомпьютеры: разработка и применение. 2010. № 12. С. 20—36.
- Куравский Л.С., Козырев А.Д., Грешников И.И. Математическая модель сопутствующей деятельности пилотов и ее применение для объективной оценки его состояния и профессиональной подготовки // Экспериментальная психология. Том 17. № 1. С. 161—180. DOI:10.17759/exppsy.2024170111
- Куравский Л.С., Юрьев Г.А., Юрьева Н.Е., Николаев И.А., Несимова А.О., Поляков Б.Ю., Козырев А.Д. Построение систем психологической диагностики на основе новых математических представлений // Экспериментальная психология. 2023. Том 16. № 2. С. 178—202. DOI: 10.17759/exppsy.2023160211
- Марковские модели в задачах диагностики и прогнозирования: учеб. пособие / Под ред. Л.С. Куравского. 2-е изд., доп. М.: Изд-во МГППУ, 2017. 197 с.
- Приказ Минтранса России 12 сентября 2008 г. № 147 об утверждении Федеральных авиационных правил «Требования к членам экипажа воздушных судов, специалистам по техническому обслуживанию воздушных судов и сотрудникам по обеспечению полетов (полетным диспетчерам) гражданской авиации». Зарегистрировано в Минюсте РФ 20 ноября 2008 г. Регистрационный № 12701 // Бюллетень нормативных актов федеральных органов исполнительной власти. 2008. 1 декабря. № 48.
- Пяткина Е.С., Шипова Л.В. Модель комплексной реабилитации инвалидов трудоспособного возраста // Цивилизация — Общество — Человек. 2018. № 6—7. С. 87—91.
- Якимович Н.В., Городецкий И.Г. Психологическое обоснование и разработка обучающих программ по формированию коммуникативных и когнитивных навыков у пилотов гражданской авиации// Труды Института психологии РАН «Актуальные проблемы психологии труда, инженерной психологии и эргономики». Вып. 5 / Под ред. А.А. Обознова, А.Л. Журавлева. М., 2013.
- Kuravsky L.S. Modeling Dynamical Behavior of Stochastic Systems: Spectral Analysis of Qubit Representations vs the Mutual Markovian Model Likelihood Estimations // Lobachevskii J. Math. 2021. Vol. 42(10). P. 2364—2376.
- Kuravsky L.S. Simplification of Solving Diagnostics Problems by Convolution of Applied Markovian Models into the Quantum Representations // Lobachevskii J. Math. 2022. 43(7). P.1669—1682.
- Kuravsky L.S., Greshnikov I.I., Kozyrev A.D., Kosachevsky S.G., Frolova L.I., Zakharcheva A.A. A mathematical model for representing the related operator professional activities and its relevant diagnostic assessment based on the quantum representations // Lobachevskii J. Math. 2024. 45(6), pp. 2549—2566. DOI: 10.1134/S1995080224602819
- Kuravsky L.S., Greshnikov I.I., Yuryev G.A., Zlatomrezhev V.I. Synthesis of Civil Aircraft Control Using Empirical Data and Quantum Filtering // Lobachevskii J. Math. 2023. 44(6). P. 2079—2100.
- Kuravsky L.S., Yuryev G.A. A novel approach for recognizing abnormal activities of operators of complex technical systems: three non-standard metrics for comparing performance patterns [Электронный ресурс] // International Journal of Advanced Research in Engineering and Technology (IJARET). 2020. Vol. 11(4). P. 119—136. URL: http://www.iaeme.com/IJARET/issues.asp?JType=IJARET&VType=11&IType=4 (дата обращения: 05.04.2024).
- Kuravsky L.S., Yuryev G.A. Detecting Abnormal Activities of Operators of Complex Technical Systems and their Causes Basing on Wavelet Representations [Электронный ресурс] //International Journal of Civil Engineering and Technology (IJCIET).2019. Vol. 10(2). P. 724—742. URL: http://www.iaeme.com/IJCIET/issues.asp?JType=IJCIET&VType=10&IType=2 (дата обращения: 05.04.2024)
- Kuravsky L.S., Yuryev G.A., Zlatomrezhev V.I. New approaches for assessing the activities of operators of complex technical systems // Experimental psychology (Russia). 2019. Vol. 12. № 4. 27—49. DOI:10.17759/exppsy.2019120403
- Nielsen Michael A. & Chuang Isaac L. Quantum Computation and Quantum Information. Cambridge University Press, 2010. 702
- Rasch G. Probabilistic models for some intelligence and attainment tests. (Copenhagen, Danish Institute for Educational Research), expanded edition with foreword and afterword by B.D. Wright. Chicago: The University of Chicago Press, 1980.
- Viste M., Skartveit H.L. Visualization of Complex Systems-The Two-Shower Mode // PsychNology J.2004. Vol. 2. № P. 229—241.
Информация об авторах
Метрики
Просмотров web
За все время: 219
В прошлом месяце: 29
В текущем месяце: 12
Скачиваний PDF
За все время: 61
В прошлом месяце: 7
В текущем месяце: 2
Всего
За все время: 280
В прошлом месяце: 36
В текущем месяце: 14