Психолого-педагогические исследования
2014. Том 6. № 2. С. 150–161
doi:10.17759/psyedu.2014060213
ISSN: 2587-6139 (online)
Рефлексия множественности возможных решений поставленной задачи как показатель метапредметного результата обучения младших школьников
Аннотация
Общая информация
Ключевые слова: профессиональный стандарт, методики диагностики метапредменых компетенций выпускников начальной школы, развивающие образовательные ситуации, обучающий эксперимент
Рубрика издания: Психология образования
Тип материала: научная статья
DOI: https://doi.org/10.17759/psyedu.2014060213
Для цитаты: Шиленкова Л.Н. Рефлексия множественности возможных решений поставленной задачи как показатель метапредметного результата обучения младших школьников [Электронный ресурс] // Психологическая наука и образование psyedu.ru. 2014. Том 6. № 2. С. 150–161. DOI: 10.17759/psyedu.2014060213
Полный текст
В связи с введением новых федеральных образовательных стандартов общего начального образования возникла необходимость разработать психолого-педагогические основы проектирования методик диагностики метапредметных образовательных результатов [Володарская , 2008; Нежнов, 2007; Федеральный государственный образовательный, 2011]. Под метапредметными образовательными результатами понимаются такие универсальные способы деятельности, которые позволяют решать задачи в различных предметных и межпредметных плоскостях [ Федеральный государственный образовательный, 2011]. В качестве основы метапредметных компетенций можно рассматривать действия анализа, планирования и рефлексии, которые специально формируются в развивающем обучении [Гуружапов; Давыдов, 2004; Давыдов, 1996; Зак, 2000], а метапредметные компетенции, таким образом, выступают выражением теоретического подхода к решению задач [Володарская , 2008]. Проектирование методик диагностики метапредметных компетенций возможно на предметном материале, в частности по математике [Гуружапов, 2012а; Гуружапов, 2013; Масленникова, 2011; Соколов, 2012].
Аналогом метапредметных образовательных результатов выступают метакогнитивные умения [ Flavell, 1979; Kesici, 2011; Panaoura, 2007; Schneider, 2010; Stel, 2010; Veenman, 2005]. В зарубежных исследованиях, посвященных проблемам обучения и развития школьников, исследуется зависимость успешности обучения от метакогниции (метапознания - metacognition). В рамках изучения особенностей проявления метакогниции в обучении исследуется проблема вклада общих и специальных метакогнитивных умений в успешность обучения и усвоения знаний по различным дисциплинам [ Kesici, 2011; Panaoura, 2007; Stel, 2010; Veenman, 2005]. В частности, было показано, что метакогнитивные умения положительно влияют на качество усвоения знаний [ Kesici, 2011; Stel, 2010]. Метакогниция принимается также в качестве одного из основных критериев прогнозирования успешности обучения [Stel, 2010].
Исследование проблемы метакогнитивных умений и регуляции собственной познавательной деятельности как их составляющей приводит к выводам о том, что эффективность обучения непосредственно связана с умением учащихся управлять собственной когнитивной деятельностью и регулировать процесс своего обучения [ Рубцов, 2010; Федеральный государственный образовательный, 2011; Flavell, 1979; Panaoura, 2007]. Основой эффективной саморегуляции когнитивной деятельности является ее рефлексивный компонент, который применительно к процессу обучения обеспечивает умение проводить оценку известного и неизвестного при решении задач [Stel, 2010].
В зарубежных исследованиях исследуется также вопрос о характере метакогнитивных способностей, в частности, развиваются ли они как общие способности или в связи с определенной областью знаний, т. е. как предметно зависимые [Stel, 2010; Veenman, 2005]. Было установлено, что при выполнении задач с высокой степенью новизны и проблематизации решения успешность их выполнения зависит от метакогнитивных способностей. В такой ситуации учащиеся вынуждены действовать «эвристически» [Stel, 2010], т. е. теоретически подходить к решению задачи. На основе полученных данных делаются выводы о том, что у школьников формирование метакогнитивных способностей должно происходить в процессе обучения различным предметам.
Мы провели собственное экспериментальное исследование умения младших школьников анализировать способы решения математической задачи и осуществлять рефлексию множественности ее возможных решений. Диагностические задания были основаны на интерпретации действий персонажей сюжетных картинок в форме математических моделей арифметических действий. Объектом исследования стал процесс решения младшими школьниками задач на моделирование отношений целого и части в содержании сюжетных картинок. Предметом исследования - связь этих процессов с метапредметным содержанием учебной деятельности младших школьников в части анализа условий адекватности отображения свойств объекта в его модели.
Нами были спроектированы два типа диагностических заданий (условные названия «Кубики» и «Вертолеты») на основе задач из учебника авторского коллектива М.И. Моро по математике для I класса [ Моро, 2011], содержащих сюжетное изображение и математическую модель действий персонажей картинки. При этом подбирались такие картинки, в сюжете которых содержится неоднозначность действий персонажей, а задание формулировалось таким образом, чтобы эта неоднозначность была актуализирована. При выполнении такого рода задачи ученик вынужден анализировать способы ее решения, а также соотносить объект и его модель и осуществлять анализ адекватности этого соотношения.
Во многих современных учебно-методических комплектах содержатся задания, связанные с моделированием содержания сюжетных картинок [Гуружапов, 2012; Гуружапов, 2012а; Гуружапов, 2013; Масленникова, 2011; Рубцов, 2010]. Учитель может их использовать в учебном процессе, изменив формулировку и условия подачи, для диагностики метапредметных образовательных результатов, в частности - наличия познавательной рефлексии. В своей работе мы проверяли, насколько подобные задания можно использовать в качестве диагностики метапредметных компетенций.
Исследование было проведено в двух московских школах с учащимися I, II и III классов в январе-феврале 2013 г. В этих школах обучение математике происходит по программе авторского коллектива М.И. Моро. Общее количество испытуемых составило 168 человек. С одной группой (экспериментальной) были проведены занятия, в которые была включена работа с заданиями на моделирование, спроектированными на основе задач из учебника математики для I класса авторского коллектива М.И. Моро [ Моро, 2011]. С другой группой (контрольной) подобные занятия проведены не были.
С учащимися из экспериментальной группы нами был проведен обучающий эксперимент, в ходе которого организовывались дискуссии и коллективная работа учащихся, а также проводилось сценирование учебно-развивающих ситуаций. Занятия проходили один-два раз в неделю. Сценирование учебно-развивающих ситуаций осуществлялось на основе материалов из учебника по математике для I класса [ Моро, 2011]. При сценировании учебно-развивающих ситуаций особое внимание уделялось множественности решений развивающих задач [Гуружапов, 2012а]. В частности, для анализа адекватности математических моделей соответствующей сюжетной картинке подбирались такие изображения, в сюжете которых присутствовала неоднозначность действий персонажей, что предполагает множественность решений поставленной задачи. В ходе урока после предъявления каждого задания среди учащихся были организованы коллективные дискуссии с обсуждением способов его выполнения. Предметное содержание этих задач существенно отличалось от предметного содержания диагностических задач.
Примером задачи на анализ соотношения объекта и модели, а также их адекватности друг другу может служить следующее задание.
Каждому ученику раздается рисунок (рис. 1).
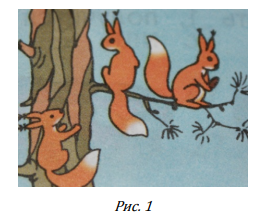
На доске делается следующая запись:

Сначала с учениками анализируется связь смысла сюжетной картинки и предлагаемой модели.
Учащимся дается следующее задание: «Определите, какой математический знак необходимо поставить между двумя квадратиками слева, если все квадраты обозначают числа».
Ученики предлагают свои варианты. Учитель просит аргументировать каждый ответ, тем самым организуя дискуссию. В результате обсуждения учащиеся приходят к выводу, что в данном случае можно поставить как знак «плюс», так и знак «минус» в зависимости от того, как интерпретировать сюжетную картинку. Далее ученикам предлагается заполнить квадратики соответствующими цифрами. Ученики предлагают множество вариантов, каждый из которых коллективно обсуждается, а те варианты, которые в ходе обсуждения приняты в качестве верных, записываются на доске. Здесь акцентируется внимание учащихся на работе с математическими действиями как моделями действий изображенных персонажей.
Отдельным моментом для обсуждения было применение нуля для обозначения действий, происходящих на сюжетной картинке: «А если белочка пробежит мимо, как будет записан пример?» (2 - « » = 2). «Что означает пустой квадратик?».
Другим примером подобного задания, использованного в обучающем эксперименте, может служить следующая задача.
Учащимся раздается следующий рисунок (рис. 2).

На доске делается запись:
3 + 2 = 5
3 + 0 = 3
5 - 2 = 3
Ученикам озвучивается следующее задание: «Посмотрите на математические записи на доске и на рисунок перед вами. Ученики одного класса составляли задачи по этой картинке. Придумывали условия задачи, а потом их решали. У них получились такие решения. Определите по решениям, какая задача или какие задачи были составлены неверно».
Приведем пример обсуждения данного задания учащимися I класса.
Протокол развивающего занятия № 4 в I классе «А» (фрагмент).
Ученик № 1. Я думаю, что третья неправильная.
Ведущий. Объясни, почему.
Ученик № 1. Пять минус два равно три. А к ним прилетели. Значит, должно быть три плюс два равно пять.
Ведущий. А второе ты считаешь правильное?
Ученик № 1. Нет.
Ведущий. Даша, а ты что хотела сказать?
Ученик № 2. Я считаю, что все правильные. Первый правильный тем, что три плюс два... К трем совушкам прилетели еще две, и их стало на ветке пять. Вторая подходит тем, что три, а две совы мимо пролетели, а последняя подходит, тем, что пять было их, а потом ... они улетели, а эти совы пролетают просто мимо.
До и после обучающего эксперимента испытуемым предлагалось диагностическое задание «Кубики» (рис. 3), спроектированное на основе картинки из учебника по математике для I класса (М.И. Моро).

Ученикам предлагались бланки, содержащие рисунок и текст задания: «Ученики составляли задачи по картинке и решали их. У них получились разные решения. Свои решения они объяснили так:
Ученик № 1. 3 + 3 = 6 (девочка поставила три кубика на три, получилось шесть).
Ученик № 2. 10 - 5 = 5 (было десять кубиков, из пяти дети построили башни).
Ученик № 3. 2 + 3 = 5 (мальчик взял два кубика и собирается поставить на них еще три, всего получится пять кубиков).
Отметь «+» правильное решение и «-» неверное».
Неверным является решение ученика № 1.
Были выделены три уровня выполнения диагностического задания данного типа:
низкий уровень - ученик выбирает вариант решения № 1 в качестве верного. То есть концентрируется на оперировании цифрами, а не соотносит их с сюжетной картинкой. Ученик не выделяет существенных отношений в условиях задачи и при анализе ее решений. Неверно сопоставляет условия задачи с сюжетной картинкой;
средний уровень - выбор в качестве правильного одного верного и одного неверного решения (№ 1 и № 2; № 1 и № 3). Данный уровень выполнения характеризуется наличием неустойчивой ориентировки на общие отношения в задаче и ее соотнесение с представленной моделью;
высокий уровень - выбор учеником двух верных решений (№ 2 и № 3). Данный уровень выполнения характеризуется ориентацией на существенные признаки, на общее отношение в задаче. Ученик соотносит модель, условия задачи и сюжетную картинку, т. е. осуществляет анализ условий их соответствия друг другу, проявляет рефлексию множественности условий задачи.
Результаты первого обследования, до проведения обучающего эксперимента представлены в табл. 1.
Таблица 1
Результаты выполнения задания «Кубики» в экспериментальной и контрольной группах (первое обследование)
|
Испытуемые |
Низкий уровень |
Средний уровень |
Высокий уровень |
|
Экспериментальная |
35 |
31 |
14 |
|
группа(80 человек) |
44 % |
39 % |
17 % |
|
Контрольная группа(88 |
36 |
37 |
15 |
|
человек) |
41 % |
42 % |
17 % |
Различия между группами по критерию t Стьюдента оказались незначимыми (р <= 0,05).
Результаты после проведения обучающего эксперимента представлены в табл. 2.
Таблица 2
Результаты выполнения задания «Кубики» в экспериментальной и контрольной группах (второе обследование)
|
Испытуемые |
Низкий уровень |
Средний уровень |
Высокий уровень |
|
Экспериментальная |
7 |
49 |
24 |
|
группа(80 человек) |
9 % |
61% |
30 % |
|
Контрольная группа(88 |
27 |
48 |
13 |
|
человек) |
31 % |
54 % |
15 % |
Различия между группами по критерию t Стьюдента оказались значимыми (р <= 0,001).
Результаты по методике «Кубики» существенно улучшились. Это позволяет сделать вывод, что присутствие в содержании учебной деятельности задач на метапредметное содержание может оказать положительное влияние на развитие умения анализировать условия задач и проявлять рефлексию множественности возможных решений поставленной задачи.
Таким образом, подтверждается валидность спроектированного диагностического задания «Кубики».
Рассмотрим другую диагностическую задачу (условное название «Вертолеты»; рис. 4).
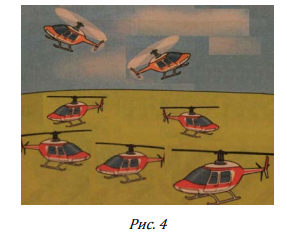
Задание предлагалось испытуемым в групповой форме на отдельных бланках, содержащих картинку и текст: «В одной школе учительница попросила учеников придумать задачи по этой картинке и решить их. У трех учеников получились следующие решения.
Ученик № 1. На аэродроме стояло 5 вертолетов, прилетело еще 2. Сколько вертолетов стало на аэродроме?
5+2=7
Ученик № 2. На аэродроме стояло 5 вертолетов, 2 вертолета пролетели мимо. Сколько вертолетов стало на аэродроме?
5-0=5
Ученик № 3. На аэродроме стояло 5 вертолетов, два вертолета улетело. Сколько вертолетов осталось на аэродроме?
5-2=3
Отметь «+» правильное решение и «-» неверное».
Неверным является решение ученика № 3.
В соответствии с общими критериями были выделены три уровня выполнения диагностического задания данного типа:
низкий уровень - ученик выбирает в качестве верного решение № 3. Это говорит об отсутствии ориентации на существенные отношения в задании. При данном уровне выполнения ученик оперирует цифрами, не соотнося их с содержанием сюжетной картинки;
среднийуровень - выбор учеником правильного и одного неправильного решения (№ 1 и № 3, № 2 и № 3). Средний уровень характеризуется неустойчивой ориентировкой на общие отношения;
высокий уровень - ученик выбирает правильные решения (№ 1 и № 2). На данном уровне выполнения ученик выделяет существенные признаки, производит соотнесение объекта и его модели, проявляет рефлексию множественности условий задачи.
Результаты до проведения обучающего эксперимента представлены в табл. 3.
Таблица 3
Результаты выполнения задания «Вертолеты» в экспериментальной и контрольной группах
(первое обследование)
|
Испытуемые |
Низкий уровень |
Средний уровень |
Высокий уровень |
|
Экспериментальная |
44 |
22 |
14 |
|
группа(80 человек) |
55 % |
28 % |
17 % |
|
Контрольная группа(88 |
57 |
18 |
13 |
|
человек) |
65 % |
20 % |
15 % |
Различия между группами по критерию t Стьюдента оказались незначимыми (р <= 0,05).
Результаты повторного тестирования, после проведения обучающего эксперимента приведены в табл. 4.
Таблица 4
Результаты выполнения задания «Вертолеты» в экспериментальной и контрольной группах
(второе обследование)
|
Испытуемые |
Низкий уровень |
Средний уровень |
Высокий уровень |
|
Экспериментальная |
53 |
12 |
15 |
|
группа(80 человек) |
66 % |
15 % |
19 % |
|
Контрольная группа(88 |
60 |
22 |
6 |
|
человек) |
68 % |
25 % |
7 % |
Различия между группами по критерию t Стьюдента оказались незначимыми.
Таким образом, в результатах выполнения задания «Вертолеты» до и после формирующего эксперимента не было обнаружено значимых различий, что может объясняться спецификой самого задания, которое в наибольшей степени связано с предметным материалом по математике, в частности с владением понятием «ноль».
При этом к концу обучающего эксперимента трудностей с применением нуля для описания действий персонажей картинки у учащихся не наблюдалось. Но поскольку истинного понимания нуля у учащихся не возникло, трудности с выполнением диагностического задания «Вертолеты» проявились снова в повторном тестировании.
Выводы. В стандартах общего образования решающая роль отведена содержанию образования, способам организации образовательной деятельности и учебного сотрудничества. Таким образом, основой учебного процесса становится организация коллективной мыслительной работы учащихся, а ее проектная часть представляет собой сценирование учебно-развивающих ситуаций [Гуружапов, 2012а; Марголис, 2010; Рубцов, 2010].
В основе проектирования учебно-развивающих ситуаций могут лежать способы анализа развивающих возможностей предметных задач и определение вариантов коллективного решения учениками этих задач на уроке, а умение анализировать условия задачи и рефлектировать множественность возможных решений поставленной задачи можно рассматривать как метапредметные образовательные результаты обучения. При этом мы предполагаем, что метапредметные компетенции тесно связаны с предметными: отсутствие предметных знаний затрудняет выполнение заданий метапредметного характера. Например, когда вводится такое сложное понятие, как «ноль», возникают определенные трудности в решении подобных заданий.
Предлагаемые нами диагностические задания могут быть использованы для оценки метапредметных образовательных результатов обучения младших школьников. Содержание задач в проведенном обучающем эксперименте может быть положено в основу проектирования развивающих образовательных ситуаций в начальной школе.
Литература
- Гуружапов В.А. К вопросу о соотношении психологической диагностики и коррекции учебной деятельности на уроках математики // Психологическая наука и образование. 2000. № 2. С. 79–85.
- Гуружапов В.А. К проблеме оценки метапредметной компетентности испытуемых [Электронный ресурс] // Психологическая наука и образование PSYEDU.ru. 2012. № 1. URL: http://www.psyedu.ru/journal/2012/1/2771.phtml (дата обращения: 28.12.2013).
- Гуружапов В.А. Учет множественности решений задач на развитие метапредметных компетенций в процессе сценирования учителем учебно-развивающих ситуаций // Психологическая наука и образование. 2012. № 1. C. 40–45.
- Гуружапов В.А., Шиленкова Л.Н. Умение анализировать условие задачи как метапредметный результат обучения [Электронный ресурс] // Психологическая наука и образование PSYEDU.ru. 2013. № 5. C. 53–60. URL: http://psyedu.ru/journal/2013/5/Guruzhapov_Shilenkova.phtml (дата обращения: 28.12.2013).
- Давыдов В.В. Проблемы развивающего обучения. М.: Издат. центр «Академия», 2004. 288 с.
- Давыдов В.В. Теория развивающего обучения. М.: Интор, 1996. 544 с.
- Зак А.З. Различия в мыслительной деятельности младших школьников. М.: Моск. психолого-социальный институт; Воронеж: Изд-во НПО «МОДЭК», 2000. 192 с.
- Как проектировать универсальные учебные действия в начальной школе: От действия к мысли: Пособие для учителя / Асмолов А.Г., Бурменская Г.В., Володарская И.А. и др.; под ред. А.Г. Асмолова. М.: Просвещение, 2008. 151 с.
- Марголис А.А., Рубцов В.В. Психолого-педагогическая подготовка учителя для новой школы // Психолого-педагогическое обеспечение национальной образовательной инициативы «Наша новая школа». М.: МГППУ. 2010. C. 68–91.
- Масленникова Л.Н. Опыт проектирования методик диагностики метапредметных компетенций младших школьников // Психологическая наука и образование. 2011. № 5. С. 14–20.
- Мониторинг учебно-предметных компетенций в начальной школе / Ред. П.Г. Нежнов, Б.И. Хасан. М.: Университетская книга, 2007. 112 с.
- Моро М.И., Волкова С.И., Степанова С.В. Математика. I класс: Учебник для общеобразоват. учреждений: В 2 ч. Ч. 1. М.: Просвещение, 2011. 127 с.
- Рубцов В.В., Марголис А.А., Гуружапов В.А. О деятельностном содержании психолого-педагогической подготовки современного учителя для новой школы // Культурно-историческая психология. 2010. № 4. C. 62–68.
- Соколов В.Л. Опыт диагностики анализа и рефлексии как универсальных учебных действий // Психологическая наука и образование. 2012. № 3. C. 29–33.
- Федеральный государственный образовательный стандарт общего (начального) образования. М.: Просвещение, 2011. 32 с.
- Flavell J.H. Metacognition and cognitive monitoring. A new area of cognitive-development inquiry // American Psychologist. 1979. Vol. 34. P. 906–911.
- Kesici S., Erdogan A., Özteke H.I. Are the dimensions of metacognitive awareness differing in prediction of mathematics and geometry achievement? // Procedia – Social and Behavioral Sciences. 2011. Vol. 15. P. 2658–2662.
- Panaoura A., Philippou G. The developmental change of young pupils’ metacognitive ability in mathematics in relation to their cognitive abilities // Cognitive Development. 2007. Vol. 22. Issue 2, June. P. 149–164.
- Schneider W., Artelt C. Metacognition and mathematics education // ZDM Mathematics Education. 2010. Vol. 42. P. 2 – 149.
- Stel M. van der, Veenman M.V.J. Development of metacognitive skillfulness: A longitudinal study // Learning and Individual Differences. 2010. Vol. 20. Issue 3, June. P. 220–224.
- Veenman M.V.J., Spaans M.A. Relation between intellectual and metacognitive skills: Age and task differences // Learning and Individual Differences. 2005. Vol. 15. Issue 2. P. 159–176.
Информация об авторах
Метрики
Просмотров web
За все время: 2377
В прошлом месяце: 28
В текущем месяце: 5
Скачиваний PDF
За все время: 948
В прошлом месяце: 11
В текущем месяце: 2
Всего
За все время: 3325
В прошлом месяце: 39
В текущем месяце: 7