Психологическая наука и образование
2021. Том 26. № 2. С. 66–77
doi:10.17759/pse.2021260206
ISSN: 1814-2052 / 2311-7273 (online)
Инициативная опора школьников на схемы в самостоятельном решении задач
Аннотация
Общая информация
Ключевые слова: учебная задача, моделирование, черновик, учебная проба
Рубрика издания: Психология образования
DOI: https://doi.org/10.17759/pse.2021260206
Благодарности. Автор благодарит за помощь в сборе данных для исследования В.Е. Адашева, Т.Н. Виноградову, М.Ю. Евтихову, В.Е. Зайцеву, Д.В. Кохановича, Д.И. Минкина, Т.В. Рубченко, А.Д. Фишер.
Для цитаты: Чудинова Е.В. Инициативная опора школьников на схемы в самостоятельном решении задач // Психологическая наука и образование. 2021. Том 26. № 2. С. 66–77. DOI: 10.17759/pse.2021260206
Полный текст
Введение
Вопросы моделирования в практике и теории обучения были подняты немногим более полувека назад в трудах отечественных психологов образования, а затем и в мировом психолого-педагогическом сообществе, и сегодня моделирование считается ключевым процессом в учении и обучении [Гальперин; Давыдов, 1996; Салмина, 1988; Эльконин, 1989; Acher]. В настоящее время еще продолжает существовать точка зрения на учебное моделирование лишь как на действие учителя, позволяющее представить изучаемое содержание для учеников так, чтобы они не искали способ решения задачи путем проб и ошибок [Palincsar; Salisu]. Но все больше практиков и исследователей говорят о том, что эффективность обучения растет, если детям предоставляется возможность моделировать самостоятельно [Айдарова, 1983; Давыдов, 1981; Рубцов; Эльконин; Acher; Effective Modelling —; Lehrer; Wouter].
Современные зарубежные исследователи и практики видят смысл учебного моделирования в начальной и основной школе преимущественно в приобщении детей к практике научного моделирования и тем самым развитии у них понятийного мышления. Обсуждается проблема соответствия научных и детских моделей, вопросы взаимодействия учителя с детьми для преобразования детских моделей и организации детского сообщества, занимающегося совместным исследованием [Acher; Lehrer; Wouter].
В концепции учебной деятельности Д.Б. Эльконина и В.В. Давыдова действие моделирования является центральным. Благодаря моделированию становится возможным выделение существенных отношений изучаемой школьниками предметной области [Давыдов, 1996; Давыдов, 1981]. При этом многолетние исследования проблемы учебного моделирования в рамках этой концепции свидетельствуют о том, что учебная модель не является копией или упрощенным вариантом исследовательской модели, существующей в некоторой предметной области науки: она специально создается коллективом разработчиков для решения задач обучения и развития детей. С другой стороны, учебная модель не является индивидуально-неповторимым порождением детского ума [Курганов, 2019] — она является, по замыслу разработчиков, некоторым культурным средством, которое должно быть в конечном счете присвоено ребенком [Давыдов, 1996; Давыдов, 1981].
Прослеживая «жизнь» учебной модели, можно выделить первый этап — этап ее разработки, или логико-предметный анализ: поиски ключевого отношения данной предметности и той знаковой (модельной) формы, в которой оно может быть фиксировано, сопровождающиеся пробами преобразования и испытания пригодности знаковой формы для ее функционирования в качестве учебной модели (логико-психологический анализ) [3; 10 и др.]. Особо следует отметить чрезвычайную важность характера знаково-символического представления и его своеобразие для каждой конкретной предметной области.
Вторая жизнь учебной модели начинается, когда она заново рождается группой (классом) совместно решающих учебные задачи учеников. Постановка учебной задачи и организация ее решения классом является задачей учителя, мастерство которого состоит в том, чтобы, зная все итоговые необходимости, дать ученикам возможность выстроить модель максимально самостоятельно. Учебная модель на этом этапе выступает для класса/группы учеников предметом построения, преобразования, испытания. Благодаря моделированию удерживаются и становятся предметом обсуждения важнейшие отношения предметной области, в модели фиксируется способ действия большого класса задач, модель обеспечивает понимание учениками учебных и других текстов в данной предметной области. Эти процессы довольно подробно рассмотрены и изучены в ряде работ [1; 3; 4; 7; 12; 14 и др.].
Значительно менее изученным является следующий этап «жизни» учебной модели. Переходя к другой предметной линии, ученики занимаются строительством иных моделей. Наступает время, когда прежняя, выстроенная классом для решения некоторых задач модель редко используется в учебной деятельности класса, но продолжает существовать в каком-то виде «в головах» учеников. Последователями Д.Б. Эльконина и В.В. Давыдова высказываются предположения о том, что для ученика переход от участия в построении, преобразовании и применении модели в совместной деятельности класса к ее использованию в качестве средства собственного действия не прост. Он связан с перефункционализаци- ей модели (Б.Д. Эльконин), обнаружением ее в качестве ресурса своего действия в учебных пробах (Е.В. Чудинова), построением функционального поля (П.Г. Нежнов) [Нежнов; Чудинова, а; Эльконин, 2010; Эльконин].
Описанное ниже исследование было предпринято для того, чтобы обнаружить следы существования учебной модели в «головах» учеников и оценить, насколько ученики склонны прибегать к моделированию в ситуации решения задачи, когда, с одной стороны, отсутствует внешнее требование действовать некоторым определенным образом, но с другой — сама задача «требует» моделирования. При подборе задач важно было, чтобы они не могли быть отнесены учениками к какому-либо типу, чтобы исключить формальный перенос знакомой схемы решения. Таким образом предполагалось достичь цели данного исследования: обнаружить и качественно описать явления самостоятельного и инициативного конструирования (реконструирования) модельных опор школьниками в ситуации отсутствия внешних требований к моделированию. Описание динамики инициативности и самостоятельности школьников в решении задач, на которых «не написан» способ их решения, важен не только с точки зрения развития теории учебной деятельности, но и в аспекте достижения практической цели современного образования — повышения уровня функциональной грамотности школьников.
Особенности формирования выборки
и метод
В предварительном исследовании приняли участие 160 шестиклассников из трех московских школ, обучавшихся по разным программам (традиционное обучение; гимназические классы с учениками, поступившими в 5 класс по конкурсу из разных школ; система Д.Б. Эльконина—В.В. Давыдова). Однако это не позволило увидеть картину возрастной динамики. Поэтому в основной части исследования приняли участие 508 учеников из 20 классов одной из московских школ (с 3 по 10 классы). Ученики третьих и четвертых классов этой школы обучались по системе Д.Б. Эльконина—В.В. Давыдова. Ученики 5—10 классов поступали в 5-ые классы из разных московских школ, то есть обучались до этого по разным программам.
Поскольку начиная с пятого класса в школе формировались разноуровневые классы, то обследование проводилось в двух разных по уровню классах параллели, чтобы увидеть весь диапазон возможных детских решений. Это обстоятельство, как и «добор» в пятые классы учеников из других школ, препятствовало проведению строгого количественного анализа данных, однако не мешало описанию предварительных наблюдений и проведению их качественного анализа.
Ученикам предлагалось решить по две задачи в текстовом формате (в двух вариантах)[Айдарова, 1983] в ходе урока не по предмету «математика». Обе задачи могли быть решены с использованием одной из первых и наиболее простых моделей, возникающих в учении, — модели числовой оси/числового луча, которая строится и начинает использоваться в первом классе. В ходе обучения по системе Д.Б. Эльконина— В.В. Давыдова модель числовой прямой последовательно строится классом под руководством учителя. Числовая прямая олицетворяет процесс измерения, фиксируя бесконечное «укладывание» мерки. В большинстве других программ начальной школы вводится близкое понятие числового луча.
На решение двух задач ученикам всех классов отводилось 10 минут. Это время вполне достаточно и зачастую избыточно для детей, многие из которых не склонны к тщательной работе и довольствуются первой мыслью, пришедшей в голову. Под текстом каждой задачи была заготовка для ответа, а рядом с ней свободное поле, на котором было написано «Место для черновика». Именно характер инициативного использования места для черновика в соотношении с правильностью решения задачи был предметом рассмотрения и анализа.
Проводящему работу была дана инструкция не произносить никаких дополнительных пояснений или указаний. В случае возникновения у ребенка вопроса о том, зачем на листе есть «Место для черновика», требовалось максимально нейтрально ответить: «Если тебе для решения нужно что-то нарисовать или написать, то это можно сделать здесь».
Эти задачи в определенных отношениях сходны. Обе характеризуются тем, что требуют для своего решения ясного представления ситуации, которое не складывается без моделирования во внешнем или во внутреннем плане. Обе задачи могут быть решены с опорой на модель числовой оси (числового луча), хотя этот способ решения не является единственным.


Анализ детских работ предполагал ответы на следующие вопросы:
• Используют ли ученики черновик для построения опор собственного действия?
• Какими знаково-символическими формами они пользуются?
• Какие попытки использования черновика можно квалифицировать как «самостоятельное построение модели»?
• Как соотносится использование черновика в целях решения задачи и успешность в ее решении?
Результаты
Предложенные задачи различаются, во-первых, тем, что задача про лифт выглядит проще и провоцирует более бытовое, житейское отношение к рассматриваемой ситуации, а задача про шкалы кажется более серьезной, научной. Может быть, именно это определяет среднюю решаемость задач: 31% правильных решений для первой и 40% для второй[Давыдов, 1996], — хотя объективно задача про шкалы труднее, так как обе мерки в первой задаче даны, а во второй их можно только построить или вычислить.
Рассмотрим способы решения учениками разных классов задачи № 1 (про лифт).
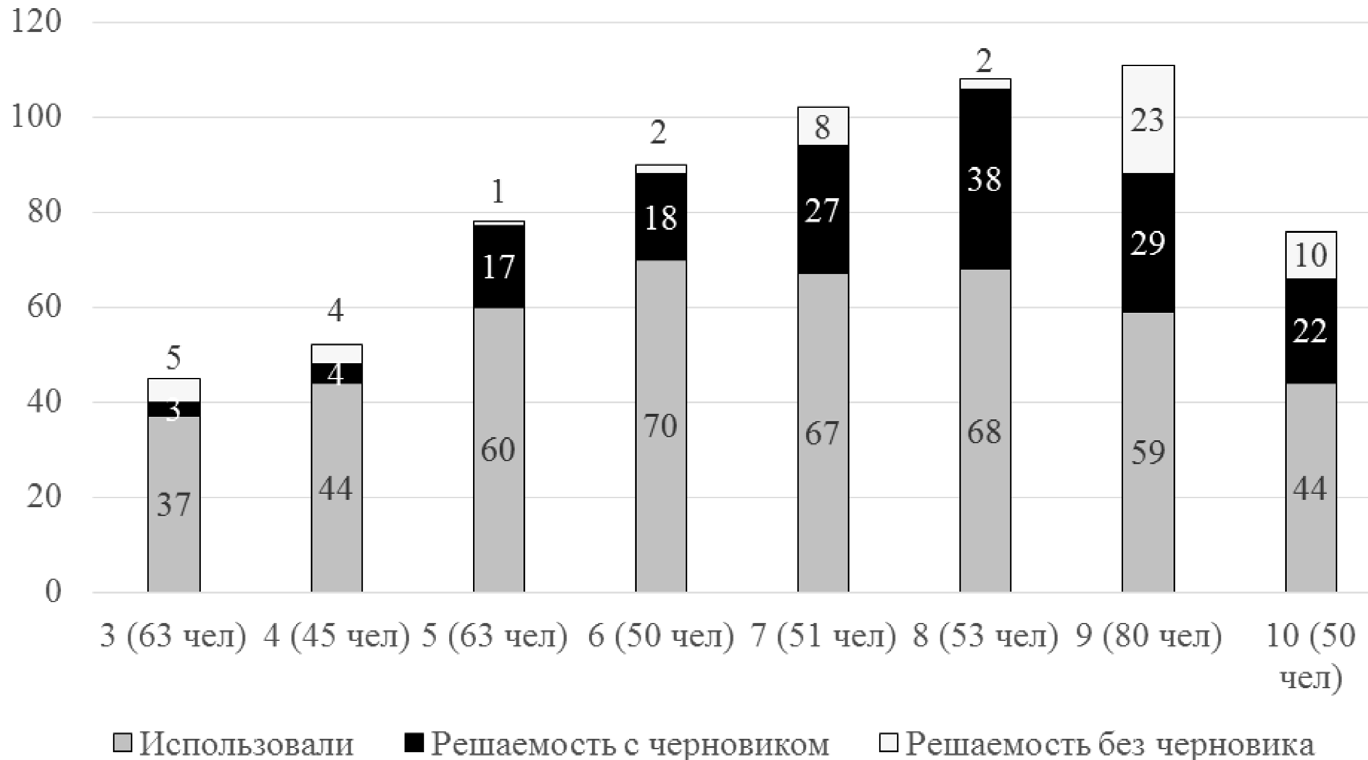
Рис. 1. Решение задачи № 1 (про лифт) учениками разных классов. По вертикальной оси — процент
учеников, использовавших место для черновика; процент учеников, верно решивших задачу
с использованием места для черновика; процент учеников, верно решивших задачу
без использования места для черновика
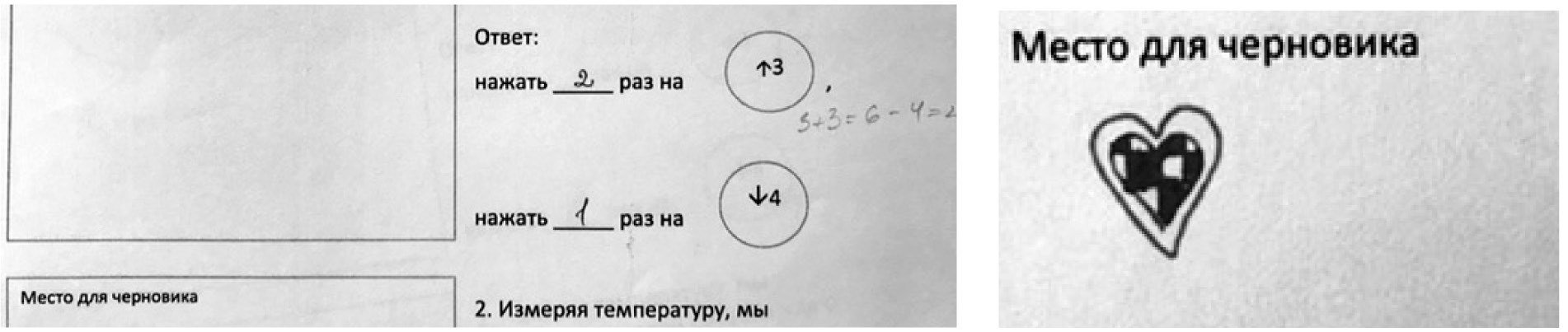
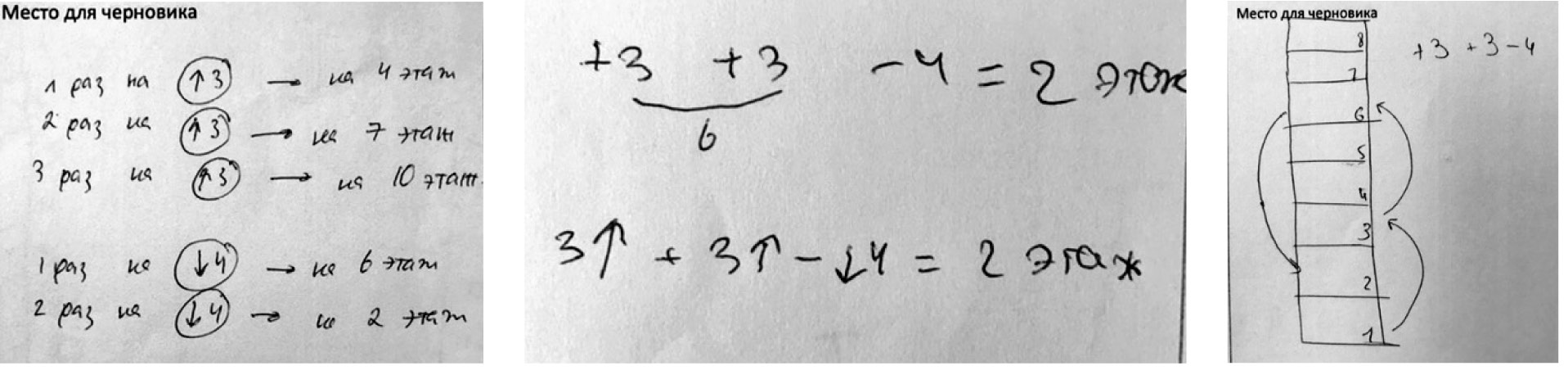
Рис. 4, 5, 6. Примеры неэффективной схематизации
По диаграмме видно, что количество учеников, пытающихся построить для себя какую-то опору и использовать ее для решения, возрастает от начальной к основной школе, но, начиная с пятого класса и до девятого, остается на уровне 60—70%. В девятом и особенно в десятом классе это количество уменьшается до 44%. По некоторым работам видно, что многие ученики старших классов считают использование черновика для решения такой простой задачи ниже своего достоинства: они стараются сделать минимальные записи и размещают их на полях работы, а не на специально выделенном месте, либо рисуют на месте для черновика не имеющее отношения к задаче изображение (см., например, рис. 2 и 3).
Использование черновика помогает найти верный ответ каждому десятому ученику начальной школы, примерно третьей части шестиклассников, более чем половине восьмиклассников. Таким образом, эффективность использования собственных построений существенно возрастает с годами. В 9—10 классах некоторые ученики начинают выполнять эти действия во внутреннем плане, прибегая иногда к проговариванию шепотом или жестикуляции, что отмечали наблюдатели, проводящие работу. Не прибегли к построению внешних опор 23% успешно решивших задачу девятиклассников против 1—8% учеников младших классов.
Вспомогательные «черновые» действия зачастую неэффективны в случаях, когда выбираются неадекватные средства схематизации, например, место для черновика служит для записи последовательных рассуждений в «полутекстовой» форме (рис. 4) или в форме математических вычислений (рис. 5).
Такая схематизация на самом деле просто отображает и фиксирует результат действий, которые совершаются «в уме». И это не позволяет ученикам заметить, что первый этаж в данном случае — это начало отсчета, ноль, а не единица на числовой оси. Иногда та же ошибка совершается в условиях, казалось бы, адекватной схематизации (см. рис. 6). Но изображенные стрелками «шаги» — этапы движения лифта — на самом деле оказываются разными, то есть мерка получается «резиновой»: первый подъем на 2 этажа, второй
подъем на 3 этажа. Это говорит о том, что решение задачи уже случилось «в уме» и на рисунке просто отображается то, что ребенку было очевидно до рисования. Иными словами, построение схемы не является в данном случае построением реальной опоры.
Умелость и тщательность рисования в данном случае не сказываются на эффективности построенной схемы. Вид «числовых прямых/лучей», построенных учениками, чрезвычайно разнообразен и никак не связан с годом обучения (см., например, рис. 7—10). Это говорит о том, что инициативное использование модели в качестве ресурса/средства собственного действия предполагает ее глубокую переработку, индивидуализацию и интеграцию в какие-то собственные знаковосимволические структуры.
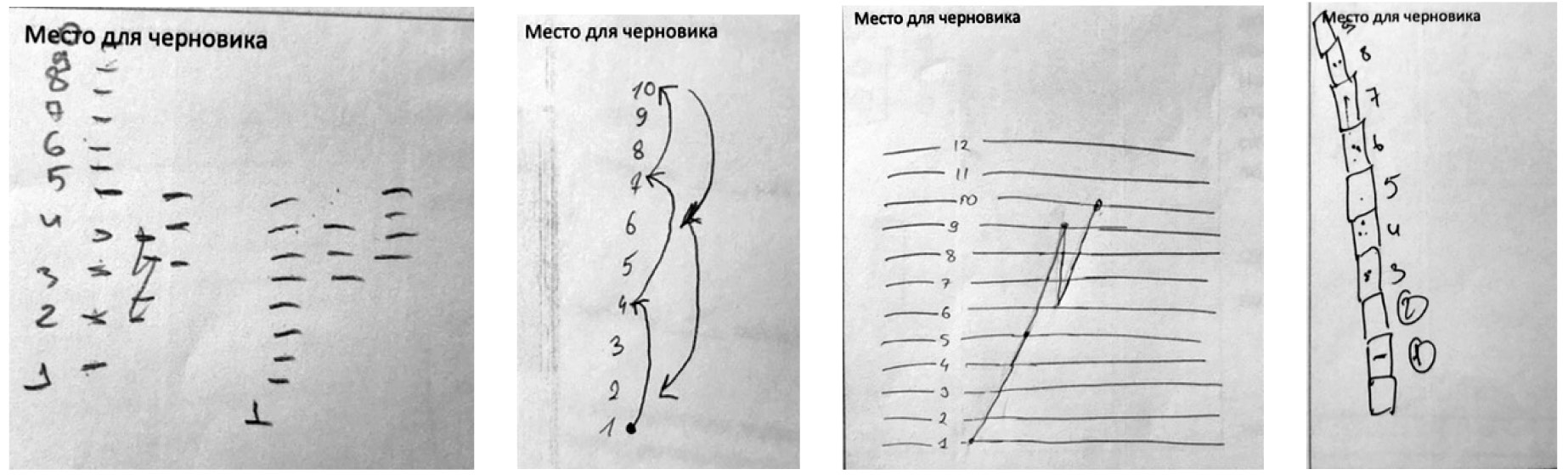
Рис. 7, 8, 9, 10. Разнообразие схем, построенных учениками в качестве опоры
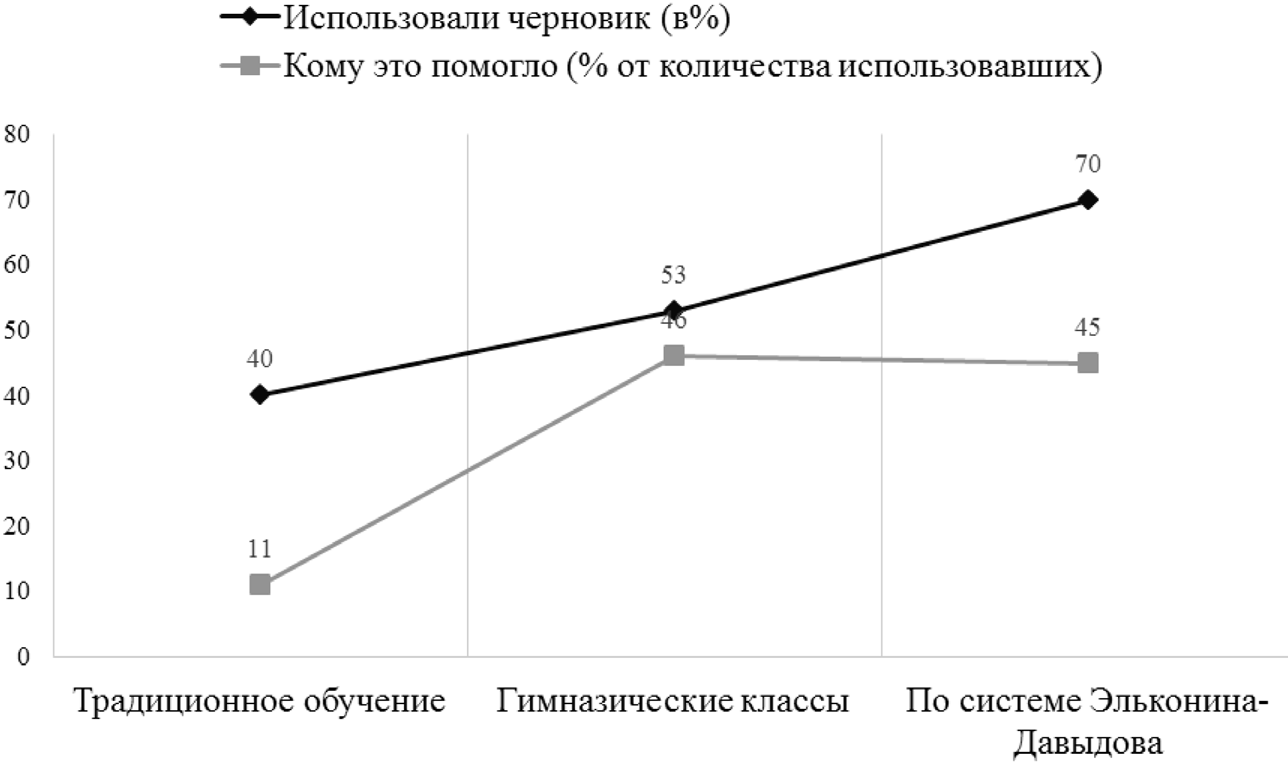
Рис. 11. Различия в работе учеников шестых классов, обучавшихся в разных школах: школа 1 — традиционное обучение; школа 2 — гимназические классы с учениками, поступившими в 5 класс по конкурсу из разных школ; школа 3 — обучение по системе Д.Б. Эльконина—В.В. Давыдова
В предварительном исследовании были задействованы шестые классы трех школ, что позволило увидеть качественные различия в работе учеников, обучающихся по разным программам (по два шестых класса из каждой школы, соответственно 56, 58 и 46 чел.). Эти различия видны совершенно явственно (рис. 11), но для получения строгих статистически достоверных результатов следует провести повторное исследование на более обширной выборке.
70% учеников шестых классов, обучающихся по системе Д.Б. Эльконина—В.В. Давыдова, пытаются рисовать схемы на месте для черновика, тогда как в традиционной школе таких попыток только 40%. Почти половине (45%) учеников, обучающихся по системе Д.Б. Эльконина—В.В. Давыдова, это помогает решить задачу верно, тогда как использование черновика учениками классов, работающих по другой программе, помогает примерно десятой части детей. Отобранные ученики-гимназисты занимают промежуточное положение по количеству использовавших черновик и делают это они столь же эффективно, как ученики классов по системе Эльконина—Давыдова (46%). Таким образом, инициативность в использовании черновика для построения опор в решении задачи почти в два раза выше, а эффективность его использования примерно в четыре-пять раз выше у учеников шестых классов, обучавшихся до этого времени по системе Д.Б. Эльконина—В.В. Давыдова. Они используют черновик столь же эффективно, как ученики, прошедшие по высокому конкурсу в гимназические классы.
Обратимся к анализу второй задачи (про шкалы). Она может быть решена наиболее простым способом через построение расположенных рядом двух числовых прямых/ лучей/отрезков с помощью разных мерок и непосредственное их соотнесение (см. пример такого решения на рис. 12). Единственная трудность такого решения — нужно быть аккуратным при разбиении одинаковых по величине отрезков на разное количество мерок. Важное условие решения — понимание самого способа деления отрезка на некоторое количество (4 или 5 примерно равных по длине частей). Ученики третьего и четвертого класса могут решить задачу именно так.
Для учеников пятых и более старших классов становятся доступны и другие способы решения: например, составлением уравнения, пропорции (см. рис. 13), которыми они начинают пользоваться. Эти способы постепенно к десятому классу полностью вытесняют «рисуночные» решения (рис. 14, 15). Лишь иногда можно наблюдать попытки рисования температурных шкал, предпринятые в основном для лучшего уяснения ситуации задачи, но сама задача решается при этом не более простым, рисуночным способом, а вычислительно-математическим.

Рис. 12. Решение задачи про шкалы путем построения двух числовых прямых
Рис. 13. Решение задачи про шкалы составлением пропорции
Рис. 14. Изображение шкал выполняется для лучшего уяснения ситуации задачи, а решение достигается вычислением
Со сменой способов решения, по-видимому, связано повышение решаемости задачи. Характерный быстрый рост случаев эффективного использования черновика можно наблюдать от пятого к седьмому классу, далее оно остается в пределах 60—75%.
Интересный эффект увеличения решаемости без черновика в размере 10—15% можно наблюдать примерно через год-два после освоения способа — от третьего-четвертого к пятому классу и от шестого к восьмому-девятому. Возможно, это свидетельствует о том, что освоение средства у некоторой части учеников завершается способностью использовать его, решая задачу во внутреннем плане. Очевидно, что для такого присвоения средства требуется продолжительное время.
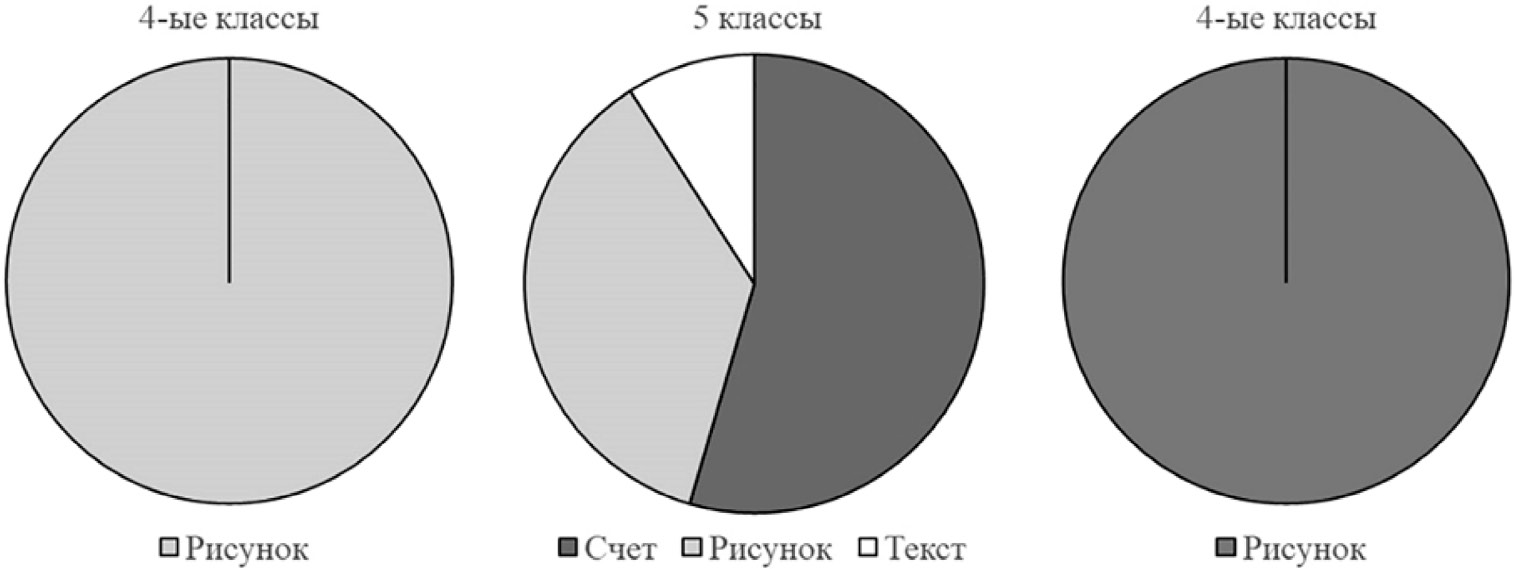
Рис. 15. Соотношение разных типов решений в разных классах
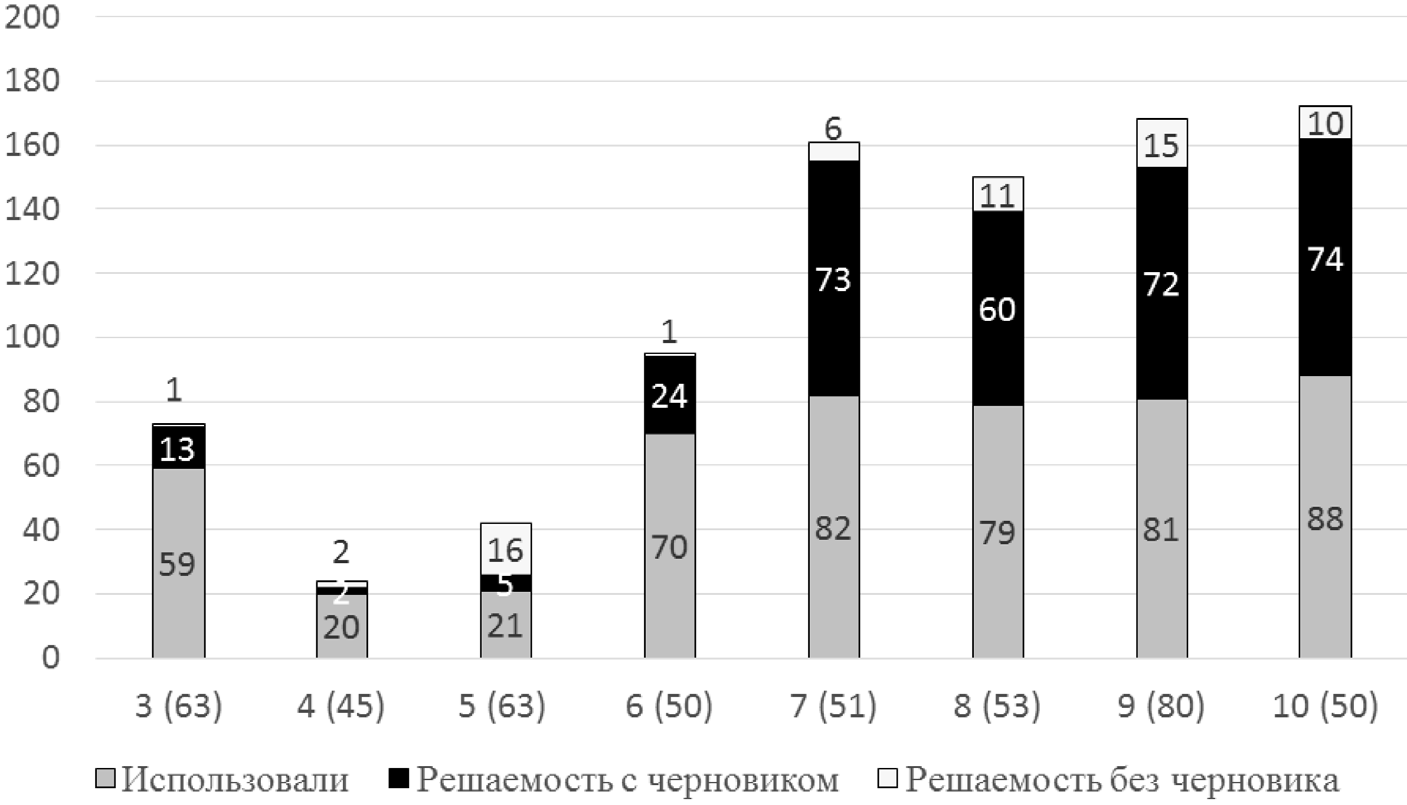
Рис. 16. Решение задачи № 2 (про шкалы) учениками разных классов.
По вертикальной оси — процент учеников, использовавших место для черновика; процент учеников, верно решивших задачу с использованием места для черновика; процент учеников, верно решивших задачу без использования места для черновика
Относительно высокий процент использования места для черновика и соответствующая более высокая решаемость задачи с использованием черновика у третьеклассников по сравнению с учениками четвертых классов может объясняться тем, что изучение темы «Измерение температуры» в курсе «Окружающий мир» происходило в конце второго года обучения, и этот материал был более «свежим» для третьеклассников.
Обсуждение
В практике современного образования вопрос о переносе приобретенного в школе знания в новые контексты является очень актуальным, особенно после обескураживающих результатов российских школьников в международном обследовании PISA. Доказано, что если задача квалифицируется учеником как относящаяся к какому-то «типу», то она значимо чаще решается «типичным, культурно-формальным» способом, однако если задача воспринимается как не относящаяся к какому-то типу, она значимо чаще решается способом подбора [Тюменева].
Проведенное исследование обнаруживает, что оказавшись один на один с новой задачей, не обусловленной прямым или контекстным указанием на способ ее решения, ученик не может решить ее с помощью формального переноса усвоенного средства/способа, но должен отыскать в себе то, что может послужить опорой, сконструировать (реконструировать/преобразовать) собственное средство и использовать выстроенные опоры для решения задачи. По-видимому, именно эти действия знаменуют собой окончательное присвоение учебной модели.
Результаты исследования показывают, что только часть учеников в начальной школе начинает инициативно использовать место для черновика, пытаясь выстроить опоры для решения задачи, однако их число возрастает в 5—7 классах. Первоначально эти попытки недостаточно эффективны, но постепенно к 7—9 классу эффективность использования черновика повышается. По-видимому, склонность прибегать к черновику для построения модельных опор собственного действия во многом определяется характером школьного обучения, объемом и характером учебного моделирования, разворачиваемого на уроках.
Эффективное самостоятельное использование черновика предполагает конструирование/реконструирование некоторой знаково-символической формы (чертежа, схемы, формулы и т.п.), которую ученик строит, опираясь на модели, выстроенные в совместном учении. Важно, что это реконструирование носит глубоко индивидуализированный характер, что свидетельствует о переосмыслении и преобразовании модели, переработке ее знаково-символической формы, «переводе» ее на свой язык.
Не все попытки инициативного использования учеником черновика можно квалифицировать как самостоятельное построение модели. Незначительная часть учеников использует черновик для посторонних целей, некоторые школьники, пытаясь выстроить опоры для решения, находят неадекватные средства, другие пользуются предоставленным местом для того, чтобы яснее представить условия задачи, но решение осуществляют «в уме». Часть учеников так и не начинает пользоваться черновиком, а к десятому классу некоторые ученики начинают «стыдиться» своего обращения к черновику. При этом очевидно, что использование черновика для построения опор в решении задачи существенно повышает вероятность верного решения.
Задачей исследователей и педагогов-практиков становится отыскание условий и организационных форм, в которых инициативное использование учениками черновика для конструирования (реконструкции) модельных опор собственного действия происходит не случайно, а систематически.
Основные итоги исследования
Можно зафиксировать следующие выявленные тенденции в качестве обоснованных гипотез:
1. После перехода из начальной в основную школу (к 6—7 классу) существенно возрастает количество инициативных обращений учеников к черновику для построения собственных опор в ходе решения задачи.
2. Примерно к этому же времени резко возрастает эффективность этих действий: попытки конструирования (реконструирования) схем, чертежей, формул, используемых в качестве моделей, чаще заканчиваются успешным решением задачи, чем оказываются безрезультатными.
3. Инициативность в использовании черновика для построения опор в решении задачи существенно зависит от характера обучения.
4. Характер использования черновика позволяет в большинстве случаев реконструировать способ действий ученика при решении задачи. Верное решение в большинстве случаев основывается на успешной реконструкции знаковосимволической формы: чертежа, формулы.
5. Реконструированные учениками средства-опоры чрезвычайно индивидуализированы, они не являются кальками тех схем, которые строились в классе. То есть, решая задачу, которую ученики не могут отнести к какому-либо классу, они строят собственные опоры, в чертах которых угадываются построенные ранее в классе модели. Видимо, инициативное использование модели в качестве ресурса/средства собственного действия предполагает действительное включение ее в глубоко индивидуализированные пласты жизненного опыта и преобразование, иногда почти до неузнаваемости.
Литература
- Айдарова Л.И. Маленькие школьники и родной язык.М.: Знание, 1983.95 с.
- Гальперин П.Я. О формировании умственных действий и понятий // Культурно-историческая психология.2010.Том 6.№ 3.С.111—114.
- Давыдов В.В. Теория развивающего обучения. М.: ИНТОР, 1996.544 с.
- Давыдов В.В., Варданян А.У. Учебная деятельность и моделирование. Ереван: Луйс, 1981.220 с.
- Курганов С.Ю. Ребенок и взрослый в учебном диалоге. Книга для учителя. М.: Образовательные проекты, 2019.250 с.
- Нежнов П.Г. Опосредствование и спонтанность в модели «культурного развития» // Вестник Моск.Ун-та. Серия 14, Психология.2007.№ 1.С.133—146.
- Рубцов В.В., Львовский В.А., Улановская И.М. Психологические особенности использования моделей при решении школьниками учебных задач // Новые исследования в психологии и возрастной физиологии.№ 2.1989.C.36—42.
- Салмина Н.Г. Знак и символ в обучении. М.: Изд-во Моск.ун-та, 1988.288 с.
- Тюменева Ю.А. и др. Что в заданиях PISA- математика мешает российским школьникам их выполнять [Электронный ресурс].URL: https://fioco.ru/Media/Default/Presentations/ТюменеваЮ.А..pdf (дата обращения: 26.11.2020).
- Чудинова Е.В. «Кухня» разработчика учебных курсов.Поиски модельной формы [Электронный ресурс].URL: https://n-bio.ru/content/kuhnya_ razrabotchika_uchebnyh_kursov_poiski_modelnoy_ formy (дата обращения: 24.11.2020).
- Чудинова Е.В. Учебная проба как проект и реальность в учебной деятельности подростков // Культурно-историческая психология.2017.Том 13.№ 2.С.24—30.DOI:10.17759/chp.2017130203
- Чудинова Е.В., Зайцева В.Е. Учебная модель как единица обучения и «зерно» развития // Культурно- историческая психология.2009.Том 5.№ 4.С.83—93.
- Эльконин Д.Б. Избранные психологические труды. М.: Педагогика, 1989.560 с.
- Эльконин Б.Д. Опосредствование. Действие. Развитие. Ижевск: ERGO, 2010.280 с.
- Эльконин Б.Д. Продуктивное Действие // Культурно-историческая психология.2019.Том 15.№ 1.С.116—122.DOI:10.17759/chp.2019150112
- Acher A. et al. Modeling as a Teaching Learning Process for Understanding Materials: A Case Study in Primary Education [Электронный ресурс].URL: https://gent.uab.cat/neussanmarti/sites/gent.uab.cat.neussanmarti/ files/20196_ftp.pdf (дата обращения: 12.11.2020).
- Constantinou C.P. et al. Framework for Modeling- Based Learning, Teaching, and Assessment [Электронный ресурс].URL: https://link.springer.com/chapter/10.1007/978-3-030-30255-9_3 (дата обращения: 10.11.2020).
- Effective Modelling — Chaucer School [Электронный ресурс].URL: http://www.chaucer.sheffield.sch.uk/images/schoolimprovement/tla/ modelling.pdf (дата обращения: 12.11.2020).
- Lehrer R. et al. Towards a Competence-Based View on Models and Modeling in Science Education [Электронный ресурс].URL: https://link.springer.com/chapter/10.1007/978-3-030-30255-9_13 (дата обращения: 10.11.2020).
- Palincsar A.S., Brown A.l. Reciprocal Teaching of Comprehension — Fostering and Comprehension — Monitoring Activities [Электронный ресурс].URL: https://people.ucsc.edu/~gwells/Files/Courses_Folder/ ED%20261%20Papers/Palincsar%20Reciprocal%20 Teaching.pdf (дата обращения: 25.11.2020).
- Salisu A., Ransom E. The role of modeling towards impacting quality education // International Letters of Social and Human Sciences.2014.Vol.32.P.54—61.DOI:10.18052/ILSHS.32.54
- Wouter R. et al. Drawing-Based Modeling in Teaching Elementary Biology as a Diagnostic Tool [Электронный ресурс].URL: https://link.springer.com/chapter/10.1007/978-3-030-30255-9_8 (дата обращения: 10.11.2020).
Информация об авторах
Метрики
Просмотров web
За все время: 841
В прошлом месяце: 33
В текущем месяце: 8
Скачиваний PDF
За все время: 293
В прошлом месяце: 13
В текущем месяце: 1
Всего
За все время: 1134
В прошлом месяце: 46
В текущем месяце: 9