Моделирование и анализ данных
2024. Том 14. № 1. С. 89–102
doi:10.17759/mda.2024140106
ISSN: 2219-3758 / 2311-9454 (online)
Моделирование деятельности экипажей при пилотировании воздушных судов
Аннотация
Рассматривается представление деятельности экипажа при пилотировании воздушного судна с помощью марковских цепей, включая моделирование в штатных и внештатных ситуациях с учетом опыта экипажа. Предложен способ оценки уровня опытности пилотов с использованием нейронной сети и алгоритм оптимизации матриц вероятностей переходов между состояниями модели. Приведены примеры моделирования для внештатной ситуации, демонстрирующие влияние уровня опытности пилота на итоговый результат.
Общая информация
Ключевые слова: моделирование, новизна полетной ситуации, Марковские цепи, Нейронная сеть
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2024140106
Получена: 18.03.2024
Принята в печать:
Для цитаты: Орищенко В.А., Грешников И.И. Моделирование деятельности экипажей при пилотировании воздушных судов // Моделирование и анализ данных. 2024. Том 14. № 1. С. 89–102. DOI: 10.17759/mda.2024140106
Полный текст
Введение
В процессе проектирования кабины экипажа воздушного судна повышенное внимание уделяется компоновке информационно-управляющего поля кабины (ИУП). Расположение компонентов ИУП кабины воздушного судна (ВС) и удобство считывания с них информации могут сыграть ключевую роль при пилотировании в критической лётной ситуации. Однако, учитывая имеющиеся данные о реальных полетах, невозможно учесть все латентные факторы, способствующие корректной деятельности пилотов. Имитационное моделирование поведения пилотов во время полетов является одним из удобных и доступных средств поиска оптимальных решений, связанных с построением ИУП.
При моделировании поведения пилотов целесообразно рассматривать конкретные ситуации, возникающие на борту ВС. Эти лётные ситуации могут быть инициированы независимо друг от друга, множество их экземпляров формирует результат выполнения данного полета.
Моделирование деятельности экипажа даёт возможность визуализировать его поведение во время полёта, включая взаимодействие с органами управления. Например, при вводе определённых данных, характеризующих лётный состав, можно в режиме реального времени наблюдать за тем, как пилот заданного уровня подготовки выполняет необходимые инструкции Руководств по лётной эксплуатации (РЛЭ), профессионально оценивая качество выполняемых действий, их своевременность и последовательность. На основании полученных оценок могут быть выявлены необходимые изменения в компоновке органов управления и интерфейсах штатных систем.
Математическая модель деятельности пилота согласно предписаниям РЛЭ может применяться для создания «виртуальных» пилотов, обеспечивающих выполнение предписаний РЛЭ ВС, оценки эффективности взаимодействия пилотов с различными вариантами информационно-управляющего поля кабины с целью принятия наилучших технических решений (включая валидацию перспективных кабин и комплексов бортового оборудования), а также для имитации деятельности пилотов/экипажей с различными уровнями профессиональной подготовки и различными психофизиологическими состояниями с целью выявления наилучших технических решений по формированию ИУП кабины ВС.
Математическая модель деятельности пилота
Деятельность пилота согласно предписаниям РЛЭ представляется марковскими процессами с дискретными состояниями и дискретным временем (марковскими цепями). В первую очередь, это обусловлено сложностью предметной области: реальный процесс пилотирования ВС находится под влиянием большого количества внешних и внутренних факторов, которые определяют поведение рассматриваемой системы. Характерная особенность марковских процессов, обусловленная влиянием только текущего состояния системы на ее будущее поведение, позволяет упростить модель без потери ее эффективности, избегая хранения значительного объёма данных об истории прохождения состояний.
Учитывая высокий темп появления событий внутри кабины экипажа во время полета (особенно при возникновении внештатных ситуаций) и необходимость оперативной реакции на них в режиме реального времени, применяется дискретная временная шкала. Полёт ВС делится на этапы, которым соответствуют различные сценарии. Сценарии представляют собой штатные и внештатные ситуации, поведение при возникновении которых регламентировано РЛЭ. Поскольку моделируется процедура выполнения (или невыполнения) пилотом регламентных инструкций, каждое из возможных состояний модели соответствует определённому шагу инструкции из РЛЭ.
Ошибки при выполнении инструкций выделяются в отдельные состояния модели. Перейдя в состояние ошибки, пилот обычно имеет возможность исправить ее, поэтому между состояниями, представляющими ошибки, и траекторией корректного выполнения инструкций имеются возможности переходов. Конечные ошибки, которые не позволяют модели положительно завершить сценарий, выделены в отдельные состояния.
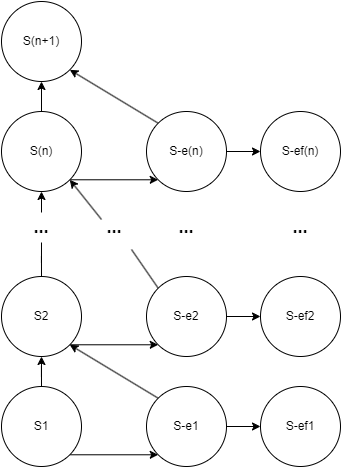
Ниже представлена общая структура марковской цепи, представляющая процедуру выполнения инструкций при возникновении штатной или внештатной ситуации (рис. 1).
Рис. 1. Марковская цепь для моделирования поведения пилота.
Данная модель представлена для сценария с n шагами. Состояния от S1 до Sn представляют предусмотренную РЛЭ деятельность пилота.
Состояние Sn+1 является конечным состоянием модели, соответствующим корректному завершению сценария.
Состояния от S-e1 до S-en представляют ошибочные действия пилота.
Состояния от S-ef1 до S-efn представляют конечные ошибочные состояния, когда сценарий или не завершен корректно и была допущена критическая ошибка, или целевое действие не было выполнено в течение приемлемого времени.
Вероятностная динамика переходов между состояниями представляется матричным уравнением:
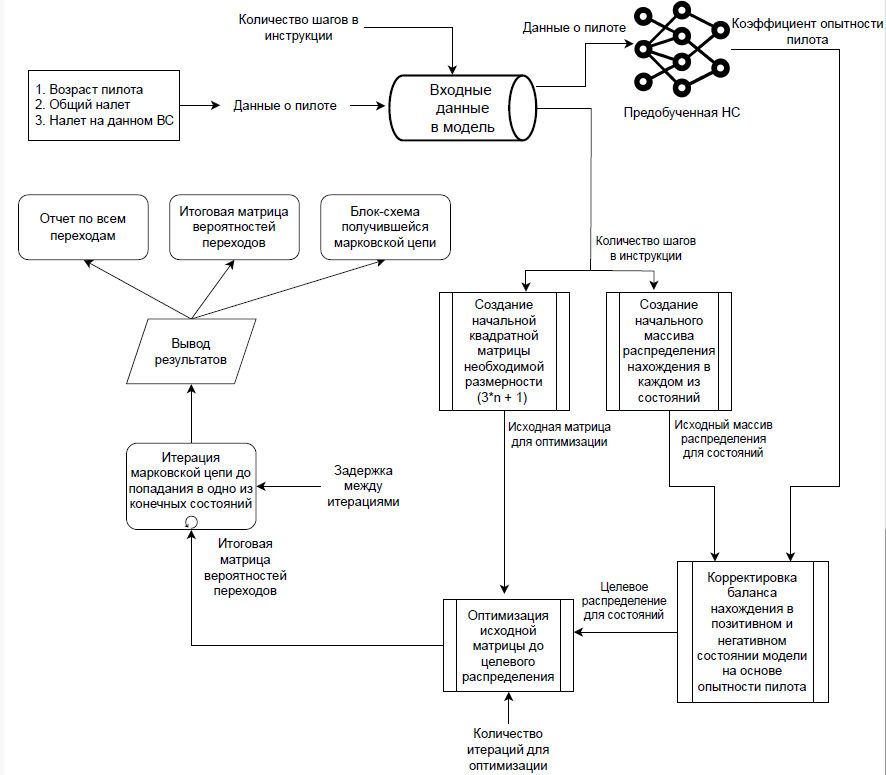
Компоненты процедуры, формирующей математическое представление деятельности пилота согласно предписаниям РЛЭ, представлены на рис. 2.
Рис. 2. Компоненты процедуры, формирующей математическое представление деятельности пилота согласно предписаниям РЛЭ
Для реализации различных вариантов поведения пилота, соответствующих различным уровням профессиональной подготовки, разработан алгоритм оценки опытности пилота воздушного судна, с помощью которого рассчитываются элементы матрицы вероятностей переходов.
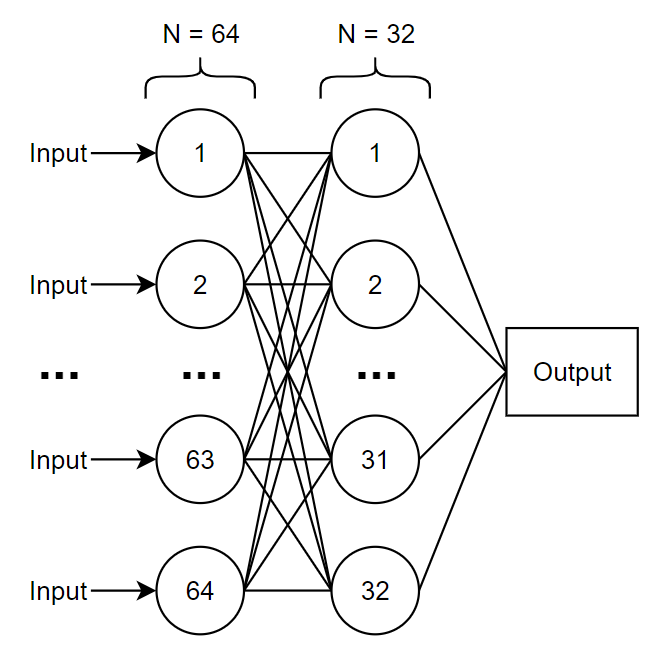
Этот алгоритм основан на использовании предобученного персептрона (рис. 3), который получает на вход данные о пилоте, включая его возраст, общий налет в часах, налет на данном воздушном судне. На выход нейронной сети поступает значение коэффициента опытности пилота в диапазоне от 0 до 1, где 0 - случай наименее опытного пилота (начинающий кадет), 1 - случай наиболее опытного пилота (имеющего более 10000 часов налета).
Рис. 3. Структура связей между элементами персептрона для получения коэффициента опытности пилота
Персептрон имеет 3 слоя (один - входной из 64 нейронов, один скрытый слой из 32 нейронов, один выходной слой с 1 нейроном). Данная сеть обучается на ограниченном наборе данных.
Матрицы вероятностей переходов между состояниями при различных психофизиологических состояниях экипажа и уровнях его профессиональной подготовки формируются, используя массивы времён пребывания в состояниях модели.
Исходный массив с временем нахождения для каждого состояния разделяется на две части: для положительных и отрицательных состояний модели (под положительными понимаются состояния, в которых корректно выполняются все инструкции сценария, под отрицательными - состояния промежуточных и конечных ошибок, предусмотренные моделью).
В зависимости от коэффициента опытности пилота происходит вычисление целевого коэффициента пропорции суммы первого массива ко второму (нахождения в благоприятных и отрицательных состояниях):
где Q - коэффициент опытности пилота, полученный из модели НС, C - коэффициент пропорции времени нахождения в положительных состояниях.
Полученный коэффициент отношения времён нахождения в положительных и отрицательных состояниях может принимать значение в диапазоне [0.5, 0.7]. Смещение значения этого коэффициента даже на одну сотую вносит существенный вклад в формирование итоговой матрицы вероятностей переходов.
После нахождения сумм для каждого из полученных массивов, содержащих информацию о нахождении в благоприятных и неблагоприятных состояниях модели, массивы нормируются. Результат представляет собой распределение выборочных оценок вероятностей нахождения в каждом из состояний модели, полученное на основе информации об опыте пилота.
Полученное распределение используется при оптимизации матрицы вероятностей переходов специальным алгоритмом, который итерационно преобразует первоначальную выборочную оценку матрицы вероятностей переходов так, чтобы приблизить определяемое этой матрицей стационарное распределение вероятностей пребывания в состояниях к указанному выше выборочному распределению [Kuravsky].
После получения итоговой матрицы вероятностей переходов проводится обход марковской цепи, при котором фиксируются все переходы за каждую итерацию. Полученный результат представляет одну инициализацию выбранного сценария для пилота определенного уровня подготовки. Данные сценарии могут быть объединены в процесс целого полета.
ПРИМЕР ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ДЛЯ СЦЕНАРИЯ С ОТКАЗОМ ДВИГАТЕЛЯ
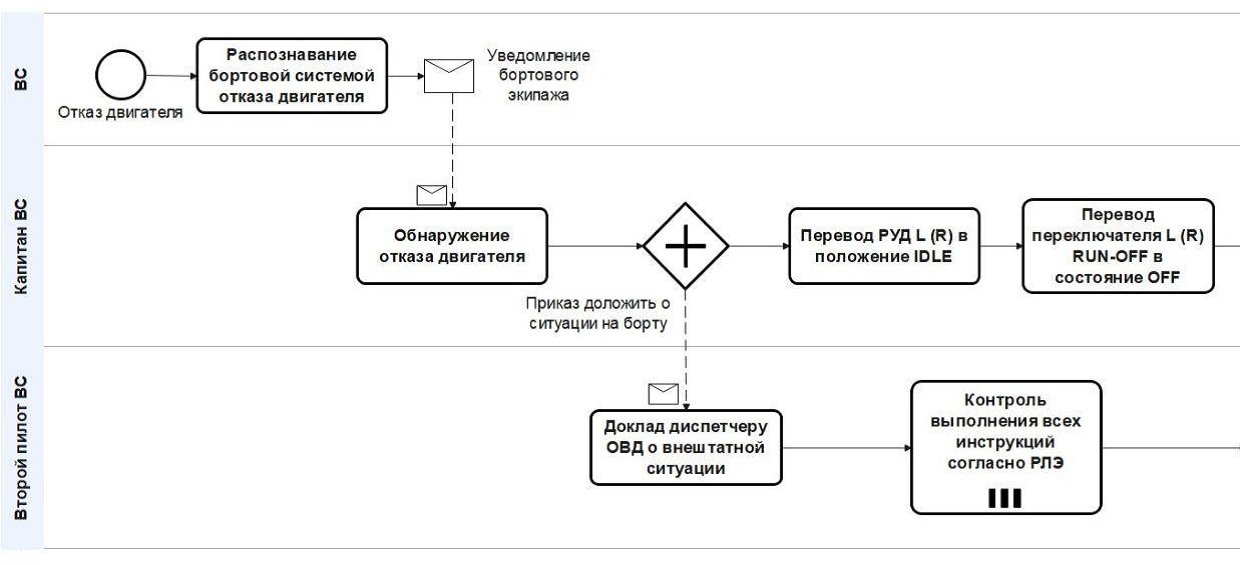
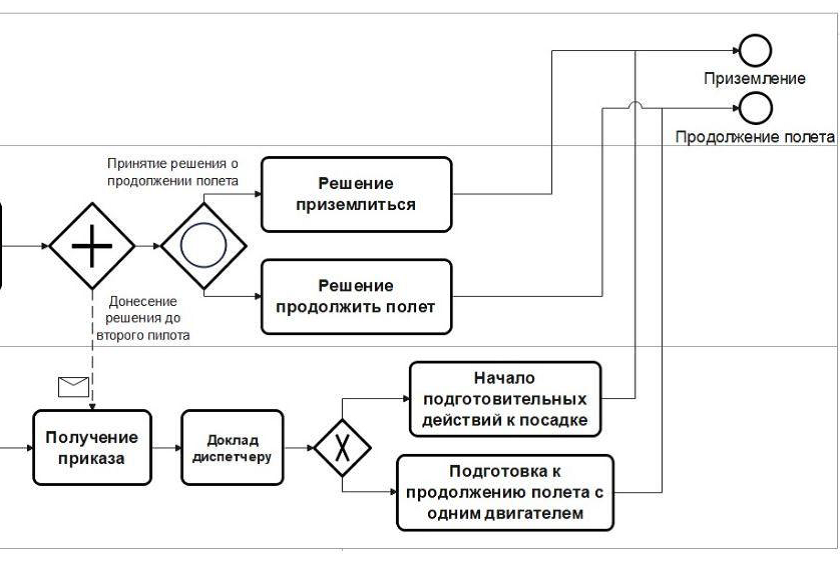
В качестве примера использован сценарий с отказом одного из двигателей во время полета самолёта MC‑21–300. Пилотирование ВС в случае данного сценария представлено в форме бизнес-процесса в нотации BPMN 2.0 (рис. 4).
Рис. 4. Схема бизнес-процесса для сценария “Отказ двигателя” в нотации BPMN 2.0.
Данный сценарий предполагает собой три целевых действия от пилотирующего экипажа: перевод РУД в положение IDLE, перевод переключателя RUN-OFF в состояние OFF, принятия правильного решения о продолжении полета.
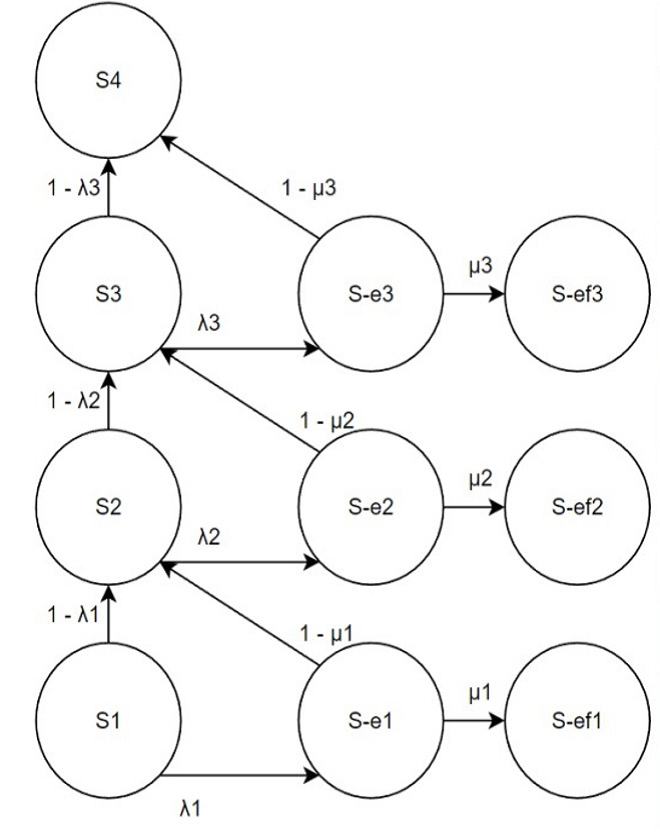
На основании данных трех действия построена модель марковской цепи для данного сценария (рис. 5).
Пример имитационного моделирования для сценария с отказом двигателя.
В качестве примера использован сценарий с отказом одного из двигателей во время полета самолёта MC-21-300. Пилотирование ВС в случае данного сценария представлено в форме бизнес-процесса в нотации BPMN 2.0 (рис. 5).
Рис. 5. Схема бизнес-процесса для сценария “Отказ двигателя” в нотации BPMN 2.0.
Данный сценарий предполагает собой три целевых действия от пилотирующего экипажа: перевод РУД в положение IDLE, перевод переключателя RUN-OFF в состояние OFF, принятия правильного решения о продолжении полета.
На основании данных трех действия построена модель марковской цепи для данного сценария (рис. 6).
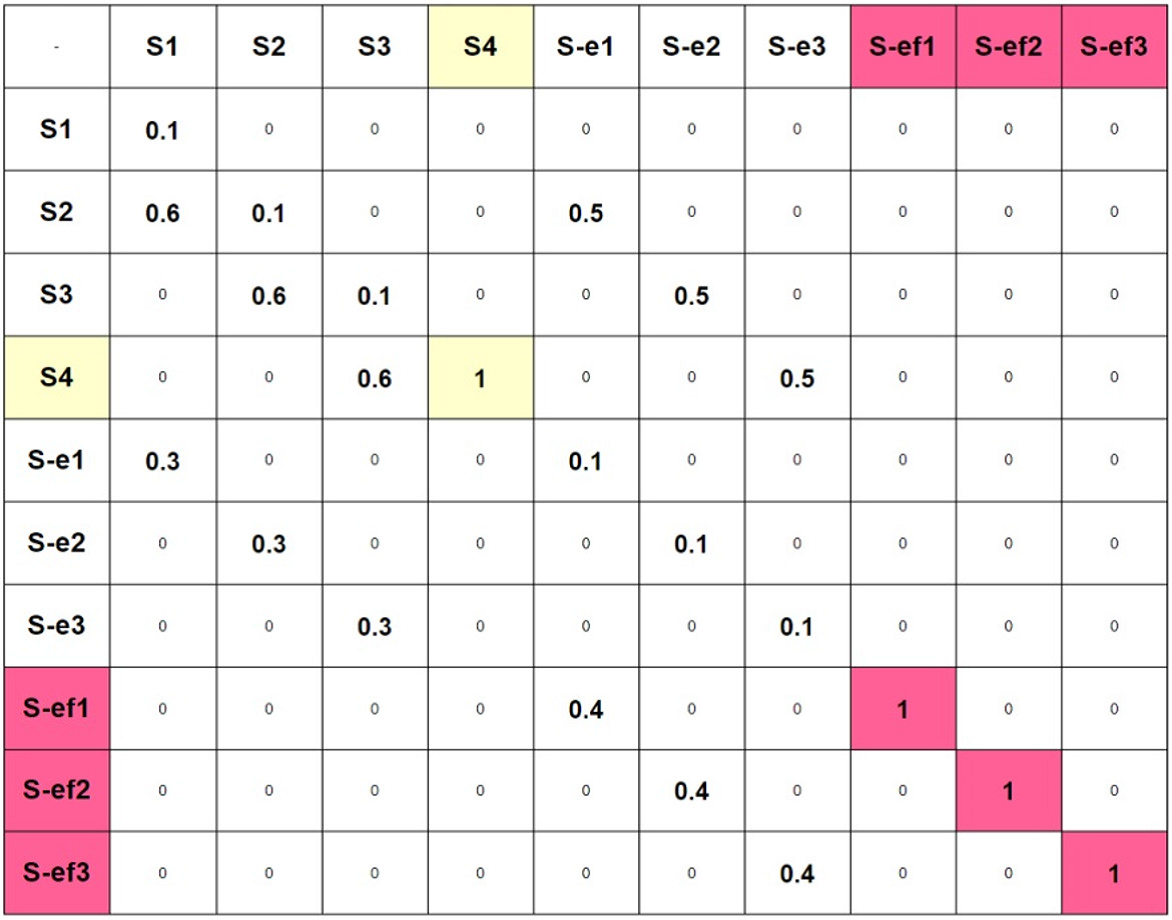
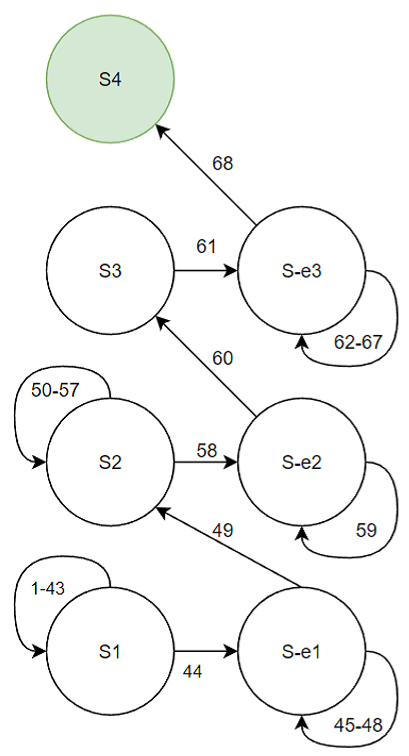
Рис. 6. Марковская модель для сценария “Отказ двигателя”
Для данного процесса была построена начальная матрица вероятностей переходов, с которой и происходят оптимизационные итерации (рис. 7). Фиолетовым цветом отмечены нежелательные конечные состояния модели (которые означают безуспешное завершение сценария). Желтым отмечено единственное конечное состояние модели, переход в которое означает успешное выполнение инструкций экипажем.
Рис. 7. Начальная матрица вероятностей переходов
Определённые элементы матрицы вероятностей переходов могут быть равны нулю или единице. Оптимизируются лишь те переходы, у которых вероятности лежат в диапазоне (0, 1).
Для проверки эффективности работы алгоритма получения итоговой матрицы вероятностей переходов с учетом опытности пилота воздушного судна выведем в рамках рассматриваемого сценария и сравним матрицы для пилота-новичка и опытного пилота.
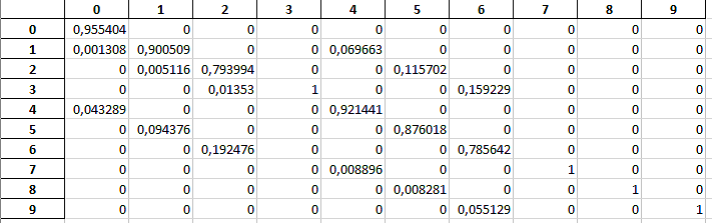
Для неопытного пилота будет использовать следующие входные данные (возраст - 23 года, общий налет - 200 часов, налет на данном типе ВС - 0 часов). Нейронная сеть выдала результат, приближенный к нулю. В таком случае получилась следующая матрица вероятностей переходов (рис. 8):
Рис. 8. Матрица вероятностей переходов для неопытного пилота
Как можно заметить по матрице - вероятности переходов в желательные состояния (например, из 0 в 1 или из 1 в 2) значительно ниже, чем в нежелательные (например, из 0 в 4 или из 1 в 5).
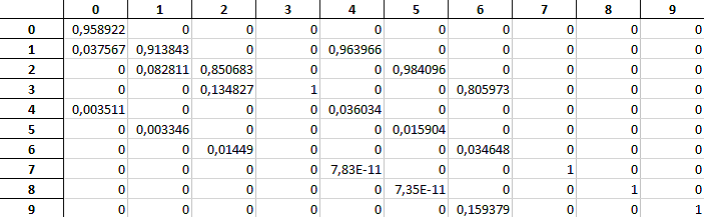
Рассмотрим теперь пример с наиболее опытным пилотом. В качестве входных возьмем следующие данные (возраст - 55 лет, общий налет - 15000 часов, налет на данном типе ВС - 5000 часов). НС выдал результат - единица. В результате получилась следующая матрица (рис. 9):
В данном случае получился существенно другой результат, что свидетельствует о том, что расчеты выполнены корректно. Однако, учитывая необходимую точность и чувствительность полученной системы, необходимо проводить дальнейшую калибровку всех коэффициентов внутри ПО, чтобы повысить точность модели.
Алгоритм успешно тестировался до сценариев, включающих до 33 шагов в инструкции (получается матрица вероятностей переходов размера 100х100). С другой стороны, если акцентировать внимание на возможные сценарии из РЛЭ, среднее количество шагов обычно не превышает 15. В таком случае механизм работает эффективно как по времени, так и по результату.
На рисунках 10-11 для сценария с отказом двигателя представлены марковские процессы, иллюстрирующие переходы между состояниями в демонстрационных вариантах поведения. Числа у стрелок показывают последовательности переходов между состояниями, включая переходы из состояний в самих себя. Очевидно, что в случае менее опытного пилота совершается значительно больше ошибок, и процесс обхода состояний включает значительно большее число шагов.
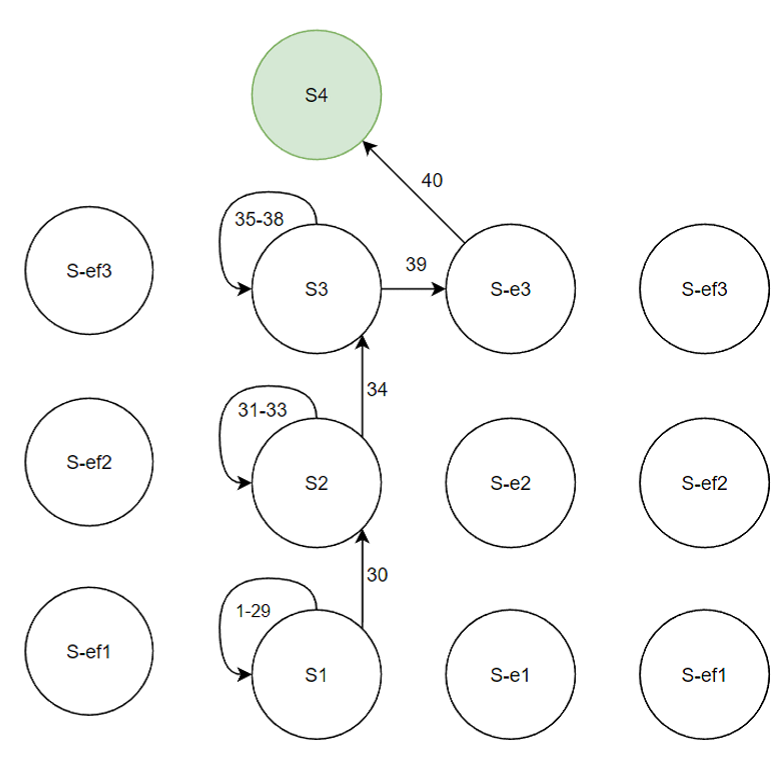
Рис. 9. Поведение при отказе двигателя в случае неопытного пилота: пример
Рис. 10. Поведение при отказе двигателя в случае опытного пилота: пример
Заключение
-
Разработана математическая модель деятельности пилота согласно предписаниям РЛЭ и программные средства для моделирования этой деятельности, построенные на её основе.
-
Математическая модель деятельности пилота согласно предписаниям РЛЭ применяется для решения следующих задач:
-
создание «виртуальных» пилотов, обеспечивающих выполнение предписаний РЛЭ ВС;
-
оценки эффективности взаимодействия пилотов с различными вариантами информационно-управляющего поля кабины с целью принятия наилучших технических решений (включая валидацию перспективных кабин и комплексов бортового оборудования);
-
имитация деятельности пилотов/экипажей с различными уровнями профессиональной подготовки и различными психофизиологическими состояниями с целью выявления наилучших технических решений по формированию информационно-управляющего поля кабины воздушного судна.
-
-
Математическая модель деятельности пилота согласно предписаниям РЛЭ представляется как марковский процесс с дискретными состояниями и дискретным временем. Полёт ВС делится на этапы, имеющие различные сценарии их выполнения. Сценарии представляют собой штатные и внештатные ситуации, поведение при возникновении которых регламентировано в РЛЭ. Каждое из возможных состояний марковского процесса соответствует определённому шагу выполнения инструкций РЛЭ.
-
Ошибки при выполнении инструкций выделяются в отдельные состояния модели. Перейдя в состояние ошибки, пилот, как правило, имеет возможность исправить её, поэтому допускаются переходы между состояниями, представляющими ошибки, и траекторией корректного выполнения инструкций РЛЭ. Конечные ошибки, не позволяющие положительно завершить сценарий, выделены в отдельные состояния.
-
Математическая модель деятельности пилота согласно предписаниям РЛЭ обеспечивает имитационное моделирование поведения пилотов во время полетов в терминах предписаний РЛЭ.
-
Рассмотренный подход может применяться при моделировании деятельности пилота как для отдельно взятых фрагментов полета, так и для полета в целом, позволяя оценивать поведение пилотов с различным уровнем профессиональной подготовки и опыта в рамках одного сценария.
Литература
- Lancaster P., Tismenetsky M. The Theory of Matrices: With Applications. Elsevier, 1985. 570 pp.
- Wilkinson J.H., The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1988).
- Cramer H., Mathematical Methods of Statistics. Princeton University Press, 1999. 575 pp.
- Г. Г. Амосов, “О марковских возмущениях группы унитарных операторов, ассоциированной со случайным процессом со стационарными приращениями”, Теория вероятн. и ее примен., 49:1 (2004), 145–155; Theory Probab. Appl., 49:1 (2005), 123–132
- Грешников И.И., Куравский Л.С., Юрьев Г.А. Принципы построения программно-аппаратного комплекса для интеллектуальной поддержки экипажа и оценки уровня его подготовки // Моделирование и анализ данных. Том 11. № 2. С. 5–30. DOI: 10.17759/mda.2021110201
- Parlett B.N., The Symmetric Eigenvalue Problem. Prentice-Hall, 1980. 348 pp.
- Куравский Л.С., Юрьев Г.А., Златомрежев В.И., Юрьева Н.Е. Оценка действий экипажа воздушного судна на основе модели рисков человеческого фактора // Экспериментальная психология. Том 13. № 2. С. 153–181. DOI: 10.17759/exppsy.2020130211
- Марковские модели в задачах диагностики и прогнозирования: Учеб. пособие. / Под ред. Л. С. Куравского. — 2-е изд., доп. — М.: Изд-во МГППУ, 2017. — 203 с.: ил. — ISBN 978–5–94051–168–7.
- G. Amosov. On Markovian Cocycle Perturbations in Classical and Quantum Probability. Int. J. Math. & Math. Sci., 2003 (54), 3443–3467 (2003).
- Куравский Л.С., Юрьев Г.А. Марковские модели адаптивного тестирования // Моделирование и анализ данных. 2011. Том 1. № 1. С. 28–40.
- Kuravsky L.S., Greshnikov I.I., Kozyrev A.D., Kosachevsky S.G., Frolova L.I., Zakharcheva A.A. “A mathematical model for representing the related operator professional activities and its relevant diagnostic assessment based on the quantum representations”, Lobachevskii J. Math., 45 (6), (2024) (в печати).
Информация об авторах
Метрики
Просмотров web
За все время: 203
В прошлом месяце: 18
В текущем месяце: 17
Скачиваний PDF
За все время: 61
В прошлом месяце: 7
В текущем месяце: 6
Всего
За все время: 264
В прошлом месяце: 25
В текущем месяце: 23