Экспертная оценка для формирования стохастических матриц поведения экипажа воздушного судна

В статье рассматривается методология экспертной оценки при формировании математической имитационной модели деятельности экипажа воздушного судна. Подход позволяет преобразовать целевой вектор времени нахождения в состояниях марковской цепи для более достоверной оптимизации матрицы вероятностей переходов. В подходе учитывается информация об относительной сложности и времени прохождения каждого из этапов ситуации согласно руководству по летной эксплуатации.

I.Моделирование поведения экипажа на борту воздушного судна

При проектировании кабины экипажа воздушного судна гражданской авиации инженеры уделяют особенное внимание компоновке информационно-управляющего поля (ИУП). Грамотное позиционирование и компоновка органов управления является одним из ключевых факторов для принятия правильных решений и осуществлению действий пилотов, особенно при возникновении серьезных внештатных ситуаций, требующих незамедлительного и верного решения. Для эффективной компоновки ИУП необходимо большое количество данных о реальных полетах, известных авиакатастрофах, вовлечение достаточного количество опытных пилотов с достаточным налетом на воздушных суднах такого типа. Не всегда это является возможным, что может быть причиной временных задержек в проектировании или в недостаточно качественном результате.

Одним из вариантов решения подобной задачи является создание математических и прикладных инструментов, которые могут заменить использование реальных данных. Создание «виртуального пилота» может существенно улучшить процесс проектирования воздушного судна не только в рамках компоновки ИУП, но и в других инженерных задачах, например, создание вспомогательных авиационных систем корректировки воздействия на органы управления и др. Также «виртуальный пилот» может быть эффективен в вопросе создания авиационных тренажеров, формированию дополнительных программ подготовки экипажа.

В рамках предыдущей работы была разработана математическая модель и сопутствующее программное обеспечение для имитационного моделирования поведения экипажа при пилотировании воздушного судна [Орищенко, 2024]. Данное решение позволяет эффективно и с приемлемыми временными затратами оценивать действия экипажа при возникновении штатных и внештатных ситуаций на борту воздушного судна согласно сценариям из руководства по летной эксплуатации (РЛЭ).

II.Математическая модель деятельности пилота 

Основой математической модели деятельности пилотов является Марковский процесс с дискретным временем и дискретным состоянием (Марковская цепь). Этот выбор обусловлен относительной простотой восприятия связи работы полученной модели с реальными действиями на борту, небольшим количеством требуемых данных для имитационного моделирования, а также несущественными требованиями к вычислительным ресурсам.

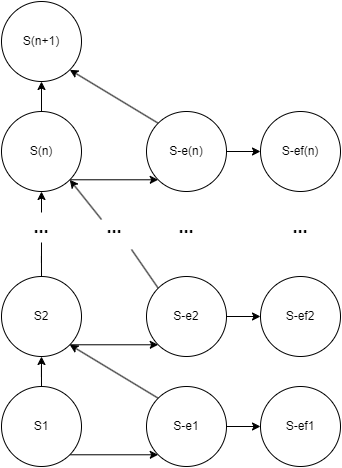
Каждая штатная или внештатная ситуация на борту представляется в виде сценария, в котором каждое целевое действие, согласно РЛЭ, представляет собой уровень (кластер). Нахождение на уровне N в сценарии подразумевает, что на данный момент у экипажа воздушного судна стоит задача в выполнении действия N из РЛЭ в рамках текущей штатной/внештатной ситуации. Для каждого сценария формируется своя Марковская цепь со своей матрицей вероятностей переходов (МВП) на основании вводных данных в модель.

 

Рисунок 1. Модель Марковской цепи поведения пилотов для сценария с n шагами.

III.Процесс формирования матриц вероятностей переходов для марковской цепи 

Матрица вероятностей переходов формируется путем итерационной оптимизации исходной стохастической матрицы к целевому вектору распределения времени нахождения в каждом состоянии. Именно от целевого вектора зависит итоговая МВП, которая и определяет качество поведения полученной модели.

Целевой вектор распределения формируется в зависимости от сложности выполнения каждого из шага сценария, а также частоты ошибок для каждого кластера. Вектор нахождения в каждом состоянии формирует эксперт (подробнее в главе 4). После изменения вектора в соответствии со сложностью выполнения каждого из действий он корректируется в соответствии с уровнем подготовки пилота, который получается с помощью предобученной нейронной сети на основании возраста, общего налета в часах, налета в часах на данном типе воздушного судна. В зависимости от коэффициента опытности пилота происходит вычисление целевого коэффициента пропорции суммы первой части вектора ко второй (нахождению в состояниях благоприятных и нежелательных состояниях):

IV.Экспертная оценка сложности и времени выполнения конкретных этапов сценариев РЛЭ 

Так как на итоговую МВП наибольшее влияние имеет целевой вектор распределения, то качество его формирования и определяет итоговое поведение пилота. В соответствии с этим от экспертной оценки зависит итоговое качество имитационного моделирования.

Для проведения достоверных и информативных исследований поведения экипажа эксперту необходимо обладать достаточным опытом в пилотировании воздушным судном (возможно в рамках полетов на авиационных тренажерах), включая знания обо всех значимых органах управления, работе информационных и управляющих системах на борту, поведении воздушного судна в разных условиях эксплуатации (включая внештатные). Также немаловажным фактором является понимание о психофизиологическом состоянии пилотов в разных состояниях и этапах полета, а также о взаимодействии экипажа друг с другом и о внешней коммуникации с диспетчерским центром. Указанные навыки и знания позволят эксперту с высокой долей достоверности определять сложность выполнения конкретных действий в рамках сценариев РЛЭ.

При необходимости моделирования нескольких сценариев оценка должна быть проведена для каждого из сценариев отдельно, предпочтительно, если она будет проведена одним экспертом для одного полета. Полученный набор исходных данных для моделирования в рамках нескольких сценариев может быть использован для имитации конкретных фрагментов полета, которые в совокупности могут отражать результат моделирования целого полета.

Основными входными данными оценки являются:

• Массив оценок сложности выполнения каждого из шага рассматриваемого сценария;

• Время, которое необходимо пилоту среднего уровня подготовки в нормальном состоянии, для завершения всего сценария;

• Массив соотношения среднего времени нахождения в каждом из кластеров;

• Ограничение по времени выполнению сценария (если оно имеется).

В рамках массива с оценками сложности каждого шага принимается массив из N элементов (для сценария с N шагами). Каждый элемент массива обозначает оценку сложности по шкале от 1 до 100, где 1 обозначает отсутствие всяких трудностей, а 100 – наиболее сложный шаг в сценарии (рис. 2). С помощью данной оценки можно классифицировать шаги в сценариях на 4 группы (легкие <25 баллов, умеренной сложности 25–50 баллов, сложные 50–75 баллов, очень сложные 75–100 баллов). При оценке рядовых и штатных ситуаций сложности будут находиться преимущественно в первых двух по сложности секциям шкалы. Для внештатных случаев, особенно для ситуаций, сопряженных с попаданием в сложные пространственные положения, требующих немедленного принятия решений, оценки будут находиться преимущественно в правой части шкалы. Таким образом получается массив из «сырых» баллов по сложности.

 

Рисунок 2. Шкала "сырой" оценки сложности

Элементы данного массива нормируются, на выходе получается массив с коэффициентами сложности, сумма всех элементов которого равна 1.

На основании заданного среднего времени формируется отношение времени нахождения в конечном успешном состоянии цепи к сумме времен нахождения во всех остальных состояниях. По умолчанию в модели указано значение для сценария с N-шагами равное 7N секунд, то есть, время нахождения в каждом кластере в среднем составляет около 7 секунд. Для более быстрых и, наоборот, тяжелых, значения могут сильно варьироваться, все зависит от экспертной оценки.

Формирование массива среднего времени для каждого из кластеров Марковской цепи происходит по аналогии с оценкой сложности – в формате оценки 100 бальной шкалы, где 1 – минимальное время, 100 – максимальное время. Далее массив нормируется аналогичным образом до суммы элементов массива, равной 1.

Первоначальный вектор для сценария с N-шагами в первую очередь преобразуется в соответствии со средним временем выполнения сценария по заданной экспертом информации. После этого вектор, который имеет одинаковое конечное распределение между кластерами (кроме состояния успешного выполнения всего сценария), преобразовывается в соответствии с нормированным массивом весов сложности каждого шага сценария.

Преобразование происходит путем обработки сначала соотношения между распределением времени внутри одного кластера между положительными, промежуточными и отрицательными состояниями (в соответствии с заданной оценкой сложности выполнения действий), а затем соотношением времени нахождения между кластерами (в соответствии с заданной оценкой длительности действий на этом кластере).

После всех итераций получается итоговый целевой вектор распределения, с помощью которого и происходит итерационная оптимизация матрицы вероятностей переходов [Орищенко, 2024], которая в таком формате будет учитывать информацию о сложности выполнения отдельных фрагментов, о длительности относительно друг друга, а также об общем времени выполнения сценария.

Стоит отметить, что в силу ограничений, связанных с отсутствием приемлемого количества эмпирически данных, итоговые коэффициенты корректировки целевого вектора распределения времени нахождения в состояниях могут быть изменены. Это требует большего количества экспериментов в реальных прикладных задачах.

V.Примеры корректировки сценариев в соответствии с их сложностью

В рамках имитационного моделирования рассмотрим сценарий с отказом одного из двигателей. В рамках данного сценария представлено 3 требуемых действия, соответственно, модель марковской цепи состоит из 4 кластеров.

Требуемые шаги в соответствии с руководством по летной эксплуатации (РЛЭ):

• Перевод РУД L (R) в положение IDLE

• Перевод переключателя L (R) RUN-OFF в состояние OFF

• Принятие решения о продолжении полета

Если рассматривать каждый шаг отдельно, становится очевидным, что первые два действия не являются сложными к выполнению, так как являются рядовыми и не требуют серьезной подготовки. Ключевым моментом будет выявление неисправности, координация верного порядка действий согласно РЛЭ. Учитывая указанные обстоятельства, а также то, что возникновение данного сценария является внештатной ситуацией, хоть и первые два действия имеют примерно одинаковую сложность, но для перевода РУД неисправного двигателя стоит задать сложность выше.

Так как по методологии имитационной модели мы учитываем состояния строго согласно РЛЭ, предшествующие действия не могут напрямую формировать кластеры состояний. Поэтому для внештатных ситуаций необходимо закладывать сложность всех подготовительных процессов (обнаружение внештатной ситуации на борту, поиск необходимого алгоритма действий в РЛЭ, координацию движений между экипажем воздушного судна) в сложность выполнения первого целевого действия. В случае со сценариями, предусмотренными штатными ситуациями, не требуется существенно закладывать сложность подготовительного этапа в первый кластер, однако, это всегда возможно и остается на решении эксперта, оценивающего сценарий.

Если говорить про шаг сценария, связанный с принятием корректного решения о продолжении полета, очевидно, что это действие является более сложным и важным, так как требует всесторонней оценки текущего состояния воздушного судна, этапа полета, показателей остальных авиационных систем, а также достаточной опытности в пилотировании воздушного судна, в том числе при возникновении внештатных ситуаций. Исходя из этого можно с уверенностью говорить, что сложность выполнения данного действия существенно выше, чем для предыдущих двух действий.

С точки зрения выполняемого времени можно предположить, что данный сценарий для пилота среднего уровня подготовки будет выполнен примерно за t = 25 с (при базовом среднем уровне выполнения сценария с 3 шагами, равном 21 секунда). Ограничение по времени для данного сценария может быть установлено в размере 50 секунд.

К примеру, исходный вектор распределения:

после осуществления всех итераций приобретает следующий вид:

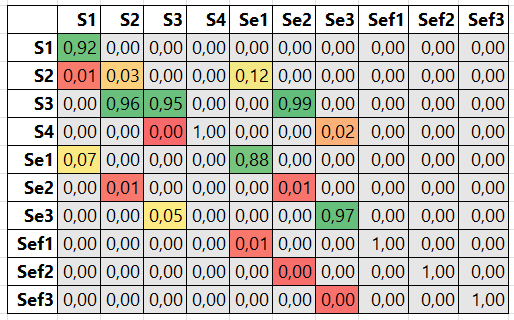
Матрица вероятностей переходов (рис. 3) для полученного вектора распределений выглядит следующим образом (серым выделены переходы, вероятности которых равно либо 0, либо 1, которые не изменяются в процессе оптимизации матрицы):

Рисунок 3. МВП для сценария с отказом двигателя.

Рассмотрим в качестве примера другой сценарий, связанный с отказом автоматической коррекции механизации крыла. Данный сценарий требует выполнения 4 целевых действий, марковская цепь будет состоять из 5 кластеров.

Список рассматриваемых действий:

• Переход на ручное управление

• Определение исправного ADS

• Ручной контроль эксплуатационных ограничений

• Посадка воздушного судна

В контексте текущего сценария начальное состояние также предполагает определенную предварительную подготовку, соответственно, это стоит учитывать в формировании сложности первого кластера. Однако в отличии от предыдущего сценария, в случае с отказом механизации нет односложных действий, которые экипаж выполняет на постоянной основе на борту. Сам по себе переход на ручное управления существенно сложнее, чем перевод ручки управления двигателем, так как предполагает постоянное управляющее воздействие на воздушное судно, а также непрерывную и качественную координацию действий экипажем.

Определение исправного ADS представляет собой более простое действие, но все же требующее определенной умственной нагрузки.

Ручной контроль эксплуатационных ограничений является сложной задачей, особенно в стрессовых условиях экипажа, тем более что контроль ограничений будет осуществляться до окончания полета.

Конечным действием является посадка воздушного судна. Сам процесс посадки является непростым и требует значимых усилий. Все это особенно усложняется техническими ограничениями, связанными с отказом механизации крыла, а также необходимостью полного ручного управления. Поэтому можно сделать вывод, что посадка в контексте рассматриваемой ситуации будет наиболее сложным действием, даже в сравнении со сценарием посадки в штатном режиме. Именно поэтому и необходимо оценивать каждый сценарий отдельно, учитывая контекст возникающей ситуации.

С точки зрения среднего времени выполнения сложно достоверно оценить конкретную ситуацию, так как есть множество влияющих на это факторов, например, высота воздушного судна в момент принятия решения об аварийной посадке, наличие возможных аэродромов поблизости. В соответствии с этими ограничениями будем имитировать процесс посадки в контексте выполнения всех необходимых для этого действий, не дожидаясь окончания приземления. Пусть весь сценарий в среднем будет занимать 90 секунд.

Ограничение по времени в рамках данного сценария задавать не будем, потому что из-за предполагаемой длительности фактическое время инициализации имитационной модели может сильно варьироваться от целевого.

На основании указанных значений оценок начальный вектор распределения следующего вида:

[0.20, 0.20, 0.20, 0.20, 7.00, 0.10, 0.10, 0.10, 0.10, 0.80, 0.80, 0.80, 1.40]

после преобразований приобретает следующий вид:

[0.35, 0.17, 0.44, 1.55, 2.18, 0.35, 0.17, 0.44, 1.55, 0.08, 0.04, 0.08, 0.57]

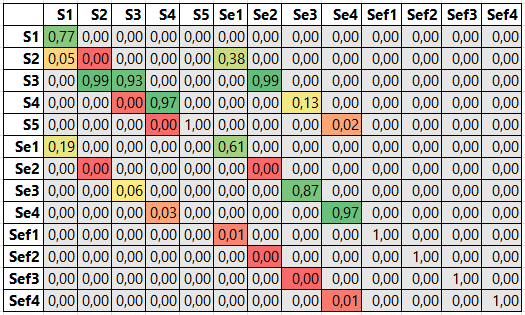
После процесса оптимизации получается следующая матрица вероятностей переходов (рис. 4).

 

Рисунок 4. МВП для сценария с отказом механизации крыла.

VI.Заключение

В рамках разработки математической модели и сопутствующего программного обеспечения для моделирования поведения экипажа воздушного судна был доработан механизм оценки каждого сценария с учетом влияния относительной сложности каждого шага сценария, общего времени выполнения сценария, а также относительному времени нахождения на каждом из кластеров.

Полученная методология позволяет более качественно и достоверно подходить к процессу предварительной подготовки отдельных фрагментов (сценариев) полета, что безусловно увеличит качество работы итоговой модели поведения. На основании экспертной оценки корректируется каждый шаг рассматриваемого сценария с учетом сложности и времени. Стоит отметить, что определяющим фактором качества модели является квалификация и уровень опыта оценивающего эксперта.

При наличии большего количества достоверных эмпирических данных возможно уточнение коэффициентов преобразования целевого массива распределений времен нахождения в состояниях.

1. Орищенко В.А., Грешников И.И. Моделирование деятельности экипажей при пилотировании воздушных судов. Моделирование и анализ данных. 2024. Том 14. № 1. C. 89–102. DOI: https://doi.org/10.17759/mda.2024140106
2. Lancaster P., Tismenetsky M. The Theory of Matrices: With Applications. Elsevier, 1985. 570 pp.
3. Wilkinson J.H., The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1988).
4. Cramer H., Mathematical Methods of Statistics. Princeton University Press, 1999. 575 pp.
5. Куравский Л. С., Козырев А. Д., Грешников И. И. Математическая модель сопутствующей деятельности пилота и ее применение для объективной оценки его состояния и профессиональной подготовки //Экспериментальная психология. – 2024. – Т. 17. – №. – С. 161-180.
6. Г. Г. Амосов, “О марковских возмущениях группы унитарных операторов, ассоциированной со случайным процессом со стационарными приращениями”, Теория вероятности и ее применение, 49:1 (2004), 145–155; Theory Probab. Appl., 49:1 (2005), 123–132
7. Грешников И.И., Куравский Л.С., Юрьев Г.А. Принципы построения программно-аппаратного комплекса для интеллектуальной поддержки экипажа и оценки уровня его подготовки // Моделирование и анализ данных. Том 11. № 2. С. 5–30. DOI: 10.17759/mda.2021110201
8. Parlett B.N., The Symmetric Eigenvalue Problem. Prentice-Hall, 1980. 348 pp.
9. Куравский Л.С., Юрьев Г.А., Златомрежев В.И., Юрьева Н.Е. Оценка действий экипажа воздушного судна на основе модели рисков человеческого фактора // Экспериментальная психология. Том 13. № 2. С. 153–181. DOI: 10.17759/exppsy.2020130211
10. Марковские модели в задачах диагностики и прогнозирования: Учеб. пособие. / Под ред. Л. С. Куравского. — 2-е изд., доп. — М.: Изд-во МГППУ, 2017. — 203 с.: ил. — ISBN 978–5–94051–168–7.
11. G. Amosov. On Markovian Cocycle Perturbations in Classical and Quantum Probability. Int. J. Math. & Math. Sci., 2003 (54), 3443–3467 (2003).
12. Куравский Л.С., Юрьев Г.А. Марковские модели адаптивного тестирования // Моделирование и анализ данных. 2011. Том 1. № 1. С. 28–40.
13. Kuravsky L. S. et al. A Mathematical Model for Representing the Related Operator Professional Activities and Their Diagnostic Assessments Based on the Quantum Representations //Lobachevskii Journal of Mathematics. – 2024. – Т. 45. – №. 6. – С. 2534-2551.