Психолого-педагогические исследования
2015. Том 7. № 1. С. 80–88
doi:10.17759/psyedu.2015070108
ISSN: 2587-6139 (online)
Проблемы понимания текстовой и символьной информации при обучении математике
Аннотация
Общая информация
Ключевые слова: понимание, восприятие языка, декодирование высказывания, обратимые конструкции, обучение математике
Рубрика издания: Психология образования
Тип материала: научная статья
DOI: https://doi.org/10.17759/psyedu.2015070108
Для цитаты: Брагина О.И. Проблемы понимания текстовой и символьной информации при обучении математике [Электронный ресурс] // Психологическая наука и образование psyedu.ru. 2015. Том 7. № 1. С. 80–88. DOI: 10.17759/psyedu.2015070108
Полный текст
Язык является системой передачи информации, с помощью которой человек поддерживает связь с социумом, приобретает свои знания и обменивается ими с другими, выражает свои мысли и эмоции. В процессе любого обучения, в том числе и математике, устная и письменная речь являются главным средством передачи информации учащимся. Обучение неизбежно затрагивает работу с информацией и распознавание языковых кодов: это восприятие речи учителя, понимание текстов учебного материала, работа с учебником и т. д. Соответственно, возникает задача по устранению препятствий, связанных с восприятием языка с целью повышения эффективности процесса обучения.
Существуют разные способы решения проблемы восприятия информации. Их предлагают психология, лингвистика, герменевтика. Важными в настоящее время представляются возможное обобщение трудов психологов, лингвистов и педагогов в вопросах восприятия языка и использование этого обобщения для обучения.
В данной статье мы попытаемся систематизировать проблемы, связанные различным образом с пониманием языка при обучении, и более подробно обсудить одну из таких проблем - раскодирование обратимых конструкций.
Учащийся, который не смог воспринять сообщение учителя или формулировку задания, оказывается вне учебного процесса в самом его начале. Когда такая ситуация повторяется несколько раз, учащийся привыкает быть отрешенным от учебной деятельности. Понимание входной информации и текстов не является достаточным условием для успешного и результативного обучения, однако является условием необходимым. Если на самом начальном этапе восприятия раскодирование не состоится, то не запустится дальнейшая работа с этой информацией.

Рис. 1. Схема раскодирования информации
На первой стадии понимания - раскодировании - учащийся переводит информацию во внутренний внеречевой план. От этого этапа зависит, активируются ли следующие этапы понимания (составляющие этих этапов уже зависят от типа входной информации и в данной работе рассматриваться не будут. Мы рассмотрим в основном проблемы, связанные с «пониманием первого уровня» - первичным раскодированием информации в письменных текстовых сообщениях).
Далее мы рассмотрим, как трактуется понятие «понимание» в разных областях знания.
В философии понятие «понимание» первоначально относилось к интерпретации текстов Священного Писания. Впоследствии на основе этой деятельности сформировалось самостоятельное направление - герменевтика. Ф. Шлейермахер [Шлейермахер Ф.Герменевтика. СПб, 2004] был одним из первых, кто предположил, что герменевтика необходима не только для толкования античных священных текстов, но и для всех текстов вообще. М. Хайдеггер [Хайдеггер М.Путь к языку, 1993] в рамках герменевтики связывал понимание с языком, причем давал понятию «понимание» субъективную характеристику, говоря, что понимание - это человеческое отношение к действительности. Г. Гадамер пытался [ГадамерГ.-Г.Актуальностьпрекрасного, 1991] определить общие условия возможности понимания. Феноменологические аспекты герменевтики изучал Э. Гуссерль [Гуссерль, 1999]. Все далее отходя от изучения интерпретации литературных текстов, К. Ясперс [Ясперс, 1997] изучал коммуникативный аспект понимания, в основе которого лежит способность людей психически сопереживать друг другу. Отметим, что в работах названных ученых интерпретация текстов как «понимание» и психологическое понимание, затрагивающее переживания человека, в начале прошлого века рассматривались в едином ключе.
В настоящее время мы можем разделять эти подходы и говорить о том, что в герменевтике работа с пониманием в философии может вестись в онтологическом смысле - в аспекте общих проблем бытия и человеческого познания. Так, в философии изучаются аспекты человеческой деятельности вообще, но не рассматриваются личностные характеристики человека. Поэтому, если мы хотим воспользоваться понятием понимания в педагогике, то необходимо, во-первых, сместить фокус с абстрактной философской периферии на динамические характеристики понятия (на его процессуальность), во-вторых, фиксировать результативность этого процесса, а в-третьих, - придать ему личностно направленную окраску.
Эти замечания приводят нас к рассмотрению понятия «понимание» в психологии.
В.В. Знаковым понимание рассматривается в качестве необходимого компонента познавательной деятельности человека как момент получения знания и наделения этого процесса смыслом [Знаков В.В, 1998]. Когнитивный подход предлагает рассматривать понимание как включение новых знаний в прошлый опыт субъекта. Такую трактовку можно дополнить взглядом логики, где пониманием следует считать способность индивида к умозаключениям. Общим во всех вышеперечисленных подходах является то, что понятие понимания зачастую связывается различным образом с процессом мышления человека. Эти подходы для педагогики актуальны, поскольку позволяют проверять степень освоения учащимися различных знаний и оценить умения применять эти знания.
Нас интересуют языковые аспекты в психологии понимания, поэтому теперь мы рассмотрим частный взгляд на понимание психолингвистов [Белянин; Жинкин, 1958]. Это позволит нам четче сформулировать задачи собственного исследования.
В психолингвистике изучается понимание письменных и устных речевых сообщений. Специфика процесса понимания текста заключается в осуществлении сложной работы, в результате которой из развернутого сообщения выделяется основная мысль, воспринимаемое сообщение компрессируется во внутренней речи реципиента до некоторого «комплекса смыслов» [Белянин]. Это происходит путем сжатия сообщения до смысловой темы, представляющей собой своеобразный внутренний код, эквивалентный содержанию воспринимаемого текста. В результате мыслительной переработки текстовой информации у читателя происходит образование некоторой модели текста [Белянин; Жинкин, 1958].
Таким образом, в психолингвистике понимание трактуется преимущественно как результат раскодирования речевого сообщения. Мы в дальнейшем будем пользоваться психолингвистическим определением понимания, подразумевая под ним восприятие или раскодирование конкретного языкового высказывания.
Язык - это система знаков, используемая для коммуникации и познания. Системность языка выражается наличием семантики, синтаксиса и словаря. При понимании языка ведется работа со всеми его тремя аспектами. Современная модель формирования речевого сообщения такова [Белянин]: мотив -^ мысль -^ внутренняя речь -^ лексическое развертывание + грамматическое конструирование -^ внешняя речь.
Процесс декодирования речи характеризуется следующей последовательностью этапов: выявление грамматических и семантических отношений между словами в пределах фразы -^ понимание синтаксической конструкции, осложненной различными деепричастными оборотами и причинно-следственными связями.
«Понимание речи - это не пассивное механическое движение от значения к смыслу, а сложный целостный психологический процесс, начинающийся с поиска общей мысли высказывания, в котором огромное значение имеют предвосхищение и установка, возникающие в языковом сознании слушателя (читателя)» [Жинкин, 1958, с. 92]. Рассматривая модель
расшифровки речевого высказывания, мы видим, что проблемы процесса декодирования разделяются на две большие группы. Первая отвечает за процессы, обеспечивающие расшифровку воспринимаемых языковых кодов (здесь важна языковая компетенция понимающего), а вторая - за воссоздание у воспринимающего контекста, позволяющего среди множества трактовок фразы подобрать оптимально подходящую.
Это разделение можно представить на схеме (рис. 2).

Рис. 2. Классификация проблем, связанных с декодированием речевого высказывания в математике
Обратимся теперь к проблеме раскодирования обратимых конструкций. Понятие «обратимые конструкции» мы заимствуем из психолингвистики [Белянин]. Обратимыми конструкциями мы будем называть структуры, построенные с помощью естественного или символьного языка, для которых выполнены следующие два условия:
1) могут существовать (быть осмысленными с точки зрения языка) отношения A~B и B~A;
2) смысл конструкций A~B и B~A неодинаков (A и B - некоторые объекты языка, ~ -
языковое отношение, в котором они находятся).
«Можно сказать: “Мальчик пошел в лес”, “Флаг развевается на крыше”, “Облако плывет по небу”, но нельзя сказать: “Лес пошел в мальчика”, “Крыша развевается на флаге” и т. д., потому что эти последние конструкции противоречат возможностям реального взаимодействия вещей. Поэтому существенное затруднение в понимании конструкций вносится их обратимостью, иначе говоря, тем обстоятельством, что как прямое, так и обратное расположение названных объектов принципиально возможно» [ЛурияА.Р. Язык и сознание, с. 212].
Мы предлагаем следующую классификацию обратимых конструкций, встречающихся в курсе математике (в определениях, заданиях, выражениях):
 обратимое отношение существования в родительном падеже; «разность квадратов» и «квадрат разности»; « функция f(x) -первообразная функции g(x)»; сюда же можно отнести отношение функции к ее аргументу; (sin x, sin(cos(x)));
обратимое отношение существования в родительном падеже; «разность квадратов» и «квадрат разности»; « функция f(x) -первообразная функции g(x)»; сюда же можно отнести отношение функции к ее аргументу; (sin x, sin(cos(x)));
 описание расположения геометрических фигур в пространстве относительно друг друга: «описанный многоугольник около окружности» и «окружность, описанная около многоугольника»; «круг внутри квадрата» и «квадрат внутри круга»;
описание расположения геометрических фигур в пространстве относительно друг друга: «описанный многоугольник около окружности» и «окружность, описанная около многоугольника»; «круг внутри квадрата» и «квадрат внутри круга»;
 отношения порядка: «x больше y» и «y меньше x»; «a правее b» или «левее ab»;
отношения порядка: «x больше y» и «y меньше x»; «a правее b» или «левее ab»;
 поcледовательность некоммутирующих операций: «после того, как к числу прибавили 5 и увеличили результат на 10 %, получилось 8»; (некоммутативность операций сложения и умножения относительно друг друга);
поcледовательность некоммутирующих операций: «после того, как к числу прибавили 5 и увеличили результат на 10 %, получилось 8»; (некоммутативность операций сложения и умножения относительно друг друга);
 субъект-объектные отношения: «Английская команда побеждена французской; 6 делится на 3; 3 делится на 6»;
субъект-объектные отношения: «Английская команда побеждена французской; 6 делится на 3; 3 делится на 6»;
 любое алгебраическое выражение также можно рассматривать как обратимую конструкцию с точки зрения перемены мест входящих в него символов (знаков действий и переменных):
любое алгебраическое выражение также можно рассматривать как обратимую конструкцию с точки зрения перемены мест входящих в него символов (знаков действий и переменных):
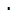 произвольные конструкции, в которых возможна перемена мест объектов с изменением при этом значения: «число с -это показатель степени, в которую надо возвести основание a, чтобы получить число b»; «3 - это такое число, при умножении которого само на себя получается 9»; «поезд следует из Адлера в Москву».
произвольные конструкции, в которых возможна перемена мест объектов с изменением при этом значения: «число с -это показатель степени, в которую надо возвести основание a, чтобы получить число b»; «3 - это такое число, при умножении которого само на себя получается 9»; «поезд следует из Адлера в Москву».
Трудность восприятия обратимых конструкций заключается в том, что, когда мы сталкиваемся с декодированием обратимого отношения A~B, у нас в сознании возникает проблема выбора, с которой сознание справляется с привлечением дополнительных усилий.
Еще больший интерес представляют конструкции, состоящие из композиции обратимых отношений, поскольку в этом случае сложность декодирования возрастает экспоненциально. Так, начав работу по декодированию конструкции A~1((B~2C)~3D), где ~1, ~2 и ~3 - обратимые конструкции, мы имеем 23 вариантов для восприятия, поэтому мгновенное раскодирование не происходит почти никогда, требуются дополнительные усилия в виде картинок, схем, различных вербальных фрагментов.
Ниже приведены задания, которые можно использовать для диагностики восприятия композиции обратимых конструкций. Конструкции могут быть как учебным материалом по математике, так и не относиться к предмету непосредственно.
Примеры заданий:
 Нарисуй треугольник слева от квадрата. Внутри треугольника нарисуй круг.
Нарисуй треугольник слева от квадрата. Внутри треугольника нарисуй круг.
 Определи, кто из мальчиков первым пришел к финишу. Быстрее Вани на соревнованиях по бегу оказались Петя и Саша. Коля был медленнее Саши. Саша пришел раньше Пети. Ваня был быстрее Коли.
Определи, кто из мальчиков первым пришел к финишу. Быстрее Вани на соревнованиях по бегу оказались Петя и Саша. Коля был медленнее Саши. Саша пришел раньше Пети. Ваня был быстрее Коли.
 Вычисли квадрат разности произведения чисел 5 и 8 и числа 7.
Вычисли квадрат разности произведения чисел 5 и 8 и числа 7.
 Найди число, которое, будучи умножено на 3, затем увеличено на 2, разделено на 7, уменьшено на 1, умножено само на себя и уменьшено на 1, дает число 2.
Найди число, которое, будучи умножено на 3, затем увеличено на 2, разделено на 7, уменьшено на 1, умножено само на себя и уменьшено на 1, дает число 2.
 Отец брата мамы сына моей сестры - кто это для меня?
Отец брата мамы сына моей сестры - кто это для меня?
Роль понимания обратимых конструкций в обучении не уточнена. Такие конструкции упоминаются в литературе по психолингвистике [Белянин; Жинкин, 1958; ЛурияА.Р. Язык и сознание] (отмечена сложность их декодирования; оказывается, что этот тип затруднений восприятия во многом зависит от работы полушарий: левое полушарие отвечает за механизм словесной передачи обратимых отношений). В статьях о семантической афазии разбираются случаи работы с людьми, имеющими системные нарушения (проблемы речи при локальных поражениях мозга) [Статников, 2001]. На необходимость понимания таких конструкций указывается в методиках
нейропсихологического тестирования детей при подготовке в школе; в некоторых исследованиях нарушения при понимании обратимых конструкций изучают вместе с формированием у ребенка двигательных функций и пространственных представлений [Кравцова Н.А, 2011].
Тем не менее в учебной литературе по математике задания на декодирование такого рода конструкций представлены несистемно. Их, как правило, классифицируют как «задания на логику», «задания на вербально-логическое мышление» без учета специфики их обратимости. В некоторых источниках эти задания являются критерием подготовки к школе детей, причем явно указывается необходимость этого материала для успешного обучения. Стоит отметить, что работа с подобными языковыми конструкциями актуальна не только в процессе обучения математике, но и во время освоения других предметов. Однако специфика математики заключается в том, что для изучения этого предмета необходима четкость и строгость мышления, критический анализ любых слов и высказываний, осознание того, что непрерывная мыслительная активность является необходимым условием для понимания информации. Существенным здесь оказывается и то, что в математике есть много операций и отношений, которые не являются коммутативными друг для друга (результат и смысл меняются при изменении порядка входящих в отношение объектов).
Беседа с учащимися, неспособными раскодировать обратимые конструкции, выявляет, что они не имеют привычки анализировать конструкцию с помощью дополнительных умственных усилий. Успешные учащиеся, напротив, изначально готовы к вспомогательному вербальному или схематическому преобразованию информации (это зависит от когнитивного стиля учащегося). На это указывает их поведение в такой ситуации (просят листочек для записи, просят дополнительное время, чтобы сосредоточиться, проговаривают вслух и т. д.)
Такие испытуемые (как взрослые - учителя математики, так и дети) отмечали, что сначала испытывали затруднения, в результате чего им приходилось использовать разные приемы для получения правильного ответа (нарисовать картинку, построить сериацию по схеме). Многие учащиеся при этом самостоятельно разбирались с принципом построения композиции - формированием цепочки, начиная с внутреннего аргумента.
При изучении обратимых конструкций и их роли в обучении с целью создания эффективной методики для обучения можно опираться на следующие положения.
1. Понимание обратимых конструкций не является простым, а требует дополнительных умственных действий со стороны воспринимающего. Осознание этого факта самими учащимися делает более эффективным процесс декодировании любой информации (т. е., решая задачу понимания при обучении математики, можно создать привычку анализировать информацию при обучении любому предмету). Понимание обратимых конструкций осложняется тем, что понимающий должен встретить подобное высказывание определенной мыслительной активностью, прилагая для этого дополнительные усилия со своей стороны. Таким образом, возникает акцент на необходимости критически оценивать свои действия и умственные усилия.
2. Обратимые конструкции в математике и обратимые конструкции естественного языка раскодируются похожим образом. Таким образом, можно создать методику обучения восприятию обратимых конструкций, основанную на материалах, в том числе не содержащих явно заданий по математике. Предполагается, что результатом у учащихся станет более эффективная работа с любыми математическими конструкциями.
3. Способ восприятия обратимой конструкции зависит от когнитивного стиля учащегося. Это некоторый образ, к которому наше сознание привыкло обращаться при столкновении с проблемами одного рода. Если этот способ сформирован, то обращение к нему становится автоматическим. В противном случае человек может оказаться беспомощным при восприятии таких конструкций и, как следствие, новой учебной информации вообще. Отрабатывать до автоматизма механику понимания таких сообщений, делая эти действия интериоризированными, следует на хорошо известном материале.
Представленный материал позволяет осознать необходимость дальнейшего детального изучения этой проблемы специалистами по психологии, педагогике и лингвистике. Этот материал может быть использован для развития теоретических концепций по восприятию информации, в том числе для решения образовательных задач.
В будущем мы планируем создать типологию заданий по раскодированию обратимых конструкций и, в зависимости от степени сформированности умений учащихся, предложить различные методические стратегии решения данной проблемы.
Литература
- Белянин В.П. Психолингвистика. М.: Флинта, Московский психолого-социальный институт, 2004. 232 с.
- ГадамерГ.-Г.Актуальностьпрекрасного. М.: Искусство, 1991. 367 с.
- Гуссерль Э. Идеи к чистой феноменологии / Пер. с нем. А.В. Михайлова. М.: ДИК, 1999. 311 c.
- Жинкин Н.И. Механизмы речи. М.: АПН РСФСР, 1958. 378с.
- Знаков В.В. Понимание в познании и общении.М.:Институт психологии РАН, 1998. 232 с.
- Кравцова Н.А., Катасонова А.В.Нейропсихология формирования двигательных функций и пространственных представлений у часто болеющих детей младшего школьного возраста [Электронный ресурс]// Психологическая наука и образование PSYEDU.ru 2011. № 2. URL:http://www.psyedu.ru/authors/a2093.phtml(дата обращения: 12.06.2014).
- ЛурияА.Р. Язык и сознание. Ростов н/Д.: Феникс, 1998. 416 с.
- Статников А.И. и др.Особенности понимания логико-грамматических конструкций при различных формах афазии / Статников А.И., Драгой О.В., Бергельсон М.Б., Искра Е.В., Маннова Е.М., Скворцов А.А.// Тезисы конференции «Когнитивная наука в Москве: новые исследования»,16 июня 2011 г./ Под ред. Е. В. Печенкова, М. В. Фаликман.М.:БукиВеди, 2001. С. 238-242.
- Хайдеггер М.Путь к языку. М.: Республика, 1993. 447с.
- Шлейермахер Ф.Герменевтика. СПб.: Европейский Дом, 2004. 242 с.
- Ясперс К. Общая психопатология. M.: Практика, 1997. 1056с.
Информация об авторах
Метрики
Просмотров
Всего: 2304
В прошлом месяце: 26
В текущем месяце: 0
Скачиваний
Всего: 932
В прошлом месяце: 4
В текущем месяце: 0