Распознавание символов на базе цепи Маркова

Введение

В процессе разработки системы распознавания и озвучивания плоскопечатных текстов El-Reader [2; 3; 4] возникла необходимость в использовании алгоритма, устойчивого к незначительным изменениям шрифтов и искажениям, возникающим в процессе выделения и обработки изображения. Анализ существующих подходов показал, что их реализация на базе основного инструмента разработки не будет обладать достаточным быстродействием (специфика задачи заключалась в том, что необходимо было обрабатывать порядка 20 символов за секунду). Было принято решение разработать алгоритм, который сможет принимать решения на основании минимального объема информации о символе.

Предварительная обработка изображения

Введенное изображение преобразуется в монохромное черно-белое представление.

Важной операцией, необходимой для корректной реконструкции связного текста, является выделение из изображения символьных строк. Задача усложняется тем, что камера, как правило, удерживается в руке и, вследствие этого, строки попадают в кадр повернутыми. Для повышения надежности распознавания при достаточно больших углах поворота необходимо восстанавливать горизонтальное положение строк. Для этого на основе анализа плотностей черных и белых точек на нескольких вертикальных срезах изображения определяют местоположение начал и концов строк, что позволяет оценить угол, на который следует повернуть графическое представление для получения удобного для анализа состояния. После такого поворота границы текстовых строк определяются повторно. На основе информации об этих границах фиксируются занимаемые символами прямоугольные фрагменты изображения.

По окончании выделения указанных прямоугольных фрагментов для всех символов в строке соответствующий ей участок вырезается из кадра, просматриваемого веб-камерой. При этом малые фрагменты, не превышающие заданный порог, удаляются из строки. Оставшиеся фрагменты рассматриваются как области, содержащие распознаваемые символы произвольного размера. Указанная процедура повторяется для всех строк из кадра, просматриваемого веб-камерой, причем информация о геометрических характеристиках как строк, так и прямоугольных фрагментов изображения, включающих в себя символы, сохраняется для последующего распознавания в порядке расположения фрагментов в кадре.

Ослабить искажения в анализируемой части изображения позволяет алгоритм коррекции локального контраста, а именно, уменьшить эффект, возникающий в связи с неравномерным освещением. При переводе в черно-белый формат невозможно установить общий уровень контраста для всего изображения, так как либо часть символов распадется и распознать их будет невозможно, либо некоторые окажутся закрашены черным целиком. Суть метода в следующем: на выделенных прямоугольных фрагментах перебираются все черные точки, из числа которых удаляются слабосвязанные (имеющие малое число одноцветных соседей). В то же время области, в которых предполагается исчезновение черных точек из-за нарушения освещенности или иных условий сканирования, заливаются черным цветом[I]. Указанный прием улучшает качество распознавания примерно на 10 %, практически не влияя на скорость работы программы.

Изображение, вводимое с веб-камеры, обычно затемнено с одного или нескольких краев и, несмотря на все использованные алгоритмы, с таким уровнем затемнения бороться бессмысленно. Эффект обусловлен непараллельностью поверхности текста и линзы, а также оптическими искажениями и недостаточным освещением. В случае значительных искажений анализируется только центральная часть графического представления.

Описание алгоритма

Каждый прямоугольник с символом переводится в контурный рисунок с помощью непрореженного вейвлет-преобразования на базе биортогонального вейвлета, прямоугольные фрагменты с контурными изображениями последовательно преобразуются в два числовых вектора. Один из них описывает распределение точек кон­
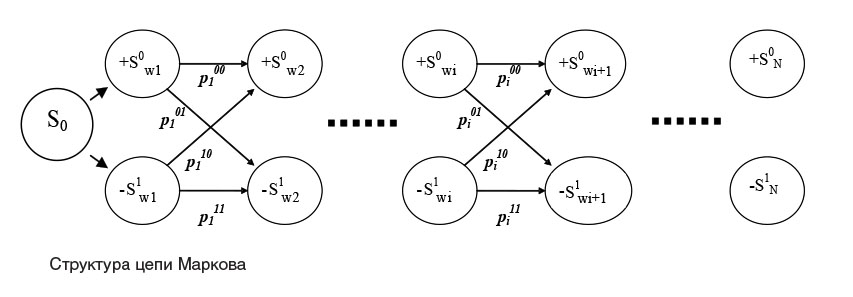
тура вдоль оси абсцисс, другой вдоль оси ординат. Таким образом, мы, теряя часть информации, получаем простой инвариант длинной в 64 числа (символы отмас- штабированы для окна 32x32), такой вектор может быть проанализирован с удовлетворяющей для задачи скоростью. Полученный вектор подвергается быстрому вейвлет-преобразованию с использованием вейвлетов Добеши 4-го порядка. Полученные подмножества последовательностей вейвлет-коэффициентов W={w}l=1 N рассматриваются как представления си м - волов и анализируются с помощью распознающей цепи Маркова, структура которой представлена на рисунке. Процедура распознавания основана на анализе знаков вейвлет-коэффициентов из указанной последовательности.

Система, описываемая данной цепью, функционирует N моментов времени, где N - длина анализируемой последовательности вейвлет-коэффициентов. В начальный момент времени система находится в состоянии S0. В i-й момент времени, где i изменяется от 1 до N, система может быть или в состоянии +S0, или в состоянии - S/, а именно: в состоянии +S0 - в случае не­отрицательности i-го элемента последовательности W и в состоянии -S1 - в случае его отрицательности. Система является нестационарной: изменяется матрица Р.=11р...11 вероятностей переходов между состояниями, такая, что р.=Р.р.-1, где р. - вектор-столбец вероятностей пребывания в состояниях цепи в i-й момент времени, причем в указанный момент времени все ее элементы равны нулю, кроме вероятностей переходов между парами состояний S1i_1 и S1,, S°„ и S1, S11 и S0, и S0k1 и S0., которые далее обозначены, соответственно, как p11, p.01, p10 и p00. В каждый из моментов времени i выполняются следующие нормировочные условия: pl11+pl10=1 и p 01+p 00=1.

Последовательности Wa, соответствующей заданному символу a, приведенные правила ставят в соответствие определенную последовательность Sa  прохождения состояний рассматриваемой цепи Маркова2
.
При обучении цепи Маркова на алфавите A={am} для каждого символа am формируется множество его эталонов3 amk, k=1,…, Km. Каждому символу am ставится в соответствие цепь Маркова, вероятности переходов между состояниями которой определяются методом максимального правдоподобия. Для этого вычисляется распределение вероятностей переходов, обеспечивающее наибольшую вероятность P появления заданного множества последовательностей состояний, соответствующих эталонам данного символа: P=Пk=1,…,Km Pk , где Pk =Пi=1,…,N pi signWi-1,k signWi,k, где k – номер эталона символа, а i – номер состояния, причем полагается, что signw0,k=1.

Указанная задача может быть решена одним из подходящих численных методов нелинейного программирования[4]. Часто удобно, с целью упрощения решения, перейти к критерию lnP, монотонно связанному с исходным критерием P, переформулировав исходную постановку в задачу оптимизации для величин \npisignW'-1ksignWik, на которые наложено условие неположительности[5] [6] [7] [8].

Распознавание поступающих на вход системы новых символов возможно после завершения обучения. При этом для цепи Маркова, соответствующей каждому из символов алфавита A, вычисляется вероятность прохождения последовательности состояний, определяемой вейвлет- коэффициентами {wjfc1 N распознаваемого символа, которая равна ’ ПЬ1 N p,signWi-1 signWi. Тип символа, который соотв е тствует цепи Маркова, имеющей наибольшую вероятность такого рода, выдается как результат распознавания.

Оценка вероятности корректного распознавания символов с помощью описанного алгоритма, полученная по результатам 1000 проб на базе асимптотической аппроксимации биномиального распределения, равна 0,791, причем нижняя и верхняя границы 95 % доверительного интервала равны 0,76 и 0,83.

Оказалось, что достаточно использовать последовательности W, состоящие из двенадцати вейвлет-коэффициентов (N=12), начиная с третьего коэффициента разложения распределений контурных точек. Расчеты выявили неинформативность первых двух вейвлет-коэффициентов этого разложения для решения задачи распознавания.

Результаты и выводы

Разработан и программно реализован новый алгоритм распознавания символов на базе цепей Маркова. Даны формальные оценки его эффективности. Алгоритм используется как один из ключевых компонентов системы распознавания и озвучивания плоскопечатных текстов El-Reader. Его преимуществами является:

•устойчивость к искажениям, вызванным особенностями процесса сканирования;

•   устойчивость к различным типам шрифтов;

•   высокое быстродействие;

•   возможность динамического уточнения текущей гипотезы за счет использования большего числа коэффициентов при анализе.

Алгоритм обладает высокой универсальностью и имеет широкие перспективы в решении задач распознавания.