Перейти к основному содержанию

Моделирование и анализ данных
2024. Том 14. № 4. С. 30–44
doi:10.17759/mda.2024140402
ISSN: 2219-3758 / 2311-9454 (online)

Об использовании дискретного преобразования Фурье в схемах подразделений

0

Битюков Ю.И., Битюков П.Ю.

PDF (RUS)
GS
Информация
в Google Scholar

Аннотация

Статья посвящена развитию метода геометрического моделирования, основанного на схемах подразделений и применению этого метода к параметрическому описанию поверхности или области по облаку точек, полученному каким-либо способом. Для нахождения начальной последовательности схемы подразделений применяется метод наименьших квадратов, но непосредственное его использование затруднительно из-за огромных размеров матриц. Поскольку схемы подразделений основаны на свертках последовательностей, для устранения проблемы размеров матриц, используется дискретное преобразование Фурье и методом наименьших квадратов находится не сама начальная последовательность, а ее преобразование Фурье

Общая информация

Ключевые слова: схема подразделений, вейвлет-анализ, вейвлет преобразование, дискретное преобразование Фурье, геометрическое моделирование

Рубрика издания: Анализ данных

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140402

Получена: 19.11.2024

Принята в печать:

Для цитаты: Битюков Ю.И., Битюков П.Ю. Об использовании дискретного преобразования Фурье в схемах подразделений // Моделирование и анализ данных. 2024. Том 14. № 4. С. 30–44. DOI: 10.17759/mda.2024140402

Полный текст

Введение

Схемы подразделений появились в задачах геометрического моделирования, причем в последствии обнаружилась тесная их связь с вейвлетами [1]. В частности вейвлеты и масштабирующие функции можно получать посредством схем подразеделений, в которых в качестве маски схемы выступает масштабная последовательность [1,2]. Схема подъема, использующая схемы подразделений, представленная в статье [3], позволяет строить биортогональные вейвлеты с заданными свойствами. Использованию схем подразделений и вейвлетов в задачах геометрического моделирования посвящены, например статьи [4-9]. Схема подъема и схема подразделений позволяет построить парметрическое семейство биортогональных вейвлетов, которое предоставляет параметрическое семейство фильтров. Такое семейство было использовано в статье [10] в задаче подрисовки изображений и нужный вейвлет выбирается не из общих соображений, а из решения оптимизационной задачи. По схемам подразделений следует отметить монографию [11], в которой даказываются основные результаты относящиеся к ним и работу [12], в которой исследуется сходимость схем.

В работах [13,14] изучаются основанные на вейвлет-фреймах алгоритмы для 3D-реконструкции поверхности или области по облаку точек. Так, в работе [13] с помощью фреймов аппроксимируется характеристическая функция множества, граница которого представленна облаком точек, а в работе [14] таже задача решается построением аппроксимации функции u ( x , y , z ) линейной комбинацией масштабирующих функций. Сама поверхность (граница области), построенная по облаку точек задается уравнением u ( x , y , z ) =0 . В обеих работах аппроксимация ищется с помощью алогритма Брегмана. Недостаток метода, основанного на масштабирующих функциях состоит в том, что они редко когда известны в аналитическом виде и матрицу системы линейных уравнений составить затруднительно.

В настоящей работе на основе статей [13,14] развивается метод реконструкции поверхности или области по облаку точек. В этом методе поверхность (область) описывается с помощью линейной комбинации масштабирующих функций, но при этом сами функции не находятся, а функция описывающая поверхность (область) находится через схему подразделений. Причем преобразование Фурье начальной последовательности к этой схеме определяется методом наименьших квадратов. Полученная линейная комбинация аппроксимирует характеристическую функцию множества, граница которого содержит данное облако точек. Все примеры, представленные в статье, созданны с использованием языка программирования Python и библиотек Numpy и Plotly. Облака точек, полученных лазерным сканированием, взяты с сайта https://sites.cc.gatech.edu/projects/large_models/.

Схемы подразделений. Основные результаты

В данном разделе приводятся основные результаты, касающиеся стационарных схем подразделений, которые будут использованы в дальнейшем. Схема подразделений [11] определяется заданной последовательностью a = { a α } α ∈ Z s , s ∈ N . Мы будем предполагать, что supp a = { α : a α ≠ 0 } – конечное множество. Обозначим l ∞ ( Z s ) линейное нормированное пространство ограниченных последовательностей ν = { ν α } α ∈ Z s , в котором норма определяется равенством ∥ ν ∥ ∞ = α ∈ Z s ν α ∨ . Введем в рассмотрение оператор S a : l ∞ ( Z s ) → l ∞ ( Z s ) , который определим формулой Последовательность { a α } α ∈ Z s будем называть маской схемы подразделений, а S a – оператором схемы подразделений.

Определение 1. [11] Будем говорить, что схема подразделений

ν m = S a ν m − 1 =
сходится в l ∞ ( Z s ) , если существует непрерывная функция ( S a ∞ ν ) : R s → R такая, что
lim m → + ∞ ‖ ( S a ∞ ν ) ( ⋅ 2 m ) − ν m ‖ ∞ = 0 . (1)
Если функция ( S a ∞ ν ) удовлетворяет дополнительному свойству ( S a ∞ ν ) ( k ) = ν k , k ∈ Z s , то она называется интерполяционной.
Следует заметить, что для интерполяционной схемы должно быть выполнено условие [11] a 2 k = δ k , где δ k = 1 при k = 0 и δ k = 0 в остальных случаях.
Теорема 1. (Необходимое условие сходимости схемы подразделений [11]) Пусть s = 1 . Предположим, что схема подразделений сходится для некоторого ν ∈ l ∞ ( Z ) и ( S a ∞ ν ) ≡ ´ 0 . Тогда маска удовлетворяет условию ∑ β ∈ Z a 2 β = 1 ; ∑ β ∈ Z a 2 β + 1 = 1 .
Введем в рассмотрение многочлен Лорана A ( z ) = ∑ n ∈ Z a n z n . Тогда из необходимого условия сходимости схемы подразделений получаем: A ( − 1 ) = 0 ; A ( 1 ) = 2. Из первого равенства следует, что, если маска имеет конечный носитель, т.е. A ( z ) = z − k R ( z ) , где R ( z ) – многочлен, то этот многочлен делится нацело на ( z + 1 ) . Поэтому A ( z ) = ( 1 + z ) Q ( z ) , Q ( 1 ) = 1. Пусть Q ( z ) = ∑ n ∈ Z q n z n и q = { q n } n ∈ Z .
Теорема 2. [12] Пусть s = 1 . Схема S a сходится при любом выборе начальной последовательности ν 0 , если существует L ∈ N такое, что ∥ .
Если обозначить Q L ( z ) = Q ( z ) Q ( z 2 ) … Q ( z 2 L − 1 ) = ∑ j q j [ L ] z j , то имеет место равенство [12]:
∥ .
Теорема 3. [12] Пусть s = 1 и A ( z ) = ( 1 + z 2 ) n Q ( z ) . Если S q сходится при любом выборе начальной последовательности, то ( S a ∞ ν ) ∈ C n ( R ) для любой начальной последовательности ν и d n d t n ( S a ∞ ν ) ( t ) = ( S b ∞ ( Δ n ν ) ) ( t ) , где Δ n ν = Δ ( Δ n − 1 ν ) и , k ∈ Z .
Теорема 4. [11] Предположим, что схема подразделений сходится для всех ν ∈ l ∞ ( Z s ) и для некоторого ν ∈ l ∞ ( Z s ) функция ( S a ∞ ν ) ≡ ´ 0 . Тогда маска { a α } α ∈ Z s определяет единственную непрерывную функцию с компактным носителем φ = S a ∞ δ , удовлетворяющую условиям:
φ ( t ) = ∑ α ∈ Z a α φ ( 2 t − α ) , t ∈ R s , ∑ α ∈ Z φ ( t − α ) = 1 , ∀ t ∈ R s .
Более того, ( S a ∞ ν ) ( t ) = ∑ α ∈ Z s ν α φ ( t − α ) , t ∈ R s .

Применение дискретного преобразования Фурье к нахождению итераций схемы подразделений

Пусть λ = { λ k } k ∈ Z s , s ∈ N . Определим последовательность
Если ω m = e 2 πi / m , m ∈ N и a = { a k } k ∈ Z s — периодическая последовательность a n + k = a k , n = ( n 1 … n s ) T , для всех k ∈ Z s , то дискретное преобразование Фурье последовательности a определяется равенством [1]:
a ^ k 1 , … , k s = ∑ j 1 = 0 n 1 − 1 … ∑ j s = 0 n s − 1 a j 1 , … , j s ω n 1 − j 1 ⋅ k 1 … ω n s − j s ⋅ k s
для 0 ≤ k j < n j , j = 1 ,2 , … , s и последовательность a ^ также является периодической. В дальнейшем периодическую последовательность будем указывать на периоде, т.е. a = { a k 1 , … , k s } k 1 , … , k s = 0 n 1 − 1 , … , n s − 1 .
Обратное преобразование Фурье последовательности a определяется равенством:
a ˇ k 1 , … , k s = 1 n 1 … n s ∑ j 1 = 0 n 1 − 1 … ∑ j s = 0 n s − 1 a j 1 , … , j s ω n 1 j 1 ⋅ k 1 … ω n s j s ⋅ k s
Лемма 1. Если задана периодическая последовательность a = { a k 1 , … , k s } k 1 , … , k s = 0 n 1 − 1 , … , n s − 1 , то справедливо равенство

↑ a ^ k 1 , … , k s = a ^ k 1 , … , k s , k j = 0 ,1 , … ,2 n s − 1 , j = 1 , … , s .

Доказательство. Имеем

↑ a ^ k 1 , … , k s = ∑ j 1 = 0 2 n 1 − 1 … ∑ j s = 0 2 n s − 1
∑ j 1 = 0 n 1 − 1 … ∑ j s = 0 n s − 1 a j 1 , … , j s ω 2 n 1 − 2 j 1 k 1 … ω 2 n s − 2 j s k s = ∑ j 1 = 0 n 1 − 1 … ∑ j s = 0 n s − 1 a j 1 , … , j s ω n 1 − j 1 k 1 … ω n s − j s k s = a ^ k 1 , … , k s .
Определение 2. Пусть даны две периодические последовательности a = { a k 1 , … , k s } k 1 , … , k s = 0 n 1 − 1 , … , n s − 1 , b = { b k 1 , … , k s } k 1 , … , k s = 0 n 1 − 1 , … , n s − 1 . Циклическая свертка таких последовательностей c = a ∗ b представляет собой периодическую последовательность, которая определяется равенством
c k 1 , … , k s = ∑ λ 1 , … , λ s = 0 n 1 − 1 , … , n s − 1 a k 1 − λ 1 , … , k s − λ s b λ 1 , … , λ s = ∑ λ 1 , … , λ s = 0 n 1 − 1 , … , n s − 1 b k 1 − λ 1 , … , k s − λ s a λ 1 , … , λ s ,
k 1 = 0 ,1 , … , n 1 − 1 , … , k s = 0 ,1 , … , n s − 1.
Как известно [1], имеет место равенство c ^ = a ^ ⋅ b ^ . Пусть D = и натуральные числа n 1 , … , n s являются четными. Введем обозначение
D 1 =
D 2 s − 1 =
При этом D i , k = .

Лемма 2. Если дано преобразование вида

c j = ( ↑ c j − 1 ) ∗ a j , j = 1 ,2 , … , (1)
где a j — заданная последовательность и C j = c j ^ , A j = a j ^ , то
C α 1 , … , α j j = A α 1 , … , α j j ∙ A α 2 , … , α j j − 1 ∙ … ∙ A α j 1 ∙ C 0 , α 1 , … , α j = 1 ,2 , … , 2 s . (2)

Доказательство. Согласно лемме 1, для преобразования (1) получим (произведение поэлементное)

C α 1 j = A α 1 j ⋅ C j − 1 , α 1 = 1 ,2 , … , 2 s .

Отсюда получаем утверждение леммы.

Заметим, что в схемах подразделений используются не циклические, а линейные свертки. Определение итераций схем подразделений с помощью дискретного преобразования Фурье дается следующей теоремой.

Теорема 5. Пусть дана схема подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 1 , … , j , где
x 0 = { x β 1 , … , β s 0 } β 1 , … , β s ∈ Z , supp x 0 ⊂ ∏ β = 1 s [ k β ,0 0 , k β ,1 0 ] ∩ Z s ,
a = { a β 1 , … , β s } β 1 , … , β s ∈ Z , supp a ⊂
Если n β 0 = k β ,1 0 − k β ,0 0 + 2 r , n β λ = 2 λ n β 0 , k β ,0 λ = 2 k β ,0 λ − 1 − r , k β ,1 λ = 2 k β ,1 λ − 1 + r и периодическую последовательность a λ на множестве ∏ β = 1 s [ 0 ; n β λ − 1 ] ∩ Z s определить равенством
a α 1 , … , α s λ = { a α 1 − r , … , α s − r , α β = 0 ,1 , … ,2 r , β = 1 , … , s ; 0 , 2 r + 1 ≤ α β ≤ n β λ − 1 , β = 1 , … , s , λ = 0 ,1 , … , j ,
то x α 1 , … , α s j = y α 1 − k 10 j , … , α s − k s ,0 j j , α β ∈ [ k β ,0 j ; k β ,1 j ] , β = 1 , … , s , где y j = Y j ˇ ,
Y α 1 , … , α j j = A α 1 , … , α j j ∙ A α 2 , … , α j j − 1 ∙ … ∙ A α j 1 ∙ Y 0 , α 1 , … , α j = 1 ,2 , … , 2 s , Y 0 = y 0 ^ ,
и y α 1 , … , α s 0 = x α 1 + k 1 ,0 0 , … , α s + k s ,0 0 0 , α β = 0 ,1 , … , n β 0 − 1 .

Доказательство. В схеме подразделений

x α 1 , … , α s λ = ∑ β 1 , … , β s a α 1 − 2 β 1 , … , α s − 2 β s x β 1 , … , β s λ − 1 = ∑ β 1 , … , β s a α 1 − β 1 , … , α s − β s
которую можно записать в виде x λ = a ∗ ( ↑ x λ − 1 ) , ненулевые значения x α 1 , … , α s λ могут быть полученны лишь при α β ∈ [ k β ,0 λ ; k β ,1 λ ] , где k β ,0 λ = 2 k β ,0 λ − 1 − r , k β ,1 λ = 2 k β ,1 λ − 1 + r . Таким образом,
k β ,0 λ = 2 k β ,0 λ − 1 − r = 2 2 k β ,0 λ − 2 − 2 r − r = … = 2 λ k β ,0 0 − r ∑ k = 0 λ − 1 2 k = 2 λ k β ,0 0 − r ( 2 λ − 1 ) ,
k β ,1 λ = 2 k β ,1 λ − 1 + r = 2 2 k β ,1 λ − 2 + 2 r + r = … = 2 λ k β ,1 0 + r ∑ k = 0 λ − 1 2 k = 2 λ k β ,1 0 + r ( 2 λ − 1 ) .

Рассмотрим преобразование

y α 1 , … , α s λ = ∑ β 1 = 0 n 1 λ − 1 … ∑ β s = 0 n s λ − 1
∑ β 1 , … , β s = 0 2 r
где n β λ = 2 n β λ − 1 , β = 1 , … , s . Пусть supp y λ − 1 ⊂ ∏ β = 1 s [ η λ − 1 ; η λ − 1 + L s λ − 1 ] . Тогда ненулевые значения y α 1 , … , α s λ могут получаться только при 2 η λ − 1 ≤ α μ − r − β μ ≤ 2 η λ − 1 + 2 L μ λ − 1 , т.е. при η λ ≤ α μ ≤ η λ + L μ λ , где η λ = 2 η λ − 1 , L μ λ = 2 L μ λ − 1 + 2 r .
Пусть η 0 = 0 и L β 0 = k β ,1 0 − k β ,0 0 , n β 0 = L β 0 + 2 r , β = 1 , … , s . Тогда η λ = 0 , ∀ λ и n β λ = 2 λ n β 0 = 2 λ L β 0 + 2 λ + 1 r . С другой стороны
L β λ = 2 L β λ − 1 + 2 r = 2 2 L β λ − 2 + 2 2 r + 2 r = … = 2 λ L β 0 + ∑ k = 1 λ 2 k r =
2 λ L β 0 + 2 r ∑ k = 1 λ 2 k − 1 = 2 λ L β 0 + 2 r ( 2 λ − 1 ) < n β λ − 1.
Пусть y α 1 , … , α s 0 = x α 1 + k 1 ,0 0 , … , α s + k s ,0 0 0 , α β = 0 ,1 , … , n β 0 − 1 . Замечая, что при α s − β s = 2 γ s , s = 1 ,2
получаем x α 1 , … , α s 1 = y α 1 − k 10 1 , … , α s − k s ,0 1 1 . Продолжая рассуждение, находим x α 1 , … , α s j = y α 1 − k 10 λ , … , α s − k s ,0 λ j . Тот факт, что y j = Y j ˇ следует из леммы 2.

Определение начальной последовательности схемы подразделений

В данном разделе использованы обозначения из теоремы 5. Пусть известны значения f l некоторой функции в точках 2 − j l , l ∈ Z s , j ∈ N , при этом supp f ⊂ ∏ β = 1 s [ k β ,0 j ; k β ,1 j ] ∩ Z s . Будем искать начальную последовательность x 0 схемы подразделений x λ = a ∗ ( ↑ x λ − 1 ) , x 0 = x , λ = 1 ,2 , … , j из условия
x 0 = arg min x ‖ x j − f ‖ 2 , supp x ⊂ ∏ β = 1 s [ k β ,1 0 ; k β ,0 0 ] . (3)
Введем в рассмотрение последовательности F = f ∙ + k 0 j ^ , где k 0 j = ( k 1 ,0 j , … , k s ,0 j ) и , α β = 0 ,1 , … , n β j − 1 , β = 1 , … , s . Тогда вместо задачи (3) можно рассмотреть задачу Y 0 = arg min y 0 ‖ F − Y j ‖ 2 . Как показано в теореме 5
Y α 1 , … , α j j = A α 1 , … , α j j ∙ A α 2 , … , α j j − 1 ∙ … ∙ A α j 1 ∙ Y 0 , α β = 1 , … 2 s , β = 1 , … , j .
Если обозначить Q α 1 , … , α j = A α 1 , … , α j j ⋅ A α 2 , … , α j j − 1 … A α j 1 , то можно рассмотреть переопределенную систему линейных уравнений
Q α 1 , … , α j ⋅ Y 0 = F α 1 , … , α j , α β = 1 , … 2 s , β = 1 , … , j . (4)
При этом нужно заметить, что в левой части каждого уравнения произведение поэлементное. Если обозначить Y ¯ 0 , F ¯ α 1 , … , α j , Q ¯ α 1 , … , α j — вектор-столбцы, в которых в некотором порядке (одинаковом) перечислены все элементы Y 0 , F α 1 , … , α j и Q α 1 , … , α j , соответственно, а Q ~ α 1 , … , α j = diag Q ¯ α 1 , … , α j — диагональная матрица, у которой на диагонали стоят элементы вектор-столбца Q ¯ α 1 , … , α m , то каждое уравнение (4) можно записать в матричном виде Q ~ α 1 , … , α j Y ¯ 0 = F ¯ α 1 , … , α j .
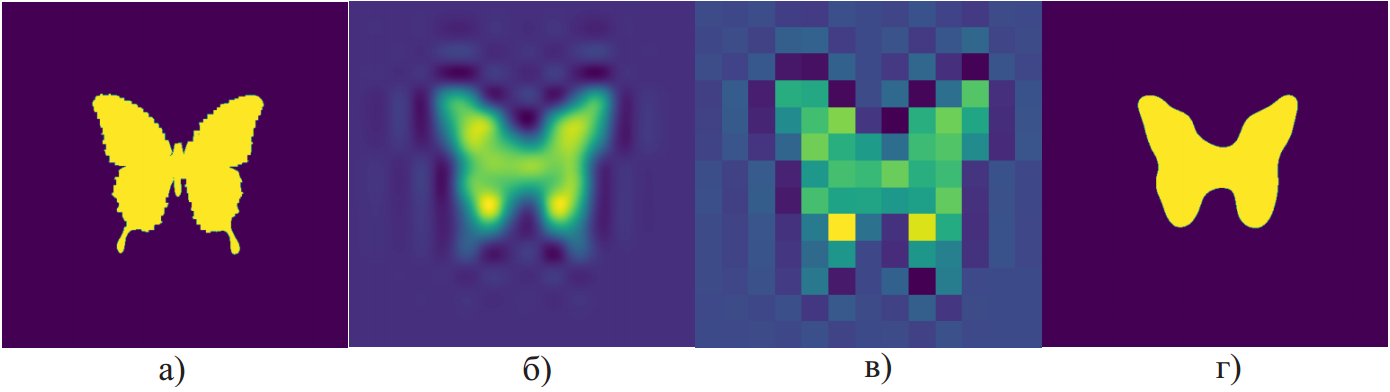
 Рис. 1. Последовательности а) f , б) x7 , в) x2 , г) xθ7 , для θ=0,5
Рис. 1. Последовательности а) f , б) x 7 , в) x 2 , г) x θ 7 , для θ = 0 ,5
 Рис. 2. Последовательности а) f , б) x7 , в) x4 , г) xθ7 , для θ=0,4
Рис. 2. Последовательности а) f , б) x 7 , в) x 4 , г) x θ 7 , для θ = 0 ,4
Обозначим B — блочную матрицу, блоки которой представляют собой матрицы Q ~ α 1 , … , α j , расположенные друг под другом. соответственно, F ¯ — вектор-столбец, у которого F ¯ α 1 , … , α j расположены друг под другом. Таким образом, Y 0 = arg min y 0 ‖ F − Y j ‖ 2 представляет собой решение методом наименьших квадратов системы линейных уравнений B Y ¯ 0 = F ¯ . Отсюда Y ¯ 0 = . Заметим, что B T B представляет собой диагональную матрицу, у которой на главной диагонали перечислены все элементы ∑ β 1 , … , β j = 1 2 s Q β 1 , … , β j ⋅ Q β 1 , … , β j , где произведение поэлементное. Поэтому, если под « » и «/» понимать поэлементное умножение и деление, то
Y 0 = ∑ β 1 , … , β j = 1 2 s Q β 1 , … , β j ⋅ F β 1 , … , β j ∑ β 1 , … , β j = 1 2 s Q β 1 , … , β j ⋅ Q β 1 , … , β j .
Искомая начальная последовательность x 0 определяется равенством:
x α 1 , … , α s 0 = y α 1 − k 10 0 , … , α s − k s ,0 0 0 , y 0 = Y 0 ˇ .
В примере, представленном на рис. 1 рассматривалась схема подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 3 , … ,7 . Заданная последовательность f , которая принимает значения 0 и 1 в точках ( 2 − 7 l 1 , 2 − 7 l 2 ) , l 1 , l 2 ∈ Z , представлена на рис. 1 а). Последовательность x 7 и последовательность x 2 , найденная с помощью дискретного преобразования Фурье, представлены на рис. 1 б), в) соответственно. На рис. 1 г) представлена последовательность x θ 7 = { 1 , x 7 > θ ; 0 , x 7 ≥ θ для θ = 0 ,5 . Аналогичные последовательности для схемы подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 5 , … ,7 и θ = 0 ,4 представлены на рис. 2. В обоих примерах использовалась маска a = u ⊗ u , где u = ( 1 4 , 3 4 , 3 4 , 1 4 ,0 ) .

Моделирование поверхности и области по облаку точек

Пусть задано множество точек P = { p i } i = 1 N ⊂ Z s , и 1 P — характеристическая функция множества P . Для ε > 0 определим последовательность

f l ε = min (5)

где U ε ( 0 ) = { l ∈ Z s : ‖ l ‖ < ε } . Здесь нужно отметить следующее. В статье [13] предлагается сначала построить функцию, значение которой в каждой точке Z s равно расстоянию от этой точки до множества P и с помощью нее определять уже характеристическую функцию области. Построение такой функии занимает существенно больше времени, чем построение функции (5). Если f ε задает границу замкнутой области D , то для получения харакеристической функции 1 D этой замкнутой области в статье использовался морфологический алгоритм заполнения области.
Пусть выбран кратномасштабный анализ [1] с масштабной последовательностью u и масштабирующей функцией φ = S ∞ δ ∈ C r ( R ) . Рассмотрим схему подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 1 , … , j , где a = u ⊗ … ⊗ u . Последовательность x 0 будем находить методом, описанным в предыдущем разделе, где в качестве последовательности f используется 1 D . В этом случае, по теореме 4, функция
( S ∞ x 0 ) ( t ) = ∑ α ∈ Z s x α 0 ( φ ⊗ … ⊗ φ ) ( t − α ) , t ∈ R s
является гладкой аппроксимацией функции 1 D . Соответсвенно область D можно описать неравенством ( S ∞ x 0 ) ( t ) ≥ η , где η ∈ ( 0 ; 1 ) .
 Рис. 3. а) Данное множество точек P , б) последовательность fε для ε=3 в)
Рис. 3. а) Данное множество точек P , б) последовательность f ε для ε = 3 в) характеристическая функция 1 D области D , граница которой представлена заданным множеством точек P , г) последовательность x 6 , д) последовательность x 6 после обнуления части вейвлет-коэффициентов, е) последовательность x 3 , ж) последовательность x θ 6 для θ = 0 ,4 , з) последовательность x θ 6 для θ = 0 ,4 при обнулении части вейвлет-коэффициентов
Пример моделирования области на плоскости представлен на рис. 3, где на рис. 3 а) показано исходное множество точек, на рис. 3 б) последовательность f ε , а на рис. 3 в) характеристическая функция замкнутой области, граница которой определяется f ε . В этом примере рассматривалась схема подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 4 , … ,6 и для нахождения начальной последовательности x 3 использовалась характеристическая функция 1 D . На рис. 3 г) представлена последовательность x 6 , а найденная с помощью дискрентого преобразования Фурье последовательность x 3 , показана на рис. 3 е). На рис. 3 ж) представлена последовательность x θ 6 для θ = 0 ,4 .
Для достижения еще больших сглаживающих эффектов, можно использовать алгоритм вейвлет-разложения [1,2] последовательности x 6 с последующим обнулением вейвлет-коэффициентов по модулю меньших заданного порога и вейвлет-восстановлением [1,2]. Так на рис. 3 д), з) представлены последовательности x 6 и x θ 6 после обнуления части вейвлет-коэффициентов.
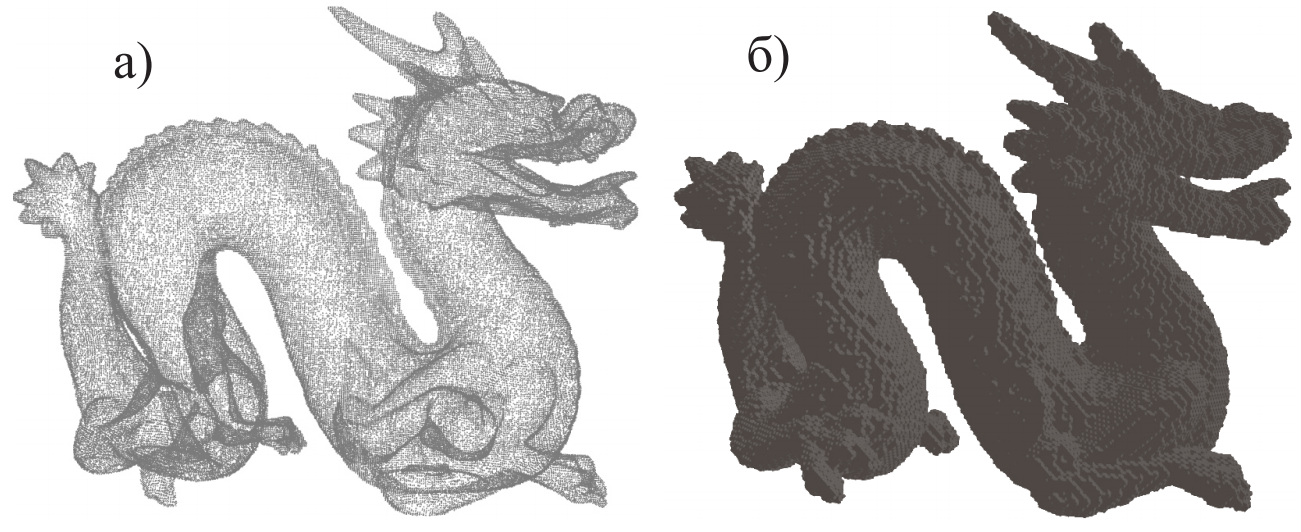
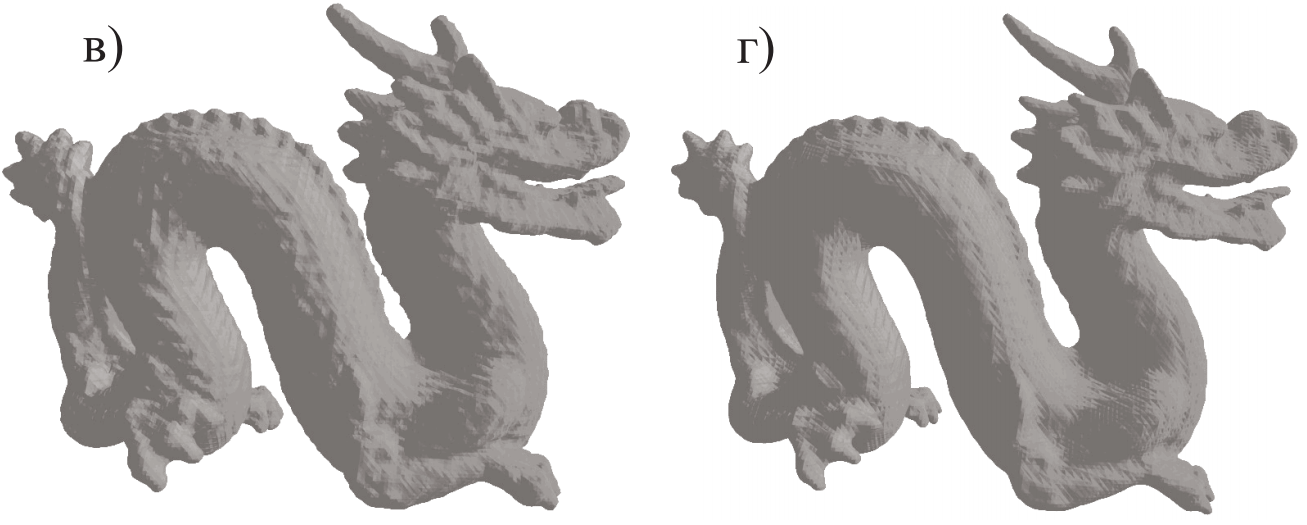
Примеры моделирования трехмерной области показаны на рис. 4 и 5. В обоих случаях рассматривалась схема подразделений x λ = a ∗ ( ↑ x λ − 1 ) , λ = 4 , … ,6 . На рис. а) показано данное облако точек, на рис. б) представлена харакетристическая функция области, на рис. в) и г) показана последовательность x 6 до и после обнуления части вейвлет-коэффициентов.
 
 
Рис. 4 а) Данное множество точек  P , б) характеристическая функция 1 D области D , граница которой представлена заданным множеством точек P , в) последовательность x 6 , д) последовательность x 6 после обнуления части вейвлет-коэффициентов
 
Рис. 5 а) Данное множество точек  P , б) характеристическая функция 1 D области D , граница которой представлена заданным множеством точек P , в) последовательность x 6 , д) последовательность x 6 после обнуления части вейвлет-коэффициентов

Заключение

В данной статье представленно развитие метода геометрического моделирования, основанного на схемах подразделений. Нужно заметить, что к таким схемам относятся часто используемые в задачах геометрического моделирования В-сплайн кривые и поверхности, поскольку сами В-сплайны могут быть получены через схемы подразделений. Статья опирается на результаты, полученные в работах [13,14]. Представлен способ нахождения начальной последовательности схемы посредством дискретного преобразования Фурье и метода наименьших квадратов (МНК). Следует отметить, что без преобразования использовать МНК затруднительно, поскольку размеры матриц велики, а с преобразованием Фурье МНК записывается в очень простой форме и построение матрицы как таковой не требуется.

Литература

  1. Frazier Michael W. An introduction to wavelets through linear algebra. 1999. Springer. 503 p.
  2. Блаттер К. Вейвлет-анализ. Основы теории. Москва, 2004. – 280 с.
  3. Sweldens Wim, The lifting scheme: A custom-design construction of biorthogonal wavelets. Applied and Computational Harmonic Analysis, volume3, issue 2, 1996, pp. 186-200.
  4. Hering-Bertram Martin, Duchaineau Mark, Hamann Bernd and Joy Kenneth. Generalized B-Spline Subdivision-Surface Wavelets for Geometry Compression. IEEE transactions on visualization and computer graphics. (2004) 10. 326-38.
  5. Lounsbery John. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. ACM Transactions on Graphics (TOG), volume 16, issue 1, 1994, pp 34 – 73
  6. Derose T., Kass Michael and Truong Tien. Subdivision Surfaces in Character Animation. Seminal Graphics Papers: Pushing the Boundaries, Volume 2, 2023, pp.801-810
  7. Stollnitz Eric, Derose T. and Salesin David. Wavelets for Computer Graphics: A Primer Part 1. IEEE Computer Graphics and Applications, volume: 15, issue: 3, May 1995, pp. 1-8.
  8. Stollnitz, Eric and Derose, T. and Salesin, David. Wavelets for Computer Graphics: A Primer, Part 2. Computer Graphics and Applications, IEEE. 15. 1995, 75-85.
  9. Hassan Mohamed and Dodgson Neil. Reverse Subdivision, Advances in Multiresolution for Geometric Modelling 2005, pp. 271-283
  10. Битюков Ю.И., Битюков П.Ю. Построение параметрического семейства вейвлетов и использование его в обработке изображений Моделирование и анализ данных, 2023, Том 13, № 4 С. 7–22.
  11. Cavaretta A.S., Dahmen W., and Micchelli C. A., Stationary Subdivision Schemes, Mem. Amer. Math. Soc. 93, 1-186.
  12. Nira Dyn, Analysis of Convergence and Smoothness by the Formalism of Laurent Polynomials. Tutorials on Multiresolution in Geometric Modelling, 2002, 51–68
  13. Dong Bin and Shen Zuowei. Wavelet Frame Based Surface Reconstruction from Unorganized Points. Journal of Computational Physics. 2011, 230, pp 8247-8255.
  14. Dong Bin and Shen Zuowei. MRA-Based Wavelet Frames and Applications. IAS Lecture Note Series, 2013, p 156.

Информация об авторах

Битюков Юрий Иванович, доктор технических наук, доцент, профессор кафедры «Теория вероятностей и компьютерное моделирование», Московский авиационный институт (национальный исследовательский университет) (МАИ), Москва, Россия, ORCID: https://orcid.org/0009-0008-6384-0564, e-mail: yib72@mail.ru

Битюков Павел Юрьевич, студент-магистр, Московский энергетический институт (национальный исследовательский университет) (МЭИ), Москва, Россия, ORCID: https://orcid.org/0009-0000-8697-7047, e-mail: p.bityukoff@yandex.ru

Метрики

Просмотров

Всего: 3
В прошлом месяце: 0
В текущем месяце: 3

Скачиваний

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0