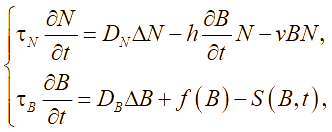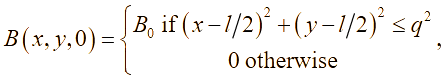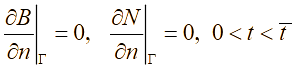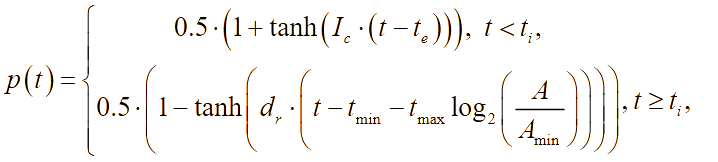Моделирование и анализ данных
2025. Том 15. № 1. С. 19–34
doi:10.17759/mda.2025150102
ISSN: 2219-3758 / 2311-9454 (online)
Система моделирования пространственной динамики бактериальной популяции при вариации режимов антимикробной обработки
Аннотация
Работа посвящена разработке и реализации модели эволюции бактериальной популяции, выращенной на питательной среде, в условиях контролируемого ингибирования биомассы антимикробным препаратом. Для формализации модели использован непрерывно-детерминированный подход. Математическая модель описывается начально-граничной задачей для системы реакционно-диффузионных уравнений, определяющих пространственно-временные распределения питательного субстрата и биомассы с учетом интеграции с фармакокинетической моделью для однократной антимикробной обработки. Модель реализована методом конечных элементов с использованием системы конечно-элементного анализа – платформы COMSOL Multiphysics. Проведена серия вычислительных экспериментов для установления численных закономерностей изменений концентрации бактериальной массы при вариации дозы антимикробного воздействия. Представлено обсуждение потенциальной возможности применения данного подхода для исследования вопроса об устойчивости бактерий к антибиотикам.
Общая информация
Ключевые слова: реакционно-диффузионная система, модель роста бактерий, питательный субстрат, метод конечных элементов, модель логистического роста, фармакокинетика, устойчивость бактерий
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2025150102
Финансирование. Работа выполнена в рамках Программы стратегического академического лидерства Казанского федерального университета («ПРИОРИТЕТ-2030»)
Благодарности. Автор благодарит за помощь в подготовке публикации своего научного руководителя – профессора Масловскую А.Г.
Получена: 05.02.2025
Принята в печать:
Для цитаты: Шуай И. Система моделирования пространственной динамики бактериальной популяции при вариации режимов антимикробной обработки // Моделирование и анализ данных. 2025. Том 15. № 1. С. 19–34. DOI: 10.17759/mda.2025150102
Полный текст
Введение
Методы математического моделирования и инструменты для проведения in silico исследований играют ключевую роль в решении одной из главных проблем современной медицины – выборе оптимальных стратегий применения антибактериальных препаратов для борьбы с инфекциями, вызванными микроорганизмами. Важно отметить, что, несмотря на значимость открытия и использования антибиотиков в истории медицины, на сегодняшний день острой проблемой является развитие устойчивости многих патогенов к широкому спектру применяемых препаратов. Это обуславливает необходимость понимания взаимосвязей между антибактериальной активностью, концентрацией лекарственных средств и механизмами действия антибиотиков, а также требует применения оптимальных стратегий лечения данными препаратами [1–3].
В междисциплинарных исследованиях важную роль играют математические и компьютерные модели кинетики роста биомассы и модели, описывающие взаимосвязь между антибактериальной активностью популяции бактерий и концентрацией лекарственного средства. Один из наиболее распространенных подходов – это детерминированное моделирование пространственно-временных распределений концентрации бактерий и питательного субстрата. Модели типа «реакция-диффузия», адаптированные для изучения микробиологических систем, часто рассматриваются как вариации моделей соперничества. Они представляют собой реакционно-диффузионную модификацию модели Колмогорова-Фишера или пространственно-временную аналогию моделей Моно и Друпа [4–5]. Возможные модификации подходов включают в себя случайный характер роста биомассы для создания натуралистических паттернов, а также зависимость диффузионного процесса от наличия питательных веществ [6–7]. Кроме того, можно учитывать пороговые зависимости в качестве «триггерной» точки для начала роста популяции с учетом эффекта Олли в рамках концепции модели Аллена-Кана [8–10].
Один из простейших методов моделирования взаимосвязи между антибактериальной активностью и концентрацией лекарственного средства – это использование формализации кинетики действия антибиотиков на бактерии на основе уравнения Михаэлиса – Ментен. Для чувствительных к антибиотикам бактерий можно описать связь между действием ингибирующего препарата и его концентрацией [Mueller, 2004]. При низкой концентрации антибиотика скорость роста бактерий может быть прямо пропорциональна концентрации препарата, но по мере увеличения концентрации антибиотика эволюция бактерий может становиться все более подавленным. Связь между антибактериальной активностью и концентрацией лекарственного средства тесно зависит от модели кинетики роста бактерий [Nielsen, 2013]. В отсутствие антибиотиков бактерии развиваются в соответствии с собственной кинетической моделью роста. При введении антибиотиков различные параметры модели антимикробной активности начинают влиять на скорость роста бактерий в зависимости от концентрации лекарства. При низкой концентрации антибиотиков их ингибирующее воздействие на рост бактерий относительно слабое, и рост бактерий преимущественно определяется их собственной кинетикой, однако с увеличением концентрации лекарства скорость роста начнет снижаться из-за присутствия антибиотиков. Эффект действия препарата, согласно модельному подходу, увеличивается постепенно, приводя к более значительному ингибирующему действию на бактериальную биомассу. При достаточно высокой концентрации лекарства происходит остановка или гибель бактерий [Sy, 2016]. Понимание этих двух концепций и их взаимосвязи играет важную роль для построения модели процесса действия антибиотиков в организме. Синтезированный подход помогает объяснить, почему антибактериальный эффект препарата меняется в зависимости от его концентрации. Интеграция обеих моделей обеспечивает более точную информацию для оптимального использования лекарств. Кроме того, эти модели могут быть применены в процессе тестирования новых антибиотиков для предварительной оценки их антибактериального потенциала. Они также позволяют рассмотреть эффективность препарата с учетом пространственно-временной динамики популяций бактерий, что способствует эффективности исследований и построения прогнозов.
В цикле авторских исследований мы развиваем детерминированные модели бактериальной коммуникации [14–15], вследствие которой у многих патогенных бактерий развиваются факторы вирулентности, формируется резистентность к антибиотикам, а также бактериальные сообщества проявляют способность к формированию плотных структур, таких как, например, биопленки. В аспекте этого научного направления чрезвычайно важным является этап формализации и численной реализации модели пространственно-временной эволюции бактериальной массы в зависимости от потребляемого питания и, в случае открытой системы – при наличии факторов ингибирования. Следует отметить, что кинетические модели антимикробной терапии, основанные на применении аппарата обыкновенных дифференциальных уравнений, достаточно хорошо развиты и описаны в литературе, однако их расширения и гибридизация с моделями пространственно-временной динамики биомассы практически отсутствуют (особенно в части связи этих процессов с управлением бактериальной коммуникацией). Данная работа направлена на развитие реакционно-диффузионного подхода в концепции численного моделирования динамики бактериальной популяции, выращенной на питательной среде, в условиях контролируемого ингибирования биомассы антимикробным препаратом. Особый акцент в настоящем исследовании сделан на установлении закономерностей (на основе данных вычислительных экспериментов) взаимосвязи между различными концентрациями антибиотиков и ростом бактериальных культур в неравновесных условиях.
Математическая постановка задачи
Общая математическая формализация двумерной по пространственным координатам модели представляется в виде начально-граничной задачи для системы полулинейных уравнений параболического типа
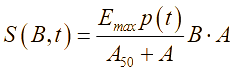 , (3)
, (3)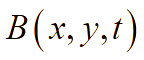
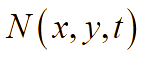
В лабораторных условиях антибиотики обычно добавляют во время приготовления питательной среды, поэтому будем предполагать, что антибиотики равномерно распределены по области (по «чашке Петри»). Известно, что ряд бактерий при постоянном воздействии на них антибактериальными препаратами (например, в госпитальных условиях) постепенно вырабатывают устойчивость (или факторы резистентности). Сущность роста популяции бактерий во многом определяется процессами адаптации к окружающей среде – акт добавления антибиотиков можно понимать как перемещение бактерий из более комфортной среды обитания в среду с чрезвычайно суровыми условиями жизни, в результате чего и вырабатывается способность бактерий выживать при ингибирующих внешних факторах. В результате, жизненный цикл можно разделить на четыре стадии: латентный период, период быстрого уничтожения популяции, период стабильности и период повышения антибактериальной устойчивости. Этот процесс, в части описательной динамики, очень похож на четыре стадии роста бактериальной популяции. В соответствии с принципом аналогии, формализуем эти четыре этапа с помощью аппроксимирующей функции p(t):
где tmin – параметр, отвечающий за продолжительность действия антибиотика в состоянии насыщения, час; te – время достижения состояния насыщения для действия антибиотика, час; Ic – интенсивность действия антибиотиков, 1/час; ti – параметр времени, определяющий интервал активного действия антибиотика, час; dr – параметр, отвечающий за интенсивность бактериальной резистентности, 1/час; tmax – параметр времени, отвечающий за усиление резистентности, час; Amin – минимальная эффективная концентрация антибиотиков в эксперименте, отн.ед./м3.
Результаты вычислительных экспериментов
Реализация математической модели, описываемой системой соотношений (1)–(6), проводилась с использованием метода конечных элементов в среде пакета COMSOL Multiphysics®.
При планировании вычислительных экспериментов мы приняли во внимание, что в лабораторных условиях единицы измерения концентрации бактериальной биомассы отличаются от единиц измерения концентрации антибактериальных препаратов и питательных веществ. В рамках реализуемой пространственно-временной модели мы установили нормализованные значения концентраций бактерий, антибиотиков и питательных веществ, используя шкалу [0, 1]. Так, например, максимальное значение концентрации бактерий равно единице, минимальное – нулю, соответственно, в области, не содержащей биомассу. Как было отмечено выше, для концентрации биомассы B(x,y,t) принята единица измерения – отн.ед./м3. Аналогично, значение минимальной концентрации антибиотиков, которое позволяет полностью деградировать бактерии, равно 1 отн.ед./м3, в случае, если антибиотик отсутствует, значение концентрации A(t)=0 отн.ед./м3. Наконец, для численной оценки питательных веществ: максимальная концентрация питательных веществ в среде равна 1 отн.ед./м3, минимальная (среда не содержит питания, обеспечивающего рост биомассы) – 0 отн.ед./м3.
Основной целью вычислительных экспериментов являлось установление закономерностей эволюции бактериальных популяций, выращенных на питательных средах (например, в чашке Петри), в условиях, соответствующих лабораторным, при контроле процесса ингибирования биомассы грамотрицательных бактерий антимикробным препаратом. Значения параметров, инициализированные для вычислительных экспериментов, представлены в таблице 1.
Таблица 1. Значения параметров модели
|
Имя |
Значение |
Описание |
|
DB |
110-10 |
Коэффициент диффузии биомассы, м2/час |
|
DN |
10-8 |
Коэффициент диффузии нутриента, м2/час |
|
B |
0.066 |
Масштабирующий параметр для времени для бактериального роста, 1 |
|
N |
11 |
Масштабирующий параметр для нутриента, 1 |
|
a |
0.5 |
Собственный темп роста биомассы, м3/(отн.ед.час) |
|
b |
1 |
Параметр «несущей способности» для бактерий, отн.ед./м3 |
|
h |
10 |
Скорость, с которой питательные вещества поглощаются внешним краем колонии, м3/отн.ед. |
|
v |
1.5 |
Скорость, с которой питательные вещества поглощаются внутренней зоной колонии, м3/(отн.ед.час) |
|
N0 |
1 |
Начальная концентрация нутриента, отн.ед./м3 |
|
B0 |
1 |
Начальная концентрация бактерий, отн.ед./м3 |
|
Emax |
0.53 |
Параметр скорости, соответствующий максимальному эффекту действия антибиотика, 1/час |
|
A50 |
0.01 |
Концентрация антибиотика, обеспечивающая 50% максимального эффекта действия антибиотика, отн.ед. /м3 |
|
tmin |
4 |
Продолжительность действия антибиотика в состоянии насыщения, час |
|
te |
4 |
Время достижения состояния насыщения для действия антибиотика, час |
|
dr |
0.2 |
Интенсивность бактериальной резистентности, 1 |
|
Ic |
4 |
Интенсивность действия антибиотиков, 1/час |
|
Amin |
0.0009896 |
Минимальная эффективная концентрация антибиотиков в эксперименте, отн.ед./м3 |
|
ti |
4 |
параметр времени, определяющий интервал активного действия антибиотика, час |
Опираясь на результаты, описанные в исследовании [Firsov, 1997], проанализируем закон динамики эффекта действия антибиотиков в эксперименте. Если пренебречь диффузией в пространстве и временно установить перманентную скорость роста бактерий постоянной – r (1/час), то скорость изменения биомассы бактерий, на которую влияют антибиотики, равна
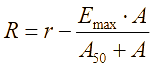 , 1/час. (7)
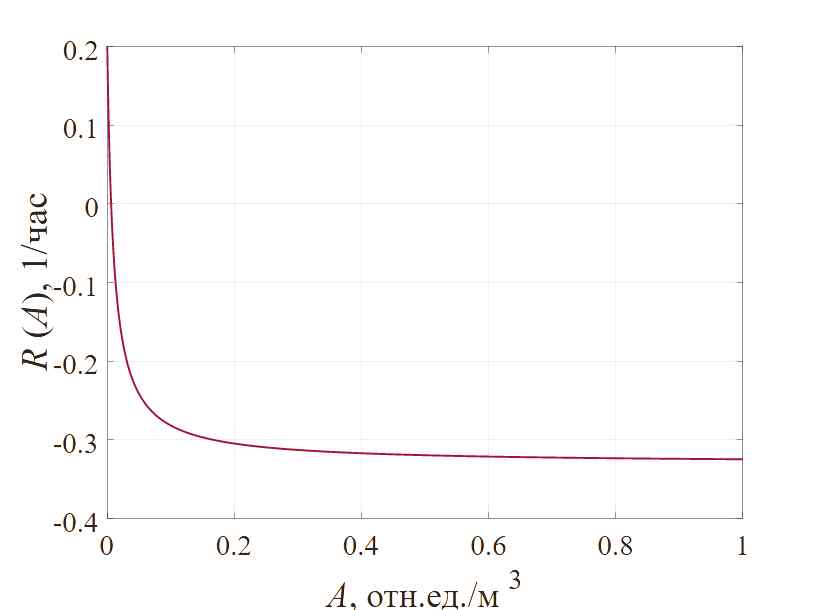
, 1/час. (7)В эксперименте [Firsov, 1997] при начальной концентрации антибиотика 0.038 – 9.6 мкг/мл, количество бактерий сначала уменьшается, а затем происходит «регенерация» – увеличение биомассы. В то же время, при концентрации антибиотиков менее 0.019 мкг/мл, колония сохраняется; если же концентрация антибиотиков превышает 19.2 мкг/мл, популяция бактерий уничтожается полностью. Согласно экспериментальным данным [Firsov, 1997], концентрация антибиотиков возрастала экспоненциально. Если значение параметра A50 принять 0.0039 отн.ед./м3, а максимальную скорость ингибирования – 0.3 1/час, тогда визуализация зависимости (7) будет иметь вид, показанный на рисунке 1. Можно отметить, что существует порог между концентрацией антибиотика и скоростью роста, и когда концентрация антибиотика достигает определенного значения, скорость роста бактерий становится отрицательной.
Рис. 1. Зависимость скорости изменения биомассы бактерий от концентрации антибиотика
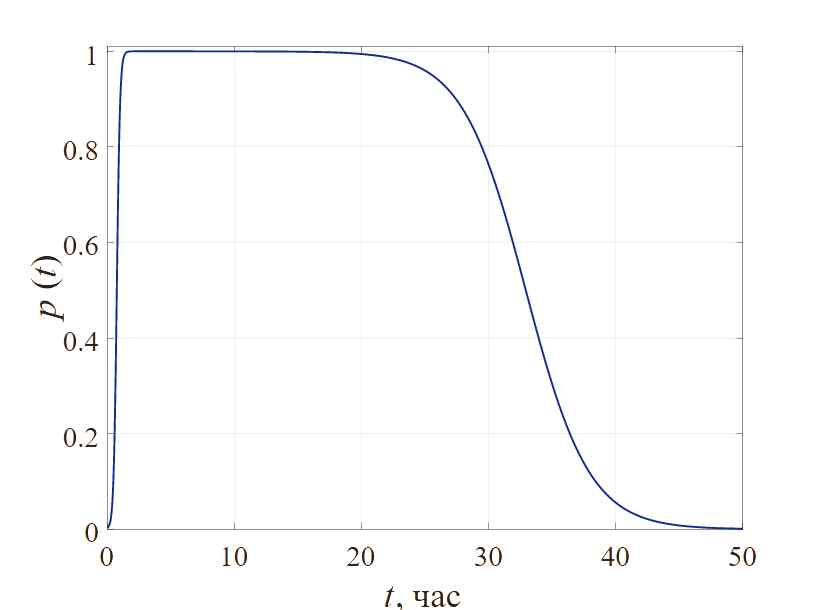
Для аналитического описания функции p(t) воспользуемся соотношением (6). Придавая значения параметрам (таблица 1), представим график функциональной зависимости, отражающий реакцию биосистемы на ингибитор, как показано на рисунке 2.
Кривая отображает процесс формирования бактериальной резистентности, в котором можно выделить пять стадий: инкубационный период, период быстрой стерилизации, период насыщения (фаза стабилизации), период повышенной резистентности и полное развитие лекарственной устойчивости бактериальной популяции. По мере роста концентрации антибиотиков время развития устойчивости бактерий будет постепенно увеличиваться. Если установить различные значения концентрации антибиотика, продолжительность фазы стабилизации также будет разной. Зависимость между временем развития устойчивости и концентрацией антибиотиков подтверждается данными экспериментальным исследований (например, [Firsov, 1997]).
Для более глубокого понимания механизмов, определяющих поведение модели, визуализируем взаимосвязь между скоростью роста бактерий и скоростью их деградации за счет антибиотиков, игнорируя влияние устойчивости бактерий, то есть зависимость f(B)–S(B,t) как функцию концентрации биомассы В.
Рис. 2. Общий вид модельной зависимости p(t)
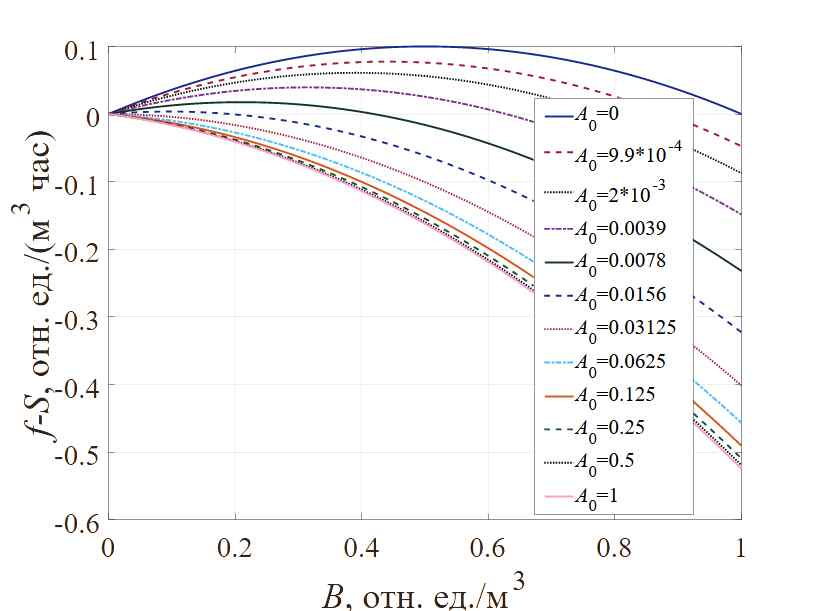
Учитывая только взаимосвязь между тремя факторами: скоростью роста бактериальной популяции, насыщенностью локальной популяции и концентрацией антибиотиков в определенный момент периода стабилизации в среде, содержащей антибиотики, визуализируем зависимости, как показано на рисунке 3. Представленная графическая интерпретация демонстрирует влияние различных концентраций антибиотиков на скорость роста популяции бактерий.
Рис. 3. Зависимость скорости роста бактерий при вариации начальной концентрации антибиотика
Можно отдельно отметить, что в силу законов, формализованных в модели, когда концентрация антибиотика превышает 0.0625 отн.ед. /м3, рост бактерий прекращается при любой плотности популяции. По мере увеличения концентрации антибиотика скорость роста бактериальной популяции будет в определенной степени снижаться, как и локальная максимальная плотность бактериальной популяции также будет уменьшаться, причем степень того и другого снижения согласуется с функциональной зависимостью, представленной на рисунке 1.
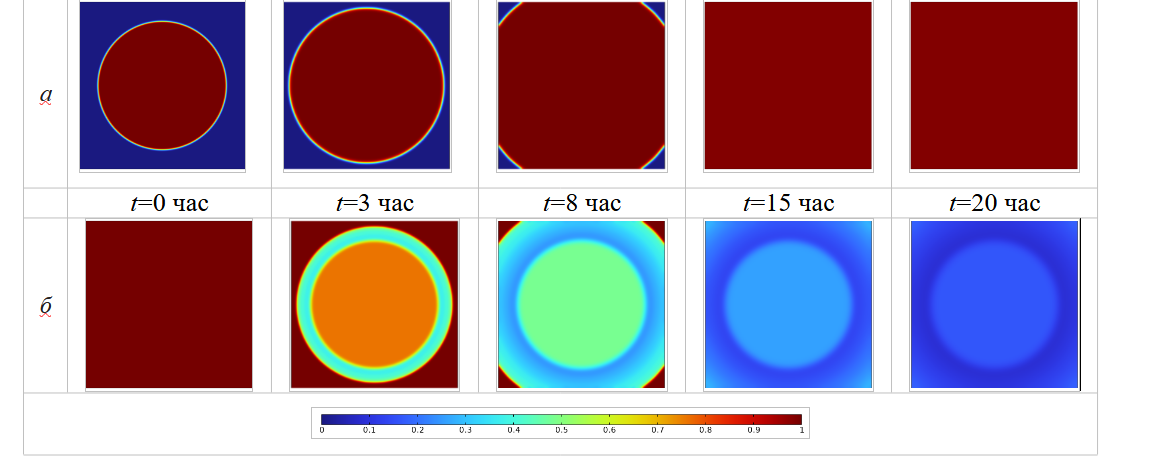
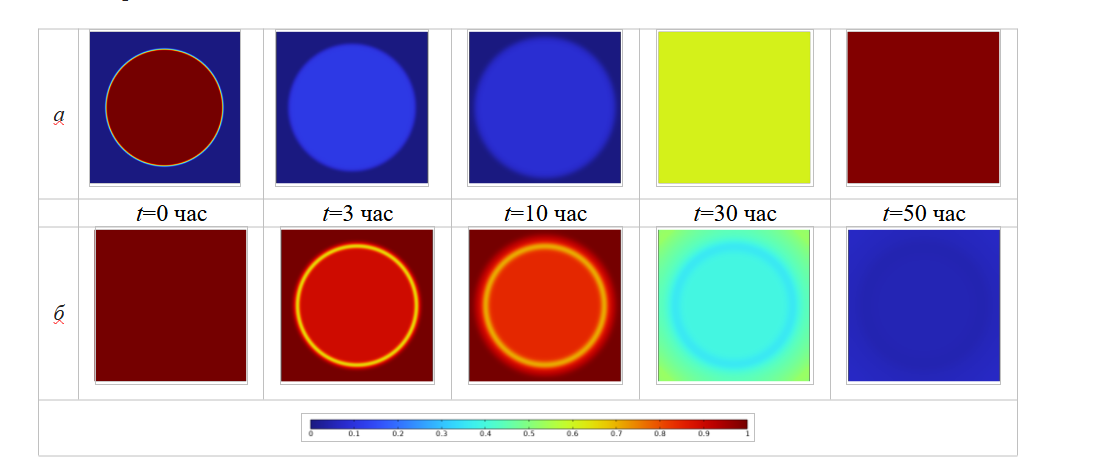
Далее рассмотрим пространственно-временную связь между ростом бактериальной биомассы, потреблением питательных веществ и воздействием антибактериальным препаратом. Для системы уравнений (1)–(6) рассмотрим две серии вычислительных экспериментов. Первая группа представляет собой контрольный эксперимент, целью которого является анализ процесса роста бактериальной колонии в чашке Петри без добавления антибиотиков. В вычислительном эксперименте для визуализации поверхностного распределения биомассы и питательного субстрата зафиксируем следующие моменты времени: t=0, 3, 8, 15, 20 час. Для второй серии экспериментов введем учет процедуры ингибирования антибактериальным препаратом, который в начальный момент t=0 час имеет концентрацию 0.00625 отн.ед./м3 (поверхностные распределения биомассы и питательного субстрата визуализируем для фиксированных моментов времени t=0, 3, 10, 30, 50 час). Результаты симуляций представлены на рисунках 4 и 5 соответственно.
Рис. 4. Пространственные распределения концентраций: биомассы – а; питательных веществ – б
На рисунке 4 a, сохраняя неизменной плотность бактериальной популяции внутри колонии, биомасса со временем постепенно расширялась и заполняла всю предоставленную площадь. Этот процесс также сопровождается потреблением питательных веществ, как показано на рисунке 4 б. В определенный временной диапазон (как показано на рисунке, около 3 час) в распределении питательного субстрата можно выделить две характерные области, имеющие формы колец, а именно – внешний край и внутреннюю часть бактериальной колонии. При принятых параметрах модельного расчета, внешний край потребляет питательные вещества с большей скоростью, чем внутренняя зона, поэтому питательные вещества не распределяются в форме концентрических кругов по мере роста бактериальной колонии. Концентрация питательных веществ будет постепенно снижаться по мере биологической активности бактерий, как показано на рисунке 4 б, пока все доступное питание не будет потреблено окончательно.
В случае деградации биомассы за счет действия антибактериальным препаратом в начальный момент времени (как показано на рисунке 5 б) плотность бактериальной популяции быстро снижается. Сравнение площадей, занимаемых колониями, в момент времени t=3 час., позволяет заключить, что сразу после добавления антибиотика колония перерастает расширяться. Это обусловлено базовыми механизмами математической модели, соответствующими экспериментально наблюдаемым: когда плотность бактериальной популяции снижается, скорость расширения бактериальных колоний, вызванная градиентом концентрации, также снижается.
Рис. 5. Пространственные распределения концентраций: биомассы – а; питательных веществ – б с учетом действия антибиотиков
Далее, в процессе эволюции бактериальных колонии (после t=20 час) наблюдается процесс развития устойчивости бактерий по отношению антибактериального препарата. В этот период эффективность действия антибиотиков постепенно снижается, а плотность бактериальной популяции начинает увеличиваться до тех пор, пока не достигнет максимально возможного значения в данной области, как показано на рисунке 5 а (t=50 час). Поскольку антибиотики влияют на рост популяции бактерий, это приводит и к опосредованному влиянию на потребление питательных веществ. Сравнение результатов симуляции, представленных на рисунках 4 и 5, б (при t=3 час) свидетельствуют, что скорость потребления питательных веществ в случае добавления антибиотиков значительно меньше, чем в отсутствие внешнего воздействия на колонию.
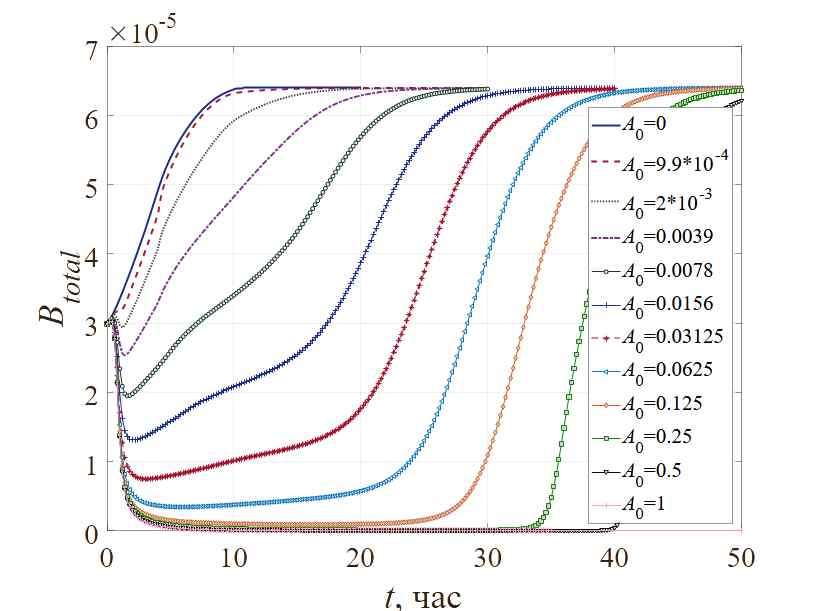
Для дальнейшего анализа введем в рассмотрение дополнительно оцениваемую в вычислительных экспериментах величину – интегральное значение концентрации биомассы Btotal, вычисленное в каждый момент времени. Графики на рисунке 6 показывают динамику изменения этого интегрального значения с течением времени. Для всех представленных доз антибактериального препарата в течение первого часа рост бактерий классической логистической кривой. Далее, накопленный эффект действия антибиотика приведет к деградации биомассы в зависимости от уровня концентрации ингибитора в начальный момент времени (разные концентрации антибиотиков вызывают уничтожение бактерий с разной скоростью, что приводит к изменению общего вида функциональной зависимости Btotal(t)). В то время как одна часть бактериальной колонии погибает под действием антибиотика, другая, «живая», часть развивает резистентность в ходе метаболического процесса. Этот процесс обладает устойчивостью – когда толерантные к ингибитору бактерии достигнут определенной концентрации в среде, популяция будет быстро расти и далее (при наличии питания) сохранять свою численность постоянной.
Рис. 6. Динамика изменения общего концентрации бактерий при вариации значений концентраций антибиотиков
Кроме того, при отсутствии ингибитора (А0=0) характер роста общей бактериальной популяции на участке соответствует логистической модели. Популяция бактерий не уменьшается при самой низкой концентрации антибиотика А0=0.0009896 отн.ед./м3, а при самой высокой концентрации антибиотика А0=1 отн.ед./м3 регенерация популяции отсутствует. Поскольку концентрация антибиотиков постепенно увеличивается, время развития устойчивости бактерий также постепенно увеличивается до тех пор, пока не будет достигнута полная ингибирующая концентрация антибиотиков в этой среде, и бактерии больше не смогут регенерировать. Следует отметить, что данная модель может быть применена и для прогнозирования эффектов ингибирования биомассы при использовании методик многократной обработки.
Заключение
Таким образом, настоящее исследование обобщает результаты реализации реакционно-диффузионной модели динамики бактериальной популяции, выращенной на питательной среде, в условиях контролируемого ингибирования биомассы антимикробным препаратом. Была предложена авторская модификация модели, включающая классическую модель популяционной динамики, формализуемой с помощью уравнения Колмогорова – Петровского – Пискунова – Фишера с учетом влияния ингибитора, а также модель пространственно-временной эволюции питательного субстрата, динамически зависящего от концентрации биомассы, и функциональную зависимость, описывающая процесс деградации колонии в зависимости от реакции биосистемы на ингибитор. Проведена численная реализация модели с исполдзованием метода конечных элементов в пакете COMSOL Multiphysics. Представлены законы действия антибиотиков при определенных параметрах, формализованы механизмы формирования резистентности бактерий и закономерности скорости роста бактерий под действием различных концентраций антибиотиков. Результаты вычислительных экспериментов (для фиксированного набора условий и параметров) позволяют установить динамику формирования факторов резистентности бактерий по отношению к антимикробным препаратам, а также прогнозировать уровни доз антибиотика, необходимых при достижении цели полного уничтожения популяции. Перспективу настоящего исследования представляет реализация более сложного варианта модели формирования бактериальных паттернов [Shuai, 2024] на основе модификации модели Аллена-Кана в условиях многократной антибактериальной обработки, а также формализации связи между резистентностью микробов и уровнем бактериального кворума [14-15].
Литература
- Aslam B., Wang W., Arshad M.I., Khurshid M., Muzammil S., Rasool M.H., Nisar M.A., Alvi R.F., Aslam M.A., Qamar M.U., Salamat M.K. Antibiotic resistance: a rundown of a global crisis // Infection and drug resistance. 2018. Vol. 10. P. 1645–1658. DOI: 10.2147/IDR.S173867
- Frieri M., Kumar K., Boutin A., Antibiotic resistance // Journal of infection and public health. 2017. Vol. 10. № 4. P. 369–378. DOI:10.1016/j.jiph.2016.08.007
- Golding I., Kozlovsky Y., Cohen I., Ben-Jacob E. Studies of bacterial branching growth using reaction–diffusion models for colonial development // Physica A: Statistical Mechanics and its Applications. 1998. Vol. 260. № 3–4. P. 510–554. DOI:10.1016/S0378-4371(98)00345-8
- Eberl H.J., Parker D.F., van Loosdrecht M.C.M. A new deterministic spatio‐temporal continuum model for biofilm development // Computational and Mathematical Methods in Medicine. 2001. Vol. 3. № 3. P. 161-175. DOI:10.1080/10273660108833072
- Mimura M., Sakaguchi H., Matsushita M. Reaction-diffusion modelling of bacterial colony patterns // Physica A: Statistical Mechanics and its Applications. 2000. Vol. 282. № 1–2. P. 283–303. DOI:10.1016/S0378-4371(00)00085-6
- Kawasaki K., Mochizuki A., Matsushita M., Umeda T., Shigesada N. Modeling spatio-temporal patterns generated bybacillus subtilis // Journal of theoretical biology. 1997. Vol. 188. № 2. P. 177–185. DOI:10.1006/jtbi.1997.0462
- Шевкун И.А., Масловская А.Г. Гибридный подход к моделированию и оценке структурных особенностей паттернов культивированных бактерий // Математическое моделирование. 2024. Т. 36. № 6. С. 59–73. DOI:10.20948/mm-2024-06-04
- Jornet M. Modeling of Allee effect in biofilm formation via the stochastic bistable Allen–Cahn partial differential equation // Stochastic Analysis and Applications. 2020. Vol. 39. № 1. P. 22–32. DOI:10.1080/07362994.2020.1777163
- Tijani Y.O., Appadu A.R. Unconditionally positive NSFD and classical finite difference schemes for biofilm formation on medical implant using Allen-Cahn equation // Demonstratio Mathematica. 2022. Vol. 55. № 1. P. 40–60. DOI:10.1515/dema-2022-0006
- Shuai Y., Maslovskaya A. Computer-assisted approach to study of bacterial communication for Landau-based model of population growth // 2024 Applied Mathematics, Computational Science and Mechanics: Current Problems (AMCSM), Voronezh, Russian Federation. 2024. P. 1–7. DOI:10.1109/AMCSM59829.2023.10525808
- Mueller M., de la Pena A., Derendorf H. Issues in pharmacokinetics and pharmacodynamics of anti-infective agents: kill curves versus MIC // Antimicrobial agents and chemotherapy. 2004. Vol. 48. № 2. P. 369–377. DOI:10.1128/aac.48.2.369-377.2004
- Nielsen E.I., Friberg L.E. Pharmacokinetic-pharmacodynamic modeling of antibacterial drugs // Pharmacological reviews. 2013. Vol. 65. № 3. P. 1053–1090. DOI: 10.1124/pr.111.005769
- Sy S.K., Zhuang L., Derendorf H. Pharmacokinetics and pharmacodynamics in antibiotic dose optimization // Expert opinion on drug metabolism & toxicology. 2016. Vol. 12. № 1. P.93–114. DOI:10.1517/17425255.2016.1123250
- Shuai Y., Maslovskaya A., Kuttler C. 2D reaction-diffusion model of quorum sensing characteristics during all phases of bacterial growth // Far Eastern Mathematical Journal. 2022. Vol. 22. № 2. P. 232-237. DOI:10.47910/FEMJ202231
- Shuai Y., Maslovskaya A.G., Kuttler C. Modeling of bacterial communication in the extended range of population dynamics // Mathematical Biology and Bioinformatics. 2023. Vol. 18. № 1. P. 89–104.DOI:10.17537/2023.18.89
- Martínez-Calvo A., Bhattacharjee T., Bay R.K., Luu H.N., Hancock A.M., Wingreen N.S., Datta S.S. Morphological instability and roughening of growing 3D bacterial colonies // Proceedings of the National Academy of Sciences. 2022. Vol. 119. № 43. P. e2208019119. DOI:10.1073/pnas.2208019119
- Firsov A.A., Vostrov S.N., Shevchenko A.A., Cornaglia G. Parameters of bacterial killing and regrowth kinetics and antimicrobial effect examined in terms of area under the concentration-time curve relationships: action of ciprofloxacin against Escherichia coli in an in vitro dynamic model // Antimicrobial agents and chemotherapy. 1997. Vol. 41. № 6. P. 1281–1287. DOI:10.1128/aac.41.6.1281
- Roberts P.A., Huebinger R.M., Keen E., Krachler A.M., Jabbari S. Mathematical model predicts anti-adhesion-antibiotic-debridement combination therapies can clear an antibiotic resistant infection // PLoS Comput Biol. 2019. Vol. 15. № 7. P. e1007211. DOI: 10.1371/journal.pcbi.1007211
Информация об авторах
Метрики
Просмотров web
За все время: 21
В прошлом месяце: 0
В текущем месяце: 21
Скачиваний PDF
За все время: 6
В прошлом месяце: 0
В текущем месяце: 6
Всего
За все время: 27
В прошлом месяце: 0
В текущем месяце: 27