Применение машинного обучения для оценки растворимости лекарственных соединений: сравнение различных представлений молекулярных данных

Растворимость является одной из ключевых характеристик лекарств и важна для определения на ранних этапах разработки препарата. Алгоритмы, основанные на машинном обучении (ML), предлагают более быстрое решение этой задачи по сравнению с вычислительно более затратными методами, использующими расчеты энергии, квантовую динамику и расчеты молекулярной динамики. В данной работе несколько алгоритмов ML, использующих различные подходы к представлению молекулярных данных, а именно сверточные нейронные сети, графовые нейронные сети и градиентный бустинг на основе решающих деревьев, применяются к открытому набору данных из недавно опубликованного конкурса Kaggle по растворимости, содержащему более чем 70 000 соединений. Производительность моделей оценивается на тестовом наборе данных, предоставленном на данном соревновании, а также на локально созданном независимом наборе данных. Результаты показывают более высокую точность модели градиентного бустинга, обученной на табличном представлении молекул, в сравнении с другими обученными методами. Данная модель также демонстрирует сравнимые результаты с другими решениями, представленными в таблице лидеров выбранного конкурса Kaggle.

Введение

Одним из ключевых физико-химических свойств, которые учитываются при разработке лекарств, является водная растворимость. Растворимость может влиять на вариабельность пероральной биодоступности, вызывать недостаточное всасывание и, следовательно, недостаточную эффективность препарата. Кроме того, низкая растворимость затрудняет тестирование активности соединения и вызывает нежелательные побочные эффекты [Fink, 2020]. Поэтому фармацевтические компании приоритизируют растворимость как один из ключевых этапов оптимизации лекарств [Ameta, 2023]. Однако оценка растворимости соединений остается сложной задачей. Появляется все больше информации, подтверждающей, что растворимость лекарств in vitro может недооценивать настоящую растворимость in vivo [Fink, 2020]. Исследование, проведенное в 2010 году, оценило, что 40% доступных лекарств обладают низкой растворимостью [Loftsson, 2010], а проведенное уже в 2014 году исследование оценило, что около 70% молекул, находящихся в разработке, имеют низкую растворимость [Basavaraj, 2014].

Было разработано множество алгоритмов для прогнозирования растворимости: полуэмпирические методы, такие как модифицированное уравнение растворимости [Ran, 2001], которое не использует подогнанные параметры, UNIFAC, метод, который объединяет концепцию функциональных групп с коэффициентами активности, основанными на квазихимической теории жидких смесей [Fredenslund, 1975], методы, основанные на минимизации энергии, которые используют симуляции кристаллической решетки и свободной энергии [Palmer, 2012], методы молекулярной динамики [Li, 2017], [Boothroyd, 2019], модели, основанные на количественных данных взаимосвязи между структурой и активностью [Duchowicz, 2009], [Yu, 2006]. Решения, использующие ML, также применялись для этой задачи, стремясь обеспечить более высокую точность по сравнению с полуэмпирическими методами, для которых требуются более длительные и сложные расчеты, основанные на минимизации энергии и динамическом моделировании. Были исследованы различные подходы ML к прогнозированию растворимости: в [Palmer, 2007] было проведено сравнение случайного леса (RF), метода частичных наименьших квадратов, метода опорных векторов и искусственных нейронных сетей, в [Deng, 2019] были разработаны модели с применением сверточной нейронной сети (CNN), рекуррентной нейронной сети, глубокой нейронной сети и спайковых нейронных сетей. В [Lusci, 2013] был реализован ансамбль рекурсивных нейронных сетей. Комбинации различных архитектур ML и вычислительной химии также использовались для этой задачи в [Boobier, 2020].

Большинство доступных наборов данных о соединениях с известной растворимостью предоставляют информацию о соединениях в их упрощенной молекулярной входной строковой записи (SMILES), которая является широко признанной формой описания молекулярных структур. В результате многие существующие модели используют признаки, полученные из SMILES, и важным отличительным аспектом решений на основе ML является то, как они представляют молекулу в пространстве признаков. Сбор физико-химических свойств (например, число тяжелых атомов или молекулярный вес) является общим шагом для почти всех существующих решений на основе ML, однако подход к извлечению структурных данных может различаться. В данной работе рассматриваются три часто используемых подхода к декодированию SMILES молекул: представление в виде отпечатков Моргана [Morgan, 1965], токенизация символов SMILES и их рассмотрение как последовательности закодированных токенов, а также построение молекулярного графа на основе доступной информации об атомах и их связях. Используя публично доступный набор данных, содержащий более 70 000 молекул с известной растворимостью, были обучены и сравнены ML -модели на основе трех различных алгоритмов и подходов к представлению данных: модель градиентного бустинга в реализации CatBoost [Prokhorenkova, 2018], одномерная сверточная нейронная сеть (1D CNN) и графовая нейронная сеть на основе механизма внимания.

Материалы и методы

ML алгоритмы

Относительно недавний подход к представлению молекулярных данных заключается в кодировании символов SMILES в токены, создании обучаемых векторных представлений для этих токенов и обработке молекулы как последовательности этих обученных векторных представлений. Архитектура 1D CNN является одним из возможных подходов к построению нейронной сети, которая может быть обучена на таких данных. Этот подход набирает популярность как инструмент работы с молекулярными данными. Он показал высокую производительность в недавнем открытом конкурсе по предсказанию молекулярных свойств [Blevins, 2024]. 1D CNN выполняет свёртку по последовательности векторных представлений токенизированного SMILES, что позволяет извлекать структурные закономерности. В данном исследовании использовалась реализация 1D CNN из библиотеки PyTorch [Paszke], которая учитывает взаимную корреляцию и может в общих чертах быть описана следующим образом (предполагая, что фильтр перебирает элементы по одному) [Cacciari, 2024]:

Кроме того, в свёртку также включается обучаемый параметр суммируемого смещения. Помимо токенизированной последовательности, 1D CNN также был обучен использовать вышеупомянутые 11 физико-химических дескрипторов, чтобы обеспечить глобальное представление молекулярных свойств. Дополнительные признаки были объединены с выводом блока 1D CNN слоев для использования в последующих линейных слоях.

Графическое представление является одним из распространённых способов описания молекулярных структур, и открывает возможности для использования графовых нейронных сетей, применение которых набирает популярность в области биоинформатики и разработки лекарств. Графовая нейронная сеть обрабатывает молекулярный граф как комбинацию узлов и рёбер, где узлы представлены набором признаков, соответствующих данному атому, а рёбра представлены списками пар индексов узловых признаков. В данной работе признаки на ребрах графа были определены дескрипторами гибридизации и типом связи и также использовались графовой нейронной сетью. Существует множество архитектур операторов графовых нейронных сетей, основным различием которых являются используемые методы передачи сообщений и обновления информации узлов. Выбранный графовый нейронный оператор [Shi] использует механизм многоголового внимания, широко применяемый в архитектурах трансформеров, и может быть описан следующим образом:

Обученная модель GNN использовала графовое представление последовательности SMILES в качестве входных данных, где свойства атомов (например, имя атома, гибридизация) хранились в виде признаков узлов, а информация о связях — на ребрах графа. Кроме того, вышеупомянутые 11 физико-химических дескрипторов были использованы в качестве дополнительных признаков, которые конкатенируются с результирующим объединённым вектором выходных данных GNN, чтобы далее использоваться в последующих линейных слоях.

Описание набора данных и их предобработка

Набор данных был взят из недавно опубликованного соревнования Kaggle «1st EUOS/SLAS Joint Challenge: Compound Solubility», для которого данные подготовила организация EU-OPENSCREEN ERIC [Zaliani, 2022]. Набор данных содержит 101 017 соединений, из которых 70 710 доступны для обучения моделей, а 30 307 зарезервированы для тестирования моделей. Каждое соединение записано в формате SMILES, дополнительно предоставлены идентификаторы соединений. Целью конкурса было правильно предсказать метку растворимости соединения, которая могла быть высокой, средней или низкой (в предоставленном наборе данных обозначены как 2, 1 и 0 соответственно). В обучающей выборке из 70 710 соединений содержалось 65 834 соединения с высокой растворимостью, 2 835 соединений со средней растворимостью и 2 041 соединение с низкой растворимостью. В рамках данного исследования обучающая часть опубликованного набора данных была использована для подготовки обучающих, валидационных и независимых тестовых наборов данных для обучения и сравнения разработанных моделей. 30 307 соединений из исходного набора данных также были использованы для дополнительного тестирования.

В рамках предобработки данных была проанализирована длина строковых описаний соединений в формате SMILES. Хотя 99,8% всех соединений в формате SMILES содержали от 18 до 95 символов, были выявлены некоторые выбросы, достигающие 226 символов и минимально 7 символов. Поскольку все 3 разрабатываемые модели чувствительны к размеру входной структуры, выбросы были удалены. Для сравнения был сформирован внутренний независимый тестовый набор путем отделения 10% данных случайным образом. Оставшиеся данные были разделены на 5 случайных обучающих и валидационных разбиений. Одни и те же разбиения были использованы для обучения моделей всех трех алгоритмов, чтобы обеспечить более объективное сравнение. Для учета несбалансированности набора данных к предсказаниям моделей были применены экспоненциальные балансировочные коэффициенты. Коэффициенты были настроены для получения максимального квадратичного коэффициента Каппа (коэффициента Каппа) на обучающем наборе данных, используя реализацию алгоритма минимизации Пауэлла [Powell, 1964] в библиотеке Python Sklearn [Pedregosa et, 2011].

Подготовка и обучение моделей

Входные признаки для модели Catboost состояли из 11 физико-химических дескрипторов и вектора отпечатка Моргана размером 1024 бита с радиусом 2. Для настройки гиперпараметров модели был выполнен поиск по сетке с пятикратной кросс-валидацией на объединении валидационной и обучающей выборок. Итоговые параметры для модели градиентного бустинга были следующими: скорость обучения 0,1, глубина дерева 10 и регуляризация листьев L2 1. Для каждого из пяти тренировочных и валидационных разделений данных была обучена отдельная модель. Обучение останавливалось, если значение функции потерь на валидации не улучшалось в течение 400 итераций, с фиксацией итерации с наименьшим значением потери на валидации. Обучение одной модели требовало около 2,5 секунд на 100 итераций.

Для модели 1D CNN входная последовательность состояла из токенизированной последовательности символов. Чтобы токенизировать строковое представление SMILES, числовые значения были присвоены часто встречающимся символам (с комбинациями, обозначающими единственное свойство или имя атома, например "Cl" или "Na", закодированными как один токен). Общее количество уникальных токенов (включая токены, зарезервированные для заполнения или неизвестных случаев) составило 40. Все последовательности SMILES были токенизированы данным образом, с максимальным размером последовательности 95, соответствующим максимальному размеру строки SMILES, найденному в обучающих данных после исключения выбросов. Разработанная модель 1D CNN включала слой с размерностью 256 для обучения векторных представлений токенов. Векторное представление передавалось в блок CNN, состоящий из пяти слоев 1D CNN, каждый из которых имел увеличивающееся количество фильтров, начиная с 64 и удваивающееся в каждом последующем слое, с фильтром размерностью 5, использующим функцию активации линейный выпрямитель (ReLU). Средний и максимальный ответы слоев CNN для данной последовательности получались с помощью слоев средней и максимальной субдискретизации соответственно. Эти ответы затем объединялись с 11 физико-химическими дескрипторами и обрабатывались многослойным линейным блоком, который использовал функцию активации ReLU с «утечкой» и включал пакетную нормализацию и слои обнуления с вероятностью обнуления 20%. Модель обучалась пакетами размером 2048, со скоростью обучения 10-4, используя алгоритм оптимизации Adam и функцию потери перекрестной энтропии. Для каждого из пяти тренировочных и валидационных разделений обучение проводилось в течение 60 эпох, с возможностью ранней остановки, если значение функции потерь на валидации не улучшалось в течение 10 эпох. Веса моделей с наименьшим значением функции потерь на валидации были выбраны как итоговые. Обучение одной модели требовало около двух секунд на одну обучающую эпоху.

Для подготовки данных для модели GNN были извлечены следующие признаки из описания SMILES молекул (с применением библиотеки RDkit) для каждого атома: имя атома (12 категорий), тип гибридизации (5 категорий), степень атома, определенная количеством связанных с ним соседей (в диапазоне от 0 до 5), общее количество неявных и явных водородов (в диапазоне от 0 до 5), неявная валентность (в диапазоне от 0 до 5), является ли атом частью кольца и является ли он ароматическим (бинарные значения). Все числовые признаки были нормализованы. Были собраны следующие признаки связей, соединяющих атомы: тип связи (4 категории), является ли связь частью кольца и является ли она сопряженной (бинарные признаки).

При формировании графов, признаки атомов хранились на узлах графа, а признаки связей хранились на ребрах графа. Ребра образовывались только между атомами, имеющими связи. Графы были неориентированными. Для категориальных признаков узлов и ребер были созданы обучаемые векторные представления: 16-мерные векторы генерировались для признаков имени атома и гибридизации, и 8-мерный вектор генерировался для признака типа связи. Результирующие векторы затем объединялись с оставшимися числовыми признаками ребер и узлов. Признаки связей дополнительно передавались через многослойный линейный блок с выходным размером 16.

Результирующие 37-мерные векторы узлов и 16-мерные векторы ребер передавались в блок из 7 слоев GNN с 8 головами внимания и 64 нейронами, с 20% слоем обнуления на уровне узлов (кроме первого слоя GNN в блоке) и пакетной нормализацией. Выход последнего слоя GNN объединялся с помощью суммирующей, максимальной и средней субдискретизации. Результирующие 3 вектора объединялись, проходили пакетную нормализацию, объединялись с 11 ранее упомянутыми физико-химическими дескрипторами и передавались в многослойный линейный блок, с 50% слоем обнуления и пакетной нормализацией между линейными слоями, который давал окончательный ответ. Использовалась функция активации ReLU с «утечкой» с параметром отрицательного наклона 0,2. Модель обучалась пакетами размером 2048, со скоростью обучения 10-3, используя алгоритм оптимизации Adam и функцию потери перекрестной энтропии. Для каждого из пяти тренировочных и валидационных разделений обучение проводилось в течение 100 эпох, с возможностью ранней остановки, если значение функции потерь на валидации не улучшалось в течение 10 эпох. Веса моделей с наименьшим значением функции потерь на валидации были выбраны как итоговые. Обучение одной модели требовало около 7 секунд на одну эпоху.

Все модели были обучены на графической карте NVIDIA RTX 4090 с 24 Гб видеопамяти.

Статистика и воспроизводимость

Статистический анализ проводился с помощью библиотеки SciPy Python [Virtanen, 2020]. Распределение данных коэффициентов Каппа проверялось с помощью теста Шапиро-Уилка. Если распределения были нормальными, выполнялся т-тест Стьюдента, в противном случае выполнялся тест Манна-Уитни. Для коэффициентов Каппа и AP, полученных из усредненных прогнозов, использовался бутстрэп с 5000 образцами. Различия считались значимыми для p-значений ниже 0,05.

Результаты и обсуждение

Результаты на независимом тестовом наборе

Сравнение алгоритмов было произведено по коэффициенту Каппа Коэна, так как он был выбран организаторами конкурса в качестве основного оценочного показателя, а также по средней точности (AP). Для обеспечения более надежного сравнения, предсказания моделей обученных моделей в рамках каждого алгоритма были усреднены. Для коэффициента Каппа были использованы коэффициенты балансировки (полученные как описано выше).

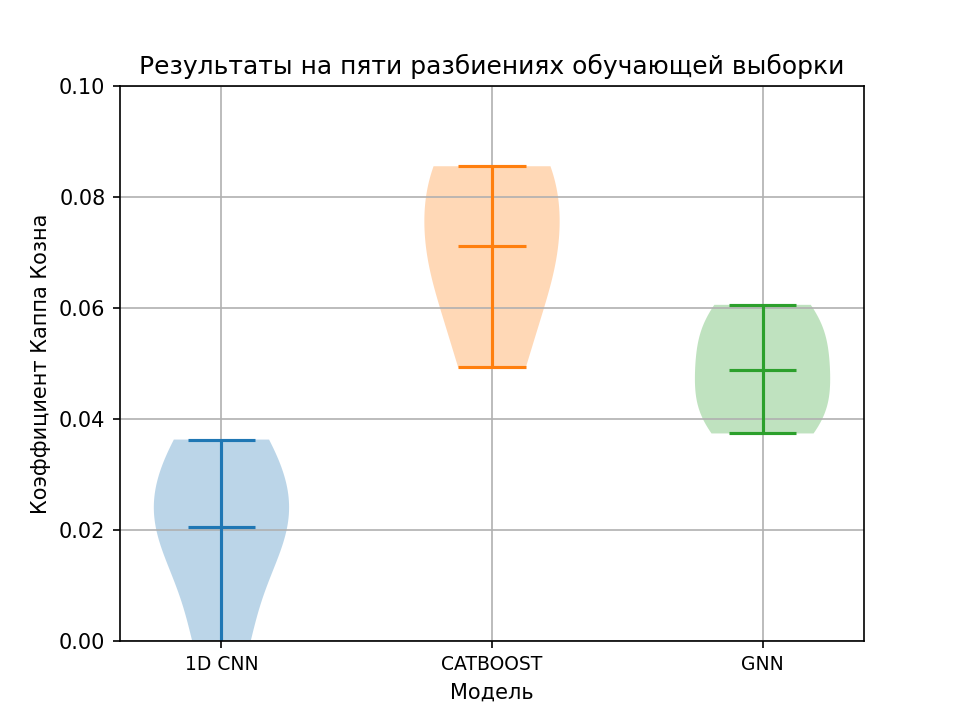
Усредненные предсказания моделей 1D CNN, GNN и CatBoost показали коэффициенты Каппа 0.0356, 0.0597 и 0.0708 соответственно. Модели показали значительное различие (p-значение < 0.05) между собой по данной метрике. Также было проведено сравнение предсказаний моделей, обученных на пяти разных разбиениях обучающей выборки, по отдельности (Рис. 1).

Рис. 1. Сравнение обученных моделей на независимой выборке данных

Как можно видеть, разные разбиения обучающей выборки показали схожие результаты: модели CatBoost дали лучшие результаты, а 1D CNN - наименьшие, с статистически значимой разницей (p-значения < 0,05). Оценка усредненных предсказаний моделей с использованием метрики AP была в пользу CatBoost, но с меньшей разницей в полученных метриках между моделями: 0,347, 0,343 и 0,337 для моделей CatBoost, GNN и 1D CNN соответственно, с статистически значимой разницей (p-значения < 0,05). В ходе этого теста также было обнаружено, что все модели рассматриваемых алгоритмов показали значительно более слабые результаты на классах с низкой и средней растворимостью: например, при показателе AP 0,94 для класса с высокой растворимостью, модель CatBoost показала только 0,05 AP для классов с низкой и средней растворимостью. Такие результаты могут быть связаны с природой данных, а не с выбранными алгоритмами, поскольку, как будет показано в следующем разделе, разработанные модели показали результаты, сравнимые с лучшими решениями, представленными на «1st EUOS/SLAS Joint Challenge: Compound Solubility».

Результаты на независимом тестовом наборе

Тестовый набор данных, созданный организаторами, был равномерно разделен на закрытые и открытые наборы. Эти наборы использовались для дополнительного сравнения моделей на данных, значительно отличающихся от тренировочных данных. Открытый набор использовался во время конкурса для того, чтобы участники могли оценивать свои решения, а закрытый набор использовался для финальной оценки и выбора победителей. Поскольку правильные метки не были публично доступны, оценка обученных моделей на этих данных осуществлялась путем отправки аннотированных таблиц через веб-сайт Kaggle для получения коэффициента Каппа, определяемого скриптом организаторов конкурса.

Аннотация данных проводилась тем же методом, что и при локальном независимом тестировании: усредненные прогнозы 5 обученных моделей для каждого из рассматриваемых алгоритмов, с применением балансирующих коэффициентов к каждому из 3 предсказанных классов, использовались для разметки каждого соединения из тестового набора. Модели 1D CNN показали наименьшие оценки, с 0,06678 на закрытом наборе и 0,07219 на открытом наборе. GNN модели показали более высокие оценки, с 0,07047 на приватном наборе и 0,11456 на публичном наборе. Модели Catboost показали наивысшие оценки, с 0,09676 на приватном наборе и 0,11903 на публичном наборе. Как можно видеть, результаты на этих наборах данных схожи с результатами, полученными на локальном независимом тестовом наборе: модели Catboost показали наилучшие результаты, а модели 1D CNN показали наименее точные результаты. При этом GNN модели показали наибольшую разницу в своей точности между открытым и закрытым наборами данных.

Следует отметить, что этот набор данных был использован в основном для сравнения моделей, разработанных в целях этого исследования, а не для сравнения с другими решениями, представленными на соревновании “1st EUOS/SLAS Joint Challenge: Compound Solubility”. Одной из основных причин этого является то, что модели, разработанные для получения высоких результатов в каком-либо соревновании по машинному обучению, обычно адаптированы к конкретному набору данных, тогда как целью этого исследования было сравнить подходы к представлению данных в более общей форме. Например, одним из признаков, использованных в победивших решениях, был идентификационный номер соединения, поскольку во время соревнования было обнаружено, что он коррелирует с целевыми классами. Если использовать этот признак во время обучения, то он улучшает точность моделей на этом наборе данных, хотя идентификатор соединения не влияет на растворимость и не должен оказывать никакого влияния на точность предсказаний. Чтобы продемонстрировать этот эффект на практике, были обучены пять моделей CatBoost, которые дополнительно учитывали идентификаторы соединений, при этом процедура обучения проводилась так же, как описано выше. Усреднение полученных в результате пяти моделей показало оценку 0,10903 на закрытой выборке и оценку 0,13323 на открытое выборке, что позволило бы этому решению занять третье место в соревновании, где лучшее решение показало коэффициент Каппа 0,11562 (исключая четыре решения, которые были дисквалифицированы организаторами соревнования). Одна из пяти обученных моделей показала еще более высокую оценку 0,11021 на закрытой выборке.

Заключение

В этом исследовании были протестированы несколько подходов к представлению молекулярных данных на задаче предсказания растворимости с использованием большого открытого набора данных, содержащего более 70 000 соединений, подготовленного EU-OPENSCREEN ERIC и опубликованного в недавнем соревновании на платформе Kaggle. Модели 1D CNN были обучены на векторных представлениях токенизированных SMILES молекул, рассматривая их как последовательность, модели GNN были обучены на графовом представлении молекул, а модели градиентного бустинга Catboost были обучены на представлении молекул с использованием отпечатков Моргана. Также эти пространства признаков были дополнены 11 физико-химическими дескрипторами для лучшего представления глобальных молекулярных свойств. Проведенные эксперименты на пяти разных разделениях выборки на обучение и валидацию показали модели CatBoost как наиболее точные, как на локально подготовленном независимом тестовом наборе, так и на тестовых наборах, опубликованных в вышеупомянутом соревновании. Все обученные модели продемонстрировали значительно более сильную предсказательную способность для класса высокой растворимости, чем для классов средней и низкой растворимости. Подобный результат может быть связан с природой самого набора данных, поскольку лучшее из обученных решений также продемонстрировало результаты, сравнимые с лучшими решениями, представленными на соревновании (на основе метрики, выбранной организаторами соревнования). Полученные результаты показывают, что представления молекул, извлеченных из SMILES в виде графов или векторных представлений символов, не обязательно превосходят более традиционные табличные представления, состоящие из отпечатков Моргана и химических дескрипторов. Это исследование также продемонстрировало, что предсказание растворимости остается сложной задачей для алгоритмов, основанных на машинном обучении. Лучшие из локально обученных моделей, а также решения, представленные на вышеупомянутом соревновании (исключая модели, которые использовали идентификационный номер соединения в качестве признака), могли достичь коэффициента Каппа около 0,10, что указывает на достаточно слабую предсказательную способность. Подобные результаты могут быть объяснены потенциальным шумом и неточностями в самих данных, но эти аспекты не были исследованы в данной работе.

1. Fink, C., Sun, D., Wagner, K., Schneider, M., Bauer, H., Dolgos, H., Mäder, K., Peters, S.-A. Evaluating the Role of Solubility in Oral Absorption of Poorly Water-Soluble Drugs Using Physiologically-Based Pharmacokinetic Modeling // Clin. Pharmacol. Ther. 2020. 107: 650-661. DOI: 10.1002/cpt.1672
2. Ameta, R.K., Soni, K., Bhattarai, A. Recent Advances in Improving the Bioavailability of Hydrophobic/Lipophilic Drugs and Their Delivery via Self Emulsifying Formulations // Colloids Interfaces. 2023. 7. 16. DOI: 10.3390/colloids7010016
3. Loftsson, T., Brewster, M.E. Pharmaceutical applications of cyclodextrins: basic science and product development // Journal of Pharmacy and Pharmacology. 2010. Volume 62, Issue 11, November 2010, Pages 1607–1621. DOI: 10.1111/j.2042-7158.2010.01030.x
4. Basavaraj, S., Guru V. Betageri, G.V. Can formulation and drug delivery reduce attrition during drug discovery and development—review of feasibility, benefits and challenges // Acta Pharmaceutica Sinica B. 2014. Volume 4, Issue 1. Pages 3-17, ISSN 2211-3835. DOI: 10.1016/j.apsb.2013.12.003
5. Ran, Y., Samuel H. Yalkowsky, S.H. Prediction of Drug Solubility by the General Solubility Equation (GSE) // Journal of Chemical Information and Computer Sciences. 2001. 41 (2). 354-357. DOI: 10.1021/ci000338c
6. Fredenslund, A., Jones, R.L. Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures // AIChE J. 1975. 21: 1975, 1086-1099. DOI: 10.1002/aic.690210607
7. Palmer, D.S., McDonagh, J.L., Mitchell, J.B.O., Mourik, T., Fedorov, M.V. First-Principles Calculation of the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules // Journal of Chemical Theory and Computation. 2012. 8. (9), 3322-3337. DOI: 10.1021/ct300345m
8. Li, L., Totton, T., Frenkel, D. Computational methodology for solubility prediction: Application to the sparingly soluble solutes // J. Chem. Phys. 2017. 146 (21): 214110. DOI: 10.1063/1.4983754
9. Boothroyd, S., Anwar, J. Solubility prediction for a soluble organic molecule via chemical potentials from density of states // The Journal of Chemical Physics. 2019. 151, 184113. DOI: 10.1063/1.5117281
10. Duchowicz, P.R., Castro, E.A. QSPR Studies on Aqueous Solubilities of Drug-Like Compounds // Int. J. Mol. Sci. 2009. 10, 2558-2577. DOI: 10.3390/ijms10062558
11. Yu, X., Wang, X., Wang, H., Li, X.,Gao, J. Prediction of Solubility Parameters for Polymers by a QSPR Model // QSAR Comb. Sci. 2006. 25: 156-161. DOI: 10.1002/qsar.200530138
12. Palmer, D.S., O'Boyle, N.M., Glen, R.C., Mitchell, J.B.O. Random Forest Models To Predict Aqueous Solubility // Journal of Chemical Information and Modeling. 2007. 47 (1), 150-158. DOI: 10.1021/ci060164k
13. Deng, T., Jia, G. Prediction of aqueous solubility of compounds based on neural network // Molecular Physics. 2019. 118:2, DOI: 10.1080/00268976.2019.1600754.
14. Lusci, A., Pollastri, G., Baldi, P. Deep Architectures and Deep Learning in Chemoinformatics: The Prediction of Aqueous Solubility for Drug-Like Molecules // Journal of Chemical Information and Modeling. 2013. 53 (7), 1563-1575. DOI: 10.1021/ci400187y
15. Boobier, S., Hose, D.R.J., Blacker, A.J. et al. Machine learning with physicochemical relationships: solubility prediction in organic solvents and water // Nature Communciations. 2020. 11, 5753. DOI: 10.1038/s41467-020-19594-z
16. Morgan, H.L. The generation of a unique machine description for chemical structures — a technique developed at chemical abstracts service // Journal of Chemical Documentation. 1965. Doc 5:107–113. DOI: 10.1021/c160017a018
17. Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A.V., Gulin, A. CatBoost: unbiased boosting with categorical features // NeurIPS. 2018. DOI: 10.48550/arXiv.1706.09516
18. Capecchi, A., Probst, D., Reymond, J.L. One molecular fingerprint to rule them all: drugs, biomolecules, and the metabolome // Journal of Cheminformatics. 2020. 12. 43. DOI: 10.1186/s13321-020-00445-4
19. Платонов Е.Н., Мартынова И.Р. Семантический анализ отзывов об организациях методами машинного обучения // Моделирование и анализ данных. 2024. Том 14. № 1. С. 7–26. DOI: 10.17759/mda.2024140101
20. Blevins, A., Quigley, K., I., Halverson, J., B., Wilkinson, N., Levin, S., R., Pulapaka, A., Reade, W., Howard, A. NeurIPS 2024 - Predict New Medicines with BELKA. Kaggle. 2024. https://kaggle.com/competitions/leash-BELKA.
21. Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library // In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32, pp. 1–12.
22. Cacciari, I., Ranfagni, A. Hands-On Fundamentals of 1D Convolutional Neural Networks — A Tutorial for Beginner Users // Applied Sciences. 2024. 14(18), 8500. DOI: 10.3390/app14188500
23. Shi, Y., Huang, Z., Wang, W., Zhong, H., Feng, S., Sun, Y. Masked Label Prediction: Unified Massage Passing Model for Semi-Supervised Classification // Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence. 202. pp 1548−1554. DOI: 10.24963/ijcai.2021/214
24. Zaliani, A., Tang, J., Martin, J., Harmel, R., Wang, W. 1st EUOS/SLAS Joint Challenge: Compound Solubility. https://kaggle.com/competitions/euos-slas, 2022. Kaggle.
25. Powell, M. J. D. An efficient method for finding the minimum of a function of several variables without calculating derivatives // The Computer Journal. 1964. Volume 7, Issue 2, Pages 155–162. DOI: 10.1093/comjnl/7.2.155
26. Pedregosa et al. Scikit-learn: Machine Learning in Python // Journal of Machine Learning Research. 2011. 12(85):2825−2830.
27. Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.; Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python // Nat. Methods. 2020. 17, 261−272. DOI: 10.1038/s41592-019-0686-2