Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения

Куланин Е.Д.; Степанов М.Е.

doi:10.17759/mda.2024140310

Моделирование и анализ данных
2024. Том 14. № 3. С. 174–202
doi:10.17759/mda.2024140310
ISSN: 2219-3758 / 2311-9454 (online)

Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения

13

Куланин Е.Д., Степанов М.Е.

Аннотация

Статья продолжает цикл ([1] – [13]) методических разработок авторов. В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

Общая информация

Ключевые слова: высшее образование, методика преподавания математики, симметрические множества, комбинаторика, алгебра многочленов, теория вероятностей

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140310

Получена: 09.07.2024

Принята в печать: 07.08.2024

Для цитаты: Куланин Е.Д., Степанов М.Е. Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения // Моделирование и анализ данных. 2024. Том 14. № 3. С. 174–202. DOI: 10.17759/mda.2024140310

Полный текст

ВВЕДЕНИЕ

Данная статья в известном смысле продолжает и дополняет статью авторов «Вычислительный эксперимент в преподавании высшей математики на примере теории чисел» [13]. Приведём цитату из статьи [13], чтобы объяснить цели, с которыми были задуманы статьи, посвящённые вычислениям различного характера.

«Учебная работа со студентами-математиками, кроме всего прочего, включает в себя развитие их интереса к математике как таковой. Добиться даже минимальных результатов в этом направлении можно, только предлагая учащимся задания, имеющие характер научного исследования. Поиск таких задач связан с определёнными трудностями. Действительно, с одной стороны задача должна быть посильной, а с другой – представлять возможности для получения новых результатов.

Авторы статьи считают, что для этих целей как раз и можно использовать задачи вычислительного характера. Данная статья посвящена рассмотрению ряда примеров таких вопросов, связанных с теорией чисел. В дальнейшем предполагается также и написание статей, которые касаются вычислений в общей алгебре, геометрии, математическом анализе и т. д.»

Данная статья направлена на рассмотрение задач комбинаторики. В одном из своих больших разделов – теории перечислений – комбинаторика целиком ориентирована на вычисления [14]. В рамках общего курса математики в высшей школе комбинаторика как отдельный предмет не выделяется. Однако важность и широкая сфера применения многих её формул требует включения некоторых вопросов комбинаторики в рамки других предметов. В первую очередь речь идёт о теории вероятностей, где методы решения ряда задач основываются на комбинаторных формулах.

В этой статье авторы рассматривают некоторые вопросы комбинаторики сами по себе, а затем показывают их применение в других разделах математики.

НЕКОТОРЫЕ ФАКТЫ ТЕОРИИ ПЕРЕЧИСЛЕНИЙ

Начнём с рассмотрения ряда известных формул.

Число пар. Пусть заданы два множества М и N. Прямым произведение этих множеств называется множество упорядоченных пар

{(m; n) ∣ m \in M, n \in N}

. Если множества М и N являются конечными, то общее число пар равно произведению количества элементов первого множества на количество элементов второго. Множество пар при небольшом количестве элементов в исходных множествах можно наглядно изобразить в виде прямоугольной таблицы.

Перестановки. Всякое упорядоченное множество (то есть множество, элементы которого занумерованы) называется перестановкой его элементов. Число всевозможных перестановок, которые могут быть образованы из n элементов равно n-факториал, то есть Рn = 1∙2∙…∙n = n!.

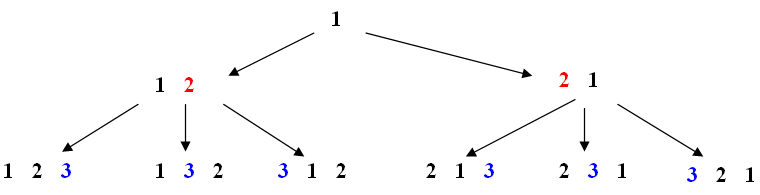
Пояснение. Один элемент можно переставить одним способом. Если добавиться второй элемент, то его можно поставить справа и слева от первого – два способа. Если добавить третий элемент, то в любую перестановку из двух его можно поставить справа, в середину и в центр, то есть из каждой перестановки из двух элементов получится три перестановки из трёх – всего шесть способов и т. д.

Задание 1. Вычислить 10! без использования калькулятора.

Решение. Основной приём, который следует применять при вычислениях, – использование коммутативности умножения и дистрибутивности. Итак, 10! = 1∙2∙3∙4∙5∙6∙7∙8∙9∙10 = 7∙(3∙6∙9)∙(4∙8)∙100 = 7∙81∙64∙100 = 7∙81∙64∙100 = 7∙ (80∙64 + 64)∙100 = 7∙ (5120 + 64)∙100 = 7∙5184∙100 = (35000 + 700 + 560 + 28) ∙100 = 36288∙100 = 3628800.

Задание 2. На одной книжной полке стоит n книг, на второй m. Книги с полки на полку переносить нельзя, но их можно переставлять на каждой из полок произвольным образом. Сколько различных перестановок при этом возникнет.

Решение. Мы имеем дело с двумя множествами – множество перестановок книг на первой полке и множество перестановок книг на второй полке. Число элементов первого множества равно n!, а второго – m!. Поскольку каждой перестановке книг на первой полке может соответствовать любая перестановка книг на второй полке, то общее количество перестановок равно числу соответствующих пар. Таким образом, искомое число равно n!∙m!.

Задание 3. Сочетанием из n элементов, взятых по k, называется подмножество, содержащее k элементов данного множества. Число сочетаний из n по k обозначается через

C_{n}^{k}

и равно

\frac{n!}{(n - k)! k!}

.

Пояснение. На полке n книг можно расставить n! способами. Выберем k книг и разделим полку на две части. Справа будем всевозможными способами переставлять k книг, а слева n – k книг. Всего получится k!(n – k)! вариантов (смотри задание 2). Таким образом, на каждое сочетание приходится k!(n – k)! вариантов. Следовательно, общее число сочетаний равно

\frac{n!}{(n - k)! k!}

.

Задание 4. Устно вычислить, сколькими способами можно из 9 предметов выбрать 5.

Решение. Главным правилом, которому нужно следовать при вычислении в данном случае, является проведение сокращений дроби. Перемножение чисел следует начинать только после того, как знаменатель станет равен единице.

C_{9}^{5} = \frac{9!}{5! 4!} = \frac{9 ∙ 8 ∙ 7 ∙ 6}{2 ∙ 3 ∙ 4}

= 9

∙ 2 ∙ 7

= 18

∙ 7

= 126.

Размещения. Размещением из n элементов по k называется всякая упорядоченная часть данного множества, содержащая k элементов. Число размещений из n по k обозначается через

A_{n}^{k}

и равно

\frac{n!}{(n - k)!}

.

Пояснение. Для размещения выбирают k книг и на правую часть полки ставят в определённом порядке, а слева n – k книг переставляют всевозможными способами. Рассуждая по аналогии с сочетаниями, устанавливаем, что число размещений равно

\frac{n!}{(n - k)!}

.

Перестановки с повторением. Пусть алфавит содержит n букв. Тогда перестановкой из n элементов по k с повторениями называется слово из k букв (буквы могут повторяться). Общее количество таких число равно nk.

Пояснение. Размещение из n элементов по k с повторениями можно рассматривать как позиционную запись числа по основанию k, состоящего из n цифр. Минимальным из этих чисел является 0, а максимальное равно nk – 1, то есть всего таких чисел nk.

Выводя формулу для числа сочетаний, мы решили следующую задачу: сколькими способами можно разбить множество с n элементами на два множества, содержащие k и n – k элементов. Эту задачу можно обобщить.

Задание 5. Множество, содержащее n элементов, разбивают на m непересекающихся множеств, содержащих соответственно n1, n2, …, nm элементов, при этом n1 + n2 + … + nm = n. Получить формулу для вычисления количества таких разбиений, обозначив это количество через

P (n_{1}, n_{2}, \dots, n_{m})

.

Пояснение. Сначала отметим, что вместо множества пар в задании рассматриваются кортежи, имеющие длину m. Их количество равно произведению числа элементов каждого множества.

Вывод соответствующей формулы полностью повторяет рассуждения, проведённые в заданиях 2 и 3. Разделим полку на m секций и разобьём книги на соответствующие подмножества. Число перестановок книг в каждой из этих секций равно

n_{1}!

,

n_{2}!

, …

n_{m}!

. А общее число равно произведению этих факториалов. Число перестановок книг без секций равно n!. Таким образом,

P (n_{1}, n_{2}, \dots, n_{m}) = \frac{n!}{n_{1}! n_{2}! \dots n_{m}!}

.

Задание 6. Определить, сколькими способами 10 книг можно разбить на блоки по две книги. Вычисления провести устно.

Решение. Соответствующее число равно

\frac{10!}{2^{5}} = 2 ∙ 3 ∙ 5 ∙ 6 ∙ 7 ∙ 9 = 10 ∙

126 ∙9 = 10 ∙ (100 + 20 + 6) ∙ 9 = 9000 + 1800 + 540 = 11340.

ПЕРЕМНОЖЕНИЕ СКОБОК

В дальнейшем нам понадобится умение осознанно перемножать скобки, каждая из которых содержит сумму нескольких переменных.

Со времён Древней Греции используется геометрическое истолкование умножения. При многократном сложении (b раз) нескольких равных куч (по a предметов), можно заменить каждую кучу полосой из a единичных квадратов и сложить b полос одну под другой. В итоге получится прямоугольник a на b, площадь которого равна a

b. Его можно повернуть на 90º и представить, что он сложен из a горизонтальных полос, содержащих по b единичных квадратов. Площадь его не изменилась, следовательно, a

b = b

a (рисунок 1).

Рисунок 1

При рассмотрении произведения трёх чисел a

b

с предметы можно заменить единичными кубами и сложить из них параллелепипед. Его можно сложить из с горизонтальных пластин размером a на b, или же из а вертикальных пластин размером b на с. Произведение a

b

с равно объёму параллелепипеда, а, значит, (a

b)

с = a

(b

с). Так же как и в случае сложения, закон ассоциативности позволяет использовать запись произведения нескольких сомножителей вообще без скобок (рисунок 2).

Рисунок 2

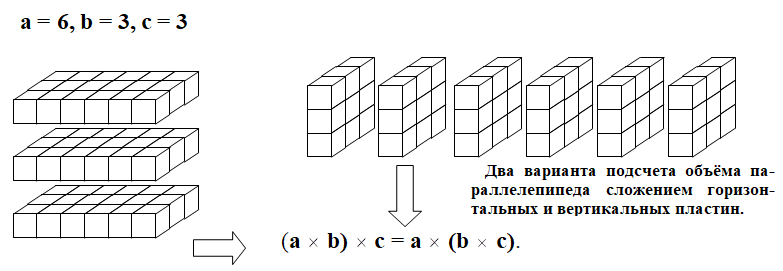
Наличие геометрического истолкования умножения и его большая практическая важность указывает на существование глубокой связи числовых отношений и простых геометрических форм. По крайней мере, становится ясным, что истолкование смысла арифметических операций хотя бы отчасти связано с упорядоченным расположением предметов в пространстве.

Тот факт, что перемножение двух сумм связано с вычислением площади прямоугольника, помогает технически облегчить процесс перемножения двух скобок, содержащих суммы, с помощью прямоугольной таблицы. Слагаемые одной скобки соотносятся со строками, а другой – со столбцами.

Например, перемножим суммы

(a + b + c)

и

(x + y + z)

. Построим таблицу 3 на 3 и заполним её. Затем суммируем содержимое всех клеток таблицы.

	x	y	z
a	ax	ay	az
b	bx	by	bz
c	cx	cy	cz

В итоге получаем:

(a + b + c) (x + y + z) = ax + bx + cx + ay + by + cy +

az + by + cz

Если теперь отстранится от таблицы, можно сформулировать правило: произведение двух сумм складывается из всех произведений вида «каждое слагаемое первой суммы умножено на каждое слагаемое второй суммы».

При перемножении нескольких сумм можно сначала перемножить первые две скобки, а затем результат умножить на третью скобку. Новый результат с помощью таблицы нужно умножить на четвёртую скобку и т. д.

И снова, если отстранится от таблиц, можно сформулировать правило: произведение нескольких сумм складывается из всех произведений вида «слагаемое первой скобки умножено на слагаемое второй скобки, затем на слагаемое третьей скобки и т. д. во всех возможных вариантах».

Таким образом, при перемножении сумм нужно научиться выбирать из скобок по одному элементу всеми возможными способами. Аналогичные рассуждения можно провести при возведении суммы в какую-либо степень.

Задание 7. Бином Ньютона – это формула для возведения двучлена (p + q) в n-ю степень. Вывести эту формулу.

Пояснение. При перемножении n скобок вида (p + q) из каждой скобки выбирают либо слагаемое р, либо слагаемое q. В итоге будет получена сумма членов вида pkqn–k, где k меняется от нуля до n. Многие члены будут при этом повторяться. Подсчитывая число членов pkqn–k при конкретном значении k, можно рассуждать так. Всего перемножается n скобок. Из них нужно выбрать k скобок. Сделать это можно

C_{n}^{k}

способами. В итоге формула бинома Ньютона выглядит следующим образом:

(p + q)^{n} = p^{n} + C_{n}^{1} p^{n - 1} q + . . . + C_{n}^{k} p^{n - k} q^{k} + . . . + C_{n}^{n - 1} {pq}^{n - 1} + q^{n}

.

Задание 8. Возвести комплексное число 1 + i в четвёртую степень.

Решение. Используем формулу бинома Ньютона:

Задание 9. Написать программу, которая позволяет вычислить

C_{n}^{k}

. Построить диаграмму из коэффициентов формулы бинома Ньютона для степени n.

Решение. Поскольку для вычисления числа сочетаний есть формула, представляется, что проблем с написанием программы не будет. Однако это не совсем так. Дело в том, что в случае предварительного вычисления факториалов будут получены очень большие числа. Последующее деление этих чисел друг на друга может привести к потере точности.

По этой причине будем вычислять число сочетаний перемножая дроби

C_{n}^{m} = \frac{n}{m} ∙ \frac{n - 1}{m - 1} ∙ \dots ∙ \frac{n - m}{1}

.

Затем округлим результат до ближайшего целого.

n = 10

GraphicsWindow.PenColor = "black"

GraphicsWindow.Width = 400

GraphicsWindow.Height = 700

x = 50

For m = 0 To n

'Подпрограмма вычисления числа сочетаний

sotsh()

EndFor

'Подпрограмма

Sub sotsh

nt = n

mt = m

cnm = 1

If m > n/2 Then

mt = n - m

EndIf

If m = 0 Then

Goto met

EndIf

For i = mt To 1 Step -1

cnm = cnm*nt/i

nt = nt - 1

EndFor

'Округление до ближайшего целого

cnm = Math.Round(cnm)

met:

GraphicsWindow.DrawText(x,650,cnm)

GraphicsWindow.DrawRectangle(x, 620 - cnm*2, 20, cnm*2)

x = x + 30

EndSub

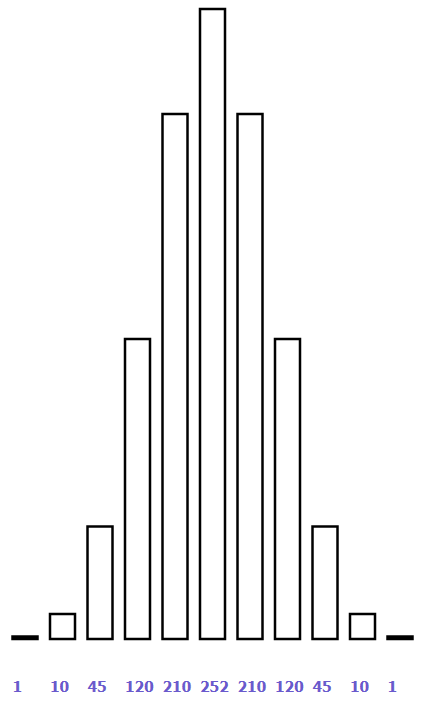
Результат работы программы показан на рисунке 3.

Рисунок 3

Задание 10. Написать программу для возведения числа вида

a + b ∙ \sqrt{5}

в n-ю степень, где

a

и

b

– целые числа. Результат должен быть представлен в таком же виде.

Решение. Результаты работы программы показаны на рисунке 4.

n = 7

'Исходное число

a = 3

b = -1

y = 50

as = Math.Power(a, n)

GraphicsWindow.DrawText(50,y,as)

y = y + 20

bs = 0

cht = 1

For m = 1 To n

'Подпрограмма вычисления числа сочетаний

sotsh()

If cht = 0 Then

'Чётная степень корня

sl = cnm*Math.Power(a, n-m)*Math.Power(5, m/2)*Math.Power(b, m)

as = as + sl

GraphicsWindow.DrawText(50,y,sl)

Else

'Нечётная степень корня

sl = cnm*Math.Power(a, n-m)*Math.Power(5, (m - 1)/2)*Math.Power(b, m)

bs = bs + sl

GraphicsWindow.DrawText(80,y,sl)

EndIf

cht = 1 - cht

y = y + 20

EndFor

GraphicsWindow.BrushColor ="black"

GraphicsWindow.DrawText(50,350,as)

GraphicsWindow.DrawText(100,350,bs)

GraphicsWindow.FontSize = 20

GraphicsWindow.DrawText(150,346,"V")

GraphicsWindow.DrawLine(160,350,180,350)

GraphicsWindow.DrawText(162,347,"5")

'Проверка

sq5 = Math.SquareRoot(5)

r1 = Math.Power(a+b*sq5,n)

r2 = as + bs*sq5

GraphicsWindow.DrawText(300,170,"Проверка")

GraphicsWindow.DrawText(300,200,r1)

GraphicsWindow.DrawText(300,230,r2)

'Подпрограмма

Sub sotsh

nt = n

mt = m

cnm = 1

If m > n/2 Then

mt = n - m

EndIf

If m = 0 Then

Goto met

EndIf

For i = mt To 1 Step -1

cnm = cnm*nt/i

nt = nt - 1

EndFor

'Округление до ближайшего целого

cnm = Math.Round(cnm)

met:

EndSub

Рисунок 4

Теперь рассмотрим вопрос об обобщении формулы бинома Ньютона на случай возведения в n-ю степень сумм более, чем двух слагаемых. Чтобы разобраться с этим вопросом, необходимо выяснить, сколько одночленов останется в итоговой сумме после раскрытия скобок и приведения подобных. Также нужно выяснить, какие перед ними будут стоять коэффициенты. Задача эта достаточно трудная. По этой причине будем двигаться к её решению от более простых задач к задачам более сложным. Возможно, удастся на основе вычислений частного вида выдвинуть и доказать общую гипотезу.

Все одночлены, которые возникают после раскрытия скобок, имеют n-ю степень. Чтобы в обозримой форме представить их, свяжем каждый одночлен со словом из n букв. Если буквы внутри слова переставить по алфавиту, то факт совпадения двух слов, полученных из разных одночленов, указывает на подобие этих одночленов. Например, в биноме Ньютона из одночленов

p^{2} qp

и

q p^{3}

будет получено слово

pppq = p^{3} q

. Итак, среди слов, составленных из букв, которые упорядочены по алфавиту, не должно быть одинаковых. Число этих слов как раз и будет количеством одночленов в итоговой сумме после раскрытия скобок и приведения подобных.

Чтобы получить все эти слова, будем их формировать и располагать в алфавитном порядке, как ранее поступили с буквами. Чтобы это упорядочение легко воспринималось, в качестве обозначения слагаемых в исходной скобке используем буквы латинского алфавита, начиная с a. Таким образом, в n-ю степень будут возводиться суммы вида

a, a + b, a + b + c, a + b + c + d, \dots

Последующие задания могут показаться слишком частными, но именно они помогут разобраться в ситуации.

Задание 11. Вывести формулу, аналогичную формуле бинома Ньютона, для возведения в квадрат суммы трёх слагаемых.

Решение. По договорённости будем выводить формулу для выражения

. Правило перемножения скобок позволяет перечислить все одночлены, из которых складывается итоговое выражение (они же могут рассматриваться как соответствующие слова). Перечисляемые одночлены расположим в алфавитном порядке

a^{2}, ab, ac, b^{2}, bc, c^{2}

.

Их шесть. Разберёмся, почему. Если обратиться к степеням 0 и 1, то для

– одно слагаемое, а для

– три слагаемых. Вернёмся к квадрату. Все перечисленные многочлены, из которых и складывается квадрат суммы, можно связать со следующими выражениями:

a^{2} ∙

a ∙

Здесь как раз и видно, что после приведения подобных будет получено ровно 6 = 1 + 2 + 3 слагаемых. При этом числа 1, 2 и 3 задают количество слагаемых в биномах степеней 0, 1, 2. Подобная ситуация, позволяющая вычислять количество более длинных слов, отправляясь от количеств, связанных со словами более короткими, сохранится и в дальнейшем.

Что касается коэффициентов, то их вычисление фактически описано в задании 5. Итак,

a^{2} + 2 ab + 2 ac + b^{2} + 2 bc + c^{2}

.

Уже на этом этапе можно сделать ряд предположений. Если известно количество членов в любых степенях сумм с m – 1 слагаемым, то можно получить количество членов в выражении для k-й степени суммы с m слагаемыми. Попытаемся это сделать.

Пусть нужно вычислить n-ю степень суммы m слагаемых

, тогда все члены, составляющие итоговую сумму могут быть получены следующим образом: они являются одночленами всех многочленов вида

. Если многочлен

состоит из

s_{k}

слагаемых, то n-я степень суммы m слагаемых

состоит из суммы

s_{0} + s_{1} + \dots + s_{n}

членов.

Пока это не даёт возможности получить итоговую общую формулу для числа членов. Но для степеней трёх слагаемых такая возможность появилась. Дело в том, что число членов бинома в n-й степени равно n + 1. Из этого и предыдущих рассуждений следует, что число членов степени

равно сумме натуральных чисел от 1 до n + 1. Эту сумму легко вычислить. Она равна

\frac{(n + 1) ∙ (n + 2)}{2}

.

Теперь открывается возможность выдвигать новые гипотезы. Но сначала рассмотрим два задания проверочного и закрепляющего характера.

Задание 12. Вывести формулу, аналогичную формуле бинома Ньютона, для возведения в третью степень (

n = 3

) суммы трёх слагаемых.

Решение. Выведем формулу для выражения

. Перечислим все одночлены, из которых складывается итоговое выражение. Перечисляемые одночлены расположим в алфавитном порядке

a^{3}, a^{2} b, a^{2} c, a b^{2}, abc, a c^{2}, b^{3},

b^{2} c, b c^{2}, c^{3}

.

Их число равно 10 = 1 + 2 + 3 + 4 =

\frac{4 ∙ 5}{2}

, что подтверждает полученный ранее результат. Остаётся найти коэффициенты. Для

a^{3}, b^{3},

c^{3}

этот коэффициент равен 1. Для

a^{2} b, a^{2} c, a b^{2}, a c^{2},

b^{2} c, b c^{2}

коэффициент равен

\frac{3!}{2! 1!}

= 3. Для

abc

коэффициент равен

\frac{3!}{1! 1! 1!}

= 6.

Задание 13. Вывести формулу, аналогичную формуле бинома Ньютона, для возведения в пятую степень (

n = 5

) суммы трёх слагаемых.

Решение. Вычисляя выражение

перечислим все одночлены, из которых складывается итоговое выражение. Их количество равно 21 = 1 + 2 + 3 + 4 + 5 + 6 =

\frac{6 ∙ 7}{2}

a^{5}, a^{4} b, a^{4} c, a^{3} b^{2}, a^{3} bc, a^{3} c^{2}, a^{2} b^{3}, a^{2} b^{2} c, a^{2} b c^{2}, a^{2} c^{3}

{a b^{4}, a b^{3} c, a b^{2} c^{2}, a {bc}^{3}, a c^{4}, b}^{5},

b^{4} c, b^{3} c^{2}, b^{2} c^{3}, b c^{4}, c^{5}

.

Коэффициенты вычисляются аналогично.

Задание 14. Сумма m одночленов возведена в n-ю степень. Каково число одночленов, из которых складывается итоговое выражение? Какие коэффициенты возникнут после приведения подобных? Каково число слагаемых после приведения подобных? Высказать гипотезу.

Решение. Начнём с того, что число одночленов, из которых складывается итоговое выражение или, что то же самое, число слов без повторений, называется количеством всевозможных упорядоченных разбиений числа n на m целых неотрицательных чисел.

Фактически на данном этапе есть возможность последовательно вычислять нужные числа, суммируя соответствующие последовательности. Для возведения в квадрат суммирование уже проведено и получен результат: количество всевозможных упорядоченных разбиений числа n на 3 целых неотрицательных числа равно

\frac{(n + 1) ∙ (n + 2)}{2}

.

Попытаемся получить количество всевозможных упорядоченных разбиений числа n на 4 целых неотрицательных числа. Для этого просуммируем последовательность чисел

\frac{1 ∙ 2}{2} + \frac{2 ∙ 3}{2}

+ … +

\frac{(n + 2) ∙ (n + 3)}{2}

. Для получения результата используем формулу суммирования квадратов натуральных чисел:

1^{2} + 2^{2} + \dots + \frac{n ∙ (n + 1) ∙ (2 n + 1)}{6} [15]

.

Итак,

\frac{1 ∙ 2}{2} + \frac{2 ∙ 3}{2}

+ … +

\frac{(n + 2) ∙ (n + 3)}{2} = \frac{1}{2} ∙

=

\frac{1}{2} ∙ (\frac{(n + 2) ∙ (n + 3) ∙ (4 n + 5)}{6} + \frac{(n + 2) ∙ (n + 3)}{2})

=

\frac{(n + 2) ∙ (n + 3)}{4} ∙ (\frac{4 n + 5}{6} + \frac{1}{2}) =

\frac{(n + 2) ∙ (n + 3) ∙ (n + 4)}{3!} ∙

Теперь можно заметить, что все количества всевозможных упорядоченных разбиений выражаются как число сочетаний – для m = 2 это

C_{n + 1}^{1}

, для m = 3 это

C_{n + 2}^{2}

, для m = 4 это

C_{n + 3}^{3}

. В качестве гипотезы выскажем следующее предположение: количество всевозможных упорядоченных разбиений числа n на m целых неотрицательных чисел выражаются как число сочетаний

C_{n + m - 1}^{m - 1}

. Это, с учётом наших рассуждений означает, что для всех n и m выполняется равенство

{C_{0 + m - 1}^{m - 1} + C}_{1 + m - 1}^{m - 1} + C_{2 + m - 1}^{m - 1} + \dots + C_{(n - 1) + m - 1}^{m - 1} + C_{n + m - 1}^{m - 1} = C_{(n + 1) + m}^{m}

Отметим, что в этом равенстве можно сумму любого набора последовательных слагаемых, начиная с первого, в левой части можно свернуть в соответствующее сочетание.

Чтобы доказать формулу, используем метод математической индукции. Для малых значений числа m проверка уже сделана. Кроме того, формула верна для любых m при n = 1.

Предположим, что формула верна для некоторого m при

n \leq k

. И, кроме того, она верна для всех n при всех меньших значениях m. Докажем, что она верна и для m при

n = k + 1

. Для этого достаточно доказать, что

C_{k + 1 + m}^{m} + C_{k + 1 + m}^{m - 1} = C_{k + 2 + m}^{m}

.

Здесь свёрнута в сочетание сумма всех слагаемых кроме последнего, что допустимо по предположению индукции. .

Эта формула действительно верна.

C_{k + 1 + m}^{m} + C_{k + 1 + m}^{m - 1} = \frac{(k + 1 + m)!}{m! (k + 1)!} + \frac{(k + 1 + m)!}{(m - 1)! (k + 2)!}

=

\frac{(k + 1 + m)!}{(m - 1)! (k + 1)!}

∙(

\frac{1}{m} + \frac{1}{k + 2}

=

\frac{(k + 2 + m)!}{m! (k + 2)!} = C_{k + 2 + m}^{m}

.

Перейдём к приложениям комбинаторики.

КОМБИНАТОРИКА И ЗАДАЧИ ТЕОРИИ ВЕРОЯТНОСТЕЙ

В качестве теоретико-вероятностных задач будем искать распределения дискретных случайных величин. Напомним, что дискретной случайной величиной называется величина, при испытаниях принимающая случайные значения (х1, х2, х3, … хn) с вероятностями р1, р2, р3, …, рn. Вектор (р1, р2, р3, …, рn) называется распределением вероятностей случайной величины.

Начнём с задач, относящихся к области классической вероятности. Классическое определение вероятности, основано на понятии равновероятности. Если какие-то события должны происходить с одинаковой частотой (например, из соображений симметрии), то они называются равновероятными. Примером равновероятных событий является выпадение какой-то из граней игрального кубика.

Вычисления классических вероятностей производится по следующему правилу. Пусть общее число равновероятных событий равно n, и пусть m из них по условию задачи считаются благоприятными, тогда вероятность благоприятного события равна отношению

\frac{m}{n}

.

Задание 15. В урне находится n чёрных шаров и m белых. Из урны наугад вынимают k шаров (

n > k, m > k

. Описать множество возможных исходов. Ввести дискретную случайную величину, связанную с этими исходами и найти её распределение.

Решение. Характер исхода определяется количеством вынутых из урны шаров одного цвета. Для определённости будем ориентироваться на количество вынутых чёрных шаров. Таким образом, возможен k + 1 исход, поскольку число вынутых чёрных шаров меняется от нуля до k. Перейдём к вычислению вероятностей каждого из этих исходов.

Пусть из урны вынули i чёрных шаров и

k - i

белых. Общее число вариантов, которыми из урны можно вынуть k шаров равно

C_{n + m}^{k}

. Общее число вариантов, которыми из урны можно вынуть i чёрных шаров равно

C_{n}^{i}

. Общее число вариантов, которыми из урны можно вынуть k

- i

шаров равно

C_{m}^{k - i}

. Значит, общее число вариантов, которыми из урны можно вынуть i чёрных шаров и k

- i

белых шаров равно

C_{n}^{i} ∙ C_{m}^{k - i}

. Следовательно, исход, связанный с тем, что из урны вынуто i чёрных шаров равен

p_{i} = \frac{C_{n}^{i} ∙ C_{m}^{k - i}}{C_{n + m}^{k}}

. Тем самым, распределение соответствующей дискретной случайной величины найдено.

Задание 16. Написать программу для вычисления вероятностей событий из предыдущего задания.

Решение. В программе используется подпрограмма вычисления числа сочетаний. Результат работы программы показан на рисунке 5.

n = 6

m = 7

k = 6

nt = n+m

mt = k

sotsh()

c3 = cnm

GraphicsWindow.BrushColor = "black"

GraphicsWindow.Width = 400

GraphicsWindow.Height = 400

GraphicsWindow.DrawText(10,20,"Число чёрных шаров")

GraphicsWindow.DrawText(170,20,"Вероятность")

y = 50

w = 0

'i – количество чёрных шаров

For i = 0 To k

nt = n

mt = i

sotsh()

c1 = cnm

nt = m

mt = k-i

sotsh()

c2 = cnm

'Вероятность выборки с i чёрными шарами

p = (c1*c2)/c3

'Сумма вероятностей

w = w + p

GraphicsWindow.DrawText(50,y,i)

GraphicsWindow.DrawText(150,y,p)

y = y +30

EndFor

GraphicsWindow.DrawText(10,y,"Сумма вероятностей")

GraphicsWindow.DrawText(150,y,w)

'Подпрограмма

Sub sotsh

cnm = 1

If mt = 0 Then

Goto met

EndIf

For j = mt To 1 Step -1

cnm = cnm*nt/j

nt = nt - 1

EndFor

cnm = Math.Round(cnm)

met:

EndSub

Рисунок 5

Задание 17. Написать программу, для вычисления вероятностей из предыдущего задания в виде обыкновенных дробей.

Пояснение. Нужно найти числитель дроби, выражающей соответствующую вероятность, то есть

C_{n}^{i} ∙ C_{m}^{k - i}

, а затем найти наибольший общий делитель числителя и знаменателя и сократить дробь. Вычисление НОД двух натуральных чисел описано в статье авторов [13].

При вычислении вероятности наступления объединения двух несовместных событий их вероятности складываются, а при вычислении вероятности совместного наступления нескольких независимых событий их вероятности перемножаются. Из этого обстоятельства следует, что вычисление совокупности вероятностей полной системы событий в некоторых случаях можно связать с перемножением скобок. Хорошим примером является задача о стрелках.

Ограничимся случаем трёх стрелков, которые поражают цель с вероятностями

p_{1}, p_{2,} p_{3}

. Соответственно вероятности их промахов равны

{q_{1} = 1 - p}_{1}, q_{2} = 1 - p_{2,} {q_{3} = 1 - p}_{3}

. Для этих стрелков полная система событий такова: все трое попали, не попал только первый, не попал только второй, не попал только третий, попал только первый, попал только второй, попал только третий, все трое не попали. Чтобы получить полное решение задачи о вычислении вероятностей этих событий, нужно перемножить три скобки:

(p1 + q1) (p2 + q2) (p3 + q3) =

= p1p2p3 + q1p2p3 + p1q2p3 + p1p2q3 + p1q2q3 + q1p2q3 + q1q2p3 + q1q2q3.

Каждое слагаемое с одной стороны определяет характер события: буква p указывает на попадание, а индекс, на номер попавшего стрелка. Буква q точно так же указывает на промах. С другой стороны соответствующее слагаемое как раз и задаёт вероятность соответствующего события.

Часто требуется найти вероятности объединённых событий, например, событие «попал только один стрелок» складывается из трёх событий «попал только первый», «попал только второй», «попал только третий». Итак, вероятность события «попал только один стрелок» равна p1q2q3 + q1p2q3 + q1q2p3.

Перейдём к рассмотрению схемы Бернулли. Проведённые только что рассуждения позволяют связать схему испытаний Бернулли с биномом Ньютона. Напомним, что в схеме испытаний Бернулли многократно выполняются однотипные опыты, приводящие к наступлению (с вероятностью р) или ненаступлению (с вероятностью q = 1 – р) одного и того же события А. Например, такая ситуация возникает при многократных выстрелах по цели одного и того же стрелка. Результаты опытов предполагаются независимыми. По этой причине вероятности событий перемножаются как выше в задаче о стрелках.

Таким образом, каждое испытание Бернулли можно уподобить выстрелу одного и того же стрелка. В случае испытаний Бернулли этот стрелок стреляет последовательно. Для двух выстрелов вероятность двух попаданий равна р2. Вероятность двух промахов равна q2. Наконец, вероятность одного попадания складывается из вероятностей двух несовместных событий – (попадание, промах) и (промах, попадание), то есть эта вероятность равна 2pq.

Легко понять, что указанные вероятности равны слагаемым бинома Ньютона: (p + q)2 = p2 + 2pq + q2. Можно понять, что при многочисленных испытаниях возникнет сходная ситуация.

Пусть проведено n испытаний Бернулли. Обозначим через P(n, k) вероятность того, что в n испытаниях благоприятное событие А наступило ровно k раз (k меняется от нуля до n). Тогда на основе того, что вероятности совместного наступления независимых событий перемножаются и с помощью бинома, получим формулу: P(n, k) =

C_{n}^{k} p^{k} q^{n - k}

. Если рассмотреть все вероятности числа успехов, будет получено так называемое биномиальное распределение вероятностей.

Задание 18. Написать программу для вычисления биномиального распределения вероятностей и построения соответствующей диаграммы.

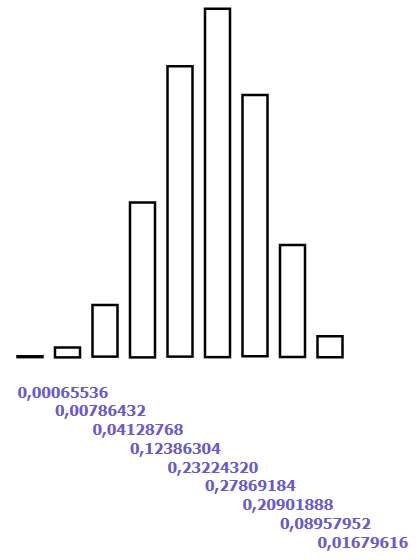
Решение. Программа может быть получена из программы задания 9 с помощью достаточно очевидной модификации. Нужно ввести вероятность успешного испытания. Кроме того, следует значительно увеличить коэффициент, определяющий высоту прямоугольников, составляющих диаграмму. При выводе на экран соответствующих вероятностей нужно избежать наложения чисел друг на друга. Результаты работы программы показаны на рисунке 6.

n = 8

p = .6

q = 1 - p

GraphicsWindow.PenColor = "black"

GraphicsWindow.Width = 400

GraphicsWindow.Height = 550

x = 50

y = 370

For m = 0 To n

'Подпрограмма вычисления числа сочетаний

sotsh()

EndFor

'Подпрограмма

Sub sotsh

nt = n

mt = m

cnm = 1

If m > n/2 Then

mt = n - m

EndIf

If m = 0 Then

Goto met

EndIf

For i = mt To 1 Step -1

cnm = cnm*nt/i

nt = nt - 1

EndFor

'Округление до ближайшего целого

cnm = Math.Round(cnm)

met:

pq = cnm * Math.Power(p, m) * Math.Power(q, n - m)

GraphicsWindow.DrawText(x, y, pq)

GraphicsWindow.DrawRectangle(x, 350 - pq*1000, 20, pq*1000)

x = x + 30

y = y + 15

EndSub

Рисунок 6

Схема Бернулли может быть обобщена на случай, когда каждое из стандартных испытаний имеет более двух исходов. Это обобщение называют полиномиальной схемой. Хорошим примером этой схемы является одновременное бросание нескольких игральных кубиков. При этом рассматривается дискретная случайная величина, равная сумме выпавших очков. Как и следует ожидать, вычисление вероятностей, определяющих распределение этой случайной величины, можно связать с возведением в степень, равную числу кубиков, суммы из шести слагаемых. Однако возможны и иные подходы к этой задаче.

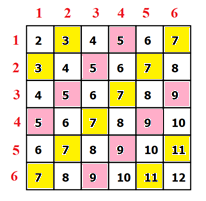
Рассмотрим конкретные примеры. Начнём со случая бросания двух кубиков. Он наиболее прост и нагляден. В частности, множество всех событий можно представить в виде квадратной таблицы (рисунок 7).

Рисунок 7

Задание 19. Получить распределение вероятностей полиномиального распределения вероятностей, возникающего при бросании двух игральных костей.

Решение. Отметим, что при практической реализации данной схемы можно либо бросать один раз сразу две кости, либо последовательно бросать одну кость два раза.

Поскольку целью является подсчёт слов, приводящих к одинаковым суммам, следует именно на этой задаче сосредоточить внимание. Дело в том, что разные слова-одночлены могут соответствовать одинаковым суммам. Именно суммы и надо перечислять. Из-за наличия наглядного представления ситуации можно просто подсчитать число клеток с равными суммами и разделить на общее число клеток. Однако мы поступим несколько иначе, нацеливаясь на более сложную задачу и готовясь к её решению. Итак, приступим к перечислению одинаковых сумм.

Суммы меняются от 2 до 12. Будем выписывать разложение этих сумм на слагаемые от 1 до 6 , располагая сомножители по возрастанию.

Сумма 2 получается единственным образом (1, 1). Вероятность равна $\frac{1}{36}$ .
Сумма 3 получается либо из слагаемых (1, 2), либо из перестановки (2, 1). Имеем два варианта. Вероятность равна $\frac{1}{18}$ .
Сумма 4 получается либо из слагаемых (1, 3) и (2, 2), либо из перестановки (3, 1). Имеем три варианта. Вероятность равна $\frac{1}{12}$ .
Сумма 5 получается либо из слагаемых (1, 4) и (2, 3), либо из перестановок (4, 1) и (3, 2). Имеем четыре варианта. Вероятность равна $\frac{1}{9}$ .
Сумма 6 получается либо из слагаемых (1, 5), (2, 4) и 3, 3), либо из перестановок (5, 1) и (4, 2). Имеем пять вариантов. Вероятность равна $\frac{5}{36}$ .
Сумма 7 получается либо из слагаемых (1, 6), (2, 5) и (3, 4), либо из перестановок (6, 1), (5, 2) и (4, 3). Имеем шесть вариантов. Вероятность равна $\frac{1}{6}$ .
Суммы 8, 9, 10, 11 и 12 в известном смысле получаются симметрично суммам от 6 до 1. Вероятности соответственно равны $\frac{5}{36}, \frac{1}{9}, \frac{1}{12}, \frac{1}{18}, \frac{1}{36}$ .

Задание 19. Получить распределение вероятностей полиномиального распределения вероятностей, возникающего при бросании трёх игральных костей.

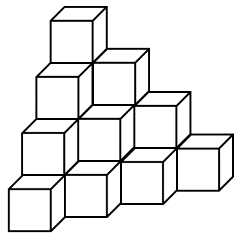
Решение. Наглядность соответствующей геометрической конструкции значительно понижена, хотя ещё сохраняется возможность хотя бы частичного изображения трёхмерной таблицы (рисунок 8).

Рисунок 8

Этот рисунок позволяет понять, что решаемая задача связана с вопросом геометрического характера, а именно с подсчётом числа единичных кубиков, составляющих большой куб, центры которых лежат на плоскости перпендикулярной одной из диагоналей большого куба. Отметим, что число единичных кубиков, слагающих большой куб, равно 216,

Перейдём к подсчётам.

Суммы меняются от 3 до 18. Будем выписывать разложение этих сумм на слагаемые от 1 до 6 , располагая сомножители по возрастанию.

Сумма 3 получается единственным образом (1, 1, 1). Вероятность равна $\frac{1}{216}$ .
Сумма 4 получается из слагаемых (1, 1, 2), дающих три перестановки. Имеем три варианта. Вероятность равна $\frac{1}{72}$ .
Сумма 5 получается из слагаемых (1, 1, 3) и (1, 2, 2). Каждая сумма с помощью перестановок даёт три варианта. Имеем шесть вариантов. Вероятность равна $\frac{1}{36}$ .
Сумма 6 получается из слагаемых (1, 1, 4) – три варианта, (1, 2, 3) – шесть вариантов после перестановок, (2, 2, 2) – один вариант. Всего имеем десять вариантов (они как раз соответствуют рисунку 8). Вероятность равна $\frac{5}{108}$ .
Сумма 7 получается из слагаемых (1, 1, 5) – три варианта, (1, 2, 5) – шесть вариантов, (1, 3, 3) – три варианта, , (2, 2, 3) – три варианта. Всего имеем пятнадцать вариантов. Вероятность равна $\frac{5}{72}$ .
Сумма 8 получается из слагаемых (1, 1, 6) – три варианта, (1, 2, 4) – шесть вариантов, (1, 3, 4) – шесть вариантов, (2, 2, 4) – три варианта, , (2, 3, 3) – три варианта. Всего имеем двадцать один вариант. Вероятность равна $\frac{7}{72}$ .
Сумма 9 получается из слагаемых (1, 2, 6) – шесть вариантов, (1, 3, 5) – шесть вариантов, (1, 4, 4) – три варианта, (2, 2, 5) – три варианта, (2, 3, 4) – шесть вариантов, (3, 3, 3) – один вариант. Всего имеем двадцать пять вариантов. Вероятность равна $\frac{25}{216}$ .
Сумма 10 получается из слагаемых (1, 3, 6) – шесть вариантов, (1, 4, 5) – шесть вариантов, (2, 2, 6) – три варианта, (2, 3, 5) – шесть вариантов, (2, 4, 4) – три варианта, (3, 3, 4) – три варианта. Всего имеем двадцать семь вариантов. Вероятность равна $\frac{1}{8}$ .
Суммы от 11 от 18 в известном смысле получаются симметрично суммам от 10 до 3. Вероятности соответственно равны $\frac{1}{8}, \frac{25}{216}, \frac{7}{72}, \frac{5}{72}, \frac{5}{108}, \frac{1}{36}, \frac{1}{72}, \frac{1}{216}$ .

Для проверки найдём сумму всех вариантов:

2∙(1 + 3 + 6 + 10 + 15 + 21 + 25 + 27) = 2∙108 = 216.

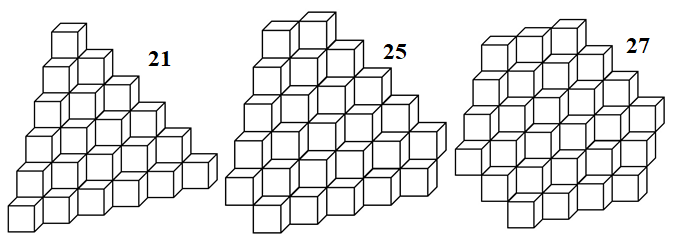
Задание 20. Изобразить сечения куба, соответствующие суммам очков 8, 9 и 10 с указанием числа вариантов.

Решение. Изображения показаны на рисунке 9.

Рисунок 9

Задание 21. Разобраться, как соответствующие сечения складываются в большой куб.

Пояснение. Следующее сечение куба также соответствует сумме очков 11. Оно, как и сечение, соответствующее 10 очкам, складывается из 27вариантов, но перевёрнуто. Далее прикладываются перевёрнутые сечения в обратном порядке из числа вариантов 25, 21, 15…

СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ

Вернёмся к перемножению скобок и обратимся к задачам высшей алгебры, связанным с симметрическими многочленами [16].

Одним из объектов высшей алгебры являются многочлены от нескольких переменных. Будем обозначать соответствующие переменные буквами некоторого алфавита. Тогда каждый член многочлена можно рассматривать как слово, составленное из букв этого алфавита. Кроме того, при таком подходе можно располагать члены в алфавитном (лексиграфическом) порядке. Мы уже делали нечто подобное.

Многочлен называется симметрическим, если он не меняется при любой перестановке переменных. Некоторые симметрические многочлены особенно важны. Они называются элементарными симметрическими многочленами. Для алфавита, состоящего из n букв, определены n таких многочленов, обозначаемых через

σ_{1}

,

σ_{2}

, …

σ_{n}

. Членs элементарного симметрического многочлена

σ_{k}

соответствуют всем различным словам из k букв. При этом любая буква алфавита не может входить в слово более одного раза.

В курсе высшей алгебры доказывается теорема основная теорема о симметрических многочленах. Согласно ей каждый симметрический многочлен может быть выражен как многочлен от элементарных симметрических многочленов. Например, при

n = 2

,

σ_{1} = x + y

и

σ_{2} = x ∙ y

. Симметрический многочлен

x^{2} + y^{2}

выражается через элементарные:

x^{2} + y^{2} = σ_{1}^{2} - 2 ∙ σ_{2}

.

В примере, конечно, рассмотрен очень простой случай. Но на самом деле при росте числа слагаемых и степеней вычисления становятся всё более сложными. Убедимся в этом.

Задание 22. Рассмотрим многочлены с четырьмя переменными

x, y, z, t

. В этом случае σ1(x, y, z, t) = x + y + z + t. Вычислить

σ_{1}^{6} =

(x + y + z + t)6.

Решение. Перед нами задача, связанная с перемножением скобок и рассмотренная выше. Сейчас, проводя более сложные, чем ранее, вычисления, будем подробно комментировать наши действия, порой повторяя выше сказанное.

Поскольку (x + y + z + t)6 = (x + y + z + t) (x + y + z + t) (x + y + z + t) (x + y + z + t) (x + y + z + t) (x + y + z + t), в каждой из этих шести скобок выбирается по одной букве из четырёх. По этой причине после раскрытия скобок получится 4*4*4*4*4*4 = 46 = (22)6 = (22)6 = 212 = 210 22 = 4*210 = 4*1024 = 4096 = 4 Кб слагаемых. Уже одно это число показывает, насколько объёмна решаемая задача.

Естественно, что среди слагаемых будут подобные. Количество подобных равно коэффициенту в полиномиальной формуле перед

x^{k_{1}} y^{k_{2}} z^{k_{3}} t^{k_{4}}

, где k1 + k2 + k3 + k4 = 6.

Этот коэффициент равен

P (k_{1}, k_{2}, k_{3}, k_{4}) = \frac{6!}{k_{1}! k_{2}! k_{3}! k_{4}!}

.

В нашем случае полиномиальная формула будет иметь следующий вид:

(x + y + z + t)6 = ∑

P (k_{1}, k_{2}, k_{3}, k_{4}) x^{k_{1}} y^{k_{2}} z^{k_{3}} t^{k_{4}}

, (1),

где сумма распространена на всевозможные разбиения числа 6 на 4 целых неотрицательных слагаемых: k1 + k2 + k3 + k4 = 6.

Поскольку

P (k_{1}, k_{2}, k_{3}, k_{4}) = \frac{(k 1 + k 2 + k 3 + k 4)!}{k_{1}! k_{2}! k_{3}! k_{4}!}

=

\frac{6!}{k_{1}! k_{2}! k_{3}! k_{4}!}

, то ясно, что если набор чисел (s1, s2, s3, s4 ) получается перестановкой из набора

(k_{1}, k_{2}, k_{3}, k_{4})

, то

P (s_{1}, s_{2}, s_{3}, s_{4}) = P (k_{1}, k_{2}, k_{3}, k_{4})

. Поэтому, например, в разложении (1) коэффициенты при x2t2yz и y2z2xt будут равны. Отсюда следует, что достаточно найти коэффициенты для таких разбиений 6 = k1 + k2 + k3 + k4 , что k1 ≥ k2 ≥ k3 ≥ k4 ≥ 0, а затем переставлять показатели всеми возможными способами.

Запишем все разбиения числа 6 на 4 целых неотрицательных слагаемых, располагая их в порядке убывания:

1. (6, 0, 0,0).

2. (5, 1, 0, 0).

3. (4, 2, 0, 0).

4. (4, 1, 1, 0).

5. (3, 3, 0, 0).

6. (3 ,2, 1, 0).

7. (3, 1, 1, 1).

8. (2, 2, 2, 0).

9. (2, 2, 1, 1).

Всего получилось 9 основных типов разбиений. Остальные разбиения получаются из основных всевозможными перестановками. Теперь выпишем для каждого типа полиномиальный коэффициент, число Sk слагаемых, соответствующих этому коэффициенту, а также сами эти слагаемые.

1.

P_{6} (6,0,0,0) =

\frac{6!}{6! 0! 0! 0!}

= 1. В этом случае S1 = Р4(1, 3) =

\frac{4!}{1! 3!}

= 4, так как число S1 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых три повторяются. Выпишем все четыре слагаемых, соответствующих коэффициенту 1:

x6 + y6 + z6 + t6.

2.

P_{6} (5,1,0,0) =

\frac{6!}{5! 1! 0! 0!}

= 6. В этом случае S2 = Р4(1, 1, 2) =

\frac{4!}{1! 1! 2!}

= 12, так как число S2 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых два повторяются. Выписываем все двенадцать слагаемых, соответствующих коэффициенту 6:

6x5y + 6x5z + 6x5t + 6y5x + 6y5z + 6y5t + 6z5x + 6z5y + 6z5t + 6t5x + 6t5y + + 6t5z.

3.

P_{6} (4,2,0,0) =

\frac{6!}{4! 2! 0! 0!}

= 15. В этом случае S3 = Р4(1, 1, 2) =

\frac{4!}{1! 1! 2!}

= 12, так как число S3 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых два повторяются. Выписываем все двенадцать слагаемых, соответствующих коэффициенту 15:

15x4y2 + 15x4z2 + 15x4t2 + 15y4x2 + 15 y4z2 + 15y4t2 +

+ 15z4x2 + 15z4y2 + 15z4t2 + + 15t4x2 + 15t4y2 + 15t4z2.

4.

P_{6} (4,1,1,0) =

\frac{6!}{4! 1! 1! 0!}

= 30. В этом случае S4 = Р4(1, 1, 2) =

\frac{4!}{1! 1! 2!}

= 12, так как число S4 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых два повторяются. Выписываем все двенадцать слагаемых, соответствующих коэффициенту 30:

30x4yz + 30x4yt + 30x4zt + 30y4xz + 30y4xt + 30y4zt +

+ 30z4xy + 30z4xt + 30z4yt + 30t4xy + 30t4xz + 30t4yz.

5.

P_{6} (3,3,0,0) =

\frac{6!}{3! 3! 0! 0!}

= 20. В этом случае S5 = Р4(1, 1, 2) =

\frac{4!}{2! 2!}

= 6, так как число S5 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых два элемента повторяются два раза. Выписываем все шесть слагаемых, соответствующих коэффициенту 20:

20x3y3 + 20x3z3 + 20x3t3 + 20 y3z3 + 20y3t3 + 20z3t3.

6.

P_{6} (3,2,1,0) =

\frac{6!}{3! 2! 1! 0!}

= 60. В этом случае S6 = Р4 = 4! = 24, так как число S6 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов без повторений. Выписываем все двадцать четыре слагаемых, соответствующих коэффициенту 60:

60x3y2z + 60x3y2t + 60x3z2y + 60x3z2t + 60x3t2y + 60x3t2z + 60y3x2z + 60y3x2z +

+ 60y3x2t + 60y3z2x + 60y3z2t + 60y3t2z + 60z3x2y + 60z3x2t + 60z3y2x + 60z3y2t +

+ 60z3t2x + 60z3t2y + 60t3x2y + 60t3x2z + 60t3y2x + 60t3y2z + +60t3z2x + 60t3z2y.

7.

P_{7} (3,1,1,1) =

\frac{6!}{3! 1! 1! 1!}

= 120. В этом случае S7 = Р4(1, 1, 2) =

\frac{4!}{3! 1!}

= 4, так как число S7 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых три повторяются. Выписываем все четыре слагаемых, соответствующих коэффициенту 120:

120x3yzt + 120y3xzt + 120z3xyt + 120t3yz.

8.

P_{6} (2,2,2,0) =

\frac{6!}{2! 2! 2! 0!}

= 90. В этом случае S8 = Р4(3, 1) =

\frac{4!}{3! 1!}

= 4, так как число S8 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых три повторяются. Выписываем все четыре слагаемых, соответствующих коэффициенту 90:

90x2y2z2 + 90y2z2t2 + 90z2t2x2 + 90t2x2y2.

9.

P_{6} (2,2,1,1) =

\frac{6!}{2! 2! 1! 1!}

= 180. В этом случае S9 = Р4(3, 1) =

\frac{4!}{2! 2!}

= 6, так как число S9 слагаемых, соответствующих этому коэффициенту, равно количеству перестановок четырёх элементов, из которых два элемента повторяются два раза. Выписываем все 6 слагаемых, соответствующих коэффициенту 180:

180x2y2zt + 180x2z2yt + 180x2t2yz + 180y2z2xt + 180y2t2xz + 180z2t2xy.

Полученные результаты сведём в таблицу.

Тип	Коэффициент	Число слагаемых	Число слагаемых до приведения подобных
1. (6, 0, 0,0)	1	4	4
2. (5,1, 0, 0)	6	12	72
3. (4, 2, 0, 0)	15	12	180
4. (4,1, 1, 0)	30	12	360
5. (3, 3, 0, 0)	20	6	120
6. (3, 2, 1, 0)	60	24	1440
7. (3,1, 1, 1)	120	4	480
8. (2, 2, 2, 0)	90	4	360
9. (2, 2, 1, 1)	180	6	1080

Всего получилось 4 + 72 + (180 + 120) + (360 + 1440) + 480 + 360 + 1080 = 76 + 300 + 1800 + 480 + 1440 = 376 + 2280 + 1440 = 2656 + 1440 = (2600 + 1400) + (56 + 40) = 4000 + 96 = 4096 слагаемых до приведения подобных.

Подсчитаем число слагаемых после приведения подобных, т.е. просуммируем третий столбец таблицы: 4 + 12∙3 + 6 + 24 + 4∙2 + 6 = 10 + 36 + 24 + 14 = 24 + 60 = 84. Мы помним, что количество всевозможных упорядоченных разбиений числа n на m целых неотрицательных чисел выражаются как число сочетаний

C_{n + m - 1}^{m - 1}

. В нашем случае n = 6 и m = 4. Следовательно, число членов после приведения подобных равно

C_{9}^{3} = \frac{9!}{3! 6!} = \frac{9 ∙ 8 ∙ 7}{2 ∙ 3}

= 84. Таким образом, наши теоретические результаты подтверждены практическим примером.

Чтобы оценить объём проделанной нами работы, запишем окончательный результат:

(x + y + z + t)6 = x6 + y6 + z6 + t6 +

+ 6x5y + 6x5z + 6x5t + 6y5x + 6y5z + 6y5t + 6z5x + 6z5y + 6z5t + 6t5x + 6t5y + 6t5z +

15x4y2 + 15x4z2 + 15x4t2 + 15y4x2 + 15 y4z2 + 15y4t2 + 15z4x2 + 15z4y2 + 15z4t2 + + 15t4x2 + 15t4y2 + 15t4z2 +

+ 30x4yz + 30x4yt + 30x4zt + 30y4xz + 30y4xt + 30y4zt + 30z4xy + 30z4xt + 30z4yt + 30t4xy + 30t4xz + 30t4yz +

+ 20x3y3 + 20x3z3 + 20x3t3 + 20 y3z3 + 20y3t3 + 20z3t3 +

60x3y2z + 60x3y2t + 60x3z2y + 60x3z2t + 60x3t2y + 60x3t2z + 60y3x2z + 60y3x2z + 60y3x2t + 60y3z2x + 60y3z2t + 60y3t2z + 60z3x2y + 60z3x2t + 60 z3y2x + 60z3y2t + 60z3t2x + 60z3t2y + 60t3x2y + 60t3x2z + 60t3y2x + 60t3y2z + +60t3z2x + 60t3z2y +

120x3yzt + 120y3xzt + 120z3xyt + 120t3yz +

90x2y2z2 + 90y2z2t2 + 90z2t2x2 + 90t2x2y2 +

180x2y2zt + 180x2z2yt + 180x2t2yz + 180y2z2xt + 180y2t2xz + 180z2t2xy.

Понятно, что произвольный симметрический многочлен четырёх переменных шестой степени может и более сложным образом выражаться через элементарные, чем в разобранном нами примере. Но этот пример дал нам возможность «пощупать» многочлен σ16 = (x + y + z + t)6 своими руками и заодно потренироваться в вычислении перестановок с повторениями, а в одном случае без повторений.

ЗАКЛЮЧЕНИЕ

Авторы надеются, что их методические идеи могут оказаться полезными для молодых преподавателей и помочь в их нелёгкой работе. По этой же причине предполагается написание ещё ряда статей, связанных с вычислениями в различных областях математики.

Литература

Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. 2019. № 4. С.127-144.
Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. 2019. № 4. С.145-156.
Куланин Е.Д.,Степанов М. Е., Нуркаева И.М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. 2020. Т.10. №2 С.110 - 128.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ данных. 2020. Т.11. №1. С.40 - 60.
Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. 2017. №1. С.54-94.
Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения Моделирование и анализ данных. 2022. Т.12. №3. С.58 – 70.
Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. Моделирование и анализ данных. 2022. Т.12. №4. С.67 – 84.
Куланин Е.Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. Моделирование и анализ данных. 2022. Т.12. №4. С.94 - 104.
Куланин Е.Д., Степанов М. Е., Панфилов А.Д., Потонышев И.С. Системный подход к методике тифлопедагогики на примере задач математического анализа. 2022. Т.12. №2. С.34 - 82.
Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики на примере теории чисел. Моделирование и анализ данных. 2024. Т.14. №1. С.170 - 195.
Холл М. Комбинаторика. М., Мир, 1970.
Натансон И. П. Суммирование бесконечно малых величин. М., Физматгиз, 1960.
Курош А. Г. Курс высшей алгебры. М., Физматгиз, 1962.

Информация об авторах

Куланин Евгений Дмитриевич, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Степанов Михаил Евграфович, кандидат педагогических наук, доцент, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Метрики

Просмотров

Всего: 28
В прошлом месяце: 18
В текущем месяце: 10

Скачиваний

Всего: 13
В прошлом месяце: 10
В текущем месяце: 3

PlumX

Метрики публикации