Моделирование и анализ данных
2023. Том 13. № 2. С. 99–122
doi:10.17759/mda.2023130206
ISSN: 2219-3758 / 2311-9454 (online)
Псевдоспектральный метод поиска оптимального управления пучками траекторий на базе мультиагентных алгоритмов оптимизации
Аннотация
Рассмотрен класс задач оптимального управления нелинейными непрерывными детерминированными системами в условиях неопределенности. Для решения поставленной задачи сформирован численный алгоритм поиска оптимального управления, в котором применяется параметризация закона управления, зависящего от времени и набора координат вектора состояния, доступных измерению. Данный подход основан на аппроксимации закона управления рядом по системе базисных функций с неизвестными коэффициентами. Поиск неизвестных коэффициентов в разложении закона управления, реализуется с применением мультиагентных методов оптимизации: гибридного мультиагентного алгоритма интерполяционного поиска и мультиагентного алгоритма, основанного на использовании линейных регуляторов управления движением агентов. Разработан комплекс программ и решены два модельных примера и прикладная задача о стабилизации спутника с помощью установленных на нем двигателей.
Общая информация
Ключевые слова: управление, теория оптимизации, алгоритм глобальной оптимизации, полиномы Чебышева, псевдоспектральный метод
Рубрика издания: Методы оптимизации
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130206
Получена: 17.03.2023
Принята в печать:
Для цитаты: Каранэ М.С. Псевдоспектральный метод поиска оптимального управления пучками траекторий на базе мультиагентных алгоритмов оптимизации // Моделирование и анализ данных. 2023. Том 13. № 2. С. 99–122. DOI: 10.17759/mda.2023130206
Полный текст
Введение
При решении многих прикладных проблем теории управления возникают задачи синтеза систем управления, которые описываются нелинейными обыкновенными дифференциальными уравнениями с неопределенно заданными начальными условиями [1–2]. Подобные задачи рассматривались во многих работах [1–6] и решались с помощью различных методов. Одним из возможных подходов к решению задачи является описание и последующее управление всей совокупностью траекторий, исходящих из заданного множества возможных начальных состояний, называемой пучком траекторий.
В статье формулируется стратегия для решения задачи поиска оптимального управления пучками траекторий с неполной обратной связью, где управление зависит от времени и от части координат вектора состояния, информация о значениях которых предполагается известной.
В силу сложности решения нелинейных прикладных задач оптимального управления [7, 8], как правило, применяются численные методы, которые можно разделить на прямые и косвенные. Основная идея прямого подхода заключается в том, что нелинейная динамическая задача оптимального управления сводится к задаче нелинейного математического программирования [Deng, 2020; Пантелеев, 2020]. Косвенный подход основан на применении необходимых условий оптимальности (принципе максимума Понтрягина) или достаточных условий оптимальности (принципе оптимальности Беллмана или принципе расширения Кротова–Гурмана) [Бортаковский, 2016].
В статье предлагается прямой подход к решению поставленной задачи с параметризацией закона управления. Для этого используется псевдоспектральный метод [7–11], в котором управление аппроксимируется глобальным многочленом, а коллокация выполняется в специально выбранных точках (точках коллокации). Глобальный многочлен подбирает к точкам коллокации сглаживающую функцию. В этом методе фиксируется набор точек коллокации, а степень используемого многочлена может изменяться. В качестве базисных функций обычно рассматриваются полиномы Чебышева или Лагранжа, а управление представляется в виде ряда по базисным функциям с неизвестными коэффициентами. В силу особых свойств полиномов Чебышева [Garg, 2017], в качестве ограничений на коэффициенты используются ограничения, наложенные на управление. Решение представляется в виде значений в –й точках коллокации, которые однозначно определяют полином, аппроксимирующий решение. Наличие естественных ограничений на коэффициенты, следующих из постановки задачи, является преимуществом псевдоспектрального метода по сравнению со спектральным [Tang, 2016], где никакой априорной информации о коэффициентах нет.
В численных методах поиска оптимального управления при прямом подходе для оптимизации критерия качества управления требуется использовать методы оптимизации, которые могут быть как классическими, так и основанными на эвристических процедурах. Для этой цели успешно применяются метаэвристические алгоритмы [6; 13–23], а также их подгруппа – мультиагентные алгоритмы [17–20], принципиальной особенностью которых является использование агентов. Если рассматривать целевую функцию , то агент – это набор параметров Агенты имеют возможность обмениваться информацией с целью достижения наилучшего результата. Мультиагентные алгоритмы имеют достаточно широкое применение и используются во многих отраслях науки. В статье используются два мультиагентных метода: гибридный мультиагентный алгоритм интерполяционного поиска [Panteleev, 2021; Panteleev, 2020] и метод, основанный на использовании линейных регуляторов управления движением агентов [17–19]. Особенность гибридного мультиагентного алгоритма интерполяционного поиска заключается в построении интерполяционных кривых: Безье, Катмулла–Рома и В-сплайна, и в различной аппроксимации набора точек. Построение интерполяционных кривых дает возможность подстроиться под локально изменяющуюся структуру поверхности уровня целевой функции, а их применение позволяет перейти к задачам одномерной параметрической минимизации с целью нахождения новых агентов по информации о текущем положении агентов, образующих популяцию. Также в алгоритме используется метод роевого интеллекта для минимизации вдоль интерполяционной кривой [Wang, 2019; Davendra, 2016] и самоорганизующийся миграционный алгоритм (Self-Organizing Migrating Algorithm, SOMA) [Финкельштейн, 2018]. Особенность метода, основанного на использовании линейных регуляторов управления движением агентов, состроит в том, что движение агентов описывается системой дифференциальных уравнений. Для разных групп агентов используются различные типы критериев и типы оптимального или субоптимального управления с полной обратной связью.
В данной работе на базе этих мультиагентных алгоритмов и идей псевдоспектрального метода сформирован алгоритм поиска оптимального программного управления в условиях неопределенности задания начального состояния, как частного случая управления с неполной обратной связью.
Решены модельные примеры [Крылов, 1968], в которых система управления описывается нелинейной системой дифференциальных уравнений, а ограниченное управление входит линейно. Помимо этого решена задача гашения вращательного движения спутника при помощи установленных на нем двигателей [Karane, 2022].
В следующем разделе описана постановка задачи управления пучками траекторий. В третьем разделе излагается стратегия поиска решения поставленной задачи, приведены общие идеи и способы ее решения. В четвертом разделе сформирован пошаговый алгоритм поиска оптимального управления пучками траекторий. Модельные примеры и прикладная задача о стабилизации спутника решены в пятом и шестом разделах соответственно.
Постановка задачи
Поведение нелинейной непрерывной детерминированной модели объекта управления описывается уравнением
(1)
где – вектор состояния системы, ; – непрерывное время, , моменты начала процесса и окончания процесса управления считаются заданными; – вектор управления, ; – множество допустимых значений управления, представляющее собой прямое произведение отрезков , ; – непрерывно дифференцируемая вектор-функция.
Начальные условия заданы компактным множеством положительной меры с кусочно-гладкой границей:
(2)
где множество характеризует неопределенность задания начальных условий.
Предполагается, что при управлении используется информация о времени и о части координат вектора состояния (без ограничения общности считается, что это первые координат). Таким образом, о компонентах вектора известна текущая информация, а о компонентах вектора она отсутствует, при этом . Если , информация о векторе состояния отсутствует, а если , то имеется полная информация о векторе состояния.
Управление, применяемое в каждый момент времени , имеет вид управления с неполной обратной связью: . Если , система управления будет разомкнутой по состоянию, а соответствующее управление – программным, а если , то система управления будет замкнутой с полной обратной связью, определяемой управлением . Множество допустимых управлений образуют такие функции , что управление кусочно-непрерывно, а функция такова, что решение уравнения (1) с начальным условием (2) существует и единственно. Множество допустимых процессов – множество пар , включающих траекторию и кусочно-непрерывное допустимое управление , где , удовлетворяющих уравнению состояния (1) и начальному условию (2).
На множестве определен функционал качества управления отдельной траекторией:
(3)
где , – заданные непрерывные функции.
Каждому допустимому управлению и множеству поставим в соответствие пучок (ансамбль) траекторий уравнения (1) [Куржанский, 1977]:
(4)
т.е. объединение решений уравнения (1) по всем возможным начальным состояниям (2). Пучок траекторий порождается множеством и управлением .
Качество управления пучком траекторий предлагается оценивать величиной функционала
(5)
или
(6)
где – мера множества .
Требуется найти управление , минимизирующее функционал (5) или (6):
(7)
Искомое управление называется оптимальным в среднем, когда минимизируется значение функционала (5), т.е. среднее значение функционала (3) на множестве начальных состояний , или гарантирующим (минимаксным), когда минимизируется функционал (6).
Стратегия поиска решения
Для решения поставленной задачи определим способ вычисления критерия оптимальности управления пучком траекторий, а также способ параметризации закона управления. Эти процедуры можно разделить на два этапа.
I этап. Приближенное вычисление значения функционала (5) и (6).
Пусть множество начальных состояний представляет собой параллелепипед, определенный прямым произведением отрезков , т.е. Все отрезки , с помощью шага разбиваются на отрезков, а параллелепипед делится на элементарных подмножеств . В каждом элементарном подмножестве задается начальное состояние – центр параллелепипеда .
Для каждого начального состояния , из множества начальных состояний следует проинтегрировать систему дифференциальных уравнений (1) с управлением одним из численных методов, например методом Рунге–Кутты 4-го порядка. В результате получаются пары , образованные управлением и соответствующими траекториями . Следовательно, можно найти приближенное значение функционалов (5) или (6) соответственно:
(8)
или
. (9)
II этап. Параметризация закона управления.
Процедуру поиска решения задачи (7) сведем к проблеме поиска наилучших значений параметров, которые задают структуру управления. Управление ищется в параметрическом виде, который определяется числом коэффициентов в разложении управления по системе базисных функций и их значениями. В качестве базисных функций предлагается использовать полиномы Чебышева. Применение разложений по многочленам Чебышева широко используется в псевдоспектральных методах [7–11].
Предполагается, что известна оценка множества возможных состояний, которая представляется прямым произведением , где – нижняя и верхняя границы по каждой координате соответственно, определяемые физическим смыслом решаемой задачи.
Закон управления будем искать в виде функции насыщения sat, гарантирующей выполнение параллелепипедных ограничений на управление [Пантелеев, 2020]:
. (9)
Здесь
, (10)
где , а аргументы функции насыщения предлагается искать в виде линейной комбинации базисных функций. Используем систему многочленов Чебышева первого рода , ортогональных с весом на отрезке :
(11)
При этом
Тогда аргументы функции насыщения находятся по формуле
(12)
Здесь – неизвестные коэффициенты; – масштабы усечения по времени и координатам вектора состояния, используемым в управлении. Решение ищется как расширенная матрица-столбец вида
(13)
с ограничениями
целые; , (14)
где значение задается исходя из возможных требований к точности решения и лимиту вычислительных затрат, и – параметры ограничений на управление, известные из постановки задачи.
Таким образом, ищется решение на множестве векторов, полученных путем конкатенации векторов, состоящих из коэффициентов разложения для управлений и векторов масштабов усечения по времени и координатам вектора состояния.
Так как полиномы Чебышева рассматриваются на отрезке , то требуется преобразовать отрезки к стандартному отрезку , применив линейные преобразования:
где – нижняя и верхняя границы по каждой координате соответственно.
В результате уравнение (1) и функционал (3) перепишем в следующей форме:
(15)
Рассмотрим частный случай, когда система разомкнута по состоянию ( ). Следовательно, будем искать программное управление . Тогда для этого случая требуется переписать рассмотренный способ параметризации. Используя многочлены Чебышева, в качестве узлов интерполяции выберем положения экстремумов многочлена Чебышева степени и крайние точки отрезка интерполяции: На отрезке они располагаются так: и называются точками коллокации Чебышева–Гаусса–Лобатто (CGL (Chebyshev–Gauss–Lobatto)).
Поскольку многочлены Чебышева можно записать в форме то их значения в узлах найдем в виде
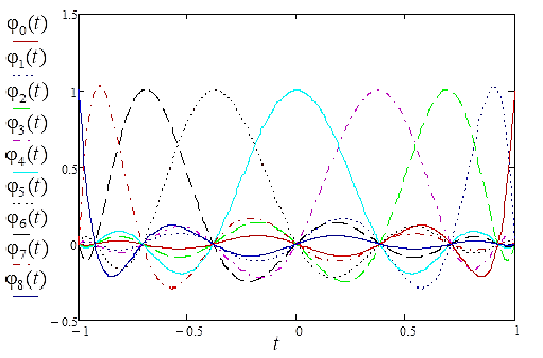
В качестве базисной системы (рис. 1) предлагается использовать [Garg, 2017]:
Тогда закон управления запишем в виде
(16)
где неизвестные величины.
При этом в узлах выполняются соотношения где символ Кронекера. На коэффициенты разложения накладываются ограничения, следующие из постановки задачи:
В задаче требуется найти координаты расширенного вектора
(17)
содержащего блок целочисленных переменных и блок действительных переменных , на которые накладываются ограничения вида (14).
Таким образом, предлагается искать значения координат блочных расширенных векторов (17), содержащих блок целочисленных переменных и блок действительных переменных, на которые наложены интервальные ограничения.
Рис. 1. Графики системы базисных функций для многочлена Чебышева 8-й степени
Вычислительный алгоритм
Описанный способ параметризации управления приводит к необходимости решения смешанной целочисленно-непрерывной задачи условной оптимизации:
(18)
где .
Для ее решения используются гибридные метаэвристические алгоритмы, относящиеся к группе мультиагентных. Они хорошо зарекомендовали себя при решении задач оптимизации типовых тестовых функций и параметров технических систем [Karane, 2020], а также в задачах поиска оптимального программного управления [Panteleev, 2020; Wang, 2018].
Поскольку вектор подбираемых параметров содержит как целочисленные, так и непрерывные координаты, то формируется алгоритм, реализующий два вида поиска: процедуру целочисленного линейного поиска для целочисленных переменных и процедуру поиска по непрерывным переменным, основанную на мультиагентных алгоритмах условной оптимизации. В связи с этим, предлагается последовательная схема решения, включающая описанные ниже шаги.
Шаг 1. Привести исходную постановку задачи к требуемому виду: отрезок привести к стандартному отрезку по формуле
Тогда модель объекта управления будет иметь вид
, ,
.
Задать параметры выбранного мультиагентного алгоритма и максимальную степень многочлена Чебышева Положить счетчик числа итерации
Шаг 2. Генерирование начального приближения.
Для целочисленных переменных:
,
где число, генерируемое согласно равномерному закону распределения, операция выделения целой части числа.
Для непрерывных переменных требуется сгенерировать начальную популяцию, состоящую из агентов на интервале . Каждый агент соответствует коэффициентам в разложении (16):
Шаг 3. Реализация процедуры поиска на множестве по целочисленным переменным при известных значениях координат вектора . Применяется процедура целочисленного линейного поиска для решения непрерывных задач оптимизации. При этом значения координат вектора в блочном векторе считаются фиксированными.
Шаг 3.1. Упорядочить переменные , случайным образом. Положить New = false – индикатор наличия улучшения, .
Шаг 3.2. Пусть на -м месте стоит -я переменная. “Просканировать” множество решений вида где единичный орт, составленный из всех нулей и одной единицы на -м месте; знак неравенства понимается покоординатно.
Шаг 3.3. Если среди полученных в результате сканирования решений имеется наилучшее, удовлетворяющее условию то заменить на и положить .
Действия, описанные на Шаге 3.2 и 3.3, назовем проходом (положим, что число проходов не превосходит максимального числа итераций ).
Шаг 4. Реализация процедуры поиска на множестве по непрерывным переменным при фиксированных координатах вектора .
Шаг 4.1. Разбить отрезок : , где , где – количество промежуточных точек отрезка известно из Шага 3.
Шаг 4.2. По сгенерированным коэффициентам (см. Шаг 2) сформировать управление в виде функции насыщения sat, гарантирующей выполнение ограничений на управление:
,
В качестве базисной системы функций рассматриваются многочлены Чебышева. Базисная система имеет следующие свойства:
– внутри интервала:
где ,
– в узлах:
Шаг 4.3. Проинтегрировать систем дифференциальных уравнений (см. Шаг 1) с управлениями , например, методом Рунге–Кутты 4-го порядка для каждого начального состояния из множества . Для каждого агента и для каждого начального состояния получить соответствующие траектории и вычислить значения функционала Найти среднее значение критерия качества управления пучком по формуле (8) (или соответствующее гарантирующему управлению по формуле (9)).
Шаг 4.4. Выполнить очередную итерацию выбранного метода минимизации функционала (8) (или (9)). Получить новые положения агентов (векторы значений коэффициентов разложения по системе базисных функций).
Шаг 4.5. Проверка критериев окончания поиска.
Если и достигнуто максимально число проходов, завершить процедуру целочисленного линейного поиска и фиксировать найденные значения координат вектора . Перейти к шагу 4.2.
Если и не достигнуто максимально число проходов, то перейти к шагу 3.1.
Если , завершить процедуру поиска значений непрерывных переменных и перейти к Шагу 5.
Шаг 5. Завершение поиска. На последней итерации выбирается лучший агент, т.е. вектор с координатами , а также соответствующие ему управление и пучок траекторий, а также значение функционала (8) (или (9)) принимаются за приближенное решение задачи с найденными коэффициентами , и значениями координат вектора .
Модельные примеры
Пример 1. Исходная постановка задачи [Крылов, 1968], приведенная в табл. 1, приводится к виду, удобному для применения описанного псевдоспектрального алгоритма с использованием полиномов Чебышева. Формула преобразования времени ( ):
Тогда отрезок времени будет иметь вид , а система дифференциальных уравнений перепишется в форме
Таблица 1
Постановка задачи
Значения параметров гибридного алгоритма интерполяционного поиска: и метода, основанного на применении линейных регуляторов управления движением агентов: , Множество начальных состояний .
В табл. 2 приведено численное решение задачи двумя мультиагентными алгоритмами и подсчитано среднее значение критерия, а в табл. 3 – значение критерия для гарантирующего управления. Исходя из полученных результатов, можно сделать вывод о том, что оба алгоритма успешно справились с поставленной задачей, но гибридный мультиагентный алгоритм интерполяционного поиска уступает мультиагентному алгоритму, основанному на применении линейных регуляторов управления движением агентов, в смысле значения функционала, однако при этом было затрачено больше ресурсов на вычисления.
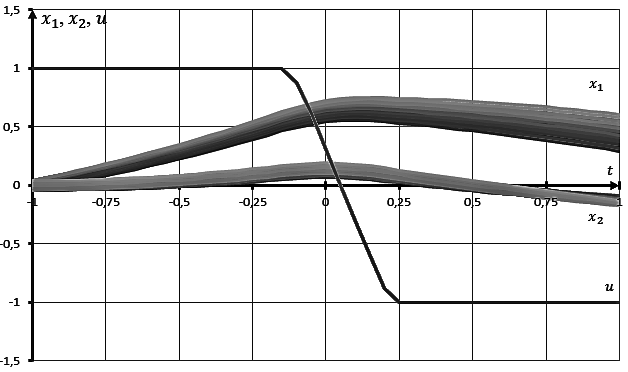
На рис. 2 изображены найденные пучки траекторий и управление для случая поиска среднего значения функционала (3) мультиагентным алгоритмом, основанным на применении линейных регуляторов управления движением агентов.
Рис. 2. Графики пучков траекторий и управления. Пример 1
Результаты, приведенные в табл. 2,3, сравнивались с известным решением, полученным при известном фиксированном начальном состоянии [Крылов, 1968]: координаты вектора состояния в конце времени функционирования системы , значение функционала (3): –0,13599. Также в [Panteleev, 2020] получены результаты решения рассматриваемой задачи в условиях неопределенности начального состояния системы. Минимизировалось среднее значение функционала (3) и искалось оптимальное в среднем управление гибридным мультиагентным алгоритмом интерполяционного поиска, с использованием спектрального разложения по системе нестационарных косинусоид. Получены следующие результаты: среднее значение функционала (3): –0,1337.
Пример 2. Исходная постановка задачи [Крылов, 1968], приведенная в табл. 4, приводится к виду, удобному для применения описанного псевдоспектрального алгоритма с использованием полиномов Чебышева. Формула преобразования времени ( ):
Таблица 4 Постановка задачи

Тогда будет справедливо, что , а система дифференциальных уравнений перепишется в виде
Значения параметров гибридного алгоритма интерполяционного поиска: метода, основанного на применении линейных регуляторов управления движением агентов: , Множество начальных состояний .
Таблица 5

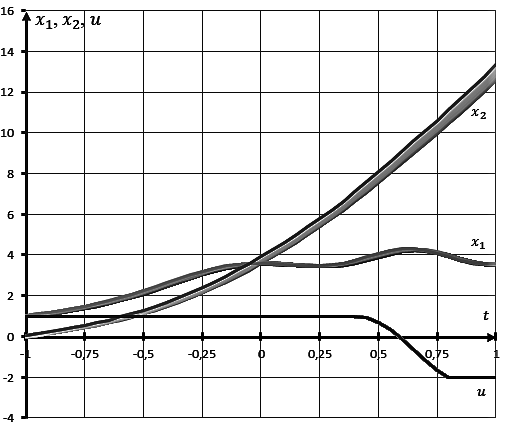
Решение задачи при поиске оптимального в среднем и гарантирующего управлений представлено в табл. 5 и 6 соответственно. Указано найденное наилучшее количество точек коллокации и значения коэффициентов в управлении. Вычисления проводятся с использованием двух мультиагентных алгоритмов. Исходя из полученных результатов, видно, что при использовании гибридного мультиагентного алгоритма интерполяционного поиска значение функционала было минимальным, по сравнению с другим мультиагентным алгоритмом, но при этом было затрачено большее время процессора. На рис. 3 приведены графики пучков траекторий и график управления. При анализе численных и графических результатов, можно сказать, что оба алгоритма успешно справились с поставленной задачей.
Рис. 3. Графики пучков траекторий и управления. Пример 2
Результат сравнивался с решением, полученным при известном фиксированном начальном состоянии, которое приводится в [Крылов, 1968]: координаты вектора состояния в конце времени функционирования системы , значение функционала (3): –2,98086. В [Panteleev, 2020] получены результаты решения рассматриваемой задачи в условиях неопределенности задания начального состояния системы. Минимизировалось среднее значение функционала и искалось оптимальное в среднем управление гибридным мультиагентным алгоритмом интерполяционного поиска, с использованием спектрального разложения по системе нестационарных косинусоид. Были получены следующие результаты: среднее значение функционала (3): –2,96042.
Исходя из приведенных данных для двух модельных примеров, можно заключить, что предложенный подход с использованием полиномов Чебышева показал результаты чуть лучше, чем метод, основанный на спектральном разложении по системе нестационарных косинусоид [Panteleev, 2020].
Прикладная задача
6.1. Постановка задачи
Рассматривается задача гашения вращательного движения спутника с помощью установленных на нем двигателей [Karane, 2022]. Движение твердого тела относительно центра инерции после перехода к безразмерным переменным, имеет вид:
(19)
где – проекции угловой скорости на главные центральные оси инерции, а – управления, которые характеризуют тяги двигателей, расположенных на спутнике. Ограничение на управление: . Начальное состояние системы задано множеством начальных состояний: В момент окончания функционирования системы должны выполняться условия:
Функционал качества управления характеризует затраты топлива при работе реактивных двигателей и степень выполнения конечных условий:
(20)
где – параметры штрафа. Для удобства численной реализации преобразуем задачу Больца (20) к задаче Майера с помощью введения дополнительного дифференциального уравнения:
(21)
Требуется найти оптимальное в среднем программное управление и соответствующий ему пучок траекторий, минимизирующие среднее значение функционала (20) на множестве начальных условий .
6.2. Решение задачи
В связи с тем, что поставленная задача будет решена описанным выше алгоритмом поиска оптимального программного управления пучками траекторий на основе псевдоспектрального метода, требуется привести исходную постановку задачи к виду, требуемому на Шаге 1. Формула преобразования времени ( , ):
тогда модель объекта управления перепишется следующим образом:
а начальный и конечный момент функционирования системы: .
Зададим параметры гибридного мультиагентного алгоритма интерполяционного поиска: , , , , , , , и метода, основанного на применении линейных регуляторов управления движением агентов: Множество начальных состояний .
Таблица 7
Решение прикладной задачи
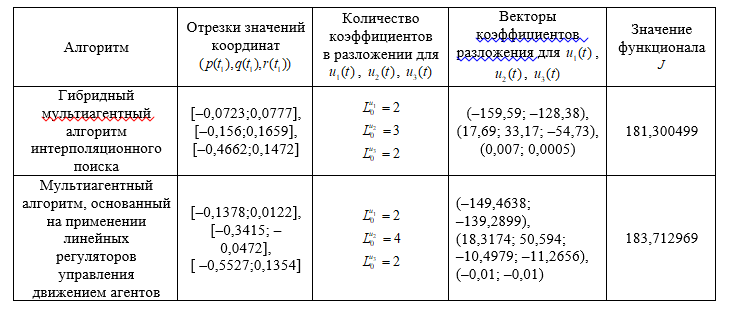
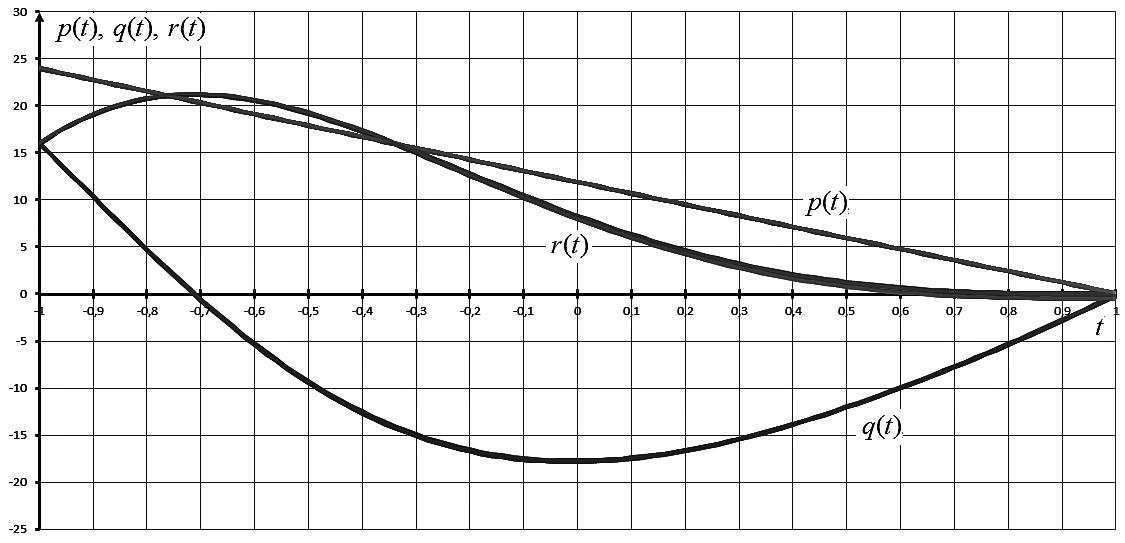
В табл. 7 приведены численные результаты, полученные двумя мультиагентными алгоритмами. Наилучшие результаты (минимальное значение функционала) получены при использовании гибридного мультиагентного алгоритма интерполяционного поиска. Для этого случая изображены графики пучков траекторий на рис. 4, а графики управления на рис. 5. Также найден вектор коэффициентов в разложении (16) для управлений , , .
В ходе решения задачи были получены данные о вычислительных затратах (времени решения задачи). Использовался процессор 11th Gen Intel(R) Core(TM) i7-1165G7 с частотой 2.80GHz. При решении гибридным мультиагентным алгоритмом интерполяционного поиска на выполнение задачи было затрачено 686 секунд, а методом, основанном на применении линейных регуляторов управления движением агентов, 895 секунд.
Численный результат сравнивался с решением, полученным с помощью мультиагентного метода, имитирующего поведение стаи криля [Wang, 2019], с параметрами: Результат решения задачи этим алгоритмом при заданных параметрах приведен в табл. 8.
Рис. 4. Задача о стабилизации спутника. Графики пучков траекторий
Рис. 5. Задача о стабилизации спутника. Программное управление
Таблица 8
Решение прикладной задачи
Заключение
Использован прямой подход для решения задачи оптимального программного управления пучками траекторий. Сформирован алгоритм поиска оптимального управления непрерывными детерминированными системами в условиях неопределенности, который базируется на применении псевдоспектрального алгоритма с использованием полиномов Чебышева и мультиагентных алгоритмов условной оптимизации. В частности, в статье рассмотрены два мультиагентных алгоритма: гибридный мультиагентный алгоритм интерполяционного поиска и метод, основанный на использовании линейных регуляторов управления движением агентов. На основе этих алгоритмов разработано программное обеспечение, с использованием которого продемонстрирована эффективность данного подхода на модельных примерах, а также на прикладной задаче о стабилизации спутника. Результаты прикладной задачи сравнивались с решением, полученным мультиагентным методом, имитирующим поведение стаи криля, а результаты модельных примеров – со спектральным мультиагентным алгоритмом, использующим разложение по системе нестационарных косинусоид. Разработанный алгоритм может быть применен в различных областях, таких как гидравлика, электротехника, а также областях связанных с поиском управления авиационно-космическими системами, например в задаче о планирующем спуске летательного аппарата, задаче о перехвате, задаче об управлении солнечным парусом и др.
Литература
- Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.: Изд-во Наука, 1977. 392 с.
- Овсянников Д.А., Мизинцева М.А., Балабанов М.Ю., Дуркин А.П., Едаменко Н.С., Котина Е.Д., Овсянников А.Д. Оптимизация динамики пучков траекторий c использованием гладких и негладких функционалов // Ч.1. Вестн. СПбГУ. Сер.10. Прикладная математика. Информатика. Процессы управления. 2020. Т. 16. №1. С. 73–84.
- Henrion D., Korda M. Convex Computation of the Region of Attraction of Polynomial Control Systems // European Control Conf, (ECC). Zurich, 2013. P. 676–681.
- Deng H., Zhang W., Shen C. Stability Analysis of Optimal Trajectory for Nonlinear Optimal Control Problems // Journal of Mathematics. 2020. P.1–5. doi:10.1155/2020/1392705.
- Бортаковский А.С. Оптимальное и субоптимальное управления пучками траекторий детерминированных систем автоматного типа // Изв. РАН. ТиСУ. 2016. №1. С. 5–26.
- Пантелеев А.В. Метаэвристические алгоритмы оптимизации законов управления динамическими системами. М.: Изд-во Факториал, 2020. 564 с.
- Афанасьев В. Н., Фролова Н. А. Дифференциальная игра в задаче управления нелинейным объектом с ограничениями на управляющие воздействия // Труды Института системного анализа РАН. 2020. Т. 70. № 3. С. 56-64. doi:10.14357/20790279200307
- Liu M., Zhao J., Hoogendoorn S., Wang M. An optimal control approach of integrating traffic signals and cooperative vehicle trajectories at intersections // Transportmetrica B: Transport Dynamics. 2021. No. 10. P.1–17. doi:10.1080/21680566.2021.1991505.
- Rybakov K.A. Applying Spectral Form of Mathematical Description for Representation of Iterated Stochastic Integrals // Differencialnie Uravnenia i Protsesy Upravlenia. 2019. No. 4. P. 1–31.
- Косников Ю.Н. Особенности применения радиальных базисных функций в геометрическом моделировании трехмерных объектов визуализации // Модели, системы, сети в экономике, технике, природе и обществе. 2020. №4.
- Garg D., Patterson M., Hager W., Rao A., Benson D. An overview of three pseudospectral methods for the numerical solution of optimal control problems // Advances in the Astronautical Sciences. 2017. V.135, P.1–17.
- Tang X., Hu Z.L. New results on pseudospectral methods for optimal control // Automatica. Vol.65. 2016, P.160-163. doi:10.1016/j.automatica.2015.11.035
- Mehrpouya M. A., Peng H. A robust pseudospectral method for numerical solution of nonlinear optimal control problems // International Journal of Computer Mathematics. 2021, no.98(6), P.1146–1165, doi: 10.1080/00207160.2020.1807521
- Hager W. W., Liu J., Mohapatra S., Rao A. V., Wang X. -S. A pseudospectral method for optimal control based on collocation at the Gauss points // IEEE Conference on Decision and Control (CDC). 2018, P. 2490–2495, doi: 10.1109/CDC.2018.8618929.
- Li Y., Chen W., Yang L. Linear Pseudospectral Method with Chebyshev Collocation for Optimal Control Problems with Unspecified Terminal Time //Aerospace 2022, no. 9. doi:10.3390/aerospace9080458
- Gendreau M., Potvin J-Y. Handbook of Metaheuristic. N.Y.: Springer, 2019. 604 p.
- Panteleev A., Karane M. Application of Multi-agent Optimization Methods Based on the Use of Linear Regulators and Interpolation Search for a Single Class of Optimal Deterministic Control Systems // Applied Mathematics and Computational Mechanics for Smart Applications. Singapore: Springer, 2021. P. 217–244
- Panteleev A., Karane M. Multi-agent Optimization Algorithms for a Single Class of Optimal Deterministic Control Systems // Advances in Theory and Practice of Computational Mechanics. Singapore: Springer, 2020. pp. 271–291
- Karane M., Panteleev A. Benchmark Analysis of Novel Multi-agent Optimization Algorithm Using Linear Regulators for Agents Motion Control // IOP Conf. Series: Materials Science and Engineering. Alushta, 2020. doi:10.1088/1757-899X/927/1/012023
- Wang D., Tan D., Liu L. Particle swarm optimization algorithm: an overview // Soft Computing, 2018, 22(2), P.387–408. doi:10.1007/s00500-016-2474-6.
- Wang G., Gandomi A., Alavi A., Gong D. A comprehensive review of krill herd algorithm: variants, hybrids and applications // Artificial Intelligence Review. 2019, no. 51, P.119–148. doi:10.1007/s10462-017-9559-1.
- Davendra D., Zelinka I. Self-Organizing Migrating Algorithm. Methodology and Implementation. Studies in Computational Intelligence. Springer 2016. 626 p.
- Финкельштейн Е.А. Вычислительные технологии аппроксимации множества достижимости управляемой системы: Автореф. дисс. ... канд. техн. наук. Иркутск, 2018. 19 с.
- Крылов И.А. Численное решение задачи об оптимальной стабилизации спутника // ЖВМ и МФ. 1968. Т.8. №1. С. 203–208.
- Karane, M.M., Panteleev, A.V. Multiagent Algorithms for Optimizing Bundles of Trajectories of Deterministic Systems with Incomplete Instant Feedback // J. Comput. Syst. Sci. Int. 61. 2022. P.751–775. doi:10.1134/S1064230722050082
Информация об авторах
Метрики
Просмотров web
За все время: 193
В прошлом месяце: 16
В текущем месяце: 11
Скачиваний PDF
За все время: 147
В прошлом месяце: 12
В текущем месяце: 4
Всего
За все время: 340
В прошлом месяце: 28
В текущем месяце: 15