Моделирование и анализ данных
2018. Том 8. № 1. С. 3–38
ISSN: 2219-3758 / 2311-9454 (online)
Компьютерные технологии как средство приобщения учащегося к математической реальности
Аннотация
Общая информация
Ключевые слова: методика преподавания математики, аналитическая геометрия, математический анализ, дифференциальная геометрия, линейная алгебра, алгебра многочленов, дифференциальные уравнения, уравнения математической физики, теория вероятностей, вычислительная математика, линейное программирование, компьютерные технологии, высшее образование
Тип материала: научная статья
Для цитаты: Степанов М.Е. Компьютерные технологии как средство приобщения учащегося к математической реальности // Моделирование и анализ данных. 2018. Том 8. № 1. С. 3–38.
Полный текст
1. ВВЕДЕНИЕ
Данная статья по содержанию примыкает к предыдущей статье автора «Некоторые вопросы методики преподавания высшей математики» [М. Е. Степанов, 2017] и развивает точку зрения, которая была там высказана: «При рассмотрении содержания математики, принято говорить о математическом понятии, вне зависимости от того, идёт ли речь о творческом развитии математического знания, об обучении математике или же о разработке методик преподавания. Нам, однако, более обоснованным представляется использование термина «объект математической реальности». Его введение позволяет детализировать процесс обучения и разделить его на формирование представления об объекте математической реальности как о понятии и как об образе. Только такое разделение позволяет достичь итогового соединения, условно говоря, логических аспектов владения объектом и аспектов интуитивного овладения им. Именно этот подход позволяет достигнуть того уровня видения математической реальности, которое называется пониманием».
В этой связи следует отметить, что развитие информатики привело к возникновению компьютерных технологий, которые оказались исключительно эффективным инструментом соединения логических аспектов познания объекта и аспектов интуитивного видения этого объекта и умения манипулировать им в виде пластического образа.
Автор отдаёт себе отчёт в том, что компьютерные технологии многогранны и предоставляют пользователю разнообразные средства опредмечивания математических объектов. Однако он сосредоточивает своё внимание на использовании для этой цели языков програм- 3
мирования. Если говорить более конкретно, речь идёт о языке Small Basic, разработанном в 2010 году специально под Windows. Конечно, нет оснований для отказа от использования в том же ключе и других языков программирования. Однако язык Small Basic освобождает от программистской формалистики и упрощает написание программ до предела.
Предлагаемые в дальнейшем подходы к обучению высшей математике опираются на использование языка программирования, как средства приобщения учащегося к математической реальности, и направлены на получение следующих результатов:
-
Студент должен увидеть, как теоретические положения и абстрактные формулы с помощью простой компьютерной программы превращаются в зримые образы.
-
Эти образы должны помочь студенту разобраться в смысле соответствующих математических понятий.
-
Студент должен научиться с достаточной степенью свободы преобразовывать математические идеи и формулы в алгоритмы соответствующих программ.
Ниже автор широко использует материалы из своей неизданной рукописи «Компьютерная геометрия, тт. 1 - 2).
2. ПРИМЕРЫ ЗАДАНИЙ
Растровая компьютерная графика основана на декартовой системе координат. По этой причине наиболее естественным исходным пунктом в деле использования компьютерных программ для иллюстрирования математических понятий является аналитическая геометрия на плоскости. Задания, которые можно предложить студенту на начальном этапе изучения аналитической геометрии, состоят в том, что нужно построить на экране некоторое изображение. При этом для его построения нужно произвести расчёты, основанные на хорошем понимании координатного метода. Когда соответствующая этому методу, пусть и простая, математика начинает работать, студент сразу ощущает, что речь идёт не об абстракциях, а о полезном и эффективном инструменте.
Первые изображения можно строить с помощью программ без переменных, в которых все операнды графических команд задаются числами. Далее необходим переход к написанию программ с переменными. И, как показывает опыт, для некоторых студентов этот шаг довольно некомфортен, поскольку думать о числах и думать о переменных - всё же разный уровень интеллектуального развития.
Конечной же целью заданий такого типа является освоение основ векторной алгебры и выход на должный уровень понимая аксиоматики Вейля, связывающей воедино точки и вектора. Дело в том, что студенты часто воспринимают точки и вектора порознь. Цель заданий на построение изображений состоит в том, чтобы донести до студента смысл точечновекторного равенства типа В = А + АВ.
Продемонстрируем одно из подобных заданий. Но предварим его инструкцией, которая предоставляется студентам и направлена на то, чтобы они поняли - написание соответствующей программы должно основываться не на смутных ощущениях, переходящих клацанье клавишами клавиатуры, а на математических расчётах.
Конечно, ряд студентов может произвести правильные и быстрые расчёты без упоминаемого ниже чертежа, но в настоящее время они, к сожалению, составляют меньшинство.
Кроме того, у студентов часто проявляется способность успешно проводить вычисления с конкретными числами, но переход к более абстрактным, но по содержанию совершенно аналогичным, вычислениям с переменными величинами ставит их в тупик. Конечно, такое положение дел является совершенно ненормальным. Предлагаемые нами задания на построение изображений должны помочь в устранении подобных недоработок школьной педагогики.
Инструкция по построению изображений на координатной плоскости.
-
Нарисуйте изображение на бумаге. Если можно, разбейте его на независимые части, каждую из которых можно рисовать, не обращая внимания на другие части полного изображения.
-
Выделите на рисунке опорные точки: концы отрезков; вершины прямоугольников; центры окружностей и эллипсов; обособленные точки.
-
Среди опорных точек выберите одну - исходную. Обозначьте её координаты через х и у.
-
Определите максимальный линейный размер изображения в пикселях, исходя из размеров экрана. Выберите конкретные значения для смещений по вертикали и горизонтали между опорными точками, а также значения радиусов.
-
Подберите конкретные значения координат х и у исходной точки, учитывая положение изображения на экране.
-
Вычислите, отправляясь от исходной точки, координаты всех опорных точек.
-
Определите порядок построения линий и фигур.
-
Напишите программу, наберите её и запустите.
-
В случае надобности займитесь поиском ошибок - отладкой программы.
Переходя к первому заданию ещё раз подчеркнём, что задания такого типа направлены на практическое освоение азов векторной алгебры. Кроме того, отметим, что некоторые задания мы будем сопровождать пояснениями, предназначенными для студентов.
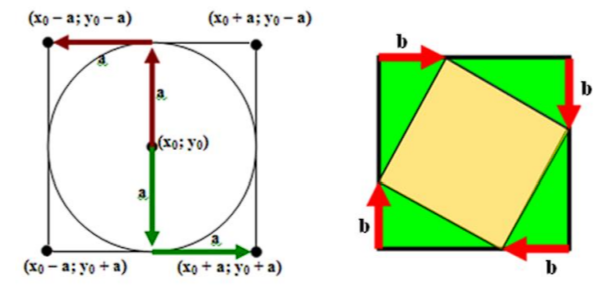
Задание 1. Построить на экране наклонный квадрат.
Поскольку нет графического примитива, который строит прямоугольники со сторонами, имеющими негоризонтальное и невертикальное направления, нужно строить стороны квадрата с помощью примитивов-отрезков. Принцип расчёта координат, отправляясь от его центра, показан на чертеже.
x0 = 320
y0 = 220
a = 150
b = 50
x1 = x0 - a + b
y1 = y0 - a
x2 = x0 + a
y2 = y0 - a + b x3 = x0 + a - b
y3 = y0 + a x4 = x0 - a
y4 = y0 + a - b
GraphicsWindow.DrawLine(x1,y1,x2,y2)
GraphicsWindow.DrawLine(x2,y2,x3,y3)
GraphicsWindow.DrawLine(x3,y3,x4,y4)
GraphicsWindow.DrawLine(x4,y4,x1,y1)
Отметим, что использование переменных позволяет в цикле строить семейства соответствующих фигур. При этом цикл вызывает изменение одной или нескольких переменных. В результате мы ведём подготовку к такому важнейшему понятию как преобразование, в данном случае речь идёт о преобразованиях геометрического характера.
Задание 2. Построить на экране семейство «концентрических» наклонных квадратов.
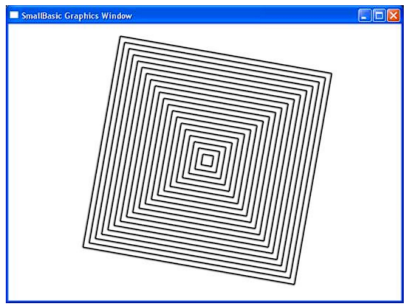
Вынесем все вычисления в подпрограмму. Для сохранения наклона квадратов введём коэффициент пропорциональности между переменными а и b
x0 = 320
y0 = 220
k = .3
For a = 10 To 200 Step 10 b = a*k
Наклонный_квадрат()
EndFor
Sub Наклонный_квадрат x1 = x0 - a + b
y1 = y0 - a
x2 = x0 + a
y2 = y0 - a + b
x3 = x0 + a - b
y3 = y0 + a
x4 = x0 - a
y4 = y0 + a - b
GraphicsWindow.DrawLine(x1,y1,x2,y2)
GraphicsWindow.DrawLine(x2,y2,x3,y3)
GraphicsWindow.DrawLine(x3,y3,x4,y4)
GraphicsWindow.DrawLine(x4,y4,x1,y1) EndSub
Нелишне на простом примере показать, что интерпретация вектора как сдвига вполне оправдана.
Задание 3. Построить ломаную по координатам вершин А, В, С, D. Сдвинуть её на заданный вектор. (Такой сдвиг называется параллельным, так как любой отрезок при переносе остаётся параллельным себе).
Пусть вектор сдвига равен (50;100), а вершины ломаной имеют координаты А (100; 100), В (200; 180), С (300; 70) и D (400; 150).

GraphicsWindow.DrawLine(100,100,200,180)
GraphicsWindow.DrawLine(200,180,300,70)
GraphicsWindow.DrawLine(300,70,400,150)
GraphicsWindow.PenColor="red"
GraphicsWindow.PenWidth=10
GraphicsWindow.DrawLine(100+50,100+100,200+50,180+100)
GraphicsWindow.DrawLine(200+50,180+100,300+50,70+100)
GraphicsWindow.DrawLine(300+50,70+100,400+50,150+100)
Пока мы делали упор на разложении векторов по двум направлениям. Теперь более внимательно рассмотрим операцию сложения векторов.
Поскольку смысл вектора состоит в сдвиге из точки в точку, легко понять, что сдвиг из точки А в точку В, а затем из В в точку С, приводит к сдвигу из точки А в точку С. И, кроме того, ясно, что если АВ(х1; у1) и ВС(х2;у2), то вектор АС имеет координаты (х1 + х2; у1 + у2). Нами введена операция сложения векторов. Геометрическая запись для суммы такова: АС = АВ + ВС, а алгебраическая запись имеет форму: (х1; у1) + (х2; у2) = (х1 + х2; у1 + у2).
Задание 4. Сложение двух векторов с геометрической точки зрения производится по правилу параллелограмма. Ориентируясь на чертёж, сформулируйте это правило. На экране компьютера выполните следующие построения.
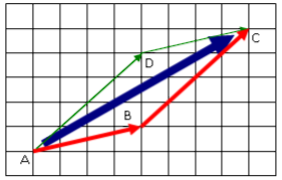
А) Заданы координаты точек А, В и D. Построить точку С и параллелограмм.
Б) Заданы координаты точек А, В и С. Построить точку D и параллелограмм.
Правило параллелограмма: сумма двух векторов АВ и AD является диагональю параллелограмма, сторонами которого являются отрезки АВ и AD. В координатах правило параллелограмма можно записать так: xc = xa + xab + xad, yc = ya + yab + yad.
Пункт А. Пусть А (100; 100), В (200; 180) и D (300; 150). Проведём предварительные вычисления, которые затем будут использованы в программе: xab = 200 - 100 = 100, yab = 180 - 100 = 80; xad = 300 - 100 = 200, yad = 150 - 100 = 50. Тогда xc = xa + xab + xad, yc = ya + yab + yad или xc = 100 + 100 + 200 = 400, yc = 100 + 80 + 50 =230. Программа:
GraphicsWindow.DrawEllipse (100 - 5, 100 - 5, 10,10)
GraphicsWindow.DrawEllipse (200 - 5, 180 - 5,10,10)
GraphicsWindow.DrawEllipse (300 - 5, 150 - 5,10,10)
GraphicsWindow.DrawEllipse (400 - 5, 230 - 5,10,10)
GraphicsWindow.DrawLine (100, 100, 200,180)
GraphicsWindow.DrawLine (200, 180,400,230)
GraphicsWindow.DrawLine (400, 230,300,150)
GraphicsWindow.DrawLine (300, 150,100,100)
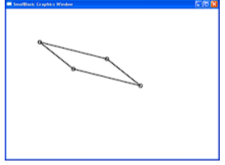
Пункт Б. Пусть А (100; 100), В (200; 180) и С (400; 230). Тогда xbc = 400 - 200 = 200, ybc = 230 - 180 = 50. Тогда xd = xa + xbc, yd = ya + ybc или xd = 100 + 200 = 300, yd = 100 + 50 =150. Программа аналогична предыдущей.
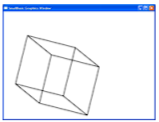
Задание 5. Постройте объёмное изображение параллелепипеда. Согласно Большой Советской Энциклопедии: «Параллелепипед (греч. parallelepipedon, от parallelos — параллельный и epipedon — плоскость), шестигранник, противоположные грани которого попарно параллельны. Параллелепипед имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы».
Зададим координаты трёх вершин параллелепипеда на его верхней грани: А (100; 100), В (200; 180) и D (300; 150). И, кроме того, сдвиг (-50; 200), соответствующий боковому ребру параллелепипеда. Верхняя грань строится по пункту А предыдущего задания. Нижняя грань строится с помощью сдвига, как в задании 8. Наконец, должны быть построены и рёбра.
GraphicsWindow.DrawLine (100, 100, 200,180)
GraphicsWindow.DrawLine (200, 180,400,230)
GraphicsWindow.DrawLine (400, 230,300,150)
GraphicsWindow.DrawLine (300, 150,100,100)
GraphicsWindow.DrawLine (100 - 50, 100+200, 200 - 50,180+200)
GraphicsWindow.DrawLine (200 - 50, 180+200,400 - 50,230+200)
GraphicsWindow.DrawLine (400 - 50, 230+200,300 - 50,150+200)
GraphicsWindow.DrawLine (300 - 50, 150+200,100 - 50,100+200)
GraphicsWindow.DrawLine (100, 100, 100 - 50, 100+200)
GraphicsWindow.DrawLine (200, 180,200 - 50, 180+200)
GraphicsWindow.DrawLine (400, 230,400 - 50, 230+200)
GraphicsWindow.DrawLine (300, 150,300 - 50, 150+200)
Задание 6. На плоскости заданы две точки А(х1; у1) и В(х2; у2). Построить третью точку С, которая делит отрезок АВ так, что AC/CB= 2 . Построить две окружности с центрами в точках А и В, проходящие через точку С.
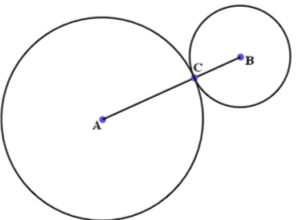
В программе нужно одновременно и делить отрезок, и вычислять расстояния между точками.
xa = 200
ya = 250
GraphicsWindow.FillEllipse(xa – 5,ya – 5,10,10)
xb = 400
yb = 150
GraphicsWindow.FillEllipse(xb – 5,yb – 5,10,10)
xc = xa + 2*(xb – xa)/3
yc = ya + 2*(yb – ya)/3
GraphicsWindow.DrawLine(xa,ya,xb,yb)
GraphicsWindow.FillEllipse(xc – 5,yc – 5,10,10)
ra = Math.SquareRoot((xa – xc)*(xa – xc)+(ya – yc)*(ya – yc))
rb = Math.SquareRoot((xb – xc)*(xb – xc)+(yb – yc)*(yb – yc))
GraphicsWindow.DrawEllipse(xa – ra,ya – ra,2*ra,2*ra)
GraphicsWindow.DrawEllipse(xb – rb,yb – rb,2*rb,2*rb)
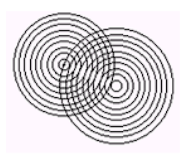
Задание 7. На плоскости заданы две точки А и В. Построить два семейства концентрических окружностей с центрами в этих точках, так чтобы каждая окружность одного семейства касалась одной из окружностей другого семейства.
xa = 200
ya = 250
GraphicsWindow.FillEllipse(xa – 5,ya – 5,10,10)
xb = 400
yb = 150
GraphicsWindow.FillEllipse(xb – 5,yb – 5,10,10)
For lmb = 0 To 1 Step 1/10
xc = xa + lmb*(xb – xa)
yc = ya + lmb*(yb – ya)
GraphicsWindow.DrawLine(xa,ya,xb,yb)
GraphicsWindow.FillEllipse(xc – 5,yc – 5,10,10)
ra = Math.SquareRoot((xa – xc)*(xa – xc)+(ya – yc)*(ya – yc))
rb = Math.SquareRoot((xb – xc)*(xb – xc)+(yb – yc)*(yb – yc))
GraphicsWindow.DrawEllipse(xa – ra,ya – ra,2*ra,2*ra)
GraphicsWindow.DrawEllipse(xb – rb,yb – rb,2*rb,2*rb)
EndFor
Задание 8. С помощью параметрических уравнений прямой постойте пунктирный отрезок.
x0 = 50
y0 = 100
GraphicsWindow.FillEllipse(x0 - 5,y0 - 5,10,10)
x1 = 600
y1 = 400
GraphicsWindow.FillEllipse(x1 - 5,y1 - 5,10,10)
For lmb = 0 To 1 Step 1/100
x = x0 + lmb*(x1 - x0)
y = y0 + lmb*(y1 - y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
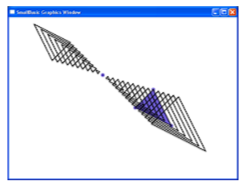
Задание 9. Постройте семейство гомотетичных треугольников.
x0 = 260
y0 = 160
GraphicsWindow.FillEllipse(x0 - 5,y0 - 5,10,10)
xa = 400
ya = 200
GraphicsWindow.FillEllipse(xa - 5,ya - 5,10,10)
xb = 450
yb = 300
GraphicsWindow.FillEllipse(xb - 5,yb - 5,10,10)
xc = 350
yc = 250
GraphicsWindow.FillEllipse(xc - 5,yc - 5,10,10)
GraphicsWindow.FillTriangle(xa,ya,xb,yb,xc,yc)
For lmb = -1 To 1.5 Step 1/10
x1 = x0 + lmb*(xa - x0)
y1 = y0 + lmb*(ya - y0)
x2 = x0 + lmb*(xb - x0)
y2 = y0 + lmb*(yb - y0)
x3 = x0 + lmb*(xc - x0)
y3 = y0 + lmb*(yc - y0)
GraphicsWindow.DrawTriangle(x1,y1,x2,y2,x3,y3)
EndFor
Задание 10. С помощью предыдущей программы создайте анимационный эффект, демонстрирующий гомотетию в динамике.
Для создания анимационного эффекта нужно уменьшить шаг в цикле до одной сотой и перед EndFor вставить три строки, которые осуществляют задержку кадра для фиксации глазом и очистку экрана:
For tm = 1 To 50000
EndFor
GraphicsWindow.Clear()
Приведём ещё три задания, направленных на освоение осознанной работы с параметрическими уравнениями прямой, расстояниями и отношениями длин отрезков.
Задание 11. На плоскости заданы две точки А и В. Построить на прямой АВ точку А1, такую, чтобы длина отрезка АА1 равнялась 100 пикселам. Подтвердить результат, построив окружность с центром в точке А и радиусом 100.
xa = 200
ya = 250
GraphicsWindow.FillEllipse(xa – 5,ya – 5,10,10)
xb = 400
yb = 150
GraphicsWindow.FillEllipse(xb – 5,yb – 5,10,10)
GraphicsWindow.DrawLine(xa,ya,xb,yb)
dl = Math.SquareRoot((xa – xb)*(xa – xb)+(ya – yb)*(ya – yb))
lmb = 100/dl
xc = xa + lmb*(xb – xa)
yc = ya + lmb*(yb – ya)
GraphicsWindow.FillEllipse(xc – 5,yc – 5,10,10)
GraphicsWindow.DrawEllipse(xa – 100,ya – 100,200,200)
Задание 12. На плоскости заданы две точки А и В. Построить на прямой АВ несколько точек А1, А2, А3 … таких, что АА1 = А1А2 = А2А3 = … = 20.

xa = 200
ya = 250
GraphicsWindow.FillEllipse(xa – 5,ya – 5,10,10)
xb = 400
yb = 150
GraphicsWindow.FillEllipse(xb – 5,yb – 5,10,10)
GraphicsWindow.DrawLine(xa,ya,xb,yb)
dl = Math.SquareRoot((xa – xb)*(xa – xb)+(ya – yb)*(ya – yb))
lmb = 20/dl
For n = 0 To 10
xc = xa + n*lmb*(xb – xa)
yc = ya + n*lmb*(yb – ya)
GraphicsWindow.FillEllipse(xc – 2,yc – 2,4,4)
GraphicsWindow.DrawEllipse(xc – 10,yc – 10,20,20)
EndFor
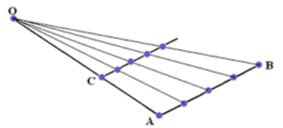
Задание 13. На плоскости заданы отрезок ОА и точка В. Выбрать на отрезке ОА точку С, провести прямую АВ и параллельную ей линию через точку С. Построить равномерную последовательность точек на АВ, а также их центральные проекции из точки О на вторую прямую.
xo = 50
yo = 50
GraphicsWindow.FillEllipse(xo – 5,yo – 5,10,10)
xa = 320
ya = 400
GraphicsWindow.FillEllipse(xa – 5,ya – 5,10,10)
xb = 600
yb = 200
GraphicsWindow.FillEllipse(xb – 5,yb – 5,10,10)
GraphicsWindow.DrawLine(xo,yo,xa,ya)
GraphicsWindow.DrawLine(xb,yb,xa,ya)
lmbc = 2/3
xc = xo + lmbc*(xa – xo)
yc = yo + lmbc*(ya – yo)
GraphicsWindow.FillEllipse(xc – 5,yc – 5,10,10)
xd = xo + lmbc*(xb – xo)
yd = yo + lmbc*(yb – yo)
GraphicsWindow.DrawLine(xc,yc,xd,yd)
For lmbc = 0 To 1 Step 1/20
xx = xa + lmbc*(xb – xa)
yy = ya + lmbc*(yb – ya)
GraphicsWindow.FillEllipse(xx – 5,yy – 5,10,10)
GraphicsWindow.DrawLine(xo,yo,xx,yy)
xx = xc + lmbc*(xd – xc)
yy = yc + lmbc*(yd – yc)
GraphicsWindow.FillEllipse(xx – 5,yy – 5,10,10)
EndFor
Отметим, что задачи на построение компьютерных чертежей, относящихся к элементарной планиметрии, требуют применения методов аналитической геометрии.
Задание 14. Постройте медианы треугольника, выделите маленькими окружностями вершины треугольника, середины сторон и точку пересечения медиан.
xa = 200
ya = 300
xb = 400
yb = 100
xc = 500
yc = 350
GraphicsWindow.DrawTriangle(xa,ya,xb,yb,xc,yc)
xma = (xb + xc)/2
yma = (yb + yc)/2
GraphicsWindow.FillEllipse(xma – 5, yma – 5,10,10)
GraphicsWindow.DrawLine(xa,ya,xma,yma)
xmb = (xa + xc)/2
ymb = (ya + yc)/2
GraphicsWindow.FillEllipse(xmb – 5, ymb – 5,10,10)
GraphicsWindow.DrawLine(xb,yb,xmb,ymb)
xmc = (xb + xa)/2
ymc = (yb + ya)/2
GraphicsWindow.FillEllipse(xmc – 5, ymc – 5,10,10)
GraphicsWindow.DrawLine(xc,yc,xmc,ymc)
xmed = xma + (xa – xma)/3
ymed = yma + (ya – yma)/3
GraphicsWindow.FillEllipse(xmed – 5, ymed – 5,10,10)
Задание 15. Теорема о биссектрисе треугольника гласит: биссектриса АР угла А треугольника АВС делит сторону ВС на отрезки ВР и РС, такие что ВР : РС = АВ : АС. Используя этот факт, постройте биссектрисы треугольника, выделите маленькими окружностями вершины треугольника, точки пересечения биссектрис со сторонами и точку пересечения биссектрис.
xa = 200
ya = 300
xb = 400
yb = 100
xc = 500
yc = 350
GraphicsWindow.DrawTriangle(xa,ya,xb,yb,xc,yc)
a = Math.SquareRoot((xb – xc)*(xb – xc)+(yb – yc)*(yb – yc))
b = Math.SquareRoot((xa – xc)*(xa – xc)+(ya – yc)*(ya – yc))
c = Math.SquareRoot((xb – xa)*(xb – xa)+(yb – ya)*(yb – ya))
xa1 = xb + c*(xc – xb)/(b+c)
ya1 = yb + c*(yc – yb)/(b+c)
GraphicsWindow.FillEllipse(xa1 – 5, ya1 – 5,10,10)
GraphicsWindow.DrawLine(xa,ya,xa1,ya1)
xb1 = xc + a*(xa – xc)/(a+c)
yb1 = yc + a*(ya – yc)/(a+c)
GraphicsWindow.FillEllipse(xb1 – 5, yb1 – 5,10,10)
GraphicsWindow.DrawLine(xb,yb,xb1,yb1)
xc1 = xa + b*(xb – xa)/(b+a)
yc1 = ya + b*(yb – ya)/(b+a)
GraphicsWindow.FillEllipse(xc1 – 5, yc1 – 5,10,10)
GraphicsWindow.DrawLine(xc,yc,xc1,yc1)
otr = Math.SquareRoot((xb – xa1)*(xb – xa1)+(yb – ya1)*(yb – ya1))
xbis = xa1 + otr*(xa – xa1)/(c+otr)
ybis = ya1 + otr*(ya – ya1)/(c+otr)
GraphicsWindow.FillEllipse(xbis – 5, ybis – 5,10,10)
Конечно, все приведённые выше задания элементарны, однако не следует забывать, что они используются для того, чтобы студент мог свободно пользоваться исходными понятиями аналитической геометрии. Кроме того, задания в предлагаемой форме перестают быть школярскими упражнениями, а превращаются, пусть и в простую, на инженерную задачу. При этом теоретические представления опредмечиваются и воплощаются в зримый образ.
Следующим этапом освоения аналитической геометрии после изучения метода координат является знакомство с кривыми, описываемыми алгебраическими уравнениями первого и второго порядка.
При этом возникает проблема масштабирования, состоящая в следующем. Экранное пространство имеет координатное поле с жёстко заданными координатами. При построении кривых нужно гибко менять характер системы координат, приноравливая её к математическим нуждам. Вопрос решается достаточно просто. Векторное уравнение прямой X = A + λ*AB ставит в соответствие точке Х, имеющей некоторую экранную координату, теоретическую координату λ. Таким образом, при построении алгебраических кривых можно поступать следующим образом. Выберем на экране точку (х0; у0) в качестве начала координат. Предположим, что из неё исходят два вектора - горизонтальный и вертикальный. При этом вектора имеют одинаковую длину а (в пикселях). Тогда экранные координаты точки М, соответствующей теоретическим координатам (t; u) вычисляются по формулам: xe = x0 + t·a, ye
= y0 – u·a.
Наличие знака минус во второй формуле связано с тем, что в экранной системе координат ось ординат направлена вниз, и мы должны её перевернуть в привычное положение.
Как известно, прямая, проходящая через точку (х0; у0) перпендикулярно вектору (a;b), имеет уравнение a*(x-x0)+b*(y-y0)=0. Эта прямая делит плоскость на две полуплоскости. Если в уравнение прямой подставить координаты точки, не лежащей на прямой, то для точек одной из упомянутых полуплоскостей значение всегда будет больше нуля, а для другой - меньше. Аналогичная ситуация имеет место и для любого неявного уравнения F(x, y) = 0, описывающего некоторую кривую. Причины этого обстоятельства нетрудно объяснить. Пусть нам задано неравенство F(x1, x2) ≤ 0. Рассмотрим функцию от двух переменных z = F(x1, x2). Она задаёт поверхность в трёхмерном пространстве. Пересечение этой поверхности с плоскостью z = 0 является некоторой кривой (её уравнение F(x1, x2) = 0), разбивающей плоскость на две области. В одной области F(x1, x2) ≤ 0, а в другой F(x1, x2) ≥ 0. Итак, неравенство F(xi, x2) < 0 задаёт на плоскости область, ограниченную кривой F(x1, x2) = 0. Используя этот факт, мы можем, пусть и неэкономным образом, строить на экране кривые. Более того, мы одновременно получаем геометрическое решение неравенств вида F(xi, x2) ≤ 0. Способ построения таков. Сканируем экранное пространство с помощью вложенного цикла по теоретическим переменным t и u и вычисляем значение функции z = F(xi, x2). Если z больше нуля, ставим точку одним цветом, в противном случае - другим.
Задание 16. Построить на экране прямую вида ax + by + c = 0 и решить соответствующие неравенства геометрически.

GraphicsWindow.Width = 600
GraphicsWindow.Height = 600
x0 = 300
y0 = 300
ed = 100
a = 2
b = 3
c =1
For t = –3 To 3 Step .01
For u = –3 To 3 Step .01
xe = x0 + ed*t
ye = y0 – ed*u
If a*t + b*u + c < 0 Then
GraphicsWindow.SetPixel(xe,ye,"green")
Else
GraphicsWindow.SetPixel(xe,ye,"red")
EndIf
EndFor
EndFor
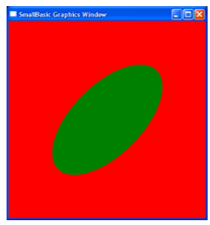
Задание 17. Построить на экране кривую вида ax2 + bxy + cy2 + d = 0 и решить соответствующие неравенства геометрически.
GraphicsWindow.Width = 400
GraphicsWindow.Height = 400
x0 = 200
y0 = 200
ed = 100
a = 5
b = –6
c = 5
d = –4
For t = –2 To 2 Step .01
For u = –2 To 2 Step .01
xe = x0 + ed*t
ye = y0 – ed*u
If a*t*t + b*t*u + c*u*u + d < 0 Then
GraphicsWindow.SetPixel(xe,ye,"green")
Else
GraphicsWindow.SetPixel(xe,ye,"red")
EndIf
EndFor
EndFor
Важной составляющей частью аналитической геометрии на плоскости является раздел, изучающий прямые линии. Здесь рассматриваются различные виды уравнений, описывающих прямые, и изучаются вопросы, связанные с пересечением прямых, с определением углов между прямыми и вычислением расстояний от прямых до точек. Следует отметить, что, казалось бы несложный вопрос о вычислении координат точки пересечения двух прямых, органично связывает аналитическую геометрию с проективной.
Перечислим основные виды уравнений, описывающих прямые. На их основе могут быть предложены многочисленные задания.
-
Параметрические уравнения прямой: х = хА + λр и у = уА + λq. При построении прямой в цикле изменяется параметр λ. Точка (хА; уА) лежит на прямой, вектор (р; q) указывает направление прямой.
-
Если задана точка (хА; уА) и угол наклона u прямой, то p = cos u и q = sin u.
-
Каноническое уравнение прямой: y = kx + b. При построении прямой в цикле изменяется независимый аргумент х. Коэффициент k является тангенсом угла наклона прямой.
-
Если задана точка (х0; у0) через которую проходит прямая и тангенс её угла наклона k, то уравнение прямой принимает вид y = k-x + y0 - k^x0.
-
Если заданы две точки (х0; у0) и (х1; у1), через которые проходит прямая, то тангенс угла наклона прямой равен k = (y1-y0)/(x1-x0).
-
Прямые с уравнениями y = k-x + b1 и y = k-x + b2 параллельны.
-
Если тангенс угла наклона исходной прямой равен k, то тангенс угла наклона прямой, перпендикулярной к ней, равен k = -1/k
-
Уравнение прямой общего вида: a*(x - x0) + b*(y - yo) = 0 или ax + by + c = 0, где c = -x0*a - yo*b. Это уравнение непосредственно для построения прямой не используется. Оно требует предварительного преобразования, после которого либо у выражается через х, либо х - через у. Уравнение содержит в себе возможность описания горизонтальных (у = у0) и вертикальных (х = х0) прямых. Анализ уравнения может проводиться непосредственно в программе с помощью условных операторов. Прямая, описываемая уравнением a*(x - x0) + b*(У — Yo) = 0, проходит через точку (x0,y0) перпендикулярно к вектору (a; b).
Рассмотрим несколько заданий, математической основой которых являются перечисленные нами уравнения. При комментировании для краткости будем ссылаться на номера пунктов, содержащих описание нужных уравнений.
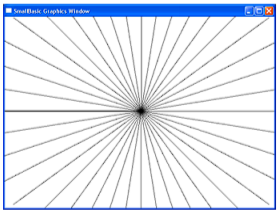
Задание 18. Множество прямых на плоскости, проходящих через одну точку, называется пучком прямых. Построить пучок с центром вначале координат.
При решении задачи используем пункт 2. Меняя в цикле угол, то есть, вращая направляющий вектор, поочерёдно строим прямые пучка. Для этого в свою очередь во внутреннем цикле меняем параметр λ.
pi= Math.Pi
x0 = 320
y0 = 220
ed=100
For u=0 To pi Step pi/20
p= Math.Cos(u)
q= Math.Sin(u)
For lmb= –3.7 To 3.7 Step .01
x = x0 + lmb*p*ed
y = y0 – lmb*q*ed
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
Интересен тот факт, что на уравнения х = хА + λ·cos u и у = уА + λ·sinu можно посмотреть двояким образом. Если изменяется параметр λ, перед нами параметрические уравнения прямой. Если же изменяется параметр u, перед нами параметрические уравнения окружности радиуса λ.
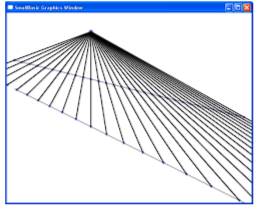
Задание 19. Построить пучок прямых с центром вначале координат и семейство концентрических окружностей с центром в центре пучка прямых.

pi= Math.Pi
x0 = 320
y0 = 220
ed=100
For u=0 To pi Step pi/20
p= Math.Cos(u)
q= Math.Sin(u)
lmb = –3.7
x1 = x0 + lmb*p*ed
y1 = y0 – lmb*q*ed
lmb = 3.7
x2 = x0 + lmb*p*ed
y2 = y0 – lmb*q*ed
GraphicsWindow.DrawLine(x1,y1,x2,y2)
EndFor
For u=0 To 2*pi Step pi/500
p= Math.Cos(u)
q= Math.Sin(u)
For lmb= 0 To 3.6 Step .3
x = x0 + lmb*p*ed
y = y0 – lmb*q*ed
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
Задание 20. Используя правило Крамера для решения систем уравнений построить точку пересечения двух прямых, заданных уравнениями a1·x + а2·y + а3 = 0 и b1·x + b2·y + b3 = 0.
Формулировка правила Крамера. Пусть задана система двух линейных уравнений с двумя неизвестными:
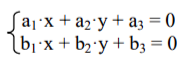
Чтобы найти её решение, из матрицы коэффициентов поочерёдно вычёркивают первый, второй и третий столбцы, а оставшиеся не вычеркнутыми столбцы располагают в циклическом порядке (за тройкой следует единица). Для трёх полученных матриц вычисляют определители (из произведения элементов, стоящих на главной диагонали, вычитают произведение элементов, стоящих на побочной диагонали) Δ1, Δ2, Δ3. Тогда x = -Δ1/Δ3 и o' = Δ2/Δ3.
Теперь свяжем уравнения прямых с воображаемой плоскостью (координаты t и u). Для перехода к экранной системе координат необходимо указать начало системы координат (х0; у0) и масштаб (ed). Уравнения, описывающие прямые, можно привести к каноническому виду: ![]() . Прямые строятся в цикле с параметром t, пробегающим отрезок от - 4 до 4.
. Прямые строятся в цикле с параметром t, пробегающим отрезок от - 4 до 4.
Наконец точка пересечения определяется по правилу Крамера: вычисляем три определителя и находим координаты tperesech и uperesech, а затем преобразуем их в экранные координаты.
x0 = 320
y0 = 220
ed = 100
a1 = 1
a2 = 1
a3 = 1
b1 = –1
b2 = 2
b3 = –3
For t = –4 To 4 Step .01
u = (–a1*t – a3)/a2
x = x0 + ed*t
y = y0 – ed*u
GraphicsWindow.SetPixel(x,y,"")
u = (–b1*t – b3)/b2
x = x0 + ed*t
y = y0 – ed*u
GraphicsWindow.SetPixel(x,y,"")
EndFor
delta1 = a2*b3 – a3*b2
delta2 = a3*b1 – a1*b3
delta3 = a1*b2 – a2*b1
tperesech = delta1/delta3
uperesech = delta2/delta3
x = x0 + ed*tperesech
y = y0 – ed*uperesech
GraphicsWindow.FillEllipse(x – 5,y – 5,10,10)
Поскольку в предыдущем задании для точки пересечения двух прямых фактически были найдены её проективные координаты, уместно будет рассмотреть принцип двойственности. Его суть состоит в том, что прямые и точки в проективной геометрии становятся как бы зеркальным отражением друг друга. Например, утверждение «через любые две точки проходит единственная прямая» после «отражения» превращается в утверждение «две любые прямые пересекаются в единственной точке».
Существуют и вычислительные аспекты принципа двойственности. Итак, положение точек определяется проективными координатами, то есть тройками чисел (х1; х2; х3), а уравнения прямых принимают форму: а1х1 + а2х2 + а3х3 = 0. При этом возврат к исходным координатам и уравнениям весьма прост. Положив õ = õ1/õ3 и õ = õ2/õ3, приходим к от уравнения а1х1 + а2х2 + а3х3 = 0 к уравнению вида а1х + а2у + а3 = 0.
Уравнение а1х1 + а2х2 + а3х3 = 0 прекрасно отражает принцип двойственности. Тройки чисел (а1; а2; а3) и (х1; х2; х3) занимают в нём симметричное положение. Это позволяет решить следующую задачу. На плоскости с помощью проективных координат заданы две точки (х1; х2; х3) и (у1; у2; у3). Найти уравнение прямой, проходящей через эти точки.
Ясно, что при подстановке координат точек в искомое уравнение, оно будет выполняться. По этой причине мы приходим к системе двух линейных уравнений с неизвестными а1; а2 и а3:
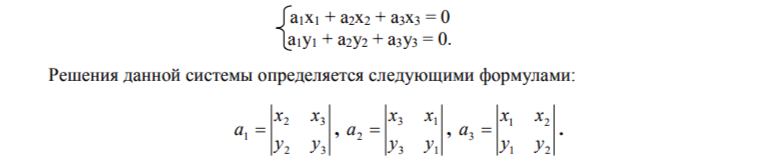
Таким образом, вычислительные процедуры для нахождения уравнения прямой, проходящей через две заданные точки и для нахождения координат точки пересечения двух прямых одинаковы. Коэффициенты а1; а2 и а3 называют проективными координатами прямой.
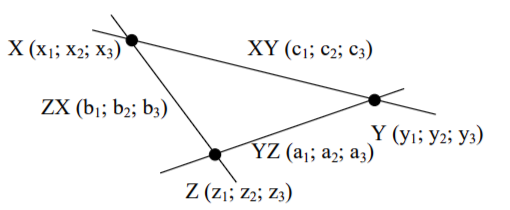
Задание 21. Проверить идентичность описанных выше вычислительных процедур с помощью специальной программы.
Для проведения соответствующей проверки с помощью проективных координат зададим на плоскости три точки X, Y и Z. Затем найдём уравнения прямых XY, YZ и ZX, после чего вычислим координаты их точек пересечения и сравним с исходными координатами точек X, Y, Z. На чертеже показаны обозначения, которые мы даём проективным координатам соответствующих точек и прямых.
x0 = 320
y0 = 240
ed = 100
x1 = –1
x2 = 1
x3 = 1
GraphicsWindow.FillEllipse(x0+ed*(x1/x3) – 5,y0 – ed*(x2/x3) – 5,10,10)
y1 = 1
y2 = 2
y3 = 1
GraphicsWindow.FillEllipse(x0+ed*(y1/y3) – 5,y0 – ed*(y2/y3) – 5,10,10)
z1 = 0
z2 = –1
z3 = 1
GraphicsWindow.FillEllipse(x0+ed*(z1/z3) – 5,y0 – ed*(z2/z3) – 5,10,10)
a1 = y2*z3 – y3*z2
a2 = y3*z1 – y1*z3
a3 = y1*z2 – y2*z1
For t = –4 To 4 Step .01
u = (–a1*t – a3)/a2
GraphicsWindow.SetPixel(x0+ed*t,y0 – ed*u,"")
EndFor
b1 = x2*z3 – x3*z2
b2 = x3*z1 – x1*z3
b3 = x1*z2 – x2*z1
For t = –4 To 4 Step .01
u = (–b1*t – b3)/b2
GraphicsWindow.SetPixel(x0+ed*t,y0 – ed*u,"")
EndFor
c1 = x2*y3 – x3*y2
c2 = x3*y1 – x1*y3
c3 = x1*y2 – x2*y1
For t = –4 To 4 Step .01
u = (–c1*t – c3)/c2
GraphicsWindow.SetPixel(x0+ed*t,y0 – ed*u,"")
EndFor
x1 = b2*c3 – b3*c2
x2 = b3*c1 – b1*c3
x3 = b1*c2 – b2*c1
X (x1; x2; x3)
Y (y1; y2; y3)
Z (z1; z2; z3)
XY (c1; c2; c3)
ZX (b1; b2; b3)
YZ (a1; a2; a3)
GraphicsWindow.DrawEllipse(x0+ed*(x1/x3) – 10,y0 – ed*(x2/x3) – 10,20,20)
y1 = a2*c3 – a3*c2
y2 = a3*c1 – a1*c3
y3 = a1*c2 – a2*c1
GraphicsWindow.DrawEllipse(x0+ed*(y1/y3) – 10,y0 – ed*(y2/y3) – 10,20,20)
z1 = a2*b3 – a3*b2
z2 = a3*b1 – a1*b3
z3 = a1*b2 – a2*b1
GraphicsWindow.DrawEllipse(x0+ed*(z1/z3) – 10,y0 – ed*(z2/z3) – 10,20,20)
Задание 22. На плоскости заданы точка S и две прямые р1 и р2. Написать программу, которая позволит из центра S проективно отобразить прямую р1 на прямую р2.
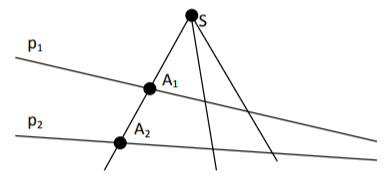
Пусть прямая р1 задана точкой М с декартовыми координатами (m1; m2) и вектором (p; q). Тогда любая лежащая на ней точка А1 имеет проективные координаты (m1 + λ*p; m2 + λ*q; 1). Если параметр λ пробегает все действительные значения от минус до плюс бесконечности, то точка А1 заметает всю прямую р1.
Таким образом, меняя параметр λ, мы фактически перебираем все прямые SA1, образующие пучок с центром в точке S. Чтобы решить задачу, нам необходимо найти координаты точки пересечения прямой р2 с прямой SA1. Прямую р2 зададим с помощью трёх коэффициентов с1, с2 и с3.
GraphicsWindow.Width=640
GraphicsWindow.Height=500
x0=320
y0=250
ed=100
s1=–1
s2=2
s3=1
xs=x0+s1*ed
ys=y0–s2*ed
GraphicsWindow.FillEllipse(xs – 5,ys – 5,10,10)
m1= –2
m2= 1
p= 1
q= –.25
For lmb= –1 To 5 Step .01
t1=m1+lmb*p
t2=m2+lmb*q
x=x0+t1*ed
y=y0 – t2*ed
GraphicsWindow.SetPixel(x,y,"")
EndFor
c1=1
c2=2
c3=2
For t=-3 To 3 Step .01
S
А1
р1
р2 А2
u=(–c1*t – c3)/c2
x=x0+t*ed
y=y0 – u*ed
GraphicsWindow.SetPixel(x,y,"")
EndFor
For lmb= –1 To 5 Step .2
t1=m1+lmb*p
t2=m2+lmb*q
t3=1
x1=x0+ed*t1/t3
y1=y0 – ed*t2/t3
GraphicsWindow.FillEllipse(x1 – 3,y1 – 3,6,6)
d1=t2*s3 – t3*s2
d2=t3*s1 – t1*s3
d3=t1*s2 – t2*s1
tt1=d2*c3 – d3*c2
tt2=d3*c1 – d1*c3
tt3=d1*c2 – d2*c1
x2=x0+ed*tt1/tt3
y2=y0 – ed*tt2/tt3
GraphicsWindow.FillEllipse(x2 – 3,y2 – 3,6,6)
GraphicsWindow.DrawLine(xs,ys,x2,y2)
For tm=1 To 50000
EndFor
EndFor
Ещё раз вернёмся к вопросам, связанным с систем решением неравенств с несколькими переменными (см. задания 16 и 17), и дадим геометрическое решение задачи линейного программирования для случая двух переменных.
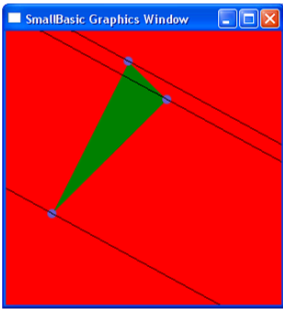
Задание 23. Найти максимум и минимум линейной формы z = 17x + 23y при условии выполнения системы неравенств
x - y +1 ≤ 0 ;
x + y — 2 ≤ 0 ;
- 2 x + y — 3 ≤ 0.
Сначала построим область, заданную системой неравенств. Затем вычислим координаты вершин этой области и проведём через эти вершины линии уровня линейной формы.
GraphicsWindow.Width = 300
GraphicsWindow.Height = 300
x0 = 150
y0 = 150
ed = 50
c1 = 17
c2 = 31
a1[М. Е. Степанов, 2017] = 1
a2[М. Е. Степанов, 2017] = –1
a3[М. Е. Степанов, 2017] = 1
a1[А. Г. Школьник, 1963] = 1
a2[А. Г. Школьник, 1963] = 1
a3[А. Г. Школьник, 1963] = –2
a1[Н. И. Ахиезер, 1965] = –2
a2[Н. И. Ахиезер, 1965] = 1
a3[Н. И. Ахиезер, 1965] = –3
For t = –3 To 3 Step .02
For u = –3 To 3 Step .02
xe = x0 + ed*t
ye = y0 – ed*u
For i=1 To 3
znak[i]=a1[i]*t+a2[i]*u+a3[i]
EndFor
If znak[М. Е. Степанов, 2017]<0 And znak[А. Г. Школьник, 1963]<0 And znak[Н. И. Ахиезер, 1965]<0 Then
GraphicsWindow.SetPixel(xe,ye,"green")
Else
GraphicsWindow.SetPixel(xe,ye,"red")
EndIf
EndFor
EndFor
For i=1 To 3
If i<3 Then
j = i+1
Else
j = 1
EndIf
d1 = a2[i]*a3[j] – a2[j]*a3[i]
d2 = a3[i]*a1[j] – a3[j]*a1[i]
d3 = a1[i]*a2[j] – a1[j]*a2[i]
tw[i] = d1/d3
uw[i] = d2/d3
x[i] = x0 + ed*tw[i]
y[i] = y0 – ed*uw[i]
GraphicsWindow.FillEllipse(x[i] – 5,y[i] – 5,10,10)
EndFor
For i=1 To 3
For t = –3 To 3 Step .02
u = –c1*t/c2 + c1*tw[i]/c2 + uw[i]
xe = x0 + ed*t
ye = y0– ed*u
GraphicsWindow.SetPixel(xe,ye,"black")
EndFor
EndFor
А теперь обратимся к вопросам построения прямых, окружностей и кривых второго порядка, а также к нахождению их точек пересечения и проведению касательных.
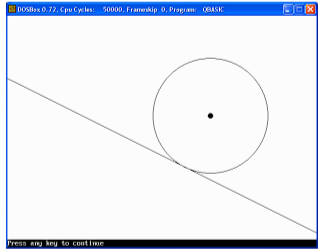
Задание 24. На плоскости заданы прямая a*x + b*y + с = 0 и точка (x1,y1). Построить окружность, касающуюся заданной прямой и имеющей центр в заданной точке.
x0 = 320
y0 = 240
ed = 100
a = 1
b = 2
c = 1
t1 = 1
u1 = 1 / 3
For t = –3.2 to 3.2 step .01
u = – (a * t + c) / b
x = x0 + ed * t
y = y0 – ed * u
GraphicsWindow.SetPixel(x,y,"")
EndFor
x1 = x0 + ed * t1
y1 = y0 – ed * u1
GraphicsWindow.FillEllipse(x1 – 3,y1 – 3,6,6)
r = ed * Math.Abs((a*t1 + b*u1 + c) / Math.SquareRoot(a*a + b*b))
GraphicsWindow.DrawEllipse(x1 – r, y1 – r, 2*r,2*r)
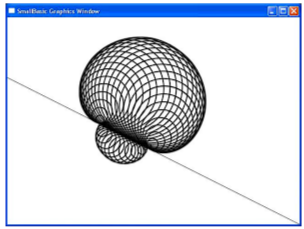
Задание 25. Построить семейство окружностей, центры которых расположены на заданной окружности, а сами эти окружности касаются некоторой прямой.
Pi = 3.14159
n=50
x0 = 320
y0 = 240
ed = 100
a = 1
b = 2
c = 1
For t= –4 To 4 Step .01
u= –(a*t+c)/b
x=x0+t*ed
y=y0 – u*ed
GraphicsWindow.SetPixel(x,y,"")
EndFor
tokr = –.5
uokr = .2
rokr = .7
For i=0 to n
t=tokr+rokr*Math.Cos(2*pi*i/n)
x=x0+t*ed
u=uokr – rokr*Math.Sin(2*pi*i/n)
y=y0 – u*ed
l=(a*t+b*u+c)/ Math.SquareRoot(a*a+b*b)
r= Math.Abs(l)*ed
GraphicsWindow.DrawEllipse(x – r,y – r,2*r,2*r)
EndFor
Задание 26. На плоскости заданы окружность с центром в точке А и радиусом r, а также точка В вне окружности. Провести через эту точку касательную к окружности.
В программе отсутствует ожидаемое решение квадратного уравнения, поскольку используется следующая планиметрическая задача: построить прямоугольный треугольник по гипотенузе и катету.
xa=200
ya=250
GraphicsWindow.FillEllipse(xa – 5,ya – 5,2*5,2*5)
r=100
GraphicsWindow.DrawEllipse(xa – r, ya – r,2*r,2*r)
xb=400
yb=130
GraphicsWindow.FillEllipse(xb – 5,yb – 5,2*5,2*5)
Касательные()
Sub Касательные
b=r
xba=xa – xb
yba=ya – yb
c=Math.SquareRoot((xa – xb)*(xa – xb)+(ya – yb)*(ya – yb))
a=Math.SquareRoot(c*c – b*b)
h=a*b/c
lhb=Math.SquareRoot(a*a – h*h)
xh=xb+lhb*xba/c
yh=yb+lhb*yba/c
xc=xh+h*yba/c
yc=yh – h*xba/c
GraphicsWindow.FillEllipse(xc–5,yc–5,2*5,2*5)
GraphicsWindow.DrawLine(xb,yb,xc,yc)
xc=xh – h*yba/c
yc=yh+h*xba/c
GraphicsWindow.FillEllipse(xc–5,yc–5,2*5,2*5)
GraphicsWindow.DrawLine(xb,yb,xc,yc)
EndSub
Задание 27. На плоскости заданы три точки. Провести через них окружность.
x1 = 200
y1 = 100
GraphicsWindow.FillEllipse(x1 – 5, y1 – 5,10,10)
x2 = 350
y2 = 200
GraphicsWindow.FillEllipse(x2 – 5, y2 - 5,10,10)
x3 = 260
y3 = 300
GraphicsWindow.FillEllipse(x3 – 5,y3 – 5,10,10)
xa = (x2 + x3)/2
ya = (y2 + y3)/2
xb = (x1 + x3)/2
yb = (y1 + y3)/2
ka = – (x3 – x2)/(y3 – y2)
kb = – (x3 – x1)/(y3 – y1)
ba = ya – ka*xa
bb = yb – kb*xb
xc = (bb – ba)/(ka – kb)
yc = ka*xc + ba
GraphicsWindow.FillEllipse(xc – 5,yc – 5,10,10)
r = Math.SquareRoot((x1 – xc)*(x1 – xc) + (y1 – yc)*(y1 – yc))
GraphicsWindow.DrawEllipse(xc – r, yc – r, 2*r, 2*r)
Задание 28. Построить на экране кривую вида ax2 + bxy + cy2 + d = 0, не закрашивая областей.
GraphicsWindow.Width = 400
GraphicsWindow.Height = 400
pi =Math.Pi
x0 = 200
y0 = 200
ed = 100
a = 5
b = –6
c = 5
d = –4
For u = 0 To 2*pi Step pi/1000
p = Math.Cos(u)
q = Math.Sin(u)
lmb = Math.SquareRoot(–d/(a*p*p + b*p*q + c*q*q))
xe = x0 + ed*lmb*p
ye = y0 – ed*lmb*q
GraphicsWindow.SetPixel(xe,ye,"")
EndFor
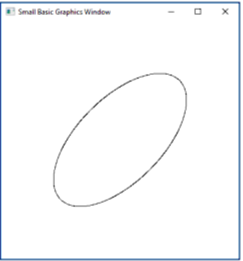
Задание 29. Дан эллипс, главные полуоси которого имеют длины a и b. Построить касательную к этому эллипсу в точке М, задаваемой абсциссой хМ и лежащей в верхней полуплоскости.
Pi = Math.Pi
x0 = 320
y0 = 220
a = 200
b = 100
c = Math.SquareRoot(a*a – b*b)
xf1 = x0 – c
GraphicsWindow.FillEllipse(xf1 – 5,y0 – 5,10,10)
xf2 = x0 + c
GraphicsWindow.FillEllipse(xf2 – 5,y0 – 5,10,10)
For ug = 0 To 2*Pi Step pi/1000
x = x0 + a* Math.Cos(ug)
y = y0 – b* Math.Sin(ug)
GraphicsWindow.SetPixel(x, y , "")
EndFor
lmb = 1/3
dx = a*lmb
xm = x0 + dx
ym = y0 – b*Math.SquareRoot(a*a – dx*dx)/a
GraphicsWindow.FillEllipse(xm – 5,ym – 5,10,10)
p1 = xm - xf1
q1 = ym – y0
s1 = Math.SquareRoot(p1*p1 + q1*q1)
ИКТ как средство приобщения учащегося к математической реальности, 2018, №1, с.3-38
25
p1 = p1 / s1
q1 = q1 /s1
p2 = xm – xf2
q2 = ym – y0
s2 = Math.SquareRoot(p2*p2 + q2*q2)
p2 = p2 / s2
q2 = q2 /s2
p3 = p1 + p2
q3 = q1 + q2
For n = - 200 To 200
x = xm + q3*n
y = ym – p3*n
GraphicsWindow.SetPixel(x, y , "red")
EndFor
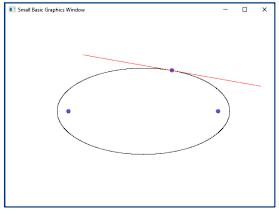
Задание 30. Построить семейства софокусных эллипсов и гипербол.
При построении используется параметризация эллипса с помощью синуса и косинуса, а также параметризация гиперболы гиперболическими функциями.
e = 2.71828
x0 = 320
y0 = 220
c = 100
For a = c + 1 To 400 Step 10
b = Math.SquareRoot(a*a -c*c)
For u = 0 To 2* Math.Pi Step Math.Pi/1000
x = x0 + a* Math.Cos(u)
y = y0 – b* Math.Sin(u)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
For a = 1 To c – 1 Step 5
b = Math.SquareRoot(c*c – a*a)
For t = –2 To 2 Step 1/1000
p = Math.Power(e,t)
q = 1/p
x = x0 + a*(p+q)/2
y = y0 – b*(p – q)/2
GraphicsWindow.SetPixel(x,y,"")
x = x0 – a*(p+q)/2
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor

Перейдём теперь к визуализации объектов математического анализа. При этом мы достаточно часто будем пользоваться и методами линейной алгебры. Говоря более конкретно, речь идёт о линейных преобразованиях. Кроме того, мы порой будем рассматривать объекты дифференциальной геометрии и теории дифференциальных уравнений, поскольку соответствующие задачи естественным образом вытекают из задач математического анализа.
Задание 31. Построить на экране график некоторой функции, предварительно разбив экран на единичные квадраты.
'Начало координат и единичный отрезок
x0 = 320
y0 = 220
GraphicsWindow.FillEllipse(x0 - 5, y0 - 5, 10, 10)
ed = 100
'Оси системы координат
GraphicsWindow.DrawLine(0, y0, 640, y0)
GraphicsWindow.DrawLine(x0, 0, x0, 440)
'Единичные квадраты
For t = –4 To 4 Step .01
For u = –3 To 3 Step 1
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "")
EndFor
EndFor
For t = –4 To 4 Step 1
For u = –3 To 3 Step .01
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "")
EndFor
EndFor
'Построение графика
For t = –4 To 4 Step .001
u = (t – 2)*(t + 1)* (t +2)/4
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "red")
EndFor
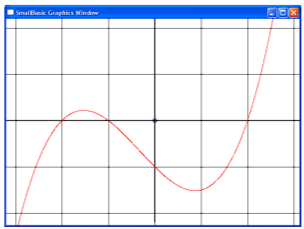
Задание 32. На графике из предыдущего задания выделить точку и провести через неё касательную и нормаль к графику.
Добавим к предыдущей программе следующие строки.
tm = 1
um = (tm – 2)*(tm + 1)* (tm +2)/4
xm = x0 + tm*ed
ym = y0 – um*ed
GraphicsWindow.FillEllipse(xm – 5, ym – 5, 10, 10)
k1 = (3*tm*tm + 2*tm – 4)/4
k2 = –1/k1
b1 = um – k1*tm
b2 = um – k2*tm
For t = –4 To 4 Step .001
u = k1*t + b1
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "blue")
u = k2*t + b2
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "green")
EndFor
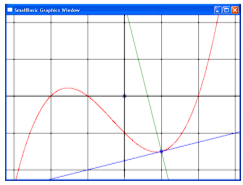
Задание 33. Построить семейство нормалей к параболе.
x0=320
y0=320
ed=100
For t= –2 To 2 Step .001
u= t*t
x=x0+ed*t
y=y0 – ed*u
GraphicsWindow.SetPixel(x,y,"")
EndFor
For t1= –2 To 2 Step .1
u1= t1*t1
x1=x0+ed*t1
y1=y0 – e d*u1
GraphicsWindow.FillEllipse(x1 – 5,y1 –
5,10,10)
t2=t1+.001
u2= t2*t2
k=(u2 – u1)/(t2 – t1)
p=1/ Math.SquareRoot(1+k*k)
q=k/ Math.SquareRoot(1+k*k)
For t= –400 To 400 Step 1
x=x1+t*q
y=y1+t*p
GraphicsWindow.SetPixel(x,y,"red")
EndFor
EndFor
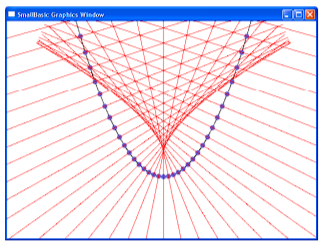
Задание 34. Огибающая нормалей кривой называется каустикой этой кривой. Построить каустику параболы.
Каждая из точек каустики будет приближённо строиться как точка пересечения двух соседних нормалей.
x0=320
y0=320
ed=100
For t= –2 To 2 Step .001
u= t*t
x=x0+ed*t
y=y0 – ed*u
GraphicsWindow.SetPixel(x,y,"")
EndFor
For t1= –4 To 4 Step .001
u1= t1*t1
t2=t1+.001
u2= t2*t2
k1=(u2 – u1)/(t2 – t1)
t3=t2+.001
u3= t3*t3
k2=(u3 – u2)/(t3 – t2)
If Math.Abs(k1)>.01 Then
a1= –1/k1
a2= –1
a3=u1+t1/k1
Else
a1=1
a2=0
a3= –t1
EndIf
If Math.Abs(k2)>.01 Then
b1= –1/k2
b2= –1
b3=u2+t2/k2
Else
b1=1
b2=0
b3= –t2
EndIf
xk=a2*b3 – a3*b2
yk=a3*b1 – a1*b3
zk=a1*b2 – a2*b1
If Math.Abs(xk)<4*Math.Abs(zk) And Math.Abs(yk)<4*Math.Abs(zk) Then
x=x0+ed*xk/zk
y=y0 – ed*yk/zk
GraphicsWindow.SetPixel(x,y,"red")
EndIf
EndFor
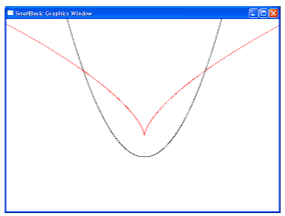
Задание 35. По формуле F(x, у, с) = 0 построить семейство графиков.
'Начало координат и единичный отрезок
x0 = 320
y0 = 220
GraphicsWindow.FillEllipse(x0 – 5, y0 – 5, 10, 10)
ed = 100
'Оси системы координат
GraphicsWindow.DrawLine(0, y0, 640, y0)
GraphicsWindow.DrawLine(x0, 0, x0, 440)
'Единичные квадраты
For t = –4 To 4 Step .1
For u = –3 To 3 Step 1
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "")
EndFor
EndFor
For t = –4 To 4 Step 1
For u = –3 To 3 Step .1
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "")
EndFor
EndFor
'Построение семейства графиков
For u = –2 To 2 Step .01
For c = 0 To 5 Step .5
t = u*u*u/c
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x, y, "red")
y = y0 + u*ed
GraphicsWindow.SetPixel(x, y, "red")
EndFor
EndFor
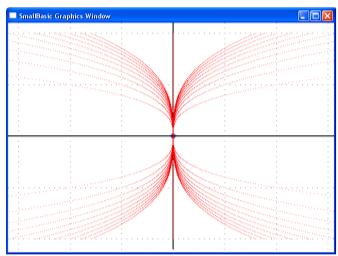
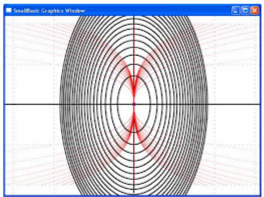
Задание 36. По семейству графиков из предыдущего задания построить ортогональную сеть.
Ортогональная сеть строится для семейства функций, заданных уравнением y3 = cx . Это уравнение следует продифференцировать: 3y2y' = c. Затем исключаем параметр с и получаем дифференциальное уравнение y = 3y'x. Далее строится уравнение для ортогональной сети y • y' = -3x. Это уравнение с разделяющимися переменными. В итоге ортогональная сеть состоит из эллипсов с полуосями √q и √q/3.
Подробнее см. например [А. Г. Школьник, 1963] .
For q = .5 To 3 Step .5
a = Math.SquareRoot(q/3)
b = Math.SquareRoot(q)
For ug = 0 To 2* Math.Pi Step Math.Pi/100
x = x0 + a* Math.Cos(ug)*ed
y = y0 – b* Math.Sin(ug)*ed
GraphicsWindow.SetPixel(x, y, "green")
EndFor
EndFor
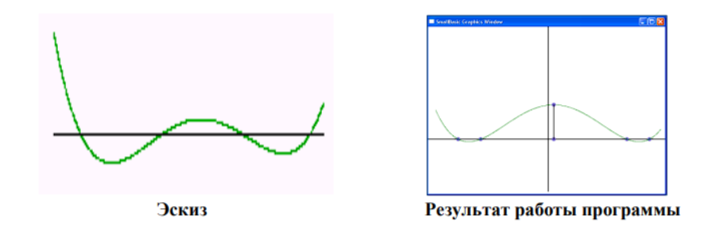
Задание 37. Построить на отрезке [-1; 1] график алгебраического многочлена по эскизу и найти максимум на этом отрезке.
x0 = 320
y0 = 300
ed = 300
GraphicsWindow.DrawLine(x0,0,x0,440)
GraphicsWindow.DrawLine(0,y0,640,y0)
t1 = .9
GraphicsWindow.FillEllipse(x0 + t1*ed – 5, y0 – 5, 10, 10)
t2 = .7
GraphicsWindow.FillEllipse(x0 + t2*ed – 5, y0 – 5, 10, 10)
t3 = –.6
GraphicsWindow.FillEllipse(x0 + t3*ed – 5, y0 – 5, 10, 10)
t4 = –.8
GraphicsWindow.FillEllipse(x0 + t4*ed – 5, y0 – 5, 10, 10)
max = (–1–t1)*( –1–t2)*( –1–t3)*( –1–t4)
xm = –1
For t= –1 To 1 Step .001
x = x0 + ed*t
u = (t–t1)*(t–t2)*(t–t3)*(t–t4)
If u>max Then
max = u
xm = x
EndIf
y = y0 – ed*u
GraphicsWindow.SetPixel(x,y,"green")
EndFor
GraphicsWindow.FillEllipse(xm – 5,y0 – 5, 10, 10)
GraphicsWindow.FillEllipse(xm – 5,y0 – max*ed -5, 10, 10)
GraphicsWindow.DrawLine(xm,y0,xm,y0 – max*ed)
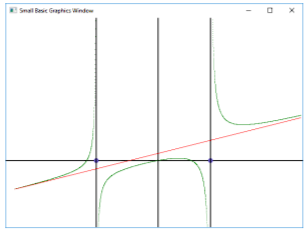
Задание 38. Построить на отрезке [-3; 3] график функции и провести асимптоты.
Уравнение наклонной асимптоты является частным при делении с остатком многочлена, стоящего в числителе, на многочлен, стоящий в знаменателе.
x0 = 320
y0 = 300
ed = 100
GraphicsWindow.DrawLine(x0,0,x0,440)
GraphicsWindow.DrawLine(0,y0,640,y0)
t1 = –1.5
t2 = .7
t3 = –1.3
x3 = x0 +t3*ed
GraphicsWindow.FillEllipse(x3 – 5, y0 – 5, 10, 10)
GraphicsWindow.DrawLine(x3,0,x3,440)
t4 = 1.1
x4 = x0 +t4*ed
GraphicsWindow.FillEllipse(x4 – 5, y0 -5, 10, 10)
GraphicsWindow.DrawLine(x4,0,x4,440)
For t=-3.001 To 3 Step .01
x = x0 + ed*t
ИКТ как средство приобщения учащегося к математической реальности, 2018, №1, с.3-38
31
u = t*(t–t1)*(t–t2)/(4*(t–t3)*(t–t4))
y = y0 – ed*u
GraphicsWindow.SetPixel(x,y,"green")
u = t/4 + .15
y = y0 – ed*u
GraphicsWindow.SetPixel(x,y,"red")
EndFor
Задание 39. Постройте многочлен Чебышева n-й степени (см. [П. К. Суетин, 1976]), имеющий корни в точках cos((2k - 1)п/2n), где k = 1, ... n. Постройте также многочлен той же степени со случайными корнями. Оцените уклонения многочленов от оси абсцисс.
x0 = 320
y0 = 220
ed = 200
GraphicsWindow.DrawLine(x0 – ed,y0,x0+ed,y0)
pi = Math.Pi
n = 5
For k = 1 To n Step 1
p[k] = Math.Cos((2*k – 1)*pi/(2*n))
x = x0 + p[k]*ed
GraphicsWindow.DrawEllipse(x – 5, y0 – 5, 10, 10)
q[k] = (Math.GetRandomNumber(200) – 100)/100
x = x0 + q[k]*ed
GraphicsWindow.DrawEllipse(x – 3, y0 – 3, 6, 6)
EndFor
For t = –1 To 1 Step .001
u1 = 1
u2 = 1
For k = 1 To n Step 1
u1 = u1*(t – p[k])
u2 = u2*(t – q[k])
EndFor
x = x0 + t*ed
y1 = y0 – u1*ed
y2 = y0 – u2*ed
GraphicsWindow.BrushColor="red"
GraphicsWindow.FillEllipse(x – 3,y1 – 3, 6, 6)
GraphicsWindow.BrushColor="green"
GraphicsWindow.FillEllipse(x – 3,y2 – 3, 6, 6)
EndFor

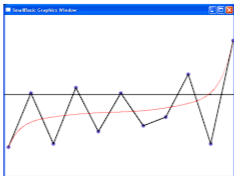
Задание 40. Отправляясь от доказательства первой теоремы Вейерштрасса, данного С. Н. Бернштейном, построить на отрезке [0; М. Е. Степанов, 2017] многочлен, аппроксимирующий непрерывную функцию y = f(x) (см. [Н. И. Ахиезер, 1965], стр. 39).
Многочлен, который мы будем строить, задаётся формулой ![]()
Выполняя построение многочлена для заданного n, мы на роль функции возьмём ло- kk маную с вершинами в точках вида (k/n; f(k/n)) .
x0 = 10
y0 = 220
ed = 620
GraphicsWindow.DrawLine(0,y0,640,y0)
n = 10
For k = 0 To n
f[k] = (Math.GetRandomNumber(100) – 50)/200
xf[k] = x0 + ed*k/n
yf[k] = y0 – ed*f[k]
GraphicsWindow.FillEllipse(xf[k] – 5,yf[k] – 5,10,10)
EndFor
For k = 1 To n
GraphicsWindow.DrawLine(xf[k–1],yf[k–1],xf[k],yf[k])
EndFor
For t = 0 To 1 Step .001
u = 0
c = 1
For k = 0 To n
u = u + c* Math.Power(t,k)* Math.Power(1–t,n–k)*f[k]
c = c*(n–k)/(k+1)
EndFor
x = x0 + t*ed
y = y0 – u*ed
GraphicsWindow.SetPixel(x,y,"red")
EndFor
Задание 41. Построить график плотности нормального распределения ![]() и график функции распределения Ф(х).
и график функции распределения Ф(х).
x0 = 320
y0 = 300
ed = 100
e = 2.71828
pi = Math.Pi
dt = .001
f1 = 1/2
f2 = 1/2
GraphicsWindow.DrawLine(x0,0,x0,440)
GraphicsWindow.DrawLine(0,y0,640,y0)
For t = 0 To 3 Step dt
x1 = x0 + ed*t
x2 = x0 – ed*t
u = Math.Power(e, –t*t/2)/ Math.SquareRoot(2*pi)
y = y0 – ed*u
f1 = f1 + u*dt
f2 = f2 – u*dt
y1 = y0 – ed*f1
y2 = y0 – ed*f2
GraphicsWindow.SetPixel(x1,y,"green")
GraphicsWindow.SetPixel(x2,y,"green")
GraphicsWindow.SetPixel(x1,y1,"red")
GraphicsWindow.SetPixel(x2,y2,"red")
EndFor
Ряд заданий будет связан с линейными преобразованиями плоскости. В статье [М. Е. Степанов, 2011] дано удобное для использования кинематическое истолкование линейных преобразований. В дальнейшем мы будем ориентироваться именно на него.
Задание 42. Построить график функции в системе координат, наклонённой под заданным углом к горизонтали.
x0 = 320
y0 = 220
ed = 100
ug = Math.Pi/6
x1 = x0 + ed* Math.Cos(ug)
y1 = y0 – ed* Math.Sin(ug)
x2 = x0 – ed* Math.Sin(ug)
y2 = y0 – ed* Math.Cos(ug)
For t1 = –4 To 4 Step .01
For t2 = –3 To 3 Step 1
x = x0 + t1*(x1 – x0) + t2*(x2 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
For t1 = –4 To 4 Step 1
For t2 = –3 To 3 Step .01
x = x0 + t1*(x1 – x0) + t2*(x2 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
For t1 = –4 To 4 Step .001
t2 = Math.Sin(10*t1)
x = x0 + t1*(x1 – x0) + t2*(x2 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
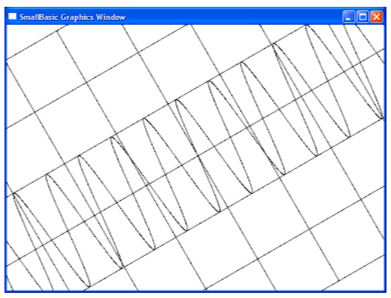
Задание 43. Построить эллипс, наклонённый под заданным углом к горизонтали и имеющий заданные длины полуосей.
x0 = 320
y0 = 220
GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)
ed = 100
a = 2
b = 1
ug = Math.Pi/6
x1 = x0 + ed* Math.Cos(ug)
y1 = y0 – ed* Math.Sin(ug)
GraphicsWindow.FillEllipse(x1–5,y1–5,10,10)
x2 = x0 – ed* Math.Sin(ug)
y2 = y0 – ed* Math.Cos(ug)
GraphicsWindow.FillEllipse(x2–5,y2–5,10,10)
For u = 0 To 2* Math.Pi Step Math.Pi/200
t1 = a*Math.Cos(u)
t2 = b*Math.Sin(u)
x = x0 + t1*(x1 – x0) + t2*(x2 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
Задание 44. Создать анимационный эффект, связанный с группой вращений плоскости относительно заданной точки.
pi=3.14159
nstor=9
m=5
ugol=2*pi*m/nstor
xa=320
ya=240
r=180
For u=0 to 10*pi step pi/20
Звезда()
For tmpause=1 to 50000
EndFor
GraphicsWindow.Clear()
EndFor
Sub Звезда
For n=0 to nstor
x1=xa+r*Math.Cos(ugol*n+u)
y1=ya – r*Math.Sin(ugol*n+u)
x2=xa+r*Math.Cos(ugol*(n+1)+u)
y2=ya – r*Math.Sin(ugol*(n+1)+u)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
EndFor
EndSub
Задание 45 Создать анимационный эффект вращения объёмного аксонометрическое изображения усечённой пирамиды.
pi=3.14159
n=7
x0=320
y0=300
rniz=150
rwerh=60
h=200
k=1/3
For u=0 to 10*pi step pi/20
Пирамида()
For tmpause=1 to 90000
EndFor
GraphicsWindow.Clear()
EndFor
Sub Пирамида
For i=1 To n
ug=u+i*2*pi/n
xniz1=x0+rniz* Math.Cos(ug)
yniz1=y0 – rniz* Math.Sin(ug)*k
xniz2=x0+rniz* Math.Cos(ug+2*pi/n)
yniz2=y0 – rniz* Math.Sin(ug+2*pi/n)*k
xwerh1=x0+rwerh* Math.Cos(ug)
ywerh1=y0 – rwerh* Math.Sin(ug)*k-h
xwerh2=x0+rwerh* Math.Cos(ug+2*pi/n)
ywerh2=y0 – rwerh* Math.Sin(ug+2*pi/n)*k-h
GraphicsWindow.DrawLine(xniz1,yniz1,xniz2,yniz2)
GraphicsWindow.DrawLine(xwerh1,ywerh1,xwerh2,ywerh2)
GraphicsWindow.DrawLine(xniz1,yniz1,xwerh1,ywerh1)
EndFor
EndSub
Задание 46. Построить поверхность, описываемую уравнением z = F(x, y).
В нашем случае используется частный вариант уравнения: z = F1(x) + F2(y).
pi = Math.Pi
u = pi/3
x0 = 320
y0 = 200
ed = 100
k = 1/3
x1 = x0 + ed * Math.Cos(u)
y1 = y0 – ed * Math.Sin(u)
x2 = x0 + ed * Math.Cos(u+pi/2)
y2 = y0 – ed * Math.Sin(u+pi/2)
x3 = x0
y3 = y0 – ed
For t1 = –1 To 1 Step .01
For t2 = –1 To 1 Step .1
t3 = t1*t1 – t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
For t1 = –1 To 1 Step .1
For t2 = –1 To 1 Step .01
t3 = t1*t1 – t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
GraphicsWindow.BrushColor="red"
For t1 = 0 To 0 Step .01
For t2 = –1 To 1 Step .01
t3 = t1*t1 – t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.FillEllipse(x – 2,y – 2,4,4)
EndFor
EndFor
GraphicsWindow.BrushColor="green"
For t1 = –1 To 1 Step .01
For t2 = 0 To 0 Step .01
t3 = t1*t1 – t 2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.FillEllipse(x – 2,y – 2,4,4)
EndFor
EndFor
GraphicsWindow.BrushColor="blue"
t1 = 0
t2 = 0
t3 = t1*t1 – t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.FillEllipse(x – 5,y – 5,10,10)
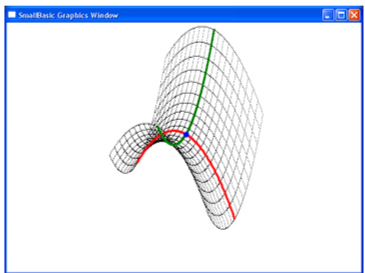
Задание 47. Построить сечение некоторой поверхности плоскостью.
pi = Math.Pi
u = pi/3
x0 = 320
y0 = 350
ed = 100
k = 1/3
x1 = x0 + ed * Math.Cos(u)
y1 = y0 – ed * Math.Sin(u)
x2 = x0 + ed * Math.Cos(u+pi/2)
y2 = y0 – ed * Math.Sin(u+pi/2)
x3 = x0
y3 = y0 – ed
For t1 = –1 To 1 Step .01
For t2 = –1 To 1 Step .1
t3 = t1*t1 + t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
For t1 = –1 To 1 Step .1
For t2 = –1 To 1 Step .01
t3 = t1*t1 + t2*t2
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.SetPixel(x,y,"")
EndFor
EndFor
GraphicsWindow.BrushColor="red"
For t1 = –1 To 1 Step .01
For t2 = –1 To 1 Step .01
t3 = t1*t1 + t2*t2
t4 = .2*t1 – .9*t2 +.3
If Math.Abs(t3 - t4) < .01 Then
x = x0 + t1*(x1 – x0) + t2*(x2 – x0) + t3*(x3 – x0)
y = y0 + t1*(y1 – y0) + t2*(y2 – y0) + t3*(y3 – y0)
GraphicsWindow.FillEllipse(x–2,y–2,4,4)
EndIf
EndFor
EndFor
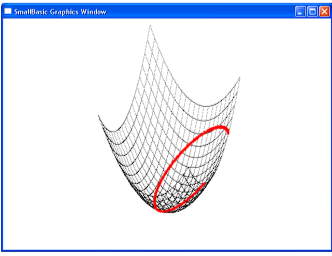
Задание 48. Создать анимационный эффект колебания струны.
x0 = 320
y0 = 220
ed = 100
pi = Math.Pi
For u = –10*pi To 10*pi Step pi/100
For t = –.5 To .5 Step .005
x = x0 + ed*t
a = Math.Sin(3*pi*t)/10 + Math.Sin(5*pi*t)/2 – Math.Sin(17*pi*t)/5
a = a* Math.Sin(u)
y = y0 – end*a
GraphicsWindow.SetPixel(x,y,"green")
EndFor
For tm = 1 To 50000
EndFor
GraphicsWindow.Clear()
EndFor
3. ЗАКЛЮЧЕНИЕ
Представляется уместным в процессе изучения высшей математики использовать задания, целью которых является написание компьютерных программ, визуализирующих изучаемые математические понятия. При этом абстрактное теоретическое знание обретает конкретное образное воплощение. Часто при этом достигается повышение уровня понимания и стимулируется более высокая степень мотивации, направленной на достижение более глубоких математических знаний.
Учащимся могут быть предложены задания различного уровня сложности, от простейших до достаточно сложных. Успешное выполнение любого из таких заданий требует активного использования математических понятий. Сложные задания иногда требуют обращения сразу к нескольким разделам математики, что также поднимает уровень математических знаний.
Кроме того, для современного математика обязательным является владение широким спектром компьютерных технологий, включая и программирование.
Литература
- М. Е. Степанов. Некоторые вопросы методики преподавания высшей математики. М., Моделирование и анализ данных. Научный журнал. МГППУ, №1, 2017.
- А. Г. Школьник. Дифференциальные уравнения. М., Учпедгиз, 1963.
- Н. И. Ахиезер. Лекции по теории аппроксимации. М. Наука, 1965.
- П. К. Суетин. Классические ортогональные многочлены. М. Наука, 1976.
- М. Е. Степанов. Метод сложных движений в компьютерной геометрии. М., Моделирова-ние и анализ данных. МГППУ, №1, 2011.
Информация об авторах
Метрики
Просмотров web
За все время: 587
В прошлом месяце: 7
В текущем месяце: 7
Скачиваний PDF
За все время: 459
В прошлом месяце: 3
В текущем месяце: 1
Всего
За все время: 1046
В прошлом месяце: 10
В текущем месяце: 8