Современная зарубежная психология
2016. Том 5. № 3. С. 7–27
doi:10.17759/jmfp.2016050301
ISSN: 2304-4977 (online)
Дискалькулия детского возраста как системная проблема обучения
Аннотация
Общая информация
Ключевые слова: дискалькулия, дислексия, школьный и дошкольный возраст, онтогенез, оптимизация обучения, математическая грамотность
Рубрика издания: Психология образования и педагогическая психология
DOI: https://doi.org/10.17759/jmfp.2016050301
Для цитаты: Ермолова Т.В., Пономарева В.В., Флорова Н.Б. Дискалькулия детского возраста как системная проблема обучения [Электронный ресурс] // Современная зарубежная психология. 2016. Том 5. № 3. С. 7–27. DOI: 10.17759/jmfp.2016050301
Полный текст
Ермолова Т.В., кандидат психологических наук, заведующая кафедрой зарубежной и русской филологии, профессор кафедры зарубежной и русской филологии, ФГБОУ ВО МГППУ, Москва, Россия, yermolova@mail.ru
Пономарева В.В., заместитель директора библиотеки по электронным ресурсам, ФГБОУ ВО МГППУ, Москва, Россия, ponomarevavv@mgppu.ru
Флорова Н.Б., кандидат биологических наук, сотрудник реферативно-аналитического сектора Фундаментальной библиотеки, ФГБОУ ВО МГППУ, Москва, Россия, ninaflorova@yandex.ru
В тематическом обзоре анализируются исследования ряда зарубежных и отечественных ученых по проблеме дискалькулии. Это позволило проследить динамику представлений о дискалькулии, ее диагностических критериях и стратегиях целевого вмешательства для детей старшего дошкольного и младшего школьного возраста. В анализируемых работах речь идет о современном понимании основных свойств дискаль- кулии — гетерогенности и дистанционности, нейроанатомических предпосылках ее формирования и рисках неадекватной интерпретации эмпирических данных. В них также дается определение первичной и вторичной дискалькулии и представление о диапазоне оптимизирующих образовательных технологий. В обзоре очерчены особенности зарубежной и отечественной научной школы применительно к данной проблеме. Представляется, что приоритетность проблемы дискалькулии остается недооцененной относительно дислексии и иных системных психолого-педагогических проблем детского возраста.
Низкая математическая грамотность представляет собой не только образовательную, но и социальноэкономическую и этическую проблему. Сегодня специалисты признают, что фактор недостаточной сфор- мированности математических компетенций в детстве снижает качество жизни взрослых людей даже сильнее, чем низкая грамотность. Эмпирически доказано, что люди с трудностями владения арифметическими навыками счета имеют меньше шансов на достойный социоэкономический статус и менее законопослушны. При этом дискалькулия не является признаком нарушения интеллекта, т. е. человек с неспособностью обучаться базовым арифметическим действиям адекватен в других областях математических знаний и в жизни в целом. В то же время дис- калькулия часто встречается в сочетании с дислексией и иными расстройствами.
Сегодня мы располагаем определенным объемом знаний о характерных проявлениях дискалькулии детского возраста. Это: непонимание смысла чисел (невозможность увязать число и его «величину»), отсутствие представления о числовой иерархии и многие другие особенности. Если в норме ребенок способен быстро и «на глаз» определить количество предметов, то дискалькулия вынуждает его пересчитывать каждый предмет отдельно, при этом часто прибегая к помощи пальцевого счета — психологически незрелой и первичной в онтогенезе (самой ранней) стратегии. Как будет показано ниже, за такие нарушения несут ответственность неразвитые структуры различных участков коры головного мозга, прежде всего, внутритеменной борозды, а также префронтальной коры и веретеновидной извилины.
В полемической статье журнала «Science» за 2011 год «От мозга к обучению» (From Brian to Education») специалисты Австралии, США и Великобритании Brian Butterworth, Sashank Varma, Diana Laurillard [Butterworth Brian, Varma, 2011] совместно указали на серьезную недооцененность дискальку- лии и выразили надежду на эффективность уже имеющихся стратегий вмешательства, ориентированных на «внешние проявления» расстройства. Они полагают, что необходимо работать в направлении поиска компенсаторных обходных путей и резервов организма, которые бы позволили оптимизировать формирование арифметической, базовой грамотности.
Зарубежный научно-практический опыт исследования дискалькулии
В кратком обзоре (журнал «Cognitive Development» за 2009 год), освещающем историю исследований и место дискалькулии в ряду трудностей обучения, психолог университета Оксфорд Ann Dowker и психолог университета Зальцбург Liane Kaufmann [Dowker Ann, Kaufmann, 2009] опубликовали согласованное определение дискалькулии как атипичного развития цифровой когнитивной функции, которое, хотя и не связано с общим нарушением интеллекта или отсутствием образовательных возможностей, тем не менее вызывает серьезные затруднения уже при обучении арифметическим действиям в начальной школе и может усугубляться по мере усложнения учебного материала. Проблема низкой чувствительности (восприимчивости) отдельных групп учащихся к математическим символам и операциям достигла такого масштаба, что в 2001 г. Департаментом образования и профессионального обучения Великобритании она была официально признана специфической неспособностью к обучению.
Однако, как подчеркивают авторы, проблема дис- калькулии отстает по степени эмпирической проработанности от других трудностей в обучении, например, дислексии. Причиной этого может быть продолжающаяся дискуссия по поводу формализации представления о природе дискалькулии — является ли она нозо- логически самостоятельным расстройством или же представляет собой просто «нижний уровень» континуума способностей и достижений в работе с цифровым материалом. В литературе есть такие критерии трудностей обучения математике (арифметике), как появившиеся в начале 2000 гг. «критерий тяжести математической адинамии», или критерий постоянства «математического бессилия (отставания, слабости)».
Следует также иметь в виду, что «...большинство ведущих теорий о цифровой (числовой) когнитивной функции опираются на исследования взрослых людей и, соответственно, многие онтогенетические исследования содержат расчетные модели, применимые к взрослым, сформировавшимся, но не к развивающимся мозгу и когнитивным функциям и системам» [Dowker Ann, Kaufmann, 2009].
Авторы выразили уверенность: ученые располагают достаточными доказательствами того, что дискалькулия не является обособленной от других проблемой развития, а лежащие в ее основе нейрофизиологические механизмы могут вызывать широкий спектр поведенческих и функциональных нарушений у индивидов, причем можно фиксировать как единичные, так и множественные расстройства у каждого отдельного индивида, имеющие разную природу. Следовательно, дискалькулию можно рассматривать как гетерогенное расстройство с масштабной несогласованностью составляющих и широким спектром возникающих в связи с этим симптомов [Dowker Ann, Kaufmann, 2009].
В начале 2000-х гг. на базе ведущих университетов США, в том числе с привлечением европейских специалистов, были проведены методологически простые, но разнообразные исследования детей с дискалькули- ей. Использовалась, в частности, технология окулогра- фии (eye-tracking — отслеживание движения глаз), позволяющая оценить способность детей к субитиза- ции (мгновенному подсчету объектов в поле зрения. — Ред.), которая показала, что дети с дискалькулией имеют проблемы с количеством фиксаций, необходимых для кодирования даже самых малых объемов числовой информации, тогда как в норме не возникает проблем с обработкой малых объемов числовой информации. Дети с дискалькулией фактически вынуждены производить подсчеты в диапазоне, в котором в норме они могут субитизироваться без подсчетов. В тестах на сопоставление одноразрядных (однозначных) чисел дети с дискалькулией демонстрировали сопоставимые с контрольной группой данные по времени реагирования, но одновременно более высокий уровень ошибочных результатов. В тестах на сопоставление двуразрядных (двузначных) чисел они показывали более выраженный отдаленный эффект по сравнению с контрольной группой и испытывали сложность в восприятии задачи как таковой. Это может означать, что величины (числовые значения) в меньшей степени дифференцируются детьми с онтогенетической дискалькули- ей, нежели детьми без этого расстройства.
Одна из исследователей, входящих в эту группу ученых, Ann Dowker в 2009 г. дополнительно изучала использование 6—7-летними школьниками стратегий дифференцирования фактов (derived fact strategies). Обнаружилось, что дети с дискалькулией широко использовали стратегии, основанные на идентичности и коммутативности, и гораздо меньше использовали какие-либо другие стратегии, например, основанные на инверсионном принципе добавления/вычитания. Это позволило расширить представление о механизмах, лежащих в основе атипичного математического мышления у детей.
Следует обратить внимание на результаты еще одного исследования, выполненного в 2009 г. генетиками Murphy и Mazzocco [Murphy, 2009]. Они изучали изменения в рабочей памяти и способностях к математике у девочек 10—12 лет с расстройством, которое, как считается, влияет на обучение математике: синдромом хрупкой X-хромосомы (синдром Мартин-Белл). Эти авторы обнаружили, что траектория формирования математических навыков и становление рабочей памяти у девочек с данным синдромом отличается от траекторий, характерных для здоровых детей, и полагают, что рабочая память может оказаться прогностичной с точки зрения успешности и результативности усвоения математики. Так, девочки с синдромом хрупкой Х-хромосомы продемонстрировали нарастание выраженных нарушений в освоении математики при повышенных требованиях к рабочей памяти, что свидетельствует о сравнительно низком пороге их рабочей памяти.
До определенного времени истинная причина трудностей обучения арифметике — несостоятельность анатомических структур мозга — оставалась в тени и на первый план выдвигались многие иные причины.
Ближе к концу 2000-х гг. стали более активно развиваться перспективные направления исполнительных функций мозга в связи с проблемой обработки числовой информации. Было выдвинуто предположение, что онтогенетическая дискалькулия в большей мере связана с проблемным контролем исполнения, чем с обработкой даже очень простых (однозначных) чисел.
Уже ранние попытки применения высокотехнологичной методологии (функционального магнитного резонанса fMRI) с участием одного из авторов обзора показали, что для детей с онтогенетической дискалькулией характерно снижение активации зон теменной доли в процессах выстраивания числового ряда, что не позволяет им формировать представления о числовом ряде. У обычно развивающихся детей формирование представлений о порядковом ряде числовой и нечисловой типологии коррелирует с механизмами активации зон теменной доли коры головного мозга.
С позиций исторической справедливости следует отметить, что еще раньше, в 2005 г., в своей публикации в журнале «Journal of Learning Disabilities» специалисты университета Орегон Russell Gersten, Nancy C. Jordan, Jonathan R. Flojo [Dyscalculia from a, 2013] указали на другую сторону проблемы — отсутствие надежных инструментов раннего скрининга математических способностей и их прогнозирования наряду со сформированными алгоритмами скрининга готовности к обучению чтению.
Эти авторы выразили надежду, что своей работой дадут импульс исследованиям, которые будут проводить сравнительное изучение эффективности различных подходов в стратегиях вмешательства для младших учащихся, предположительно склонных к тревожности из-за проблем с математикой. В частности, они фиксируют сопоставимость имеющихся в науке данных, что, с их точки зрения, позволяет приблизиться к пониманию личностных траекторий учащихся с математическими трудностями (МТ) и пониманию их уязвимых мест, требующих интенсивной поддержки. Фактически авторы поставили перед собой цель формализации инструментов раннего скрининга и опережающей интервенции при профилактике трудностей обучения счету.
Авторы рассматриваемой ниже обширной публикации [Gersten Russell, Jordan, 2005] относят начало широких активных и, главное, системных исследований проблемы дискалькулии у детей к концу 1980—х гт., а именно к работам 1987-1988-х гт. (Goldman, Pellegrino, & Mertz; Hasselbring, Goin, & Bransford), показавшим, что учащиеся с математическими трудностями (МТ) в первые годы обучения в начальной школе неспособны к автоматическому поиску и извлечению математической информации (arithmetic facts, например 4 + 3 = 7 или 9 х 8 = 72) из ресурсов памяти.
Выражаясь точнее, учащиеся с МТ неспособны достигать такого уровня мастерства, при котором реализация навыков и умений происходит быстро и точно с минимальным сознательным контролем или совсем без него, при этом ресурсы концентрации внимания могут быть распределены на другие задачи и цели, включая повышение уровня исполнительной или регулирующей функции (Goldman & Pellegrino, 1987). Обнаруженная дефи- цитарность, или дисфункциональность, означает подавление способности к математической логике и усвоению более сложных алгебраических понятий.
Известно, что дети с трудностями обучения математике (арифметике) имеют сопутствующие трудности с обучением чтению (ЧТ). На примере исследований, проведенных Jordan с соавторами в начале 2000-х гг., можно проследить логику становления навыков работы с цифровым материалом у детей младшего школьного возраста, имеющих такие сочетанные дефициты обучения.
Считается, что в связи с комплексным характером любого математического действия при его осуществлении происходит одновременное обращение к самым разнообразным когнитивным процессам. Это позволило Jordan с соавторами в 2003 г. выдвинуть гипотезу, согласно которой математические способности могут в разной мере проявлять себя в различных областях математической компетенции, особенно среди детей с МТ (только МТ).
Начиная с работы Hanich et al. 2001 г., в лонгитюдных исследованиях стало общепринятым дифференцирование детей на группы соответственно диагностированным расстройствам обучения — только МТ, МТ+ЧТ, только ЧТ и обычная успеваемость (ОУ) по чтению и математике (арифметике) в начале второго года обучения.
Jordan, Kaplan, and Hanich (2002) в течение двух лет исследовали успеваемость в каждой такой группе, пользуясь инструментом Woodcock-Johnson Psycho- educational Battery-Revised.
В 2003 г. они предположили, что именно недостаточность пространственных представлений, связанных с численными величинами (в большей степени, чем недостаточность вербальных представлений), определяет дефицитарность фактора быстрого поиска готовых решений в рабочей памяти.
Рассматривая перспективы оптимизации образовательного процесса для детей с МТ, исследователи приходят к заключению, что дефицитарность беглости счета является одной из основных причин математических трудностей.
Одной из зафиксированных причин трудностей в изучении математики у детей является смена образовательной среды (детский сад — начальная школа). Исследования этого этапа позволяют проследить динамику данных расстройств и оценить возможности их смягчения.
Мы обнаружили лишь одно исследование, охватывающее достаточно длительный интервал изучения этого периода — пять лет [Mathematical Cognition Deficits, 2012]. Его содержание и результаты описаны ниже.
С 2008—2009 гг. за рубежом начались активные поиски механизмов формирования арифметического мышления и навыка счета у детей в детском саду с применением стратегий компьютерного вмешательства (computer-assisted intervention-CAI) и образовательных игр: The Number Race и Graphogame-Math. Было выявлено, что дети с пониженными математическими способностями могут развить в себе умение сравнивать числа. Однако в этом случае обучать счету необходимо начинать в раннем возрасте. Именно тогда у ребенка закладываются основы так называемого «арифметического мышления» (своеобразная чувствительность к математическим знакам и действиям).
Основоположники концепции «позитивного арифметического мышления» (Okamoto & Case, 1996; Kalchman, Moss, & Case, 2001) включают в структуру этого понятия: а) беглость оценки и суждений о величинах; b) способность признать результаты необоснованными; с) гибкость при мысленных вычислениях; d) способность ориентироваться в системе представлений и выбирать наиболее подходящие.
Case, Harris, and Graham в 1992 г. обнаружили, что когда воспитанникам детского сада показали две группы предметов (т. е. пять чипсов и восемь чипсов), то большинство детей могли выбрать более объемную группу предметов и знали, что в более объемной группе больше предметов (кусочков). Тем не менее, только дети с хорошо развитым арифметическим мышлением могли знать, что 8 на 3 больше, чем 5. Точно так же только дети с развитым арифметическим мышлением могли знать, что 12 намного больше чем 3, тогда как 5 лишь ненамного больше трех.
Эти наблюдения высветили необходимость разработки дифференцированных методических рекомендаций по обучению основам математики в детских садах.
Okamoto в 2000 г. идентифицировал два различных фактора, определяющих математические умения детей в детских садах. Первый имеет отношение к счету, ключевому индикатору цифровой, последовательной, вербальной структуры; второй фактор связан с умением определять количество (quantity discrimination) (т. е. скажи мне, что больше — 5 или 3?). Например, Okamoto и Case еще в 1996 г. обнаружили, что некоторые учащиеся, в том числе умеющие считать до пяти без ошибок, не имели представления о том, какое число больше — 4 или 2.
Эти авторы пришли к выводу, что у детей старшего дошкольного возраста два ключевых компонента арифметического мышления не вполне прочно связаны между собой и являются, скорее, прототипами других компонентов арифметического мышления — это способности оценивать (суждения) и способности ориентироваться в системе представлений.
Дополнительным свидетельством важности умения определять количество (quantity discrimination) и его потенциального влияния на общие способности к математике стала работа Griffin, Case, and Siegler (1994) по раннему скринингу. Эти авторы показали, что посещающие детский сад различаются по способности отвечать на вопросы, подразумевающие владение навыком «определения количества» (например, «какое число больше — 5 или 4?»), даже если они умеют считать и производить простые арифметические действия.
В целом, согласно мнению Case и его коллег (1992), арифметическое мышление представляет собой концептуальную структуру, опирающуюся на множество связей между математическими отношениями, математическими правилами и законами и математическими операциями. Раннее формирование таких связок может быть решающим для получения математических знаний в более старшем возрасте. Детям, не выработавшим таких связей, может впоследствии потребоваться вмешательство, направленное на их формирование.
В научной литературе по проблеме дискалькулии активно анализируются оценочные технологии раннего скрининга трудностей обучения математике среди воспитанников детских садов, т. е. непосредственно перед началом школьного обучения. Практика показала надежность теста Number Knowledge Test. Он представляет собой индивид-ориентированный оценочный инструмент, позволяющий не только оценить знание детьми законов и операций базовой арифметики, но и глубину понимания ими действий с помощью набора структурных проб, выявляющих уровень понимания величин, концепции «больше чем» и стратегий, используемых при счете. Number Knowledge Test, как инструмент с наибольшим диапазоном показателей, был признан одним из лучших прогностических инструментом в ряду оценочных процедур по протоколам SAT-9 Procedures and Problem Solving. Содержащиеся в нем оценочные критерии, относящиеся к математике, можно считать предикторами умений более высокого порядка, в том числе тех, которые к математике не относятся, например, Phoneme Segmentation (оценочный критерий фонематической осведомленности) — беглость наименования букв и способность назвать цвета и изображения.
Кроме того, следует сказать, что для целей скрининга оказались полезными и перспективными задания по сравнению величин (the magnitude comparison task) и счет в обратном направлении (digit span backward task). Три относительно компактных оценочных параметра также представляются весьма перспективными: а) quantity discrimination, или сравнение величин (magnitude comparison); b) идентификация отсутствующей цифры/числа в последовательном ряду как критерий знаний о счете; с) способность к идентификации чисел/цифр.
Другими словами, учащиеся, все еще медленно использующие пальцевый счет, чтобы рассчитать такую комбинацию, как, например, 7 + 8, скорее всего абсолютно не воспринимают предлагаемый им учителем новый формат операций, а педагоги остаются в неведении и продолжают пользоваться привычным игровым приемом как базовым для объяснения вариантов решения задач или понимания происходящего.
Необходимо направить больше усилий на то, чтобы связать разработку специфических мер, ориентированных на ранний скрининг и идентификацию детей с МТ, с теориями относительно МТ как явления. Например, в первом классе начальной школы сдвиг от конкретики к действиям в уме представляется самым важным для развития беглости счета (Jordan & Hanich, 2003; Jordan et al., 2003). Оценочный аппарат раннего скрининга может охарактеризовать стратегии счета у детей на разных уровнях становления их арифметического мышления.
На актуальность возможно более раннего формирования арифметического мышления указывает Evelyn Kroesbergen (университет Утрехт) [Mathematical learning difficulties, 2015]. По ее мнению, способность к арифметическому мышлению является полезным базовым свойством, которое следует формировать у детей как можно раньше. Особенно важны для детей знания символов, слов, обозначающих числа и цифры, основ счета. По мнению этого автора, данные количественные представления служат хорошей основой для дальнейших успехов в усвоении математики. Если у детей не сформированы должным образом базовые навыки арифметического мышления, они попадают в группу риска и могут столкнуться с трудностями в изучении математики.
Раскрывая содержание арифметического мышления, E. Kroesbergen пишет, что знакомство с образами и символами создает основу для дальнейшего развития числовых навыков (так называемых до-математических навыков или знания о числах и вычислениях (Aunio et. al, 2005; Jordan et al., 2010)), а также более продвинутых числовых навыков (понимание и беглое пользование числами и операциями (McIntosh et al., 1992)). Однако наиболее важные навыки, которыми, с ее точки зрения, должны овладеть дети — это комбинирование различных представлений об информации, заключенной в числах. Они получили название «навыки картирования, или навыки отображения».
Эти навыки отображения особенно важны для того, чтобы придать смысл словам, обозначающим числа, и арабским цифрам/числам, путем ассоциирования их с количеством, которое они представляют (Geary, 2013; Mazzocco et al., 2011).
Таким (в самом первом приближении) предстает путь научного знания и его практического применения в сфере трудностей обучения на середину 2000-х гг. прошлого столетия. С течением времени возрастающий объем научного знания о дискалькулии позволил предложить методологически более совершенные стратегии вмешательства, которые позволяют оптимизировать школьное обучение детей с математическими трудностями. Стала очевидной необходимость подключения научного знания к практическим разработкам.
Так, многонациональная исследовательская группа психологов — Roi Cohen Kadosh, Ann Dowker, Angela Heine, Liane Kaufmann, Karin Kucian [Kadosh Cohen, 2013], представляющая четыре ведущих европейских университета, разместила в журнале «Trends in Neuroscience and Education» статью, обосновывающую направления оптимизации существующих стратегий корректирующего вмешательства для обучения детей с онтогенетической дискалькулией (developmental dyscalculia, DD), или расстройством, выражающимся в трудностях обучения математике (арифметике, англ. mathematical learning disability, MLD). По данным авторов этой статьи, такие трудности испытывают, начиная с детства, от 3 до 13% населения, а 20% людей имеют низкие способности к усвоению математики.
Предпосылки к успеху вмешательств лежат, по мнению авторов, прежде всего в новом понимании дискалькулии как анатомически и нейробиологически обусловленного расстройства; сегодня специалисты сходятся во мнении, что с дискалькулией связана двойная дисфункция нижележащих зон теменных долей мозга, отвечающих за метаболизм и навыки счета.
Второй определяющий момент в проблеме дискаль- кулии авторы видят в том, что арифметика, как учебная дисциплина, многокомпонентна, и за различные ее компоненты ответственны различные зоны и локусы головного мозга. Поэтому, по мнению авторов, необходимы стратегии вмешательства, сфокусированные не на каком-то конкретном компоненте, а более комплексные и эффективные, учитывающие, что математические трудности у разных детей не всегда аналогичны.
С этих позиций авторы рассмотрели набор целевых вмешательств, имеющийся в распоряжении системы образования. Они выделяют среди учащихся 8—10 лет группу со средним уровнем трудностей базового обучения математике (арифметике).
Для этой группы авторы рекомендуют структурированную целевую программу индивидуального обучения Catch Up Numeracy, ориентированную на 15-минутные занятия дважды в неделю на протяжении учебного года; в ней развиваются навыки по десяти ключевым компонентам грамотного счета, в том числе устный счет; счет объектов (предметов); чтение и письмо; сотни, десятки и единицы; оценка; проблемы со словами; перенесение (перемещение); порядковые числительные. Занятия проводятся специально подготовленными педагогами, имеющими сертификаты по программам «Catch Up Numeracy learner profile» и «Catch Up Numeracy formative assessments».
Учитывая, что дети с MLD/DD имеют поведенческие нарушения, а также атипичную активность и анатомию головного мозга, авторы наглядно продемонстрировали, каким образом вмешательство игрового формата (например, программа Calcularis) может оказать воздействие на поведение и функции мозга. С помощью ряда высокотехнологичных инструментов (электро- и магнитоэнцефалография, функциональный магнитный резонанс, позитронная эмиссионная томография, ближне-инфракрасная спектроскопия и др.) они провели картирование головного мозга в момент игрового вмешательства.
Анализируя результаты картирования в совокупности с литературными данными, авторы приходят к заключению, что при атипичном DD-онтогенезе следует говорить о нейронных коррелятах в ходе обработки математических материалов и выполнения операций счета. Получены конвергентные доказательства того, что атипичность наблюдается преимущественно в борозде теменной доли, а также в верхней и нижней теменной доле, которые, как известно, являются основными зонами, ответственными за математические способности и овладение математикой. Кроме теменных областей, другие кортикальные и субкортикальные области, которые вносят свой вклад в работу с математическим материалом, могут также быть ассоциированы с математическими трудностями. В частности, было выявлено снижение объема серого вещества и дефицит связанности нервных волокон.
Вместе с тем, у детей с DD выявлены компенсаторные механизмы; они обычно характеризуются усилением подкреплений в виде мобилизации ресурсов рабочей памяти, внимания, контролирующей функции, стратегией счета, аналогичных счету на пальцах. Возрастающая потребность в таких поддерживающих функциях может объясняться недостаточным развитием числовых представлений или отсутствием автоматизированного навыка оперирования числами. Тем самым авторы обращают внимание читателя на наличие поддерживающих функций, обеспечивающих оптимизацию формирования начальных математических компетенций, о чем говорилось в начале статьи.
Авторы интерпретируют имеющиеся в литературе результаты вмешательства с помощью компьютерной программы «Rescue Calcularis», длившегося 5 недель. Они подчеркивают, что результаты обучения по этой программе проявляются в виде модуляций мозговых функций. Метод fMRI демонстрирует снижение активности ряда областей головного мозга после окончания занятий, главным образом лобных долей, билатеральных IPS-участков и левых веретенообразных извилин. Снижение активности мозга в этих локусах и особенно в лобных долях представляется авторам показателем автоматизации когнитивных процессов, необходимых для понимания математики. Спустя 5 недель по окончании занятий у детей с DD было отмечено значительное увеличение активности теменных областей мозга. Поскольку IPS-структуры играют центральную роль в формировании математических представлений, эти результаты показывают, что после обучения по программе требуется время, чтобы сформировать нейронные механизмы математических представлений.
Можно с определенной долей уверенности говорить о том, что игровой формат эффективен для трансформирования активности головного мозга, атипичной по времени и локализации, в «типичную активацию», а значит о том, что оптимизация образовательного процесса при данных расстройствах возможна посредством активации резервных мощностей мозга. В качестве одного из таких путей оптимизации авторы обсуждают метод транскраниальной электростимуляции, пролонгировано повышающей корковую возбудимость, как дополнительный электрофизиологический метод стимуляции в периоде начального обучения.
Концептуально значима публикация журнала «Frontiers in Psychology» в 2013 г., представляющая системный взгляд на дискалькулию большого коллектива специалистов из шести стран мира [Dyscalculia from a, 2013]. Эта публикация важна своей методологической направленностью, поскольку в ней дано современное определение дискалькулии и дифференцированы ее проявления на поведенческом, когнитивном и нейробиологическом уровне, а также перечень индивидуальных ресурсов, позволяющих противостоять трудностям в обучении.
Авторы четко дистанцируют онтогенетическую дис- калькулию (Developmental Dyscalkulia — DD) от трудностей обучения математике, относя это расстройство исключительно к обучению арифметике и поясняя, что термины «арифметическое» и «математическое» не являются синонимами, поскольку первый относится к навыкам вычисления (т. е. выполнению базовых арифметических действий, таких как сложение/вычитание/ разложение), а второй охватывает остальные аспекты цифрового мышления, такие как алгебра, геометрия и т. д. Кроме того, истинная DD присуща меньшинству (в популяции. — Ред.) и может существовать в скрытой форме на фоне иных расстройств личности.
Далее авторы констатируют, что компетенции в области арифметики включают в себя ряд компонентов (запоминание фактического материала, выполнение операций, понимание, пользование арифметическими закона- ми/принципами (Desoete et al., 2004; Dowker, 2005, 2008), каждый из которых субъективен, индивидуален, сохраняется в зрелом возрасте (Dowker, 2005; Kaufmann et al., 2011a) и может способствовать распространенности слабо развитых навыков счета (Geary et al., 2013).
Выдвигая гетерогенность дискалькулии на первый план как ее неотъемлемое свойство, авторы пишут, что индивидуальные различия должны обсуждаться при наличии четкого определения DD, так как предположения о едином дефицитарном механизме (Butterworth, 2005) не подтверждаются наблюдаемым в реальности диaпaзономклиническихпроявленийDD.Гетерогенность DD и других математических трудностей поддерживается также средовыми факторами, классифицируемыми как культуральные (характер и степень школьного образования, характеристики системы счета) или как эффекты пре/постнатального заболевания и/или социо-эмоциональной отягощенности (например, тревожности, связанной с математикой).
Отсюда следует, что сегодня мы можем четко представлять себе истинный масштаб трудностей с обучением математике и распределение этих трудностей на подлежащие и не подлежащие коррекции и профилактике, что, в свою очередь, чрезвычайно важно в образовательной политике. Узкое место здесь — диагностическое дифференцирование детской популяции.
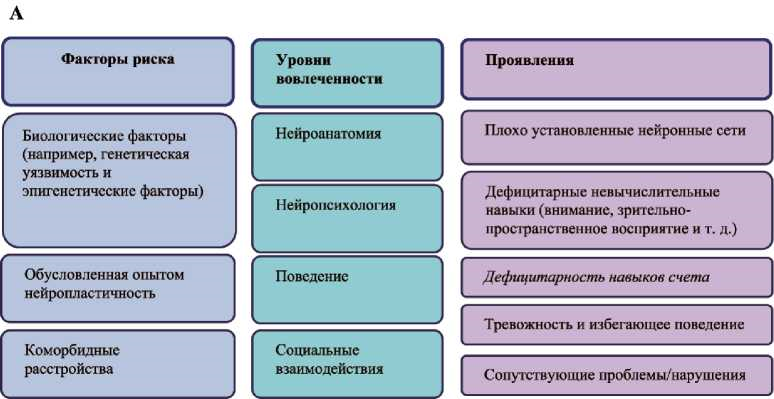
В этой небольшой, но чрезвычайно насыщенной (рис. 1 А, В, С), иллюстрирующая гетерогенность этого статье предлагается схема концепта DD из трех частей явления.

|
Рис. 1 (А) Связанные с развитием и интегративные аспекты DD. (B) представления о возможных клинических манифестациях DD. (С) представления о ключевых областях знания для будущих исследований, ориентированных на разработку адекватных концепций DD, связанных с развитием личности. Направления, обозначенные в серых кругах, не являются предметом данной статьи, но необходимы для понимания системного характера будущих разработок [10, c. 2] |
В блоке А представлены взаимосвязи факторов риска, уровней вовлечения систем организма в ответную реакцию и манифестации (проявления).
К биологическим факторам относятся генетическая узявимость и эпигенетические факторы; уровень их вовлечения — нейроанатомический и нейропсихологический; манифестантные проявления — соответственно «плохо установленные» нейронные сети и несовершенные (дефицитарные) не-вычислительные навыки (внимание, визуально-пространственное восприятие).
Факторы риска, относящиеся к нейропластичности, проявляются на уровне поведения дефицитарно- стью навыков счета, тревожностью и избеганием.
Наконец, коморбидные расстройства на уровне межличностных взаимодействий чреваты различными сопутствующими расстройствами личности ассоциативного характера.
В блоке В показано, какие последствия являются ожидаемыми при совместном давлении со стороны домен-генерализованных проблем (эмоциональных, моторных, социальных, коморбидных, когнитивных не-вычислительных) и домен-специфичных дефицитов (дефицитарность представлений о числах и дефи- цитарность базовых вычислительных действий). Показаны различные уровни проявления последствий — дома, в школе, на индивидуальном уровне и в обществе. Так, например, в обществе это могут быть проблемы социализации, в семье — проблемы, связанные с низкой успеваемостью.
В блоке С представлены проблемы (исследовательские тренды), сопряженные с проблемой дискальку- лии, это диагностирование, гетерогенность, траектории развития, вязкость, прогнозирование, значение для социума.
Авторы формулируют общеметодологические проблемы, стоящие перед специалистами, работающими с проблемой дискалькулии. Таких вопросов два. Первый — действительно ли DD представляет собой конечную стадию континуума (или нескольких континуумов) математических способностей? Второй — в какой мере арифметические трудности, ассоциированные с DD, количественно отличны от более общих математических трудностей. Анализируя обширный литературный материал, они приходят к выводу, что существуют данные в поддержку и той и другой позиции. Арифметические трудности могут отражать индивидуальные различия как в цифровой/числовой, так и в нечисловой/нецифровой функциях.
Авторы выделили несколько рискованных моментов в применении результатов подобных исследований и предупреждают об этом педагогов, диагностов- дефектологов и других специалистов. Так, если, например, у детей имеются серьезные проблемы с извлечением арифметических фактов, но адекватно развиты навыки решения других числовых и арифметически задач, они не могут быть классифицированы как имеющие дискалькулию или даже нарушения арифметической грамотности.
При выстраивании алгоритма научной работы в формате группового исследования, описанные дефициты могут остаться незамеченными, поскольку усреднение как внутри выборки, так и в изучаемых процессах может маскировать дефициты, проявляемые у меньшинства в выборке (Siegler, 1987).
Существует и риск другой крайности: дети могут оказаться «маркированными» (стигматизированными. — Ред.) сами собой или окружающими как слабые и испытывающие трудности в определенных навыках арифметики, невзирая на высокие способности в других областях этой дисциплины. Это может привести к самореализующимся («накликанным») неприятностям или способствовать формированию масштабной тревожности, связанной с математикой. На самом деле, среди детей младшего возраста, как показывают многие исследования, имеет место относительно слабая связь между тревожностью и успеваемостью, тогда как у более старших детей и взрослых эта связь прочна и зачастую тревожность воздействует на успеваемость, а слабая успеваемость повышает тревожность (Ashcraft and Kirk, 2001; Mazzone et al., 2007; Pixner and Kaufmann, 2013).
Некоторые авторы особо подчеркивают риск неадекватной оценки эмпирических данных при исследовании дискалькулии. В частности, Moeller и его коллеги (2012) сообщают о наличии слабой согласованности мнений специалистов в том, какие дети относятся к той или иной целевой группе (DD, расстройства, связанные с обучением математике и т. д.). Методологические подходы различаются по терминологии «момента отсекания» для классификационных критериев (в диапазоне от <10 до < 35 процентилей), при том что указанные процентили отражают лишь стандартизированные или единично-выборочные рейтинги или же девиации, полученные на уровне популяции и величин SD.
Более того, когда в исследованиях используются различные подходы, к ним привлекаются очень разнородные выборки, и таким образом могут контролироваться различные фоновые характеристики. В них могут быть включены даже дети с генерализованными когнитивными дефицитами, если значительное расхождение между усредненными интеллектуальными способностями и субсредними навыками в математике не заявлены в качестве определительного критерия (как указано в действующем документе «Diagnostic and Statistical Manual of Mental Disorders (DSM)» (Ehlert et al., 2012)).
Еще один ведущий тренд с высоким риском интерпретации — действенная дифференциальная диагностическая классификация в исследованиях, посвященных DD. В то время как ряд исследований используют дискретные числовые технологии (например, отмечаемые точками или пунктиром перечисления), другие исследования используют стандартизированные математические тесты, которые могут включать логические рассуждения или тексты, требующие осмысления.
В совокупности эти предостережения отражают общую тенденцию, когда современные инновационные исследования «натыкаются» на отсутствие единого терминологического, классификационного и методологического инструментария, а явно противоречащие друг другу умозаключения относительно того, включаются ли в структуру DD дефициты базовых или более общих (системных) способностей работать с числами, могут возникать в результате использования разных классификационных задач в разных исследованиях. Противоречивые наблюдения могут также отражать различия в исследуемых выборках детей, которые заведомо все отнесены к имеющим DD.
Резюмируя свои позиции, авторы предлагают вооружить специалистов понятиями первичной и вторичной дискалькулии.
Первичная DD представляет собой гетерогенное расстройство, возникающее вследствие индивидуального дефицита числового или арифметического функционирования на поведенческом, когнитивном/ней- ропсихологическом и нейронном уровнях.
Термин Вторичная DD может быть использован, если числовые/арифметические дисфункции полностью вызваны нечисловыми повреждающими факторами (например, расстройством внимания).
В докладе Pekka Rasanen (университет Ювяскюля) были очерчены серьезные методологические проблемы, мешающие прийти к единому определению феномена DD (всего шесть).
В нем прозвучало, что применительно к проблеме DD все еще нет универсальных инструментов скрининга или ратификации так называемых «основных дефицитов» («core deficits»), вследствие чего исследователи работают в определенном диапазоне инструментального обеспечения. Эти оценочные инструменты (технологии) часто варьируют даже в рамках одного конструкта (такого как «вычисление» или «сравнение величин») и при проведении стандартизированных тестов, а оценочные нормативы отличаются от страны к стране. Такая фрагментация исследовательского пространства приводит к проблемам сопоставимости результатов одного исследования с другими. Исследования, воспроизводящие предыдущие наблюдения и использующие тот же самый набор оценочных методов и технологий, являются редкими исключениями.
Может создаться впечатление, что возрастающее количество вмешательств с использованием технологии компьютерных программ вмешательства (computer- assisted intervention CAI) могло бы изменить ситуацию. К сожалению, это не тот случай. Исследователи склонны вводить в свою экспериментальную работу новые продвинутые инструменты и не используют старые идеи и технологии возрастом всего несколько лет. Новый исследовательский проект от плана до публикации длится несколько лет. Так что прикладной инструментарий, запланированный в начале проекта, к концу его технически устаревает, и начинается новый цикл усовершенствования проектов, что ведет к фрагментации исследовательского пространства.
Авторами доклада представлен сравнительно новый аспект проблемы — фенотипические и генотипические факторы развития дискалькулии. Они полагают, что многие дети, не испытывая трудностей с обучением, плохо успевают по математике. Термин «онтогенетическая дискалькулия» не охватывает все формы математических трудностей, встречающихся в детском возрасте. Некоторые дети фенотипически проявляют признаки DD в некоторых точках жизненного цикла, но их трудности не имеют отношения к генотипу DD; это явление более общего характера, встречающееся среди детей с неадекватной домашней или школьной обучающей средой, связанной с бедностью. Это хорошо показано в аналитических межнациональных обзорах. Внутри одной страны и между странами разрыв большой, калькуляционные навыки у детей варьируют от одной страны к другой. Поэтому математические навыки в категории наиболее низких показателей (10— 15%) в различных странах на самом деле отражают различия в фенотипах. Трудно разделить факторы образовательной и домашней жизненной среды, дифференцируя фенотипические и генотипические факторы.
Дополнительно к этому ученые отмечают отсутствие единой терминологии. Например, расстройство, связанное с необучаемостью математике (MLD), используется как синоним DD, но в то же время используется как отличное от DD. Особое внимание к MLD понятно, если принять во внимание, что все такие дети нуждаются в том, чтобы их проблему изучали и система образования учитывала их особенности. Однако не все такие дети имеют серьезные специфичные расстройства, связанные с математикой, которые относятся к DD.
В литературе по дискалькулии довольно четко обозначены перспективы исследований в данной области. Например, указывается необходимость раннего «воспитания» рабочей памяти (Maria Chiara Passolunghi, университет Триест); причем этому автору удалось экспериментально показать, что группа, получившая целевое обучение, направленное на рабочую память, проявила одновременно значительное улучшение и в функциональных способностях рабочей памяти, и в ранних способностях к работе с числами (к умению считать).
Кроме того, были представлены пилотные стратегии интервенции для детей с трудностями обучения математике (Pirjo Aunio & Anna Tapola, университет Хельсинки). Эти авторы рассказали о своем опыте создания специализированного образовательного портала ThinkMath-webservice.
Главная цель проекта ThinkMath-webservice состоит в том, чтобы разработать обучающие материалы для специалистов системы образования по поддержанию мышления и математических навыков. Материал предназначен для воспитанников детских садов, учащихся первого и второго года обучения в школе (средний возраст 5—8 лет) со слабо развитым мышлением или математическими навыками. Целью также было дать специалистам образования знание о теоретических основах мышления и математических навыков, исполнительных функций, мотивации, коррекционного воздействия.
Материалы вмешательства были подобраны на основании исследования, показавшего, что точное и подробное (эксплицитное) обучение на конкретно- представленном абстрактном уровне (concrete- representational-abstract levels-CRA) и структурирование чисел (например, десятичная система) — это адекватные инструменты поддержания образовательного процесса в группе слабо успевающих.
Авторы подчеркивают, что им удалось выделить четыре фактора, определяющие базовые математические способности в возрастной группе 5—8 лет. Эти четыре фактора: невербальное и символическое арифметическое мышление; знание чисел; базовые навыки счета и арифметики и понимание математических взаимосвязей.
Для большинства детей приобретение этих базовых навыков не составляет проблемы и проходит без чрезмерных усилий. Детям необходим каждый из перечисленных навыков для того, чтобы они могли учиться и понимать то, что говорит им педагог на школьных уроках математики.
Если обобщить данные зарубежных исследований дискалькулии у детей дошкольного и младшего школьного возраста за последние два десятилетия, то совершенно четко прослеживаются следующие позитивные тенденции:
• становление научно-практического знания: постоянное обогащение ведущих концепций, расширение спектра образовательных продуктов (простых и сложных) применительно к трудностям обучения математике (арифметике) — от гомогенности к гетерогенности проблемы; от визуальных краткосрочных и локальных исследований к лонгитюдам с участием разных образовательных учреждений и высокотехнологичным сопровождением; от школьного возраста к дошкольному и т. д.;
• участие зарубежной высшей школы в разработке образовательных программ и обучающих продуктов;
• зарубежные научные и научно-практические исследования разных авторов не воспроизводят друг друга, но, по сути, все являются самостоятельными, независимыми и инновационными, привносящими новое знание в понимание проблемы;
• трансляция научного знания в международное междисциплинарное наукометрическое пространство, в структуру которого входят разработчики образовательных технологий, психологи системы образования, педагоги, социологи, экономисты и иные специалисты;
• создание профессионального международного сообщества дефектологов и всех специалистов, работающих с детьми, имеющими трудности в обучении математике (арифметике) и чтению, т. е. имеющими первичную дискалькулию;
• фиксация отсроченного эффекта дискалькулии детского возраста на последующие годы школьного обучения, социализацию, приобретение профессии и реализацию в жизни;
• признание проблемы дискалькулии среди детей как недооцененной.
Опыт проведения долгосрочного лонгитюдного исследования сочетанной дискалькулии и дислексии при смене образовательной среды
Изучая проблемы усвоения математики и формирования навыков чтения, David C. Geary, Mary K. Hoard, Lara Nugent and Drew H. Bailey (Университет Миссури, штат Колумбия, США) рассмотрели возможности компенсации математического когнитивного дефицита у детей старшего дошкольного возраста и с первого по пятый год обучения в школе. В их лонгитюдном исследовании (Journal of Educational Psychology, 2012) [Mathematical Cognition Deficits, 2012] участвовали три группы обучающихся: дети, страдающие расстройствами, связанными с трудностями обучения математике (mathematical learning disability MLD, n=16), дети с общей устойчивой малой эффективностью обучения (persistent low achievement LA, n=29) и дети с обычной успеваемостью (typical achievement ТА, n=132) — контрольная группа.
Обосновывая актуальность проведенного ими исследования, авторы высказали мнение, что «... индивиды, не владеющие базовыми математическими компетенциями на момент окончания средней школы, будут лишены благоприятных условий при адаптации на рынке рабочей силы XXI века и окажутся ущербными в своей способности осуществлять многие действия, составляющие ежедневную рутинную жизненную среду».
Статистические данные о числовой неграмотности взрослого населения свидетельствуют, что к MLD могут быть отнесены в среднем 7% учащихся (4%—14% в зависимости от метода классификации), и еще 10% учащихся могут быть отнесены к имеющим умеренно выраженные, но постоянные трудности обучения и в будущем оказываются слабо успевающими (LA). В пересчете на процентили дети с MLD составляют ниже 10 процентилей на большей части ступеней обучения, тогда как дети с LA обычно занимают от 11 до 25 процентилей в популяции.
Учитывая предшествующий опыт и методологические недостатки предыдущих исследований, авторы поставили основной целью своего исследования составление карты стартовых позиций учащихся и построение 5-ти летних траекторий развития ключевых числовых и арифметических компетенций у детей с MLD и их сверстников с LA в сравнении с контрольной группой ТА. Вторая цель состояла в том, чтобы определить, в какой степени эти компетенции и их формирование связаны с различиями в математических достижениях на момент поступления в школу и в течение пяти лет школьного обучения.
Начиная со второго года обучения, авторы оценивали интеллект испытуемых (уровень развития понятийного аппарата), их рабочую память, скорость обработки информации, внимание на уроке, а также проводили тестирование их математических способностей. На момент поступления в школу ученикам в группе MLD были свойственны низкий уровень достижений в математике и низкий уровень овладения чтением. Первый из уровней характеризовался низкой беглостью обработки информации или оперирования количественными категориями, что могло быть связано с малыми объемами знакомых им чисел и соответствующих арабских цифр, тогда как второму была свойственна низкая автоматизация называния (перечисления) букв и цифр.
Группы MLD и LA продемонстрировали слабую успеваемость по математике при переходе с одной ступени обучения на другую. Дифференциация групп по признаку повышения успеваемости была определена по критериям скорости обработки числовой информации, наличия или отсутствия способности извлекать базовые данные из долговременной памяти и анализировать числовую информацию при решении задач, а также с учетом ключевых исполнительных структур рабочей памяти и способности сосредоточиваться на занятиях в классе.
Для того, чтобы определить конкретные числовые и арифметические дефициты при анализе групповых различий в усвоении математики, необходимо было выяснить, одинаковые или разные факторы отвечают за овладение навыками работы с буквой/словом и регулируют вклад общих когнитивных способностей в обучаемость по многим, если не по всем, учебным дисциплинам. Кроме того, в ходе эксперимента педагоги контролировали внимание (сосредоточенность) учащихся на уроке.
Авторы считают, что полученные ими данные способствуют пониманию основных причин трудностей в обучении математике: «Это исследование — одно из немногих, где сведены воедино многолетние оценки числовых и арифметических когнитивных особенностей, общего состояния когнитивной сферы и внимания на уроках с тем, чтобы выделить дефициты, специфичные для слабо успевающих по математике учеников».
Проведя анализ литературных источников по данной тематике, они отмечают, что, несмотря на значимость влияния интеллекта (понятливости), рабочей памяти, скорости обработки информации на успеваемость по математике и развитие математических способностей, в большинстве работ эти факторы (параметры) никогда не изучались в совокупности. В тех же исследованиях, где рассматривались три указанные способности, они не изучались в возрастной динамике и в течение длительного промежутка времени.
Для четкой дифференциации MLD- и LA-групп испытуемых авторы использовали ряд методик, таких как создание кластеров и построение кривых роста применительно к оценке математических достижений. Результаты, однако, показали, что ключевая «математическая стартовая точка» и переменные роста имеют единое распределение, т. е. группы MLA и LA не выделись как самостоятельные фракции (подгруппы).
Эти результаты концептуально важны, поскольку означают, что показатели детей с MLD и их ровесников с LA являются частью нормального распределения математических компетенций, но с различными точками разделения (D.C. Geary, M.K. Hoard, D.H. Bailey, 2012).
Знание о том, что дети с MLD и LA в литературе отнесены к нижним границам простого нормального распределения, бесполезно при разработке приемлемых критериев для специальных образовательных программ и соответствующих коррекционных мероприятий, также оно бессмысленно и для обобщения данных. Поэтому к эксперименту были привлечены гомогенные выборки MLD и LA, которые позволили провести такое обобщение и разработать методики для образовательных учреждений.
К участию в эксперименте были привлечены выпускники детских садов из 12-ти начальных школ, воспитывавшихся в семьях с разным социоэкономиче- ским статусом.
Математический учебный план на тот момент, когда дети начинали школьное обучение, был представлен разработкой Investigations in Number, Data, and Space (Russell, S. J., Tierney, C., Mokros, J. 1999).
В качестве инструментов авторы использовали методики определения вербального и невербального IQ, а также полномасштабную шкалу IQ в соответствии с национальными нормативами.
Чтобы идентифицировать группы MLD и LA, была проанализирована динамика математической успеваемости у испытуемых (от детсадовцев до учащихся, окончивших пятую ступень обучения) с использованием модельной кластеризации (Mclust).
Чтобы оценить стартовые позиции и переменные для описания роста навыков, использовалась модель свободной кривой с угловыми коэффициентами (имеется в виду, что свободная кривая состоит из сегментов, на которых можно определить контрольные точки. — Ред.), в версии Mplus Version 5.21 (Muthe'n, L.K., & Muthe'n, B.O., 1998—2007). Эта модель оценивает некое промежуточное положение кривой, которое может быть интерпретировано как уровень достижений каждого участника эксперимента, независимо от траектории роста, в точке, где уровень и траектория наиболее близки к ортогональному взаимному расположению.
Стандартизированные измерения, проведенные авторами
Интеллект. Для оценки интеллекта использовались цветные прогрессивные матрицы Равена (Raven’s Coloured Progressive Matrices, далее — CPM), признанные отличным инструментом оценки подвижного интеллекта (fluid intelligence), и сокращенная шкала интеллекта Векслера (Wechsler Abbreviated Scale of Intelligence, далее — WASI), раздел с субтестами на словарный запас и абстрактное мышление (Vocabulary and Matrix Reasoning). Оценки по CPM были стандартизированными, полученными на выборке из 287 детей, прошедших тест (M =100, SD = 15), и соответственно стандартизированными были оценки по WASI. Субтест на словарный запас был использован как оценочный критерий вербального IQ, а значения CPM и тест на абстрактное мышление были использованы как тесты на невербальный IQ.
Успеваемость (достижения). Успеваемость в математике и чтении были оценены по результатам субтестов «Числовые операции» и «Чтение слов» (Numerical Operations and Word Reading subtests), из теста Индивидуальных Достижений Векслера (Тест-II — сокращенный — Wechsler Individual Achievement Test- II: Abbreviated). «Более легкие тесты по математике (Numerical Operations — числовые операции) ориентированы на оценку распознавания чисел и цифр, механического запоминания, продуцирования чисел, знания основ сложения и вычитания. Более трудные задания включали в себя мультизначимые операции сложения и вычитания, умножение и деление, решение задач с рациональными числами с карандашом на бумаге. Более легкие тесты на чтение слов (Word Reading) требуют навыков сопоставления и идентификации букв, рифм, начала и конца слов и фонемных “сочетаний”. Более трудные задания позволяют оценить точность чтения постепенно усложняющихся слов».
Используемые в исследовании математические задания
Выбор стратегии сложения. В центре экрана монитора компьютера по горизонтали одновременно располагали четырнадцать простых заданий на сложение и шесть более сложных заданий. В простых заданиях применялись числа от 2 до 9 с ограничением, не позволяющим использовать в одной задаче одинаковые целые числа (например, 2 + 2). /2 часть задач была на сложение до 10 и менее, при этом меньшее по величине слагаемое стояло на первом месте в половине задач. Сложными задачами считались 16 + 7, 3 + 18, 9 + 15, 17 + 4, 6 + 19 и 14 + 8.
Детей просили решить каждую задачу (без карандаша и бумаги) так быстро, как это возможно, и без большого количества ошибок. Ребенок сам мог выбрать стратегию решения задачи, ответ он должен был произнести вслух в микрофон с целью фиксирования времени реакции (response time — RT), требующегося для формулировки и произнесения ответа. Также от испытуемых требовалось описать процедуру получения суммы. В результате пробных испытаний были выделены самые распространенные стратегии решения задач: пальцевый счет, устный счет, извлечение и разложение. Вычислительные пробы были затем классифицированы как минимальные, суммарные, максимальные (min, sum, max). Следует отметить, что при пальцевом счете время реакции было наиболее продолжительным, затем в ряду по убыванию располагаются устный счет, разложение, прямое извлечение.
В ходе тестирования для формирования представлений о детских компетенциях в решении задач на сложение были выделены четыре переменных — две для простых задач и две для более сложных.
Первая из переменных давала представление о степени использования процессов обработки информации, связанных с памятью, при решении задач. При корректном использовании стратегий, связанных с памятью, дети непосредственно (напрямую) извлекали (из ресурсов памяти. — Ред.) ответ, затрачивая на это 62% времени реакции, и пользовались разложением, затрачивая на него 38% этого же времени. Основной стратегией, относящейся к памяти, для решения сложных задач, являлось разложение, тогда как прямое извлечение использовалось редко.
Вторая переменная, характеризующая операционную компетенцию, была закодирована таким образом, что по высоким баллам можно было судить о частоте и точности пользования min-процедурой.
Для детей, пользовавшихся вычислениями только при решении задач на подмножество, баллы были установлены, исходя из процентной доли выполненных заданий. Максимальные баллы составили соответственно 28 и 12 для простых и сложных операций сложения.
Числовые наборы. Участникам эксперимента были предложены стимульные материалы в виде домино, на полудюймовых квадратах которых были изображены предметы (например, звездочки) и арабские цифры (18-м кеглем), представленные в различных комбинациях. Эти домино располагались на листе рядами по пять штук в каждом. Последние два ряда занимали три прямоугольника- домино втрое большей площади. Заданные изначально суммы (5 или 9) были показаны крупным шрифтом в верхней части листа. На каждом листе цели соответствовали 18 объектам; из них 12 имели большее значение, чем заданная сумма, 6 — меньше, и 6 содержало 0 или пустую картинку на квадрате размером в полдюйма.
Испытатель начинает с объяснения двух заданий, в которых нужно получить заданную сумму 4, и затем использует заданную сумму 3 для примера. Проводится тест. Ребенку предлагается двигаться по каждой линии на листе слева направо без пропусков; «выделить (очертить) какие-либо группы, которые можно объединить с тем, чтобы получилось число, обозначенное наверху листа, — «5 (9)» и сделать это так быстро, как только возможно, без большого количества ошибок». Ребенку давалось 60 секунд на достижение цели «5» и 90 секунд — на достижение цели «9». Ограничения по времени были установлены, чтобы избежать «потолочных эффектов» (максимальных показателей) и чтобы оценить беглость распознавания и манипуляции с количествами.
По результатам анализа полученных данных было показано наличие групповых различий уже в начале первого года обучения. Дети групп MLD и LA демонстрировали некоторый прорыв до уровня своих ТА-сверстников в период с первого по второй год обучения, но после этой точки рост в группах был практически параллельным (рис. 2, диаграмма А).
Значение промежуточного показателя представляет собой оценку в баллах детей контрольной ТА-группы первого года обучения, а аналогичный показатель MLD и LA отражает различия в промежуточных показателях этих групп с ТА (ps = 0,0001, d = 2,21, 0,88 соответственно, для баллов первого года обучения). Переменные линейного наклона позволяют оценить усредненные линейные изменения на разных ступенях обучения в группе ТА, тогда как квадратическая переменная градиента оценивает ускорение или замедление скорости изменений в процессе образовательного школьного процесса.
Положительный линейный наклон MLD и LA-эффектов означает, что средняя скорость изменений для этих групп была выше, чем у детей контрольной ТА-группы, но отрицательный квадратичный контраст показывает, что скорость наверстывания снижалась по мере перехода с одной ступени обучения на другую. В самом деле, изучение графика (рис. 2, диаграмма А) свидетельствует о том, что большинство наверстываний имеет место между первым и вторым годом обучения, а смешанная модель, включающая только интервал обучения от 2 до 5 года, демонстрирует отсутствие сколько-нибудь значительного линейного или квадратического наклона (градиента) эффектов MLD и LA (ps = 0,15). Контрастность групп MLD и LA подтверждает существенную разницу промежуточных показателей (p = 0,0005), но линейный и квадратичный градиент применительно к эффекту для MLD не был значительным (ps = 0,25), а это означает, что изменения в этих группах шли параллельно по мере обучения в школе.
Работа с числовой линией

|
Детям были предъявлены серии из 24-х 25-сантиметровых числовых линий, содержащих пустую строку с двумя конечными точками (0 и 100) с заданными числами (например, 45), изображенными крупным шрифтом над линией. Задачей ребенка было выделить строку, где могло бы находиться заданное число. На первом году обучения разрешалось пользоваться карандашом и бумагой, в компьютерной версии ребенок отмечал нужную линию мышкой. Чтобы сделать выводы о том, как дети решают задачи размещения, использовался принцип медианных групповых размещений с использованием линейных и логарифмических моделей; для индивидуального дифференциального анализа использовался критерий точности.
Групповые различия были очевидны в начале первого года обучения, но разрыв между группами ТА и LA стал сглаживаться к концу пятого года обучения. Величина разрыва между группами ТА и MLD уменьшалась примерно на треть по мере обучения, но все равно оставалась значительной к концу пятого года обучения (см. рис. 1, диаграмма В). В первый год обучения группа ТА делала меньше ошибок, чем группа MLD (d = 1,55) и LA (d = 0,92), но значительный линейный градиент эффектов MLD и LA указывает на наверстывание на последующих этапах.
Сравнение попарных значений (действительно значимый тест на различия) показало, что преимущество детей группы ТА над группой LA было значительным в первый год обучения (d = 0,97) и вплоть до конца четвертого года (d = 0,60) (ps = 0,05), но не пятого (p = 0,05). Дети группы ТА проявляли существенные преимущества перед своими сверстниками группы MLD в течение всех лет обучения (ps = 0,05), но разрыв уменьшался по величине с первого (d = 1,55) по пятый (d = = 0,97) год. По контрасту, постоянный разрыв между группами MLD и LA был заметен с первого (d = 0,59) по пятый (d = 0,78) год обучения.
Для оценки рабочей памяти и скорости обработки информации использовалась батарея тестов The Working Memory Test Battery for Children (WMTB-C), состоящая из 9 субтестов, позволяющих оценить центральные исполнительные нейронные структуры, фонологическую петлю, зрительно-пространственную «записную книжку».
Нейронные механизмы центральных исполнительных структур мозга оценивались тремя «двузадачными» субтестами. При прослушивании записей текстов (Test Recall) ребенок должен был определить, является ли звучащее высказывание истинным или ложным и повторить последнее слово в этой серии воспринятых на слух предложений. Тест Counting Recall (на припоминание итогов счета) предлагал ребенку подсчитать точки на карточке (4, 5, 6 или 7) и затем назвать общее количество подсчитанных точек в конце серии таких карточек. Еще один тест Backward Digit Recall предлагал ребенку совершить операции подсчета в обратном порядке.
Фонологическая петля. Тесты Digit Recall, Word List Recall и Nonword List Recall представляют собой стандартные диапазонные задачи с различными числовыми раздражителями (стимулами); задача ребенка состояла в повторении вслед за исследователем произносимых им слов, в том же порядке. В задаче Word List Matching ребенку предлагались наборы слов, начинающиеся с двух слов и продолжающиеся добавлением по одному слову при каждом успешном выполнении предыдущего упражнения. Одинаковые слова, но, возможно, в другом порядке, повторялись затем вновь, и задачей ребенка было определить, отличается ли второй вариант порядка слов от первого или нет.
Зрительно-пространственная «записная книжка». В задании Block Recall раздражитель (стимульный материал) представляет собой доску с девятью рельефными кубиками «случайного» расположения. Кубики пронумерованы на одной стороне, которую (только ее) экспериментатор не может видеть со своего места. Экспериментатор смешивает кубики (перемещая один или несколько), и задача ребенка состоит в том, чтобы разложить кубики в том же порядке, в каком их изначально предложил экспериментатор (восстановить порядок). В задании Mazes Memory ребенку предлагается лабиринт с более чем одним решением и картинка идентичного лабиринта, на которой указан путь к одному решению (выходу). Картинку убирают, и задача ребенка в том, чтобы продублировать этот путь на своем игровом поле. На каждом уровне лабиринты все более усложняются на одну стену.
Скорость обработки информации. Две задачи на быстрое автоматическое называние (rapid automatized naming, далее — RAN) позволили оценить скорость обработки информации.
Смешанные модели показали, что группа ТА характеризуется более низкими показателями (более быстрым стартом RT по сравнению с MLD и LA), но линейные и квадратические наклон-эффекты на MLD были более существенными (ps < 0,0001) и отражали наверстывание по мере обучения. Был выявлен тренд линейного наклона (градиента) с LA-эффектом (p = 0,07), также указывающим на наверстывание. Сопоставление групп LA—MLD выявило существенное преимущество в промежуточных показателях группы MLD и существенный линейный и квадратичный градиент MLD-эффекта (ps < 0,001); преимущество группы LA исчезало по мере обучения. Попарное сравнение значений выявило отсутствие различий групп LA—TA за весь период наблюдений (ps > 0,05); группа ТА имела преимущество над MLD в первый (d = 1,88), второй (d = 1,0) и четвертый (d = 0,73) годы обучения.
Исходя из потенциальной дефицитарности обработки числовой информации у детей с MLD и их LA сверстниками, был проведен повторный репликаторный анализ переменных с типом объекта (числом или буквой) и годом обучения как внутриобъектными факторами и группой, так и межсубъектными факторами. Групповые различия в скорости обработки информации были сопоставимы, но факторные взаимодействия объект-группа (р > 0,50) и год—группа (р >0,50) были незначительными; это означает, что групповые различия в скорости обработки информации были неспецифичны для чисел.
Для оценки внимания в классе использовался инструмент The Strength and Weaknesses of ADHD-Symptoms and Normal-Behavior (SWAN). Предполагалось, что выполняемые в его контексте задачи помогают оценить остроту дефицита внимания и гиперактивности, а полученные показатели будут иметь нормальное распределение и соответствовать поведению обычного ребенка в классе.
В процессе анализа результатов SWAN F (2,174) = = 30,67, p < 0,0001) выявлено, что групповые различия были существенными. Группа ТА (M = 5.20, SD = 1.02) отличалась более высокими баллами по сравнению с группами MLD (M = 3,43, SD = 0,79, d = 1,96) и LA (M = 4,07, SD = 1.03, d = 1,01).
Основные результаты исследования
Полученные результаты позволяют сделать вывод, что низкий старт и медленный рост показателей были вызваны некоторыми специфичными дефицитами математической когнитивности, относящимися к разряду дефицита управления (регулирования).
Было подтверждено, что дети с MLD, как правило, отличаются слабыми навыками чтения. В литературе есть указания на то, что низкий уровень их навыков чтения на момент поступления в школу определяется иным механизмом (скоростью извлечения букв и цифр из долговременной памяти) отличающимся от механизма, ответственного за низкие успехи в математике. Слабо успевающие дети часто имеют преимущество в интеллекте и способности к чтению, но, тем не менее, неизменно низкие баллы — ниже 25-го процентиля — по тестам на достижения в математике.
Следует подчеркнуть, что выборка детей с LA, представленная в исследовании, характеризовалась типичным (нормальным) уровнем подготовки по математике на момент поступления в школу, но в процессе обучения рост их достижений шел параллельно детям с MLD, не превышая его. Отмечено, что дети с риском MLD относятся к нижней квартили базовых количественных компетенций в детском саду, но, в то же время, идентификация детей с LA по росту компетенций по математике в первые два года обучения в школе требует дополнительных документированных данных и анализа.
У детей с LA в период с третьего по пятый год обучения укрепление способности решать простые задачи прямым извлечением зависит от надежности извлечения из памяти при использовании обеих стратегий. Установлено, что компетенции извлечения у детей с MLD укрепляются медленно и не происходит параллельного улучшения в выполнении операций разложения. Предположительно, дети с MLD могут не иметь сформированного концептуального представления о том, как разложить число и решить тем самым задачу.
Авторы акцентируют внимание будущих исследователей проблемы детской дискалькулии на том, насколько важно в этом возрасте возможно более раннее формирование понятия number sense, о чем неоднократно упоминалось в данной статье.
Применительно к этому аспекту, авторы указывают на важность формирования таких числовых компетенций, как скорость и точность оценки количеств в небольших по объему числовых комбинациях, для чего необходимо, в свою очередь, знать арабские цифры. Более того, анализ литературных данных показал, что способность отобразить арабские цифры/числа в соответствующих количественных категориях может быть критичным навыком (Rousselle and Noel, 2007). Вместе с тем, само понятие number sense сегодня еще не может быть полностью оценено и понято.
Другое важное мнение авторов состоит в том, что: 1) ранние математические способности важны на уровне не только предметном (арифметическом), но и гораздо более высоком, связанном с развитием «генерализованных способностей к обучению как таковому», и 2) они автономны по отношению к способностям ребенка обучаться чтению.
Как видно из материала статьи, вопрос о приоритетности навыков чтения и счета остается дискуссионным.
Таким образом, мы видим, что за рубежом исследовательская и концептуальная составляющие проблемы дискалькулии учащихся продолжают развиваться и совершенствоваться.
Отечественный опыт исследования проблемы дискалькулии
В имеющихся на сегодняшний день немногочисленных аналитических обзорах по проблеме дискаль- кулии у учащихся появление отечественных концепций дискалькулии относится в среднем к тому же периоду, что и в зарубежной литературе, т. е. к 2004— 2009 гг. [Берестенко, 2016].
Можно выделить основные тренды исследования проблемы дискалькулии — это создание научных концепций, классификация и профилактика в образовательной среде.
При этом, как указано в обнаруженных нами публикациях, отечественная научная школа дискалькулии насчитывает три основных концепции. В первой (авторы А. Гермаковская, С. Мнухин, Р. Лалаева) ведущими механизмами дискалькулии считаются нарушения гностико-праксических функций; во второй (авторы С. Мнухин, Г. Капустина) нарушения вычислительных компетенций связываются с незрелостью операций синтеза и обобщения и высокой психической истоща- емостью и инертностью; в третьей (авторы Ю. Демьянов, А. Гермаковска, Р. Лалаева) формирование навыков счета и проведения вычислительных операций связываются с несформированностью фонематических функций, системными нарушениями речи, недоразвитием лексической и грамматической сторон речи, а также нарушениями чтения и письма.
Иными словами, ведущими трендами стали изначальная взаимосвязанность речевых и счетных психологических и психических нарушений, т. е. нарушения речи были признаны ведущим симптомом трудностей обучения счету.
В своем теоретическом обзоре 2011 года по проблеме детской дискалькулии А. Грибанов и Н. Рысина (Поморский государственный университет) постулируют, что у детей с дискалькулией на первый план выходят проблемы «...недостаточной сформированности аналитического и мотивационного компонента когнитивного поведения, что может приводить к принятию неадекватной стратегии деятельности и малой вариативности поведенческого реагирования» [Рысина, 2011]. То есть особенности когнитивной сферы и поведения у детей с дискалькулией можно описать как отсутствие быстрого и адекватного реагирования на условия среды, что согласуется с позициями зарубежных исследователей, изложенными выше.
Эти авторы сопоставляют дискалькулию, грубые нарушения логического математического мышления и способности к выполнению основных мыслительных операций, дефицитарность памяти и пространственное восприятие. Развитие памяти и ее объем, возможность понимать речь и действенно ее использовать рассматриваются авторами как основы формирования и развития математических компетенций. Иными словами, дис- калькулия, по мнению отечественных авторов, вторична по отношению к речевым расстройствам, которые приоритетны для профилактики и оптимизации.
Детально рассматривая литературный материал о значении функций зрения и слуха для формирования математических навыков, они пишут: «В развитии математических понятий важную роль играет функция контроля глазных мышц_ <...> при ослабленном контроле глазных мышц, у детей плохо развиваются навыки чтения, усвоение порядка чисел в числовом ряду, им трудно расшифровывать математические формулы. Неспособность к различению звуков препятствует формированию представлений о числах и особо сказывается при овладении устным счетом. При овладении понятием натурального числа и математическими действиями значительную роль выполняют зрительный и слуховой симультанный анализ и синтез» [Murphy, 2009].
В своем научно-практическом исследовании эти авторы (Н. Рысина и А. Грибанов) [Грибанов, 2011] изучили особенности поведенческого реагирования детей с дискалькулией в различных условиях среды. В эксперименте лонгитюдного характера (6 месяцев) участвовали дети 8—9 лет, учащиеся начальных классов. Изучалось поведенческое реагирование в стохастической, вероятностной и детерминированной средах с помощью тестовой компьютерной системы «Бинатест-К», в смоделированной игровой ситуации для возрастного диапазона 6—15 лет.
Исследование проводилось в трех режимах: «Свободный выбор», «Управляемый выбор», «Вероятностный выбор».
Оказалось, что «.нейродинамика организации новой функциональной системы у детей с дискальку- лией протекает медленнее. Замедленные или слабо выраженные операции процесса обработки информации могут расцениваться как проявления нарушений в области восприятия, что, в свою очередь, увеличивает время поисковой активности и время выбора ответа у детей с трудностями по математике. В режиме “Вероятностный выбор” наиболее явно и значимо проявилось ускорение реакции выбора у детей с дискаль- кулией по сравнению с детьми контрольной группы и в сравнении с их же временем реакции в режиме «Свободный выбор». По данным нашего исследования, в этой группе детей значимо чаще отмечены проявления импульсивности и значимо ниже показатели по уровню развития операций мышления по сравнению с детьми контрольной группы, что также может значительно затруднять адекватный анализ ситуации и принятие верного решения».
По результатам исследования, авторы предложили режим «Управляемый выбор» в качестве экспресс- метода выявления трудностей в обучении и поведенческих рисков.
Далее, в отечественной литературе встречается классификация дискалькулии на врожденную и приобретенную (С. Мнухин), первичную и вторичную (Л. Цветкова); признается также имеющей право на существование классификация на вербальную, прак- тогностическую, дислексическую, графическую, операциональную, по данным зарубежных источников.
Ближе к концу 2000-х гг. (О. Степкова, 2008 г., Российский государственный педагогический университет имени А.И. Герцена) были определены основные направления профилактики дискалькулии у детей: формирование сенсомоторных функций; формирование логических операций; формирование сукцессив- ных и симультанных процессов; формирование количественных представлений; формирование речевых предпосылок овладения математическими знаниями, умениями и навыками.
В 2009 г. Л. Томме (Омский государственный педагогический университет) впервые предложила прогностическую симптоматику недостаточной готовности к обучению математике. Ею было доказано, что полноценность усвоения математического материала детьми с нарушениями речи определяется степенью развития деятельностного, речевого и когнитивного компонентов. Были разработаны содержание и методы системной коррекционной работы по формированию готовности к обучению математике и предложена трехэтапная программа изучения перечисленных компонентов (первый этап — оценка состояния когнитивных и деятельностных предпосылок усвоения математики; второй этап — оценка математических представлений и третий этап — оценка речевой готовности детей к изучению математики) [Томме, 2008].
Анализ недавних отечественных научных и научнопрактических публикаций по проблеме (случайная выборка, по данным e-library.ru) показал, что практически всегда исследование дискалькулии проводится среди детей, имеющих нарушения речи разной степени и/или ограниченные возможности здоровья, связанные с поражением нервной системы.
Следует отметить, что в зарубежных работах, приведенных в нашем обзоре, такой четкой привязки именно к конкретным речевым нарушениям и нарушениям функций центральной нервной системы не просматривается, и внимание уделяется самой дискалькулии как явлению, независимо от фоновых нарушений.
Можно также предположить, что для отечественных разработок по дискалькулии характерна скорее более выраженная детализация профилактики и оптимизации различных видов дискалькулии, нежели концептуальные аспекты проблемы дискалькулии как таковой.
В этом ряду выделяется ряд публикаций в отечественных психологических журналах С. Кондратьевой (Российский государственный педагогический университет, Санкт-Петербург), отличающихся концептуальной обоснованностью, глубиной разработки, прикладным характером и острой актуальностью.
Так, одна из работ С. Кондратьевой посвящена самостоятельному виду дискалькулии — графической дискаль- кулии [Кондратьева, 2016а], для которой характерны затруднения «...в усвоении зрительных образов геометрических фигур, математических знаков и цифр, многие из которых кажутся детям дошкольного возраста похожими». Данные трудности связаны с несформированностью зрительно-пространственных представлений, что проявляется несостоятельностью в сравнении длины предметов и оценке их пространственного соотношения. Таким детям трудно усвоить понятия «вверху» и «внизу», «справа» и «слева» и запомнить правила написания математических знаков, символов и воспроизведения геометрических фигур. В речи таких детей отсутствуют предлоги и наречия, описывающие пространственные соотношения предметов и образов. Они неспособны к трехмерному конструированию и рисованию в перспективе.
Автор выделила факторы риска предрасположенности к графической дискалькулии: нарушение ручной моторики; замедленность в формировании зрительнодвигательной координации, аналитико-синтетической деятельности, пространственного восприятия, зрительной памяти; несформированность представлений о форме, величине, математической символике.
С. Кондратьева предложила детально проработанную систему мер по формированию измерительных компетенций в детском саду, куда вошли «.формирование пространственных представлений, развитие глазомера, восприятия величины. Обучение измерению начинается с использования условных мерок, что делает измерение доступным для маленьких детей. В бытовой деятельности педагог учит детей измерять длину комнаты большими и маленькими шагами; количество крупы стаканами, ложками; воду банкой, кружкой». Программа ориентирована также на формирование письменной речи (умение записывать математические символы, решать примеры). Автор подчеркивает в своей методической разработке, что «.для овладения механизмом письма ребенку необходимо сделать основное открытие — рисовать можно не только вещи, но и речь, т. е. буквы, цифры, знаки, фигуры». То есть, математические умения оказываются вторичными по отношению к навыкам письма (что мы и наблюдаем на практике).
Этот автор проводит исследования по выявлению и профилактике вербальной дискалькулии у детей, имеющих тяжелые нарушения речи (ТНР) [Кондратьева, 2016]. В этой публикации автор излагает разработанный ею концептуальный подход, основанный на том, что «. от эффективности математического развития ребенка в дошкольном детстве зависит его успешность обучения математике в начальной школе.. Цель занятий математикой — дать ребенку ощущение уверенности в своих собственных силах, основанное на том, что мир имеет свой порядок и потому постижим и предсказуем для человека. Целенаправленное математическое развитие ребенка-дошкольника предполагает, прежде всего, воспитание у него привычки аргументировать свои действия. Отсутствие речи у дошкольников с ТНР не может не отразиться на овладении и математическими знаниями и умениями. У детей с речевыми нарушениями, как правило, запаздывает сенсорное развитие, не возникает самостоятельная ориентировка в окружающей обстановке, времени и др.
В рамках исследования автор разработала для родителей методические рекомендации по профилактике вербальной дискалькулии, рекомендовав, чтобы родители «. как можно чаще. в присутствии детей устанавливали отношения сходства, различия между объектами, используя в своей речи слова «такой же», «одинаковые», «не такой», «разные»; использовали термины: вверху, внизу, впереди, сзади, перед, за, между и т. д.; «.использовали в своей речи понятия, отражающие форму, цвет, величину, пространство, время и т. д; учили с детьми считалки и использовать их в игровом опыте детей; заучивали стихи и сочиняли сказки с математическим содержанием. Необходимо постоянно поощрять ребенка, который использует в своей речи новые математические термины».
Как в домашней среде, так и в дошкольном учреждении автор рекомендует «.использовать познавательное, эмоциональное и воспитательное значение художественных произведений. . Литературные произведения используются и для того, чтобы научить детей отличать задачу от рассказа. К этой работе можно приступать при условии приобретения детьми элементарных навыков решения задачи и умения понимать, называть и различать жанр литературного произведения (рассказ, сказка, загадка, стихотворение). Для этого задачу и рассказ целесообразно строить на едином сюжете. Внимание детей с ТНР необходимо сосредоточивать на языковом материале текста задачи. Для этого текст задачи читается медленно и выразительно, разбирается содержание текста в вопросно-ответной форме. Вопросы, подготовленные педагогом, должны быть направлены на выделение основных моментов сюжетного действия, их последовательность, на математические термины, на понимание вопросительного слова и т. д. В процессе разбора целесообразно применять иллюстративный материал, помогающий понять содержание задачи. Дошкольников с речевыми нарушениями необходимо специально обучать пересказу текста задачи, используя для этого на начальных этапах иллюстративный материал и помощь педагога. Процесс обучения решению арифметических задач должен строиться с учетом оптимальных условий, побуждающих детей что-то сказать, решая задачу, сообщить ответ, спросить, выделить числительные, ключевые слова (антонимические пары) и т. п.».
С. Кондратьева разработала и предложила методологию выявления и прогнозирования дискалькулии для детей с тяжелыми поражениями центральной нервной системы, основываясь на постулате, что в старшем дошкольном возрасте дети с ограниченными возможностями здоровья должны получать адекватную коррекционно-логопедическую помощь, в противном случае велик риск вторичных нарушений развития, в том числе математических [Кондратьева, 2016б].
В структуру такой помощи автор включает специальные диагностические методики изучения познавательных (когнитивных) и речевых (вербальных) функций. Автор предложила алгоритм обследования таких детей с целью выявления предрасположенности к формированию различных тппов дискалькулии, в том числе графической и операциональной. При этом математика (арифметика) позиционировалась как компонент культуры познания окружающего мира в целом.
Сравнивались дети с нормальным речевым развитием (НРР), тяжелыми нарушениями речи (ТНР), задержкой психического развития (ЗПР).
Оказалось, что даже в контрольной группе (НРР) при том что у 80% детей не выявлена предрасположенность к дискалькулии, у 20% она может быть отнесена к разным видам рассстройства (5% — к графической; по 4 % к практогностической, операциональной и вербальной и 3 % — к дислексической), то есть дислексическая форма была выражена минимально.
В группе ТНР у 37% дошкольников была выявлена предрасположенность к дискалькулии, распределенная несколько иначе (10% — к графической; 9% — к вербальной; 7% — к дислексической; 6% — к операциональной и 5% — к практогностической), т. е. преимущественно к графической, вербальной и дислексической форме, минимальной была практогностическая форма.
В группе ЗПР предрасположенность к дискалькулии была максимально выражена — 57% выборки; распределение форм выглядело следующим образом: 13% — операциональная; по 12% — вербальная и дислексическая, 11% — графическая и 9% — практогностическая.
На основании проведенных экспериментов автор предложила репрезентативные задания для выявления дискалькулии у дошкольников.
Это, например, «Конструирование кубиками» и «Черно-белые круги» (по типу паззлов), ориентированные на выявление предрасположенности к графической дискалькулии. Если ребенок самостоятельно выполняет задание без ошибок и составляет правильное изображение, представленное на рисунке, то «...определяется “зона актуального развития” данного навыка. Если ребенок ошибается, но сам пытается исправить ошибки, то это говорит о том, что данный навык находится в стадии формирования и можно определить “зону его ближайшего развития”. Если же совершаются стойкие ошибки при составлении узоров, то можно говорить о нарушениях в восприятии изображения» [Кондратьева, 2016б].
Задание «Определение правильности временных конструкций» направлено на выявление предрасположенности к вербальной дискалькулии; задание «Восприятие ритма» «Копилка» (методика Марии Фидлер) по сопоставлению количества звуков и черточек на рисунке — на выявление предрасположенности к практогностической дискалькулии. Если ребенок не может правильно сосчитать количество звуков и количество черточек, то можно предполагать несформированность у него навыков счета, зрительного и слухового восприятия.
Задание «Найди нужную фигуру по схеме с кодом отрицания «не» (Методика М. Фидлер) направлено на выявление предрасположенности к дислексической дискалькулии. Если ребенок правильно находит фигуру в соответствии со схемой, но путается при назывании ее характеристик, но самостоятельно исправляет ошибку при указании на нее, то это говорит о процессе формирования навыка. Если ребенок допускает стойкие ошибки, не может самостоятельно их исправить, не использует помощь со стороны взрослого, то у него однозначно имеются нарушения зрительных представлений о геометрических фигурах, их цвете, форме, величине.
«Задача про цветы» на копирование заданного паззла (методика А.В. Белошистой) выявляет предрасположенность к операциональной дискалькулии. Если ребенок ошибается при составлении задачи, использует не то количество геометрических фигур или не те числа, которые представлены в модели, то у него не сформировано умение производить необходимые математические операции [Кондратьева, 2016б].
Таким образом, автор фактически разработала, апробировала и предложила к применению простые в реализации способы мониторирования групп детей старшего дошкольного возраста еще перед поступлением в школу. По существу, этот подход представляет собой инструмент профилактики дискалькулии применительно к детям с ограниченными возможностями здоровья.
Подводя итоги исследований отечественных ученых по проблеме дискалькулии, отметим:
• исследования проблемы детской дискалькулии отличаются большей проработкой деталей, безусловной практической ориентированностью и более доступным инструментарием мониторинга и профилактики по сравнению с зарубежными аналогами;
• отечественные концепции дискалькулии, равно как и зарубежные, по умолчанию построены на принципе первичности проблемы нарушений речи и иных ограниченных возможностей здоровья (со стороны высших психических функций);
• в исследования по данной проблеме и, соответственно, в научно-практическую дискуссию вовлечен более узкий круг высших учебных заведений, по сравнению с зарубежным глобальным научным пространством.
Заключение
Вслед за зарубежными и отечественными специалистами различного профиля приходится признать, что дискалькулия, наряду с дислексией, представляет собой серьезное личностное нарушение психосоматической природы у ребенка дошкольного и младшего школьного возраста. Она характеризуется изначальным отсутствием у ребенка абстрактного мышления, «чувства числа» (number sense), представлений о величине и масштабе чисел, числовом ряде, трудностями в обучении простейшим операциям вычисления, пользованием незрелыми стратегиями счета (пальцевой, в частности). Со стороны педагогов в настоящее время еще нет достаточного понимания того, что таким детям необходимо, во-первых, время для усвоения математической информации, и, во-вторых, они нуждаются в активной помощи. Максимально возможная по многим обстоятельствам (состояние психосоматической сферы, качество образовательной среды, семейное окружение, статус семьи, сопутствующие невротические симптомы и многое другое) компенсация данного нарушения оптимизирует возможности дальнейшего школьного обучения и жизненные перспективы, однако требует от широкого круга специалистов больших усилий. Объем имеющейся на сегодняшний день информации о психофизиологических, анатомо-морфологических, психоэмоциональных, психоневрологических и иных механизмах, лежащих в основе дискалькулии, а также об опыте оптимизации обучения позволяет надеяться, что рано или поздно дискалькулия и дислексия будут рассматриваться по меньшей мере с позиций паритета и в комплексе. Так же комплексно следует в будущем подходить и к разработке стратегий вмешательства и профилактики отягощения названными расстройствами (трудностями) обучения детей в старших группах детского сада и начальной школе. Алгоритмы таких стратегий, в которые должны войти разработанные простые технологии и, при необходимости, высокотехнологичные инструменты обучения, могут быть выстроены с учетом закономерностей, выявляемых в ходе лонгитюдных исследований выборок детей с сочетанными трудностями обучения как чтению, так и счету, и/или имеющих какое-либо одно из этих расстройств.
Литература
- Берестенко Ю.А. Теоретический анализ проблемы дискалькулии у детей дошкольного возраста // Научное сообщество студентов: материалы IX Междунар. студенч. науч.–практ. конф.: Чебоксары, 31 мая 2016 г. / Ред.: О.Н. Широков [и др.]. Чебоксары: ЦНС «Интерактив плюс», 2016. С. 81–84.
- Грибанов А.В. Рысина Н.Н. Особенности поведенческого реагирования у детей с дискалькулией // Экология человека. 2011. № 3. С. 56–60.
- Кондратьева С.Ю. Профилактика вербальной дискалькулии у детей с тяжелыми нарушениями речи (ТНР) // Казанский педагогический журнал. 2016. № 1 (114). С. 178–181.
- Кондратьева С.Ю. Профилактика графической дискалькулии у дошкольников с тяжелыми нарушениями речи // Проблемы современного педагогического образования. 2016. № 51-4. С. 194–201.
- Кондратьева С.Ю. Профилактика дискалькулии у детей с ограниченными возможностями здоровья (ОВЗ) // Проблемы современного педагогического образования. 2016. № 52-7. С. 184–196.
- Рысина Н.Н., Грибанов А.В. Понятие о дискалькулии: психофизиологические аспекты развития: Обзор [Электронный ресурс] // Вестник Северного (Арктического) федерального университета. Серия: Естественные науки. 2011. № 1. С. 77–88. URL: http://cyberleninka.ru/article/n/ponyatie-o-diskalkulii-psihofiziologicheskie-aspekty-razvitiya-obzor (дата обращения: 05.09.2016).
- Томме Л.Е. Развитие речевых предпосылок усвоения математики у детей с общим недоразвитием речи [Электронный ресурс] // Дефектология. 2008. № 5. С. 35–40. URL: http://childrens-needs.com/katalog/katalog/izuchenie-i-korrekcija-vyjavlennyh-narushenij/razvitie-rechevyh-predposylok-usvoenija-matematiki (дата обращения: 05.09.2016).
- Butterworth Brian, Varma Sashank, Laurillard Diana. Dyscalculia: From Brain to Education // Science. 2011. Vol. 332. № 6033. P. 1049–1053. doi: 10.1126/science.1201536
- Dowker Ann, Kaufmann Liane. Atypical development of numerical cognition: Characteristics of developmental dyscalculia // Cognitive Development. 2009. Vol. 24. P. 339–342. doi:10.1016/j.cogdev.2009.09.010
- Dyscalculia from a developmental and differential perspective / Kaufmann Liane [et al.] // Frontiers in psychology. 2013. Vol. 4. Article 515. P. 168–171. doi: 10.3389/fpsyg.2013.00516
- Gersten Russell, Jordan Nancy C., Flojo Jonathan R. Early Identification and Interventions for Students With Mathematics Difficulties // Journal of Learning Disabilities. 2005. Vol. 38. № 4. P. 293–304. doi: 10.1177/00222194050380040301
- Interventions for improving numerical abilities: Present and future / Kadosh Cohen R. [et al.] // Trends in Neuroscience and Education. 2013. Vol. 2. № 2. P. 85–93. doi: 10.1016/j.tine.2013.04.001
- Mathematical Cognition Deficits in Children With Learning Disabilities and Persistent Low Achievement: A Five Year Prospective Study / Geary David C. [et al.] // Journal of Educational Psychology. 2012. Vol. 104. № 1. P. 206–223. doi: 10.1037/a0025398
- Mathematical learning difficulties – snapshots of current European research [Электронный ресурс] / Eds. Pirjo Aunio, Riikka Mononen ja Anu Laine // LUMAT. 2015. № 3(5). P. 650–667. URL: http://luma.fi/lumat-en/3989 (дата обращения: 05.09.2016).
- Murphy M.M., Mazzocco M.M.M. The trajectory of mathematics skills and working memory thresholds in girls with fragile X syndrome // Cognitive Development. 2009. Vol. 24. №. 4. P. 430–449. doi: 10.1016/j.cogdev.2009.09.004
Информация об авторах
Метрики
Просмотров web
За все время: 3565
В прошлом месяце: 47
В текущем месяце: 33
Скачиваний PDF
За все время: 3333
В прошлом месяце: 18
В текущем месяце: 16
Всего
За все время: 6898
В прошлом месяце: 65
В текущем месяце: 49