Изучение понимания непереходности превосходства с использованием «нетранзитивных» объектов
Аннотация
Общая информация
Ключевые слова: транзитивность – нетранзитивность отношения превосходства, мышление, нетранзитивные объекты
Рубрика издания: Эксперимент в когнитивной психологии
Тип материала: материалы конференции
Для цитаты: Поддьяков А.Н. Изучение понимания непереходности превосходства с использованием «нетранзитивных» объектов // Экспериментальная психология в России: традиции и перспективы.
Фрагмент статьи
Постановка проблемы
В логике транзитивность (переходность) определяется как такое свойство отношений, при котором из того, что 1-й элемент находится в определенном отношении ко 2-му, а 2-й к 3-му, следует, что 1-й элемент находится в этом же отношении к 3-му (из aRb и bRc следует aRc). Овладение транзитивными рассуждениями считается одним из важнейших этапов умственного развития человека. Оно связано со способностью делать дедуктивные заключения, с пониманием сущности измерения, принципов сохранения, по Ж. Пиаже, и т. д. В ряде работ показано, что в онтогенезе первые транзитивные умозаключения начинают осуществляться примерно с 5 лет. (Пример задачи на транзитивное заключение для детей: «Петя выше Бори. Боря выше Гены. Кто выше всех?»)
Особое место в дискуссиях занимает транзитивность – нетранзитивность превосходства. В классической логике сравнения транзитивность превосходства вводится как аксиома, считающаяся ключевым критерием рациональных действий: если первое превосходит второе в определенном отношении, а второе превосходит третье, то первое превосходит третье в указанном отношении (Козелецкий, 1979).
Но начиная со времен Кондорсе вокруг принципа транзитивности превосходства ведутся споры. В ряде работ доказывается, что транзитивность превосходства может нарушаться в случае сравнения сложных многопараметрических объектов. Один из классических примеров – «нетранзитивные» игральные кубики Б. Эфрона, выигрывающие друг у друга по кругу. Интерес к проблеме нетранзитивности усилился в последнее время в связи с новыми данными: показано, что отношения «бойцовской силы» между биологическими видами могут не быть транзитивны, а подчиняться принципу игры «камень, ножницы, бумага» (1-й вид организмов вытесняет 2-й вид, 2-й вытесняет 3-й, а тот, в свою очередь, вытесняет 1-й) (Reichenbach et al., 2007), это относится и к группам людей, использующих разные экономические стратегии (Semmann et al., 2003).
В целом, есть теоретические аргументы и эмпирические данные и в пользу переходности отношения превосходства в некоторых областях, и в пользу непереходности. Проблема состоит в том, чтобы раскрыть, какие отношения транзитивны, а какие нет, а затем попытаться найти общие правила, которые позволили бы идентифицировать эти отношения в различных ситуациях (Roberts, 2004).
Полный текст
Постановка проблемы
В логике транзитивность (переходность) определяется как такое свойство отношений, при котором из того, что 1-й элемент находится в определенном отношении ко 2-му, а 2-й к 3-му, следует, что 1-й элемент находится в этом же отношении к 3-му (из aRb и bRc следует aRc). Овладение транзитивными рассуждениями считается одним из важнейших этапов умственного развития человека. Оно связано со способностью делать дедуктивные заключения, с пониманием сущности измерения, принципов сохранения, по Ж. Пиаже, и т. д. В ряде работ показано, что в онтогенезе первые транзитивные умозаключения начинают осуществляться примерно с 5 лет. (Пример задачи на транзитивное заключение для детей: «Петя выше Бори. Боря выше Гены. Кто выше всех?»)
Особое место в дискуссиях занимает транзитивность – нетранзитивность превосходства. В классической логике сравнения транзитивность превосходства вводится как аксиома, считающаяся ключевым критерием рациональных действий: если первое превосходит второе в определенном отношении, а второе превосходит третье, то первое превосходит третье в указанном отношении (Козелецкий, 1979).
Но начиная со времен Кондорсе вокруг принципа транзитивности превосходства ведутся споры. В ряде работ доказывается, что транзитивность превосходства может нарушаться в случае сравнения сложных многопараметрических объектов. Один из классических примеров – «нетранзитивные» игральные кубики Б. Эфрона, выигрывающие друг у друга по кругу. Интерес к проблеме нетранзитивности усилился в последнее время в связи с новыми данными: показано, что отношения «бойцовской силы» между биологическими видами могут не быть транзитивны, а подчиняться принципу игры «камень, ножницы, бумага» (1-й вид организмов вытесняет 2-й вид, 2-й вытесняет 3-й, а тот, в свою очередь, вытесняет 1-й) (Reichenbach et al., 2007), это относится и к группам людей, использующих разные экономические стратегии (Semmann et al., 2003).
В целом, есть теоретические аргументы и эмпирические данные и в пользу переходности отношения превосходства в некоторых областях, и в пользу непереходности. Проблема состоит в том, чтобы раскрыть, какие отношения транзитивны, а какие нет, а затем попытаться найти общие правила, которые позволили бы идентифицировать эти отношения в различных ситуациях (Roberts, 2004).
В свою очередь, мы исходим из того, что нетранзитивность превосходства – не менее фундаментальное свойство мира, чем транзитивность, а понимание нетранзитивности отношений превосходства – не менее важная линия когнитивного развития, чем понимание транзитивности (Поддьяков, 2006). Это две взаимосвязанные линии развития познания, и изучать их тоже нужно во взаимной связи. В реальности же имеется значительная асимметрия. Есть много исследований, в которых изучаются овладение транзитивным выводом у детей (Flavell et al., 2002), ошибки отказа от принципа транзитивности в случаях, когда ему необходимо следовать (Tversky, 1969), и т. д., но нет исследований, в которых изучалось бы развитие понимания нетранзитивности – в социо-, онто- и актуалгенезе.
В рамках создания комплекса экспериментальных объектов для изучения мышления детей и взрослых, направленного на понимание многофакторных зависимостей, мы разработали демонстрационные модели нетранзитивных отношений превосходства (доминирования и т. д.). Это, например, геометрические пластины такой формы, что пластина А выводит из равновесия при столкновении пластину В (но не наоборот), В выводит из равновесия С, но С выводит из равновесия А; фигурки зверей такой формы, что зверек А может покормить с ложечки зверька В (но не наоборот), В кормит С, а С кормит А (модель нетранзитивных отношений при взаимопомощи) и др. Эти объекты можно использовать как для диагностики особенностей мышления при решении задач на транзитивность – нетранзитивность, так и в обучении.
Цель пилотажного эмпирического исследования: изучить влияние наблюдения испытуемыми объектов, находящихся в нетранзитивных отношениях превосходства, на изменение суждений о возможности – невозможности существования других «нетранзитивных» объектов в различных областях.
Методика
Испытуемым предлагается опросник со следующими вопросами.
- Есть три прямых, жестких, недеформируемых стержня. Они разной длины: 1-й стержень длиннее 2-го, 2-й стержень длиннее 3-го. Может ли при этом 3-й стержень быть длиннее 1-го?
- Есть три предмета разной массы. Масса каждого предмета неизменна. Масса 1-го предмета больше массы 2-го предмета; масса 2-го предмета больше массы 3-го. Может ли при этом масса 3-го предмета быть больше массы 1-го?
- Есть три шахматных компьютера, играющих друг с другом в шахматы. Известно, что 1-й компьютер чаще выигрывает у 2-го, чем проигрывает ему. 2-й компьютер чаще выигрывает у 3-го, чем проигрывает ему. Может ли быть так, что при этом 3-й компьютер чаще выигрывает у 1-го, чем проигрывает ему?
- Есть три различающихся набора карандашей. В каждом наборе по 6 карандашей разной длины. Сравниваем по длине каждый карандаш с каждым. Известно, что карандаши из 1-го набора чаще оказывались длиннее карандашей из 2-го набора. Карандаши из 2-го набора чаще оказывались длиннее карандашей из 3-го набора. Может ли при этом быть так, что карандаши из 3-го набора чаще оказывались длиннее карандашей из 1-го набора?
- Есть три команды борцов, в каждой команде по 6 борцов. В турнире каждый борец одной команды встречался с каждым из борцов двух других команд. Известно, что: 1-я команда победила 2-ю по соотношению индивидуальных побед (т. е. борцы 1-й команды одержали больше побед над борцами 2-й команды, чем потерпели от них поражений); 2-я команда победила 3-ю по соотношению индивидуальных побед (т. е. борцы 2-й команды одержали больше побед над борцами 3-й команды, чем потерпели от них поражений). Может ли при этом быть так, что 3-я команда победила 1-ю по соотношению индивидуальных побед (т. е. борцы 3-й команды одержали больше побед над борцами 1-й команды, чем потерпели от них поражений)?
- Есть три вида микроорганизмов. Микроорганизмы 1-го вида вытесняются с занятой территории микроорганизмами 2-го вида. Микроорганизмы 2-го вида вытесняются с занятой территории микроорганизмами 3-го вида. Может ли при этом быть так, что микроорганизмы 3-го вида затем вытесняются с занятой территории микроорганизмами 1-го вида?
- Есть три вида оружия – гуляй-башни разной конфигурации, соревнующиеся, кто поставит на другой цветную метку. Гуляй-башня, поставившая в ходе столкновения цветную метку на другой, считается победителем, а другая – побежденной (как в пейнтболе). Известно, что: 1-я гуляй-башня сконструирована так, что ставит метку на 2-й гуляй-башне, оставаясь не помеченной ею (т. е. побеждает ее); 2-я гуляй-башня сконструирована так, что ставит метку на 3-й гуляй-башне, оставаясь не помеченной ею (т. е. побеждает ее). Может ли при этом быть так, что 3-я гуляй-башня ставит метку на 1-й гуляй-башне, оставаясь не помеченной ею (т. е. побеждает ее)?
- Есть три зубчатые передачи (шестеренки на осях, соединяемые друг с другом). Известно, что: ось 1 вращается с большей частотой вращения, чем ось 2, при сцеплении их шестерней; ось 2 вращается с большей частотой вращения, чем ось 3, при сцеплении их шестерней. Может ли при этом быть так, что ось 3 вращается с большей частотой вращения, чем ось 1, при сцеплении их шестерней?
Варианты ответов: «да, может»; «нет, не может»; «затрудняюсь ответить».
Затем испытуемым предъявлялась тройка объектов, находящихся в нетранзи тивных отношениях превосходства, и их схематическое изображение. В экспери ментальной группе 1 предъявлялись «нетранзитивные» гуляй-башни (рисунок 1), в группе 2 – «нетранзитивные» шестерни (рисунок 2).
После этого испытуемым снова предлагалось ответить на те же вопросы, подтверждая, что их оценки остались прежними, или, наоборот, в чем-то изменяя их.
Рис. 1. Гуляй-башни, поражающие друг друга «по кругу»: 1-я гуляй-башня побеждает 2-ю, 2-я побеждает 3-ю, а 3-я побеждает 1-ю
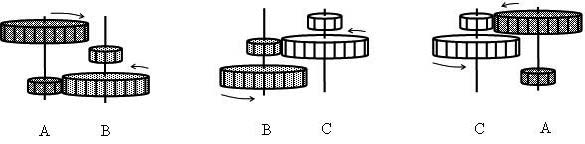
Рис. 2. Три зубчатые передачи, скомпонованные так, что: передача А вращается с большей частотой, чем передача В; В вращается быстрее С, С вращается быстрее А
Испытуемые
89 студентов гуманитарных факультетов ГУ-ВШЭ 17–21 года (64 женщины, 25 мужчин); из них 40 человек в группе 1, 49 – в группе 2, примерно уравненные по полу и возрасту.
Результаты
До показа «нетранзитивных» объектов между группами не было значимых различий. В группе 1 было дано 68% правильных ответов на все вопросы, 28 % неправильных, 4 % – «затрудняюсь ответить»; в группе 2–74% правильных ответов, 25 % неправильных, 1 % – «затрудняюсь ответить». В обеих группах абсолютное большинство испытуемых (от 94 % до 97%) правильно считало невозможной нетранзитивность длин недеформируемых стержней и неизменных масс объектов. Также в обеих группах большинство считало, что «нетранзитивные» гуляй-башни возможны (90 % испытуемых в группе 1 и 88 % испытуемых в группе 2), а «нетранзитивные» шестерни невозможны (65 % испытуемых в группе 1 и 67% испытуемых в группе 2).
Ситуация существенно изменилась после показа «нетранзитивных» объектов.
В группе 1 после показа башен все 100 % испытуемых стали считать, что «нетранзитивные» гуляй-башни возможны. Количество правильных ответов на другие вопросы выросло на 10%, при полном отсутствии замен правильных ответов на неправильные. В целом, общее число правильных ответов составило 74%, неправильных – 22 %, «затрудняюсь ответить» – 4 %. Улучшение статистически незначимо для ответов на вопрос о «нетранзитивных» башнях (башни и до показа абсолютное большинство испытуемых считало возможными), но значимо для всего массива вопросов (критерий знаков, p<0,01). Парадокс ситуации состоит в том, что на изменения суждений участников о множестве других объектов повлияло наблюдение объектов, относительно которых они и так знали правильный ответ. Возможная причина состоит в том, что хотя существование «нетранзитивных» гуляй-башен участники допускали, но конкретного механизма реализации не представляли. Знакомство с этим механизмом позволило расширить правильные представления о «нетранзитивных» объектах и в других областях.
В группе 2 после показа шестерней 96 % испытуемых (на 43% больше, чем до показа) стали считать, что «нетранзитивные» шестерни возможны (4% по-прежнему ответили, что невозможны – возможно, они сочли демонстрацию фокусом). Однако, в отличие от группы 1, это существенное улучшение коснулось только вопроса о тех объектах, которые были показаны, – о шестернях. Хотя произошли изменения в 12% ответов и на другие вопросы, они распределились так: 8 % – положительные изменения, а 4% – отрицательные (в совокупности изменения статистически незначимы). Таким образом, в целом, некоторая тенденция к улучшению имела место, но общий рост числа правильных ответов (до 84% – что даже больше доли правильных ответов в группе 1 после показа) достигнут практически полностью за счет вопроса о шестернях, а не за счет роста доли правильных ответов на вопросы об объектах, которые не были показаны, – как в группе 1).
Итак, знакомство с «нетранзитивными» шестернями вызвало не столь выраженные изменения в ответах на другие вопросы, как знакомство с «нетранзитивными» гуляй-башнями. И эти изменения, в отличие от группы 1, были двойственными – и положительными, и отрицательными (происходила замена некоторых правильных ответов на неправильные).
Выводы
- Представления о нетранзитивных отношениях превосходства являются в исследованной выборке предметно-специфическими: участники допускают существование одних объектов, находящихся в нетранзитивных отношениях превосходства, и не допускают существования других (хотя реально они тоже возможны). Аксиома транзитивности, если и используется участниками, то выборочно – для тех или иных областей и объектов.
- Демонстрация различных объектов, находящихся в нетранзитивных отношениях превосходства, вела к разным эффектам. Результаты показывают: разработка «нетранзитивных» объектов, знакомство с которыми оказывает положительное влияние на изменение представлений о возможности существования других «нетранзитивных» объектов в других областях, возможна и целесообразна. Также есть «нетранзитивные» объекты, знакомство с которыми оказывает двойственное (как положительное, так и отрицательное) влияние на изменение этих представлений. И те, и другие объекты могут быть использованы для исследования понимания транзитивности–нетранзитивности превосходства.
- Необходима программа изучения исторического и онтогенетического развития понимания транзитивности–нетранзитивности отношений превосходства как фундаментальных свойств мира. Динамика постановки и решения (или признания неразрешимости) различных задач о транзитивности–нетранзитивности, происходящая в социо- и онтогенезе – это важнейшая составляющая процесса познавательного развития в целом.
Литература
- Козелецкий Ю. Психологическая теория решений. М.: Прогресс, 1979.
- Поддьяков А. Н. Непереходность (нетранзитивность) отношений превосходства и принятие решений // Психология. Журнал Высшей школы экономики. 2006. № 3. С. 88–111.
- Flavell J. H., Miller P. H., Miller S. A. Cognitive development. N. J.: Prentice-Hall, 2002.
- Reichenbach T. et al. Mobility promotes and jeopardizes biodiversity in rock–paper–scissors games // Nature. 2007. № 448. P. 1046–1049.
- Roberts T. S. A ham sandwich is better than nothing: Some thoughts about transitivity // Australian Senior Mathematics Journal. 2004. № 18 (2). P. 60–64.
- Semmann D., Krambeck H.-J., Milinski M. Volunteering leads to rock–paper–scissors dynamics in a public goods game // Nature. 2003. № 425. P. 390–393.
- Tversky A. Intransitivity of preferences // Psychological review. 1969. № 76. P. 31–48.
Информация об авторах
Метрики
Просмотров web
За все время: 2317
В прошлом месяце: 22
В текущем месяце: 3
Скачиваний PDF
За все время: 83
В прошлом месяце: 5
В текущем месяце: 0
Всего
За все время: 2400
В прошлом месяце: 27
В текущем месяце: 3