Психологическая наука и образование
2010. Том 15. № 1. С. 94–110
ISSN: 1814-2052 / 2311-7273 (online)
Факторный анализ показателей нравственного состояния общества в европейских странах
Аннотация
Общая информация
Ключевые слова: нравственность, сети Маркова, факторный анализ, индекс нраственного состояния общества
Рубрика издания: Социальная психология
Тип материала: научная статья
Для цитаты: Куравский Л.С., Юревич А.В., Мармалюк П.А., Иванова Е.Г. Факторный анализ показателей нравственного состояния общества в европейских странах // Психологическая наука и образование. 2010. Том 15. № 1. С. 94–110.
Полный текст
1. Введение
Нравственность - одна из проблем, к которым психологическая наука обращается нечасто и неохотно по разным причинам, среди них можно выделить следующие:
• психологи часто воспринимают эту проблему как «закрепленную» за философией, в первую очередь, за таким ее разделом, как этика;
• она плохо поддается эмпирическому изучению и «препарированию» в психологических лабораториях;
• естественнонаучная психология, в соответствии с традициями естественной науки, трактует объективность научного исследования как предполагающую абстрагирование от ценностей, что едва ли возможно при изучении таких проблем, как нравственность.
Так или иначе, хотя многие традиционные объекты психологического изучения - ценности, установки и др., имеют непосредственное отношение к морали и нравственности, последняя оказалась вынесенной за пределы основного русла психологической проблематики. Вместе с тем, значительная доля работ в этой области, в том числе и ведущихся в современной отечественной психологии, так или иначе ее затрагивает. В частности, в таком наиболее актуальном для современной России аспекте, как нравственное состояние современного российского общества.
В Институте психологии РАН в русле развиваемой в нем количественной макропсихологии [Юревич; Юревич, 2007] разработан «Индекс нравственного состояния общества» (ИНСО), основанный на интеграции следующих показателей: 1) убийств; 2) беспризорных детей (число на 100 000 жителей); 3) индекс коррупции; 4) индекс Джини, выражающий неравномерность распределения доходов.
Методика вычисления ИНСО такова. Первичные индексы вычисляются как базисные. Значение показателя России за 1996 г. (Vo) считается равным 100 баллам. Нормализация значений показателей (Vi) за более поздние или более ранние годы осуществляется путем их соотнесения со значением за 1996 г. (чем выше балл, тем благополучнее общество по соответствующему параметру). Для нормализации значений показателей социального сиротства, смертности от убийств и индекса Джини, увеличение значений которых указывает на ухудшение состояния в обществе, используется формула
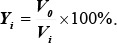
Начиная с 1996 г. интегральный индекс рассчитывается как среднее геометрическое значение четырех первичных индексов:
смертности от убийств;
численности выявленных детей, оставшихся без попечительства родителей;
коррупции;
неравномерности доходов (индекс Джини).
Ввиду того что до 1996 г. индекс коррупции не рассчитывался, композитный индекс за 1990-1995 гг. строится по трем первичным индексам.
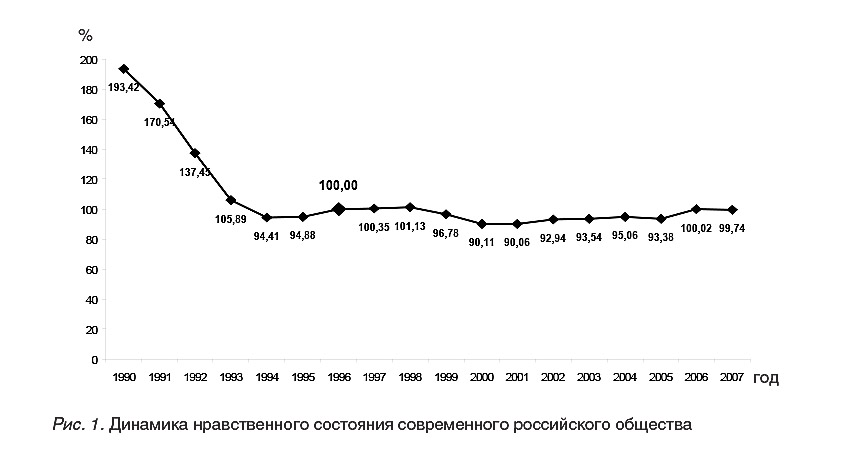
Динамика нравственного состояния российского общества в годы реформ, количественно оцененного таким образом, показана на рис. 1, из которого видно, что нравственное состояние нашего общества ежегодно ухудшалось с 1991 по 1994 гг., затем улучшалось до «дефолтного» 1998 г., после чего вновь ухудшалось до 2002 г., а потом обнаружило тенденцию к ежегодному улучшению (за 2007 и 2008 гг. индекс не рассчитан ввиду того, что статистические данные, лежащие в основе его расчетов, пока отсутствуют). Не подвергая интерпретации выявленную динамику, отметим, что она почти полностью соответствует динамике макропсихологического состояния современного российского общества, оцененной на основе других показателей [Юревич, 2007а], а также временно́й развертке его характеристик, вычисляемых социологами (социальные настроения, социальный оптимизм и др.), что говорит о синхронном проявлении подобной динамики в самых различных сферах. Количественная оценнка нравственного состояния нашего общества по
казывает, что в первые годы реформ оно ухудшалось высокими темпами, что свидетельствует о связи данного явления именно с реформами и с сопутствовавшими им событиями. Полученные данные показывают, что в течение последующих после реформ лет обнаруживается нелинейная, «волнообразная» динамика, показатели которой уступают уровню 1990 г. почти в два раза.
Большой интерес для исследования нравственного состояния общества представляет анализ динамики развития и взаимодействия составляющих «Индекс нравственного состояния общества» показателей, а также выявление факторов, которыми обусловлена их изменчивость. Анализ данных европейских стран по указанным выше показателям при помощи традиционных методов, включая регрессионный и корреляционный анализ, не позволил выявить значимые линейные зависимости между выделенными величинами, которые были бы достаточны для их содержательной интерпретации. Поиск нелинейных зависимостей с помощью аппарата нейронных сетей также не дал положительных результатов, что сделало актуальными разработку и применение новых, более сложных методов анализа исследуемых показателей. В данной работе рассматриваются два из них: «Альтернативный вариант конфирматорного факторного анализа» и «Обучаемые сети Маркова», позволившие выявить ряд частных закономерностей развития проблемных характеристик.
2 . Факторный анализ
Выявление закономерностей развития и взаимных связей исследуемых характеристик является одной из актуальных задач, возникающих при анализе результатов социологических исследований. Как правило, рассматривается временная динамика наблюдаемых переменных, которые в различных контрольных точках формально рассматриваются как отдельно анализируемые величины. Для решения задачи используются различные методы статистического анализа, наиболее эффективным из которых является симплекс-метод конфирматорного факторного анализа (КФА) [Jöreskog]. Однако практическое применение этого подхода обусловлено рядом серьезных ограничений, которые зачастую делают его использование невозможным. Кроме того, существенным недостатком традиционного КФА является необходимость решения трудоемкой задачи многомерной локальной оптимизации для оценки величин свободных параметров модели, что, как правило, не позволяет найти глобальный минимум и приводит к неоднозначности решения.Чтобы преодолеть указанные проблемы, был разработан новый подход, опирающийся на возможности вейвлетпреобразований и обучаемых факторных структур [Kuravsky]. К его особенностям и преимуществам относятся:
• возможность нахождения оценок свободных параметров модели прямыми (неитерационными) методами, гарантирующими однозначное оптимальное решение;
• гибкие средства для исследования взаимодействия факторов;
• применимость для анализа ковариационных и корреляционных матриц произвольной структуры.
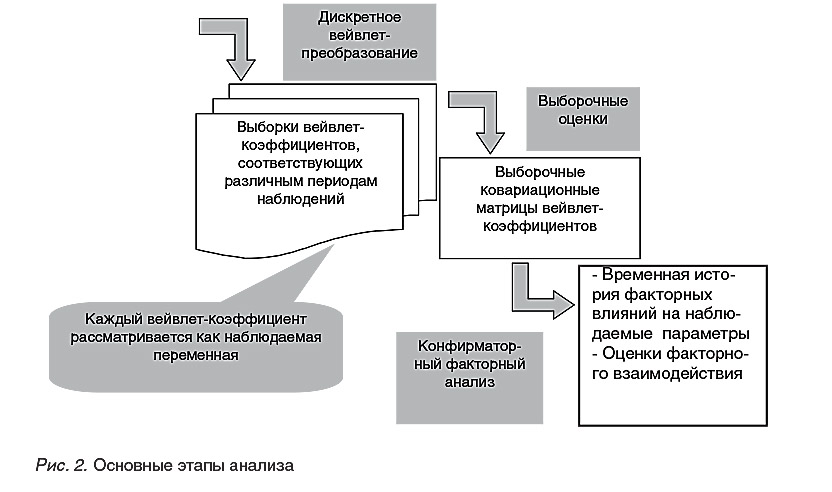
2.1. Основные этапы факторного анализа
Основные этапы предложенного подхода представлены на рис. 2. Выборки коэффициентов, полученных в результате кратномасштабного вейвлет-анализа временных рядов значений исследуемого параметра и соответствующих различным периодам наблюдений, в последующем конфирматорном факторном анализе рассматриваются как значения наблюдаемых переменных, которые позволяют выявить временную историю факторных влияний и оценки факторного взаимодействия. Представление данных, полученное с помощью вейвлет-преобразований, дает возможность выявить различия в характеристиках процесса в различных шкалах, что особенно важно при большом числе контрольных моментов времени, связанных с проведением измерений. Идентификация свободных параметров факторной модели (обычно корреляций или ковариаций) выполняется с помощью новой прямой (неитерационной) процедуры, которая опирается на «Метод максимального правдоподобия» (ММП) и является альтернативой традиционному итерационному способу решения задач локальной оптимизации.
Рабочие представления анализируемых процессов формируются с помощью вейвлет-преобразования, которое позволяет выявлять отличия в их характеристиках при использовании различных шкал измерений на всем протяжении интервала наблюдений. Если исследуемый процесс есть функция одной переменной, то его вейвлет-спектр - функция двух аргументов, один из которых характеризует период составляющих компонентов, а другой - смещение вычисляемых показателей вдоль оси времени. Для вычисления вейвлет-спектров используются вейвлеты - особые функции в форме коротких волн («всплесков») с нулевым интегральным значением и локализацией по оси независимой переменной, способные к сдвигу по этой оси и масштабированию.
Вейвлет-анализ имеет очевидные преимущества перед традиционным спектральным анализом, поскольку он обеспечивает корректные результаты в случае нестационарных процессов и содержит более полную информацию о поведении изучаемого объекта. Это сделало данный подход популярным среди исследователей разных специальностей. Далее применялся дискретный вариант этого метода, позволивший представить анализируемые процессы в виде элементов определенного метрического функционального пространства с вейвлет-базисом.
2.2 . Альтернативный вариант конфирматорного факторного анализа
Основные компоненты КФА представлены на рис. 3.
КФА предполагает наличие строго определенной факторной модели изучаемого явления. Факторная модель, связывающая латентные и наблюдаемые переменные, формируется, опираясь на знание предметной области. Объектами данного вида анализа являются ковариационные или корреляционные матрицы наблюдаемых переменных. Цель работы - выявить значения параметров модели, которая с приемлемыми ошибками объясняет изменчивость наблюдений.
Для определения свободных параметров модели традиционный КФА предполагает решение трудоемкой задачи многомерной локальной оптимизации. Это приводит к невозможности определения глобального минимума и неоднозначности решения.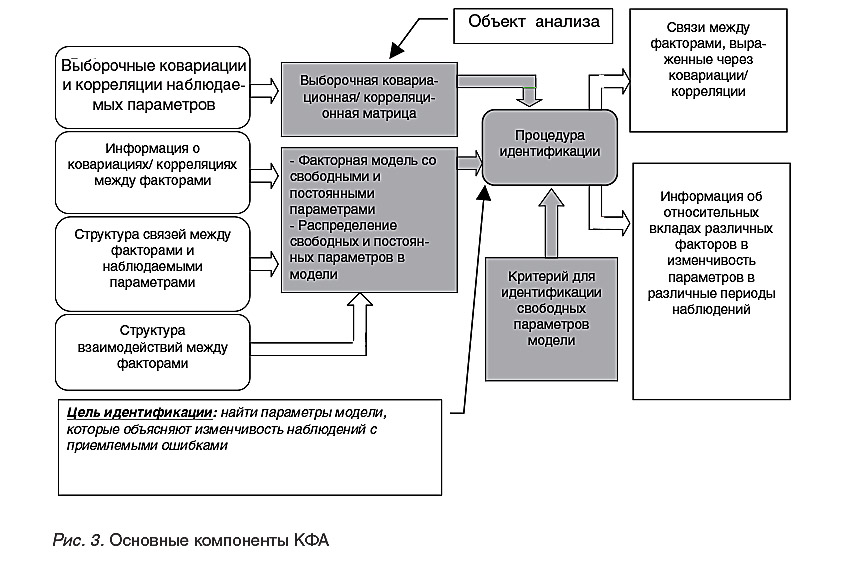
Рассматриваемый далее альтернативный вариант КФА позволяет находить единственное оптимальное решение прямыми (неитерационными) методами. Процедура решения включает в себя:
1) составление переопределенной системы алгебраических уравнений при выражении выборочных дисперсий и ковариации через аналогичные факторные показатели1;
2) решение системы прямым (неитерационным) методом, используя ММП2 [Куравский, 2007; Kuravsky, 2004];
3) проверку адекватности полученных моделей наблюдениям при опоре на статистические критерии согласия.
Чтобы избежать составления сложных для решения нелинейных систем уравнений относительно коэффициентов корреляции и факторных нагрузок, используется путевая модель дисперсионных составляющих (рис. 4) [Kuravsky, 2007], в которой факторные нагрузки равны единице. Каждой наблюдаемой дисперсии и ковариации ставится в соответствие алгебраическое уравнение, которое связывает ее выборочную оценку с соответствующей прогнозируемой величиной, выраженной аналитически через неопределенные дисперсии и ковариации латентных переменных [Bollen, 1989]. В путевых диаграммах3 для этого, в частности, могут быть использованы правила обхода путей4. В результате получается система, число уравнений которой равно числу наблюдаемых дисперсий и ковариаций.
Представим полученную переопределенную систему n уравнений в матричной форме
Ax=b,
где A - матрица системы, коэффициенты которой определяются факторной моделью; b - вектор-столбец n выборочных дисперсий и ковариаций, определяемых результатами наблюдений; x - вектор- столбец m искомых дисперсий и ковариаций латентных переменных.
Теперь рассмотрим вектор ε=Ax* –b, представляющий полученную методом наименьших квадратов невязку псевдорешения x* переопределенной системы. Полагая в общем случае, что компоненты вектора невязок коррелированны, выразим их невырожденную ковариационную матрицу как σ2 V.
Сделав замены b=V½b0 и A= V½A0, где V=V½V½. 5, перейдем к системе A0 x=b0, ковариационная матрица вектора невязок ε0 =V-½ε которой имеет вид σ2 E, где E – единичная матрица.
Если рассматриваемая система невырождена (rank A = m, где m – число свободных параметров модели), вектор невязки ε0 имеет многомерное нормальное распределение, а x = (A0 T A0 )-1A0 Tb0 = (ATV-1A)-1ATV-1b – псевдорешение, полученное методом наименьших квадратов, это псевдорешение является оценкой максимального правдоподобия, а статистика X2 =(b0 -A0 x ) T(b0 -A0 x )/σ2 =(b-Ax )
TV-1(b-Ax* )/σ2 имеет распределение χ2 с n-m степенями свободы.
гипотезу о представимости выборочных дисперсий и ковариаций, составляющих вектор b, дисперсиями и ковариациями латентных переменных, содержащихся в исследуемой модели. Область принятия гипотезы есть X2<y_2nma , где а есть уровень значимости критерия.’
При реализации данного подхода удобно сделать следующие упрощающие предположения, обусловленные особенностями искомого решения:
• компоненты вектора невязок е являются некоррелированными;
• значения среднеквадратических отклонений различных компонентов вектора невязок е составляют одну и ту же фиксированную долю (процент) от соответствующих компонентов вектора b6.
Чтобы обеспечить сопоставимость оценок, указанная доля (процент) подбирается так, чтобы равенство 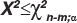 выполнялось при а=0,05. Для оценки степени допустимости вычисленной характеристики для нее удобно установить разумное критическое значение, например, 0,1. Таким образом, вместо уровня значимости появляется новый показатель - критический процент.
выполнялось при а=0,05. Для оценки степени допустимости вычисленной характеристики для нее удобно установить разумное критическое значение, например, 0,1. Таким образом, вместо уровня значимости появляется новый показатель - критический процент.
Преимуществом предложенного подхода является то, что он не сводит решение к трудоемкой процедуре многомерной локальной оптимизации, которая не гарантирует нахождение глобальных минимумов, обеспечивая при этом однозначность результата.
Как и в традиционном КФА, рассматриваемый метод дает возможность строить заключения о статистической значимости различных компонентов модели, используя статистические критерии согласия [Куравский, 2009].
2.3. Факторные модели для анализа результатов вейвлет-преобразований
В данной работе применяется модель дисперсионных составляющих. Пример типового варианта таких моделей показан на рис. 4. Состав вейвлет-коэффициентов, используемых при анализе в качестве наблюдаемых переменных, зависит от рассматриваемой прикладной задачи и может меняться. Обычно предполагается, что число моментов времени, в которые производятся наблюдения, является степенью числа 2.
Аналитические выражения для ковариаций и дисперсий вейвлет-коэффициентов Wt линейны:
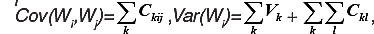
где k и l- индексы факторов, V* - дисперсии, C** и C*** - ковариации между факторами.
Такие модели дают возможность получать прямые оценки свободных параметров, используя рассмотренный выше альтернативный вариант КФА, и применять данную модель на практике.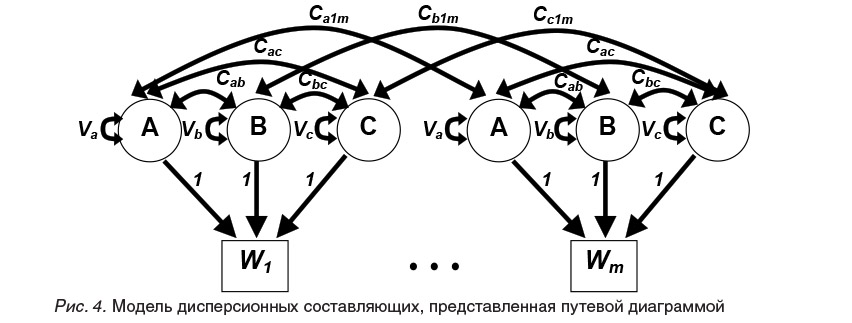
Интерпретация результатов рассмотренного варианта факторного анализа обычно опирается:
• на оценки свободных7 факторных дисперсий и ковариаций;
• оценки свободных корреляций между различными факторами в одни и те же моменты времени;
• оценки свободных корреляций между одинаковыми факторами в разные моменты времени;
• оценки статистической значимости различных компонентов модели.
2 .4. Факторные модели и результаты расчетов
Данные для анализа содержали значения индекса коррупции K, индекса Джини D и показателя убийств U, измеренные в 22 европейских странах с 1998 по 2001 г.
Гипотеза о наличии общего фактора, влияющего на социально-экономические показатели, в первом приближении частично подтверждается оценками индекса надёжности Кронбаха, приведенными в табл. 18.
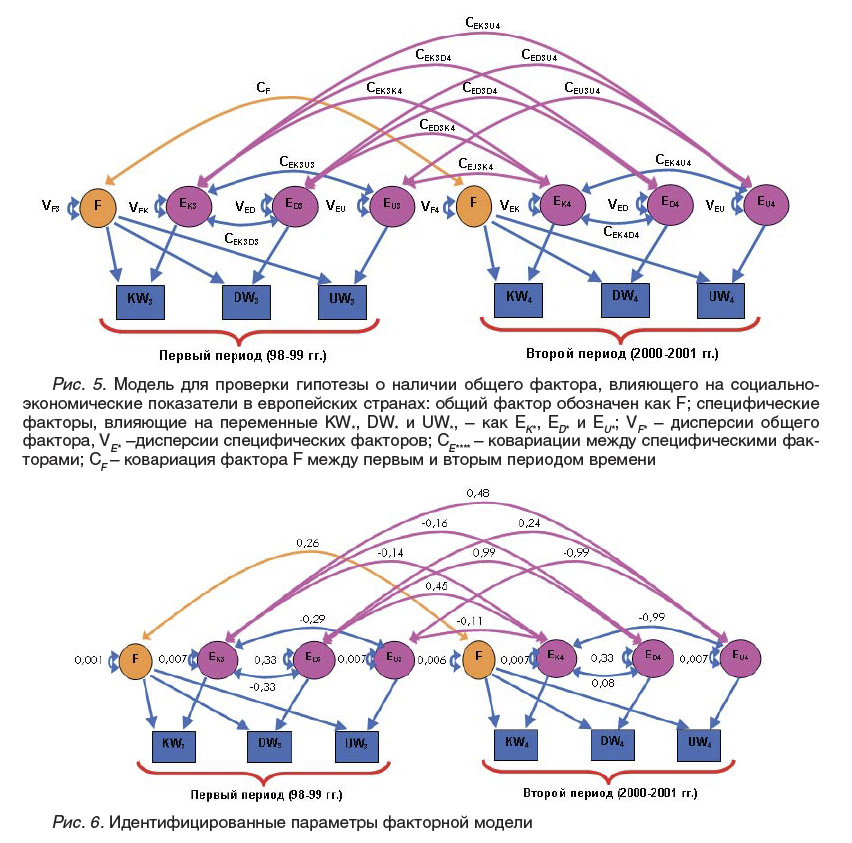
Для последующего анализа, проведенного с помощью представленной на рис. 5 факторной модели дисперсионных составляющих, использовались вейвлет- коэффициенты, соответствующие периодам наблюдений с 1998 по 1999 г. и с 2000 по 2001 г. Вейвлет-коэффициенты, соответствующие периоду с 1998 по 1999 г., обозначены как KW3, DW3u UW3, а коэффициенты, соответствующие периоду с 2000 по 2001 год, - как KW4, DW4 и UW4. Указанная модель использовалась для выявления степени факторного взаимодействия и проверки гипотезы о наличии общего фактора, влияющего на наблюдаемые переменные.
В этой модели отсутствуют корреляции между факторами ED3 и EU3, ED4 и EU4, и EU3 и ED4, поскольку их наличие приводит к неоднозначности решения, которая обусловлена появлением зависимостей между свободными параметрами модели и проявляется в дефекте матрицы системы уравнений, определяемой факторной моделью. Способ устранения зависимых переменных описан в статье об используемых методах альтернативного конфирматорного анализа [Куравский, 2009].
Идентифицированные дисперсии и корреляции представлены на рис. 69.
Для проверки гипотезы о наличии общего фактора F исследовалась значимость самого этого фактора, а также значимость ковариации данного фактора между первым и вторым периодом. В табл. 2 приведены значения статистики X2 для соответствующих упрощений модели и оценки статистической значимости исключенных компонентов.
Статистические значимости фактора F и его ковариации в разные периоды времени свидетельствуют о наличии общего фактора, влияющего на наблюдаемые переменные. Умеренная корреляция между значениями этого фактора в разные периоды наблюдений позволяет говорить о его временной изменчивости, обусловленной появлением новых составляющих.
Таблица 1
Группы переменных с высоким значением индекса надежности Кронбаха
|
Группа переменных |
Индекс надежности Кронбаха |
|
U1998, D1998, K2000 |
0,52 |
|
K1998, U1999, D2000, D2001 |
0,63 |
|
K1998, U1999, D2000 |
0,75 |
 Дальнейшие расчеты (табл. 3) показали незначительность влияния общего фактора на изменчивость индекса Джини. Однако удаление соответствующих влияний приводит к вырожденности матрицы переопределенной системы уравнений и появлению зависимых переменных, устранение которых вызывает качественное изменение типа системы и несогласованность полной и упрощённых моделей из табл. 2. Это позволяет говорить о целесоообразности сохранения указанных связей.
Дальнейшие расчеты (табл. 3) показали незначительность влияния общего фактора на изменчивость индекса Джини. Однако удаление соответствующих влияний приводит к вырожденности матрицы переопределенной системы уравнений и появлению зависимых переменных, устранение которых вызывает качественное изменение типа системы и несогласованность полной и упрощённых моделей из табл. 2. Это позволяет говорить о целесоообразности сохранения указанных связей.
2.5. Анализ с помощью факторных моделей: основные выводы
Факторный анализ индекса коррупции, индекса Джини и показателя убийств в европейских странах свидетельствует о наличии статистически значимого общего фактора, действием которого обусловлена изменчивость указанных показателей, причем влияние данного фактора подвержено определенным временным изменениям.
Таблица 2
Оценки статистической значимости исследуемых компонентов модели
|
Модель |
Статистика X2 |
Число степеней свободы |
р-значе- ние |
Разность оценок X2 по сравнению с полной моделью |
Разность в числе степеней свободы по сравнению с полной моделью |
р-значе- ние для разности оценок X2 |
Значимость исключенного компонента |
|
Модель с общим фактором F (полная модель) |
6,764 |
3 |
0,054 |
— |
— |
— |
— |
|
Модель без ковариации между фактором F в 1-м и 2-м периодах наблюдений |
11,195 |
4 |
0,024 |
4,430 |
1 |
0,035 |
Значим |
|
Модель без общего фактора F |
18,993 |
6 |
0,004 |
12,228 |
3 |
0,007 |
Значим |
Таблица 3
Оценки балансов факторных влияний на изменчивость наблюдаемых переменных10
|
Баланс факторных влияний в первом периоде |
Баланс факторных влияний во втором периоде |
||
|
Составляющие дисперсии KW3 |
Составляющие дисперсии KW4 |
||
|
VF3 |
17 % |
VF4 |
44 % |
|
VEK |
87 % |
VEK |
52 % |
|
Необъясненная |
0 % |
Необъясненная |
4 % |
|
Составляющие дисперсии DW3 |
Составляющие дисперсии DW4 |
||
|
VF3 |
0 % |
VF4 |
3 % |
|
VED |
36 % |
VED |
163 % |
|
Необъясненная |
64 % |
Необъясненная |
0 % |
|
Составляющие дисперсии UW3 |
Составляющие дисперсии UW4 |
||
|
VF3 |
27 % |
VF4 |
24 % |
|
VEU |
132 % |
VEU |
26 % |
|
Необъясненная |
0 % |
Необъясненная |
50 % |
Используя результаты, представленные в табл. 3 и на рис. 6, можно сделать следующие выводы о балансе влияний общего и специфических факторов на каждый показатель, а также об изменении факторных влияний во времени:
• индекс коррупции и показатель убийств испытывают сопоставимые влияния общего и специфического факторов, причем в 1998-99 гг. влияние специфических факторов на изменчивость указанных характеристик значительно преобладает, а в 2000-01 гг. указанные влияния выравниваются;
• в случае индекса Джини влияние общего фактора пренебрежимо мало по сравнению с влиянием специфического фактора, причем в 2000-01 гг. специфический фактор практически полностью определяет всю изменчивость данной характеристики;
• имеет место существенная отрицательная корреляция между специфическими факторами, воздействующими на индекс коррупции и показатель убийств, усилившаяся во втором периоде наблюдений;
• имеет место сильная отрицательная корреляция между специфическими факторами, воздействующими на показатель убийств в первом и втором периоде наблюдений;
• имеет место сильная положительная корреляция между специфическими факторами, воздействующими на индекс Джини в первом и втором периоде наблюдений.
3 . Сети Маркова
Второй метод анализа - «Сети Маркова» - рассматривается здесь как дополнение к представленному выше подходу [Machinery Failure Prevention, 2008]. Его применение позволяет исследовать динамику развития и взаимосвязь исследуемых характеристик, восстанавливать вероятностные характеристики исследуемых величин в произвольные моменты времени, находящиеся между контрольными точками, а также извлекать из экспериментальных результатов новые показатели, недоступные для других методов исследования. Непосредственно анализируемыми объектами являются гистограммы, представляющие распределения наблюдаемых значений исследуемых характеристик в контрольные моменты времени.
3.1. Основные принципы построения
Анализируемой величиной являются диапазоны значений (уровни) исследуемой характеристики. Весь диапазон допустимых значений заданной величины делится на несколько интервалов. Каждый интервал рассматривается как отдельное состояние, в котором исследуемая величина может находиться с некоторой вероятностью, отражающей частоту ее появления в популяции, переходя из одного состояния в другое по определенным правилам. Для описания, как вероятности нахождения в заданных состояниях изменяются со временем, применяются сети Маркова.
По результатам накопленных наблюдений проводится прогнозирование указанных вероятностей с использованием параметрических математических моделей, описываемых марковскими случайными процессами с дискретными состояниями и непрерывным временем.
Модель для описания динамики этих переходов представляется ориентированным графом, в котором вершины соответствуют состояниям, а дуги соответствуют переходам. Процесс переходов между состояниями может рассматриваться как случайное блуждание по графу из одного состояния в другое согласно направлениям дуг. Переходы между состояниями мгновенны и происходят в случайные моменты времени.
Можно показать, что в рассматриваемых потоках число событий Х, попадающих в любой временной интервал длины т, начинающийся в момент t, распределено согласно закону Пуассона:
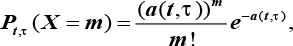
где PtT(X=m) - вероятность появления m событий в течение рассматриваемого интервала, a(t, T) - среднее число событий, попадающих в интервал длины т, начинающийся в момент времени t.
Далее будут рассматриваться только стационарные потоки (в которых a(t,r)=nr, n=const). Параметр п называется интенсивностью стационарного потока. Он равен среднему числу событий в единицу времени. Средняя продолжительность времени между двумя смежными событиями в этом случае равна 1/ц.
При указанных предположениях динамика изменения во времени вероятностей пребывания системы в различных состояниях описывается системой обыкновенных дифференциальных уравнений Колмогорова, в которой каждому состоянию соответствует уравнение
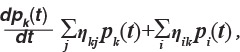
где k- номер состояния; Pk и P- вероятности нахождения в k-м и i-м состояниях; nkj- интенсивности потоков, выходящих из состояния k; nik - интенсивности потоков, входящих в состояние k.
Для интегрирования указанной системы уравнений необходимо задать начальные условия
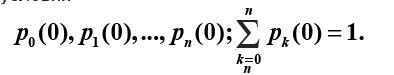
Нормализующее условие 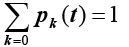
k=0 выполняется в любой момент времени.
Интенсивности потоков событий являются свободными параметрами модели. Здесь рассматривается обратная постановка задачи. Значения свободных параметров определяются путем сравнения наблюдаемых и прогнозируемых гистограмм, описывающих наблюдаемые распределения исследуемой характеристики, а именно: вычисляются значения, обеспечивающие наилучшее соответствие наблюдаемых и ожидаемых частот попадания в определенное состояние системы в заданные моменты времени. Прогнозируемые вероятности нахождения в состояниях получаются путем численного интегрирования систем уравнений Колмогорова.
Прогнозируемая частота попадания в k-е состояние равна pkN, где N - число элементов в выборке. Соответствующие наблюдаемые частоты Fk определяются по распределениям наработок до отказа, зарегистрированным на практике. Статистика Пирсона

используется как мера соответствия в том смысле, что ее большие значения означают плохое согласование прогнозируемых и наблюдаемых результатов, а малые значения - хорошее согласование. Сумма этих статистик минимизируется в те моменты времени, для которых имеются результаты наблюдений.
Данный способ идентификации свободных параметров называется методом минимума X [Крамер, 1976] и дает решения, близкие к полученным ММП [Крамер, 1976, с. 461-462]. Это позволяет использовать его для проверки гипотезы, что полученный прогноз согласуется с результатами наблюдений.
3 .2 . Многофакторные сети Маркова
Для того чтобы модель более детально представляла исследуемые характеристики, удобно использовать двух- и многофакторные сети Маркова [Kuravsky, 2005]. Типовая структура двухфакторной сети показана на рис. 7. Данная модель учитывает два определяемых исследователем фактора различной природы, значимых для исследуемой характеристики. Каждый фактор соответствует одному из двух ортогональных направлений на плоскости: вертикальному или горизонтальному. Каждая строка (столбец) состояний сети соответствует определенному уровню значений фактора. Переходы между состояниями возможны только вдоль указанных ортогональных направлений («манхэттенские переходы»), а именно: интенсивности I. соответствуют правым горизонтальным переходам, интенсивности рг. - левым, интенсивности 0.. соответствуют вертикальным переходам вниз, а интенсивности п. - вертикальным переходам вверх. В общем случае эти интенсивности переходов являются функциями их позиции в диаграмме
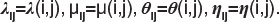
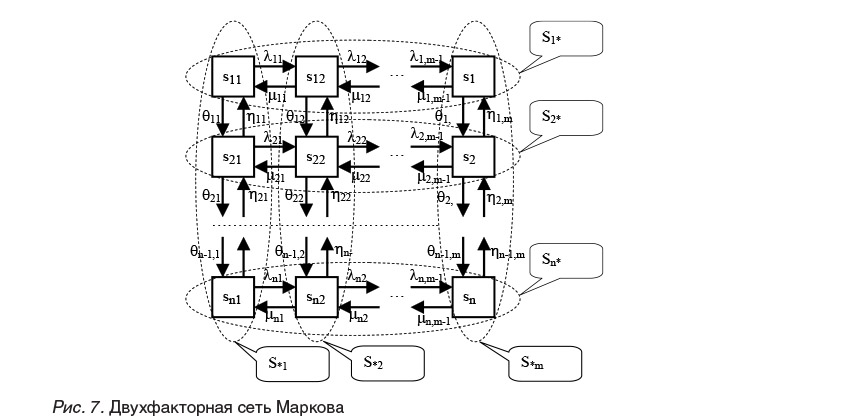
Подобные функции позволяют отразить в модели тонкие особенности поведения исследуемой системы.
В практически важных случаях идентификация свободных параметров двух- и многофакторных моделей является сложной вычислительной задачей. Однако имеется эффективный прием, позволяющий упростить эту работу. Рассмотрим его на примере двухфакторной модели.
Строки и столбцы состояний исходной сети могут быть объединены в «сгруппированные» состояния, а именно: нахождение в состоянии S(i=1,2,...,n) равносильно нахождению в одном из состояний si1, si2 sim, а нахождение в состоянии Sej (j=1,2,...,m) равносильно нахождению в одном из состояний s1j, s2j snj. Согласно теоремам о суммах пуассоновских потоков событий, переходы между сгруппированными состояниями также удовлетворяют свойствам пуассоновских потоков событий, а их интенсивности являются суммами аналогичных характеристик в соответствующих направлениях:
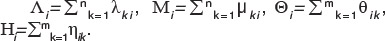
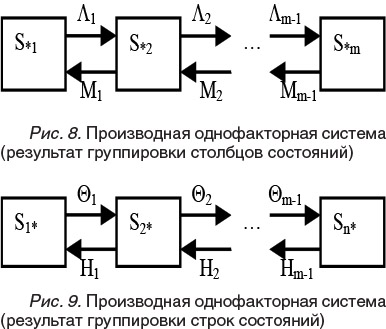
Таким образом, исследование исходной двухфакторной системы сводится к анализу двух производных однофакторных систем (рис. 8 и 9), которые могут быть идентифицированы и интерпретированы, как показано выше. Возврат к исходной системе прост: вероятность р.. нахождения в состоянии sij может быть вычислена как произведение вероятностей P. и P, пребывания в «сгруппированных» состояниях S,. и Sej, соответственно. Наличие такого простого способа декомпозиции является важным преимуществом рассматриваемых систем. В практических приложениях представленная выше общая модель может быть упрощена и конкретизирована.
3.3. Исследование с помощью двухфакторных сетей Маркова
Для исследования взаимодействия и эволюции факторов, определяющих ИНСО, использованы двухфакторные сети Маркова. Исследовался период времени с 2000 по 2006 г. Построены три двухфакторных модели, выявляющие попарное взаимодействие и развитие трех составляющих, определяющих индекс нравственности (рис. 10):• модель индекс Джини/уровень коррупции;
• модель индекс Джини/уровень убийств;
• модель уровень коррупции/уровень
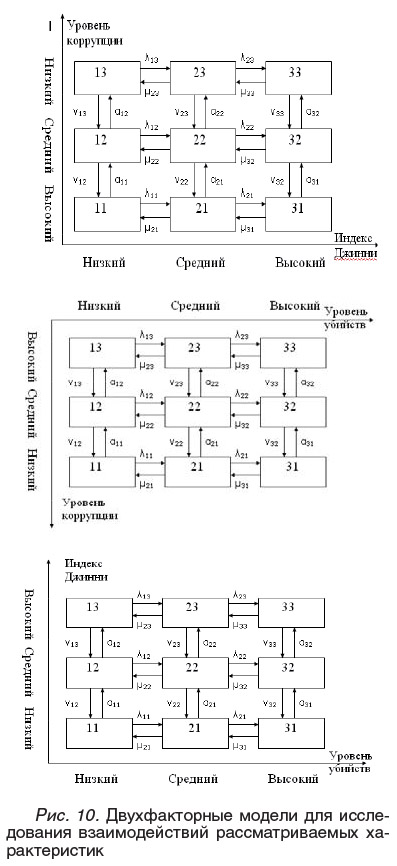
• каждая страна должна быть оценена по двум факторам, включенным в модель;
• каждое ортогональное направление включает в себя три состояния, так как именно это количество позволяют исходные данные;
• начальными распределениями моделей являются наблюдаемые распределения в предыдущей контрольной точке (в 2000 г.);
• неявный параметр системы - время. Время измеряется в годах;
• свободными параметрами системы являются параметры показателей интенсивности перехода.
Взаимные связи интенсивностей потоков событий описываются следующими формулами:
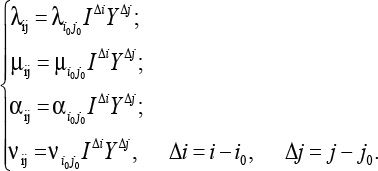
λi0j0, μi0j0, αi0j0, νi0j0 – «начальные» интенсивности. Начальной полагается нижняя левая интенсивность. Например, v^^= v12, где i - номер состояния по горизонтали, а j - по вертикали.
Таким образом, свободными идентифицируемыми параметрами являются «начальные» интенсивности и
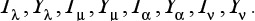
Если
I >1, то с ростом i увеличится интенсивность потоков вниз (v);
I <1, то с ростом i увеличится интенсивность потоков вверх (а);
Y >1, то с ростом j уменьшится интенсивность потоков вниз (v);
Y <1, то с ростом i уменьшится интенсивность потоков вверх (а).
При девяти состояниях в разработанной системе соотношений минимизировалась сумма двух статистик Пирсона, вычисленных в двух контрольных точках. Проведенные расчеты показали хорошее согласование прогнозируемых и наблюдаемых гистограмм.
В модели индекс Джини/уровень коррупции значение суммарной статистики Пирсона равно 1,564 (df=5, р=0,906). Для модели индекс Джини/уровень убийств этот показатель составляет 3,064 (df=5, р=0,69), а для модели уровень убийств/ уровень коррупции - 2,115 (df=5, р=0,833). Полученные характеристики свидетельствуют о достаточно высокой степени соответствия модели наблюдениям.
3.4. Анализ с помощью сетей Маркова: основные выводы
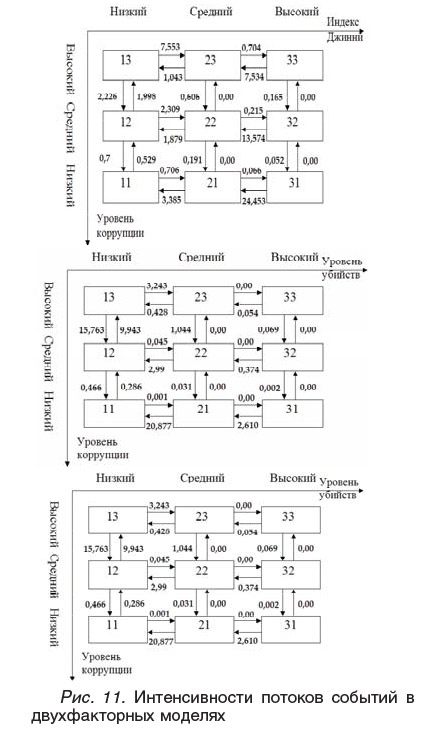
Полученные оценки интенсивностей потоков событий (рис. 11) позволяют сделать следующие выводы.
1. Модель «уровень коррупции/ уровень убийств». Тенденция к уменьшению уровня коррупции преобладает над тенденцией к его увеличению. При этом чем ниже уровень убийств, тем быстрее будет уменьшаться коррупция. При низких и средних значениях показателя уровня коррупции существует тенденция к уменьшению числа убийств, в отличие от высокого уровня коррупции, при котором уровень убийств стремится к средним значениям.
2. Модель «уровень коррупции/индекс Джини». Значения индекса Джини стремятся к средним показателям при средних и высоких значениях уровня коррупции. При низких показателях уровня коррупции видна тенденция к уменьшению значений индекса Джини. Тенденция к уменьшению уровня коррупции преобладает над тенденцией к его увеличению, при этом чем меньше индекс Джини, тем быстрее уменьшается коррупция.
3. Модель «индекс Джини/уровень убийств». Тенденция к уменьшению числа убийств преобладает над тенденцией к его увеличению. Значения индекса Джини имеют тенденцию к уменьшению при низких показателях уровня убийств. При высоком и среднем уровне убийств существует тенденция к увеличению значений индекса Джини, при этом чем больше был индекс Джини, тем быстрее.
Таким образом, осуществленный анализ продемонстрировал правомерность использования разработанного Институтом психологии РАН индекса нравственного состояния общества, а также высветил взаимосвязи его составляющих.2 В другой форме, нежели при традиционном КФА.
3 В путевых диаграммах (рис. 3–7 и 11) овалы (круги) соответствуют латентным переменным, прямоугольники соответствуют наблюдаемым переменным, однонаправленные стрелки соответствуют
причинным связям, двунаправленные стрелки соответствуют ковариациям, дисперсиям или корреляциям.
4 Обход начинается против причинной связи, затем происходит поворот по ковариационной связи,
после чего движение продолжается вдоль причинной связи. При движении запрещается дважды обходить ковариационную связь.
5 Для любой симметричной неотрицательно определенной матрицы V (именно к этому классу относятся ковариационные матрицы) существует единственная симметричная неотрицательно определенная матрица V1/2, называемая квадратным корнем из V, такая, что (V1/2)2=V.
8 Индексы переменных К, D и U обозначают год.
9 Идентифицированные ковариации между факторами для удобства интерпретации пересчитаны в корреляции.
Литература
- Крамер Г. Математические методы статистики. М., 1976.
- Куравский Л. С., Корниенко П. А. Применение нейронных сетей для идентификации локусов количественных признаков в психогенетике //Нейрокомпьютеры: разработка и применение. 2007. № 4.
- Куравский Л. С., Мармалюк П. А., Баранов С. Н., Абрамочкина В. И., Петрова Е. А.Факторный анализ результатов вейвлетпреобразований лонгитюдных данных как новый метод исследования динамических характеристик сложных систем // Нейрокомпьютеры: разработка и применение. 2009. № 9.
- Юревич А. В. Нравственность как психологическая проблема // Вопросы психологии.2009. № 4.
- Юревич А. В., Ушаков Д. В. Макропсихология как новая область психологических исследований // Вопросы психологии. 2007. № 4.
- Юревич А. В., Ушаков Д. В., Цапенко И. П.
Количественная оценка макропсихологиче-
ского состояния современного российского
общества // Психологический журнал. 2007.№ 4. - Bollen K. A. Structural equations with latent
variables. N. Y., 1989. - Jöreskog K. G. Estimation and testing of
simplex models // British Journal of Mathematical and Statistical Psychology. Vol. 23. - Kuravsky L. S., Baranov S. N. The concept of
multifactor Markov networks and its application to forecasting and diagnostics of technical systems //In: Proc. Condition Monitoring 2005, Cambridge,United Kingdom, 2005. - Kuravsky L. S. and Baranov S. N.Development of the wavelet-based confirmatory factor analysis for monitoring of system factors // In: Proc. 5th International Conference on Condition Monitoring
- Machinery Failure Prevention Technologies,Edinburgh, United Kingdom, 2008.
- Kuravsky L. S. and Baranov S. N. Neural
networks in fatigue damage recognition: diagnostics and statistical analysis // In: Proc.11th International Congress on Sound and
Vibration, St.-Petersburg, Russia, 2004. - Kuravsky L. S., Kornienko P. A. On the approach to identifying quantitative trait loci in behavior genetics. In: Proc. 2nd World Congress on Engineering Asset Management and 4th International Conference on Condition Monitoring, Harrogate, United Kingdom, 2007.
- Neale M. C., Cardon L. R. Methodology for
genetic studies of twins and families. Dordrecht,the Netherlands, Kluwer Academic Publishers, 1992.
Информация об авторах
Метрики
Просмотров
Всего: 2348
В прошлом месяце: 14
В текущем месяце: 12
Скачиваний
Всего: 1015
В прошлом месяце: 3
В текущем месяце: 2