Формирование доверительного множества поглощения в задаче прогнозирования скорости ветра

Склезнева К.А.; Соболь В.Р.

doi:10.17759/mda.2025150108

Моделирование и анализ данных
2025. Том 15. № 1. С. 145–157
doi:10.17759/mda.2025150108
ISSN: 2219-3758 / 2311-9454 (online)

Формирование доверительного множества поглощения в задаче прогнозирования скорости ветра

3

Склезнева К.А., Соболь В.Р.

Аннотация

В статье исследуется задача определения множества допустимых прогнозных векторов скоростей ветра, измеренных перед вылетом самолета, при которых скорость ветра к моменту посадки окажется в допустимых пределах с вероятностью не меньше заданной. Отклонения направления и модуля скорости ветра от прогнозных полагаются случайными. Рассматривается случай, когда в аэропорту назначения есть две взлетно-посадочные полосы, расположенные под углом друг к другу. Задача сведена к задаче определения линии уровня для функции вероятности специального вида. Предложен численный алгоритм построения аппроксимации линии уровня. Приведены численные примеры, демонстрирующие зависимость формы искомого множества от параметров задачи.

Общая информация

Ключевые слова: доверительное множество поглощения, функция вероятности, диффузионная аппроксимация, изокванта

Рубрика издания: Математическое моделирование

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2025150108

Получена: 19.02.2025

Принята в печать: 03.03.2025

Для цитаты: Склезнева К.А., Соболь В.Р. Формирование доверительного множества поглощения в задаче прогнозирования скорости ветра // Моделирование и анализ данных. 2025. Том 15. № 1. С. 145–157. DOI: 10.17759/mda.2025150108

Полный текст

ВВЕДЕНИЕ

Важной прикладной областью задач стохастического программирования является обеспечение безопасности полетов [1, 2]. Это связано с тем, что ключевые факторы неопределенности – погодные условия и надежность компонент – успешно описываются и моделируются с помощью аппарата теории вероятностей. Хорошо изученные примеры таких задач [Кан, 2009] – задача минимизации площади взлетно-посадочной полосы при ограничении на вероятность успешной посадки и задача определения множества допустимых скоростей ветра в пункте назначения, измеренных до начала полета, при которых с вероятностью не меньше заданной условия для посадки будут благоприятны. Для обеих указанных задач сперва были получены приближенные (гарантирующие) решения с помощью доверительного метода [Кан, 2009], также известного как обобщенный минимаксный подход [Кибзун, 1984]. Позднее были получены также приближенные, но более точные решения с применением гладкой аппроксимации функции вероятности и градиентных методов оптимизации [Sobol, 2021]. Для второй задачи также был предложен способ решения, основанный на алгоритме построения доверительного множества поглощения [5, 6]. Остановимся на второй задаче подробнее.

Представим, что из пункта А вылетает самолет и через некоторое время t прибывает в пункт В. Прямо перед вылетом измеряются скорость и направление ветра, продольная и боковая составляющие скорости ветра в аэропорту прилета В и строится прогноз скорости и направления ветра к моменту прилета. При подлете на основе фактической скорости и направления ветра принимается решение выдавать ли разрешение на посадку. Для каждого типа воздушного судна существуют свои предельно допустимые скорости попутного, встречного и бокового ветра, при которых допускается посадка. Эти величины могут зависеть от материала и состояния взлетно-посадочной полосы, режима работы тормозной системы и других параметров, но во всех вариантах предельно допустимые скорости являются фиксированными для конкретного типа воздушного судна. Если самолет получил разрешение на взлет, но условия для посадки в итоге признаются небезопасными, то самолет может быть перенаправлен на запасной аэродром или будет вынужден ожидать разрешения на посадку в воздухе, что приводит к дополнительным расходам для авиакомпании. Следовательно, разрешение на взлет при высокой вероятности реализации такого сценария скорее всего является нецелесообразным. С другой стороны, если разрешение на взлет будет даваться только при крайне низкой вероятности неблагоприятного сценария, то это может приводить к задержкам вылетов, что также влечет дополнительные расходы. Таким образом, возникает необходимость определения множества допустимых прогнозных/фактических скоростей ветра до вылета, при которых разрешение на посадку будет дано с достаточно высокой вероятностью. Определение множества начальных условий, при которых выполняется вероятностное ограничение на конечное состояние системы, является примером задачи построения доверительного множества поглощения [Кибзун, 2020а].

Если направление скорости ветра близко или совпадает с направлением взлетно-посадочной полосы (ВПП), то разрешение на посадку может быть дано при достаточно высоких абсолютных значениях скорости ветра. Отклонение самолета от расчетной точки касания будет компенсироваться запасом длины ВПП. При этом максимально допустимые величины попутного и встречного ветра могут отличаться. В то же время, боковой ветер оказывает более существенное влияние как в силу меньшего запаса ВПП по ширине, так и в силу влияния на способность выдерживать требуемый курс (возникает вращательный момент). В силу вышесказанного, можно ожидать, что искомое множество допустимых скоростей ветра имеет эллипсообразную форму, симметричную относительно направления ВПП. Это подтверждается ранее полученными результатами [2, 4, 5].

Более сложным случаем является тот, когда в аэропорту назначения есть две ВПП, расположенные под углом друг к другу. В этом случае, в зависимости от направления и скорости ветра может быть выбрана более подходящая полоса. Например, пересекающиеся ВПП можно увидеть в аэропорту имени Бредли (Коннектикут), в аэропортах Огасты в Джорджии, Лас-Вегаса, Нью-Йорка, Де-Мойна и в ряде других. В аэропортах Шереметьево и Домодедово г. Москвы ВПП параллельны друг другу, но, например, в аэропорту Гумрак г. Волгограда новая и старая ВПП расположены под углом. Без ограничения общности будем считать, что точка пересечения совпадает с расчетной точкой посадки. В данной статье предлагается алгоритм определения множества векторов скорости ветра, гарантирующих безопасную посадку с заданным уровнем доверительной вероятности. Как будет показано в расчетных примерах, конфигурация и свойства получаемого множества существенно зависят от параметров задачи. В частности, множество допустимых скоростей ветра может быть невыпуклым, в отличие от случая с одной полосой. Работа является продолжением исследования в [Sobol, 2021] и использует подход, основанный на построении линии уровня для функции вероятности специального вида. Задача определения линии уровня сводится к решению дифференциального уравнения специального вида, а для расчета производных функции вероятности используется ее гладкая аппроксимация [Соболь]. Стоит отметить, что в [Кан, 2009] предполагалось, что перед вылетом измеряются текущие скорость и направление ветра, а фактические величины к моменту посадки моделировались через случайные отклонения от соответствующих величин в момент вылета. Такое предположение игнорирует использование метеорологических прогнозов. Более адекватным представляется использование прогнозных величин для принятия решения и их случайные отклонения для моделирования фактических величин.

1.МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Пусть начало координат совпадает с расчетной точкой касания ВПП при посадке и находится на пересечении полос. Пусть Ох направлена вдоль полосы 1, Оy – поперек. Полоса 2 расположена под углом

γ

к полосе 1.

Пусть

v

и

β

– прогнозные модуль скорости и угол направления ветра относительно Ох в аэропорту города В, зафиксированные перед вылетом. Пусть

w_{x 1}^{0}, w_{y 1}^{0}

– случайные продольная и боковая компоненты скорости ветра для полосы 1,

w_{x 2}^{0}, w_{y 2}^{0}

– для второй полосы соответственно. Выразим их в полярных координатах:

w_{x 1}^{0} = vcosβ,

(1)

w_{y 1}^{0} = vsinβ,

(2)

w_{x 2}^{0} = vcos (γ - β),

(3)

w_{y 2}^{0} = vsin (γ - β) .

(4)

Пусть

ξ

и

ε

– случайные отклонения вектора скорости по абсолютной величине и по направлению за время полета относительно прогнозных параметров в момент вылета. Предполагается, что случайные величины

ξ

и

ε

независимы и имеют нормальное распределение с нулевым математическим ожиданием и дисперсиями, равными

σ_{ξ}^{2}

и

σ_{ε}^{2}

соответственно.

Свяжем прогнозные и реализовавшиеся компоненты вектора скорости ветра через случайные отклонения:

w_{x 1} = (v + ξ) \cos (β + ε)

, (5)

w_{y 1} = (v + ξ) \sin (β + ε)

, (6)

w_{x 2} = (v + ξ) \cos (γ - β - ε)

, (7)

w_{y 2} = (v + ξ) \sin (γ - β - ε)

. (8)

Введем события:

A_{1}

– условия для посадки на полосу 1 безопасны к моменту прибытия самолета,

A_{2}

– аналогично для полосы 2. Тогда получим вероятности событий

A_{1}

и

A_{2}

через условия того, что фактические компоненты скорости ветра не превысят установленных границ:

P (A_{1}) = P (w_{xmin} \leq w_{x 1} \leq w_{xmax}; w_{ymax}^{2} - w_{y 1}^{2} \geq 0)

, (9)

P (A_{2}) = P (w_{xmin} \leq w_{x 2} \leq w_{xmax}; w_{ymax}^{2} - w_{y 2}^{2} \geq 0)

, (10)

где

w_{xmax}

и

w_{xmin}

– максимальная и минимальная допустимые скорости для встречного и попутного ветра,

w_{ymax}

– максимально допустимая скорость поперечного ветра.

Вероятность того, что самолет получит разрешение на посадку на одну из полос, определяется как вероятность суммы зависимых случайных событий:

$P (A_{1} + A_{2}) = P (A_{1}) + P (A_{2}) - P (A_{1} A_{2})$ . (11)

Пусть задан уровень надежности

α

. Вероятность

P (A_{1} + A_{2})

может быть рассмотрена как функция от

vиβ

. Задача определения множества допустимых векторов скорости ветра в начальный момент времени сводится к нахождению множества точек

W = (v, β)

, для которых выполняется вероятностное ограничение:

P (v, β) = P (A_{1} + A_{2}) \geq α, \forall (v, β) ϵW

. (12)

2.ИДЕЯ АЛГОРИТМА

Предположим, что нам доступен практический способ расчета функции

P (v, β)

и ее производных. В качестве стартовой точки (

v_{0}, β_{0}

), лежащей на границе искомого множества можно найти максимальную скорость попутного ветра, направленного вдоль ВПП 1, при которой выполняется ограничение (12). Для этого численно решим уравнение, взяв

β_{0} = 0

:

P (v_{0},0) = α .

(13)

После нахождения стартовой точки поворачиваем вектор скорости ветра с заданным шагом

Δβ

так, чтобы вероятность оставалась неизменной, то есть выполнялось условие:

\frac{\partial}{\partial β} P (v, β) Δβ + \frac{\partial}{\partial v} P (v, β) Δv = 0.

(14)

Необходимо найти изокванту функции

P (v, β)

, то есть ее поверхность уровня. Изокванта будет содержать семейство векторов

c = [v, β]

, при которых значение функции остается постоянным. Множество таких векторов будет удовлетворять дифференциальному уравнению специального вида:

\frac{dv}{dβ} = \frac{- \partial P (v, β)}{\partial β} {(\frac{\partial P (v, β)}{\partial v})}^{- 1}

(15)

с начальным условием:

v (0) = v_{0} .

(16)

3.ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ И ИХ ПРОИЗВОДНЫХ

Для реализации подобного алгоритма требуется определить выражение для неизвестной вероятности. Вероятности

P (A_{1})

,

P (A_{2})

и

P (A_{1} A_{2})

, входящие в выражение для

P (v, β)

, могут быть записаны в форме математических ожиданий:

P (A_{1}) = M [I {w_{xmin} \leq w_{x 1} \leq w_{xmax}} I {w_{ymax}^{2} - w_{y 1}^{2} \geq 0}]

, (17)

P (A_{2}) = M [I {w_{xmin} \leq w_{x 2} \leq w_{xmax}} I {w_{ymax}^{2} - w_{y 2}^{2} \geq 0}]

, (18)

P (A_{1} A_{2}) = M [I {w_{xmin} \leq w_{x 1} \leq w_{xmax}} I {w_{ymax}^{2} \geq w_{y 1}^{2}} I {w_{xmin} \leq w_{x 2} \leq w_{xmax}} I {w_{ymax}^{2} \geq w_{y 2}^{2}}],

(19)

где

I

– индикаторная функция.

Функция Хевисайда является аналитическим представлением индикаторной функции:

Θ (y) = {\begin{matrix} 1, y \geq 0, \\ 0, y < 0. \end{matrix}

(20)

Следовательно, вероятности могут быть переписаны в виде:

P (A_{1}) = M [Θ (w_{xmax} - w_{x 1}) Θ (w_{x 1} - w_{xmin}) Θ (w_{ymax}^{2} - w_{y 1}^{2})]

, (21)

P (A_{2}) = M [Θ (w_{xmax} - w_{x 2}) Θ (w_{x 2} - w_{xmin}) Θ (w_{ymax}^{2} - w_{y 2}^{2})]

, (22)

P (A_{1} A_{2}) = M

[

Θ (w_{xmax} - w_{x 1}) Θ (w_{x 1} - w_{xmin}) Θ (w_{xmax} - w_{x 2}) Θ (w_{x 2} - w_{xmin}) Θ (w_{ymax}^{2} - w_{y 1}^{2}) Θ (w_{ymax}^{2} - w_{y 2}^{2})

]. (23)

Вероятности (21)-(23), записанные в форме математического ожидания, могут быть эффективно вычислены с помощью метода Монте-Карло. Однако, вычисление их производных напрямую затруднительно. Известно [Кибзун, 1997], что градиент функции вероятности может быть выражен в форме интеграла Лебега по поверхности, являющейся границей области реализаций случайного вектора. Для некоторых частных случаев показано [Uryasev S.., 1995], что этот интеграл может сводиться как минимум к сумме объемного и поверхностного интегралов. Поверхностные интегралы не могут быть вычислены с помощью метода Монте-Карло, что ограничивает практические возможности расчета производных функции (12).

Решением данной проблемы может стать применение гладкой аппроксимации функции вероятности и ее производных [Соболь]. Ранее такой подход применялся в решении задачи с одной ВПП [Sobol, 2021], а также, например, в задаче аппроксимации α-ядра вероятностной меры. Идея аппроксимации заключается в замене функции Хевисайда в выражении для функции вероятности на сигмоиду:

S_{θ} (y) = \frac{1}{1 + e^{- θy}}, θ > 0.

(24)

Для гладких функций потерь и абсолютно непрерывных распределений случайных параметров доказана [Соболь] сходимость аппроксимаций функции вероятности и ее производных. Вероятности (21)-(23) заменим на их приближенные значения:

P (A_{1}) \approx M [S_{θ} (w_{xmax} - w_{x 1}) S_{θ} (w_{x 1} - w_{xmin}) S_{θ} (w_{ymax}^{2} - w_{y 1}^{2})]

, (25)

P (A_{2}) \approx M [S_{θ} (w_{xmax} - w_{x 2}) S_{θ} (w_{x 2} - w_{xmin}) S_{θ} (w_{ymax}^{2} - w_{y 2}^{2})]

, (26)

P (A_{1} A_{2}) \approx M

[

S_{θ} (w_{xmax} - w_{x 1}) S_{θ} (w_{x 1} - w_{xmin}) S_{θ} (w_{xmax} - w_{x 2}) S_{θ} (w_{x 2} - w_{xmin}) S_{θ} (w_{ymax}^{2} - w_{y 1}^{2}) S_{θ} (w_{ymax}^{2} - w_{y 2}^{2})

]. (27)

Их производные по параметрам

v

и

β

вычисляются непосредственно по правилам дифференцирования сложной функции. Производная сигмоиды определяется следующим образом:

S_{θ}^{'} (y) = {θS}_{θ} (y) (1 - S_{θ} (y)) .

(28)

Следовательно, аппроксимации значений и производных функции

P (v, β)

определены.

4.АЛГОРИТМ ПОСТРОЕНИЯ ВНЕШНЕЙ АППРОКСИМАЦИИ

ГРАНИЦЫ МНОЖЕСТВА

Предложим алгоритм построения аппроксимации границы искомого доверительного множества, основанный на численном решении дифференциального уравнения:

1) задать начальное значение параметра алгоритма

β_{0}

, шага

Δβ

, параметра аппроксимации

θ

;

2) используя метод дихотомии, определить значение

v_{0}

из условия (13);

3) найти частные производные функции вероятности при текущих

β_{k}, v_{k}

;

4) вычислить отношение производных

\frac{dv}{dβ}

по формуле (15) и найти текущее значение

v_{k} = v_{k - 1} + \frac{dv}{dβ} Δβ

;

5) полученную точку проверить на выполнение вероятностного ограничения. Если ограничение выполняется, увеличить

v_{k}

на шаг 𝛿, умноженный на частную производную по v. В противном случае уменьшить

v_{k}

на шаг 𝛿, пропорциональный производной по v. Повторять шаг до тех пор, пока выполняется ограничение (12);

6) задать

β_{k + 1} = β_{k} + Δβ

;

7) повторять шаги 2-6, пока выполняется

β_{k + 1} \leq 2 π .

Таким образом, на каждом шаге алгоритма происходит поворот угла

β

и корректировка допустимой скорости. Результатом работы алгоритма является внутренняя аппроксимация искомого множества.

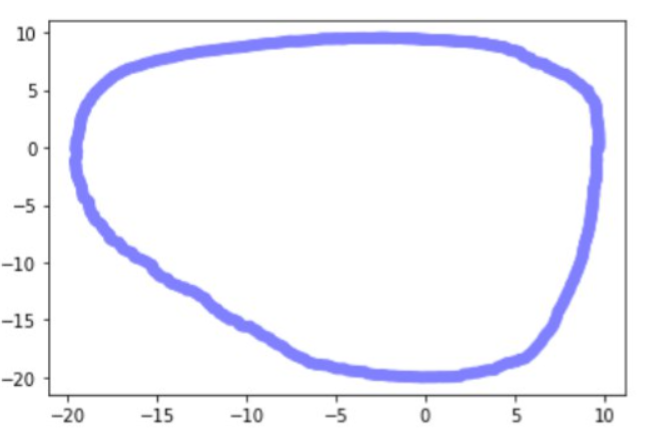
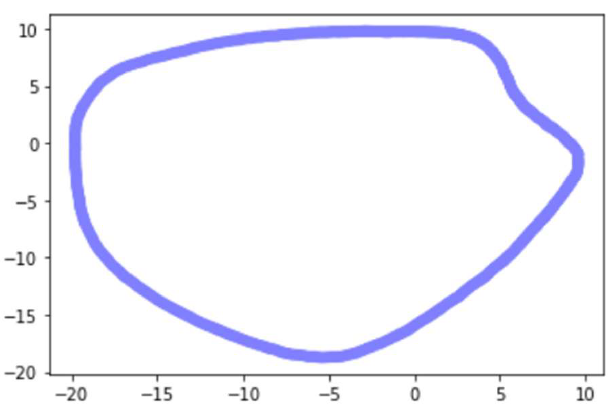
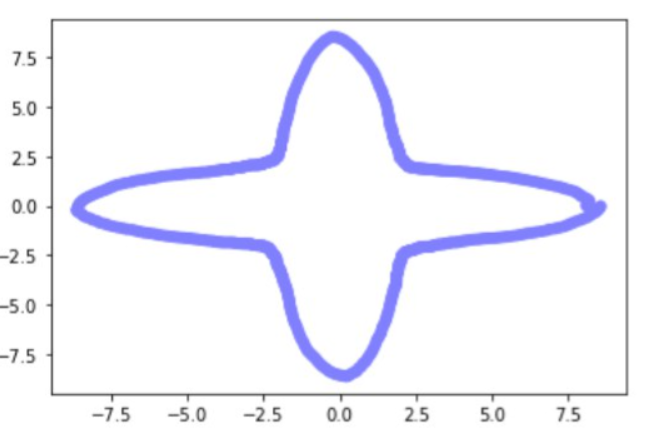
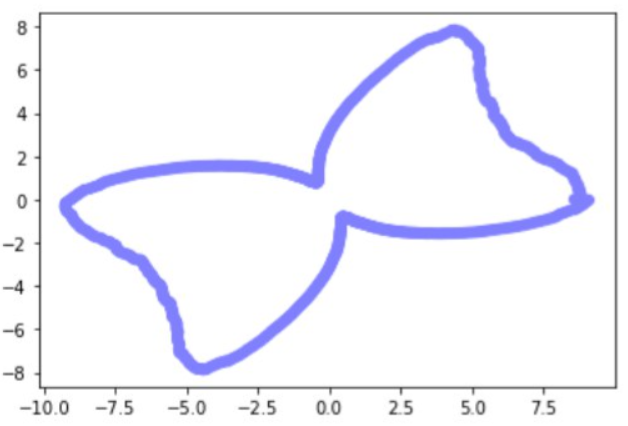
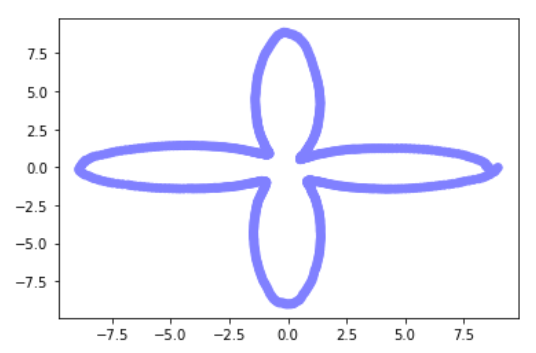
5.ПРИМЕР ПОСТРОЕНИЯ ПРИБЛИЖЕННОЙ ГРАНИЦЫ МНОЖЕСТВА ДЛЯ ДВУХ ВЗЛЕТНО-ПОСАДОЧНЫХ ПОЛОС

Для реализации алгоритма были использованы элементы программного комплекса, описанного в [Торишный]. Начальные данные, отражающие изменение ветра, взяты из [Кан, 2009]:

σ_{ξ} = 3 \frac{м}{сек}, σ_{ε} = 15 °, γ = \frac{π}{2}, α = 0,99,

w_{ymax} = 15 \frac{м}{сек}, w_{xmin} = - 25 \frac{м}{сек}, w_{xmax} = 10 \frac{м}{сек} .

Найденная начальная точка:

v_{0} = 9.678

,

β_{0} = 0

. Приближенную границу множества представим на Рис. 1.

Рис. 1. Приближенная граница множества для двух ВПП при

γ = \frac{π}{2}

Возьмем теперь угол

γ = \frac{π}{3}

при тех же параметрах.

Найденная начальная точка:

v_{0} = 9.248

,

β_{0} = 0

. Полученная приближенная граница множества представлена на Рис. 2:

Рис. 2. Приближенная граница множества для двух ВПП при

γ = \frac{π}{3}

Теперь уменьшим предел бокового ветра до

5 \frac{м}{сек}

и немного расширим допустимые границы для продольного ветра:

w_{xmin} = - 20 \frac{м}{сек}, w_{xmax} = 20 \frac{м}{сек}

. Угол между полосами

γ = \frac{π}{2}

. Начальная точка:

v_{0} = 8.057

,

β_{0} = 0

.

Получаем новую границу, похожую на крест (Рис. 3). Применим те же самые параметры для случая

γ = \frac{π}{3}

(Рис. 4).

Рис. 3. Приближенная граница множества для двух ВПП при

γ = \frac{π}{2}

и минимальном

w_{ymax}

Рис. 4. Приближенная граница множества для двух ВПП при

γ = \frac{π}{3}

и минимальном

w_{ymax}

Начальная точка:

v_{0} = 8.486

,

β_{0} = 0

.

Таким образом, получаем, что при небольшом боковом ветре и достаточно больших пределах продольного ветра искомое множество похоже на крест. Например, как на Рис. 3 при угле

\frac{π}{2}

. При увеличении бокового ветра множество стремится к виду, изображённому на Рис. 1. Аналогично для любого угла.

Дальше представим иные характерные формы получаемых множеств и их параметры.

На Рис. 5 изображена граница множества при достаточно большой максимальной боковой скорости и небольших границах продольной с параметрами

σ_{ξ} = 3.8 \frac{м}{сек}, σ_{ε} = 13 °

.

Рис. 5. Приближенная граница множества для двух ВПП при большом боковом ветре для угла

\frac{π}{2}

Полученная начальная точка в таком случае:

v_{0} = 9.287

,

β_{0} = 0

.

Приближенная граница множества с параметрами

σ_{ξ} = 1.9 \frac{м}{сек}, σ_{ε} = 15 °

,

w_{ymax} = 5 \frac{м}{сек}, w_{xmin} = - 20 \frac{м}{сек}, w_{xmax} = 10 \frac{м}{сек}

представлена на Рис. 6.

Получаем начальную точку границы множества:

v_{0} = 6,57

,

β_{0} = 0

.

Рис. 6. Приближенная граница при маленьком боковом ветре для угла

\frac{π}{3}

ЗАКЛЮЧЕНИЕ

Основным результатом работы является алгоритм нахождения допустимого множества векторов скорости ветра. Для достижения этой цели была использована гладкая аппроксимация функции вероятности.

Боковой ветер представляет больший риск при посадке, чем продольный ветер, что требует строгих ограничений. Это приводит к формированию области безопасности в виде эллипса на взлетно-посадочной полосе. А в случае двух пересекающихся ВПП такое сочетание параметров задачи, как ограничения на скорость ветра и конфигурация полосы, позволяет получить большое количество разных характерных форм множества.

Литература

Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления летательными аппаратами // М.: Машиностроение, 1987 – 302 с.
Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероятностными критериями // М.: Физматлит, 2009. - 372 с.
Кибзун А.И., Малышев В.В. Обобщенный минимаксный подход к решению задач с вероятностными ограничениями // Изв. АН СССР. Техническая кибернетика. 1984. № 1. С. 20–29.
Sobol V.R., Torishnyy R.O., Pokhvalenskaya A.M. Application of the smooth approximation of the probability function in some applied stochastic programming problems // Вестн. ЮУрГУ. Сер. Матем. Моделирование и программирование. 14:3. 2021. С. 33-45.
Кибзун А.И., Иванов С.В., Степанова А.С. Построение доверительного множества поглощения в задачах анализа стохастических систем // Автомат. и телемех., 2020, С. 21-36.
Кибзун А.И., Иванов С.В. Построение доверительных множеств поглощения с помощью статистических методов // Автомат. и телемех., 2020, С. 82-99.
Соболь В.Р., Торишный Р.О. О гладкой аппроксимации вероятностных критериев в задачах стохастического программирования // Тр. СПИИРАН, 2020 – 38 с.
Кибзун А.И., Третьяков Г.Л. Дифференцируемость функции вероятности // Доклады Академии наук, 1997, С. 159-161.
Uryasev S.. Derivatives of probability functions and some applications. // Annals of Operations Research. 1995, Vol. 56. № 1. pp. 287–311.
Торишный Р.О. Программный комплекс для анализа задач стохастического программирования с вероятностным критерием // М.: ВКиТ, 2022 – 12 с.

Информация об авторах

Склезнева Ксения Андреевна, студент, кафедра «Теория вероятностей и компьютерное моделирование», Московский Авиационный Институт (национальный исследовательский университет) (МАИ), Москва, Российская Федерация, e-mail: xenia.sklezneva@gmail.com

Соболь Виталий Романович, кандидат физико-математических наук, доцент кафедры «Теория вероятностей и компьютерное моделирование», Московский Авиационный Институт (национальный исследовательский университет) (МАИ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0002-1275-0445, e-mail: vitsobol@mail.ru

Метрики

Просмотров web

За все время: 21
В прошлом месяце: 0
В текущем месяце: 21

Скачиваний PDF

За все время: 3
В прошлом месяце: 0
В текущем месяце: 3

Всего

За все время: 24
В прошлом месяце: 0
В текущем месяце: 24

PlumX

Метрики публикации