Математическая модель процесса ингибирования газосборных шлейфов

Паранук  А.А.; Терещенко И.А.; Шишков В.С.

doi:10.17759/mda.2024140405

Моделирование и анализ данных
2024. Том 14. № 4. С. 78–90
doi:10.17759/mda.2024140405
ISSN: 2219-3758 / 2311-9454 (online)

Математическая модель процесса ингибирования газосборных шлейфов

0

Паранук А.А., Терещенко И.А., Шишков В.С.

Аннотация

В работе представлена оригинальная математическая модель определения термобарических параметров промыслового шлейфа, в которой учитывается конвективный теплоперенос, турбулентное ядро, возникающее в полости газосборного шлейфа. В представленной математической модели теплоперенос, теплообмен и турбулентное ядро описывается двумя безразмерными коэффициентами. Также в работе приводится авторское уравнение определение влагосодержания природного газа, которая позволяет точнее проводить расчеты процесса ингибирования метанолом в газосборных шлейфах (промысловых газопроводах). Методика расчета ингибитора, которая рассматривается в работе, может применяться для ликвидации гидратов при их образовании в газосборных шлейфах. В методике учитывается фазовый переход газ-гидрат, режим работы газопровода, расход в шлейфе, давление, температура и концентрация ингибитора. Верификация методики проводилась при помощи промысловых данных, полученных с действующего газового месторождения Краснодарского края.

Общая информация

Ключевые слова: гидраты природного газа, влагосодержание природного газа, клатратное соединение, ингибитор, теплопотери, промысловый газопровод, конвективный теплоперенос

Рубрика издания: Анализ данных

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140405

Получена: 06.11.2024

Принята в печать: 02.12.2024

Для цитаты: Паранук А.А., Терещенко И.А., Шишков В.С. Математическая модель процесса ингибирования газосборных шлейфов // Моделирование и анализ данных. 2024. Том 14. № 4. С. 78–90. DOI: 10.17759/mda.2024140405

Полный текст

Введение

При добыче природного газа, в зимний период возникает проблема образования гидратов в промысловых системах сбора природного газа. Так как, природный газ, поступающий из скважины не обработанный, и содержит различные нежелательные компоненты (вода, жидкие углеводороды, соли жесткости), которые приводят к авариям и аварийным инцидентам в шлейфах газопроводов.

Основным компонентом, который является катализатором образования гидратов природного газа, является избыточное содержание влаги в добываемом природном газе. Вода, которая содержится в добываемом природном газе при определенных термобарических параметрах, кристаллизуются и образует клатратное соединение «гидрат». В целях обеспечения работоспособности газосборного шлейфа, и ликвидации гидратов в полость газопровода подают ингибитор (метанол), согласно утвержденным технологическим картам. Использование данной технологий приводит перерасходу ингибитора, а также к дополнительным материальным затратам на хранение и транспортировку ингибитора. Для материальных затрат и сокращения расходов на процесс ингибирования, необходимо использовать дозированную подачу метанола, что влечет за собой достаточно сложный технологический расчеты, который включает несколько математических моделей. К этим математическим моделям относятся: определение температуры и давления природного газа по всей длине газосборного шлейфа, определение температуры фазового перехода, определение объема влаги, который содержится в природном газе, теплопотери шлейфа за счета процесса теплопередачи в окружающую среду и т.д.

Математическое моделирования и постановка задачи

Для моделирования термобарических параметров газосборного шлейфа воспользуемся оригинальной математической моделью, которая приводится в работах авторов [1-3]

Предположим, что внутри сечение газового потока в полости трубопровода возникает турбулентное ядро [4], в нем происходит интенсивный конвективный теплоперенос (процесс, обусловленный передачей тепловой энергии между молекулами газа), тогда считаем усреднению температуру температурой ядра. При этом в турбулентном режиме потока газа у стенки возникает пограничный слой, который можно характеризовать средним значением скорости потока

ϑ

. Распределение температуры по сечению промыслового трубопровода, принимаем переменной, так как происходит теплообмен между стенкой и окружающей средой. Тогда для промыслового газопровода, принимаем две координаты (x, r). Причем х отсчитывается из выхода со скважины, а r – осевая линия промыслового газопровода (см.рис.1).

Рис. 1- Участок промыслового газопровода (шлейфа)

Запишем уравнение теплопроводности для рисунка 1 в цилиндрических системе координат. (r, , х) при условии что процесс стационарный с конвективным переносом тепла для шлейфа получим [1-4]:

\frac{\partial T}{\partial t} = χ (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} T}{\partial θ^{2}} + \frac{\partial^{2} T}{{\partial x}^{2}}),

(1)

где

T

– температура газа, °С;

χ

- коэффициент температуропроводности

(χ = \frac{λ}{ρс})

, м2/с; содержит

λ

– коэффициент теплопроводности газа, Вт/(град∙м);

ρ

– плотность газа, кг/м3.

В рассматриваемом уравнении (1) температурное поле не зависит от угла

θ

, поэтому полагая что

\frac{\partial^{2} T}{\partial θ^{2}} = 0

. Тогда получим уравнение теплопроводности в виде:

\frac{\partial T}{\partial t} = χ (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r} + \frac{\partial^{2} T}{{\partial x}^{2}}),

(2)

При условии, что температура газопровода зависит от координат

T (x, r)

, и считая, что течение газа стационарно, т.е.

\frac{\partial T}{\partial t} = 0

при конвективном переносе вдоль газопровода

ϑ_{r} = 0

, при

ϑ_{x} = ϑ

уравнение (2) примет вид:

ϑ \frac{\partial T}{\partial x} = χ (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r} + \frac{\partial^{2} T}{{\partial x}^{2}})

(3)

Далее в уравнении (3) обезразмерим по

x = RX

(R - шлейфа) и масштабируем координату

R - r = RY \sqrt{ε}

, и также произведем замену переменных

(x, r) = (X, Y)

, введем безразмерный параметр

ε = \frac{χ}{ϑR}

, тогда уравнение примет следующий вид [3]:

\frac{\partial T}{\partial X} = \frac{\partial^{2} T}{{\partial Y}^{2}} - \frac{\sqrt{ε}}{1 - Y \sqrt{ε}} \frac{\partial T}{\partial Y} + ε \frac{\partial^{2} T}{{\partial Х}^{2}}

. (4)

Принимая, что

ε = \frac{χ}{ϑR} ≪ 1

, для промысловых шлейфов, тогда проведя оценку порядка величин получим

10^{- 5}

, тогда двумя последними слагаемыми в правой части уравнения (4) можно пренебречь по сравнению с первым уравнением [1-3].

Для проверки, слагаемых воспользуемся следующими рассуждениями, принимая температуру газа равной 200С, а стенки 100С, принимаем, что на расстоянии 1 см от стенки температура равняется средней температуре по сечению. Тогда изменение температуры

∆ T = 1 0^{0} С

, соответственно изменение радиуса

∆ r = R - r = 1 см

. Далее принимая R=10 см, произведем следующую оценку порядка величин для промыслового шлейфа:

Y = \frac{R - r}{R \sqrt{ε}} \approx \frac{0,1}{3,0 - 10^{- 3}} \approx 30

, соответственно

∆ Y \approx \frac{Y}{10} \approx 3

; тогда

\frac{\partial T}{\partial Y} \approx \frac{∆ T}{∆ Y} \approx \frac{10}{3} \approx 3,3

; порядок второго слагаемого в правой части уравнения (4) оценивается для газовых шлейфов как

Y = \frac{\sqrt{ε}}{1 - Y \sqrt{ε}} \frac{\partial T}{\partial Y} \approx \frac{0,003}{1 - 30 \times 3,1 \times 10^{- 3}} \approx 0,01

.

Тогда, при отбрасывании слагаемого

\frac{\sqrt{ε}}{1 - Y \sqrt{ε}} \frac{\partial T}{\partial Y}

в уравнении (4), считая остальные слагаемые порядка единицы, составляет величину равную 1%.

Таким образом, для моделирования изменения температуры природного газа

T (X, Y)

при X,Y > 0 в тепловом пограничном слое принимается одномерное уравнение теплопроводности [1-4],

\frac{\partial T}{\partial Y} = \frac{\partial^{2} T}{\partial Y^{2}}

при граничных условиях

T (X,0) = T_{0}

получим;

T (0, Y) = T_{} .

(5)

где

T_{0}

– температура внутренней стенки трубы, а

T_{}

– температура газа в ядре потока (вдали от стенки), соответственно полагается, что

T_{} > T_{0}

. Решение задачи (5), в частности, дает следующий результат, где

y = Y \sqrt{ε}

:

{\frac{\partial T}{\partial y} |}_{y = 0} = \frac{T_{} - T_{0}}{\sqrt{πεX}}

, (6)

Переходим в уравнении (6) к физическим размерным величинами и получается:

{\frac{\partial T}{\partial r} |}_{r = R} = - (T_{} - T_{0}) \sqrt{\frac{ϑ}{xπ χ}}

. (7)

В уравнениях (6,7) температура

T_{0}

и

T_{}

постоянны при решении уравнения (5), а дальше они считаются меняющими вдоль оси шлейфа –

T_{0} (x)

и

T (x) = T_{}

, фактически – это свидетельствует об изменении температуры в пределах погрешности математической модели вдоль шлейфа газопровода с длиной много большей характерной толщины теплового пограничного слоя

R \sqrt{ε}

.

В математической модели принимаем, что q(t) удельное (по длине шлейфа) теплосодержание единичного «объема» природного газа (при условий, что газ движется со скоростью в шлейфа

ϑ

), внутренний диаметр газопровода D=2R, в метрах; через

T (x) = T_{}

- температура природного газа в ядре потока, которая зависит от координаты вдоль шлейфа.

Обозначим температуру на внешней стенке

T_{+}

(стенка включает теплоизоляцию), тогда для газосборного коллектора (шлейфа) запишем следующее выражение с учетом теплопередачи от природного газа к стенке [3,4]:

\frac{dq}{dt} = ϑ \frac{dq}{dx} = λ πD {\frac{dT}{dr} |}_{r = R} = λD (T_{0} - T) \sqrt{\frac{ϑ π}{χx}},

(8)

Тогда уравнение теплопередачи через стенку шлейфа и теплоизоляцию во внешнюю среду можно записать в виде:

ϑ \frac{d T}{dx} = \frac{π D^{2}}{4} ρc =

Λ

π D

(9)

где Λ – коэффициент теплопередачи через стенку коллектора единицы измерения Вт/(К∙м2, а определяется сопоставлением расчета с данными измерения как усредненная характеристика теплопередающих свойств стенки шлейфа вместе с теплоизоляцией. Полученные данные соответствует классической теории конвективного теплообмена, которая входит в число Нуссельта

Nu = \frac{D Λ}{λ}

, согласно источнику [5].

Аналитическое выражение температуры внешней стенки шлейфа полагаем не зависящей от температуры

T_{+}

(постоянно), тогда температура внутренней стенки

T_{0} (x)

будет зависящей. Согласно уравнению (9), выражение для определения температуры внутренней стенки примет следующий вид:

T_{0} = T_{+ - \frac{Dc ϑ ρ}{4 Λ} \frac{dT}{dx} .}

(10)

Подставляя уравнение (10) выражение (8), с учетом вида левой части уравнения (9) получим:

\frac{π D^{2}}{4} ρ cϑ \frac{dT}{dx} = λ D

, (11)

Тогда производная по температуре, зависящая от координаты в ядре потока выражается уравнением:

\frac{dT}{dx} = \frac{4 λ}{ρ cϑD} \sqrt{\frac{ϑ π}{χx}} \frac{T_{+ - T}}{π \frac{λ}{Λ} \sqrt{\frac{ϑ π}{χx}}}

(12)

Продифференцировав уравнение (12) с учетом

χ = \frac{λ}{ρс}

, запишем выражение в следующем виде:

\frac{dT}{dx} = \frac{4 λ}{D} \sqrt{\frac{χ π}{ϑx}} \frac{T_{+ - T}}{π + \frac{λ}{Λ} \sqrt{\frac{ϑ π}{χx}}}

(13)

Введем коэффициент потерь тепла

\frac{λ}{Λ} \sqrt{\frac{ϑ π}{χx}}

и коэффициент переноса тепла

β = \frac{8}{D} \sqrt{\frac{χ}{π ϑ}}

. При интегрировании уравнение (13) примет вид:

\int_{T_{1}}^{T_{2}} \frac{dT}{T_{+ - T}} = β \int_{0}^{L} \frac{\sqrt{x}}{\sqrt{x} +} d \sqrt{x}

(14)

Получим после интегрирования выражение:

\ln \frac{T_{+ - T_{1}}}{T_{+ - T_{2}}} = β

(15)

После тождественного преобразования уравнение (15) принимает вид:

T_{2} = T_{+ +}

(16)

где

\frac{2}{πD Λ} \sqrt{cQ λ}

;

β = 4 \sqrt{\frac{λ}{cQ}}

– коэффициенты отражают изменение температуры от ядра к стенке; Q – расход природного газа, с – теплоемкость природного газа, Дж/(кг∙К);

Уравнение (16) описывает потери тепла шлейфа в окружающую среду, но и возможен и обратный подвод тепла к природному газу, при этом

T_{1} (0)

и

T_{2} (L)

.

Поскольку модель для определения термобарических параметров промыслового газопровода построена, предложим уравнение для определения распределения влаги в шлейфе по длине до установки подготовки газа к транспорту [6]:

W (x) = (Y_{w} \frac{\sum M_{g}}{M_{w}}) \frac{0.457}{P (x)} e^{0.0735 T (x) - 0.00027 T {(x)}^{2}} + 0.0418 e^{0.054 T (x) - 0.00027 T {(x)}^{2}}

(17)

где Yw

-

молярная доля воды в газе, определяется по ГОСТ 34807-2021 с помощью переносного гигрометра Hygrovision-mini;

\sum M_{g} -

средний молекулярный вес газовой смеси г/моль; Mw

-

молекулярная масса воды, г/моль.

Давление внутри промыслового шлейфа будем вычислять по закону линейного изменения его квадрата

0 < x < L .

Тогда выражение для определения давления в произвольные точки примет вид;

P

(18)

Для определения температуры образования воспользуемся известной моделью из источников [7 - 9]

T_{Г} (r) = T_{н} + \frac{({T_{ф} - T}_{н})}{\ln \frac{R_{0}}{R_{0} - ξ}} \ln \frac{r}{R_{0}}

(19)

где

ξ

– толщина гидратного слоя, в метрах; Tф – температура фазового перехода Tф= Tф(P,T); TГ – температура гидрата, К; Tн – температура на внешней поверхности стенки газопровода, К; R0 – радиус чистой трубы (

{r = R}_{0} - ξ

), в метрах;

Уравнение (19) позволяет определить температуру образования гидратов в промысловых трубопроводах, так как общая постановка модели включает фазовый переход и описывается задачей Стефана. Она особенно актуальна при различных режимах эксплуатации газосборного шлейфа.

Для определения температуры фазового перехода воспользуемся следующим уравнением [7-9]

T_{ф} = T_{ф}^{0} (P) - {ΔT}_{ф} (C)

(20)

где

T_{ф}^{0} (P)

– величина температуры фазового перехода газ – гидрат при отсутствий ингибитора, который определяется индивидуально непосредственно для конкретного месторождения природного газа (экспериментально).

{ΔT}_{ф} (C) = \frac{KC}{M (100 - C)}

(21)

где K- константа, зависящая от конкретного ингибитора (метанол М = 32,04 г/моль); C- концентрация метанола %;

{ΔT}_{ф} (C)

- сдвиг равновесной температуры образования гидратов в присутствии ингибитора

Для определения концентрации ингибитора, который приводит к сдвигу температуры образования гидратов на величину

{ΔT}_{ф} (C)

определяется

C_{г} = \frac{M {ΔT}_{ф}}{M {ΔT}_{ф} (C) + K}

(22)

При эксплуатации промысловых газопроводов в метанол подается с концентрацией от 90 до 95% [9].

Для определения расхода метанола в газосборных шлейфах воспользуемся выражением:

G = \frac{W C_{г}}{C_{0} - C_{г}} + \frac{100 - C_{г}}{C_{0} - C_{г}} (q_{g 1} - q_{g 2} + q_{k 1} - q_{k 2})

(23)

где W – количество содержащейся в природном газе воды г/м3;

q_{g 1}

– количество метанола, содержащегося в поступающем природном газе;

q_{g 2}

– количество метанола в газовой фазе при его концентрации в водном растворе СТ;

q_{k 1}

– количество метанола, содержащегося в поступающем с газом углеводородном конденсате;

q_{k 2}

– количество метанола, растворяющегося в углеводородном конденсате при концентрации водного раствора метанола СТ [10].

Верификация математической модели

Для проверки математической модели будем использовать реальные промысловые данные, полученные с действующего газового месторождения Краснодарского края. Исходные данные по месторождению приведены в таблице 1.

Таблица 1. Исходные данные для верификации математической модели

№ скважины	Диаметр шлейфа м	Длина шлейфа км	Давление Р1, МПа	Давление Р2, МПа	Температура Т1, 0С	Расход природного газа млн.м3/сутки	Толщина стенки трубы мм
1	200	8	3,4	2,8	10	0,96	6,0
2	300	6	4,5	3,2	9,5	0,98	8,0
3	250	5	3,2	2,6	11	0,83	7,0
4	400	3	4,5	3,6	8,5	0,89	9,9
5	200	3	3,2	2,9	10,5	0,82	6,0
6	200	2,2	3,0	2,8	9,7	0,95	6,0
7	300	1,8	4,2	3,75	8,8	0,98	8,0

Продолжение таблицы 1

8	400	7	5,2	3,6	10,1	0,78	9,9
9	200	1,8	2,2	2,1	9,4	0,87	6,0
10	300	1,2	4,5	3,9	10,1	0,92	8,0
11	200	10	3,5	2,2	9,8	0,93	6,0
12	200	3	3,1	2,85	9,7	0,95	6,0
13	300	15	4,25	3,65	9,4	0,91	8,0
14	400	6	3,9	3,5	8,9	0,91	9,9
15	200	8	4,4	3,3	10,12	0,92	6,0
16	250	9	3,2	2,9	8,9	0,98	7,0
17	300	12,4	4,12	3,5	10	0,89	8,0
18	300	13,5	4,25	3,45	9,8	0,88	8,0
19	200	7,6	3,1	2,8	8,9	0,85	6,0
20	200	15,6	3,75	3,02	9,85	0,84	6,0

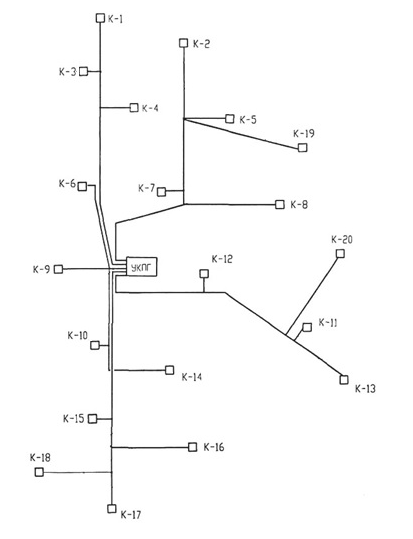
Рис.2 – Газосборная сеть Анастасиевско – Троицкое нефтегазоконденсатного месторождения

Для расчета принимаем, что теплоемкость природного газа с= 2483 Дж/(кг*К); молярная масса природного газа μ = 0.016 г/моль; коэффициент теплопередачи через стенку коллектора Λ= 0,2 Вт/(м2* 0С). Изоляция коллектора усиленная, состоит их 3 слоев ленты толщиной 1,2 мм; коэффициент теплопроводности газа

λ

= 0,2, температура окружающей среды -50С. Для определения распределения влаги в промысловом газопроводе будем использовать для расчета по формуле (15) шаг c 400 м по длине шлейфа. В таблицу 2 будем вносить максимальное значение влагосодержания исследуемых промысловых шлейфов.

Таблица 2. Расчетные данные по предложенной математической модели

№ скважины	Температура Т2,0С	Макс. влагосодержание природного газа $W (x)$ г/моль	Скорость газа $ϑ$ , кг/с	Коэффициенты отражают изменение температуры от ядра к стенке		Расход природного газа кг/с
№ скважины	Температура Т2,0С	Макс. влагосодержание природного газа $W (x)$ г/моль	Скорость газа $ϑ$ , кг/с		$β$	Расход природного газа кг/с
1	8,52	2,252	778,8	0,54639	0,00233	237,3
2	8,53	2,251	528,2	0,36803	0,00231	242,27
3	9,898	2,253	537,57	0,40643	0,00251	205,19
4	8,19	2,249	359,1	0,26304	0,002420	220,02
5	9,86	2,252	665,2	0,50497	0,002521	202,72
6	9,4	2,251	770,7	0,54353	0,002342	234,86
7	8,79	2,249	528,2	0,36803	0,002306	242,27
8	8,71	2,252	314,69	0,24625	0,002585	192,83
9	9,09	2,251	705,81	0,52014	0,002447	215,08
10	8,26	2,252	495,88	0,35659	0,002380	227,44
11	8,0	2,251	754,48	0,53778	0,002367	229,91
12	9,21	2,251	770,71	0,54353	0,002342	234,86
13	7,1	2,251	490,49	0,35464	0,002393	224,97
14	7,97	2,249	367,14	0,26598	0,002393	224,97
15	8,6	2,251	746,37	0,53488	0,002380	227,44
16	7,36	2,249	582,9	0,42323	0,002406	222,5
17	7,89	2,251	479,71	0,35072	0,002420	220,02
18	7,56	2,251	474,32	0,34875	0,002433	217,55
19	7,45	2,249	689,58	0,51413	0,002476	210,13
20	7,18	2,25	681,47	0,51110	0,002491	207,66

Выводы

На основании анализа данных таблицы 1 установлено, что в исследуемых промысловых шлейфах при температуре окружающей среды (-50С) и принятых расчетных параметрах, образование гидратов в шлейфах не происходит, то есть промысловые газосборные шлейфы не подвергаются облитерации из-за достаточно высокой температуры природного газа, которая поступает из скважины. Также в работе не применяются расчеты по формулам (17-21) так как их используют только при образовании и ликвидации гидратов. Данные формулы приводятся в статье для предоставления единой методики расчета при различных режимах работы промысловых шлейфов. Также в предложенной математической модели определения термобарических параметров применяются безразмерные коэффициенты, которые отражают изменение температуры от ядра к стенке и конвективный теплоперенос.

Литература

Бунякин А. В., Паранук А. А., Мамий С. А., Кешоков М. В. Моделирование тепловых характеристик промысловых шлейфов и проверка условия образования гидратов природного газа /, , , // Технологии нефти и газа. – 2019. – № 5(124). – С. 47-52. – DOI 10.32935/1815-2600-2019-124-5-47-52.
Быков И. Ю. , Паранук А.А., Бунякин А.В. Математическое моделирование температурных условий гидратообразования в промысловых газосборных коллекторах Западно-Песцовой площади Уренгойского НГКМ // Инженерно-физический журнал. – 2022. – Т. 95, № 1. – С. 225-231.
Паранук А.А. Косвенный контроль газосборной сети // Нефтегазовое дело. 2012. Т. 10. № 1. С. 36 –
Юдаев Б.Н. Теплопередача: учебник для вузов. – 2- е.изд., перераб. и доп. –М.: Высш.школа,1981. 319 с.
Паточкина О. Л., Казаринов Ю. Г., Ткаченко В. И. Физическая модель зависимости числа Нуссельта от числа Рэлея // Журнал технической физики. – 2016. – Т. 86, № 11. – С. 23-29.
Паранук А.А. Дунаев В.И. Приходько М.Г. Об одной методике определения влагосодержания природного газа в трубопроводных системах //Физико-математическое моделирование. Нефть, газ, энергетика. Том 10. № 3 (39) – С. 60-72.
Буц, В. В. Модель образования гидратов в трубопроводах в присутствии ингибитора // Территория Нефтегаз. – 2010. – № 6. – С. 20-25.
Воеводин А.Ф. Газотермодинамический расчет потоков в простых и сложных трубопроводах // Известия СО АН СССР. Сер. Техн. науки. 1969. Вып. 2. №8. С. 45-55.
Бондарев Э.А., Васильев В.И., Воеводин А.Ф., Павлов Н.Н., Шадрина А.П. Термодинамика систем добычи и транспорта газа// М.; Наука, 1988. 270 с.
Буц В. В. Математическое моделирование процесса ингибирования образования гидратов в газопроводах с оптимизацией расхода ингибитора: специальность 05.13.18 – Математическое моделирование, численные методы и комплексы программ: диссертация на соискание ученой степени кандидата технических наук – г.Саратов, 2012. – 153 с.

Информация об авторах

Паранук Арамбий Асланович, кандидат технических наук, Доцент кафедры систем транспортировки газа и нефти и оборудования нефтегазовой промышленности, Кубанский государственный технологический университет (ФГБОУ ВО КубГТУ), Краснодар, Россия, ORCID: https://orcid.org/0000-0003-2443-683X, e-mail: rambi.paranuk@gmail.com

Терещенко Иван Анатольевич, Старший преподаватель кафедры систем транспортировки газа и нефти и оборудования нефтегазовой промышленности, Кубанский государственный технологический университет (ФГБОУ ВО КубГТУ), Краснодар, Россия, ORCID: https://orcid.org/0000-0002-4804-4251, e-mail: ongptr@mail.ru

Шишков Валерий Сергеевич, кандидат технических наук, Доцент кафедры нефти и газа и землеустройства, Филиал ФГБОУ ВО Майкопский государственный технологический университет (МГТУ), Россия, ORCID: https://orcid.org/0000-0003-2112-1605, e-mail: vsshishkov@gmail.com

Метрики

Просмотров

Всего: 6
В прошлом месяце: 0
В текущем месяце: 6

Скачиваний

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0

PlumX

Метрики публикации