Моделирование и анализ данных
2024. Том 14. № 2. С. 23–44
doi:10.17759/mda.2024140202
ISSN: 2219-3758 / 2311-9454 (online)
Применение статистик m* и d* для оценки качества данных психологического исследования с помощью закона Бенфорда (на примере измерения времени реакции)
Аннотация
Целью предлагаемого исследования было рассмотрение свойств статистик, используемых для изучения согласия распределения первой значащей цифры закону Бенфорда, m^* и d^* при достаточно скромных объёмах выборки (10≤n ≤70). Для достижения цели было проведено симуляционное исследование. Симулировались данные лог-нормального распределения с параметрами, имитирующими распределение измерений времени реакции. Распределение первой значащей цифры изучалось у стандартизированных значений, возведённых в степень γ; 5≤γ≤100. Выяснилось, что статистика m* не зависит от степени числа в отличие от d*. Были установлены критические значения для выборок объёмом от 10 до 70 наблюдений с шагом h = 10. Оказалось, что критические значения при малых n статистики d* близки к асимптотическим, в то время как критические значения статистики m* существенно больше. Функциональность установленных критических значений проверялась в рамках экспериментального исследования: один респондент выполнял когнитивный тест Струпа в соответствии с инструкцией (контрольный случай), другой – нарушал её (экспериментальный случай). Обнаружено, что статистика d* не позволяет дифференцировать поведение испытуемых. В свою очередь m* оказалась чувствительной к изменениям в поведении респондентов и в экспериментальном случае существенно чаще позволяла отвергнуть нулевую гипотезу о соответствии распределения первой значащей цифры стандартизированного значения времени реакции закону Бенфорда в сравнении с контрольным. Таким образом, делается предварительный вывод о том, что статистика m* в сравнении с d* более функциональна при изучении качества данных о времени реакции при небольших n.
Общая информация
Ключевые слова: закон Бенфорда, время реакции, статистика
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2024140202
Получена: 13.03.2024
Принята в печать:
Для цитаты: Колачев Н.И. Применение статистик m* и d* для оценки качества данных психологического исследования с помощью закона Бенфорда (на примере измерения времени реакции) // Моделирование и анализ данных. 2024. Том 14. № 2. С. 23–44. DOI: 10.17759/mda.2024140202
Полный текст
Введение
Высокое качество собранных данных имеет ключевое значение для формулирования выводов во многих эмпирических исследованиях. На достоверность собираемых данных могут влиять различные факторы: несовершенства измерительного инструмента, методические погрешности, отсутствие стандартизации процедуры сбора данных и многое другое. Особого внимания требуют результаты измерения нефизических величин (например, мотивации, когнитивных процессов и пр.), которые не поддаются непосредственному, прямому измерению, и, как правило, подвержены влиянию флуктуаций в поведении респондента (испытуемого).
В части исследования качества многое сделано для оценки достоверности данных, собираемых опросно-анкетными методами. К примеру, хорошо известно, как справляться с таким фактором недостоверности самоотчётных данных, как социальная желательность [Осин, 2011]. Более того, разработаны специальные подходы для измерения характеристик личности, которые могут подвергаться искажениям при самоотчёте. К числу таких подходов относятся методы поведенческих сценариев [Peng, 1997], якорных виньеток [Primi, 2016], сценарных шкал [Antipkina, 2020].
При этом необходимо констатировать, что на сегодняшний день не предложены методы анализа достоверности данных о времени реакции, что делает настоящую работу особенно актуальной, ведь измерение времени реакции является основой когнитивной психологии [Психология высших когнитивных, 2004].
Время реакции
Время реакции широко распространено и обычно используется в науках о поведении для оценки и моделирования когнитивных процессов, чаще всего внимания [Dutilh, 2019]. Под временем реакции понимают временной интервал между появлением какого-либо стимула и ответом (реакцией) на этот стимул со стороны испытуемого [Карпенко, 1998]. Обычно измеряется в миллисекундах (мс). В исследованиях с использованием показателя времени реакции выделяют три вида возможных реакций [Зайцев, 2002]:
-
Простая сенсомоторная реакция (реакция на появление любого стимула);
-
Дифференцировочная реакция простого выбора (реакция на стимулы определенного типа и игнорирование всех остальных);
-
Дифференцировочная реакция сложного выбора (ответ на каждый тип стимула должен сопровождаться определенной реакцией).
На протяжении многих лет время реакции служило основой для значимых открытий в экспериментальной, когнитивной психологии, нейрофизиологии, таких как эффект Струпа [Stroop, 1935], аффективный прайминг [Zhang, 2012] и др. По сей день вопросы работы со временем реакции являются актуальными для исследователей. Так, известно, что распределение времени реакции во многих исследованиях имеет правостороннюю асимметрию [Whelan, 2008], поэтому в качестве меры центральной тенденции рекомендуют использовать медиану или моду, а не среднее арифметическое. Кроме того, ряд исследователей говорит о лог-нормальности распределения времени реакции, то есть логарифм времени реакции имеет нормальное распределение [Marmolejo-Ramos, 2015]. Некоторые исследователи указывают, что распределение времени реакции подчиняется так называемому экс-гауссовскому распределению (смесь гауссовского и экспоненциального) [Whelan, 2008].
Основным фактором, влияющим на качество данных о времени реакции, является невыполнение испытуемым поставленной задачи. Если испытуемый хаотично, бессистемно реагирует на стимулы (например, нажимать клавиши на клавиатуре компьютера, ведь большая часть современных исследований проводится в компьютерном формате, даже онлайн [R Core Team, 2021]), то исследователи получают недостоверные данные, ничего не свидетельствующие об особенностях познавательных процессов испытуемого. Существующие рекомендации по работе с данными о времени реакции лишь предлагают способы «подгонки» данных под существующие статистические методы, как, например, исключение выбросов по правилу «±2 стандартных отклонения», или методы работы с пропущенными данными [Lachaud, 2011]. Все эти рекомендации не позволяют судить о достоверности собранных данных. В связи с этим возникает острая необходимость в поиске способов проверки качества получаемых или генерируемых данных. Одним из вариантов может выступить использование закона Бенфорда.
Закон Бенфорда
Стоит отметить, что не все переменные подчиняются закону Бенфорда. Так, считается, что «почтовые индексы, выигрышные номера в лото и рулетку, номера телефонов и любые объемы данных, размер которых не достаточен для применения статистических методов» [Кувакина, 2013, с. 76]. Кроме того, время реакции в пределах от 100 до 200 мс может быть, например, результатом быстрой догадки. Такие быстрые реакции легко выявляются, и их обычно исключают из анализа [Whelan, 2008]. При этом такие значения встречаются в распределении реже, чем, допустим, значения в интервале от 400 до 500 мс, что говорит о низкой согласованности первой значащей цифры исходных данных о времени реакции с законом Бенфорда, поскольку, согласно этому закону, цифры 1 и 2 встречаются чаще, чем 4 и 5.
Другой существенной проблемой применения закона Бенфорда является подбор подходящих методов оценки согласия эмпирических данных с этим законом. Тестирование гипотезы о соответствии эмпирического распределения значащих цифр закону Бенфорда обычно происходит методом хи-квадрата или с помощью критерия Колмогорова [Morrow, 2014]. Как полагает Джон Морроу, эти тесты являются достаточно консервативными, то есть довольно часто не позволяют отклонить нулевую гипотезу в ситуации, когда данные не согласуются с законом Бенфорда (другими словами, имеют высокую вероятность ошибки II рода). В связи с этим возникла необходимость разработки новых тестов для проверки гипотезы о соответствии данных этому закону.
Модификации статистических тестов согласия с законом Бенфорда
Решением проблемы консервативности статистических тестов занялся Джон Морроу [Morrow, 2014]. В своей работе он доказал следующую теорему:
пусть X – непрерывная случайная величина, B – закон Бенфорда, тогда
Также учёный показал, что предложенные им статистические тесты достигают достаточной мощности при объёме выборки, превышающем 80 наблюдений (при уровне значимости α=0.01).
-
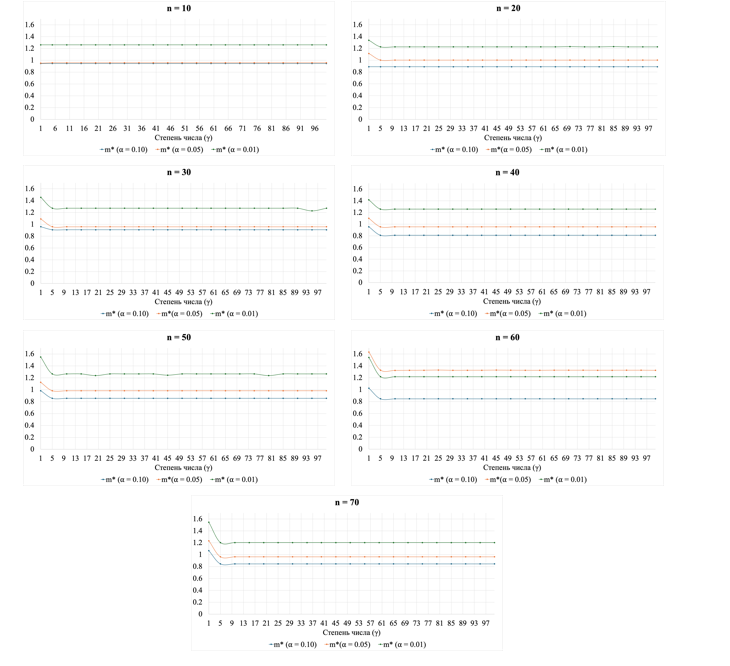
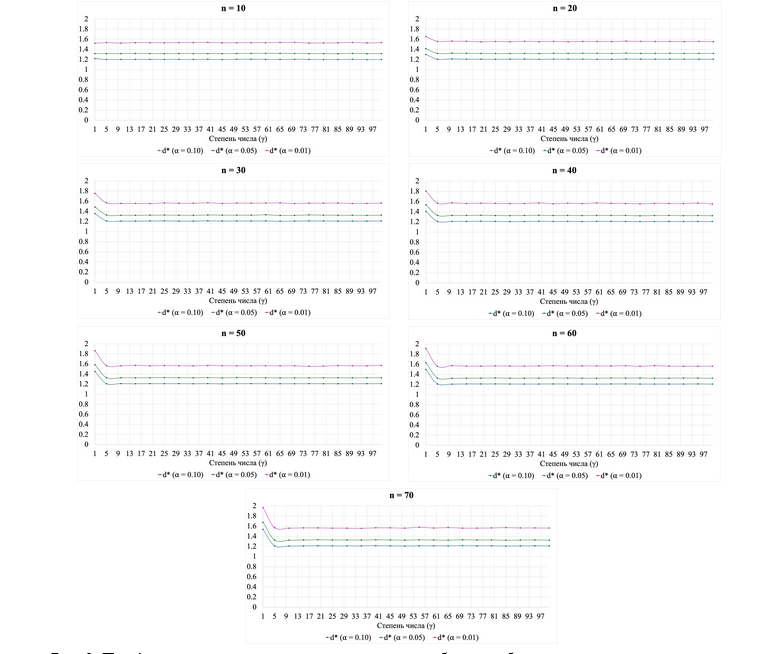
1.Изучить, различаются ли значения и в зависимости от объёма выборки;
-
2.Исследовать, зависят ли значения статистик и от степени, в которую возводят стандартизированное значение времени реакции, при контроле объёма выборки;
-
3.Установить критические значения статистик и для небольших по объёму выборок ( ) на основе симуляций из лог-нормального распределения;
-
4.Проверить функциональность установленных критических значений на экспериментальном (эмпирическом) примере.
Дисперсионный анализ основан на вычислении межгрупповой и внутригрупповой дисперсии и расчёте статистики Фишера (F-статистики):
Симуляционное исследование дополнено экспериментальным (эмпирическим). В рамках этого исследования два респондента прошли когнитивный тест (тест Струпа), который заключается в том, что испытуемые нажимают нужные клавиши на клавиатуре компьютера в зависимости от цвета краски появившегося слова по следующему правилу: «←» – красный, «↑» – жёлтый, «↓» – зелёный, «→» – синий. Причём появившееся слово обычно означает цвет, тем самым возникает семантическая интерференция. В ходе выполнения теста фиксируется время реакции и правильность нажимания клавиши. Некоторые стимулы являлись нейтральными (например, вместо слова показывался набор символов «XXXXX»). На рисунке 1 представлен пример стимула.
Рис. 1. Пример стимула в тесте Струпа.
Первый респондент (контрольный случай) выполнял тест, согласно стандартной инструкции: «Ваша задача – как можно быстрее и точнее реагировать на окраску слова ведущей рукой. Для ответа необходимо использовать стрелки на клавиатуре: ВЛЕВО – для красного, ВВЕРХ – для желтого, ВНИЗ – для зелёного и ВПРАВО – для синего». Второй респондент (экспериментальный случай) был инструктирован выполнять тест в хаотичном, бессистемном режиме, игнорируя инструкцию к тесту.
Затем шанс экспериментального условия делился на шанс контрольного, тем самым получалось отношение шансов (odds ratio, OR):
Для интерпретации отношения шансов использованы данные исследования Чена и коллег [Chen, 2010]. Согласно их исследованию, малый эффект наблюдается при отношении шансов, находящемся в полуинтервале [1,52; 2,74), средний – в полуинтервале [2,74; 4,72), большой – в полуинтервале [4,72; +∞).
Симуляция данных выполнена в среде R [R Core Team, 2021] с использованием базовых функций «rlnorm» и «sample». Статистическая обработка данных проходила в программе jamovi [The jamovi project, 2023]. Визуализация выполнена с помощью Microsoft® Excel [Microsoft Corporation. Microsoft, 2018].
Результаты
Симуляционное исследование
Таблица 1. Корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики с учётом исключения выбросов
|
Объём выборки (n) |
|
|
|
|
10 |
0,00 |
0,00 |
0,00 |
|
20 |
0,00 |
0,00 |
0,29 |
|
30 |
0,00 |
0,00 |
-0,34 |
|
40 |
0,00 |
0,00 |
0,00 |
|
50 |
0,00 |
0,00 |
0,06 |
|
60 |
0,00 |
0,00 |
0,00 |
|
70 |
0,00 |
0,00 |
0,00 |
Таблица 2. Корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики с учётом исключения выбросов
|
Объём выборки (n) |
|
|
|
|
10 |
-0,17 |
0,03 |
-0,08 |
|
20 |
-0,20 |
0,01 |
-0,23 |
|
30 |
-0,01 |
-0,18 |
-0,06 |
|
40 |
-0,37 |
-0,55* |
-0,38 |
|
50 |
-0,11 |
-0,33 |
-0,24 |
|
60 |
-0,40 |
0,01 |
-0,29 |
|
70 |
0,05 |
-0,15 |
0,04 |
|
Прим. * p < 0,05 |
|||
Таблица 3. Критические значения для при разных уровнях значимости
|
Объём выборки |
|
|
|
|
10 |
0,946 |
0,958 |
1,262 |
|
20 |
0,890 |
1,002 |
1,225 |
|
30 |
0,907 |
0,958 |
1,273 |
|
40 |
0,809 |
0,955 |
1,259 |
|
50 |
0,856 |
0,983 |
1,266 |
|
60 |
0,847 |
0,968 |
1,219 |
|
70 |
0,845 |
0,965 |
1,204 |
|
Дж. Морроу (n > 80) |
0,851 |
0,967 |
1,212 |
Таблица 4. Критические значения для при разных уровнях значимости
|
Объём выборки |
|
|
|
|
10 |
1,204 |
1,321 |
1,538 |
|
20 |
1,208 |
1,326 |
1,563 |
|
30 |
1,211 |
1,331 |
1,569 |
|
40 |
1,213 |
1,330 |
1,574 |
|
50 |
1,211 |
1,329 |
1,572 |
|
60 |
1,212 |
1,330 |
1,571 |
|
70 |
1,214 |
1,333 |
1,578 |
|
Дж. Морроу (n > 80) |
1,212 |
1,330 |
1,569 |
Экспериментальное исследование
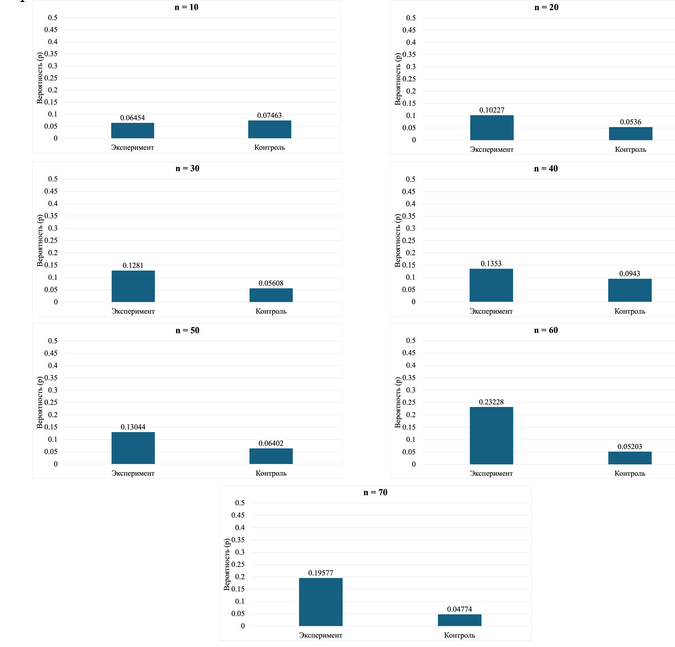
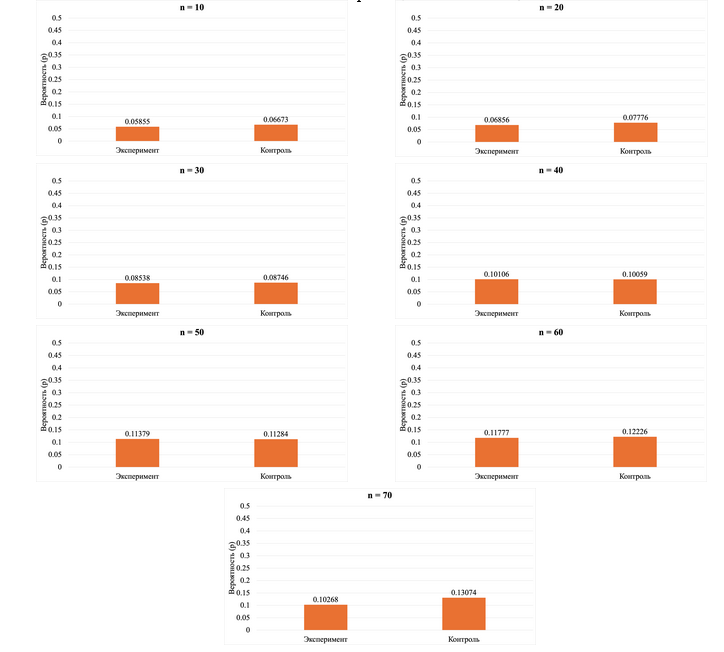
На рисунке 4 представлены вероятности отвержения нулевой гипотезы о соответствии распределения первой значащей цифры закону Бенфорда для экспериментального и контрольного случаев в разрезе разных объёмов выборки. Можно заметить, что распределение вероятности для контрольного случая флуктуирует в районе значения 0,06, при этом для экспериментального увеличивается при увеличении объёма выборки. Также на основе представленных вероятностей можно рассчитать отношение шансов при сравнении экспериментального и контрольного случаев.
На основе границ размеров эффекта можно сделать вывод, что при объёме выборки от 10 до 50 различия между экспериментальным и контрольным случаем довольно малы. В то же время при n = 60 и n = 70 различия являются большими.
Заключение
Ограничения исследования
Литература
- Зайцев А.В., Лупандин В.И., Сурнина О.Е. Время реакции в теоретических и прикладных исследованиях // Психологический вестник Уральского государственного университета. Вып. 3. 2002. Электронный ресурс: https://elar.urfu.ru/bitstream/10995/3964/3/pv-01-03.pdf (дата обращения: 03.03.2024).
- Зенков А.В. Отклонения от закона Бенфорда и распознавание авторских особенностей в текстах // Компьютерные исследования и моделирование. 2015. Том 7. № 1. С. 197–201. DOI:10.20537/2076-7633-2015-7-1-197-201
- Карпенко Л.А., Петровский А.В., Ярошевский М.Г. Краткий психологической словарь. Ростов-на-Дону, «ФЕНИКС», 1998. 505 с.
- Кувакина Л.В., Долгополова А.Ф. Закон Бенфорда: сущность и применение //Современные наукоемкие технологии. 2013. № 6. С. 74–76.
- Куликова А.А., Прохоров Ю.В. Односторонние устойчивые распределения и закон Бенфорда // Теория вероятностей и ее применения. 2004. Том 49. № 1. С. 178–184. DOI:10.4213/tvp244
- Лонэ М. Теорема зонтика, или искусство правильно смотреть на мир через призму математики. Бомбора, 2022. 352 с.
- Осин Е.Н. Проблема социальной желательности в исследованиях личностного потенциала. 2011. Электронный ресурс: https://www.hse.ru/data/2012/08/28/1242770673/Осин%202011.pdf?ysclid=lt46qcsjlj468944400 (дата обращения: 27.02.2024)
- Попина О.Ю., Савельева М.Ю., Бородина Ю.Б. Оценка качества отчетов о движении денежных средств российских организаций с использованием закона Бенфорда // Научные исследования: от теории к практике. 2016. № 4-2. С. 187–190.
- Психология высших когнитивных процессов / Под ред. Т. Н. Ушаковой, Н. И. Чуприковой. М.: Ин-т психологии РАН, 2004. 303 с.
- Старунова О.А., Руднев С.Г., Иванова А.Е., Семенова В.Г., Стародубов В.И. Применение закона Бенфорда для оценки качества данных профилактического скрининга // Математическая биология и биоинформатика. 2022. Том 17. № 2. С. 230–249. DOI:10.17537/2022.17.230
- Antipkina I., Ludlow L.H. Parental involvement as a holistic concept using Rasch/Guttman scenario scales // Journal of Psychoeducational Assessment. 2020. Vol. 38. № 7. P. 846–865. DOI:10.1177/0734282920903164
- Benford F. The law of anomalous numbers // Proceedings of the American philosophical society. 1938. P. 551–572.
- Campanelli L. On the Euclidean distance statistic of Benford’s law // Communications in Statistics-Theory and Methods. 2024. Vol. 53. № 2. P. 451–474. DOI:10.1080/03610926.2022.2082480
- Chen H., Cohen P., Chen S. How big is a big odds ratio? Interpreting the magnitudes of odds ratios in epidemiological studies // Communications in Statistics—simulation and Computation®. 2010. Vol. 39. № 4. P. 860-864. DOI:10.1080/03610911003650383
- Dixon P. The p-value fallacy and how to avoid it // Canadian Journal of Experimental Psychology/ Revue canadienne de psychologie expérimentale. 2003. – Vol. 57. № 3. P. 189–202. DOI:10.1037/h0087425
- Dutilh G. et al. The quality of response time data inference: A blinded, collaborative assessment of the validity of cognitive models // Psychonomic bulletin & review. 2019. Vol. 26. P. 1051–1069. DOI:10.3758/s13423-017-1417-2
- Lachaud C.M., Renaud O. A tutorial for analyzing human reaction times: How to filter data, manage missing values, and choose a statistical model // Applied Psycholinguistics. 2011. Vol. 32. № 2. P. 389–416. DOI:10.1017/S0142716410000457
- Marmolejo-Ramos F. et al. On the efficacy of procedures to normalize Ex-Gaussian distributions // Frontiers in psychology. 2015. Vol. 5. DOI:10.3389/fpsyg.2014.01548
- Marszalek J. M., Barber C., Kohlhart J., Cooper B. H. Sample size in psychological research over the past 30 years // Perceptual and motor skills. 2011. Vol. 112. № 2. P. 331–348. DOI:10.2466/03.11.PMS.112.2.331-348
- Microsoft Corporation. Microsoft Excel. 2018. URL: https://office.microsoft.com/excel (Accessed: 02.03.2024)
- Morrow J. Benford's Law, Families of Distributions and a Test Basis // CEP Discussion Papers dp1291, Centre for Economic Performance, LSE. 2014. URL: https://cep.lse.ac.uk/pubs/download/dp1291.pdf (Accessed: 12.03.2024)
- Peng K., Nisbett R.E., Wong N.Y.C. Validity problems comparing values across cultures and possible solutions // Psychological methods. 1997. Vol. 2. № 4. P. 329–344. DOI:10.1037/1082-989X.2.4.329
- Primi R. et al. Anchoring Vignettes: Can They Make Adolescent Self-Reports of Social-Emotional Skills More Reliable, Discriminant, and Criterion-Valid? // European Journal of Psychological Assessment. 2016. Vol. 32. № 1. P. 39–51. DOI:10.1027/1015-5759/a000336
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. 2021. URL: https://www.R-project.org/ (Accessed: 02.03.2024)
- Stoet G. PsyToolkit: A novel web-based method for running online questionnaires and reaction-time experiments // Teaching of Psychology. 2017. Vol. 44. № 1. P. 24–31. DOI:10.1177/0098628316677643
- Stroop J.R. Studies of interference in serial verbal reactions // Journal of experimental psychology. 1935. Vol. 18. №6. P. 643–662.
- The jamovi project. jamovi (Version 2.3) [Computer Software]. 2023. URL: https://www.jamovi.org (Accessed: 02.03.2024)
- Whelan R. Effective analysis of reaction time data // The psychological record. 2008. Vol. 58. P. 475–482. DOI:10.1007/BF03395630
- Zhang Q., Kong L., Jiang Y. The interaction of arousal and valence in affective priming: behavioral and electrophysiological evidence // Brain research. 2012. Vol. 1474. P. 60–72. DOI:10.1016/j.brainres.2012.07.023
Информация об авторах
Метрики
Просмотров web
За все время: 142
В прошлом месяце: 24
В текущем месяце: 23
Скачиваний PDF
За все время: 34
В прошлом месяце: 4
В текущем месяце: 2
Всего
За все время: 176
В прошлом месяце: 28
В текущем месяце: 25