Моделирование и анализ данных
2023. Том 13. № 4. С. 153–164
doi:10.17759/mda.2023130409
ISSN: 2219-3758 / 2311-9454 (online)
Моделирование процессов автоматизированного формирования рабочих программ
Аннотация
Предлагается метод формализации учебного текста в онтологию. Предлагается сохранять передачу содержащего в тексте смысла за счет оперирования минимальными учебными элементами: определениями конкретных сущностей, описанием ее свойств, производимых действий, правил, формул и тому подобные фрагментов знаний. Представляющая учебный текст формальная структура, которую можно рассматривать как ориентированный граф, вершины которого составляют описывающие учебные элементы фреймы, обеспечивает возможность разработки моделей и алгоритмов, позволяющие эффективно решать целый ряд задач в сфере образования. Эта же структура позволяет разработать модель содержательного наполнения рабочей программы, посвященной изучению находящихся в данном учебном тексте знаний.
Общая информация
Ключевые слова: учебный текст, программа, содержание, онтология, граф
Рубрика издания: Методика преподавания
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130409
Получена: 24.11.2023
Принята в печать:
Для цитаты: Вертешев С.М., Воронов М.В. Моделирование процессов автоматизированного формирования рабочих программ // Моделирование и анализ данных. 2023. Том 13. № 4. С. 153–164. DOI: 10.17759/mda.2023130409
Полный текст
Введение
Знания, как отраженный результат познавательной деятельности, передаются от поколения к поколению в процессе обучения. Если обучение осуществляется в рамках некоторого учреждения, то оно осуществляется в соответствии с конкретной образовательной программой, представляющей собой набор документов, в которых определено основное содержание подлежащих освоению знаний, умений и навыков (ЗУН) и сформулированы требования к результатам обучения [1].
Основу образовательной программы составляет упорядоченная последовательность отдельных учебных дисциплин, для каждой из которых указан отводимый ресурс учебного времени, форма отчетности и ряд других параметров. В свою очередь для учебной дисциплины разрабатывается так называемая рабочая программа, служащая ориентиром для ведущих эту дисциплину преподавателей. Разработаны подлежащие к исполнению требования к структуре рабочей программы. Последняя может быть сформирована, если будут определены: последовательность освоения и содержание каждого раздела, отводимое на них учебное время и ориентиры по уровню освоения учебного материала. Несомненно, это требует высокой компентности разработчиков и творческого отношения к такой деятельности [2, 3].
Помимо собственно разработки рабочих программ требуется их регулярная корректировка. Все эти факторы влекут за собой необходимость осуществления целого ряда бюрократических действий. Естественно поставить вопрос, решение каких вопросов при разработке рабочих программ целесообразно и возможно обеспечить с использованием вычислительной техники и имеющихся информационных технологий.
В большинстве вузов имеются информационные системы, которые ориентированы на решение задач автоматизированного формирования рабочих программ, их систематизацию и хранение, обладают удобным интерфейсом для последующего использования и корректуры рабочих программ и т.п. [4]. Однако, при этом не затрагиваются вопросы содержательного манипулирования информацией.
По своей сути учебный процесс представляет собой усвоение конкретного набора знаний, приобретение умений и навыков, причем таких, которые в перспективе в известной мере обеспечат осуществление определенной деятельности. В организационном плане учебный процесс регламентирован набором различного рода документов (законов, постановлений, приказов, стандартов, программ и т.п.). В условиях конкретного учебного заведения подготовка ведется по определенным технологиям, описанным в соответствующей образовательной программе, которая содержит: календарный учебный график, рабочие программы учебных дисциплин (модулей), оценочные и методические материалы.
Из перечня включенных в данную образовательную программу дисциплин и отводимого на их освоение объема учебного времени можно составить лишь общее представление о содержании изучаемого материала. Наиболее полные сведения об этом находится в рабочих программах. Именно они в наиболее полной мере содержат сведения о том, что, как долго и как конкретно следует изучать и осваивать.
Источниками, из которых черпается необходимая для этого информация, выступают, как правило, различного рода книги. Профессорско-преподавательский состав кафедры решает, какие разделы из каких конкретно источников подлежат изучению в рамках формируемой программы. Кстати, рабочие программы содержат список источников, на основе которых предполагается изложение преподавателем учебного материала по данной учебной дисциплине. В этой связи можно считать, что содержание рассматриваемой учебной дисциплины заключено в едином текстовом массиве, который для удобства будем называть обобщенным учебником или просто «учебником».
В данной статье делается попытка описать метод, обеспечивающий в автоматизированном режиме формирование рабочей программы данной учебной дисциплины на основе содержательной обработки подлежащих освоению знаний. Источником этих знаний является определенный массив текста, названный выше обобщенным учебником.
Учебный материал обычно изложен в виде упорядоченной последовательности ряда составляющих его разделов (частей, глав). Разделы также представляют собой последовательность еще более мелких фрагментов знаний и т.д. [5]. Предполагается, что текст учебника отображает и целостную картину деятельности обучаемого, обеспечивая ему потенциальную возможность освоения заключающихся в нем знаний как с преподавателем, так и самостоятельно [6].
Эти обстоятельства способствуют возможности представлять учебный текст в виде структуры, которую образуют самые малые находящиеся в определенных отношениях для данного изложения порции знаний и отношения между ними. Каждая такая порция, в педагогической литературе ее называют учебным элементом, представляет собой часть текста, где даны: определение конкретной сущности, описание ее свойств, действий, правил, формул и тому подобные фрагменты знаний. Выделенный учебный элемент, который несет уникальную в рамках данного текста единицу информации будем трактовать как имеющий свое имя квант знаний (KZi).
Исследования показывают, что каждый учебный текст может быть формализован в виде ориентированного графа, описывающего структуру содержащихся в нем представленных на естественном языке знаний [7]. Представленный в виде формальной структуры (математической модели) учебный материал обеспечивает возможность разработки моделей и алгоритмов, позволяющих эффективно решать целый ряд задач в сфере образования. В этой связи базовой является задача трансформации в формальную модель структуры представленного на естественном языке учебного текста.
Построение модели структуры знаний
Ставится задача: разработать метод трансформации представленного на естественном языке учебного текста в формальную знаниевую структуру.
Решение этой задачи предлагается осуществлять в ходе пошагового конструктивного процесса, каждый шаг которого заключается в выявлении и фиксации в формальной форме очередного учебного элемента и его связей с другими элементами. Этот процесс можно интерпретировать как формирование онтологии, представляющей собой формальную (математическую) модель структуры представленных в тексте знаний [8]. Выбор такого способа реализации семантических технологий обусловлен тем, что манипулирование знаниями, представленными в виде онтологий, может обеспечить проведение процедур логического вывода в автоматическом режиме [9, 10].
Поскольку онтологию можно представить в виде ориентированного графа, то далее будем пользоваться терминологией из теории графов, что позволяет более наглядно описывать процесс формирования модели.
Изложим процесс построения формальной модели представленного в вербальном виде учебного текста более детально. Пусть по мере прочтения рассматриваемого учебного текста в нем обнаруживается введение «нового», т.е. еще не введенного, кванта 〖KZ〗_k. В учебных текстах при описании кванта знаний используются ранее введенные кванты знаний, в том числе и те, которые относятся к так называемым базовым (входным) знаниям, т.е. к тем, которые предполагаются известными обучаемому до начала освоения данного материала. Пусть в рассматриваемом фрагменте текста дается описание кванта 〖KZ〗_k, в котором используется некоторое множество других квантов знаний {〖KZ〗_i,x_ik } , где x_ik – признак того, что квантор 〖KZ〗_i непосредственно используется при описании 〖KZ〗_k.
Каждому вводимому кванту знаний отвечает определенная вершина формируемого графа. Для ее формализованного описания предлагается использовать соответствующий фрейм, куда вносятся название вводимого фрагмента знаний 〖(KZ〗_k), пары из {〖KZ〗_i,x_ik }, т.е. информация о том, какие кванты знаний использованы при описании 〖{KZ〗_i} и в каком отношении они находятся, для удобства сюда целесообразно вводить собственно фрагмент текста, описывающий квант 〖KZ〗_k. Тем самым оказывается построен фрагмент формируемой модели (ее подграф)
ΔG(k)=<〖{KZ〗_i}, 〖KZ〗_k, {i,k} >,
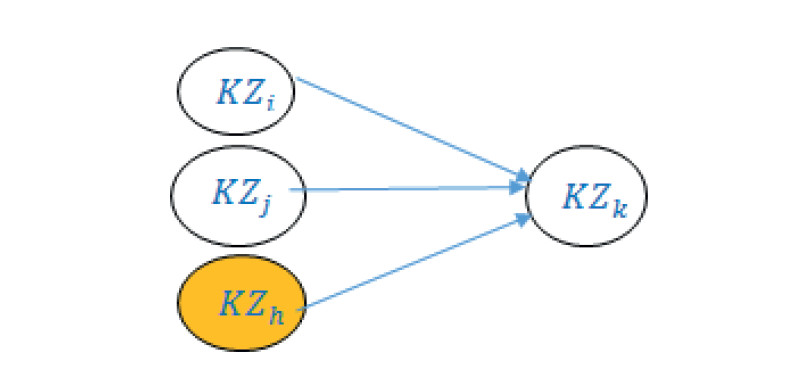
отображающей описание квантора знаний 〖KZ〗_k и его строение. Этот фрагмент имеет характерную структуру, определенный паттерн, из которых будет построена модель рассматриваемого учебного текста в целом (см. рис.1.). Подчеркнем, в нем оказываются связанными только часть фрагментов знаний, которые использованы при введении 〖KZ〗_k .
Рис 1. Структура модели, описывающий квант знаний 〖KZ〗_k
Одновременно, благодаря выявлению связей из множества {i,k} происходит автоматическое наращивание формируемой модели
G(k)=G(k-1) U ΔG(k),
поскольку ∀i: 〖{KZ〗_i}⊂ G(k-1).
Примечание. Возможны ситуации, когда среди включенных в ΔG(k) есть те кванты, которые еще не вошли в G(k-1) и не относятся к базовым. Это означает, что при описании 〖KZ〗_k используются кванты, которые в рассматриваемом тексте еще не введены, т.е. использованы понятия, которые еще не были описаны (нарушена логика изложения), либо они вообще в данном учебнике не вводятся (неполнота излагаемого учебного материала), т.е. в учебном тексте обнаружен брак.
Для фиксации таких ситуаций можно поступать таким образом. Если при формализации кванта знаний 〖KZ〗_k выявлен квант, на рис.1. это выделенный квант 〖KZ〗_h, который не присутствует в G(k-1), то в ΔG(k) включается «пустая вершина». В отображающем ее фрейме фиксируется лишь имя пустого кванта 〖KZ〗_h и делается соответствующая отметка. Имя каждого пустого кванта также заносится в специальный в список проблемных мест рассматриваемого учебного текста.
После рассмотрения всех n присутствующих в рассматриваемом тексте квантов знаний модель этого текста G(n) оказывается сформированной.
Данная модель может быть использована для построения инструментария для решения ряда учебно-методических вопросов. Это, например, оценивание соответствующих учебников на предмет их полноты и наличия искажения логики изложения материала, а также создавать системы активной поддержки процессов самоподготовки студентов [11].
Модель формирования рабочей программы
Пусть рассматривается задача разработки модели рабочей программы изучения данной учебной дисциплины. Как уже отмечалось, разработан широкий спектр программных продуктов для формирования рабочих программ, по структуре отвечающих требованиям руководящих документов. Вместе с тем не решены вопросы автоматического определения содержательных компонентов. Это, в первую очередь, какие темы изучать, в какой последовательности и каково отводимое на это время. По-видимому, полноценное решение такого рода вопросов под силу только опытному преподавателю, что называется «вручную». Вместе с тем наличие формальной структуры подлежащего освоению учебного материала обеспечивает построение модели, использование которой позволяет в значительной мере автоматизировать этот процесс.
Не вызывает сомнения следующее суждение: при прочих равных условиях, уровень освоения фиксированного объема знаний существенно зависит от объема, отводимого на это времени, причем, чем больше затрачивается времени на освоения данного раздела, тем выше может быть ожидаемый уровень его освоения. Однако на изучение учебной дисциплины всегда отводится ограниченный временной ресурс, обозначим его через время T. Следовательно, естественной выглядит попытка отведения на изучение каждого фрагмента знаний наибольшего объемы учебного времени в рамках, отводимых учебных часов на данную дисциплину в целом.
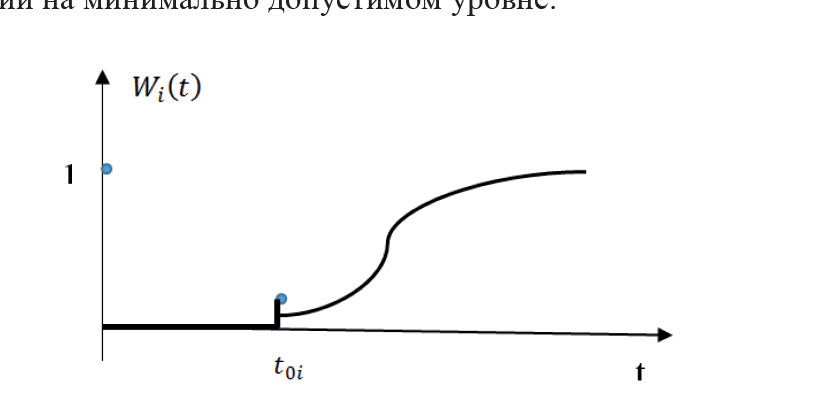
Предположим, что для каждого фрагмента учебного материала на основе анализа опыта преподавания данной учебной дисциплины построены функции, описывающие уровень освоения W_i (t), в зависимости от отпущенного на это времени. Это неубывающая монотонная зависимость, качественный вид которой представлен на рис.2, где t_0i ̶ минимальное время, которое должно быть отпущено для освоения i -го кванта знаний на минимально допустимом уровне.
Рис.2. Зависимость уровня освоения учебного материала
как функции времени.
Пусть для выбранного учебника по вышеизложенной методике построена модель, представляющую собой онтологию, элементы которой описывают содержание упомянутые в учебнике кванты знаний и связи между ними. Кроме того, сформировано множество функций времени {W_i (t)}, описывающих ожидаемый уровень освоения каждого кванта знаний. Благодаря этому, во фреймы, описывающие квант знаний, могут быть введены так называемые исходные значения уровня его освоения W_k и отпускаемое на это учебное время. Наиболее просто это осуществить, причем в автоматическом режиме, вводя их минимальные значения, т.е. 〖W_k=W〗_k (t_0k ) и t_0k. Это означает, что для достижения минимально приемлемого уровня освоения кванта знаний 〖KZ〗_k отводится время t_0k.
Разработка рабочей программы по учебной дисциплине с необходимостью должна быть адаптирована под удовлетворение условий по крайней мере в двух аспектах: временных и содержательных. Так, если из построенной онтологии, задающей исходное состояние объекта моделирования следует, что ∑_(∀k)▒〖〖argW〗_k (t_0k ) 〗>T и/или ∃k: W_k<W_k (t_0k), то при введенных ограничениях удовлетворительный вариант рабочей программ не может быть разработан. В противном случае имеет смысл поставить вопрос о разработке рабочей программы, обеспечивающей более высокий уровень освоения.
Естественно потребовать, чтобы за отпущенное время можно было обеспечить наиболее высокий уровень освоения каждого кванта знаний при гарантии достижения приемлемого уровня. Такой постановке задачи отвечает следующая математическая модель
∀k: W_k→max (1)
при условиях:
∑_(∀k)▒〖〖argW〗_k (t) 〗≤T (2)
∀k: W_k (t)≥W_k (t_0k) (3)
Задача (1-3) представляет собой задачу нелинейного программирования очень высокой размерности, что существенно ограничивает применение известных методов ее решения.
Заметим, функция W_k (t) описывает уровень освоения соответствующего фрагмента программы за время t в целом. При более строгой постановке задачи целесообразно отдельно учитывать временные затраты на приобретение знаний, умений и навыков. Это приведет к необходимости вместо одной функции W_k (t) формировать три функции (W_k (t)→(〖WЗ〗_k (t),〖WУ〗_k (t),〖WН〗_k (t). Кроме того, существенно возрастет и размерность задачи.
Обсудим возможные пути практического преодоления трудностей применения традиционных методов решения такого рода задач математического программирования. Во-первых, можно использовать прием, который неявно применяется на практике: исходя из каких-то соображений (обычно основываясь на своем опыте), учебный материал курса разделяют на ряд достаточно крупных разделов и на освоение каждого из них выделяется определенный объем учебного времени (в пределе на освоение данной учебной дисциплины отводимый бюджет учебного времени попросту назначается). При этом обоснованность принятого решения существенно снижается и применение модели (1 – 3) становится бессмысленной.
Можно предложить и иной подход. Его суть заключается в поиске тех квантов знаний, которые представляются более важными и на их освоение выделяют больше учебного времени.
Для учебных текстов характерно использование ранее введенных квантов знаний для описания квантов последующих, лишних же фрагментов знаний в учебники обычно не вводят. Иначе говоря, все они считаются необходимыми. Но можно ли ввести на их множестве обоснованную «оценку относительной полезности»?
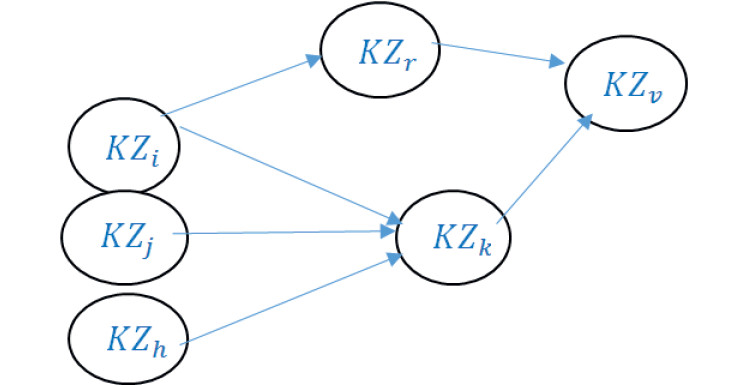
При анализе построенного графа G(n) можно заметить, что одни и те же кванты знаний используются при введении целого ряда квантов, причем как непосредственно, так и опосредованно. Например, как следует из рис.3. квант 〖KZ〗_i непосредственно используется при введении и кванта 〖KZ〗_r, и кванта 〖KZ〗_k, а квант 〖KZ〗_j с квантом 〖KZ〗_v связан лишь опосредованно через 〖KZ〗_k.
Рис 3. Иллюстрации вариантов повторного использования
одних и тех же квантов знаний
В этой связи для каждого кванта знаний 〖KZ〗_k можно ввести меру оценки относительной полезности m_k, равную количеству квантов, в которых он использован непосредственно,
m_k= ∑_(∀i)▒〖x_ik |x_ik=1〗
Эта мера вводится во все фреймы, описывающие введенные кванты знаний. Поскольку собственно величина m_k характеризует только часть полезности кванта, то в предыдущую модель целесообразно вводить величины 〖q_k=c_k∙m〗_k, где c_k – коэффициент, который впоследствии может использоваться, как настроечный параметр
Теперь модель примет вид
∀k: 〖q_k∙W〗_k→max (4)
при условиях:
∑_(∀k)▒〖〖argW〗_k (t) 〗≤T (5)
∀k: W_k (t)≥W_k (t_0k) (6)
Для некоторых квантов знаний, относительно которых есть устоявшееся мнение о достаточном уровне их освоения, можно ввести дополнительные ограничения 〖WM〗_i, и ввести дополнительное условие
∃i:W_i (t_0i)≤W_i (t_i)≤〖WM〗_i (7)
Для модели (4 - 7) появляется возможность построить конструктивный алгоритм выделения дополнительных (относительно минимальных) временных ресурсов на освоение тех квантов знаний, которые предпочтительнее по фактору учета «мощности непосредственной связи» q_k.
Заключение
Особенности учебных текстов обусловливают возможность построения формальных структур, отображающих их содержание в достаточной для практики степени. Наиболее подходящим их представлением являются популярные в настоящее время онтологические модели.
Разработан алгоритм формирования онтологической модели учебного текста, которая отображает присутствующие в тексте кванты знаний и связи между ними. Онтологические модели удобно представлять в виде взвешенных графов (графов знаний). Вершины этих графов целесообразно формировать в виде паттернов фреймов, в которых фиксируются сведения о квантах знаний, как наиболее малых порциях содержательной информации.
Наличие формальной модели учебного текста обеспечивает возможность решения целого ряда задач с автоматизированным учетом содержания текста. Среди них, в частности, оценка ряда качеств учебных текстов и формирование рабочих программ изучения учебных дисциплин в процессе решения соответствующих задач математического программирования.
Литература
- Федеральный закон от 29.12.2012 N 273-ФЗ (ред. от 04.08.2023) "Об образовании в Российской Федерации" (с изм. и доп., вступ. в силу с 01.09.2023)
- Вертешев С. М., Поляков А.О. От «фон Неймановского компьютера к мегамашине. ̶ Псков: Псковский государственный политехнический институт, 2009. 512 с.
- Вертешев С. М., Воронов М.В, Герасименко, П. В., Кремков, М. В. Принятие решений при управлении организационными системами: монография. ̶ Псков: Псковский государственный университет, 2019. 218с.
- Космачёва И. М., Квятковская И. Ю., Сибикина И. В. Автоматизированная система формирования рабочих программ учебных дисциплин //Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика, 2016, №1. С. 90–97.
- Сабинина А.А. Учебный текст: структура и прагматика. //Известия РГПУ им. А. И. Герцена. 2009; С. 222-225.
- Гурье Л.И. Проектирование педагогических систем: Учеб. пособие; Казан. гос. технол. ун-т. ̶ Казань, 2004. 212с.
- Воронов М.В., Пименов В.И. Формализация регулятивных текстов. //Информатика и автоматизация. 2021; 20(3). С. 562–590.
- Воронов М.В. Моделирование структуры представленных в учебных текстах знаний // Педагогика информатики 2022, № 1-2. С.99-108.
- Копайгородский А.Н. Применение онтологий в семантических информационных сетях // Онтология проектирования, 4(14)/2014. С. 78-89
- Надеждин Е.Н. Прикладные задачи семантического анализа текстовых документов // Фундаментальные исследования. 2017. № 1. С. 94-100.
- Воронов М.В. Система активной поддержки самоподготовки студентов //Образовательные технологии 2018. №3. С. 107-118.
Информация об авторах
Метрики
Просмотров
Всего: 97
В прошлом месяце: 11
В текущем месяце: 5
Скачиваний
Всего: 63
В прошлом месяце: 5
В текущем месяце: 0