Моделирование и анализ данных
2023. Том 13. № 2. С. 64–76
doi:10.17759/mda.2023130203
ISSN: 2219-3758 / 2311-9454 (online)
Проблемы классификации текстов естественного языка методами классического машинного обучения
Аннотация
В статье описаны проблемы методов классического машинного обучения в задаче классификации естественного языка. Одной из таких задач является классификация структурных элементов в школьных сочинениях. На её примере рассматриваются недостатки классического машинного обучения по сравнению с другими, более сложными алгоритмами.
Общая информация
Ключевые слова: анализ текста, естественный язык, автоматизация
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130203
Получена: 21.03.2023
Принята в печать:
Для цитаты: Сологуб Г.Б., Пухов В.А. Проблемы классификации текстов естественного языка методами классического машинного обучения // Моделирование и анализ данных. 2023. Том 13. № 2. С. 64–76. DOI: 10.17759/mda.2023130203
Полный текст
Введение
Задача классификации текста является одной из базовых задач анализа естественного языка.
Проблема выбор метода классификации текста возникла при решении задачи сегментации текста школьных сочинений в рамках соревнования по машинному обучению. Для проверки сочинения требуется выделить в тексте структурные элементы, такие как введение, позиция автора, аргумент и т.д.
При решении данной задачи была предложена модель машинного обучения, которая сначала разделяет структурные элементы, затем их классифицирует.
В этой статье анализируются и сравниваются методы классификации текстов на описанных выше данных.
Для обработки естественного языка был использован метод TF-IDF, впервые изложенный в [Manning]. Этот метод считает частоту вхождения слов в подстроке и взвешивает их в отношении к частоте встречаемости этого слова в документе. Таким образом, более релевантные слова получают больший вес в векторном представлении текста. Однако, такой способ не учитывает порядок слов в подстроке.
Описание алгоритмов машинного обучения и метрики их качества взяты из [Дьяконов], что позволило выбрать множество методов для анализа, критерий эффективности работы методов для задачи классификации структурных элементов школьных сочинений, а также такой способ сравнения алгоритмов как обучающая и валидационная кривые.
В работах [Alex Sherstinsky Fundamentals] и [Christopher Olah Understanding] описывается архитектура сети LSTM, выбранной в качестве исследуемого метода глубокого обучения.
Постановка задачи
Имеется датасет (Таблица 1) из 1487369 строк и 3 столбцов.
|
id |
discourse_text |
discourse_type |
|
423A1CA112E2 |
Modern humans today are always on their phone... |
Lead |
|
423A1CA112E2 |
They are some really bad consequences when stu... |
Position |
|
423A1CA112E2 |
Some certain areas in the United States ban ph... |
Evidence |
|
… |
… |
… |
|
4C471936CD75 |
it is better to seek multiple opinions instead. |
Position |
|
4C471936CD75 |
The impact of asking people to help you make a... |
Evidence |
|
4C471936CD75 |
there are many other reasons one might want to… |
Concluding Statement |
Таблица 1
Столбец id – идентификатор сочинения, discourse_text – текст структурного элемента, discourse_type – тип структурного элемента.
Возможные типы структурных элементов:
- введение (Lead);
- позиция автора сочинения (Position);
- аргумент (Claim);
- контраргумент (Counterclaim);
- опровержение контраргумента (Rebuttal);
- пример, подтверждающий аргумент (Evidence);
- вывод (Concluding Statement).
Этот набор данных описывает текстовые документы, содержащие сочинения. Каждая строка содержит id документа, подстроку соответствующего документа, выделенную как структурный элемент, и тип этого элемента.
Задача классификации формулируется так: пусть – множество описаний объектов, – множество меток классов. Существует неизвестная целевая зависимость – отображение значения которого известны только на объектах данной обучающей выборки . Требуется построить алгоритм способный классифицировать произвольный объект .
В контексте данной работы структурные элементы из данного набора данных будут рассматриваться без привязки к текстовым документам: входные признаки – тексты структурных элементов, и целевые метки классов – типы структурных элементов.
Задача этой работы заключается в сравнении нескольких алгоритмов . Целью работы ставится выявление наиболее эффективного алгоритма для классификации структурных элементов школьных сочинений с точки зрения заданной метрики.
Предобработка текста
Для работы с естественным языком были произведены преобразования исходного текста структурных элементов в векторные представления:
- количественная векторизация,
- TF-IDF.
Количественная векторизация представляет собой преобразование входного текста к матрице, где номер каждого столбца – индекс слова из словаря входного текста, номер каждой строки – порядковый номер предложения, а значение элемента матрицы – количество вхождений соответствующего слова в соответствующем предложении.
TF-IDF трансформация состоит из:
- TF (term frequency — частота слова) — отношение числа вхождений некоторого слова к общему числу слов документа. Таким образом, оценивается важность слова в пределах отдельного документа
где есть число вхождений слова в документ, а в знаменателе — общее число слов в данном документе.
- IDF (inverse document frequency – обратная частота документа) – инверсия частоты, с которой некоторое слово встречается в документах коллекции. Учёт IDF уменьшает вес широкоупотребительных слов
где – число документов в коллекции, – число документов из коллекции , в которых встречается (когда ).
- -
Формулы -приведены в главе 6 [Manning].
После того, как тексты преобразованы в векторную форму, можно применять алгоритмы классификации.
Сравнение методов классификации
При оценке качества алгоритмов машинного обучения использовалась метрика Macro F1 Score [Дьяконов]:
где – число классов структурных элементов (7); – номер класса; , – количество верно классифицированных объектов класса i; – количество объектов неверно отнесенных к классу i; – количество объектов класса i, неверно отнесенных к другому классу.
Таким образом, – суть среднее арифметическое по каждому классу. В свою очередь – среднее гармоническое точности и полноты классификации.
Подобный выбор метрики обусловлен тем, что в задаче сегментации текста сочинений нет предпочтения ложноположительным или ложноотрицательным ошибками, а количество структурных элементов в обучающем множеств – несбалансированное.
Для анализа эффективности алгоритмов использовались обучающая и валидационная кривые. Первая позволяет понять, как влияет мощность обучающей выборки на оценочную метрику. Вторая, методом скользящего контроля – какое значение гиперпараметра оптимально для решения задачи. Также, для сохранения времени исходный датасет был сокращен до 100000 структурных элементов.
Классические модели машинного обучения подразделены на метрические и неметрические. Одни используют векторное расстояние между объектами, другие – нет.
Классические неметрические алгоритмы
Наиболее совершенным классическим алгоритмом машинного обучения является градиентный бустинг. При исследовании задачи классификации рассматривались несколько его вариаций на деревьях решений: стохастический градиентный бустинг (sklearn GradientBoostingClassifier), экстремальный градиентный бустинг (XGBoost) и CatBoost.
Сравнение алгоритмов представлено в таблице 2 [Дьяконов].
|
|
GBC |
XGBoost |
CatBoost |
|
Построение деревьев |
По уровням |
По уровням |
По уровням однородно |
|
Поиск расщеплений |
Полный перебор или гистрограммный подход |
Полный перебор или гистрограммный подход |
Предварительный биннинг (дискретизация вещественных признаков) |
|
Важность признаков |
Impurity |
Gain / Frequency или Weight / Coverage |
Изменение прогнозируемых значений / функции ошибки |
|
Ранняя остановка |
+ |
- |
+ |
Таблица 2
Стохастический градиентный бустинг
На рисунках 1 и 2 представлены соответственно обучающая и валидационная кривые для стохастического градиентного бустинга.
Рис. 1. Обучающая кривая метода GBC
Рис. 2. Валидационная кривая метода GBC
XGBoost
На рисунках 3 и 4 представлены соответственно обучающая и валидационная кривые для экстремального градиентного бустинга.
Рис. 3. Обучающая кривая метода XGBoost
Рис. 4. Валидационная кривая метода XGboost
CatBoost
На рисунках 5 и 6 представлены соответственно обучающая и валидационная кривые для метода CatBoost.
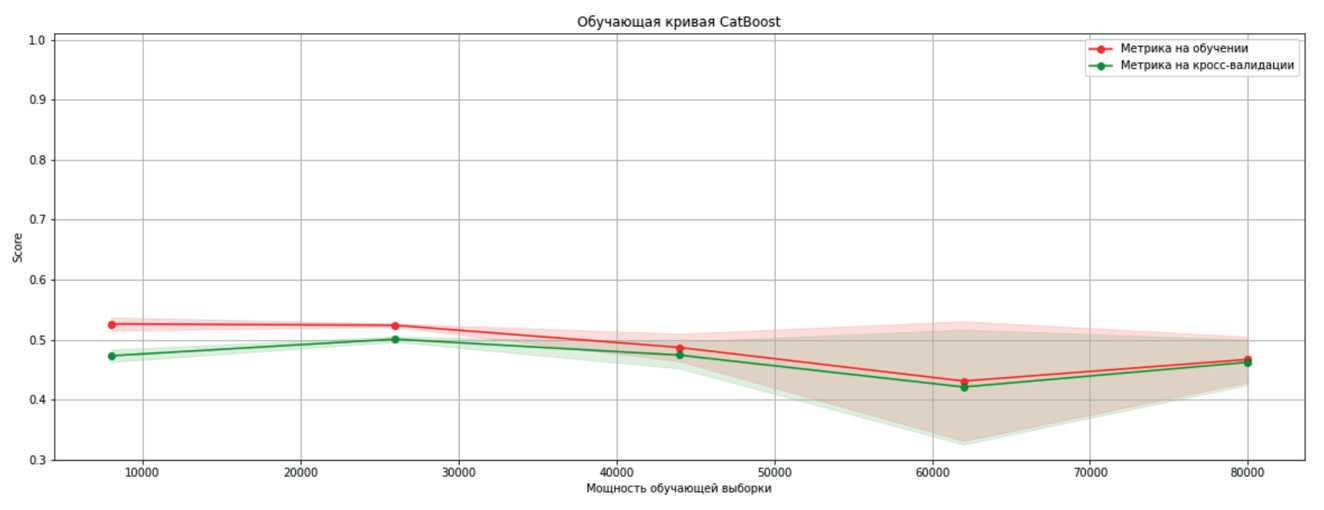
Рис. 5. Обучающая кривая метода CatBoost
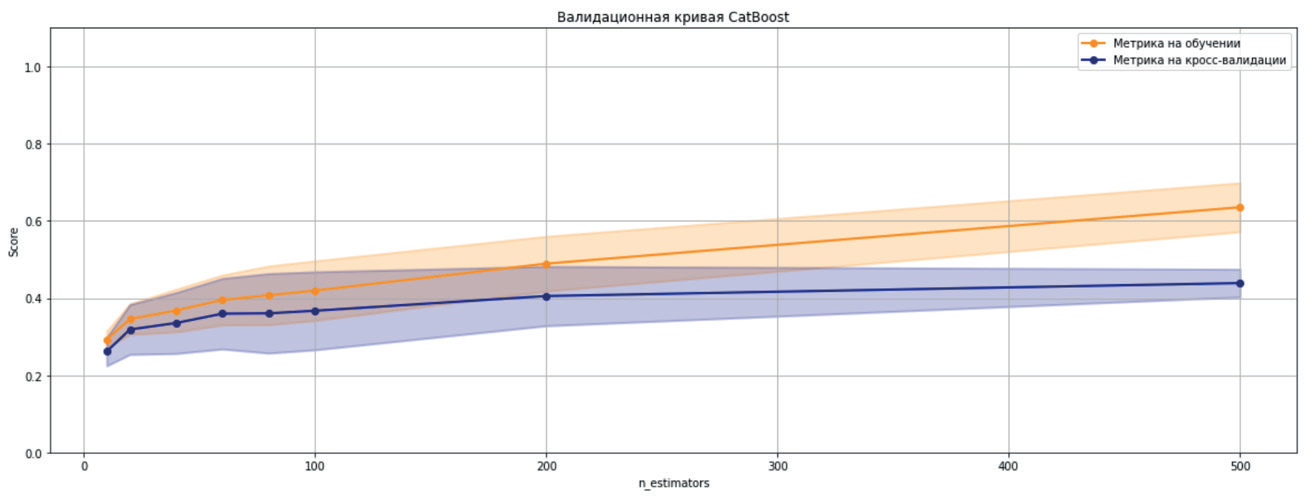 Рис. 6. Валидационная кривая метода CatBosst
Рис. 6. Валидационная кривая метода CatBosst
Анализ обучающих кривых показывает, что первые две модели перестают улучшаться при увеличении мощности обучающего множества более 70000 образцов, CatBoost имеет аналогичную картину, за исключением необычно большого разброса значения метрики на предпоследнем значении мощности тренировочной выборки.
Валидационные кривые свидетельствуют о том, что увеличение сложности моделей не влияют на целевую метрику.
Максимальное значение метрики на отложенной выборке при решении задачи классификации градиентным бустингом составило .
Классические метрические алгоритмы
Метрические модели, в основном, работают без учителя, поэтому анализировался только метод N ближайших соседей, обучающийся на данных.
На рисунках 7 и 8 представлены соответственно обучающая и валидационная кривые для метода N ближайших соседей.
Рис. 7. Обучающая кривая метода N ближайших соседей
Рис. 8. Валидационная кривая метода N ближайших соседей
В случае N ближайших соседей, обучающая кривая имеет тренд на увеличение, но само обучение замедляется с ростом обучающей выборки, так как алгоритм считает расстояние между всеми её объектами. Поэтому, учитывая выход на плато кривой валидации, этот метод не оказался более эффективным, чем бустинг.
Глубокое обучение
Далее, был исследован подход глубокого обучения. Наиболее эффективной из рассмотренных оказалась нейросеть долгой краткосрочной памяти (LSTM) [Alex Sherstinsky Fundamentals].
LSTM – рекуррентная нейронная сеть, способная удалять информацию из состояния ячейки.
Пусть – t-ое входное значение фрагмента A нейронной сети, – возвращаемое значение (рисунок 9).

Рисунок 9
LSTM слой состоит из нескольких подслоев [Christopher Olah Understanding].
- Фильтр забывания (рисунок 10). Сигмоидальный слой, возвращающий значение от 0 до 1, отвечающий за сохранение информации из ячейки .
Рис. 10. Схема фильтра забывания
где – веса слоя, – вектор смещения.
- Сигмоидальный и слой изображен на рисунке 11. Решает, какая новая информация будет храниться в состоянии ячейки.
Рис. 11. Схема обновления информации
где и – веса и смещения соответствующих индексу слоёв, – вектор значений новых кандидатов на добавление в состояние ячейки.
- Этап замены состояния на изображен на рисунке 12.
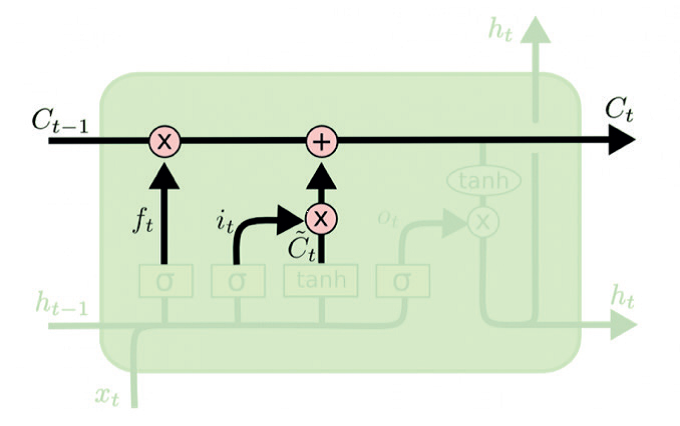 Рис. 12. Схема замены состояния ячейки
Рис. 12. Схема замены состояния ячейки
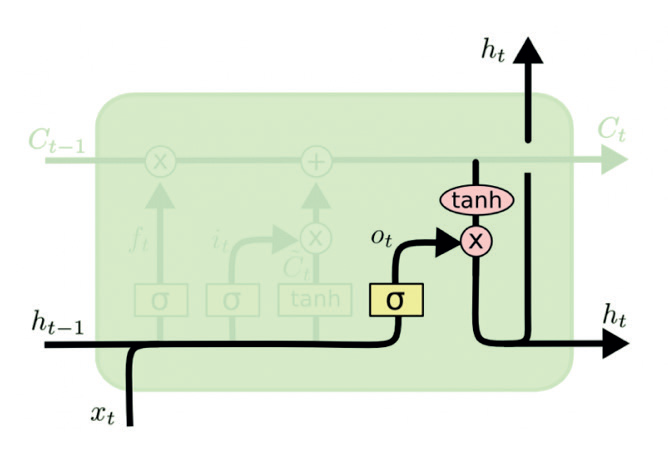
- Получение выходного значения. Схема показана на рисунке 13.
– веса выходного слоя, – выходной вектор смещения.
Рис. 13. Схема получения выходного значения ячейки
Структура полученной сети:
- эмбеддинговый слой,
- LSTM-слой из 128 нейронов,
- слой прореживания,
- LSTM-слой из 64 нейронов,
- слой прореживания,
- softmax слой.
Валиационная кривая и зависимость функции ошибки от итерации обучения построенной нейронной сети изображены на рисунке 14.
Рис. 14. Валидационная кривая и функция ошибки нейронной сети
Судя по полученным графикам, сеть полностью выучивает обучающую выборку. Тем не менее, значения метрики на отложенной выборке не убывает с каждой итерацией обучения.
Качество такой сети зависит от того, насколько тестовые примеры будут отличаться от данных в датасете. Возможно, следует понизить количество итераций обучения, если для тестовых данных исходная выборка будет не репрезентативна. Исходя из полученного значения метрики нейронные сети эффективнее решают задачу классификации текстов в сравнении с моделями классического машинного обучения.
Заключение
При анализе методов классического машинного обучения (Gradient Boosting, CatBoost, XGBoost, N ближайших соседей) и метода глубокого обучения (LSTM нейронной сети) для решения задачи классификации структурных элементов текстов школьных сочинений было выявлено, что, с точки зрения выбранной метрики, лучше справился метод глубокого обучения.
Литература
- Manning, C.D.; Raghavan, P.; Schutze, H. Scoring, term weighting, and the vector space model // Cambridge University Press. 2009 P. 109-133 DOI:10.1017/CBO9780511809071.007
- Дьяконов А.Г. Лекции [Электронный ресурс] URL: https://dyakonov.org/tag/лекции/
- Alex Sherstinsky Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network [Электронный ресурс] // Physica D: Nonlinear Phenomena 2020 P. 1-40 DOI:10.1016/j.physd.2019.132306 URL: https://sciencedirect.com/science/article/abs/pii/S0167278919305974
- Christopher Olah Understanding LSTM Networks [Электронный ресурс] // 2015 URL: http://colah.github.io/posts/2015-08-Understanding-LSTMs/
Информация об авторах
Метрики
Просмотров web
За все время: 394
В прошлом месяце: 31
В текущем месяце: 10
Скачиваний PDF
За все время: 168
В прошлом месяце: 13
В текущем месяце: 4
Всего
За все время: 562
В прошлом месяце: 44
В текущем месяце: 14