Моделирование и анализ данных
2023. Том 13. № 2. С. 123–141
doi:10.17759/mda.2023130207
ISSN: 2219-3758 / 2311-9454 (online)
Методика определения свойств компонентов композиционного материала на основе миграционных алгоритмов глобальной оптимизации
Аннотация
Сформирована математическая модель расчета упругих характеристик обобщенного материала на основе свойств поперечно-изотропного волокна и изотропной матрицы. Задача выбора параметров материалов сформулирована как проблема минимизации целевой функции на параллелепипедном множестве допустимых решений. Для ее решения применены классический и модифицированный самоорганизующиеся миграционные алгоритмы глобальной оптимизации, относящиеся к группе метаэвристических. Получены рекомендации по выбору наилучших значений параметров.
Общая информация
Ключевые слова: критерии разрушения композита, гомогенизация
Рубрика издания: Методы оптимизации
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2023130207
Получена: 21.04.2023
Принята в печать:
Для цитаты: Пантелеев А.В., Ковтунов С.С., Ракитянский В.М. Методика определения свойств компонентов композиционного материала на основе миграционных алгоритмов глобальной оптимизации // Моделирование и анализ данных. 2023. Том 13. № 2. С. 123–141. DOI: 10.17759/mda.2023130207
Полный текст
Введение
При проектировании и производстве композитных изделий важно учитывать их механические свойства. При этом у полимерных композитных материалов (ПКМ) свойства могут существенно отличаться от свойств отдельных компонентов. Из-за невозможности получения свойств составляющих композитного материала экспериментальным путем, необходимо прогнозировать их свойства с помощью математических моделей и численных методов.
Одним из основных подходов к прогнозированию свойств ПКМ является микромеханическое моделирование, которое позволяет учитывать особенности микроструктуры композита и предсказывать его общие упругие свойства.
На рис. 1 (слева) изображен представительный элемент объема (ПЭО) полимерного композитного материала в микромасштабе, который состоит из нескольких компонентов (в рассматриваемом случае это углеродное волокно и эпоксидная матрица). Волокно является армирующей (усиливающей) составляющей, так как оно намного прочнее и жестче полимерной матрицы. Матрица, в свою очередь, выступает связующим элементом для удержания волокон в определенной конфигурации. Справа представлен однородный сплошной материал с анизотропными свойствами (анизотропные свойства варьируются в зависимости от направления, изотропные свойства одинаковы в любом из направлений).
Подход гомогенизации – это математический метод для определения обобщенных упругих свойств ПКМ. Этот метод используется для расчета упругих свойств материалов, состоящих из двух или более компонентов, имеющих разные упругие свойства. При использовании подхода гомогенизации, микроструктура композитного материала рассматривается как периодическая среда, которая состоит из матрицы и включений. С помощью математических соотношений, справедливых на микроуровне, определяются эффективные упругие свойства на макроуровне.
Подход гомогенизации позволяет получить аналитические формулы для определения эффективных упругих свойств композитного материала на основе свойств его компонентов и микроструктуры. Это позволяет оптимизировать дизайн композитных материалов, прогнозировать их механические свойства и улучшать производственные процессы.
Задача заключается в том, чтобы найти упругие характеристики обобщенного материала, зная свойства поперечно-изотропного (в поперечном направлении в любой из точек свойства будут одинаковыми) волокна и изотропной матрицы.
Рисунок 1- Описание процесса гомогенизации
Формирование математической модели процесса гомогенизации
Входными параметрами для реализации процесса гомогенизации являются упругие характеристики составляющих материала.
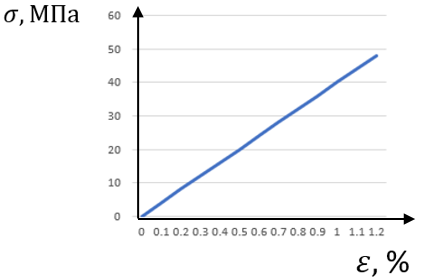
Упругие характеристики. На рис. 2 изображена диаграмма растяжения (зависимость напряжение-деформация). По закону Гука модуль упругости (его можно определить по рис. 2) равняется отношению действующего напряжения к деформации (для рассматриваемого далее прикладного примера в направлении 1 (см. рис. 7): , где направление 1 – это направление вдоль волокон в однонаправленном материале).
Рисунок 2 – График зависимости напряжение-деформация при растяжении
На рис. 3 показан типовой график зависимости продольной деформации от поперечной. Так как коэффициент Пуассона определяется отношением относительной поперечной деформации к продольной: , то на рис. 3 коэффициент Пуассона определяется тангенсом угла наклона изображенной кривой.
Рисунок 3 - График зависимости продольной деформации от поперечной
Механические характеристики составляющих композитного материала включают в себя упругие свойства поперечно-изотропного волокна и изотропной матрицы.
Упругие поперечно-изотропные волокна имеют осевой и поперечный модули упругости , а также осевой и поперечный коэффициенты Пуассона ,:
- осевой модуль упругости (модуль упругости в продольном направлении): ;
- поперечный модуль упругости (модуль упругости в поперечном направлении): ;
- осевой модуль сдвига (зависимость касательного напряжения от сдвиговой деформации): ). На рис. 4 показана диаграмма сдвига (зависимость линейная, т.е. угол сдвига пропорционален касательному напряжению).
Рисунок 4 - Диаграмма сдвига
- поперечный модуль сдвига : ;
- осевой коэффициент Пуассона : ;
- поперечный коэффициент Пуассона : .
Изотропную матрицу характеризуют:
- объемная доля волокна в материале ; объемная доля (содержание) волокна в представительном элементе объема определяется отношением объема волокна (цилиндра) к объему куба: . На рис. 5 изображен представительный элемент объема в виде куба для более наглядного изображения объемной доли волокна (синим цветом изображены волокна, зеленым цветом матрица).
Рисунок 5 – Кубический представительный элемент объема (ПЭО)
- модуль упругости матрицы;
- коэффициент Пуассона для матрицы .
Например, в координатах 123 (см. рис. 9) у волокна индексу A соответствуют свойства E1,G12, G13, n12, n13 , а индексу T – E2, E3, G3, n23.
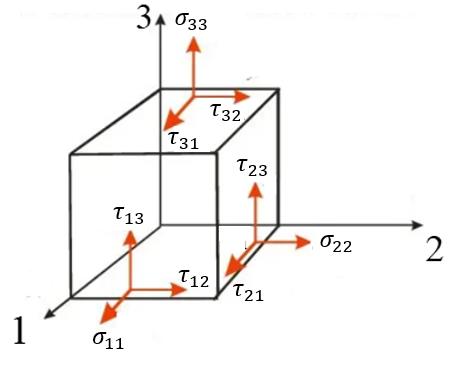
Напряжения. При деформировании в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы называются внутренними напряжениями (нормальными и касательными), которые описываются тензором 2-го ранга – тензором напряжений. На рис. 6 изображен тензор напряжений кубического элемента. В описании формул используется сокращенная система обозначений Фохта для тензора второго ранга – индексы 111, 222, 333, 126, 135, 234):
где индексы тензора напряжений записаны исходя из двух принципов:
- повторяющиеся индексы записываются только один раз (например, 11 становится 1);
- если два индекса i и j отличаются, то для сокращенной записи можно использовать следующую формулу: 9 − i − j (например, 12 становится 6).
Рисунок 6 - Тензор кубического элемента
Тензор жесткости. Тензор жесткости – это математический объект, который описывает зависимость напряжений от деформаций в упругих материалах. Он является фундаментальной характеристикой упругих свойств материалов и используется в механике твердого тела для описания и предсказания поведения материалов при механических нагрузках.
Тензор жесткости определяет связь между деформациями и напряжениями в материале и может быть выражен через обратный тензор упругости :
где – компоненты тензора напряжений, – компоненты тензора деформации, – компонент тензора жесткости. Тензор жесткости играет важную роль в механике твердого тела и используется для моделирования различных процессов, таких как деформации при растяжении, сжатии, изгибе, скручивании и т.д. [Ландау, 1987].
Деформации. На рис. 7 показано, как выглядит и выражается линейная деформация.
Рисунок 7 - Схематическое изображение того, как выглядит и выражается линейная деформация
На рис. 8 показано, как выглядит и выражается сдвиговая (угловая) деформация.
Рисунок 8 - Схематическое изображение того, как выглядит и выражается сдвиговая (угловая) деформация
Опишем выходные параметры процесса гомогенизации. На рис. 9 слева показаны обозначения направлений ПКМ, которые взяты за основу при обозначении упругих характеристик материала. Справа показаны обозначения осей симметрии в ПКМ.

Рисунок 9 - Обозначение направлений и осей в ПКМ
В задаче рассматривается поперечно-изотропный материал гомогенизированного слоя (слоя с обобщенными свойствами), описываемый пятью константами: (при этом и ):
- осевой модуль упругости слоя (физическая величина, характеризующая способность материала сопротивляться упругой деформации в продольном направлении 1);
- поперечный модуль упругости слоя (физическая величина, характеризующая способность материала сопротивляться упругой деформации в поперечном направлении);
- главный коэффициент Пуассона (представляет собой отношение поперечных деформаций к продольным при действии напряжений вдоль направления 1);
- поперечный коэффициент Пуассона (представляет собой отношение деформаций в направлении 3 к деформации в направлении 2 при действии напряжений вдоль направления 1);
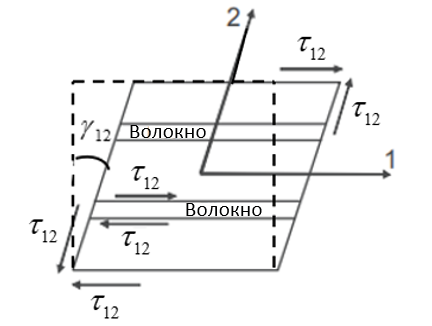
- модуль сдвига в плоскости слоя равен отношению касательного напряжения к величине угла сдвига при действии касательных напряжений в плоскости 12 (на рис. 10 дана плоскость 12 с рис. 9).
Рисунок 10- Изображение сдвига в плоскости слоя
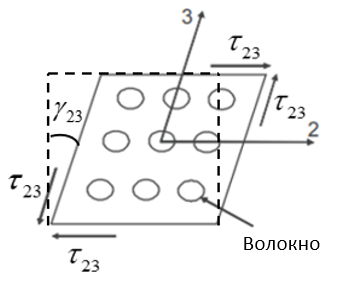
- модуль сдвига в плоскости слоя равен отношению касательного напряжения к величине угла сдвига при действии касательных напряжений в плоскости 23 (на рис. 11 дана плоскость 23 с рис. 9).
Рисунок 11 - Изображение поперечного сдвига
Для расчета гомогенизированных свойств однонаправленного слоя углепластика на основе свойств волокна и матрицы применяются формулы PMM (Periodic Microstructure Micromechanics). Это микромеханический метод, который используется для определения обобщенных механических свойств периодических микроструктур, который основывается на представлении периодической микроструктуры в виде повторяющейся единичной ячейки и на анализе поведения материала в этой ячейке [Hill, 1952]. Основные формулы PMM включают уравнения для эффективных упругих свойств (эффективный тензор жесткости и тензор релаксации).
Для определения эффективного тензора жесткости PMM использует теорию ячеек Хасена, которая описывает поведение материала внутри повторяющейся ячейки. Эффективный тензор жесткости определяется путем усреднения тензоров жесткости материалов, образующих ячейку, в соответствии с их объемными долями [Torquato, 2002]. Эффективный тензор релаксации в PMM определяется путем анализа релаксации напряжений в материале при малых деформациях. Тензор релаксации связывает временную зависимость деформаций в материале с временной зависимостью напряжений [Sanchez-Palencia, 1980].
Получаемые с помощью формул PMM [Davendra, 2016] характеристики являются предсказанными гомогенизированными свойствами однонаправленного слоя углепластика на основе свойств волокна и матрицы.
Формализация проблемы как задачи условной параметрической оптимизации
Предполагается, что в результате эксперимента известны параметры
Объемная доля волокна задана и не является искомым параметром.
Выбору подлежат следующие параметры: Множества их допустимых значений заданы отрезками.
В качестве целевой функции задачи используется
характеризующая суммарное отклонение упругих характеристик слоя ПКМ , полученных расчетным путем от экспериментальных данных. Здесь весовые коэффициенты, учитывающие важность учета каждого слагаемого и размерности входящих величин.
Требуется найти параметры сформированной модели материала, чтобы характеристики , , , , наилучшим образом совпадали с результатами эксперимента, т.е. достигалось минимальное значение целевой функции на заданном параллелепипедном множестве допустимых решений.
Для решения задачи предлагается использовать самоорганизующиеся миграционные алгоритмы глобальной оптимизации, относящиеся к группе эволюционных метаэвристических методов [6–9].
Самоорганизующийся миграционный алгоритм (Self-Organizing Migrating Algorithm – SOMA) [Пантелеев, 2023] может быть классифицирован, как эволюционный алгоритм оптимизации, основанный на самоорганизующемся поведении групп индивидов в социальном окружении. При решении задачи используются конечные наборы возможных решений, называемые популяциями, где – индивид с номером , – размер популяции. Самоорганизующийся миграционный алгоритм имитирует эволюцию начальной популяции и представляет собой итерационный процесс, исследующий множество допустимых решений. Изначально популяция создается из индивидов со случайно сгенерированными координатами из промежутка с помощью равномерного закона распределения. Далее начинаются миграционные циклы. Перед каждым циклом выявляется лидер – индивид с наилучшим значением целевой функции. В этих циклах все индивиды последовательно двигаются к лидеру по прямой их соединяющей, в том числе продвигаясь за него на некоторое расстояние вдоль той же прямой. При этом лидер остается неподвижным. Затем выбирается та позиция индивида, которой соответствует наилучшее значение целевой функции, полученное в процессе поиска, и она записывается в следующую популяцию. Алгоритм продолжается до того момента, пока разность значений целевой функции, соответствующих лидеру и худшему индивиду популяции, не станет меньше заранее заданного значения, или пока не реализуется максимальное число миграционных циклов.
При разработке модифицированного самоорганизующегося миграционного алгоритма оптимизации (MSOMA) использовалась базовая версия алгоритма SOMA [7-9]. Модификации заключаются в выделении среди индивидов, образующих популяцию, трех лидеров. Для каждого из членов популяции генерируются два клона с той же позицией. Тем самым порождаются три популяции, каждая из которых реализует миграционный цикл относительно своего лидера. Для всех членов популяции находятся наилучшие положения, достигнутые в течение цикла. В процессе поиска популяция регулярно обновляется за счет новых индивидов, генерируемых на множестве допустимых решений. Они замещают выбывающих индивидов с наихудшими значениями целевой функции. После выполнения условий окончания производится уточняющий поиск (миграционный цикл), в котором участвуют три оставшихся лидера популяции. В качестве решения предъявляется наилучший результат.
Для подсчета величины целевой функции предлагается использовать алгоритм, в котором использованы следующие обозначения:
- – заданная объемная доля волокна;
- – известные данные из эксперимента;
- – изменяемые параметры;
- , , , , – выходные параметры.
Значения используемых индексов: m – свойства матрицы, f – свойства волокна, A – осевой (Axial), T – поперечный (Transversal).
Алгоритм вычисления значения целевой функции
Шаг 1. Вычисление констант матрицы:
– коэффициент Ламе;
Шаг 2. Вычисление коэффициентов (коэффициенты , , учитывают геометрию микроструктуры, включая геометрию включений и их геометрическое расположение). Используются формулы для цилиндрических волокон:
Шаг 3. Вычисление коэффициентов в тензоре жесткости поперечно-изотропного материала:
Шаг 4. Вычислить коэффициенты для упрощенной записи компонент тензора жесткости:
Шаг 5. Вычисление компонент тензора жесткости для композита с цилиндрическими волокнами и объемной долей волокон (использован метод разложения Фурье):
Шаг 6. Вычисление элементов матрицы:
Шаг 7. Нахождение обратной матрицы вида:
(далее используются значения ,,,,, ).
Шаг 8. Вычисление выходных параметров:
Шаг 9. Вычисление значения целевой функции
Прикладная задача
Предполагается, что в результате эксперимента известны параметры
и объемная доля волокна (таблица 1).
Ограничения на искомые переменные (параметры) заданы в виде отрезков изменения их возможных значений:
МПа; МПа; МПа;
; ; МПа; .
Таблица 1
|
Экспериментальные значения параметров |
Объемная доля волокна |
||||
|
,МПа |
,МПа |
,МПа |
|||
|
337682 |
6918 |
0,3 |
0,52 |
4755 |
0,62 |
Известно решение поставленной задачи, полученное эмпирически [Cabrera Barbero, Javier].
Таблица 2
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
, МПа |
, МПа |
|||
|
517000 |
11158 |
10636 |
0,269 |
0,306 |
4629,558 |
0,363 |
Случай 1. Положим, что все слагаемые в целевой функции имеют равную важность, т.е. . Из-за разного масштаба параметров, от которых зависит целевая функция, и особенностей работы миграционных алгоритмов применяется метод нормализации. Предполагается, что значения всех независимых переменных принадлежат универсальному отрезку [0,1]. Процедура поиска производится на параллепипедном множестве допустимых решений, размерность которого определяется числом независимых переменных (в решаемой задаче ). При подсчете величины целевой функции значения всех переменных преобразуются к исходным масштабам:
Результаты, полученные при помощи алгоритма SOMA (табл. 3): минимальное значение целевой функции , затраченное время 283,7 с.
Таблица 3
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
,МПа |
|||
|
512146 |
13116 |
20442 |
0,269 |
0,228 |
3838,357 |
0,363 |
Результаты, полученные при помощи алгоритма MSOMA (табл. 4): минимальное значение целевой функции , затраченное время: 935,5 с.
Таблица 4
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
,МПа |
|||
|
484359 |
13030 |
80527 |
0,235 |
0,311 |
3232,095 |
0,385 |
Заметим, что полученные значения параметра сильно отличаются от эмпирического решения и друг от друга, поэтому в случае 2 предлагается использовать подход, связанный с добавлением регуляризирующего слагаемого в целевую функцию, влияние которого последовательно уменьшается.
Случай 2. Добавим регуляризирующее слагаемое с весовым коэффициентом . Тогда целевая функция имеет вид где ; МПа.
Результаты, полученные при помощи алгоритма SOMA (табл. 5): минимальное значение целевой функции , затраченное время 1062 с.
Таблица 5
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
, МПа |
|||
|
455936 |
9111 |
10635 |
0,260 |
0,369 |
5017,922 |
0,347 |
Результаты, полученные при помощи алгоритма MSOMA (табл. 6): минимальное значение целевой функции , затраченное время 1851,7 с.
Таблица 6
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
,МПа |
|||
|
485647 |
10237 |
10635 |
0,278 |
0,305 |
4997,997 |
0,342 |
Случай 3. Также исследован подход, при котором лучшая особь мигрирующей популяции из предыдущего запуска алгоритмов SOMA и MSOMA добавляется в начальную популяцию для следующего запуска, а значение коэффициента на пяти последовательных итерациях каждый раз уменьшается в 3 раза.
Результаты, полученные при помощи алгоритма SOMA (табл. 7): минимальное значение целевой функции , затраченное время 8301 с.
Таблица 7
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
,МПа |
|||
|
512495 |
11418 |
10636 |
0,291 |
0,225 |
4971,129 |
0,335 |
Результаты, полученные при помощи алгоритма MSOMA (табл. 8): минимальное значение целевой функции: , затраченное время 4157,7 с.
Таблица 8
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
,МПа |
|||
|
505776 |
11102 |
10636 |
0,288 |
0,248 |
4979,134 |
0,337 |
Случай 4. Предположим, что значение параметра МПа задано (найдено предварительно с помощью других подходов к решению задачи гомогенизации).
Результаты, полученные при помощи алгоритма SOMA (табл. 9): минимальное значение целевой функции , затраченное время 1049,5 с.
Таблица 9
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
,МПа |
,МПа |
, МПа |
|||
|
516018 |
11591 |
10636 |
0,293 |
0,212 |
4966,414 |
0,333 |
Результаты, полученные при помощи алгоритма MSOMA (табл. 10): минимальное значение целевой функции , затраченное время 2703,2 с.
Таблица 10
|
Свойства волокна |
Свойства матрицы |
|||||
|
,МПа |
, МПа |
, МПа |
, МПа |
|||
|
504938 |
11065 |
10636 |
0,288 |
0,251 |
4980,057 |
0,337 |
Выполненные исследования позволяют сделать вывод о том, что определение параметра является математически некорректной задачей. Использование априорной информации о значении этого параметра позволяет получить решение с применением идей регуляризации. При фиксировании значения решение задачи различными методами оптимизации становится устойчивым к изменению начальных данных и дает удовлетворительный по точности результат при приемлемых вычислительных затратах.
Заключение
Получение упругих свойств отдельных компонентов ПКМ позволяет решить проблему моделирования материала в микромасштабе, что в свою очередь позволяет учитывать особенности микроструктуры ПКМ и предсказывать их общие упругие свойства.
Кроме того, знание упругих свойств отдельных компонентов важно для эффективного выбора компонентов ПКМ при проектировании и производстве композитных изделий.
Упругие свойства отдельных компонентов могут быть использованы для определения наилучших условий изготовления композита и для контроля качества при производстве композитных изделий.
Получение таких параметров, как , на данном этапе развития научно-технического прогресса невозможно. Предложенная методика математического моделирования и параметрической оптимизации с помощью миграционных метаэвристических алгоритмов позволяет прогнозировать характеристики композитного материала с приемлемой точностью.
Литература
- Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1987. - 247 с.
- Hill, R. The elastic behavior of a crystalline aggregate. Proc. Phys. Soc. London, 65:349-354, 1952.
- Torquato, S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Springer, 2002.
- Sanchez-Palencia, E. Non-Homogeneous Media and Vibration Theory. Springer-Verlag, 1980.
- Barbero, E.J. Introduction to Composite Materials Design, Second Edition. CRC Press, 2018. ISBN 978-1-4987-5983-9.
- Davendra D., Zelinka I. Self-organizing migrating algorithm. Methodology and implementation // Studies in Computational Intelligence, Springer, 2016, Vol. 626.
- Пантелеев А.В., Скавинская Д.В. Метаэвристические стратегии и алгоритмы глобальной оптимизации.- Факториал, 2023.– 564 с.
- Panteleev A.V., Rakitianskii V.M. Application of the modified self-organizing migration algorithm MSOMA in optimal open-loop control problems // Journal of Physics: Conference Series. – 2021. Vol. 1925. Id 012017.
- Пантелеев А.В., Ракитянский В.М. Разработка модифицированного самоорганизующегося миграционного алгоритма оптимизации (MSOMA) // Моделирование и анализ данных. – 2020. № 2. – С. 62–73.
- Cabrera Barbero, Javier, "Thermal-Fatigue and Thermo-Mechanical Equivalence for Transverse Cracking Evolution in Laminated Composites" (2018). Graduate Theses, Dissertations, and Problem Reports. 3715.
Информация об авторах
Метрики
Просмотров web
За все время: 270
В прошлом месяце: 22
В текущем месяце: 13
Скачиваний PDF
За все время: 113
В прошлом месяце: 8
В текущем месяце: 5
Всего
За все время: 383
В прошлом месяце: 30
В текущем месяце: 18