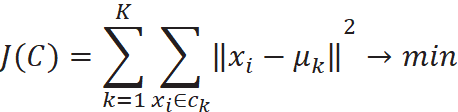Моделирование и анализ данных
2022. Том 12. № 1. С. 5–15
doi:10.17759/mda.2022120101
ISSN: 2219-3758 / 2311-9454 (online)
Кластеризация водителей по степени опасности вождения с использованием алгоритмов машинного обучения
Аннотация
Общая информация
Ключевые слова: кластеризация, гистограммы распределения, опасное вождение, системы мониторинга, машинное обучение
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2022120101
Получена: 04.03.2022
Принята в печать:
Для цитаты: Баданина Н.Д., Судаков В.А. Кластеризация водителей по степени опасности вождения с использованием алгоритмов машинного обучения // Моделирование и анализ данных. 2022. Том 12. № 1. С. 5–15. DOI: 10.17759/mda.2022120101
Полный текст
Введение
Системы мониторинга безопасности вождения транспортных средств (ТС) призваны снижать аварийность на дорогах; контролировать общее соблюдение правил дорожного движения. Частично разработки нацелены на заблаговременное предотвращение аварийных ситуаций. Такие системы безусловно важны, по причине того, что от них в прямом смысле может зависеть безопасность на дороге, жизни водителей, пассажиров и пешеходов. При должном контроле поведения водителя, существует возможность применения санкционных мер, с целью улучшить его поведение за рулем, что в перспективе может снизить риск дорожно-транспортного происшествия.
Методы анализа данных широко применяются для обработки больших данных высокой размерности. Кластеризация – разбиение множества объектов на группы (кластеры), основываясь на свойствах этих объектов. Кластер представляет собой группу объектов, имеющих общие признаки. Целью алгоритмов кластеризации является создание классов, которые максимально связаны внутри себя, но различны друг от друга [Кутуков, 2011]. Таким образом, в системах мониторинга опасности вождения можно применить алгоритмы кластеризации, с целью решения задачи группировки водителей на некоторое количество классов, соответствующее различным типам вождения.
Релевантные исследования и разработки
На рынке присутствуют как государственные реализации системы мониторинга, так и частные. К государственным относится система камер фото- и видео-фиксации ГИБДД. В их основе лежит одна из технологий искусственного интеллекта – компьютерное зрение. Эта система имеет ряд преимуществ, однако, не имеет возможности сделать вывод о безопасности вождения в любом моменте времени – необходимо обязательное наличие камер или иных средств фиксации нарушения. У органов регулировки дорожно-транспортной ситуации нет возможности обеспечить стопроцентное покрытие всех автомагистралей, дорог специализированным оборудованием, и нет возможности осуществлять мониторинг ТС на протяжении всего пути. Во многом операционная система Яндекс.Навигатор и подобные “помогают” водителям избежать нарушений, предупреждая о наличии средств контроля заранее. Это ведет к недостоверной статистике о поведении водителя. Третьим недостатком является зависимость от технологии компьютерного зрения, которая не способна работать при ненадлежащем качестве изображения, при поломке фото- или видеорегистраторов.
Альтернативные способы контроля качества вождения представлены частными компаниями. Яндекс.Про считывает данные акселерометра устройства, на которое он установлен, – смартфона или планшета. Если водитель совершает агрессивные манёвры – резкий старт и торможение, многократную смену полос, несоблюдение дистанции, – акселерометр фиксирует перегрузку и считает нарушением при систематичности [Мониторинг манеры вождения]. Недостатком является факт того, что по каждому ТС показатели собираются множество раз за все время поездки, что усложняет анализ и может вести к ложным выводам из-за ошибки оборудования или из-за факта разовых нарушений.
В исследовательской области есть ряд работ по определению опасного вождения – кластеризация водителей по стилям торможения [ 2 ] с использованием нейронной сети Кохонена; определение поведения водителей на основе мониторинга движения в реальном времени [Huaikun Xiang ,, 2021]; детекция несосредоточенности водителя с использованием изображения машины внутри и снаружи [ 6 ].
Таким образом, на рынке мониторинга безопасности вождения транспортных средств присутствует возможность внедрения новых технологий, использующих машинное обучение. В данной работе описана методика построения моделей кластеризации водителей для задачи обнаружения паттернов опасного вождения.
Гистограммы распределения как способ составления обучающего множества
В качестве данных в работе был использован датасет, собранный из информации о сигналах с ТС. К сигналам относятся значения скорости; значения ускорений по трем осям x, y, z.
Дано множество водителей
![]() . Для каждого
. Для каждого
![]() дан вектор скоростей
дан вектор скоростей
![]() , где каждое значение соответствует скорости ТС.
Аналогично заданы вектора ускорений
, где каждое значение соответствует скорости ТС.
Аналогично заданы вектора ускорений
![]() ,
,
![]() ,
,
![]() по осям x, y, z соответственно. Требуется
разделить множество
по осям x, y, z соответственно. Требуется
разделить множество
![]() на
на
![]() непересекающихся кластеров
непересекающихся кластеров
![]() .
.
Данные о сигналах поступали с некоторой периодичностью на протяжении всей поездки на ТС, даже при условии того, что фактическая скорость могла быть нулевой, то есть факт движения отсутствовал. На их основе были обучены и протестированы модели кластеризации, реализованные с помощью методов машинного обучения без учителя, то есть в данных отсутствовала разметка о принадлежности того или иного водителя к некоему классу, отвечающему за степень опасности вождения.
Данные по трекам были агрегированы. Для каждого водителя была собрана вся доступная информация по сигналам, записанным во время всех поездок. За каждую поездку могло поступить множество сигналов с разным временным промежутком. Проблема обучения моделей на таких данных состоит в том, что для каждого водителя количество собранных сигналов велико и для разных водителей их может быть разное количество, и, следовательно, вектор признаков будет иметь различную длину. С векторами различной длины нельзя составить обучающее множество. Вариант дополнения каждого вектора до максимальной длины нецелесообразен, так как может вести к существенному увеличению времени обучения модели и ложным выводам.
Решением описанной проблемы является составление частотных гистограмм распределения значений сигналов по интервалам. Гистограммы распределения указывают насколько часто встречаются те или иные значения. Рассмотрим алгоритм построения для задачи кластеризации водителей.
Выделяются сигналы одной природы. В рассматриваемой задаче
описано множество сигналов
![]() . Для каждого вектора из множества
. Для каждого вектора из множества
![]() выделяются интервалы значений. Не допускается
перекрытие промежутков и наличие пропущенных значений.
выделяются интервалы значений. Не допускается
перекрытие промежутков и наличие пропущенных значений.
· Интервалы задаются экспертом;
· Весь диапазон значений разбивается на равное количество частей с некоторым шагом;
· Оптимальное количество интервалом определяется математически, исходя из мощности выборки. Применяется формула Стерджесса
|
|
(1) |
, где
![]() – количество наблюдений.
– количество наблюдений.
После подсчета коэффициента
![]() весь диапазон значений от минимального до
максимального разбивается на равные части. Ширина интервала определяется по
формуле
весь диапазон значений от минимального до
максимального разбивается на равные части. Ширина интервала определяется по
формуле
|
|
(2) |
Тогда первый интервал начинается в
![]() , а последний (с номером
, а последний (с номером
![]() ) заканчивается в
) заканчивается в
![]() . Интервалы составляются следующим образом:
. Интервалы составляются следующим образом:
![]() .
.
После определения интервалов осуществляется подсчет частоты
попадания значений сигналов в соответствующие интервалы. Частота считается
явно: сколько из всех значений находятся внутри интервала. Пусть
![]() и
и
![]() – левая и правая граница интервала
– левая и правая граница интервала
![]() соответственно, тогда считается количество
значений
соответственно, тогда считается количество
значений
![]() , для которых выполняются неравенства
, для которых выполняются неравенства
![]() и
и
![]() .
.
Таким образом, можно подсчитать частоту попадания значений
сигналов в определенный интервал и составить обучающее множество. После
выполнения вышеописанного алгоритма был составлен датасет следующего вида:
колонки соответствуют интервалу сигнала из
![]() , строки – водителям из D, а цифры – количеству
вхождений значений сигнала в интервал.
, строки – водителям из D, а цифры – количеству
вхождений значений сигнала в интервал.
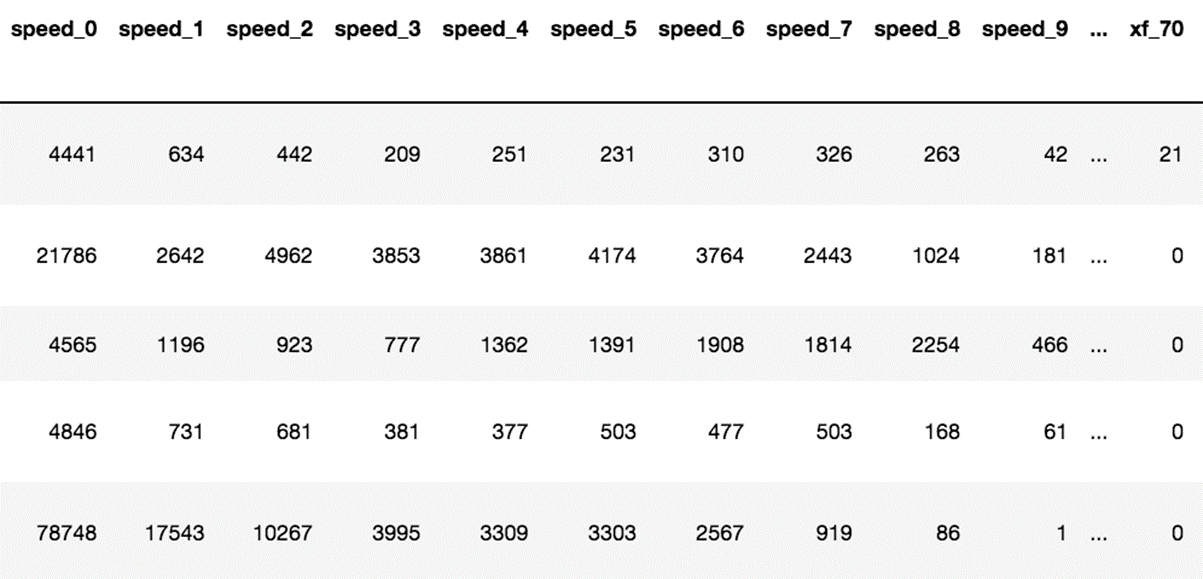
Рис. 1 Пример полученного датасета
Интервалы были заданы одинаковой длины: для скорости с шагом 10, а для ускорений с шагом 100. Каждому водителю соответствует единственная строка, в которой указано количество попадания значений сигнала в заданные промежутки значений. Такой подход позволяет
● учесть данные по всем поездкам, совершенным водителем ТС;
● создать вектор определенной неизменной длины для каждого водителя;
● объединять интервалы при необходимости сбора более обобщенной статистики;
● добавлять или исключать водителей без необходимости пересчета всего обучающего множества;
● собрать наглядную статистику по каждому доступному водителю за весь период активности;
● исключить введения штрафных санкций за разовые нарушения, которые не свойственны определенному водителю;
● перевести целочисленные значения частотности в долевые значения, указывающие какой процент значений попадает в определенный интервал по отношению ко всему множеству значений сигналов, которое было разбито на промежутки.
Построение модели кластеризации
Цель моделей кластеризации – определить
![]() количество групп для
количество групп для
![]() объектов на основании метрик сходства таким
образом, чтобы максимизировать схожесть между объектами одного класса,
одновременно минимизировав схожесть между объектами разных классов.
объектов на основании метрик сходства таким
образом, чтобы максимизировать схожесть между объектами одного класса,
одновременно минимизировав схожесть между объектами разных классов.
Пусть
![]() – множество из
– множество из
![]() точек некоторой размерности
точек некоторой размерности
![]() , которое необходимо разбить на
, которое необходимо разбить на
![]() кластеров
кластеров
![]() .
.
Алгоритм K-means стремится минимизировать суммарное
квадратичное отклонение точек кластеров от центров этих кластеров. Пусть
![]() – центр кластера
– центр кластера
![]() . Среднеквдаратическая ошибка между
. Среднеквдаратическая ошибка между
![]() и точками кластера
и точками кластера
![]() определяется как
определяется как
|
|
(3) |
Цель модели K-means – минимизировать суммарную
среднеквадратическую ошибку для всего множества кластеров
![]() [Jain, 2010].
[Jain, 2010].
|
|
(4) |
В работе были протестированы различные методы кластеризации, для каждого из которых была вычислена метрика силуэт. Коэффициент силуэт вычисляется с помощью среднего внутрикластерного расстояния и среднего расстояния до ближайшего кластера по каждому наблюдению. Силуэт вычисляется по формуле
|
|
(5) |
, где
![]() – среднее расстояние от данного объекта до
объектов из того же кластера,
– среднее расстояние от данного объекта до
объектов из того же кластера,
![]() – среднее расстояние от данного объекта до
объектов из ближайшего кластера (отличного от того, в котором лежит сам
объект). Эта метрика позволяет оценивать качество работы моделей кластеризации,
обученных без учителя.
– среднее расстояние от данного объекта до
объектов из ближайшего кластера (отличного от того, в котором лежит сам
объект). Эта метрика позволяет оценивать качество работы моделей кластеризации,
обученных без учителя.
Таблица 1
Вариации данных
|
|
Интервалы составлены с шагом 10 для скорости и с шагом 100 для ускорения |
|
Частотные долевые значения в % |
А |
|
Частотные целочисленные значения |
Б |
Таблица 2
Результаты работы алгоритмов
|
Название модели с указанием основных параметров |
Метрика силуэт |
|
|
A |
Б |
|
|
KMeans |
0.459 |
0.505 |
|
KMeans А, Б: n_clusters=2, init='k-means++', max_iter=300, algorithm= 'auto' |
0.686 |
0.801 |
|
AgglomerativeClustering |
0.449 |
0.434 |
|
AgglomerativeClustering Б: n_clusters=2, affinity='euclidean', linkage=' single' |
0.682 |
0.892 |
|
AffinityPropagation |
0.221 |
0.344 |
|
AffinityPropagation Б: damping=0.85, max_iter=200, affinity='euclidean' |
0.224 |
0.342 |
|
Birch |
0.446 |
0.434 |
|
Birch А: n_clusters=2, threshold=0.36, branching_factor=50 Б: n_clusters=2, threshold=0.1, branching_factor=50 |
0.686 |
0.804 |
|
DBSCAN A: eps=0.30, min_samples=9 Б: eps=5, min_samples=4 |
0.384 |
-0.281 |
|
DBSCAN Б: eps=9, min_samples=3, algorithm='auto' |
0.473 |
-0.277 |
|
MiniBatchKMeans n_clusters=5 |
0.442 |
0.497 |
|
MiniBatchKMeans Б: n_clusters=2, init='k-means++', max_iter=100, batch_size=64, reassignment_ratio=0.01 |
0.686 |
0.802 |
|
MeanShift() |
0.537 |
0.394 |
|
MeanShift max_iter=300, bandwidth=0.8 |
0.683 |
0.002 |
|
OPTICS А: eps=0.8, min_samples=10 Б: eps=10, min_samples=9 |
-0.643 |
-0.624 |
|
OPTICS А, Б: eps=1, min_samples=2, metric= 'euclidean', cluster_method= 'xi', algorithm= 'auto' |
-0.291 |
-0.131 |
|
SpectralClustering n_clusters=5 |
0.444 |
-0.322 |
|
SpectralClustering А: n_clusters=2, eigen_solver='arpack', gamma=0.2, affinity='rbf', assign_labels='kmeans' Б: n_clusters=2, eigen_solver='lobpcg', affinity='nearest_neighbors', assign_labels='discretize' |
0.686 |
0.352 |
|
GaussianMixture n_components=2 |
0.376 |
0.099 |
|
GaussianMixture А: covariance_type='spherical', n_components=2, init_params='kmeans' Б: covariance_type='tied', n_components=2, init_params='kmeans' |
0.682 |
0.805 |
Из Таблицы 2 видно, что метрику силуэт удалось улучшить для большинства моделей. От вида данных, подаваемых в модель зависят полученные результаты, поэтому при разработке стоит учитывать разнообразие существующих алгоритмов, уделить внимание их подбору.
Рассмотрим подробнее модель KMeans на данных типа Б, так как она показала одну из наилучших метрик, а также проста в понимании. Построим гистограммы для центров кластеров, на которые модель разделила данные. Центр можно считать средним значением по кластеру. Из Рис. 2 видно, что 3 класс можно считать классом, относящимся к опасному вождению из-за распределения значений в интервалах с высокими скоростями.
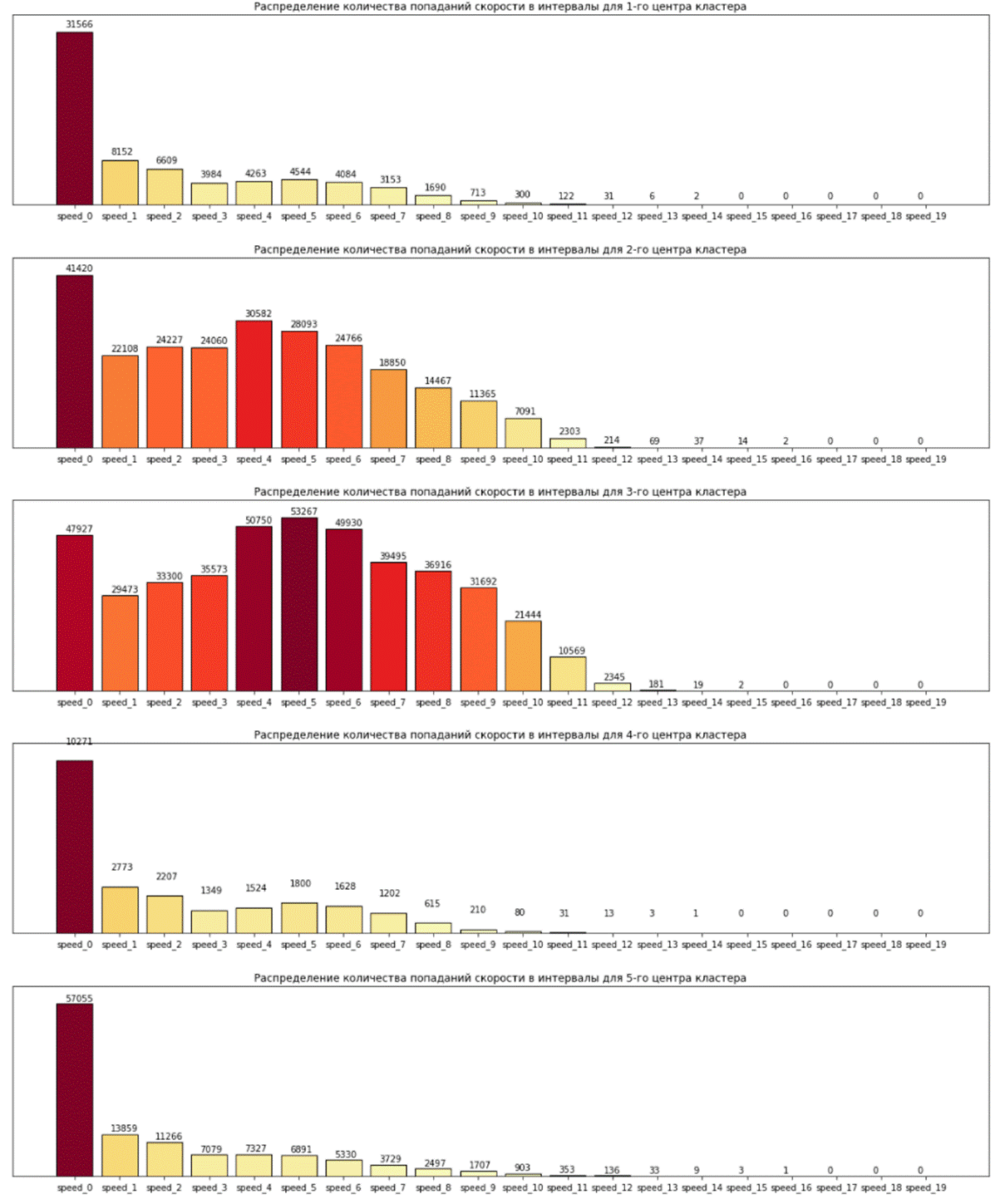
Рис. 2 Гистограммы для центров классов Для выполнения расчетов и построения моделей был выбран язык программирования Python3, с использованием среды разработки Jupyter Notebook. Выбор обусловлен наличием большого количество библиотек с готовыми реализациями математического аппарата, а также наличием мощных инструментов для визуализации готовых результатов. В ходе выполнения работы были использованы готовые библиотеки, в том числе feather для хранения больших данных. Формат feather был использован как альтернатива csv, так как позволяет уменьшить объем сохраняемых файлов, увеличивает скорость чтения и записи данных. Были обучены модели кластеризации из широко используемого пакета Scikit Learn.
Целью работы являлась реализация методов кластеризации в решении задачи разбиения множества водителей на классы, соответствующие степени опасности вождения. В качестве данных были использованы записи о сигналах водителей за некоторый временной период. Для агрегации датасета были использованы гистограммы распределения, позволяющие привести данные в формат, пригодный для обучения моделей машинного обучения, также, с помощью этого подхода была собрана собирательная статистика за все время активности водителя ТС.
В ходе выполнения работы был обучен ряд моделей кластеризации и подсчитала метрика силуэт. При принятии решения о качестве модели кластеризации, обученной без учителя, можно опираться на значение этой метрики в том случае, когда результаты работы модели совпадают с ожиданиями от поставленной задачи.
Использование описанного метода кластеризации и работы с гистограммами распределения сигналов в системах мониторинга качества вождения может улучшить контроль за поведением водителей, поможет выявлять и предотвращать поведение, способное привести к дорожно-транспортному происшествию.
Литература
- Кутуков Д.С. Применение методов кластеризации для обработки новостного потока // Технические науки: проблемы и перспективы: материалы I Междунар. науч. конф. Санкт-Петербург: Реноме, 2011. С. 77-83.
- Дик Д.И. Кластеризация водителей по стилям торможения // Курганский государственный университет. Вестник КГУ. 2012. №2(24). С. 17-20.
- Мониторинг манеры вождения [Электронный ресурс]: https://pro.yandex/ru-ru/moskva/knowledge-base/taxi/safety/monitoring-driving
- Jain A.K. Data clustering: 50 years beyond K-means // Pattern Recognition Letters, 31(8). 2010. pp. 651–666.
- Huaikun Xiang , Jiafeng Zhu , Guoyuan Liang and Yingjun Shen Prediction of Dangerous Driving Behavior Based on Vehicle Motion State and Passenger Feeling Using Cloud Model and Elman Neural Network // Frontiers in Neurorobotics. April 2021. Vol. 15. p. 16.
- Omerustaoglu Furkan, Sakar C. Okan, Kar Gorkem Distracted driver detection by combining in-vehicle and image data using deep learning // Applied Soft Computing 96(6). 2020.
- J. Hartigan Clustering Algorithms // New York: Wiley, 1975.
Информация об авторах
Метрики
Просмотров web
За все время: 506
В прошлом месяце: 22
В текущем месяце: 8
Скачиваний PDF
За все время: 210
В прошлом месяце: 5
В текущем месяце: 1
Всего
За все время: 716
В прошлом месяце: 27
В текущем месяце: 9