Моделирование и анализ данных
2019. Том 9. № 4. С. 100–111
doi:10.17759/mda.2019090408
ISSN: 2219-3758 / 2311-9454 (online)
Мультиагентное моделирование в задачах формирования расписаний
Аннотация
Общая информация
Ключевые слова: мультиагентные системы, предпочтения агентов, оптимизация, распределенные системы
Рубрика издания: Методы оптимизации
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2019090408
Финансирование. Работа выполнена при поддержке гранта РФФИ проект № 18–00–00012 (18–00–00011) КОМФИ.
Для цитаты: Судаков В.А., Сивакова Т.В. Мультиагентное моделирование в задачах формирования расписаний // Моделирование и анализ данных. 2019. Том 9. № 4. С. 100–111. DOI: 10.17759/mda.2019090408
Полный текст
В статье исследуется применение мультиагентных технологий для решения оптимизационных задач. Показано, как мультиагентные системы позволяют работать с ограничениями в распределенной вычислительной среде. Формализована задача составления расписания. Разработано программное обеспечение и проведены вычислительные эксперименты, показавшие эффективность предложенного подхода.
Введение
Рассмотрим проблему распределения множества задач на множество ресурсов (например, планирование лекций для аудиторий или пакета заданий для нескольких процессоров). Это распространенная и важная проблема, которую можно формализовать, используя мультиагентный подход.
Обработку ограничений можно рассматривать как широкую и разнообразную область исследований, объединяющую методы и алгоритмы, которые охватывают многие различные дисциплины, включая исследование операций, компьютерное зрение, искусственный интеллект и теорию принятия решений. Все эти области имеют дело со сложными проблемами, которые можно сделать более понятными, тщательно продумав ограничения, определяющие структуру проблемы.
В данной статье показано, как обработка ограничений может использоваться для решения проблем оптимизации в мультиагентных системах (MAS - multi-agent system). Рассматриваются распределенные подходы к задачам оптимизации с ограничения (DCOP - distributed constraint optimization). В DCOP набор агентов должен прийти к какому-то соглашению (обычно через какую-то форму переговоров), о том, какие действия должен предпринять каждый агент, чтобы совместно получить наилучшее решение для всей системы [A. Farinelli, M, 2013]. Эта структура успешно используется не только для планирования собраний, но и в сенсорных сетях, где датчики должны договориться о том, на какую цель они должны ориентироваться, чтобы получить наиболее точную оценку местоположения целей. Для тестирования эффективности алгоритмов решения DCOP, часто используют задачи проверки выполнимости булевых функций и раскраски графов. Общим ключевым аспектом DCOP для MAS является то, что каждый агент ведет локальные переговоры только с подмножеством других агентов (обычно называемых соседями), которые могут непосредственно влиять на его поведение. В зависимости от постановки задачи и используемой методики решения этот аспект может значительно сократить вычислительные усилия, с которыми сталкивается каждый агент, что делает сложные проблемы доступными даже для крупномасштабных систем. Так в задаче планирования собраний, агент будет напрямую вести переговоры только с теми агентами, с которыми он должен встретиться, что обычно составляет небольшое подмножество агентов, вовлеченных во всю проблему.
Наряду с мультиагентными подходами, сейчас активно развиваются метаэвристиче- ские методы оптимизации, которые хотя и не гарантируют нахождения точного решения, но обычно позволяют найти приемлемое решение за приемлемое время [Пантелеев, 2013].
Возможная формализация DCOP для задачи планирования собрания включает набор агентов, представляющих людей, участвующих в собрании, и набор переменных, которые представляют возможное время начала данного собрания в соответствии с участником. Ограничения предписывают равенство переменным, представляющим время начала одного и того же собрания разных агентов, и гарантируют, что переменные, которые представляют время начала разных встреч одного и того же агента не совпадает. Наконец, предпочтения могут быть представлены как мягкие ограничения на время начала встреч, и общая цель состоит в том, чтобы оптимизировать сумму всех мягких ограничений. Хотя в этом параметре у нас есть личные предпочтения, мы максимизируем сумму предпочтений всех агентов, и, таким образом, рассматривается сценарий, когда агенты полностью сотрудничают, то есть они готовы уменьшить свою собственную локальную полезность, если это максимизирует глобальную полезность [Сивакова, 2019].
Постановка задачи
В качестве конкретного примера применения DCOP рассмотрим задачу формирования расписания авиарейсов.


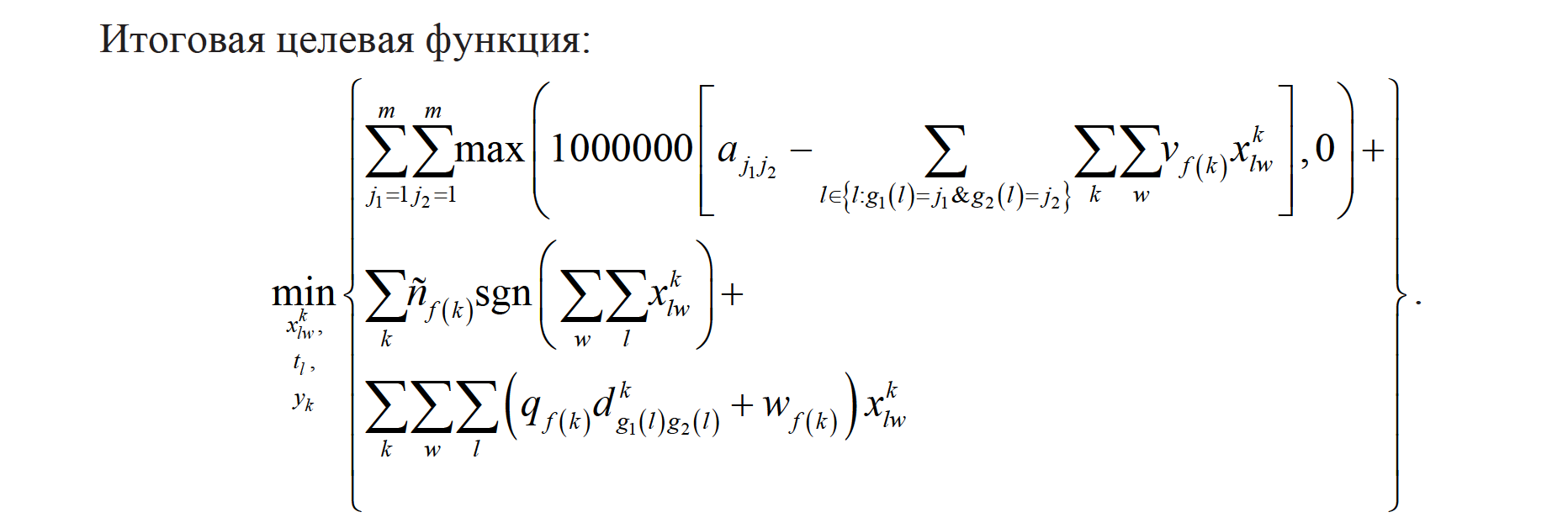
Эту проблему можно решить, и как классическую оптимизационную задачу. Однако подход DCOP обеспечивает масштабируемое решение, которое можно реализовать большом вычислительном кластере, обеспечив, таким образом, существенный рост производительности.
Определение сети ограничений
Ключевым элементом для распределенной обработки ограничений является концепция сети ограничений. Приведем стандартные формальные определения, относящиеся к сетям ограничений, а затем рассмотрим парадигму распределенной обработки ограничений.


Метод решения
Распределенное решение предполагает использование набора агентов, которые контролируют переменные и взаимодействуют, чтобы найти решение для сети ограничений. Как было сказано выше, это могут быть задачи CSP или COP, которые решаются соответствующими распределенными методами: распределенный CSP (distributed CSP - DCSP) и распределенный COP (distributed COP - DCOP). Парадигма DCSP была первоначально предложена для решения проблем координации в среде с несколькими агентами [Makoto Yokoo. Distributed, 2001], однако в последние годы платформе DCOP уделялось больше внимания, поскольку она имеет больше сценариев практического применения и CSP можно свести к COP.
DCOP представлен сетью N = (X, D, C, содержащей мягкие ограничения, плюс набор агентов A = {A1, A2,..., Ak} . Поиск оптимального решения DCOP - это NP-трудная проблема. Поэтому эмпирическая оценка методов решения DCOP является решающим моментом для оценки их возможного практического применения.
Учитывая предыдущее описание DCOP, рассмотрим точные методы решения, то есть те, которые всегда находят решение, которое соответствует наилучшему значению целевой функции (глобальный оптимум). Эти методы особенно интересны и изящны с теоретической точки зрения, но, поскольку мы имеем дело с проблемой NP-полноты, они также демонстрируют экспоненциально увеличивающиеся издержки координации (либо в размере, либо количестве сообщений, которыми обмениваются, либо в вычислениях, проводимых каждым агентом), количество агентов в системе увеличивается.
В целом, подходы можно разделить на два класса: те, которые основаны на поиске [6-10], и те, которые используют динамическое программирование [A. Petcu and, 2005]. Кроме того, подходы, основанные на поиске, делятся на синхронные, такие как SyncBB[Katsutoshi Hirayama and, 1997] и AND/ OR поиск [R. Dechter and, 2007], и асинхронные, такие как ADOPT[P.J. Modi, 2005], NCBB[A. Chechetka and, 2006] и AFB[Gershman, 2009]. В модели синхронного выполнения агенты ждут сообщений от других агентов, прежде чем вычислить и отправить новые сообщения самим. Напротив, в асинхронной модели агенты выполняют вычисления и отправляют сообщения, не ожидая сообщений от своих соседей. Асинхронная операция желательна в мультиагентном подходе, поскольку она позволяет агентам принимать решения, не дожидаясь, пока другие агенты завершат свои вычисления, полностью используя параллельные вычисления. С другой стороны, синхронная модель гарантирует, что агенты всегда обладают самой актуальной информацией перед выполнением вычислений, таким образом, сводя к минимуму избыточность как в вычислениях, так и в коммуникации.
Все вышеперечисленные методы полностью децентрализованы, в том смысле, что каждый агент имеет полный контроль над своими переменными и знает только про релевантные ограничения. Тем не менее, централизация части проблемы иногда может уменьшить усилия, необходимые для поиска оптимального в глобальном масштабе решения. Данная концепция, лежит в основе подхода оптимального асинхронного частичного наложения (Optimal Asynchronous Partial Overlay - optAPO) [R.Maillerand, V, 2004]. Алгоритм optAPO стремится обнаружить части задачи, которые особенно трудно решить децентрализованным способом (части, которые сильно взаимосвязаны). Далее он объединяет их в подзадачи, которые делегируются агентам-посредникам, действующим как централизованные решатели. Практика показала, что optAPO последовательно снижает накладные расходы на коммуникации по сравнению с другими децентрализованными методами, такими как ADOPT. Однако очень трудно предугадать, какая часть задачи будет решаться централизовано, и, следовательно, трудно предсказать затраты вычислительных ресурсов, которые потратят агенты-посредники.
В работе проведены вычислительные эксперименты на децентрализованном подходе ADOPT. Для решения поставленной задачи использовался пакет pyDCOP - это решатель DCOP написанный на языке Python[Library for research]. Он обладает следующими особенностями:
• предоставляет реализации многих классических алгоритмов DCOP;
• позволяет легко реализовать собственные алгоритмы DCOP, предоставляя всю необходимую инфраструктуру: агенты, систему обмена сообщениями, сбор метрик;
• упрощает проведение распределенных экспериментов, так как агенты могут работать на одном и том же компьютере или на разных ЭВМ;
• обеспечивает мультиплатформенность, так как может работать на Windows, Mac и Linux;
• подходит для использования в интернете вещей (IoT) и может запускать агенты на одноплатных компьютерах, таких как Raspberry Pi.
Поставленная задача формирования расписания была успешно решена на языке Python и размещена на портале веб-сервисов поддержки принятия решений ws-dss.com (см. рис. 1).
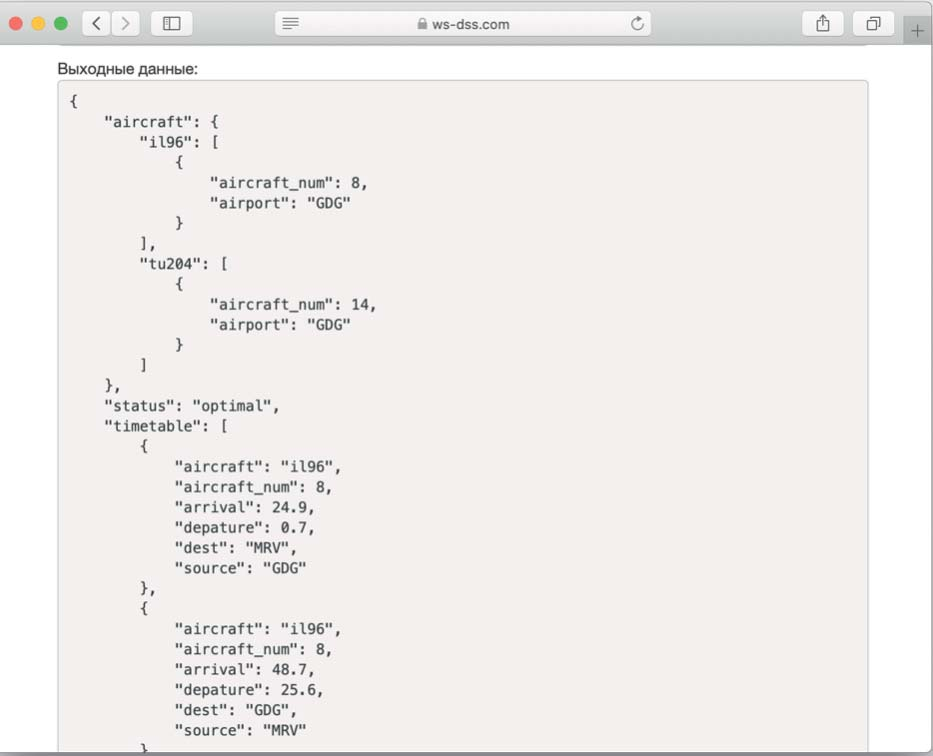
Рис. 1. Решение задачи на ws-dss.com
Несколько работ основаны на ADOPT, пытаются сократить время вычислений. Например, в работе [W. Yeoh, A, 2008] предложен метод BnB-ADOPT, который является расширением ADOPT, он последовательно сокращает время вычислений, используя различные стратегии поиска: поиск в глубину и метод ветвей и границ. В работе [S.M. Ali, 2005] предложено использование методов предварительной обработки для поиска ADOPT и показано, что это может привести к существенному увеличению производительности.
Заключение
ADOPT - эффективный мультиагентный метод, который работает в асинхронном режиме. Использование памяти каждым агентом является полиномиальным по количеству переменных, что является существенным преимуществом данного подхода по сравнению с динамическим программированием. Кроме того, все сообщения имеют фиксированный размер. Однако количество сообщений, которыми должны обмениваться агенты, в худшем случае экспоненциально по количеству переменных. Это влияет на время, необходимое для поиска оптимального решения. В частности, число циклов синхронизации сообщений определяется числом всех агентов, получивших входящие сообщения и отправивших исходящие сообщения, и является экспоненциальным. Такие экспоненциальные элементы неизбежны при поиске точного оптимального решения и могут серьезно ограничивать размерность решаемых задач.
MAS позволяет минимизировать количество информационных агентов, которые должны раскрывать информацию друг другу (таким образом, повышается уровень конфиденциальности). Это связано с тем, что в DCOP агентам необходимо знать только об ограничениях, в которые они вовлечены.
В целом, структура DCOP и алгоритмы, разрабатываемые для решения таких проблем, представляют собой активную область исследований в сообществе MAS, которая все чаще применяется в реальных условиях.
Финансирование
Работа выполнена при поддержке гранта РФФИ проект № 18-00-00012 (18-00-00011) КОМФИ.
Литература
- A. Farinelli, M. Vinyals, A. Rogers, and N. Jennings. “Distributed Constraint Handling and Optimization”, in G. Weiss (ed.), “Multiagent Systems” (second edition), MIT Press, p. 547–584, 2013.
- Пантелеев А.В., Метлицкая Д.В., Алешина Е.А. Методы глобальной оптимизации. Метаэвристические стратегии и алгоритмы. М.: Вузовская книга, 2013. 244 c.
- Сивакова Т.В., Судаков В.А. Метод нечетких областей предпочтении для оценки эффективности инноваций // XXVIII Международная научно-техническая конференция «Современные технологии в задачах управления, автоматики и обработки информации». Алушта, 14–20 сентября 2019 г. Сборник трудов. М.: Изд.-во Национальный исследовательский ядерный университет «МИФИ», 2019. С. 81–82.
- R. Dechter. Constraint Processing. Morgan Kaufmann, 2003.
- Makoto Yokoo. Distributed constraint satisfaction: Foundations of cooperation in multiagent systems. Springer-Verlag, 2001.
- P.J. Modi, W. Shen, M. Tambe, and M. Yokoo. ADOPT: Asynchronous distributed constraint optimization with quality guarantees. Artifi cial Intelligence Journal, (161):149–180, 2005.
- A. Chechetka and K. Sycara. No-commitment branch and bound search for dis- tribute constraint optimization. In Proceedings of Fifth International Joint Confer- ence on Autonomous Agents and Multiagent Systems, pages 1427–1429, 2006.
- Gershman, A. Meisels, and R. Zivan. Asynchronous forward bounding for dis- tribute COPs. Journal Artifi cial Intelligence Research, 34:61–88, 2009.
- R. Dechter and R. Mateescu. And/or search spaces for graphical models. Artifi cial Intelligence, 171:73–106, 2007.
- Katsutoshi Hirayama and Makoto Yokoo. Distributed partial constraint satisfaction problem. In Principles and Practice of Constraint Programming, pages 222–236, 1997.
- A. Petcu and B. Faltings. DPOP: A scalable method for multiagent constraint optimization. In Proceedings of the Nineteenth International Joint Conference on Arti- fi cial Intelligence, pages 266–271, 2005.
- R.Maillerand, V.Lesser. Solving distributed constraint optimization problems using cooperative mediation. In Proceedings of Third International Joint Conference on Autonomous Agents and MultiAgent Systems, pages 438–445, 2004.
- Library for research on Distributed Constraints Optimization Problems. URL: https://github.com/Orange-OpenSource/pyDcop (датаобращения: 26.10.2019)
- W. Yeoh, A. Felner, and S. Koenig. BnB-ADOPT: An asynchronous branch-and- bound DCOP algorithm. In Proceedings of the Seventh International Joint Conference on Autonomous Agents and Multiagent Systems, pages 591–598, 2008.
- S.M. Ali, S. Koenig, and M. Tambe. Preprocessing techniques for accelerating the DCOP algorithm ADOPT. In Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems, pages 1041–1048, 2005.
Информация об авторах
Метрики
Просмотров web
За все время: 572
В прошлом месяце: 18
В текущем месяце: 6
Скачиваний PDF
За все время: 190
В прошлом месяце: 2
В текущем месяце: 1
Всего
За все время: 762
В прошлом месяце: 20
В текущем месяце: 7