Моделирование и анализ данных
2019. Том 9. № 4. С. 80–87
doi:10.17759/mda.2019090406
ISSN: 2219-3758 / 2311-9454 (online)
Использование web-сервисов для повышения согласованности суждений матриц парных сравнений
Аннотация
Общая информация
Ключевые слова: парные сравнения, индекс согласованности, повышение согласованности, поддержка принятия решений, web-сервисы
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2019090406
Финансирование. Исследование выполнено при поддержке РФФИ, проект 18–01–00382а.
Для цитаты: Куренных А.Е., Судаков В.А., Осипов В.П. Использование web-сервисов для повышения согласованности суждений матриц парных сравнений // Моделирование и анализ данных. 2019. Том 9. № 4. С. 80–87. DOI: 10.17759/mda.2019090406
Полный текст
Парные сравнения критериев и альтернатив широко применяются в большом количестве актуальных технических и научных задач современности, в которых требуется провести ранжирование конечного множества объектов или выполнить оценку какого-либо объекта. Парные сравнения понятны и просты для эксперта, являются качественным и достоверным способом выставления оценок, однако стоит отметить, что сложность и размерность пространства критериев во многих задачах ведет к оказанию высокой нагрузки возникать некорректные или ошибочные ситуации, ведущие к снижению согласованности суждений, а, в следствие, к принятию нерациональных решений. Алгоритмическое обеспечение для повышения согласованности суждений является востребованными среди экспертов и исследователей, что, в совокупности с большим количеством разнообразных задач, формирует требования по разработке соответствующего программного обеспечения: возможность доступа большого числа пользователей и независимость от предметной области, которые в высокой степени удовлетворяются web- интерфейсом. В данной работе авторы приводят описание эффективного метода повышения согласованности суждений в матрицах парных сравнений. Основная задача метода - максимальное повышение согласованности суждений при минимуме изменений, вносимых в матрицу, предложенную экспертом в качестве первоначальных оценок. В качестве количественной меры согласованности суждений используется классический показатель - индекс согласованности. На основании созданного алгоритма авторами было разработано программное обеспечение, которое доступно для исследователей в распределенных web-сервисах для поддержки принятия решений ws-dss.com.
Введение
Одной из основных задач в поддержке принятия решений является ранжирование конечного множества объектов (альтернатив), которые характеризуются конечным числом критериев, благодаря которым является возможным проводить сравнение между собой предметов ранжирования. В случае сложной научной или технической задачи, когда размерность множества альтернатив достаточно велика, а каждая из них, при этом, характеризуется своим множеством критериев, их ручной анализ становится затруднительным и, как правило, невозможным, что вынуждает использовать специализированное программное обеспечение - системы поддержки принятия решений (СППР), реализующие математический аппарат теории принятия решений. Современный уровень научно-технического развития требует применения СППР в самых разнообразных областях [1-3], процессы деятельности в которых зачастую сопровождаются рисками, требуют тщательного планирования и анализа каждого управленческого решения [4, 5]. В настоящее время существует большое количество методов, позволяющих выполнять ранжирование объектов, среди которых одним из самых распространенных и известных является метод парных сравнений. Применение метода парных сравнений берет свое начало более двухсот лет назад в работах Мари Кондорсе [M. Condorcet, “Essai, 1785] и Жана-Шарля де Борда [J.C. de, 1781], посвященных проблемам голосований. В первой половине XX века метод приобрел большую популярность и с тех пор применяется в различных задачах, таких как метод анализа иерархий [T.L.Saaty, 1980], в области здравоохранения [T. Kakiashvili, M, 2012], менеджмента [10, 11] и пр.
Цель проводимого авторами исследования заключается в разработке алгоритмического и программного обеспечения, задача которого - вырабатывать рекомендации по повышению точности и корректности приводимых экспертами матриц парных сравнений за счет повышениях согласованности суждений, выражаемой индексом согласованности.
Постановка задачи
В процессе оценивания n объектов составляется квадратная положительная обратно-симметричная матрица А, на главной диагонали которой стоят единицы, а остальными ее элементами являются степени предпочтительности одного объекта над другим:
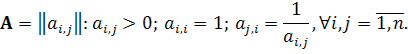
Особое внимание стало уделяется такому показателю как согласованность суждений эксперта. Наиболее известный и распространенный CIA способ количественно оценить этот показатель - использовать индекс согласованности, предложенный Томасом Л. Са- ати. Этот показатель можно вычислить, имея максимальное собственное значение ![]() матрицы и зная ее размер n:
матрицы и зная ее размер n:
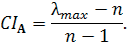
Принято считать, CIA < 0,1 что матрица парных сравнений хорошо согласована, если выполняется неравенство , однако на практике это условие часто нарушается ввиду целого ряда причин, среди которых можно отметить основные:
- многие распространенные программные средства для поддержки принятия решений и много-критериальногo анализа альтернатив имеют функционал, позволяющий только оценить индекс согласованности, но никак не могут помочь лицу, принимающему решения, или эксперту в устранении некорректных суждений;
- исправление нарушений транзитивности суждений - крайне трудоемкий процесс, который требует проведения повторного анализа предметной области, в задаче которой применяются парные сравнения.
Авторы данной работы рассматривают следующую постановку оптимизационной за- дачив процессе разработки алгоритмического и программного обеспечения для повышения согласованности суждений в матрицах парных сравнений:
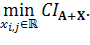
При ограничении на количество корректируемых элементов:
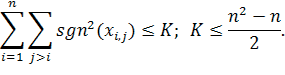

Метод решения задачи
Как уже было отмечено ранее, метод парных сравнений широко применяется в совершенно различных предметных областях, поэтому в процессе программной реализации предложенного алгоритма расчета матрицы корректировок было важно обеспечить возможность широкого доступа, инвариантность относительно предметной области а также прикладного программного обеспечения, с которым работает человек, стабильную ско
рость работы, а также следовать требованиям кросс-платформенности и независимости от используемых аппаратных средств. Удовлетворить вышеперечисленные критерии можно только с помощью web-сервисов, реализующих распределенные облачные вычисления. Примером таких сервисов является ws-dss.com, который разработан с учетом каркасной архитектуры, и содержит набор методов для проведения многокритериального анализа альтернатив, моделирования и оптимизации.
Программная реализация метода повышения согласованности была выполнена с использованием языков программирования R и Ruby, которые отвечают за функциональную составляющую алгоритма, реализующую метод Improved stochastic ranking evolution strategy (ISRES) [12, 13]. Реализация рассматриваемого алгоритма в web-среде позволила достичь следующих положительных качеств:
- к разработанному алгоритму есть доступ с любого устройства, имеющего выход в Интернет из любой точки мира, будь то персональный компьютер, планшет или смартфон;
- процессы вычислений реализованы на серверной части, что не требует высоких технических характеристик комплекса технических средств пользователя;
- разработанный метод можно вызвать из любой специализированной прикладной программы по протоколу http(s), таким же способом web-сервисы передают ответ с результатом вычислений обратно в прикладную программу. Это позволяет расширять функционал уже разработанных средств для поддержки принятия решений посредством обращений к сервисам ws-dss для дополнительной обработки данных.
Схема обмена данными между прикладной программой и web-сервисами реализована с использованием технологии RESTfulAPI, где используются стандартные методы протокола http(s), а данные передаются в формате JSON. Выбор такого формата информационного обмена обусловлен повсеместным распространением данной технологии, которая может быть реализована в любой современной системе программирования под управлением любой операционной системы.
Апробация и обсуждение результатов
Для целей апробации предложенного метода была составлена матрица парных сравнений (рис. 1). Для полученной матрицы были рассчитаны веса, максимальное собственное значение, ИС и другие показатели, приведенные на нижней части рис. 1.
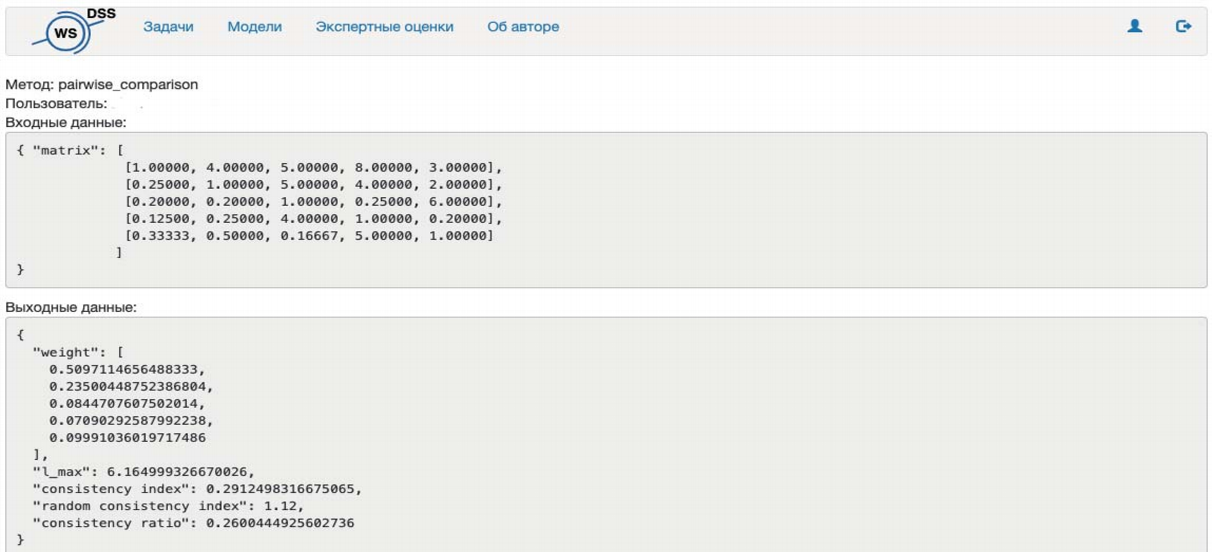
Рис. 1. Исходная матрица парных сравнений.
По значению consistency_index = 0,2912 видно, что согласованность суждений в данной матрице является недостаточной. После этого был использован предложенный алгоритм подбора вариаций двух элементов исходной матрицы и выполнен повторный расчет ИС. В результате расчетов получились следующие корректировки и новое значение ИС, которое удовлетворяет требованиям (рис. 2):
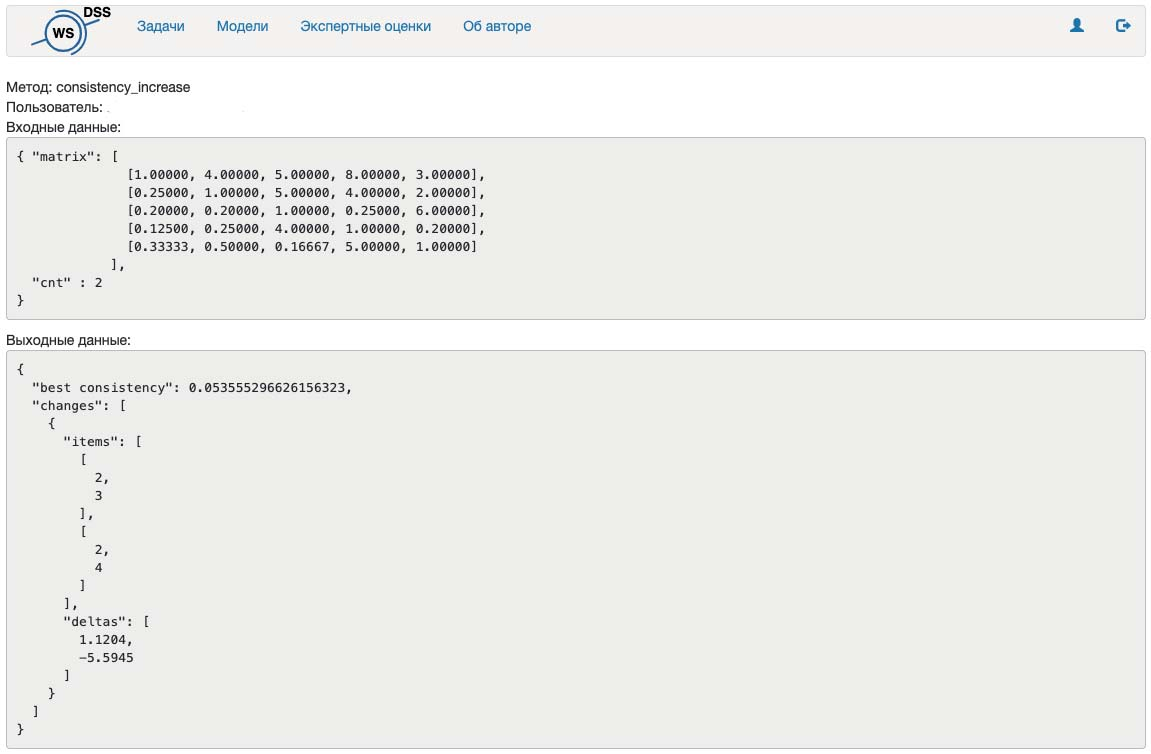
Рис. 2. Вариации элементов матрицы парных сравнений и оптимальная согласованность.
На рисунках можно видеть, что система корректно обработала введенную матрицу с учетом заданного ограничения на количество вариаций, а полученный ИС удовлетворяет условию согласованности матрицы. Соответственно, данную матрицу можно использовать для вычисления весов критериев и последующих процедур в процессе поддержки принятия решений.
Заключение
Предложенный способ реализации алгоритма повышения согласованности матриц парных сравнений показал хорошие результаты на тестовых данных и полностью удовлетворяет критерию оптимизации, а также наложенным ограничениям. Время расчетов является удовлетворительным и может сокращаться за счет применения параллельных вычислений. Разработанное программное обеспечение соответствует требованиям каркасной архитектуры, а также расположено в общем доступе для использования в сторонних системах поддержки принятия решений. Перспективным направлением продолжения исследования является масштабная апробация алгоритма с привлечением экспертов, которые смогли бы оценить результаты использования алгоритма, а также, по возможности, предложить способы повышения его эффективности.
Финансирование
Исследование выполнено при поддержке РФФИ, проект 18-01-00382а.
Литература
- T. Saaty, P. Pierfrancesco. Rethinking Design and Urban Planning for the Cities of the Future // Buildings, vol. 7, 76, pp. 1–22, 2017.
- K.F. Yuen. The fuzzy cognitive pairwise comparisons for ranking and grade clustering to build a recommender system: An application of smartphone recommendation // Engineering Applications of Artifi cial Intelligence, Vol. 61, 2017, pp. 136–151.
- M. Groves, J. Branke. Top-κ selection with pairwise comparisons // European Journal of Operational Research, Vol. 274, 2, 2019, pp. 615–626.
- Huin S.F. Managing deployment of ERP systems in SMEs using multiagents // International Journal of Project Management. Vol.22. N.6. pp.511–517. 2004.
- Batkovskiy A.M., Kurennykh A.E., Semenova E.G., Sudakov, V.A., Fomina, A.V., Balashov, V.M. Sustainable project management for multi-agent development of enterprise information systems // Entrepreneurship and Sustainability Issues 7(1). pp.278–290. 2019.
- M. Condorcet, “Essai sur l’application de l’analyse à la probabilité des décisionsrendues á lapluralité des voix”, Paris, 1785.
- J.C. de Borda, “Mémoire sur les électiones au scrutin”, Histoire de l’Académie Royale des Sciences, Paris, 1781.
- T.L.Saaty, The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation. Mcgraw-Hill, New York, 1980.
- T. Kakiashvili, M. Woodbury. Smith Improving the medical scale predictability by the pairwise comparisons method: evidence from a clinical data study. Computer Methods and Programs in Biomedicine, 105, 2012, pp. 210–216.
- K. Kułakowski, J. Szybowski, R. Tadeusiewicz, Tender with Success – The Pairwise Comparisons Approach, Procedia Computer Science, Vol. 35, 2014, pp. 1122–1131.
- A. Kalinowska, T. Trzaskalik. Bonus Distribution for Employees of a Telephone Customer Service Department: A Case Study based on Pairwise Comparisons, Procedia Computer Science, Vol. 35, 2014, pp. 1145–1154.
- T. Runarsson, X. Yao, “Stochastic ranking for constrained evolutionary optimization”, Evolutionary Computation, IEEE Transactions, on. 4, 2000, pp. 284–294.
- T. Runarsson, X. Yao, “Search Biases in Constrained Evolutionary Optimization”, Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on. 35, 2005, pp. 233–243.
Информация об авторах
Метрики
Просмотров web
За все время: 576
В прошлом месяце: 13
В текущем месяце: 9
Скачиваний PDF
За все время: 160
В прошлом месяце: 5
В текущем месяце: 3
Всего
За все время: 736
В прошлом месяце: 18
В текущем месяце: 12