Моделирование и анализ данных
2019. Том 9. № 2. С. 4–20
ISSN: 2219-3758 / 2311-9454 (online)
Оптимизационные математические модели мирного и военного подчинительных взаимодействий двух государств
Аннотация
Общая информация
Ключевые слова: Оптимизационная динамическая математическая модель, государство, взаимодействие двух государств, мирное торгово-валютное взаимодействие, военное нападательное взаимодействие
Рубрика издания: Математическое моделирование
Тип материала: научная статья
Для цитаты: Захаров В.К. Оптимизационные математические модели мирного и военного подчинительных взаимодействий двух государств // Моделирование и анализ данных. 2019. Том 9. № 2. С. 4–20.
Полный текст
На основе созданной ранее автором оптимизационной динамической математической модели одного отдельно взятого государства строятся оптимизационные динамические математические модели мирного торгово-валютного и военного нападательного подчинительных взаимодействий двух государств в пользу одного из них.
1. ВВЕДЕНИЕ
Интерес к созданию математической модели войны возник у автора после выхода в свет известной книги [Гуссейнова, 1984] под редакцией академика Н.Н. Моисеева, посвящённой имитационному моделированию Пелопонесской войны.
Однако для создания общей оптимизационной модели войны между государствами потребовалось сначала создать общую математическую оптимизационную модель государства в широком смысле (т.е. как государства-страны). Такая модель была построена и развита автором в статьях [2, 4, 5] и книгах [Захаров, 2011а, С. 153-168], [Захаров, 2016, С. 330-353], [Захаров, 2017, С. 393-399]. Математическое исследование этой модели на существование оптимального управления было проведено Кузенковым О.А. в статьях [2, 4, 5].
Продвижение же к построению на этой основе общей математической оптимизационной модели взаимодействия нескольких государств наступило только в 2018 году, когда удалось математически формализовать мирное и военное подчинительные взаимодействия двух государств [Захаров, 2019]. Именно эти виды взаимодействия оказались наиболее заметными в истории 20 и 21 веков.
Цель и мирного, и военного подчинительного взаимодействия одна и та же. Это - достижение наибольшего расхождения совокупных достояний взаимодействующих государств к концу некоторого промежутка времени в пользу одного из них. Однако способы управления при этих взаимодействиях могут качественно отличаться друг от друга.
В первой части рассматривается математическая модель мирного торгововалютного взаимодействия посредством согласованного и не согласованного управления в обоих государствах, оптимально-подчинительного в пользу одного из них. Во второй части рассматривается математическая модель военного нападательного взаимодействия посредством одностороннего управления со стороны нападающего государства, оптимальноподчинительного в его пользу.
Статья является чисто концептуальной. Никаких теоретических и практических способов решения поставленных оптимизационных задач в ней не рассматривается. Естественно, что приведённые динамические оптимизационные математические модели мирного и военного подчинительных взаимодействий двух государств опирается на разработанную ранее в указанных выше работах автора соответствующую модель управляемой деятельности одного отдельно взятого государства.
2. ОПТИМИЗАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЕЯТЕЛЬНОСТИ ОДНОГО ГОСУДАРСТВА
Для того, чтобы сделать статью замкнутой в себе, приведём основные сведения из статей [2, 4, 5].
УСТРОЙСТВО И ДЕЯТЕЛЬНОСТЬ ГОСУДАРСТВА
Каждое государство является сложным трёхуровневым системным обществом, устроенным в виде совокупности основных (под)систем, связанных друг с другом в единую систему и зависящих друг от друга так, что без каждой из этих систем государство существовать не может. Основными системами государства являются: содержательная, учётная, обеспечительная, совокупная распорядительная и верховная системы.
Содержательная система C осуществляет метааграрный (изымающий из природной среды), индустриальный (перерабатывающий) и сервисный (обслуживающий) способы жизнедеятельности. Учётная система E осуществляет производство, сбор, хранение и раздачу денег, статистических сведений и т.п. Обеспечительная система D обеспечивает порядок, охрану, законность, нравственность и пр. Распорядительные системы F, G и H ведают (управляют) деятельностью содержательной, учётной и обеспечительной систем, соответственно. Поэтому их можно именовать содержательно-распорядительной, учётнораспорядительной и обеспечительно-распорядительной системами, соответственно. Они образуют совокупную распорядительную систему. Верховная (управляющая) система P управляет деятельностью совокупной распорядительной системы.
Государство является открытой системой с тремя частями бытийной среды, называемыми природной средой A1, зарубежной надприродной средой A2 и своей теневой средой A3. Они обобщённо именуются средами государства.
Любая мысленно отмеченная часть государства и его внутренней природной среды называется достоянием государства. Используемые государством и производимые им достояния (и, в частности, состояния) располагаются в учреждениях государства и в его средах. Все эти достояния подразделяются на следующие виды: содержательное (код 1), распорядительное (код 2), верховное (код 3), обеспечительное (код 4), учётное (код 5). Объединения этих достояний по всем учреждениям основной системы дают достояния основной системы, а объединения по всем учреждениям государства дают достояния государства. Объ
единение всех достояний государства по всем видам достояний даёт совокупное достояние государства.
Каждая основная система производит достояние своего вида. При производстве соответствующего достояния каждая система использует некоторые из имеющихся в ней достояний. Все основные системы связаны между собой потоками производимых достояний. Содержательная, учётная и обеспечительная системы получают из сред государства и отдают в эти среды соответствующие достояния.
Изображение основных систем государства и имеющихся в нём достояний и потоков дано ниже на рисунке 1.
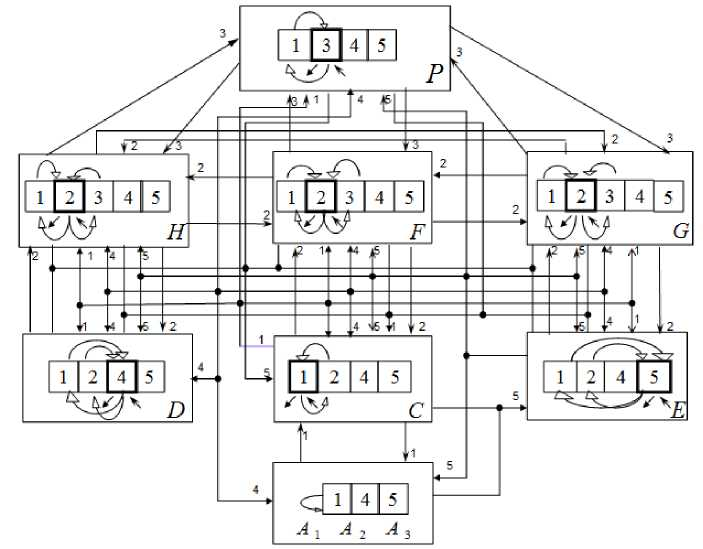
Рис. 1. Схема систем, достояний и потоков государства
ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПОТОКОВ ДОСТОЯНИЙ




3.ОПТИМИЗАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МИРНОГО ПОДЧИНИТЕЛЬНОГО ВЗАИМОДЕЙСТВИЯ ДВУХ ГОСУДАРСТВ

НАЗВАНИЕ И СМЫСЛ ДОПОЛНИТЕЛЬНЫХ ПОТОКОВ


СООТНОШЕНИЕ МЕЖДУ ДЕНЬГАМИ РАЗНЫХ ГОСУДАРСТВ И СВЯЗИ МЕЖДУ ДОПОЛНИТЕЛЬНЫМИ ПОТОКАМИ

ИЗМЕНЁННЫЕ И ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ГОСУДАРСТВА S
С учётом дополнительных потоков уравнения для государства S, написанные выше, изменятся следующим образом:

ИЗМЕНЁННЫЕ И ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ГОСУДАРСТВА S(I)

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МИРНОГО СОГЛАСОВАННОГО ПОДЧИНИТЕЛЬНОГО ВЗАИМОДЕЙСТВИЯ ДВУХ ГОСУДАРСТВ


МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МИРНОГО НЕСОГЛАСОВАННОГО ПОДЧИНИТЕЛЬНОГО ВЗАИМОДЕЙСТВИЯ ДВУХ ГОСУДАРСТВ


4. ОПТИМИЗАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВОЕННОГО ПОДЧИНИТЕЛЬНОГО ВЗАИМОДЕЙСТВИЯ ДВУХ ГОСУДАРСТВ

ДОПОЛНИТЕЛЬНЫЕ ДОСТОЯНИЯ И ПОТОКИ ПРИ ВОЕННОМ ВЗАИМОДЕЙСТВИИ ДВУХ ГОСУДАРСТВ



СВЯЗИ МЕЖДУ ДОПОЛНИТЕЛЬНЫМИ ПОТОКАМИ

СОГЛАШЕНИЯ О НЕПРЕРЫВНОСТИ ОБЩИХ ПОТОКОВ
Будем считать, что переводные и отправленные потоки «равны» в мировой валюте, т.е. связаны соотношениями
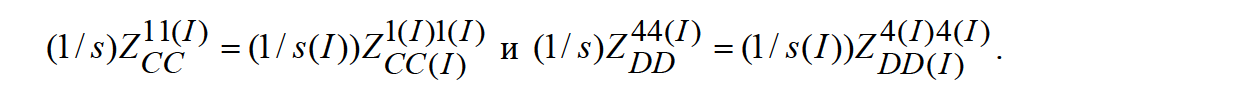

ИЗМЕНЁННЫЕ И ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ГОСУДАРСТВА S



5. ЗАКЛЮЧЕНИЕ
Предложенные модели концептуально отражают следующие важные исторические примеры взаимодействий между государствами. Во время Второй Мировой войны США военным путём обеспечили подчинительное взаимодействие в свою пользу с такими государствами, как Япония, Германия, Италия и др. После войны в течение нескольких лет США уже мирным согласованным путём продолжали обеспечивать подчинительное взаимодействие с указанными государствами. В эти же сроки США мирным несогласованным путём обеспечили подчинительное взаимодействие в свою пользу с Британской Империей. После соглашения между Робертом Никсоном и Ден Сяопином в 1972 году в течение нескольких лет США мирным согласованным путём обеспечивали подчинительное взаимодействие с КНР в свою пользу. После указанных сроков уровни прямого торгово-валютного подчинения во всех упомянутых взаимодействиях постепенно понижались, а способы подчинения становились всё более скрытными.
В указанных во введении статьях автора на основе общей концептуальной модели государства решалась конкретно-числовая игровая задача на существование, нахождение и приближённое вычисление оптимизирующего управления в системе исходных уравнений для государства S, приведённой в первой части
То же самое нужно сделать и для изложенных выше общих концептуальных динамических оптимизационных математических моделей мирного и военного подчинительных взаимодействий двух государств.
После этого можно переходить к численному моделированию перечисленных выше наличных исторических взаимодействий между государствами и сверке модельных вычислений с историческими данными.
Литература
- Гуссейнова А.С., Павловский Ю.Н., Устинов В.А. Опыт имитационного моделирования исторического процесса. − М.: Наука, 1984. − 157 с.
- Захаров В.К., Кузенков О.А. Оптимальное управление в модели государства // Моделирование и анализ данных. 2011. № 1. С. 55-75.
- Захаров В.К. Номология. Устроение и направление человеческой деятельности. − М.: МГППУ, 2011. − 216 с.
- Захаров В.К., Капитанов Д.В., Кузенков О.А. Оптимальное управление в модели государства II // Моделирование и анализ данных. 2014. № 1. С. 4-31.
- Захаров В.К., Кузенков О.А. Оптимальное управление в математической модели государства // Журнал Средневолжского математического общества. 2015. Т. 17, № 2. С. 34-38.
- Захаров В.К. Номология. Воспроизведение и обновление человеческого бытия. − М.: «Onebook.ru», 2016. − 396 с.
- Захаров В.К. Этот Новый Старый Мир. Будущее из прошлого. − М.: Издательский дом "Кислород", 2017. − 448 с.
- Захаров В.К. Математические модели мирного и военного подчинительных взаимодействий двух государств // 26 Международная конференция «Математика. Компьютер. Образование» (28 января-02 февраля 2019г.). Тезисы. − Россия, г. Пущино: Пущинский центр биологических исследований РАН, 2019. С. 238.
Информация об авторах
Метрики
Просмотров web
За все время: 565
В прошлом месяце: 15
В текущем месяце: 2
Скачиваний PDF
За все время: 174
В прошлом месяце: 4
В текущем месяце: 0
Всего
За все время: 739
В прошлом месяце: 19
В текущем месяце: 2