Вероятностные модели процесса выполнения тестовых заданий

Представлены особенности практического применения подхода к вероятностному моделированию процесса выполнения тестовых заданий на примере тестов на рабочую память. Данный подход позволяет учитывать динамику способностей испытуемых и трудностей заданий во время их выполнения. Для построения количественных оценок вводится модифицированная функция Раша, аргументы которой, в отличие от классического варианта, задаются в вероятностной шкале. Рассмотрены способы идентификации представленных расчётных зависимостей с использованием результатов прохождения тестов на рабочую память.

1. ВВЕДЕНИЕ

Компьютерное тестирование в настоящее время активно применяется в различных областях деятельности человека, решая различные задачи. Благодаря компьютерному тестированию повышаются информационные возможности процесса контроля, появляется возможность сбора дополнительных данных о динамике прохождения теста отдельными испытуемыми.

Основные преимущества компьютерного тестирования - высокая точность обработки, обеспечение одинаковых условий тестирования для испытуемых, контроль процедуры тестирования, при необходимости может быть фиксация времени каждого ответа, что особенно важно для тестов на интеллект, объективность тестирования, хранение и представление результатов тестирования, автоматизированная обработка.

Компьютерное тестирование позволяет формировать большое количество вариантов теста, используя банк тестовых заданий; создавать тесты, соответствующие различным уровням подготовленности испытуемых; управлять как содержанием теста, так и стратегией проверок в ходе тестирования; вводить временные ограничения на выполнение тестовых заданий или проводить временное отслеживание процесса тестирования, что позволяет учитывать результаты тестирования для последующих проведений тестов. Качество тестирования и достоверность его результатов в значительной степени зависят от технологий проведения тестов, которые в последние десятилетия стали предметом активных научных исследований.

В настоящее время доминирующим подходом в этой области является использование технологий, построенных на базе так называемой современной теории тестирования (Item Response Theory - IRT), основанной на латентно-структурном анализе (Rasch, G., 1960/1980; Baker F.B., 2001; Тюменева Ю.А., 2007; Шмелев А.Г., 2013). Основная концепция данного подхода, предложенного Г. Рашем в 1960 году, предполагает, что вероятность правильного ответа на задание определяется разностью уровня способностей или знаний и трудности теста. В зависимости от условий прикладной задачи на практике используются и другие, более сложные модели, построенные на базе данной концепции (Rasch, G., 1960/1980; Wright B.D., Masters G.N., 1982; Wright B.D., Stone M.N., 1979).

Применение технологии IRT приводит к следующим проблемам:

• «статичность» оценок: игнорирование того факта, что результат тестирования вследствие усталости испытуемых и других факторов может, вообще говоря, существенно изменяться со временем, принимая различные значения в процессе сеанса тестирования;

• невозможность учёта времени, затрачиваемого на решение тестовых задач, при построении расчётных оценок;

• необходимость выполнения достаточно большого числа заданий для получения оценок с приемлемой точностью;

• сравнительно сложная для практической реализации процедура оценки точности результата, связанная с применением метода максимального правдоподобия и расчётом доверительных интервалов.

Указанные проблемы сделали актуальными поиск и разработку новых принципов построения технологий тестирования. Одним из наиболее перспективных результатов в этой области стал новый подход (Куравский Л. С., Марголис А. А., Мармалюк П.А., Юрьев Г.А., Думин П.Н., 2000-2014), построенный на использовании обучаемых структур в форме марковских моделей с дискретным и непрерывным временем. Его особенностями, обеспечивающими преимущества перед аналогичными способами тестирования, являются:

• выявление и использование при построении расчётных оценок временной динамики изменения способности справляться с заданиями теста;

• возможность учёта при построении расчётных оценок времени, затрачиваемого на решение тестовых задач;

• возможность исследования временной динамики знаний или способностей, как в дискретной, так и в непрерывной временной шкале;

• меньшее по сравнению с другими подходами число заданий, которое следует предъявлять испытуемому для получения оценок знаний или способностей с заданной точностью, что ускоряет процесс тестирования;

• получение распределения вероятностей возможных результатов теста в качестве конечного результата;

• развитая техника идентификации параметров моделей.

На основе рассмотренных выше технологий тестирования были разработаны системы поддержки принятия решений (Куравский Л.С., Марголис А.А., Мармалюк П.А., Юрьев Г.А., Думин П.Н., 2013; Панфилова А.С., 2013; Марковские модели: уч. пособие, 2013), которые ускоряют процесс тестирования, оптимизируя предъявление тестовых заданий. Диагностические выводы строятся на основе уточняющихся в процессе тестирования вероятностных оценок принадлежности испытуемых к различным категориям. Подобные инструменты дают практикующему специалисту дополнительную информацию для анализа и, в случае марковских моделей, предоставляют рекомендации по выбору следующего теста, обладающего, по сравнению с прочими, наибольшей для данного испытуемого дифференцирующей способностью.

Все рассмотренные выше технологии тестирования объединяет общий признак: итоговые оценки, как правило, определяются только по формальным результатам прохождения тестовых заданий, предъявляемых испытуемому, без учёта изменений в процессе их выполнения когнитивных способностей и психофизиологического состояния человека. Это существенно ограничивает возможности измерительной процедуры.

Чтобы решить эту проблему, предложен подход к вероятностному моделированию процесса прохождения тестов, позволяющий учесть динамику способностей испытуемых и трудностей заданий во время их выполнения, при этом используется модифицированная функция Раша, аргументы которой, в отличие от классического варианта, задаются в вероятностной шкале. Внедрение нового подхода в практику компьютерного тестирования требует исследования особенностей его практического применения на конкретных примерах, а, в частности, этот подход был применен на результатах тестов на рабочую память.

Был решен ряд задач:

• адаптировать вероятностную модель и методы моделирования процесса выполнения заданий для тестирования рабочей памяти;

• реализовать указанную модель и методы в одной из современных сред программирования;

• идентифицировать созданную модель по результатам прохождения теста на рабочую память;

• провести анализ полученных зависимостей;

• определить оптимальное время, которое следует отводить для выполнения заданий теста на рабочую память.

Кроме того, актуальной для практических приложений рассматриваемого подхода задачей является проверка следующих гипотез :

• результаты теста не зависят от уровня подготовки испытуемых;

• результаты теста не зависят от фактора пола.

2. МОДЕЛИРОВАНИЕ ПРОЦЕССА ВЫПОЛНЕНИЯ ТЕСТОВЫХ ЗАДАНИЙ: ОСНОВНЫЕ ПОНЯТИЯ И МЕТОД

Определим величины, необходимые для представления процесса выполнения задания. Для этого рассмотрим конечные генеральные совокупности заданий I и испытуемых J, состоящие, соответственно, из N и M элементов. Пусть p_ij(t) есть вероятность того, что j-й испытуемый выполнит i-е задание до момента времени t включительно; v_i(t) есть вероятность того, что произвольно выбранный испытуемый не выполнит i-e задание до момента времени t включительно при условии, что все испытуемые из генеральной совокупности J имеют равную вероятность быть выбранными; u_j(t) есть вероятность того, что j-й испытуемый выполнит произвольно выбранное задание до момента времени t включительно при условии, что все задания из генеральной совокупности I имеют равную вероятность быть выбранными. Величины v_i(t) и U_j(t) рассматриваются, соответственно, как меры трудности i-го задания и способностей j-го испытуемого.

Пусть т есть продолжительность малого минимального интервала времени, в течение которого возможно выполнение задания. Эта величина является параметром исследуемой системы тестовых заданий. Тогда, рассматривая полную систему из двух событий Aj и Āj, где Aj есть наличие выполненного j-го задания в момент времени t, и используя формулу полной вероятности, вероятность Pij(t) того, что j-й испытуемый выполнит i-е задание до момента времени t+т включительно, выражается следующим образом:

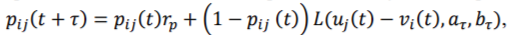
где Pij (0) = 0; Гр есть вероятность не найти ошибку в представленном ранее к моменту t решении в течение интервала времени [t; t + т]; функция L(Uj(t) — Vi(t),aT,bT) выражает вероятность выполнения задания в течение интервала времени [t; t + т] при условии, что в момент времени t задание не выполнено; ат и bт - параметры, идентифицируемые по результатам наблюдений.

Функция L зависит от разности мер способностей испытуемого Uj(t) и трудности задания Vi(t), а также некоторых параметров, обусловленных величиной т. В качестве аппроксимации этой функции целесообразно использовать модифицированную функцию Раша (Rasch, G, 1980) следующего вида:

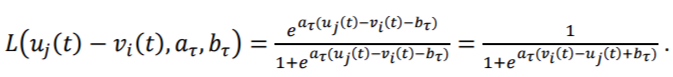
указанные выше соотношения с точностью до бесконечно малых более высокого порядка, чем о(т), можно преобразовать в следующую систему обыкновенных дифференциальных уравнений, которая интегрируется подходящими численными методами:

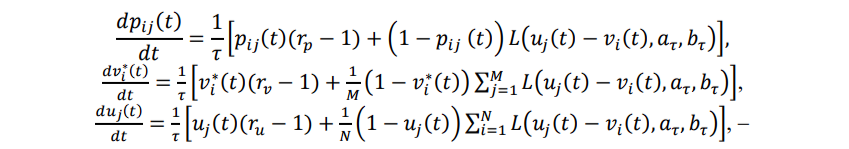
с начальными условиями Pij(O), v¡*(O) и u¡(0) и идентифицируемыми по результатам наблюдений параметрами aт, bт, rp, rv и ru. С целью уменьшения числа интегрируемых уравнений, к этой системе может быть применено указанное выше упрощение.

При решении практических задач, использование рекуррентных формул для дискретных моментов времени является предпочтительным, однако, если задача предполагает применение только модели с непрерывным временем, динамика вероятностей может прогнозироваться с помощью приведённых выше дифференциальных уравнений.

3. ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ РЕКУРРЕНТНЫХ ЗАВИСИМОСТЕЙ

4. ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ: РАБОЧАЯ ПАМЯТЬ И ЕЁ ХАРАКТЕРИСТИКИ

Память — это одна из психических функций и видов умственной деятельности, предназначенная сохранять, накапливать и воспроизводить информацию. Способность длительно хранить информацию о событиях внешнего мира и реакциях организма и многократно использовать её в сфере сознания для организации последующей деятельности.

Рабочая память - это вид памяти, который может одновременно оперировать несколькими элементами. Она отличается от других типов моментальным временем своего действия - она сразу же избавляется от ненужной переработанной информации. Это самый быстрый и часто используемый вид памяти, позволяющий решать мелкие повседневные задачи.

Например, рабочая память - это способность управлять и манипулировать запомненным: тасовать числа, складывать их, определять, четные они или нечетные, и т. д., а, если говорить о языке, то именно рабочая память позволяет нам не просто запоминать предложения, но и понимать их смысл и даже обдумывать, каких последствий стоит ждать после их произнесения. Рабочая память характеризует способность человека манипулировать информацией, хранящейся короткое время в его памяти. Такая манипуляция лежит в основе процессов мышления: рассуждения, обучения, понимания.

Для оценки рабочей памяти используются различные методики, любой человек может пройти такой тест. Хороший и правильный тест памяти, не просто дает какое-то значение результата, но и предлагает методику восстановления или улучшения памяти, исходя из полученных результатов.

Ученые пришли к выводу, что уровень интеллекта напрямую зависит от рабочей памяти. Весьма правдоподобно, что способность к решению интеллектуальных задач выше у тех людей, которые способны одновременно держать в голове большее число идей. Логические познавательные процессы также находятся в постоянной зависимости от ее состояния. Объем информации, который можно одновременно удерживать в голове, влияет непосредственно на способность делать умозаключения. Чем больше этот объем, тем логичней и быстрей будут умозаключения.

В область интеллекта проблема рабочей памяти была открыто внесена в статье П. Киллонена и Р. Кристала «Способность к рассуждению - это (немногим больше, чем) рабочая память». (Kyllonen, Christal, 1990) Авторами была разработана специальная серия тестов для измерения рабочей памяти. Она показала настолько высокие корреляции интеллекта и рабочей памяти, что, по мнению авторов, эти два понятия близки к тому, чтобы совпасть.

Различные авторы по-разному трактуют механизмы, стоящие за задачами на рабочую память. Так, Р. Ингл считает, что успешность выполнения как задач на рабочую память, так и тестов интеллекта следует искать в управляющих процессах.

Учеными доказано, что рабочая память обеспечивается тесной связью с вниманием. Внимание необходимо для качественного удержания нескольких его объектов в уме одновременно. Именно поэтому люди, имеющие большой объем кратковременной или рабочей памяти, гораздо лучше способны сосредотачиваться и длительно сохранять внимание на одном объекте. Обладающие же довольно неустойчивым вниманием, наоборот, достаточно часто отвлекаются на посторонние объекты.

Рабочая память лежит в основе понимания, усвоения и запоминания новой информации. Недостаток рабочей памяти вызывает трудности в обучении, лишает человека возможности работать в многозадачном режиме. Рабочую память можно улучшить с помощью различных тренажеров и тестов.

5. ТЕСТ НА РАБОЧУЮ ПАМЯТЬ

Параметры на рабочую память оцениваются с помощью комплексных задач на рабочую память, в которых испытуемый должен одновременно перерабатывать информацию и удерживать в памяти промежуточные результаты.

Средства для оценки рабочей памяти человека включают в себя нескольких тестов, в которых испытуемому предъявляется последовательность изображений или слов, матрицы которых необходимо запомнить. Во время тестирования длина последовательности увеличивается. Результаты заносятся в базу данных.

В настоящее время в сети Интернет функционирует несколько тестов, входящих в эту систему. Вход в систему можно осуществить по адресу: http://it-span.mgppu.ru/u3rem/.

Тесты на рабочую память разрабатываются и апробируются лабораторией психологии и психофизиологии творчества Института психологии РАН под руководством члена-корреспондента РАН Д. В. Ушакова совместно с факультетом информационных технологий МГППУ в рамках проводимых исследований влияния рабочей памяти на интеллект.

Рассмотрим один из таких тестов на рабочую память (Тест Visual MUT) и проанализируем его результаты с помощью модифицированной функции Раша.

Тест состоит в следующем: предъявляется последовательность стимулов, которые во время тестирования удлиняются и усложняются.

Испытуемому выводится на экран квадратная таблица с меткой в одной ячейке. Затем предъявляется серия знаков в виде стрелок 'вверх', 'вниз', 'вправо', 'влево'. Необходимо мысленно переместить метку в запомненной таблице в указанном направлении на одну клетку для каждого знака. Затем предъявляется пустая таблица для ответа, где следует указать, в какой из ячеек окажется метка. При прохождении теста длина серии знаков возрастает.

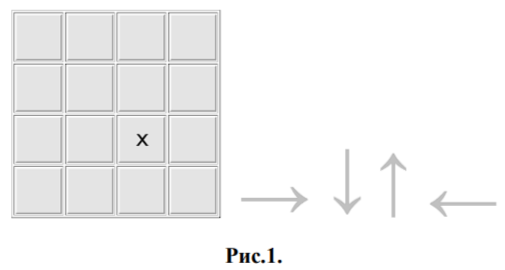
Размерность таблицы и количество матриц может меняться.

6. ПРАКТИЧЕСКАЯ ЧАСТЬ

6.1. Практическое применение

В качестве наблюдаемых зависимостей трудностей и способностей использовались выборочные оценки, полученные по результатам тестирования двух групп испытуемых, одна из которых - студенты (возраст от 19 до 22 лет), а вторая - школьники (возраст 14-15 лет).

Результаты тестирования студентов и школьников

Результаты тестирования на рабочую память студентов и школьников представлены двумя матрицами, одна из которых показывает ответы испытуемых в виде метки верно- го/неверного (1/0) ответа, а вторая матрица - время решения каждого задания.

Далее по матрице, содержащей время решения каждого задания, оцениваются выборочные зависимости трудностей всех заданий и способностей всех испытуемых-студентов и школьников от времени. Оценка выборочной зависимости трудности задания от времени выполняется следующим образом: по матрице времён выполнения заданий для каждого из значений параметра времени, выбранных с единичным шагом в диапазоне от 0 до 500 секунд, рассчитывается доля испытуемых в выборке, которые не выполнили задание к соответствующему моменту. Оценка выборочной зависимости способности испытуемого от времени выполняется аналогично: по матрице времён выполнения заданий для каждого из указанных выше значений параметра времени рассчитывается доля заданий в выборке, которые были выполнены испытуемым к соответствующему моменту.

В нижеприведенных таблицах 1-2 показаны расчеты для студентов и школьников на примере тестового задания 1.

Таблица 1. Количество заданий, которые были выполнены испытуемыми- студентами к заданному моменту времени.

	500	1000	1500	2000	2500	3000	3500	4000	4500	5000	5500	6000	6500
ti	0	3	4	6	9	9	10	14	14	14	14	14	14

Таблица 2. Количество заданий, которые были выполнены испытуемыми- школьниками к заданному моменту времени.

ti	<500	<1000	<1500	<2000	<2500	<3000	<3500	<4000	<4500
	0	2	5	7	7	7	7	7	7

6.2. Описание инструмента и метод оптимизации

Для решения задачи идентификации был использован метод, программно реализованный в среде графического программирования LabVIEW (версия 2010).

Поскольку число идентифицируемых параметров мало, а диапазоны их изменения известны и ограничены, то решение задачи осуществлялось перебором всех возможных сочетаний значений определяемых параметров с шагом, равным заданной точности решения.

6.3. Результаты идентификации модели для студентов и школьников

В результате идентификации модели получили следующие параметры для студентов:

Таблица 3. Значения идентифицируемых параметров, полученных по тестовым заданиям

	ti	t 3	t 5	t 8	t10	t 15	t 17	t 20	t 24	t 26	t 28	t 30	t 32
ат	0,8	3,8	-0,6	1,6	2,4	-0,8	-0,8	1	0,8	0,4	2,6	-0,8	-0,8
bт	2,8	0,2	-3	0,6	0,2	-2	-2	0,6	1,4	2,4	0,2	-2,6	-2,2
X2	3,28	2,59	6,72	1,33	1,77	5,43	4,60	2,70	7,06	8,72	10,39	4,41	7,84
Р- значе ние	0,99	0,99	0,88	0,99	0,99	0,49	0,97	0,99	0,53	0,56	0,94	0,93	0,80
df	12	12	4	12	12	6	12	12	8	10	12	10	9

В результате идентификации модели получили следующие параметры для школьников:

Таблица 4. Значения идентифицируемых параметров, полученных по тестовым заданиям

	t1	t 3	t 5	t 8	t10	t 15	t 17	t 20	t 24	t 26	t 28	t 30	t 32
ат	-3	-2,8	2	3,4	-3	-2,2	-2	-2,8	-3	-1,4	-2	1,4	3,2
bт	-1,4	-1,6	0,8	0,4	-1,6	-1.8	-2	-1,6	-1,4	-2,6	-2,8	2	0,6
X2	3,50	3,96	2,20	2,16	3,57	1,60	2,19	3,96	1,71	1,61	5,38	1,23	1,02
Р- значение	0,99	0,98	0,99	0,99	0,99	0,99	0,82	0,95	0,99	0,90	0,50	0,99	0,96
df	12	12	12	12	12	12	5	10	12	5	6	13	5

 

Для всех построенных моделей выбранных тестовых заданий получено высокое p- значение, позволяющее говорить об адекватности модели наблюдениям. Малые значения величины X² свидетельствуют о хорошем согласовании прогнозируемых и наблюдаемых данных.

В результате идентификации модели были получены графики вероятностей решения тестовых заданий студентами. Так, например, выглядят графики вероятностей решения задания испытуемыми - студентами задания 1(t1) (рис. 3) и испытуемыми - школьниками задания 1(t1) (рис. 4).

Кривая трудности на графиках показана белым цветом, кривая способности - красным цветом, кривая вероятности p_ij(t) - зеленым цветом.

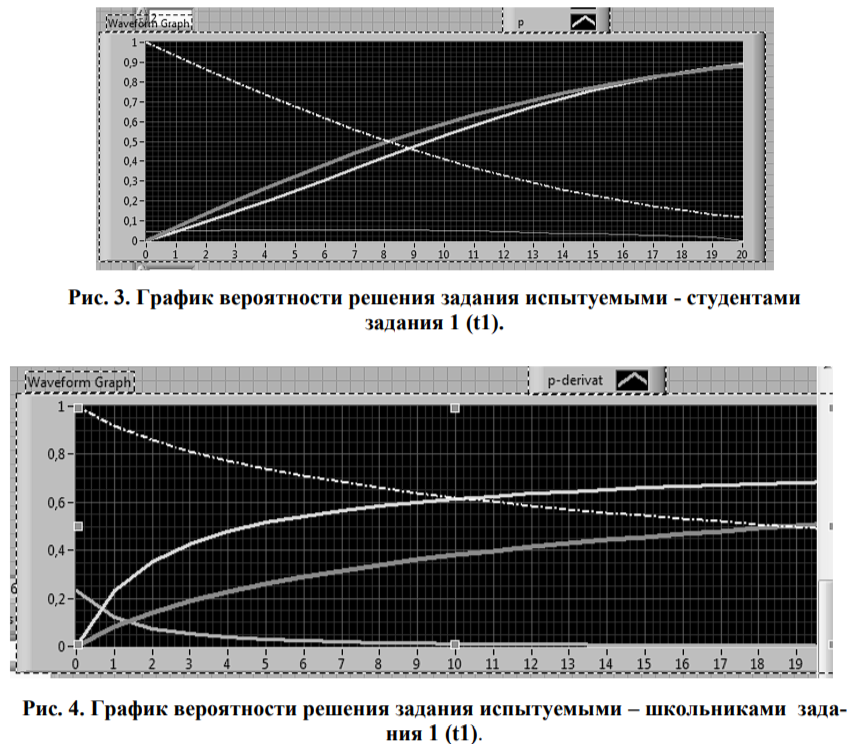
Формы выборочных зависимостей трудностей заданий и способностей испытуемых от времени демонстрируют выраженную связь с величиной трудностей заданий и способностей испытуемых в классическом понимании. Однако можно наблюдать, что вариация кривых зависимости способности испытуемых во времени содержит также необъяснённые компоненты, которые, вероятно, связаны с такими характеристиками испытуемых, как скорость принятия решений, уверенность в выбранном ответе и т.п.

Рассмотрим более детально поведение функции

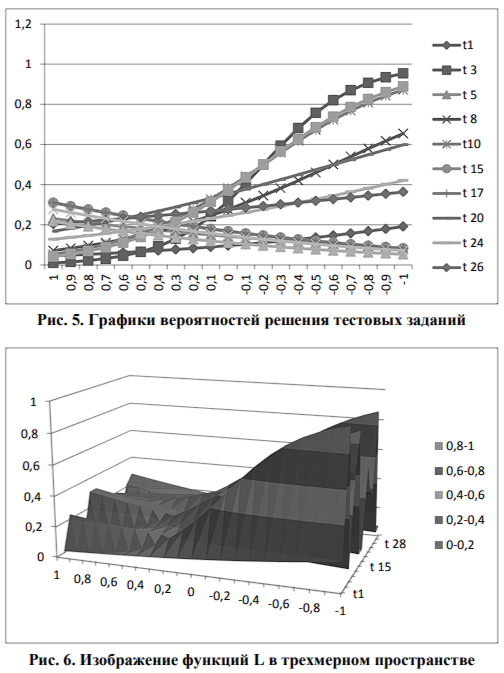
Следует отметить, что по горизонтальной оси, где принимаются отрицательные значения, уровень трудности меньше, чем уровень способности, там вероятность решения показывает большие значения, чем там, где принимаются положительные значения, уровень трудности больше уровня способности и вероятность решения показывает маленькие значения. Есть задания, которые показывают обратное, это тестовые задания 17, 30, 32, вероятность решения тестового задания 1 показывает очень маленькие результаты.

На промежутке, где функция L показывает малые вероятности, интерпретация не имеет значения (область нереализованных значений параметров u, v),

Но, в основном, большая вероятность решения задания связана с уровнем способности испытуемого, что видно из графиков.

Есть задания, которые слабо различают сильных и слабых испытуемых, т.е. это задание выполняется примерно с одинаковой вероятностью и слабыми и сильными студентами.

Оптимальным временем, отведенным на выполнения тестовых заданий, считаем время, к которому 90% всех испытуемых - студентов от асимптотического значения функции вероятности справились с заданием.

Для каждого тестового задания, выполненного студентами, время представлено в табл. 5.

Таблица 5. Оптимальное время выполнения тестовых заданий для студентов

Тестовые задания	Оптимальное время
ti	10000 мс=10с
t3	3000 мс=3,5с
t5	7500 мс=7,5 с
t8	3500 мс=3,5с
t10	2500 мс=2,5с
t13	6500 мс=6,5с
t15	6500 мс=6,5с
t17	6500 мс=6,5с
t20	2500 мс=2,5с
t24	3500 мс=3,5с
t26	3500 мс=3,5с
t28	2500 мс=2,5с
t30	9000 мс=9с
t32	7500 мс=7,5с

Графическое изображение функции L при полученных значениях ат и Ьт для второй группы испытуемых - школьников показано на рис. 6.-7.

Изменение аргумента - в пределах от -1 до 1, с шагом 0,1.

Графики вероятности решения тестовых заданий представлены на рис. 7-8.

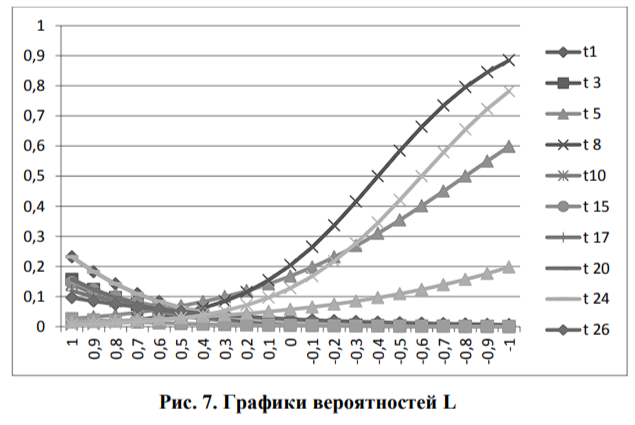
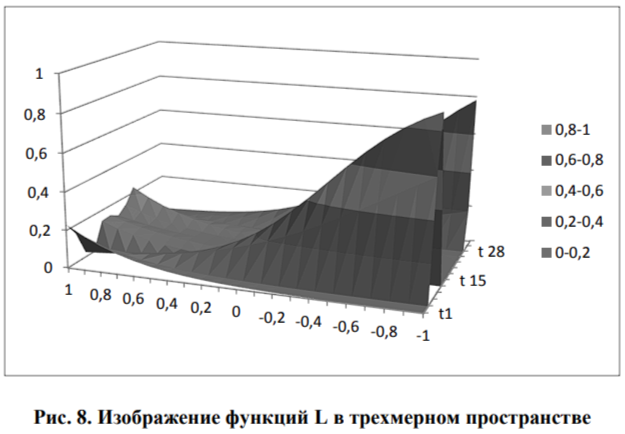
Чем больше параметр а_т, тем быстрее значение функции достигает значения 1, и вероятность решения более зависима от способности испытуемого, т.е. сильные испытуемые выполняют задание правильно с высокой вероятностью, а слабые испытуемые с малой (параметр b_т - параметр сдвига (или смещения)). Крутизна кривой говорит о дифференцирующей способности испытуемых.

По горизонтальной оси, где принимаются отрицательные значения, уровень трудности меньше, чем уровень способности, там вероятность решения показывает большие значения, чем там, где принимаются положительные значения, уровень трудности больше уровня способности и вероятность решения показывает маленькие значения. Есть задания, которые показывают обратное, это тестовые задания 20, 26, 28, вероятность решения тестового задания 30 показывает очень маленькие результаты.

Из графиков функций вероятностей видно, что большая вероятность решения задания связана с уровнем способности испытуемого.

Есть задания, которые слабо различают сильных и слабых испытуемых, т.е. это задание выполняется примерно с одинаковой вероятностью и слабыми и сильными школьниками.

Оптимальным временем, отведенным на выполнения тестовых заданий, считаем время, к которому 90% всех испытуемых - школьников от асимптотического значения функции вероятности справились с заданием.

Для каждого тестового задания, выполненного школьниками, время представлено в табл. 6.

Таблица 6. Оптимальное время выполнения тестовых заданий для школьников

Тестовые задания	Оптимальное время школьники
ti	4500 мс=4,5с
t3	7000 мс=7с
t5	5500 мс=5,5с
t8	4500 мс=4,5с
t10	5000 мс=5с
t15	6500 мс=6,5с
t17	5500 мс=5,5с
t20	5500 мс=5,5с
t24	5500 мс=5,5с
t26	5500 мс=5,5с
t28	7000 мс=7с
t30	8500 мс=8,5с
t32	6500 мс=6,5с

 

Сравнивая оптимальное время для студентов и школьников, можно заметить, что для решения тестовых заданий школьникам требуется оптимального времени больше, чем студентам. Общее время для школьников равно 77000 мс=77с., а для студентов это время составляет 68000 мс = 68с.

6.4. Проверка гипотез

Используя готовые средства, проверим выдвинутые гипотезы по уровню подготовленности и по фактору пола.

Проверим гипотезу о том, что уровень подготовленности испытуемых не влияет на результаты тестирования.

Проверим эти выборки на нормальность.

Вычислим базовые статистики: среднее, медиану и моду, и на основе этого определим отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.

Базовые статистики приведены в таблице 7.

Таблица 7. Результаты статистических данных

	студенты	школьники
сумма	591	195
среднее	49,25	24,375
медиана	27	28,5
мода	31	29

 

Анализируя полученные данные, мы видим, что базовые статистики между собой заметно отличаются.

Проверим гипотезу о нормальности с помощью критериев асимметрии (As), эксцесса (Ex).

Критерий асимметрии (As) - критерий, позволяющий проверить степень симметричности эмпирического распределения, выраженную в числовой форме.

Критерий эксцесса (Ex) - критерий, позволяющий проверить степень плоско- или узковершинности эмпирического распределения, выраженную в числовой форме (распределение является нормальным, если показатели асимметрии и эксцесса находятся в диапазоне от - 1,000 до + 1,000; распределение не является нормальным, если показатели либо асимметрии, либо эксцесса находятся в диапазоне больше -1,000 и +1,000).

С помощью программы SPSS получаются следующие результаты, в таблице 8.

Таблица 8. Результаты, полученные по критерию асимметрии (As), эксцесса (Ex)

	VAR00002	VAR00004
N Валидные	23	8
Пропущенные	8	23
Асимметрия	-2,220	-1,659
Стд. ошибка асимметрии	,481	,752
Эксцесс	4,940	1,746
Стд. ошибка эксцесса	,935	1,481

Так как показатели асимметрии и эксцесса находятся в диапазоне больше -1,000 и + 1,000, то распределение не является нормальным.

Так как распределения в целом отличаются от нормальных, применим непараметрический метод проверки гипотезы. Это U-Критерий Манна-Уитни - непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.

Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном. В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.

U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.

Обрабатываем данные в программе SPSS.

Таблица 9. Результаты, полученные по критерию Манна-Уитни

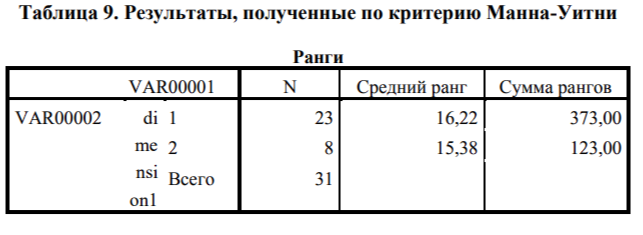
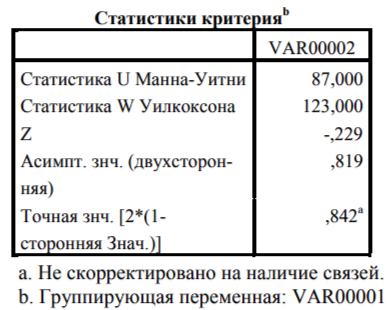
Полученные результаты говорят о том, что уровень подготовленности группы студентов не превосходит уровня подготовленности группы школьников.

Объединим эти две выборки и проверим, отличаются ли результаты теста в зависимости от фактора пола.

Разобьем на две подгруппы, юноши и девушки, в одной выборке получили 16 человек, в другой - 15 человек.

Проверим каждую из этих выборок на нормальность, вычислим базовые статистики.

Базовые статистики приведены в таблице 10

Таблица 10. Базовые статистики

	девушки	юноши
сумма	389	397
среднее	24,31	24,47
медиана	27,5	28
мода	31	31

Базовые статистики отличаются.

Проверим гипотезу о нормальности с помощью критериев асимметрии (As), эксцесса (Ex).

Результаты представлены в таблице 11.

Таблица 11. Результаты, полученные по критерию асимметрии (As), эксцесса (Ex)

	VAR00002	VAR00004
N Валидные	15	16
Пропущенные	1	0
Асимметрия	-2,591	-1,638
Стд. ошибка асимметрии	,580	,564
Эксцесс	7,973	1,780
Стд. ошибка эксцесса	1,121	1,091

Для проверки результатов по подгруппам снова воспользуемся критерием Манна- Уитни.

В таблице 12 результаты, полученные в программе SPSS.

Таблица 12. Результаты, полученные по критерию Манна-Уитни

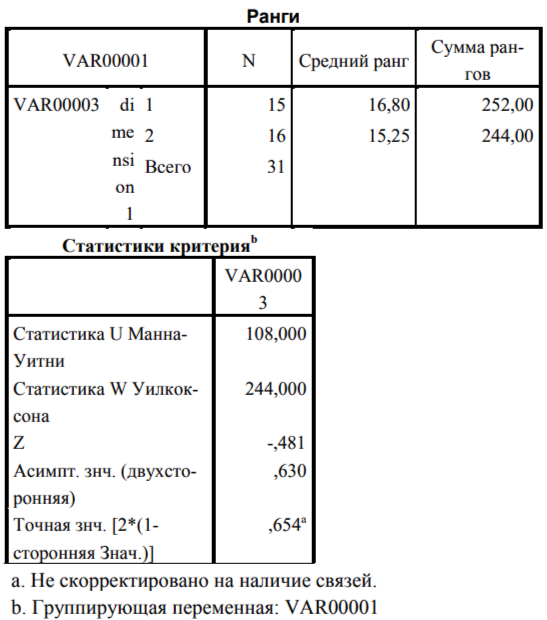
Полученные результаты свидетельствуют о том, что фактор пола также не влияет на исход полученных результатов.

7. ЗАКЛЮЧЕНИЕ

1. Исследованы особенности вероятностного моделирования процесса выполнения теста на рабочую память. Преимуществами использованного подхода являются:

• учёт динамики способностей испытуемых и трудностей заданий во время их выполнения и

• модифицированная функция Раша, аргументы которой, в отличие от классического варианта, задаются в вероятностной шкале.

2. Параметры использованной вероятностной модели идентифицированы с использованием результатов тестов на рабочую память.

3. Анализ идентифицированных зависимостей позволил определить оптимальное время, которое следует отводить для выполнения заданий теста.

4. Проведённый статистический анализ позволил принять гипотезы о независимости результатов теста на рабочую память от уровня подготовки и пола испытуемых.

1. Л.С. Куравский, П.А. Мармалюк, Г.А. Юрьев, П.Н. Думин, А.С. Панфилова. Вероятностное моделирование процесса выполнения тестовых заданий на основе модифицированной функции Раша. – Вопросы психологии, 2015, №3.
2. Л.С. Куравский, П.А. Мармалюк, Г.А. Юрьев, П.Н. Думин. Методы численной идентификации марковских моделей и их сравнительный анализ. Информационные технологии, №10, том 21, 2015.
3. L. S. Kuravsky, P. A. Marmalyuk, G. A. Yuryev, P. N. Dumin and A. S. Panfilova. Probabilistic Modeling of a Testing Procedure. - Applied Mathematical Sciences, Vol. 9, 2015, no. 82, 4053 – 4066, https://doi.org/10.12988/ams.2015.53234.
4. Куравский Л. С., Мармалюк П. А., Алхимов В. И., Юрьев Г. А. Математические основы нового подхода к построению процедур тестирования. – Экспериментальная психология, №4, том 5, стр. 75, 2012.
5. Куравский Л. С., Мармалюк П. А., Алхимов В. И., Юрьев Г. А. Новый подход к построению интеллектуальных и компетентностных тестов. Моделирование и анализ данных, №1, 2013.
6. Л.С. Куравский, А. А. Марголис, Г.А. Юрьев, П.А. Мармалюк. Концепция системы поддержки принятия решений для психологического тестирования. Психологическая наука и образование. №1, 2012.
7. Войтов В.К., Косихин В.В., Ушаков Д.В. Рабочая память как перспективный конструкт когнитивной психологии и методы его измерения // Моделирование и анализ данных. 2015. № 1. С. 57–78.
8. Войтов В. К., Сафонов М. А., Соколов Л. Ф., Разработки тестов рабочей памяти в интернете - Моделирование и анализ данных - 2014. № 1.
9. Д. В. Ушаков, Психология интеллекта и одаренности, Издательство «Институт __________психологии РАН» Москва – 2011.
10. Тюменева Ю.А., Яременко А.А., Руководство для авторов, публикующих результаты разработки оценочного инструмента, Вопросы образования, №1, 2013. Москва.
11. Шмелев А.Г., «Практическая тестология: Тестирование в образовании, прикладной психологии и управлении персоналом», М., «Маска», 2013.
12. Baker F.B. The Basics of Item Response Theory. ERIC Clearinghouse on Assessment and Evaluation, University of Maryland, College Park, MD, 2001. Портал психологических изданий PsyJournals.ru.
13. Gregory R.J. Psychological testing: History, principles, and applications (5th edition). - New York: Pearson. 2007.
14. Развитие рабочей памяти с помощью компьютерных тренажеров как средство преодоления объективных трудностей при изучении дисциплин. URL: http://cyberleninka.ru/article/n/razvitie-rabochey-pamyati-s-pomoschyu-kompyuternyhtrenazherov- kak-sredstvo-preodoleniya-obektivnyh-trudnostey-pri-izuchenii (дата обра- щения 24.03.2016).
15. Для чего нам нужна рабочая память? URL: http://hawkish.ru/%D1%80%D0%B0%D0%B1%D0%BE%D1%87%D0%B0%D1%8F- %D0%BF%D0%B0%D0%BC%D1%8F%D1%82%D1%8C/, (дата обращения 3.03.2016)
16. Компьютерные тренажеры рабочей памяти. URL: http://working-memory.ru/ (дата обращения 11.02.2016).
17. Анализ двух выборок. URL: http://www.tsput.ru/res/math/mop/lections/lection_6.htm (дата обращения 14.04.2016).
18. Закон нормального распределения и его использование при выборе параметрического или непараметрического критерия. URL: http://citoweb. yspu.org/link1/metod/met154/node6.html (дата обращения 14.04.2016).