Моделирование и анализ данных
2015. Том 5. № 1. С. 4–19
ISSN: 2219-3758 / 2311-9454 (online)
Канонический ансамбль самоизбегающих блужданий
Аннотация
Общая информация
Ключевые слова: Случайное блуждание без самопересечений, канонический ансамбль, уравнение Дайсона, квантовая теория поля
Рубрика издания: Моделирование
Тип материала: научная статья
Для цитаты: Алхимов В.И. Канонический ансамбль самоизбегающих блужданий // Моделирование и анализ данных. 2015. Том 5. № 1. С. 4–19.
Полный текст
1. ВВЕДЕНИЕ
Вначале мы кратко изложим модель самоизбегающего случайного блуждания в d - мерном евклидовом пространстве Rd , состоящего из последовательности N частичных перемещений r1, r2 , . . . , rN,, каждое из которых имеет одну и ту же плотность распределения вероятностей т(r) = т(r) со средним квадратичным перемещением Er2 = l2. При этом точки сочленения перемещений а также начало вектора r1 и конец вектора rn являются центрами взаимно непроницаемых шаров - "исключённых" объёмов диаметра r0 < l, пронумерованных от 0 до N соответственно. В результате указанного ограничения из множества всех возможных пространственных конфигураций рассматриваемого блуждания исключаются такие траектории, в которых расстояние rij = |ri+...+rj|, 1 ≤ i < j ≤ N, между центрами любой пары шаров меньше r0. Введённый запрет оказывает существенное влияние на функциональную зависимость плотности вероятностей WN(R) от расстояния R = r1N между концами траектории, состоящей из N частичных перемещений, и поэтому его называют эффектом "исключённого" объёма. Запишем искомую плотность вероятностей WN(R) в форме интеграла Фурье

2. ОСНОВНОЕ УРАВНЕНИЕ
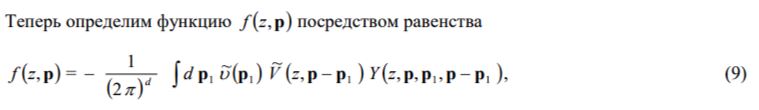



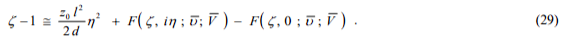
3. УРАВНЕНИЕ РЕНОРМГРУППЫ (РГ)



4. АСИМПТОТИКА РАСПРЕДЕЛЕНИЯ РАССТОЯНИЙ МЕЖДУ КОНЦАМИ САМОИЗБЕГАЮЩЕЙ ТРАЕКТОРИИ БЛУЖДАЮЩЕЙ ЧАСТИЦЫ






5. КАНОНИЧЕСКИЙ АНСАМБЛЬ САМОИЗБЕГАЮЩИХ БЛУЖДАНИЙ




Литература
- В.И. Алхимов. Случайные блуждания без самопересечений. М.: МГОБУ ВПО МГППУ, 2015 – 121 с.
- Н.Н. Боголюбов и Д.В. Ширков. Введение в теорию квантованных полей. М.: Наука, 1976.
- Л.В. Овсянников. Групповой анализ дифференциальных уравнений. М.: Наука, 1978.
- М.В. Федорюк. Метод перевала. М.: Наука, 1977.
- Керзон Хуанг. Статистическая механика. М.: Мир, 1966.
- Э. Титчмарш. Теория функций. М.: Наука, 1980.
- В. Феллер. Введение в теорию вероятностей и еѐ приложения, т. 2. М.: Мир, 1967.
Информация об авторах
Метрики
Просмотров web
За все время: 968
В прошлом месяце: 10
В текущем месяце: 5
Скачиваний PDF
За все время: 343
В прошлом месяце: 4
В текущем месяце: 2
Всего
За все время: 1311
В прошлом месяце: 14
В текущем месяце: 7