Аутизм и нарушения развития
2021. Том 19. № 2. С. 52–58
doi:10.17759/autdd.2021710206
ISSN: 1994-1617 / 2413-4317 (online)
Сравнительный анализ эффективности использования прямого и генерализованного условного подкрепления при формировании навыка решения простых арифметических задач у ребенка с РАС
Аннотация
Общая информация
Ключевые слова: прямое подкрепление, генерализованное подкрепление, математическая задача, деление, умножение, расстройства аутистического спектра, прикладной анализ поведения
Рубрика издания: Методы обучения и сопровождения
Тип материала: научная статья
DOI: https://doi.org/10.17759/autdd.2021710206
Благодарности. Автор благодарит за обучение и наставничество Юлию Михайловну Эрц, руководителя проекта «Аутизм: коррекционная работа на основе поведенческого анализа (АВА). Теория и практика».
Для цитаты: Колесникова Ю.В. Сравнительный анализ эффективности использования прямого и генерализованного условного подкрепления при формировании навыка решения простых арифметических задач у ребенка с РАС // Аутизм и нарушения развития. 2021. Том 19. № 2. С. 52–58. DOI: 10.17759/autdd.2021710206
Полный текст
Введение
Для успешной адаптации в школе необходимо, чтобы ребенок мог регулировать свое поведение, имел достаточный интеллектуальный уровень и темп деятельности. Помимо этого, у детей должны быть сформированы начальные академические навыки чтения и математических операций. Однако у многих детей с РАС, обучающихся в инклюзии, могут наблюдаться дефициты в данных сферах, и требуются специальные методики, применение которых будет способствовать овладению необходимыми навыками и умениями [Питерс, 1999; Хотылева, 2008].
Одним из самых проблемных направлений в учебной деятельности на ранних этапах является формирование навыков, связанных с решением математических задач [Levingston, 2009]. Причем, низкий уровень усвоения математических знаний не является следствием педагогической запущенности, интеллектуальной недостаточности или сложности учебной программы, а может быть связан с индивидуальными особенностями формирования высших психических функций у детей [Ахутина, 2001]. В связи с этим необходимо разрабатывать методы обучения, которые могли бы повысить успеваемость всех учащихся.
В работах зарубежных ученых можно увидеть множество исследований, направленных на изучение проблемы решения математических задач у детей со сложностями в обучении[Jitendra, 1997], предлагаются, например:
— когнитивная стратегия с выделением ключевых слов и иллюстрированием условия задачи [Case, 1992];
— решение задач с постепенным переходом обучения от слова к фразе, от фразы к предложению и от предложения к целой задаче [Miller, 1993];
— обучение на основе схематического представления материала [Jitendra, 1996];
— использование тренировочных процедур [Montague, 1993];
— использование списков с указанием шагов, необходимых для решения задач на вычитание и сложение [Cassel, 1996];
— обучение предшествующим навыкам при решении математических задач [Neef, 2003]; в данном исследовании детей обучали таким навыкам как определение начального условия, изменение условия, определение математической операции и указание ответа;
— обучение предшествующим навыкам при решении детьми задач по умножение и деление [Levingston, 2009]; в данном исследовании детей обучали таким навыкам как определение большего и меньшего числа в условии задачи, выбор нужного арифметического действия и запись ответа в нужном месте.
Самым важным фактором в прикладном анализе поведения, получившим широкое практическое применение, является положительное подкрепление. Подкрепление — это процесс, происходящий во времени и приводящий к учащению поведения. Положительное подкрепление может быть разных видов — первичное (еда, сон, вода), условное (похвала, внимание, игрушки), прямое (предоставляемое непосредственно после реакции) и генерализованное (знаки отличия, жетоны, деньги). По физическим характеристикам виды подкрепления можно разделить на пищевые и чувственные, предметные, активност- ные и социальные [Купер, 2016]. К социальным подкреплениям, в первую очередь, относится похвала, которая может быть очень эффективна при обучении навыкам типично развивающихся детей, но часто безрезультатна для детей с особенностями развития [Senn, 2020].
Для каждого ребенка подкрепление должно подбираться с учетом индивидуальных способностей и использоваться в таком формате, который приводит к максимально быстрому научению [Campanaro, 2020]. Есть данные о том, что прямое подкрепление является наиболее эффективным, особенно для людей с ограниченным поведенческим репертуаром [Koegel, 1980]. Также проводились исследования, показавшие, что даже отсроченное первичное подкрепление действует более эффективно, чем генерализованное подкрепление, для людей с тяжелыми нарушениями развития [Leon, 2016]. С другой стороны, на людей с наименее выраженными особенностями развития при обучении навыкам поощрение в форме жетонов может оказывать большее подкрепляющее воздействие [Bonfonte, 2020; Fiske, 2020]. Однако исследований, сравнивающих эффективность того или иного вида подкрепления при формировании академических навыков, пока недостаточно.
В текущем исследовании оценивалось влияние положительного подкрепления — прямого и генерализованного — в процессе обучения ребенка с высокофункциональным аутизмом на навык определения в математических задачах арифметической операции путем вычленения ключевой фразы и на умение решать задачи.
Метод
Участник и среда,
в которой проводилось вмешательство
В исследовании приняла участие девятилетняя девочка А. с диагнозом РАС. Общий уровень навыков ребенка на период проведения процедуры обучения составлял 154 балла по программе оценки VB-MAPP [Сандберг, 2013]. Девочка учится во втором классе общеобразовательной школы, но есть трудности в усвоении академических навыков, особенно математических. Девочка может считать, определять большее и меньшее число, решать примеры и задачи с простыми арифметическими операциями, но наблюдаются затруднения в дифференцировании задач на сложение и вычитание и задач на умножение и деление.
Вмешательство проводилось индивидуально в домашних условиях родителями ребенка: 5 дней в неделю 2 раза в день, в утренние и вечерние часы по 20 минут.
Зависимая переменная
Целевое поведение: после прочтения задачи ребенок подчеркивает ключевую фразу и в зависимости от нее выбирает арифметическую операцию. Например: в задаче «У Алены было 5 конфет, а у Светы в 3 раза больше. Сколько конфет было у Светы?» нужно подчеркнуть фразу «в 3 раза больше», записать и решить пример на умножение «5 х 3 = 15». А в задаче «У Алены было 5 конфет, а у Светы на 3 больше. Сколько конфет было у Светы?» нужно подчеркнуть фразу «на 3 больше», записать и решить пример на сложение «5 + 3 = 8». Аналогично в задачах на вычитание и деление арифметическая операция выбирается в зависимости от фраз «на (число) меньше» или «в (число) раз меньше».
Измерение поведения проводилось путем подсчета количества реакций, в которых ребенок верно указывал ключевую фразу и выбирал соответствующую фразе арифметическую операцию. Правильность решения задачи не учитывалась, так как девочка после выбора арифметической операции решала задачу правильно в 100% случаев.
Если ребенок выполнял оба действия самостоятельно (и подчеркивал ключевую фразу, и верно выбирал арифметическую операцию), то реакция учитывалась как правильная.
Если ребенок не выполнял одно из действий (не подчеркивал ключевую фразу, или подчеркивал неверную фразу, или выбирал неверную арифметическую операцию), реакция учитывалась как неправильная.
Вмешательство
Для обучения использовался список из 100 простых арифметических задач на умножение, деление, сложение и вычитание по типу AxB=C, A^B=C, A+B=C, A-B=C.
Перед каждой сессией проводилась оценка предпочтений методом множественных стимулов [Fisher, 1992].
Вмешательство включало три процедуры и 2 этапа.
Первый этап.
Процедура 1. Формирование навыка определения арифметического действия в задачах на умножение и сложение с использованием прямого подкрепления
Для обучения использовались 2 вида бланков с заданиями. Бланк А включал таблицу с фразами:
№ 1 — на (число от 1 до 10) больше.
№ 2 — в (число от 1 до 10) раза больше.
Таблица 1
Образец бланка А для обучения
|
на 4 больше |
|
в 1 раз больше |
|
|
в 8 раз больше |
|
на 3 больше |
|
|
на 3 больше |
|
в 5 раз больше |
|
|
на 2 больше |
|
в 4 раза больше |
|
|
в 10 раз больше |
|
на 2 больше |
|
|
на 6 больше |
|
на 7 больше |
|
|
в 1 раз больше |
|
в 9 раз больше |
|
|
на 7 больше |
|
на 8 больше |
|
|
в 9 раз больше |
|
в 6 раз больше |
|
|
в 5 раз больше |
|
на 10 больше |
|
В ячейку возле фразы ребенок должен был вписать верную арифметическую операцию. В случае правильной реакции предоставлялось прямое подкрепление в пропорции 1:1. В случае неправильной реакции производилась коррекция ошибки с предоставлением вербальной подсказки с акцентом на предлоге «на» или «в». Подкрепление не предоставлялось.
Бланк В содержал список из 10 задач со специальным свободным пространством под каждой задачей для записи решения.
Ребенок должен был найти и подчеркнуть в задаче фразу № 1 или № 2, выбрать правильное арифметическое действие и решить задачу. За каждую верно выполненную цепочку действий ребенок получал прямое подкрепление в пропорции 1:1. Если фраза или арифметическое действие были выбраны неправильно, предоставлялась вербальная и визуальная подсказки. Вербальная подсказка выражалась в словесной инструкции с предложением обратить внимание на ключевую фразу, а визуальная подсказка представляла собой карточку с образцом ключевой фразы и соответствующей ей арифметической операцией. Подкрепление не предоставлялось.
Процедура 2. Формирование навыка определения арифметического действия в задачах на деление и вычитание
с использованием генерализованного подкрепления
Здесь проводилось обучение дифференциации действий вычитания и деления. Также использовались два вида бланков. Бланк С был аналогичен бланку А и включал фразы:
№ 3 — на (число от 1 до 10) меньше.
№ 4 — в (число от 1 до 10) раз меньше.
Правильно выполненная цепочка подкреплялась генерализованным подкреплением (жетоны) в постоянной пропорции 1:1. Необходимо отметить, что жетонная система подкреплений была введена и успешно использовалась в течение 2-х лет для обучения девочки в рамках прикладного анализа поведения. Когда ребенок собирал 10 жетонов, он получал предпочитаемое поощрение.
Бланк D был аналогичен бланку В и содержал задачи на вычитание и деление. Если ребенок правильно определял опорную фразу и выбирал верную арифметическую операцию, он получал жетон в пропорции 1:1. После сбора 10 жетонов предоставлялся доступ к поощрению.
Коррекция ошибки осуществлялась так же, как в Процедуре 1.
Процедура 1 и Процедура 2 применялись на первом этапе исследования в переменном режиме. Из двух сессий в день обязательно в одной применялась Процедура 1, а в другой Процедура 2, но не было закрепленного времени суток для каждой из процедур, то есть Процедура 1 могла проводиться сегодня в утреннюю сессию, а завтра — в вечернюю. При достижении критерия правильных ответов в 80%, обучение перешло на второй этап и продолжилось по Процедуре 3.
Процедура 3. Формирование навыка определения арифметического действия в задачах на деление, вычитание, умножение и сложение с использованием прямого и генерализованного подкрепления
В данной процедуре проводилось обучение дифференциации действий вычитания и деления, а также сложения и умножения. Использовался бланк Е, в котором были записаны задачи на все четыре арифметические операции в случайном порядке. Коррекция ошибки осуществлялась так же как в Процедуре 1.
Второй этап.
На втором этапе исследования прямое и генерализованное подкрепления использовались в переменном режиме: менялось время суток для применения одного или другого вида подкрепления. Если утром применялось прямое подкрепление, то вечером — генерализованное, и наоборот.
Для исследования эффективности подкреплений использовался двухфазный альтернирующий дизайн.
Результаты
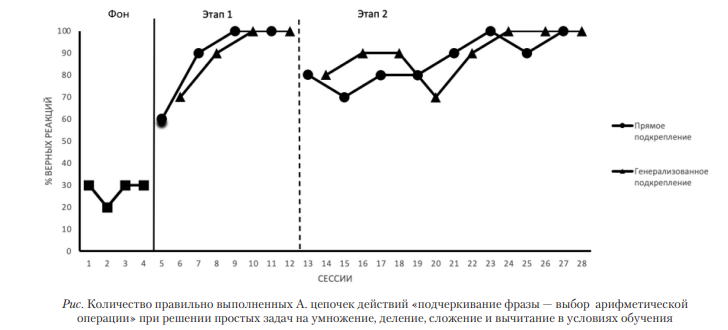
Результаты проведенного исследования показаны в графике (см. рис.). Здесь можно увидеть, что применение как прямого, так и генерализованного подкрепления в случае применения вмешательства к девочке А. оказалось одинаково эффективно в обучении навыку определения верной арифметической операции при решении простых задач. Если при фоновых условиях количество верно выполненных цепочек реакций не превышало 30%, то в конце вмешательства их количество выросло и составило 90—100% — при использовании как прямого, так и генерализованного подкрепления.
Таблица 2
Образец бланка В для обучения

Обсуждение и выводы
Результаты исследования показали одинаковую эффективность прямого и генерализованного подкрепления при обучении ребенка навыку определения арифметической операции в задачах. Возможно, это связано с уровнем функционирования ребенка, который является относительно высоким. Так как различий в эффективности подкреплений не выявлено, можно предположить, что при формировании других навыков у девочки А. возможно с одинаковым успехом использовать оба вида подкрепления, причем для формирования навыков с короткой временной продолжительностью, например, таких, как заучивание слов иностранного языка, удобнее использовать генерализованное подкрепление, а для формирования навыков с высокой временной продолжительностью, таких как написание изложения, — прямое подкрепление.
В будущих исследованиях приоритетным направлением можно выбрать проверку эффективности прямого и генерализованного подкрепления для формирования навыков решения более сложных математических задач и навыков, не связанных с математикой, например, навыка понимания прочитанного, что также вызывает большие сложности у детей с РАС.
Вместе с тем, возможно продолжить работу с целью исследования эффективности разных видов подкрепления в рамках групповой работы, например, в классе.
Литература
- Ахутина Т.В., Обухова Л.Ф., Обухова О.Б. Трудности усвоения начального курса математики в форме квазиисследовательской деятельности // Психологическая наука и образование. 2001. Т. 6. № 1. С. 65—78.
- Купер Дж.О., Херон Т.Э., Хьюард У.Л. Прикладной анализ поведения. Москва: Практика, 2016. 864 c. ISBN 978-5- 89816-157-6.
- Питерс Т. Аутизм: От теоретического понимания к педагогическому воздействию. Санкт-Петербург: Институт специальной педагогики и психологии, 1999. 192 с.
- Сандберг М.Л. VB-MAPP: Оценка вех развития вербального поведения и построение индивидуального плана вмешательства: [В 2 ч.: Ч. 2]. Руководство. Программа оценки речи и социального взаимодействия для детей с аутизмом и другими нарушениями развития. Ришон ле-Цион: MEDIAL, 2013. 275 с. ISBN 978-965-559-011-1.
- Хотылева Т.Ю., Галактионова О.Г., Борисова О.В. Формирование у детей, страдающих аутизмом, умения решать арифметические задачи // Детский аутизм: исследования и практика / ред. В.Н. Касаткин. Москва: РОО «Образование и здоровье», 2008. С. 286—301. ISBN 978-5-9900666-3-2.
- Bonfonte S.A., Bourret J.C., Lloveras L.A. Comparing the reinforcing efficacy of tokens and primary reinforces. Journal of Applied Behavior Analysis, 2020, vol. 53, no. 3, pp. 1593—1605. DOI:10.1002/jaba.675
- Campanaro A.M., Vladescu J.C., Kodak T. etal. Comparingskillacquisitionundervaryingonsetsofdifferentialreinforcement: A preliminary analysis. Journal of Applied Behavior Analysis, 2020, vol. 53, no. 2, pp. 690—706. DOI:10.1002/jaba.615
- Case L.P., Harris K.R., Graham S. Improving the mathematical problem-solving skills of students with learning disabilities: Self-regulated strategy development. The Journal of Special Education, 1992, no. 26, vol. 1, pp. 1—19. DOI:10.1177/002246699202600101
- Cassel J., Reid R. Use of a self-regulated strategy intervention to improve word problem-solving skills of students with mild disabilities. Journal of Behavioral Education, 1996, vol. 6, pp. 153—172. DOI:10.1007/BF02110230
- Fiske K.E., Isenhower R.W., Bamond M.J., Lauderdale-Littin S. An analysis of the value of token reinforcement using a multiple-schedule assessment. Journal of Applied Behavior Analysis, 2020, vol. 53, no, 1, pp. 563—571. DOI:10.1002/ jaba.613
- Fisher W., Piazza C.C., Bowman L.G. et al. A comparison of two approaches for identifying reinforcers for persons with severe and profound disabilities. Journal of Applied Behavior Analysis, 1992, vol. 25, no. 2, pp. 491—498. DOI:10.1901/ jaba.1992.25-491
- Jitendra A., Hoff K. The effect of schema-based instruction on mathematical word-problem-solving performance of students with learning disabilities. Journal of Learning Disabilities, 1996, vol. 29, no. 4, pp. 422—431. DOI:10.1177/002221949602900410
- Jitendra A., Xin Y.P. Mathematical word-problem-solving instruction for students with mild disabilities and students at risk for math failure; A research synthesis. The Journal of Special Education, 1997, vol. 30, no. 4, pp. 412—438. DOI:10.11 77/00224669050390030501
- Koegel R.L. Williams J.A. Direct versus indirect response-reinforcer relationships in teaching autistic children. Journal of Abnormal Child Psychology, 1980, vol. 8, no. 4, pp. 537—547. DOI:10.1007/BF00916505
- Leon Y., Borrero J.C., DeLeon I.G. Parametric analysis of delayed primary and conditioned reinforcers. Journal of Applied Behavior Analysis, 2016, vol. 49, no. 3, pp. 639—655. DOI:10.1002/jaba.311
- Levingston H.B., Neef N.A., Cihon T.M. The effects of teaching precurrent behaviors on children’s solution of multiplication and division word problems. Journal of Applied Behavior Analysis, 2009, vol. 42, no. 2, pp. 361—367. DOI:10.1901/ jaba.2009.42-361
- Miller S.P., Mercer C.D. Using graduated word problem sequence to promote problem-solving skills. Learning Disabilities Research and Practice, 1993, vol. 8, no. 3, pp. 169—174.
- Montague M., Applegate B., Marquard K. Cognitive strategy instruction and mathematical problem-solving performance of students with learning disabilities. Learning Disabilities Research & Practice, 1993, vol. 8, no. 4, pp. 223—232.
- Neef N.A., Nelles D., Iwata B.A., Page T.J. Analysis of precurrent skills in solving mathematics story problems. Journal of Applied Behavior Analysis, 2003, vol. 36, no. 1, pp. 21—33. DOI:10.1901/jaba.2003.36-21
- Senn L.P., Bayles M.W., Bruzek J.L. An evaluation of praise as a reinforcer for preschoolers’ behavior. Journal of Applied Behavior Analysis, 2020, vol. 53, no. 1, pp. 315—330. DOI:10.1002/jaba.591
Информация об авторах
Метрики
Просмотров web
За все время: 552
В прошлом месяце: 22
В текущем месяце: 10
Скачиваний PDF
За все время: 206
В прошлом месяце: 7
В текущем месяце: 1
Всего
За все время: 758
В прошлом месяце: 29
В текущем месяце: 11