Психологическая наука и образование
2010. Том 15. № 4. С. 91–99
ISSN: 1814-2052 / 2311-7273 (online)
Генетико-моделирующий метод и диагностика новообразований учебной деятельности
Аннотация
Общая информация
Ключевые слова: генетико-моделирующий метод, инструментальный акт, знаковое опосредствование, единица анализа, учебная деятельность, учебная задача, обобщенный способ действия
Рубрика издания: Тематические сообщения
Тип материала: научная статья
Для цитаты: Медведев А.М. Генетико-моделирующий метод и диагностика новообразований учебной деятельности // Психологическая наука и образование. 2010. Том 15. № 4. С. 91–99.
Полный текст
Иногда Л. С. Выготский характеризовал предлагаемый им метод как объективирующий: «Если методика “стимул - реакция” была объективной психологической методикой, ограничивавшей изучение лишь теми процессами, которые в поведении человека уже являлись внешними, то наша методика с полным правом может быть названа объективирующей ... Вынося наружу те вспомогательные операции, с помощью которых субъект овладевает той или иной задачей, наша методика делает их доступными для объективного изучения, иначе говоря, объективирует их» [Выготский, 1984, с. 78-79].
Наряду с этим в текстах Л. С. Выготского предлагаемый им метод определяется как инструментальный, поскольку предметом исследования выступает инструментальный акт. «... В инструментальном акте, - пишет Л. С. Выготский, - используются психологические свойства внешнего явления, стимул становится психологическим орудием в силу использования его как средства воздействия на психику и поведение. Поэтому всякое орудие является непременно стимулом; если бы оно не было непременно стимулом, т. е. не обладало способностью воздействия на поведение, оно не могло бы быть и орудием. Но не всякий стимул является орудием» [Выготский, 1982, с. 106-107].
Сравнивая существовавшие в то время в детской психологии исследовательские подходы, Л. С. Выготский отмечал, что эксперимент оказался отделенным от сравнительно-генетического подхода (воспроизводил только ставшие, устойчивые формы поведения), а сравнительногенетический метод не был связан с экспериментом (носил описательнофеноменологический характер). «... Мы идем как раз обратным путем, - писал Л. С. Выготский, - связывая обе линии исследования в единый экспериментальногенетический метод (курсив мой. - А.М.)» [Выготский, 1984, с. 79]. Именно такое название - экспериментально-генетический - или синонимичное ему - генетико-моделиру- ющий - закрепилось за методом исследования становящихся психических функций в специально построенных экспериментальных условиях.
Л. С. Выготский противопоставлял генетико-моделирующий метод методу срезов, получившему распространение в традиционной диагностике психического развития, основанной на достижениях дифференциальной психологии. Традиционная психодиагностика как прежде, так и теперь опирается на априорное предположение наличия в психической организации человека неких элементов и структур, которые прирастают в ходе развития, не изменяясь по своей качественной сути. Так называемые срезы - это тестовые испытания, показывающие возрастной (точнее, временной) прирост психических функций, соотносимый с некоторой статистической нормой.
Об ограниченности исследовательских возможностей тестов, основанных на теориях черт и факторных теориях, писали А. В. Запорожец и Д. Б. Эльконин. Однако и в самой традиции научной школы Л. С. Выготского - в практике развивающего обучения - диагностика часто строилась как «срезовая».
Диагностика как, буквально, распознание, различение предполагает анализ исследуемого явления. Анализ, в свою очередь, предполагает выделение элементов или единиц изучаемой реальности. Ориентация на элементы или на единицы определяет различные виды анализа. «. Следует различать двоякого рода анализ, применяемый в психологии, - пишет Л. С. Выготский. - . Первый способ психологического анализа можно назвать разложением сложных психических целых на элементы. Существенным признаком такого анализа является то, что в результате его получаются продукты, чужеродные по отношению к анализируемому целому, - элементы, которые не содержат в себе свойств, присущих целому как таковому.» [Выготский, 1982а, с. 13]. В противопоставление этому виду анализа Л. С. Выготский предлагает проводить «. анализ, расчленяющий сложное единое целое на единицы» [Выготский, 1982а, с. 15] и тут же определяет, что может быть единицей: «Под единицей мы подразумеваем такой продукт анализа, который в отличие от элементов обладает всеми основными свойствами, присущими целому, и который является далее неразложимыми живыми частями этого единства» [там же].
Основное требование, предъявляемое к содержательным единицам исследуемого предмета, состоит в том, что они должны нести в себе потенции развитого целого - той реальности, которая подвергается исследовательской или диагностической процедуре.
Выделение содержательных единиц требует обращения к логике - анализ операция логическая. При этом различение элементов и единиц предполагает различение двух логик: формальной и содержательной. Для первой характерно составноструктурное представление объекта изучения, при котором производится выделение элементов, предполагаемых неизменными во всех изменениях (своего рода атомов исследуемого предмета), и особенностей их связывания в целое. При этом различение элементов и единиц в формальной логике не проводится, они отождествляются. Для содержательной логики, напротив, характерно выделение единиц, которые, в отличие от элементов, несут в себе основные черты изучаемого предмета как целого и, главное, содержат потенции развития изучаемого предмета. В связи с этим содержательная логика определяется еще и как генетическая, поскольку ее предметом выступает возникающая и развивающаяся реальность.
В рассматриваемой традиции культурно-исторической психологии на необходимость различения формальной логики и генетической логики при психологопедагогическом проектировании - построении теории и практики развивающего обучения - указывал В.В. Давыдов. Следует отметить, что В. В. Давыдов связывал построенную им теорию развивающего обучения с идеей метода Л.С. Выготского. «... В процессе разработки данной теории и ее практического применения, - пишет В.В. Давыдов, - экспериментальногенетический метод исследования, введенный Л. С. Выготским и его сотрудниками, закономерно превратился в метод формирующего эксперимента или в генетикомоделирующий метод, в котором важную роль выполняет проектирование» [Давыдов, 1996, с. 517].
Учебная деятельность в системе Эльконина-Давыдова организуется по форме квазиисследования, в ходе которого учащиеся осваивают обобщенные способы действия, опосредствованные научными понятиями. Единицей этой деятельности выступает учебная задача. Входящие в ее состав учебные действия, их последовательность воспроизводят логику мысленного эксперимента, логику происхождения научного понятия. Учебная задача как единица учебной деятельности «обладает всеми основными свойствами, присущими целому». Поэтому она может служить ориентиром для диагностики развивающих эффектов учебной деятельности, если эта диагностика строится в соответствии с идеей генетико-моделирующего метода.
В лабораторных же исследованиях новообразований учебной деятельности и при построении диагностических процедур часто использовались приемы, характерные для традиционной практики психологического экспериментирования и традиционной диагностики. Так, для определения сформированности анализа использовалась методика «Кубики Кооса» [Рякина, 1983], для исследования внутреннего плана действия (ВПД) применялась задача «Ханойская башня» [Аршавина, 1982], для диагностики функции планирования - «Прогрессивные матрицы Равена» [Федекин, 2000], для диагностики рефлексии - анаграммы [Зак, 1997; Зак, 2009]. Содержание предметного материала и логика действий испытуемых в этих исследованиях в целом дают возможность фиксировать «обобщение с места» как интегральный показатель освоения обобщенного способа действия, но не позволяют оценить динамику освоения способа и опосредствования этого процесса.
Принципиально другой методический подход представляют собой исследования Л. В. Берцфаи [Берцфаи, 1963; Берцфаи, 1981], а также работы, выполненные под руководством В. В. Рубцова (в особенности это относится к работам Р.Я. Гузмана [Гузман, 1980] и В. В. Агеева [Агеев, 1985]). В них испытуемые осуществляют реальные действия-преобразования в режиме квазиисследования, а цикл выполняемых ими действий соотносим со структурой учебной задачи.
Остановимся на эксперименте Л. В. Берцфаи, поскольку именно он послужил прототипом для построения нашего эксперимента.
В исследовании применялось оригинальное техническое устройство конструкции Н.Н. Поддьякова, скомпонованное из прямоугольной площадки, фигурки и пульта управления с четырьмя кнопками, функциональное назначение которых состояло в перемещении фигурки по четырем направлениям: направо, налево, от себя и к себе. На площадку ставились лабиринты, по этим лабиринтам нужно было проводить фигурку, последовательно нажимая на разные кнопки.
В эксперименте каждому учащемуся сначала предлагалось решить практическую задачу, т. е. провести фигурку по одному из лабиринтов, поставленному на площадку. Когда ребенок допускал ряд ошибок, перед ним ставилась учебная задача: экспериментатор убирал лабиринт и предлагал, нажимая кнопки, самостоятельно научиться перемещать фигурку по «чистой» площадке. Затем испытуемого возвращали к решению практических задач.
Как пишет В.В. Давыдов, «своеобразие учебной задачи состояло в том, что ребенок в случае ее решения мог сразу овладеть общим способом проведения фигурки по лабиринтам, работая при этом с прибором, на площадке которого ни одного лабиринта не было. Особенность задачи заключалась в том, что ребенок прежде всего мог определить принцип связи направлений перемещения фигурки с расположением кнопок на пульте. Для этого ребенок должен был, работая с прибором, самостоятельно овладеть следующим обобщенным способом действия: уметь отождествлять любую точку перемещения фигурки в поле с нажимом определенной кнопки на пульте» [Давыдов, 1996, с. 189].
Соотнесем особенности этой методики с положениями базовой теории. Согласно теории учебной деятельности овладение обобщенным способом действия, с одной стороны, позволяет сразу, без долгого накопления опыта научиться решать весь класс задач в соответствии с заложенным в них принципом. С другой стороны, сам принцип основывается на генетически исходном отношении, конституирующем ту предметную область, к которой этот класс задач относится. Генетически исходное отношение непосредственно не совпадает со своими проявлениями, поэтому в процессе познания оно фиксируется в исходной абстракции, которая есть продукт моделирования. Это требует выхода в знаковосимволический план, в план знакового опосредствования.
При соотнесении этих представлений с содержанием и структурой задач, решаемых школьниками в рассматриваемом эксперименте, возникает ряд вопросов. Можно ли считать отношение нажатий на кнопки устройства и направлений движения фигурки генетически исходным? В какой абстракции (модели, понятии) это отношение фиксируется? Какой всеобщий принцип (в границах заданного класса задач) раскрывает участник эксперимента в решении этой двигательной задачи? Или, на языке Л. С. Выготского: какая натуральная форма поведения в какой его культурной форме преодолевается и чем опосредствуется этот переход? Отвечая на эти вопросы, приходится констатировать, что содержание задачи состоит в освоении технического устройства и построении на этой основе алгоритма операций. Распредмечивание, моделирование, мысленный эксперимент, т. е. то, что могло бы связывать выстраиваемый способ действия с таким прототипом, как научно-познавательная деятельность, оказывается редуцированным к построению ориентировочной основы практического действия.
При этом схема эксперимента Л. В. Берцфаи остается несомненно удачной методической находкой, позволяющей четко дифференцировать ориентацию на освоение способа и ориентацию на достижение частного результата. Мы полагали, что методика может быть улучшена, если соединить идею опосредствованного (аппаратурного) управления с идеей «живого объекта» (термин Б. Д. Эльконина), который ведет себя в соответствии с присущими ему закономерными внутренними свойствами, что и было реализовано в построенной нами компьютерной методике «Квадрат».
Технически это было сделано следующим образом. На экране компьютера испытуемому предъявлялись два изображения: в левом верхнем углу - исходное состояние объекта преобразования, в правом верхнем углу - целевое. Оба изображения - это четыре квадратика с цифрами, расположенные в границах квадратного периметра и различающиеся взаимным расположением (рис. 1). Перед испытуемым ставилась задача научиться преобразовывать левый квадрат так, чтобы цифры в нем расположились так же, как и в правом, причем сделать это за минимальное число действий.
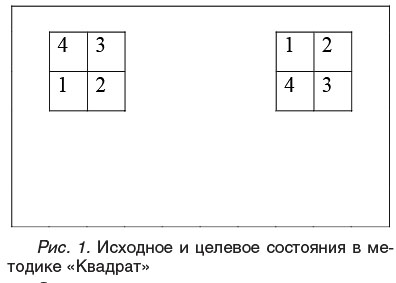
Элементарная операция состояла в «сдвиге»: одним элементом композиции - выделенным квадратом, который окрашивался зеленым при нажатии соответствующей цифры на клавиатуре компьютера, можно «толкать» (нажимая стрелку перемещения курсора) смежный с ним квадрат. Таким способом, например, можно «тройкой» сдвинуть вниз «двойку» или влево «четверку». Сам по себе, не толкая перед собой смежные квадраты, выбранный элемент перемещаться не может: программа компьютера не выполняет таких операций и не дает никаких «ответов», композиция остается неподвижной. Цепочка из операций-ходов представлена на рис. 2.
В ходе решения задачи необходимо было выстроить цепочку «сдвигов», позволяющую из одного квадрата (квадратной композиции из четырех квадратов- элементов) получить другой (квадратную композицию с другим расположением элементов). Последовательность переходов из одного состояния в другое могла быть представлена как цепочка перемещений, дающих циклическую перестановку из 6 и более ходов (см. рис. 2).
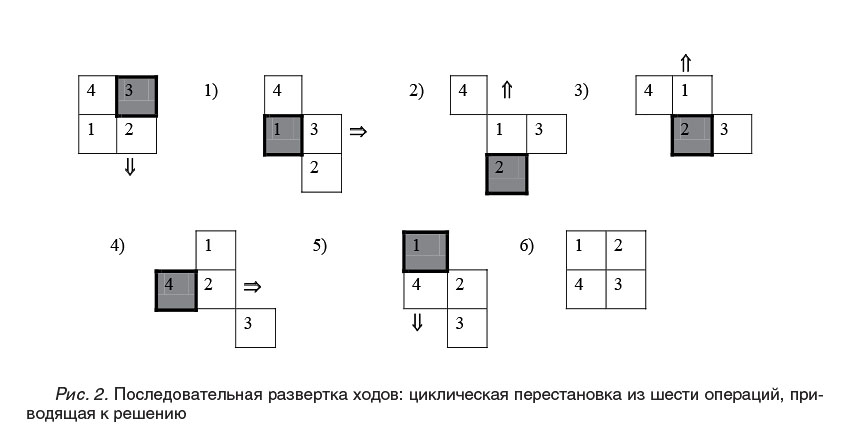
Следует заметить, что изображенная на рисунке развертка преобразований - это схема, граф решения задачи, а вовсе не то, что предстает перед испытуемым на экране компьютера. На экране он видит каждый раз одну из изображенных здесь композиций, которая при манипулировании клавиатурой сменяется (или не сменяется) другой и т. д.
Необходимо объяснить, в чем состояло нормативное решение и на какой общий способ мы рассчитывали. Как и в методике Л. В. Берцфаи, ориентация на поиск способа связывалась нами с отвлечением от решения поставленной частной задачи. Переформулирование конкретнопрактической задачи в учебную в нашем случае - это поиск способа преобразования одного квадрата в любой другой, а не только в тот, который задан на экране. Это попытка ответить на вопрос: а что с этим можно делать вообще? Но в нашем случае простого соотнесения нажатий клавиш и элементарных перемещений недостаточно. Соотнесение множества получаемых состояний объекта также может ничего не дать, кроме констатации, что все они разные. Сравнить и понять, в каком направлении происходят изменения, можно при соотнесении исходного квадрата - «завершенного гештальта», в котором элементы образуют собранный квадрат, - с каким-то вновь полученным «завершенным гештальтом». Поэтому содержательной единицей обобщенного способа становится получение из одного квадрата другого, что можно делать за четыре хода, если их правильно связать в последовательность. Таким образом, четыре взаимосвязанные операции могут стать единицей преобразования. Для того чтобы стать единицей планирования, они должны обеспечить предвидение, а оно невозможно без осмысления (моделирования) преобразования. А такое осмысление-моделирование, в свою очередь, нуждается в знаковом опосредствовании, в символизации. «... Включение символических функций в операцию, - писал Л. С. Выготский, - ... создает условия для совершенно нового характера связи элементов настоящего и будущего (актуально воспринимаемые элементы настоящей ситуации включаются в одну структурную систему с символически представленными элементами будущего), создает совершенно новое психологическое поле для действия, ведя к появлению функций образования намерения и спланированного заранее целевого действия» [Выготский, 1984, с. 49].
Как показывают полученные нами экспериментальные данные, учет всей последовательности производимых с объектом изменений становится предпосылкой общего способа в том случае, когда удается объединить их в осмысленную единицу действия, а саму эту единицу представить в знаково-символической форме. В этом случае возникает возможность перейти от ретроспективного описания уже произведенных операций к прогностическому представлению будущего преобразования и его предполагаемого результата. Поэтому полноценный анализ объекта и моделирование закономерной единицы его трансформации - логико-психологическое условие построения общего способа.
Для того чтобы представить последовательность изменений в едином образе, отражающем принцип, «механизм» трансформации, необходимо вывести происходящее в особый воображаемый план, где становится возможным «снятие» времени. «... У человека этот план, - пишет П. Я. Гальперин, - выделяется и оформляется в самостоятельный объект, наряду с миром вещей, среди которых или с которыми предстоит действовать. Таким образом, в среду природных вещей вводится новая “вещь” - план человеческого действия.
А с ним и цель в прямом смысле слова, т. е. в качестве того, чего в готовом виде нет и что еще должно быть сделано, произведено» [Гальперин, 1976, с. 146]. Симультанный образ последовательности изменений, в котором координируются все аспекты происходящей трансформации в соответствии с нашими представлениями, выступает в функции идеального предмета, отражающего механизм преобразований объекта. Этот механизм, будучи однажды построен, обеспечивает удержание множественности состояний объекта и многоаспектности его трансформаций как бы «автоматически», связывая воздействие на объект с соответствующей трансформацией как бы напрямую, т. е. без рассмотрения разворачивающейся каждый раз цепочки причинноследственных связей в последовательности фрагментарных изменений.
В экспериментах принимали участие 49 учащихся V классов лицея № 9 г. Волгограда (эксперимент проводился М. В. Ма- роковой в рамках диссертационного исследования [Марокова, 2010]). При этом 16 из них выявили закономерность и построили обобщенный способ действия. Главная особенность решения задачи этими испытуемыми - генез знакового опосредствования в ходе преобразований, что позволило им построить (смоделировать) идеальную предметность действия. В построении обобщенного способа действия можно было выделить следующие фазы: натурального оперирования, непосредственных преобразований, знакового опосредствования.
Фаза натурального оперирования
С а ш а Г.: «Если мы нажмем “3” и “=>”, тройка толкнет двойку вправо. Если так толкать, они сдвигаются, а если просто, ну вот - “3” и “<= “, то нет».
А р т е м К.: «Нажимаешь цифру и двигаешь ее в ту, которая рядом».
Далее испытуемые были заняты уже собственно преобразованиями объекта и описывали происходящее не на языке «нажатий» (операций), а на языке преобразований.
Фаза непосредственных преобразований
К о л я Г.: «Я вот делаю и смотрю: у меня уже такой квадрат получился, но не такой, другой. Сейчас еще какой-нибудь .».
М а к с и м Д.: «Когда быстро надо изменять, надо вот четыре вбок, четыре вниз. Но все время четверкой нельзя, он разъединяется и тогда ничего не выходит».
О л я П.: «Можно долго гнать четверкой тройку или. двойку. Но лучше далеко не уходить. Потом все равно возвращаться надо».
После установления границ возможных преобразований некоторые из испытуемых этой группы сосредоточились на выделении границ преобразований целесообразных. Элементы квадрата больше не перемещались по всему полю, действия были сосредоточены на опробовании возможностей получить из исходного квадрата какой-то другой квадрат. В большинстве случаев преобразования сопровождались комментариями и демонстрацией экспериментатору происходящего на экране, а также сообщениями ему своих намерений.
К о л я Г.: «Я здесь как делаю: четверкой вбок, потом ей вниз, потом единицей назад сюда, потом двойкой вверх, вот у меня новый квадрат получился».
О л я П.: «Я по такому принципу: сначала все поменяю, но однушку поставлю как надо, потом опять все поменяю и другую цифру поставлю.». В данном случае «все поменяю» описывает циклическую перестановку, после которой одна из цифр встает на требуемое место - как в целевой композиции.
Фаза знакового опосредствования
Наконец, шестеро из этой группы пришли к построению «идеализованного предмета», увидели в преобразовании «движение по кругу». Этот принцип решения, основанный на распредмечивании нашего замысла, демонстрировался экспериментатору.
Ж е н я А.: «Посмотрите, здесь вот так получается, они же друг за другом ходят!».
Раскрытие идеи предмета сопровождалось проявлениями «ага-переживаний», что выступало для нас дополнительным симптомом «квазиоткрытия».
В о в а Р.: «Я понял! Понял! Они же вот так. Они же по кругу!»
Если участник эксперимента приходил к образу кругового движения, экспериментатор просил его нарисовать на бумаге и подробно разъяснить, что именно имеется в виду.
Заметим, что образ круга прямо противоречит внешней форме объекта - квадрату, а построение этого образа по сути и есть знаковое опосредствование решения задачи. Обратим внимание на особенность знакового опосредствования, которую было чрезвычайно важно уловить в эксперименте: в знаково-символических средствах действие не просто фиксируется, оно в них строится. Здесь замысел, представляемый в знаково-символической форме, «вбрасывается» в ситуацию и апробируется в ней. «Движение по кругу» - это, конечно же, фиксация некоторого опыта, но не в этом основной смысл образа круга. Его смысл - в «овладении собственным мышлением». По Л.С. Выготскому, «мысль совершается в слове, а не выражается только в нем» [Выготский, 1982, с. 162].
Литература
- Агеев В. В., Давыдов В. В., Рубцов В.В. Опробование как механизм построения совместных действий // Психологический журнал. 1985. № 4.
- Аршавина Л. И. Развитие аналитических компонентов мышления у младших школьников при различных типах обучения: Автореф. дис. … канд. психол. наук. Киев, 1982.
- Берцфаи Л. В. Формирование двигательного навыка в условиях практической и учебной задачи // Вопросы психологии. 1963. № 4.
- Берцфаи Л. В. Опыт построения методики диагностики учебной деятельности младших школьников // Диагностика учебной деятельности и интеллектуального развития детей: Сб. науч. тр. / Под ред. Д. Б. Эльконина, А. Л. Венгера. М., 1981.
- Выготский Л. С. Собрание сочинений: В 6 т. Т. 1. М., 1982.
- Выготский Л. С. Собрание сочинений: В 6 т. Т. 2. М., 1982.
- Выготский Л. С. Собрание сочинений: В 6 т. Т. 6. М., 1984.
- Гальперин П. Я. Введение в психологию. М., 1976.
- Гузман Р. Я. Роль моделирования совместной деятельности в решении учебных задач // Вопросы психологии. 1980. № 3.
- Давыдов В.В. Теория развивающего обучения. М., 1996.
- Зак А. З. Диагностика теоретического мышления у младших школьников // Психологическая наука и образование. 1997. № 2.
- Зак А. З. Диагностика интеллектуального развития выпускников начальной школы как оценка рисков обучения в основной школе // Психологическая наука и образование. 2009. № 2.
- Марокова М. В. Формы, уровни и динамика планирующей функции мышления у младших подростков: Автореф. дисс. … канд. психол. наук. М., 2010.
- Рякина С. В. О возможностях активного формирования у младших школьников содержательного анализа (в связи с проблемой использования методики «Кубики Кооса») // Развитие психики школьников в процессе учебной деятельности / Под ред. В. В. Давыдова (отв. ред.), Т. А. Матис. М., 1983.
- Федекин И. Н. Новый метод диагностики сформированности действия планирования // Вестник Международной Ассоциации «Развивающее обучение». 2000. № 7.
Информация об авторах
Метрики
Просмотров web
За все время: 3467
В прошлом месяце: 35
В текущем месяце: 9
Скачиваний PDF
За все время: 1895
В прошлом месяце: 10
В текущем месяце: 6
Всего
За все время: 5362
В прошлом месяце: 45
В текущем месяце: 15