Моделирование и анализ данных
2022. Том 12. № 4. С. 67–84
doi:10.17759/mda.2022120405
ISSN: 2219-3758 / 2311-9454 (online)
Всестороннее рассмотрение математических понятий как методический приём
Аннотация
Статья продолжает цикл ([1]-[4], [8]-[11]) методических разработок авторов. В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.
Общая информация
Ключевые слова: высшее образование, методика преподавания, методика преподавания математики, аналитическая геометрия, геометрия, кривая , эллипс, преобразование, Экстремальные задачи
Рубрика издания: Методика преподавания
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2022120405
Получена: 07.11.2022
Принята в печать:
Для цитаты: Куланин Е.Д., Степанов М.Е. Всестороннее рассмотрение математических понятий как методический приём // Моделирование и анализ данных. 2022. Том 12. № 4. С. 67–84. DOI: 10.17759/mda.2022120405
Полный текст
Введение
На факультете информационных технологий МГППУ изучение математики проводится во многом по классической форме, выработанной отечественной высшей школой. Это касается, как набора изучаемых предметов, так и их содержания. Естественно, что каждый предмет имеет свою специфику и присущий только ему круг понятий. В то же время есть и понятия, которые являются центральными сразу для нескольких предметов. Например, понятие функции, так или иначе, рассматривается в теории множеств, математической логике, математическом анализе, комплексном анализе, теории дифференциальных уравнений, теории уравнений в частных производных, а также в других математических курсах, например, связанных с задачами оптимизации.
Преподаватель должен учитывать это обстоятельство и постоянно иметь в виду, что, преподавая свой предмет, он может дополнительно объяснить студентам, в чём состоит специфика именно изучаемого в данном предмете вида функций и в чём его отличие от других видов функций. Можно предположить, что подобные экскурсы в смежные математические курсы позволяют повышать культуру математического мышления студентов-математиков.
Очевидно, что пока речь шла только о благих пожеланиях без конкретных соображений о том, какие вопросы нужно затронуть преподавателю. Для эффективного использования подобного подхода нужна разработанная методика, направленная на установление внутренних связей между различными курсами математического цикла [Степанов, 2021].
В советское время разработкой методик занимались и высшие учебные заведения, и специализированные научные учреждения. Конечно, это в первую очередь относилось к среднему образованию, но и высшее образование попадало на соответствующую орбиту. Этот, несомненно, положительный факт обеспечивал хорошую проработку методических материалов. Была в подобной работе и отрицательная сторона. Многие методики, направленные на изучение определённой темы, руководители образования делали обязательными для всех преподавателей. Конечно, такое принуждение являлось ошибочным. Любая методика должна рассматриваться как полезный инструмент обучения, но вопрос о её применении в тех или иных случаях должен решаться преподавателем. Именно на возможность использования их методических разработок надеются авторы статьи. Не исключено, что их разработки окажут помощь кому-нибудь из их коллег.
Естественно, что и кроме понятия функции имеется целая группа важных понятий, появляющихся в математических курсах повсеместно. Речь идёт о действительных числах, многочленах, линейных пространствах, геометрических преобразованиях и т. д. Все подобные объекты напрашиваются на их всестороннее рассмотрение с позиций различных математических дисциплин. Но есть возможность выбора в качестве центрального понятия и достаточно специфического объекта, который, если и появляется в учебных курсах, то всего лишь на их периферии. В данной статье авторы как раз и рассматривают круг вопросов, связанных с подобным понятием.
Целями построения всестороннего рассмотрения второстепенных понятий являются
Демонстрация того факта, что математические теории пересекаются не только в точках первостепенной важности.
Демонстрация того, что на первый взгляд утерявшие актуальность математические понятия связаны с кругом достаточно современных идей.
Построение примера конкретной методики разностороннего рассмотрения некоторых математических понятий и связанных с ними объектов.
Рассматриваемым в статье центральным понятием является эллипс Штейнера, введённый в геометрию в девятнадцатом веке Якобом Штейнером. Поскольку эллипс Штейнера – геометрическое понятие, то важное значение при его рассмотрении являются образы. Вопрос об использовании образов математических понятий представляется авторам статьи весьма важным [2 – 4]. По этой причине в статье будут приведены программы на языке программирования Small Basic, которые позволяют строить соответствующие образы на экране компьютера, в том числе видеть их изменение в динамике.
Перейдём, наконец, к рассмотрению вопросов, связанных с эллипсом Штейнера. Изложение отдельных вопросов будет проводиться в различных формах. Речь идёт либо о постановке совокупности задач, решение которых позволяет освоить соответствующий материал, либо о последовательном описании идей и методов, используемых в изучаемой теме. Возможно и сочетание этих форм изложения.
Определение эллипса Штейнера основано на использовании аффинных преобразований. С их изучения мы и начнём. При этом следует отметить, что соответствующие вопросы изучаются в курсе аналитической геометрии.
Аффинные преобразования плоскости
Аффинные преобразования являются частным видом геометрических преобразований плоскости.
В данной статье мы будем использовать то обстоятельство, что любое геометрическое преобразование плоскости обязательно является непрерывным и взаимно однозначным отображение плоскости на себя.
Аффинным называется геометрическое преобразование плоскости, при котором любая прямая переходит в прямую [Яглом, 1962].
Задание 1. Доказать, что прямая AB, проходящая через точки декартовой плоскости с координатами A (x_1; y_1 ) и B (x_2; y_2 ), описывается параметрическими уравнениями
x= x_1+t∙(x_2- x_1);
y= y_1+t∙(y_2- y_1).
Указание. Рассмотреть вектор AB (x_2- x_1; y_2- y_1) и показать, что концы коллинеарных ему векторов, исходящих из точки A заметают прямую AB.
Задание 2. Доказать, что преобразование декартовой плоскости, заданное формулами
u= a_11∙x+ a_12∙y+ c_1,
v= a_21∙x+ a_22∙y+ c_2
является аффинным преобразованием.
Указание. Пусть точки A (x_1; y_1 ) и B (x_2; y_2 ) при соответствующем преобразовании переходят в точки A_1 (u_1; v_1 ) и B_1 (u_2; v_2 ). Тогда прямая AB переходит в прямую A_1 B_1 .
Задание 3. Какие ограничения на параметры a_11,a_12, a_21,a_22 накладывает условие взаимной однозначности отображения из предыдущего задания.
Указание. С помощью констант c_1 и c_1 задаётся параллельный перенос плоскости. Геометрическое преобразование, задаваемое матрицей ‖a_ij ‖ должно быть обратимым, то есть определитель этой матрицы должен отличаться от нуля.
Задание 4. Доказать, что при аффинном преобразовании параллельные прямые переходят в параллельные.
Указание. Показать, что допущение пересечения образов двух параллельных прямых приводит к противоречию с взаимной однозначностью аффинного преобразования.
Задание 5. Доказать, что при аффинном преобразовании сохраняется отношение длин отрезков, лежащих на одной прямой на параллельных прямых.
Указание. Использовать формулу из задания 2.
Задание 6. Доказать, что при аффинном преобразовании декартовой плоскости единичный квадрат переходит в параллелограмм (рис. 1). Таким образом, сетка единичных квадратов при аффинном преобразовании переходит в сетку из параллелограммов.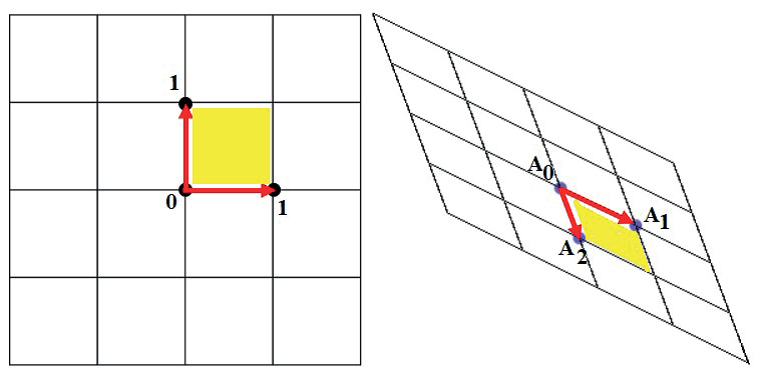
Рис. 1
Задание 7. На декартовой плоскости указаны три точки A_0 (x_0; y_0 ),A_1 (x_1; y_1 ),〖 A〗_2 (x_2; y_2 ), которые задают параллелограмм, изображённый на рис. 1. Получить формулы аффинного преобразования, описанного в предыдущем задании.
Указание. Рассматриваемое преобразование переводит базисные вектора декартовой плоскости в вектора A_0 A_1 и A_0 A_2. Таким образом, точка (x;y) переходит в точку, которая является концом вектора x∙A_0 A_1+y∙A_0 A_2. Вычислив координаты указанной точки получим уравнения аффинного преобразования.
u= x_0+x∙(x_1- x_0 )+y∙(x_2- x_0);
v= y_0+x∙(y_1- y_0 )+y∙(y_2- y_0).
Задание 8. Написать программу на языке Small Basic, которая строит сетку из параллелограммов.
Решение. Текст программы:
GraphicsWindow.Width = 600
GraphicsWindow.Height = 500
x0 = 300
y0 = 250
x1 = 380
y1 = 230
x2 = 350
y2 = 200
GraphicsWindow.FillEllipse(x0 - 5, y0 - 5, 10, 10)
GraphicsWindow.FillEllipse(x1 - 5, y1 - 5, 10, 10)
GraphicsWindow.FillEllipse(x2 - 5, y2 - 5, 10, 10)
For x = -2 To 2 Step .01
For y = -2 To 2 Step 1
u = x0 + (x1 - x0)*x + (x2 - x0)*y
v = y0 + (y1 - y0)*x + (y2 - y0)*y
GraphicsWindow.SetPixel(u, v,"")
EndFor
EndFor
For x = -2 To 2 Step 1
For y = -2 To 2 Step .01
u = x0 + (x1 - x0)*x + (x2 - x0)*y
v = y0 + (y1 - y0)*x + (y2 - y0)*y
GraphicsWindow.SetPixel(u, v,"")
EndFor
EndFor
Выбор точек A_0 (x_0; y_0 ),A_1 (x_1; y_1 ),〖 A〗_2 (x_2; y_2 ) определяет характер аффинного преобразования. В частности, аффинное преобразование, сохраняющее расстояние между точками, называется движением.
Задание 9. Доказать, что в случае когда точка А0 совпадает с началом координат О, а вектора ОА1 и ОА2 имеют единичную длину и перпендикулярны, преобразование является поворотом. Вывести формулы, описывающие поворот.
Указание. Пусть единичный вектор ОА1 наклонён к оси абсцисс под углом φ (этот угол отсчитывается против часовой стрелки). Тогда вектор ОА1 имеет координаты 〖(cos〗φ;sin〖φ)〗. Пусть вектор ОА2 повёрнут на угол 90º, а, значит, имеет координаты (-sin〖φ 〖; cos〗φ)〗. При этих условиях формула из задания 7 превращается в формулу поворота на угол φ.
u= x∙cosφ-y∙sinφ;
v= x∙sinφ+y∙cosφ.
Задание 10. Написать программу на языке Small Basic, которая строит график функции в наклонной системе координат (рис. 2).
Рис. 2
Решение. Текст программы:
GraphicsWindow.Width = 600
GraphicsWindow.Height = 600
pi = Math.Pi
xekr0 = 300
yekr0 = 300
ed = 50
u0 = pi/6
a11 = ed* Math.Cos(u0)
a12 = -ed* Math.Sin(u0)
a21 = -ed* Math.Sin(u0)
a22 = -ed* Math.Cos(u0)
For x = -8 To 8 Step 1
For y = -8 To 8 Step .01
u = xekr0 + a11* x + a21* y
v = yekr0 + a21* x + a22* y
GraphicsWindow.SetPixel(u,v,"")
EndFor
EndFor
For x = -8 To 8 Step 0.01
For y = -8 To 8 Step 1
u = xekr0 + a11* x + a21* y
v = yekr0 + a21* x + a22* y
GraphicsWindow.SetPixel(u,v,"")
EndFor
EndFor
u1 = xekr0 + a21* (-8)
v1 = yekr0 + a22* (-8)
u2 = xekr0 + a21* 8
v2 = yekr0 + a22* 8
GraphicsWindow.DrawLine(u1,v1,u2,v2)
u1 = xekr0 + a11* (-8)
v1 = yekr0 + a21* (-8)
u2 = xekr0 + a11* 8
v2 = yekr0 + a21* 8
GraphicsWindow.DrawLine(u1,v1,u2,v2)
GraphicsWindow.FillEllipse(xekr0-5,yekr0-5,10,10)
GraphicsWindow.BrushColor = "red"
For x = -5 To 5 Step 0.001
y = (x + 2)*(x + 1)*(x - .5)*(x - 1.5) - 2
u = xekr0 + a11* x + a21* y
v = yekr0 + a21* x + a22* y
GraphicsWindow.FillEllipse(u-2,v-1,4,4)
EndFor
Задание 11. Сжатием с коэффициентом k к оси абсцисс называется преобразование, при котором все вертикальные расстояния умножаются на этот коэффициент, а горизонтальные расстояния не меняются. Докажите, что это преобразование является аффинным. Выведите соответствующие формулы.
Указание. Формулы сжатия к оси абсцисс имеют вид: u=x;v=k∙y. Очевидно, что эти формулы являются частным видом аффинных преобразований. Сетка единичных квадратов переходит в сетку прямоугольников (рис. 3).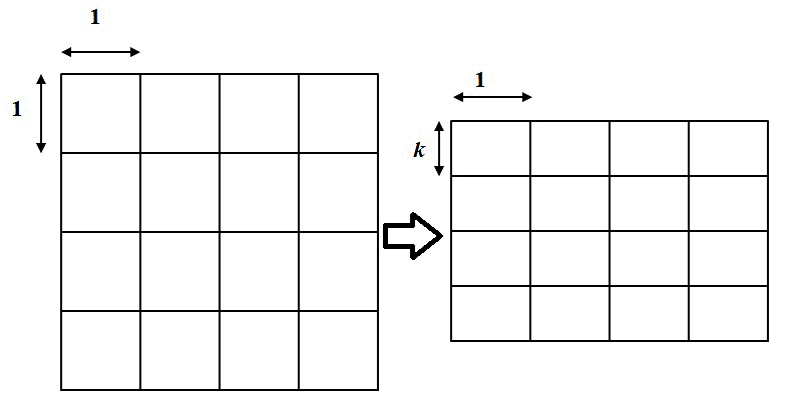
Рис. 3
Задание 12. Доказать, что существует аффинное преобразование, которое любые три точки А, В, С, не лежащие на одной прямой, переводит в произвольно выбранные точки А1, В1, С1, также не лежащие на одной прямой.
Указание. В задании 7 объясняется, как получить формулы аффинных преобразований, переводящих единичный квадрат как в точки А, В, С (обозначим это преобразование через φ), так и в точки А1, В1, С1 (обозначим это преобразование через ψ). Любое аффинное преобразование имеет обратное, которое тоже является аффинным. Преобразование φ^(-1)∙ψ является искомым.
ЭЛЛЛИПС КАК СЖАТАЯ ОКРУЖНОСТЬ И ЭЛЛИПТИЧЕСКИЙ ПОВОРОТ. Определение синуса и косинуса тесно связано с операцией, имеющей простой механический смысл. Пусть на плоскости задана декартова система координат и окружность единичного радиуса с центром в начале координат. Положение вращающегося единичного радиус-вектора определяется углом, который он образует с положительным направлением оси абсцисс. Этот угол измеряться в радианах и может включать в свой состав по нескольку оборотов. Пусть угол наклона единичного радиуса вектора равен φ, тогда синусом угла φ называется абсцисса конца радиуса-вектора, а косинусом угла φ – соответствующая ордината (рис. 4).
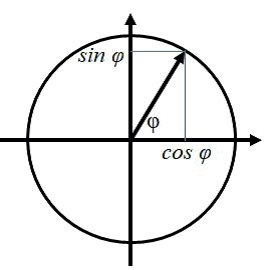
Задание 13. Получить параметрические уравнения окружности радиуса r с центром в начале координат. Параметром должно быть значение угла наклона радиуса.
Пояснение. Хотя формулы x=r∙cos〖φ;y=r ∙sinφ 〗 очевидны, следует иметь ввиду, что они описывают переход от полярной системы координат к декартовой.
Задание 14. Используя тот факт, что поворот на угол φ в полярной системе координат описывается уравнениями r_1=r; α_1= α+ φ и формулы поворота в декартовой системе координат, получить тригонометрические формулы синуса и косинуса суммы и разности углов.
Задание 15. Положение точки на окружности радиуса r определяется углом α. Положение этой же точки после поворота на угол φ определяется углом α_1= α+ φ. Написать программу, которая строит на экране правильный многоугольник, вписанный в окружность (рис. 5).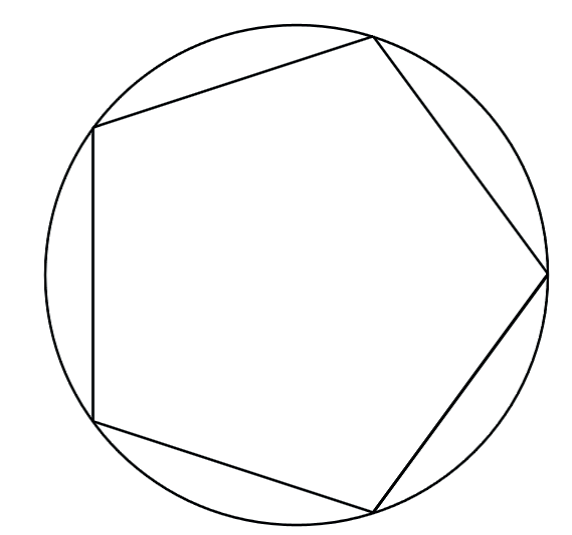
Рис. 5
Решение. Текст программы:
x0 = 320
y0 = 220
r = 200
pi = Math.Pi
n = 5
GraphicsWindow.DrawEllipse(x0-r,y0-r,2*r,2*r)
For u = 0 To 2*pi Step 2*pi/n
u1 = u + 2*pi/n
x1 = x0 + r*Math.Cos(u)
y1 = y0 + r*Math.Sin(u)
x2 = x0 + r*Math.Cos(u1)
y2 = y0 + r*Math.Sin(u1)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
EndFor
Задание 16. Написать программу, создающую анимационный эффект вращения правильного многоугольника.
Решение. Текст программы:
x0 = 320
y0 = 220
r = 200
pi = Math.Pi
n = 7
For du = 0 To 6*pi Step pi/100
GraphicsWindow.DrawEllipse(x0-r,y0-r,2*r,2*r)
For u = 0 To 2*pi Step 2*pi/n
u1 = u + 2*pi/n
x1 = x0 + r*Math.Cos(u+du)
y1 = y0 + r*Math.Sin(u+du)
x2 = x0 + r*Math.Cos(u1+du)
y2 = y0 + r*Math.Sin(u1+du)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
EndFor
Program.Delay(100)
GraphicsWindow.Clear()
EndFor
Одним из определений эллипса является следующее: эллипс – сжатая окружность. Обычно используется сжатие окружности радиуса a с центром в начале координат к оси абсцисс с коэффициентом k. При этом горизонтальный диаметр окружности переходит в горизонтальный диаметр эллипса длины 2a, вертикальный диаметр окружности переходит в вертикальный диаметр эллипса длины 2b=k∙2a.
Задание 17. Вывести параметрическое уравнение эллипса с полуосями a и b.
Указание. Окружность описывают формулы x=a∙cos〖φ;y=a ∙sinφ 〗. При сжатии к оси абсцисс первая координата останется неизменной, а вторая будет умножена на коэффициент сжатия k. Таким образом, будут получены параметрическое уравнение эллипса: =a∙cos〖φ;y=b ∙sinφ 〗.
Задание 18. Доказать, что уравнение эллипса имеет вид x^2/a^2 + y^2/b^2 =1.
Указание. Нужно подставить в уравнение параметрические выражения для x и y.
Традиционным способом определения эллипса является его свойство, связанное с так называемыми фокусами эллипса. Оно состоит в следующем.
Рассмотрим эллипс, уравнение которого имеет вид x^2/a^2 + y^2/b^2 =1. Тогда точки F_1 и F_2, лежащие на оси абсцисс и отстоящие от начала координат на расстояние c= √(a^2- b^2 ), называются фокусами эллипса (рис. 6).
Задание 19. Доказать, что сумма расстояний от произвольной точки М, лежащей на эллипсе, до фокусов постоянна и равна 2а, то есть F_1 M+ F_2 M=2a.
Рис. 6
Указание. Общий ход доказательства аналогичен выводу канонического уравнения эллипса, который можно найти в любом учебнике аналитической геометрии [Александров, 1979]. Пусть точка M на эллипсе имеет координаты (a∙cos〖φ;b ∙sinφ 〗). Тогда F_1 M+ F_2 M можно записать в виде √(〖(c+a∙cos〖φ)〗〗^2+ b^2∙〖sin〗^2 φ)+ √(〖(c-a∙cos〖φ)〗〗^2+ b^2∙〖sin〗^2 φ) = 2a. Чтобы доказать это равенство следует второй корень перенести вправо, возвести обе части уравнения в квадрат, выполнить сокращения, уединить оставшийся корень, снова возвести в квадрат и сократить всё, что можно.
Мы уже видели, как можно вращать окружность, смещая все её точки на один и тот же угол. Если параллельно рассматривать эллипс, который получен из исходной окружности с помощью сжатия, то при вращении окружности точки эллипса также будут двигаться по эллипсу, не покидая его. Фактически мы приходим к преобразованию, которое называется эллиптическим поворотом. Эллиптический поворот можно повсеместно наблюдать в быту. Дело в том, что вращающееся колесо под углом наблюдатель воспринимает как эллипс.
Пусть на эллипсе находится точка M (a∙cos〖α;b ∙sinα 〗). Тогда повороту окружности на угол φ будет соответствовать перемещение точки М в точку M1 (a∙cos〖(α+ φ);b ∙sin〖(α+ φ〗 〗)).
Задание 20. Написать программу, создающую анимационный эффект вращения пирамиды.
Решение. Текст программы:
pi=3.14159
x0 = 320
y0 = 320
r = 100
k = .3
h = 200
x3 = x0
y3 = y0 - h
For du = 0 To 6*pi Step pi/100
GraphicsWindow.DrawEllipse(x0 - r, y0 - k*r, 2*r, 2*r*k)
For u=.5 To 2*pi+.5 Step 2*pi/5
x1 = x0 + r*Math.Cos(u+du)
y1 = y0 + k*r*Math.Sin(u+du)
x2 = x0 + r*Math.Cos(u+2*pi/5+du)
y2 = y0 + k*r*Math.Sin(u+2*pi/5+du)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
GraphicsWindow.DrawLine(x1,y1,x3,y3)
EndFor
Program.Delay(100)
GraphicsWindow.Clear()
EndFor
Любые два взаимно перпендикулярных диаметра окружности переходят в два диаметра эллипса (вообще говоря, не перпендикулярных). Такие диаметры эллипса называются сопряжёнными (рис. 7).
Рис. 7
Задание 21. Доказать, что середины хорд, параллельных какому-то диаметру эллипса лежат на диаметре, сопряжённом к исходному.
Указание. Нужно доказать следующую теорему, связанную с окружностью: «Доказать, что середины хорд, параллельных какому-то диаметру окружности лежат на диаметре, перпендикулярном к исходному». Затем следует использовать свойства аффинных преобразований.
Определение эллипса Штейнера
Если подвергнуть кривую второго порядка аффинному преобразованию, она снова перейдёт в кривую второго порядка. Это следует из того, что в формулы аффинного преобразования входят либо переменные в первой степени, либо константы, и по этой причине при замене переменных в кривой второго порядка снова будет получена кривая второго порядка.
Все невырожденные кривые второго порядка распадаются на три класса: параболы, гиперболы и эллипсы. При этом только эллипсы расположены в ограниченных областях плоскости, а аффинные преобразования переводят ограниченные области в ограниченные.
Таким образом, если подвергнуть окружность не только сжатию, но и любому другому аффинному преобразованию, она превратится в эллипс.
Задание 22. Доказать, что в случае, когда аффинное отображение переводит окружность ω1 в эллипс ε1, это преобразование переводит в эллипс ε2 и любую другую окружность ω2. При этом эллипсы ε1 и ε2 можно совместить параллельным сдвигом, если окружности ω1 и ω2 равны между собой. Если же размеры окружностей различны, то эллипсы ε1 и ε2 гомотетичны.
Указание. Как было показано выше ε1 и ε2 являются эллипсами. Проводя через их центры параллельные прямые и используя сохранение отношений длин параллельных отрезков, можно доказать предлагаемое утверждение.
Теперь можно дать определение эллипса Штейнера, вернее двух эллипсов Штейнера – вписанного и описанного [Прасолов, 2006].
Пусть заданы правильный треугольник А0В0С0 и произвольный треугольник АВС. Существует аффинное преобразование, которое переводит вершины первого треугольника в соответствующие вершины второго. Образ вписанной в правильный треугольник окружности называется вписанным эллипсом Штейнера. Образ описанной вокруг правильного треугольника окружности называется описанным эллипсом Штейнера.
Задание 23. Выяснить, в каком отношении точки касания вписанного эллипса Штейнера делят стороны треугольника АВС.
Задание 24. Доказать, что вписанный и описанный эллипсы Штейнера гомотетичны. Найти центр гомотетии и коэффициент гомотетии (рис. 8).
Рис. 8
Множество треугольников, связанных с эллипсом Штейнера фиксированной формы
Определение эллипса Штейнера даёт способ построения этого эллипса для любого произвольно выбранного треугольника. Рассмотрим иную задачу, которая заключается в следующем.
Задание 25. Построить треугольник, эллипс Штейнера которого имеет заданный коэффициент сжатия k= b/a.
Указание. Нужно подвергнуть правильный треугольник сжатию с коэффициентом сжатия k= b/aк некоторой прямой, например, к одной из высот этого треугольника. Приведём программу, осуществляющую соответствующее построение, результат работы которой можно увидеть на рис. 9.
Текст программы:
pi = Math.Pi
x0 = 320
y0 = 220
r0 = 200
r1 = r0/2
k = 1/3
x1 = x0 + r0* Math.Cos(0)
y1 = y0 + k*r0* Math.Sin(0)
x2 = x0 + r0* Math.Cos(2*pi/3)
y2 = y0 + k*r0* Math.Sin(2*pi/3)
x3 = x0 + r0* Math.Cos(4*pi/3)
y3 = y0 + k*r0* Math.Sin(4*pi/3)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
GraphicsWindow.DrawLine(x2,y2,x3,y3)
GraphicsWindow.DrawLine(x3,y3,x1,y1)
GraphicsWindow.DrawEllipse(x0-r0,y0-k*r0,2*r0,2*k*r0)
GraphicsWindow.DrawEllipse(x0-r1,y0-k*r1,2*r1,2*k*r1)
GraphicsWindow.DrawLine(x0-r0,y0,x0+r0,y0)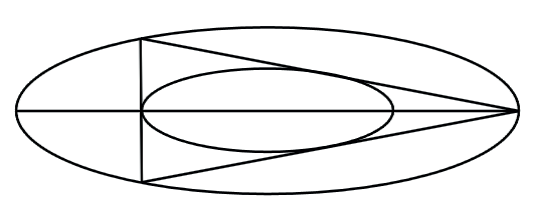
Рис. 9
Задание 26. Указать способ построения любых других треугольников, эллипс Штейнера которых имеет ту же форму (рис. 10).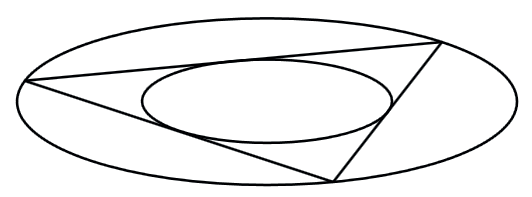
Рис. 10
Указание. Нужно использовать эллиптический поворот образа правильного треугольника. Эллипс остаётся неизменным, а треугольник, для которого этот эллипс является эллипсом Штейнера, скользит вокруг него.
Текст программы для построения рисунка 10:
pi = Math.Pi
x0 = 320
y0 = 220
r0 = 200
r1 = r0/2
k = 1/3
u = 1.3
x1 = x0 + r0* Math.Cos(u)
y1 = y0 + k*r0* Math.Sin(u)
x2 = x0 + r0* Math.Cos(u+2*pi/3)
y2 = y0 + k*r0* Math.Sin(u+2*pi/3)
x3 = x0 + r0* Math.Cos(u+4*pi/3)
y3 = y0 + k*r0* Math.Sin(u+4*pi/3)
GraphicsWindow.DrawLine(x1,y1,x2,y2)
GraphicsWindow.DrawLine(x2,y2,x3,y3)
GraphicsWindow.DrawLine(x3,y3,x1,y1)
GraphicsWindow.DrawEllipse(x0-r0,y0-k*r0,2*r0,2*k*r0)
GraphicsWindow.DrawEllipse(x0-r1,y0-k*r1,2*r1,2*k*r1)
Задание 27. Написать программу, создающую анимационный эффект вращения эллипса Штейнера.
Точки с целочисленными координатами на эллипсе Штейнера
Решим ещё одну задачу, связанную с эллипсом Штейнера.
Задание 28. Указать способ получения треугольника с целочисленными координатами вершин и вывести уравнение эллипса Штейнера этого треугольника. Построить соответствующее изображение.
Решение. Рассмотрим каноническое уравнение эллипса с неизвестными пока полуосями а и b. Пусть точка МС с целочисленными координатами (x_1;y_1) лежит на эллипсе, и её положение определяется углом α. Тогда x_1=a∙cosα, y_1=b∙sinα. Таким образом, cos〖α= x_1/a〗 и sin〖α= y_1/b〗.
Точка MA с координатами (x_1;y_1) лежит на эллипсе, и её положение определяется углом α+ 2π/3. Следовательно, x_2= -1/2 a∙cos〖α- √3/2 a ∙sinα 〗 и y_2= -1/2 b∙cos〖α+ √3/2 b ∙sinα 〗. После замены cos〖α= x_1/a〗 и sin〖α= y_1/b〗 получим формулы x_2= -x_1/2- y_1∙√3/2∙a/b и y_2= -y_1/2+ x_1∙√3/2∙b/a. Чтобы обеспечить целочисленность x_1 и y_1, нужно нейтрализовать √3. Для этого достаточно выбрать a и b так, чтобы их отношение равнялось √3. Кроме того, a^2 должно быть целым числом. В этом случае уравнение эллипса принимает вид x^2/a^2 + (3y^2)/a^2 =1. Поэтому для вычисления a^2 по значениям x_1 и y_1 можно использовать уравнение a^2= x^2+3y^2.
Положим x_1=1 и y_1=3, тогда a^2 = 28. Вычисление координат x_2 и y_2 позволяет получить точку (-5; -1). Наконец для координат x_3 и y_3 аналогичные вычисления дают точку (4; -2).
Эллипс Штейнера и соответствующий треугольник показаны на рис. 11.

Рис.11
Заключение
В статье были рассмотрены вопросы, так или иначе связанные с эллипсами Штейнера. В целом их изучение позволяет несколько с иных позиций посмотреть на аналитическую геометрию. Кроме того, самостоятельное решение предлагаемых задач позволяет повысить математическую культуру студентов.
Тематика, связанная с эллипсами Штейнера, далеко не исчерпана. Авторы продолжают её описание в следующей статье, в которой делается акцент на экстремальных свойствах эллипсов Штейнера.
Литература
- Степанов М. Е. Межпредметные связи в общем курсе высшей математики. Моделирование и анализ данных. Том 11. № 2., 2021. Моделирование и анализ данных. Том 10. № 2., 2020.
- Степанов М. Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. Научный журнал. – 2017.
- Степанов М. Е. Компьютерные технологии как средство приобщения учащегося к математической реальности. Моделирование и анализ данных. Научный журнал. – №1, 2018.
- Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. Том 10. № 2., 2020.
- Яглом И. М., Ашкинузе В. Г. Идеи и методы аффинной и проективной геометрии. Часть I. Аффинная геометрия. М. Государственное учебно-педагогическое издательство министерства просвещения РСФСР. 1962.
- Александров П. С. Курс аналитической геометрии и линейной алгебры. М., Наука, 1979.
- Прасолов В. В. Задачи по планиметрии. М., Издательство МЦИМО, 2006.
- Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
- Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. № 4. С.127-144.
- Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
- Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ дан ных. 2020. Т.11. №1. С.40 - 60.
Информация об авторах
Метрики
Просмотров web
За все время: 231
В прошлом месяце: 18
В текущем месяце: 6
Скачиваний PDF
За все время: 76
В прошлом месяце: 4
В текущем месяце: 2
Всего
За все время: 307
В прошлом месяце: 22
В текущем месяце: 8