Моделирование и анализ данных
2019. Том 9. № 3. С. 32–36
ISSN: 2219-3758 / 2311-9454 (online)
Метод оценки влияния вершин при анализе сетевых структур
Аннотация
Общая информация
Ключевые слова: Анализ сетей, центральность вершины, центральность графа, ключевые вершины
Рубрика издания: Анализ данных
Тип материала: научная статья
Для цитаты: Александрова У.В., Осипова В.А. Метод оценки влияния вершин при анализе сетевых структур // Моделирование и анализ данных. 2019. Том 9. № 3. С. 32–36.
Полный текст
В статье предложен подход к анализу оценки влияния вершин при анализе сетей. Наряду с понятием центральности вершины рассматривается понятие центральности сети. Предлагается в качестве показателя оценки влияния вершины (актора) на топологию сети рассматривать понятие ключевой вершины, а также характеристику, близкую по своей структуре к индексу Банцафа.
ВВЕДЕНИЕ
В последнее время задача анализа различных сложных сетей, в частности исследование их структуры и определение ключевых элементов, становится актуальной и занимает особое место наряду с другими исследованиями сетей. Топология сетей, отражающих взаимодействие вершин, оказывает влияние на принятие решений, связанных с их анализом. Сетевая топология представляется структурой в виде графа, вершинам (акторам, при исследовании социальных сетей) которого соответствуют узлы сети, а рёбрам — физические или информационные связи между вершинами. Различают различные виды сетевых топологий: полносвязная, неполносвязная (может применяться передача данных не напрямую между компьютерами, а через дополнительные узлы), элементарные: шина, звезда, кольцо.
Важной характеристикой сети является понятие центральности вершины. Различные определения центральности сводится к трем основным концепциям [1,5], рассмотренным ниже. Все они определяют некоторую меру, характеризующую важность актора. Наряду с понятием центральности вершины характеристикой сети выступает также понятие центральности самой сети.
В работе предлагается в качестве показателя оценки влияния вершины (актора) на топологию сети рассматривать понятие ключевой вершины, а также характеристику, близкую по своей структуре индексу к Банцафа, основанному на вычислении доли подграфов, в которых вершина является ключевой.
1. ДОСТАТОЧНАЯ ЦЕНТРАЛИЗОВАННОСТЬ СЕТИ И ОЦЕНКА ВЛИЯНИЯ ВЕШИНЫ (АКТОРА)



Рис.1 Граф кольцо

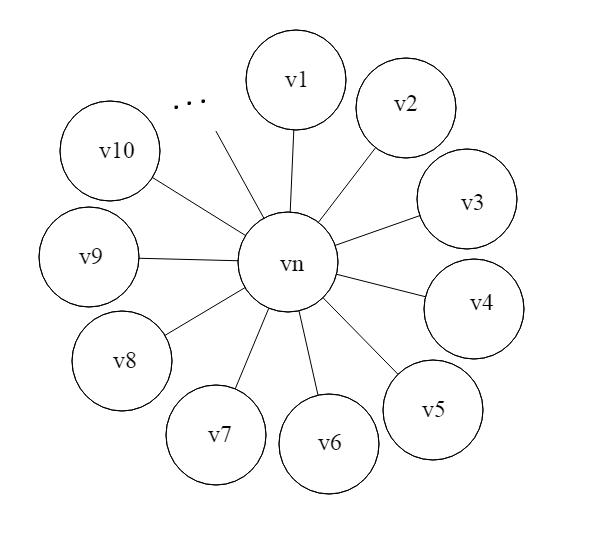
Рис.2 Граф звезда


Рис.3 Граф смешанной топологии сети с 𝒏 = 12 вершинами


Литература
- Freeman L. C. Centrality in social networks. Conceptual clarification // Soc. Networks. 1978/79. V. 1. P. 215-239.
- Leavitt H. J. Some effects of certain communication patterns on group performance // J. Ab-norm. and Soc. Psychology. 1951. V. 46. P. 38-50.
- Bavelas A. A mathematical model for group structure // Human Organization. 1948. V. 7. P. 16-30.
- Алескеров Ф.Т., Хабина Э.Л., Шварц Д.А. Бинарные отношения, графы и коллективные решения. – М.: ФИЗМАТЛИТ, 2017. – 344 с.
- Щербакова Н.Г. Меры центральности в сетях. – Институт вычислительной математики и математической геофизики СО РАН,630090, Новосибирск, 2015. – 13 с.
Информация об авторах
Метрики
Просмотров
Всего: 486
В прошлом месяце: 7
В текущем месяце: 0
Скачиваний
Всего: 300
В прошлом месяце: 6
В текущем месяце: 0