Моделирование и анализ данных
2017. Том 7. № 1. С. 54–94
ISSN: 2219-3758 / 2311-9454 (online)
Некоторые вопросы методики преподавания высшей математики
Аннотация
Общая информация
Ключевые слова: методика преподавания математики, математический анализ, линейная алгебра, дифференциальные уравнения, теория вероятностей, высшее образование
Рубрика издания: Анализ данных
Тип материала: обзорная статья
Для цитаты: Степанов М.Е. Некоторые вопросы методики преподавания высшей математики // Моделирование и анализ данных. 2017. Том 7. № 1. С. 54–94.
Полный текст
1. ВВЕДЕНИЕ
Отношение к методике преподавания математики часто является достаточно прохладным, а иногда и ироничным. Подтверждением этому факту может послужить хорошо известный анекдот, который утверждает, что математики делятся на три непустых множества. Первое составляют творцы, открывающие новые факты и доказывающие собственные теоремы. Во второе множество входят те, кто не способен получать новое знание сам, но может доносить его до других людей - это преподаватели математики. Наконец, третье множество состоит из методистов, то есть лиц, которые не могут открывать новые математические факты, а кроме того неспособны и преподавать.
Отчасти такое отношение можно объяснить свойственной ряду творческих личностей заносчивостью, что тоже можно подтвердить анекдотом. Каждый крупный математик уверен, что все математические теоремы делятся на три непустых множества. Первое составляют неверные утверждения. Во второе множество входят утверждения тривиальные. И, наконец, третье множество состоит из «МОИХ ТЕОРЕМ».
Однако есть и более основательные причины для пренебрежительного отношения к методистам и их методикам. Действительно, часто «методическое творчество» очень напоминает схоластику в её самых неприглядных формах. С другой стороны, всегда были выдающиеся учёные, которые в своей преподавательской деятельности значительное внимание придавали решению чисто методических вопросов. Ограничусь двумя примерами. На мехмате МГУ мне пришлось слушать курс Владимира Игоревича Арнольда «Обыкновенные дифференциальные уравнения» и курс Марка Иосифовича Вишика «Уравнения в частных производных».
Оба лектора не скрывали, что строятся новые курсы, и что идёт их утряска и шлифовка. В. И. Арнольд использовал смелый и необычный приём. После доказательства очередной теоремы он вдруг сообщал аудитории, что в доказательстве содержится ошибка. Это заставляло студентов более внимательно следить за рассуждениями преподавателя.
Что касается М. И. Вишика, то по окончании каждой лекции он обращался к студентам с просьбой сообщить, где они испытали затруднения, и какие детали были им неясны. Все замечания он скрупулёзно записывал. При этом, кстати, возникла довольно забавная ситуация. Один не вполне адекватный студент (множество таких учащихся не только не является пустым, но и становится в наше время всё более мощным) каждый раз задавал вопросы слишком уж элементарного характера, а иногда просто нелепые. Аудитория посмеивалась, а Марк Иосифович разводил руками и иронично пояснял всем: «Товарищ очень интересуется».
Автор данной статьи и в мыслях не имеет намерения сравнивать себя с выдающимися педагогами-математиками, но всё же надеется, что некоторые его соображения, связанные с методикой преподавания математики могут представить некоторый интерес. При этом он знает, что в методике трудно претендовать на новизну и на безусловную правильность подхода к изложению того или иного вопроса. Однако обсуждение некоторых проблем методики может стимулировать педагогическую активность других преподавателей, особенно молодых.
Хочется отметить, что данная статья, возможно, не была бы написана, если бы не проблемы, стоящие перед образованием в настоящее время. Наличие подобных проблем, кажется, готовы признать даже в сферах, осуществляющих управление образованием. В связи с этим отметим, что современная ситуация в образовании характеризуется падением уровня образования в целом и, в частности, что особенно важно для данной статьи, с ухудшением подготовки абитуриентов. Причины этого связаны не только с непродуманными управленческими решениями. Чрезвычайную роль играет также изменение мотивации молодёжи. Отметим ещё и в целом негативное влияние электронных устройств, приводящее к потере не только навыков устного счёта, но и к утрате некоторых жизненно важных интеллектуальных навыков.
Обсуждать всю совокупность перечисленных проблем мы не можем, но обязаны отметить, что эти проблемы усложняют работу преподавателя и в том числе заставляют его искать новые подходы к преподаванию, включая поиск методический.
Но переходя к обсуждению методических проблем, автор невольно вспоминает фантастический рассказ «Какая прелестная школа!...», который написал Ллойд Биггл-младший. В образовании используется телеобучение. Ученики дома смотрят уроки по телевизору, но могут свободно переключаться на любого преподавателя. Учитель, уроки которого смотрит большее число учащихся, является лучшим. По этой причине молодая учительница использует стриптиз. Но рано или поздно ученики поймут, что он никогда не дойдёт до конца. Учительницу ждёт неизбежный крах. Иное дело математик, крепкий профессионал, который прекрасно жонглирует наглядными пособиями и ловко держит кусок мела на носу. У него всегда будет аудитория, пусть и скромная.
Автор статьи надеется, что его критики всё же признают его крепким профессионалом несмотря на неизбежное наличие слабых мест в его методиках.
2. О КОМПЛЕКСЕ ОСНОВНЫХ МЕТОДИЧЕСКИХ ПРОБЛЕМ
Методические проблемы имеют различный характер. Речь может идти как о вопросах весьма общего характера, так и о вопросах частных, хотя и имеющих важное значение. Начнём с рассмотрения некоторых из проблем общего характера.
Первая проблема методического характера, о которой мы будем говорить, непосредственно не связана с трудностями, возникшими в настоящее время, хотя и обостряется из -за них. Речь идёт о важнейшем выборе преподавателя: на что ориентироваться на студента или на предмет?
Поясню суть данной дилеммы реальным конфликтом, произошедшим около десяти лет назад. Незрячие студенты, с которыми у меня сложились доверительные отношения, попросили меня побеседовать с одним из преподавателей, который слишком быстро проговаривал формулы. В результате многие студенты не могли следить за ходом его рассуждений. Я выполнил их просьбу и поговорил с этим преподавателем. В результате он с нескрываемым раздражением ответил мне, поражаясь моей бестолковости: «Слишком детально проговаривая формулы, я не успею вычитать свой курс».
Попытаюсь дать комментарий этой ситуации. Известный философ Иван Ильин в работе «О сопротивлении злу силою» показывает, что единых рецептов решения вопроса, вынесенного в заглавие его книги, не существует. Необходим конкретный анализ, который только и может дать ответ на необходимость применения силы и на степень, условно говоря, необходимой обороны. Мнение же такого великого писателя и мыслителя как Лев Толстой о том, что сила неприемлема никогда и ни при каких обстоятельствах, является неверным. Очевидно, что подобная ситуация имеет место при любых проблемных ситуациях. И если конкретный анализ такой ситуации проведён грамотно, его результаты не могут быть опровергнуты самыми крупными авторитетами.
Рассмотрим вопрос: откуда возникло стремление к слишком скрупулёзному вычитыванию курса? Думается, что оно уместно в рамках университетского образования, когда лекции читают выдающиеся учёные, порой не слишком склонные к педагогической деятельности. Важно и то, что они читают курс сильным студентам. Кроме того, очевидно, что творческими математиками станет только небольшая часть студентов, но именно они и являются целью образовательного процесса. В результате преподаватель пусть и неосознанно становится на следующую точку зрения: я должен озвучить свой курс, и те, кто способен на это, получат возможность овладеть соответствующим материалом. Главной составляющей успеха являются личные усилия студента.
Подобная точка зрения, на наш взгляд, является уязвимой даже в данной конкретной ситуации. На это в частности указывает пример В. И. Арнольда и М. И. Вишика. Но в случаях, когда состав студентов недостаточно силён или же студенты обременены особыми проблемами, например, связанными с их здоровьем, преподаватель должен преодолеть своё преклонение перед предметом как некоей неприкосновенной абстрактной ценностью и обязан повернуться лицом к студентам, чтобы помочь им.
Впрочем, такая точка зрения может вызвать осуждение ревнителей высокой науки, ибо математика для них святей не только студента, но и человека вообще. Хотелось бы показать, к какому интересному результату достаточно часто приводит такой выбор. От начала до конца занятий преподаватель находится лицом к доске и спиной к аудитории. При эт ом никаких претензий к нему предъявлено не будет - он вычитывает курс. В то же время в адрес нашей позиции возможны обвинения, в том числе и чисто бюрократического порядка: «Ну, не вычитывает он всего, что можно вычитать, Ну, не успевает. Со студентами возится во вред учебному процессу. А подать его сюда! Немедля повернись к доске передом, к студентам задом».
Так что выбор, предполагающий нацеленность преподавателя на студентов, а не на предмет, заведомо является неблагодарным.
Нужно отметить, что здесь в полной мере применима философская категория, восходящая к Гегелю и Марксу - отчуждение. Какими бы соображениями не руководствовались «вычитыватели» курсов, результатом является отчуждение непустого множества студентов от науки как таковой.
Важнее, однако, вопрос о том, как действовать преподавателю, выбравшему студентов как главную цель своей работы. Отчасти ответ очевиден. Необходимо максимально активизировать индивидуальную работу со студентами. Но столь же очевидно и то, что при этом резко возрастает нагрузка на преподавателя. Увы, преподавание требует чуть ли не самоотречения. Видимо, по этой причине некоторые власть имущие лица советуют преподавателям переходить в бизнес. Это может несколько повысить уровень их благосостояния. Правда, если удастся безболезненно вписаться в рыночную экономику.
Однако сделать выбор - это лишь малая часть дела. Дальше начинаются трудно решаемые проблемы. Например, при нацеленности на индивидуальную работу возможен уход в две крайности. Либо преимущественная работа с сильными студентами (что в целом очень естественно), либо преимущественная работа со слабыми студентами (цель - стремление поднять общий уровень аудитории при надежде на хорошую самостоятельную работу сильных студентов).
Этих крайностей желательно избегать. И именно здесь на первый план выходит продуманная методика преподавания. В общих чертах по пунктам очертим наше видение данной ситуации.
-
Необходимо стремление к максимальному личному контакту с каждым студентом для погружения его в постоянную работу. Важной целью при этом является устранения пробелов в знаниях, имеющихся именно у данного студента. В результате такого контакта преподаватель должен составить представление о возможностях каждого студента и о том, на какую проблематику его направлять в дальнейшем.
-
Важнейшим средством осуществления личного контакта являются многочисленные контрольные работы, при выполнении которых каждый студент имеет возможность подойти к преподавателю для консультации. При этом даже у слабого студента нет необходимости списывать. Преподаватель же получает возможность изучить особенности каждого студента.
-
После предварительной оценки уровня студентов необходим переход на контрольные работы с индивидуализированным содержанием и различным уровнем сложности.
-
Желательно использование помощи сильных студентов для консультирования студентов более слабых.
-
Неизбежно создание и использование гибкой системы электронных конспектов по различным разделам математики, значительно более кратких, чем стандартные учебники.
О содержании и форме контрольных работ и электронных пособий будет сказано ниже.
В случае же неудачи полезно вспоминать бессмертные слова Виктора Степановича Черномырдина и повторять их, немного перефразировав: «Хотел как лучше, а получилось как всегда. Раньше работала половина студентов, а пол не работало, а теперь всё наоборот. Не надо класть оба яйца в одну корзину. Надо делать то, что нужно нашим студентам, а не то, чем мы здесь занимаемся. Здесь вам не тут. Ну, кто меня может заменить? Убью сразу. Извините. Никогда не было, и опять».
Это неуместные шутки? Нет, необходимость. Современный преподаватель, гонимый судьбой и министерством образования, вынужден искать точку опоры, хотя бы и в Черномырдине.
Вернёмся, однако, к собственно методическим проблемам. Прежде всего, следует выделить базовые и, если так можно сказать, вечные методические проблемы. Речь идёт, например, о чёткой постановке целей математического образования. При этом определяющим фактором является вопрос о том, на подготовку специалистов с каким уклоном нацеливается высшее учебное заведение: математик, ориентированный на теоретическую работу в какой-то области математики; математик-прикладник; математик-инженер, который ориентирован на применение уже разработанных методов и теорий; наконец, педагог. Заметим, что методистов специально не готовят. Они сами рождаются как Афродита из пены.
Выбор целей преподавания определяет содержание курсов и отбор материала, а также выбор уровня строгости и определение удельного веса образного и логического мышления.
В нашем конкретном случае целью является воспитание математика-прикладника или математика-инженера, что в частности предполагает свободное владение понятиями и методами современной информатики. Ядро комплекса математических дисциплин имеет традиционный характер, то есть включает в себя курсы аналитической геометрии, алгебры и теории чисел, линейной алгебры и большой комплекс дисциплин, связанный с курсом математического анализа, вырастающий из него и его развивающий. Особое место занимает теория вероятностей, как важнейший инструмент математика-прикладника. Комплекс курсов, связанных с дискретной математикой, примыкает к курсам, связанным с информатикой, и нами рассматриваться не будет.
3. О ПОНИМАНИИ МАТЕМАТИКИ
Теперь мы переходим к обсуждению проблем более конкретного характера, оставляя при этом за собой право касаться и вопросов общего характера, в частности, связанных с проблемой понимания математических фактов. Освоить какой-то предмет, значит, понять его. Но в чём состоит суть понимания?
При рассмотрении содержания математики, принято говорить о математическом понятии, вне зависимости от того, идёт ли речь о творческом развитии математического знания, об обучении математике или же о разработке методик преподавания. Нам, однако, более обоснованным представляется использование термина «объект математической реальности». Его введение позволяет детализировать процесс обучения и разделить его на формир о- вание представления об объекте математической реальности как о понятии и как об образе. Только такое разделение позволяет достичь итогового соединения, условно говоря, логических аспектов владения объектом и аспектов интуитивного овладения им. Именно этот подход позволяет достигнуть того уровня видения математической реальности, которое называется пониманием.
Приведём цитату из [Ю. Л. Ершов, 2015], правда, используя её «поперёк мнения» автора: «Один мой остроумный коллега рассказал о недавнем разговоре с другим своим коллегой-математиком. Он сказал: «Я занимаюсь математической логикой» - и тот вполне искренне ответил следующее: «Ты знаешь, а я в своей деятельности логикой никогда не пользовался!» Должен сказать, что это почище литературного героя, который был поражён, когда узнал, что говорит прозой. И это сказал математик!»
Надо полагать, что коллега-математик подразумевал, кроме всего прочего, что до крайности формализованная логика и творческая деятельность математика, основанная на понимании некоторых математических теорий, являются мало связанными между собой сферами. И уж заведомо при обучении математике преждевременный уход в область абстракций, вроде бы сулящих единство логического восприятия разнородных конструкций, приводит к тому, что понимание математики ни в коей мере не достигается.
Борьбу за максимальное засилье абстрактно-логических тенденций в обучении математике следовало бы назвать «бурбакистикой». Малосимпатичная (см. [А. Б. Сосинский]) группа французских математиков взялась за «очищение авгиевых конюшен», то есть за наведение логического порядка в математике. При этом она между делом нанесла непоправимый вред математическому образованию, в том числе школьному.
Нельзя сказать, что причиной данного процесса явилась некая врождённая зловредность бурбакистов. Они имели основания для того, чтобы ратовать за перестройку математического образования. Математика движется вперёд, а математическое образование до сих пор основывается на «Началах» Евклида. Правильно ли это? В результате возникает дилемма: «отказ от традиций, включая интуитивное восприятие математики» или «отсталость»? Важнейшим вопросом при этом стал выбор уровня общности.
А любовь к обобщениям и «формализм» неразрывны. Печальные результаты, связанные с триумфом бурбакистов в образовании общеизвестны. Возник спор о математике, в котором часто слышатся алармистские нотки. Сначала гибло математическое образование. Теперь дело дошло до спада в самой математике. Причиной этого является как раз торжествующая формалистика и неуёмная жажда обобщений.
В. И. Арнольд активно вёл борьбу за важность понимания сущности математики, возможно, иногда в полемике, несколько перегибая палку в свою сторону и называя математику физикой, в рамках которой эксперименты являются наиболее дешёвыми. Здесь тоже проявлялись объективные основания, приводящие к спорам и конфликтам среди математиков, озабоченных состоянием математического образования. В частности, Арнольд рассматривал известную книгу Я. Б. Зельдовича «Высшая математика для начинающих» как образец учебного пособия. И это при том, что книга была подвергнута сокрушительной критике за отсутствие элементарной строгости.
Можно понять и позицию В. И. Арнольда, и позицию математиков, критикующих нестрогий, эвристический стиль рассуждений. Но, делая выбор между строгостью и эвристикой, следует помнить о результатах, полученных Леонардом Эйлером и о тех, часто весьма далёких от формальной строгости, методах рассуждений, которые великий математик применял. Следует также попытаться ответить на вопрос: чем была бы математика в настоящее время если бы не было гениальных прозрений, первоначально покоящихся на очень зыбких основаниях, у того же Эйлера, Галуа, Римана, Лобачевского? Чтобы чистить конюшни, нужно их сначала построить. Не правда ли?
Автор статьи полагает, что нельзя полностью пренебрегать строгостью математических рассуждений. Но ради этой строгости не следует выплёскивать из корыта ребёнка вместе с водой. Наилучшим решением проблемы является разделение труда. Одни стремятся к достижению строгости, другие дышат воздухом живой математики. При этом сфера математического образования должна располагаться именно во владениях живой математики.
Процитируем по этому поводу великого французского учёного Анри Пуанкаре: «... логическая безупречность рассуждений, ведущих от аксиом к теоремам, не единственное, что должно нас занимать. Разве в математике всё сводится к правилам совершенной логики? Утверждать это всё равно, что сказать, будто всё искусство шахматистов сводится к правилам хода отдельных фигур. Надо, ведь делать ещё выбор из всех комбинаций, какие только можно сделать из материалов, доставляемых логикой; истинный математик производит этот выбор правильно, потому что им руководит какой-то надёжный инстинкт, какое-то смутное сознание некоторой более глубокой, более сокровенной, геометрии, одно лишь и придающее ценность возводимому зданию. Исследовать происхождение этого инстинкта, изучить законы этой сокровенной геометрии, законы, которые чувствуются, но не формулируются - было бы всё ещё недурной задачей для философов, не признающих, чтобы логика была всем» [А. Пуанкаре, Л, 2010].
Итак, повторим, что изучение объекта математической реальности требует формирования представления об этом объекте и как о понятии, и как об образе. При этом необходимо добиваться соединения логических аспектов познания объекта и аспектов интуитивного видения этого объекта и умения манипулировать им в виде пластического образа.
В качестве примера рассмотрим некоторые этапы формирования у студентов развитого представления о числовой прямой - базового понятия аналитической геометрии и математического анализа. Здесь соединяются представления о множестве действительных чисел и о континууме, как геометрическом, а точнее топологическом образе. При этом чувственный образ континуума понимается как некое непрерывное геометрическое многообразие. На данном этапе обучения речь идёт об одномерном многообразии, а именно о кривой. В итоге у студента должен быть сформирован образ пластического перехода прямой в график функции. Далее аналогичные представления переносятся на декартову плоскость и двумерный континуум.
Обсуждая данный пример, мы затронем некоторые вопросы, о которых будем подробнее говорить ниже, а именно вопрос о повторении некоторых фактов из школьного курса математики и вопрос об использовании компьютерных технологий при изучении математики. Сейчас отметим только, что и повторение элементарных фактов, и использование компьютера являются в настоящее время необходимыми составляющими учебного процесса.
Множество действительных чисел рассматривается нами как множество десятичных дробей, поскольку эта точка зрения в большей степени соответствует духу прикладной мат е- матики, чем теория сечений Дедекинда. В то же время сведения и о теории Дедекинда могут быть доведены до студентов, как дополнительный материал.
Перечислим этапы формирования представления о числовой прямой. Некоторые пункты в основном повторительного характера в процессе обучения занимают небольшое время, хотя при этом затрагивается достаточно большое количество вопросов. Опыт показывает, что обо всех этих вопросах желательно упомянуть для систематизации общей картины в сознании студента.
-
Обзор основных видов чисел (натуральные, целые, обыкновенные дроби или рациональные числа). В том числе обсуждается вопрос о том, была ли исторически связана с натуральными числами сложная математическая проблема. Изобретение нуля. Позиционные системы счисления и их роль в математике. Недесятичные системы счисления.
-
«Физический» смысл отрицательных чисел как долгов и отрицательных температур. Шкалы, как прообразы и модели числовой прямой. Расстояние между точками с целыми координатами. Дадим как пример экономического истолкования разъяснение того, что минус единица в квадрате равна единице. Введём два вида множеств. Первое - положительные числа (наличность), изображаемые зелёными камешками. Второе - отрицательные числа (долги), изображаемые красными камешками. Промежуточным является пустое множество, не содержащее элементов (ни наличности, ни долга). Поскольку сложение и вычитание сведены к последовательному прибавлению и вычитанию единиц, мы работаем либо с множеством зелёных элементов, либо с множеством красных элементов. Любое число представимо не единственным способом, но может быть сведено к элементам одного цвета с помощью своеобразной аннигиляции. Когда речь идёт о красных элементах, удаление (вычитание) одного приводит к уменьшению долга на единицу, но к тому же результату по экономическому смыслу приводит и добавление зелёной единицы, компенсирующей единичный долг. Таким образом - (-1) = 1, то есть (-1) (-1) = 1.
-
Рациональные числа как обыкновенные дроби. Смысл приведения дробей к общему знаменателю. Разложение натуральных чисел на простые множители. Признаки делимости. Наименьшее общее кратное нескольких чисел.
-
Связь десятичных дробей и дробей обыкновенных. Перевод конечных десятичных дробей в обыкновенные дроби. Перевод обыкновенной дроби в десятичную. Причины возникновения бесконечных десятичных периодических дробей. Сумма бесконечной геометрической прогрессии. Перевод бесконечных периодических десятичных дробей в обыкновенные дроби.
-
Процедура измерения отрезков. Два метода измерения отрезков. Алгоритм Евклида и измерение отрезков. Алгоритм получения длины отрезка в форме десятичной дроби. Возможные исходы измерения при этом типе измерения. Построение отрезка, имеющего длину, заданную конечной или бесконечной десятичной дробью. Связь с понятием супремума и теоремой Вейерштрасса о монотонной ограниченной последовательности.
-
Иррациональные числа. Доказательство существования иррациональных чисел. Квадратные корни, как примеры иррациональных чисел. Символические вычисления с иррациональными числами. Конструирование иррациональных чисел, состоящее в описании конструкций бесконечных десятичных дробей, обеспечивающих их непериодичность. Решение задач следующего типа:
-
Каким числом является сумма целого и иррационального чисел?
-
Доказать, что число √2 + √3 является иррациональным.
-
Каким числом может являться сумма двух иррациональных чисел? Привести примеры.
-
Сконструировать два иррациональных числа, сумма которых рациональна.
-
Привести пример двух иррациональных чисел сумма и произведение которых является целыми числами.
-
Существуют ли два иррациональных числа сумма и разность которых является целым числом.
-
Числовая прямая и действительные числа. Построение взаимно однозначного соответствия между десятичными дробями и точками прямой с помощью процедуры измерения отрезков. Два представления множества действительных чисел - десятичные дроби и точки прямой. Расстояние между точками на числовой прямой. Взаимосвязь геометрического и алгебраического языка в курсе математического анализа.
-
Определение понятия переменной величины как свойства объекта, выраженного действительным числом. Спиртовой термометр как модель переменной величины. Геометрическая модель переменной величины - числовая прямая, по которой движется точка-указатель. Функция y = f(x) как зависимость между двумя переменными. Примечание: обычно понятие переменной сводится к процедуре произвольного выбора значений из определённого множества. При этом, хотя бы отчасти, теряется физический смысл понятия «переменная». Этот смысл состоит в том, что переменная даёт числовое выражение некоторых свойств объектов окружающего мира. Именно для этого переменные и нужны. В рамках классической математики переменные также выражают свойства объектов, например, в геометрии речь идёт о длинах, площадях, объёмах и т.д. В свою очередь, признав, что переменная является выразителем свойств, следует беспорядочный «выбор значений» заменить «изменением», то есть движением указателя вдоль числовой прямой. Именно такое интуитивное представление соответствует физическому смыслу термина «переменная». Хотя с точки зрения логики и возможности обобщений именно «выбору значений» может быть отдано предпочтение.
-
Декартова система координат на плоскости. Два представления декартовой плоскости - множество упорядоченных пар десятичных дробей (пар вещественных чисел) и точки евклидовой плоскости. График как множество точек вида (x; f(x)).
-
Пластический образ континуума. Целью данного пункта является наглядное объяснение причин, по которым график функции является кривой. Само объяснение таково. Представим себе, что на оси абсцисс в декартовой плоскости расположен пластичный, легко деформируемый стержень. Ординаты всех его точек равны нулю. Стержень можно параллельно оси абсцисс переместить вверх или вниз на некоторую величину с. При этом ординаты всех его точек примут одинаковые значения с, уже неравные нулю. С помощью этой процедуры построен график функции у = с. Пусть далее нам дана функция y = f(x). Теперь мы будем перемещать по вертикали не весь стержень целиком, а каждую его точку х сдвинем на своё особое расстояние y = f(x). При этом стержень деформируется. Он даже может разорваться, но если для близких значений абсцисс, значения ординат тоже близки, то разрывов не будет, а график функции предстанет в виде кривой. Примечание: можно отрицать необходимость приведённых рассуждений, но можно и утверждать, что они полезны. Что и делает автор.
-
Компьютерное построение графиков как материализация представления о пластическом образе континуума. Пусть нам дана некоторая функция. Требуется построить на экране компьютера график этой функции. Перед построением в нашем сознании пребывает воображаемая декартова плоскость (t; u), на которой начерчен график функции u = f(t). Обозначения переменных х и у оставлены для экранных координат. (Для по
строения использован язык программирования Small Basic). Пусть в точке (х0; у0) находится начало координат. Число а указывает, сколько пикселов содержит единичный отрезок на экране.
Строим на экране отрезок [-1; 1] оси абсцисс и поднимаем его вертикально вверх на высоту а.

Чтобы поднимать не весь отрезок целиком, а каждую его точку по отдельности на свою высоту, сделаем переменную у зависимой от параметра t. Это вполне естественное решение, поскольку разным значениям параметра t соответствуют разные точки на горизонтальном отрезке. Для этого в уже написанной программе мы заменим всего лишь одну единственную команду y = y0 - a, например, на команду y = y0 - a*t*t, что будет соответствовать построению графика функции у = х2.
Пластический образ поверхности как аналога графика функции двух переменных. Представим себе, что на декартовой плоскости расположен пластичный, легко деформируемый ковёр. Каждая точка ковра определяется парой координат (х; у). Если же нам дана функция от двух переменных z = f(x, y), мы каждую точку ковра (х; у) сдвинем по вертикали (уже в трёхмерном пространстве) на своё особое расстояние z = f(x, y). При этом ковёр деформируется и превратится в аналог графика функции от двух переменных, а именно в некоторую поверхность. Компьютерная реализация этого построения более сложна, поскольку требует владения понятием линейного отображения двумерных пространств для создания хорошей проекции объёмного изображения на экран.
4. НЕКОТОРЫЕ НАПРАВЛЕНИЯ МЕТОДИЧЕСКОЙ РАБОТЫ СВЯЗАННЫХ КАК С НЕПОСРЕДСТВЕННЫМ ПРОЦЕССОМ ПРЕПОДАВАНИЯ, ТАК И С ПОСТРОЕНИЕМ ДОЛГОВРЕМЕННЫХ КУРСОВ МАТЕМАТИКИЧЕСКИХ ДИСЦИПЛИН
Важнейшей задачей преподавателя, связанной с непосредственным процессом преподавания на младших курсах, является выяснение тех особенностей студентов, от которых существенно зависит успешность учебного процесса. Работа, конечно, очень нелёгкая и лежащая в русле индивидуальной работы со студентами. Прежде всего, речь идёт об уровне подготовки каждого учащегося. Как уже отмечалось основным инструментом здесь являются контрольные работы. С их помощью можно оценить степень знания и понимания (что не одно и то же) студентом различных фактов. Это может стать основой при восполнении пробелов в знаниях студента, в том числе в области элементарной математики. Для этого в индивидуализированные контрольные можно и нужно вносить повторительные задачи. Если говорить честно, то преподавание на современном этапе проходит под всё громче звучащем лозунгом: «Повторение - мать учения».
Вот зарисовка с натуры. Преподаватель говорит и пишет на доске: На следующем занятии будет проведена контрольная работа на тему «Дифференциальные уравнения с разделяющимися переменными». Далее он повторяет эту фразу ещё дважды и спрашивает: «Все слышали? Все поняли?» - «Все! Все!» - «Вопросы есть?» - «Да. А контрольная будет? А когда она будет? А какие такие уравнения? А что там разделяется?»
Расскажу ещё один вроде бы малозначительный случай из своей практики, который, однако, хорошо характеризует нынешних студентов с точки зрения их эрудиции, в том числе, и за пределами математики.
Несколько лет назад на нашем факультете обучался не очень прилежный студент по фамилии Макаренко. Кроме всего прочего он был склонен к ироническому комментированию некоторых действий преподавателя. Заметив, что я тяготею к повторению многих тем, он после очередного моего предложения что-то повторить воскликнул: «Ну, конечно же, повторение - мать учения». Я подошёл к нему и сказал: «Это верно». И тут же спросил: «Но знаешь ли ты, кто является отцом учения?» Он растерялся. После чего я сообщил ему, что отцом учения является Макаренко. О своём знаменитом однофамильце он и не слыхивал. Так же, как и студент по фамилии Качалин не знал великого советского футбольного тренера и даже почему-то стыдился своей фамилии. Подобные примеры можно продолжать очень долго.
Тут возникает тема, связанная со стилем общения преподавателя со студентами. Кстати, на нашем факультете эта тема особенно актуальна, поскольку преподавателю приходится работать и с аутистами, и с инвалидами - опорниками, с незрячими и плохо слышащими. Это, естественно, предъявляет повышенные требования к такту педагога. Впрочем, тут секрет очень прост - нужно относится к студентам заинтересованно и доброжелательно. Хотя, честно говоря, это тоже часто нелегко.
Немалую роль в установлении доверительного контакта с аудиторией играет юмор. Шутить иногда вполне уместно, особенно если вспомнить слова Паскаля о том, что предмет математики настолько серьёзен, что никогда не лишне сделать его хоть в какой-то мере занимательным. А юмор и занимательность хорошо дополняют друг друга. Рискну (юмор легко критиковать с достаточными основаниями) привести только два из используемых мной занимательно-юмористических текста. Один из них включён в электронный документ, посвящённый радианной мере углов как развлекающее дополнение, а второй представляет собой непритязательный анекдот, который я часто рассказываю на занятиях. Кстати, моё первое знакомство с этим анекдотом восходит к тем годам, когда я слушал лекции Арнольда и Вишика.
«Философская задача» из текста о радианной мере: «Какую форму математическая теорема «все окружности подобны» приобретает в философии?»
Ответ. Мыслитель раннего Возрождения Николай Кузанский (1401 - 1464) писал математические и философские трактаты, не стремясь к системе, но следуя божественному вдохновению. Николай виртуозно использовал математические понятия для иллюстрации философских идей.
В числе прочих геометрических фигур он обращался к окружности и кругу, а также к их основному свойству - округлости. Вот, что он писал по этому поводу: «В круге, не имеющем начала и конца, поскольку ни одна его точка не больше начало, чем конец, я вижу образ вечности. Поэтому и округлость, коль скоро она такая же, я называю образом вечности».
Итак, с позиций философии окружность - образ вечности. Вечно же лишь совершенное. Следовательно, все окружности совершенны, и теорема приобретает форму: «Все окружности бесподобны».
Анекдот о математиках в сумасшедшем доме. Один агрессивный обитатель сумасшедшего дома терроризировал своих товарищей, заявляя, что продифференцировал их. Узнав о нанесённом им ущербе, все начинали рыдать и биться в судорогах. И только один в ответ засмеялся. Террорист не хотел сдаваться и закричал: «Теперь я ещё и проинтегрировал тебя». Потенциальная жертва продолжала смеяться. Отчаявшийся террорист воскликнул: «Кто же ты такой?» - «Я е в степени икс».
Анекдотец не затейлив. Однако Гёте в своей автобиографической книге «Поэзия и правда» сообщает, что пользовался в детстве зарифмованными учебниками. И, как он считает, именно низкое качество стихов помогло ему легко запоминать все зарифмованные правила. Можно засвидетельствовать, что данный анекдот действует на студентов подобно старинным немецким учебникам.
Чрезвычайно важным моментом является достижение в процессе преподавания максимальной наглядности. В значительной мере, если следовать мысли Германа Вейля, отказ от упора на наглядность или наоборот устремлённость к ней можно рассматривать как одно из сражений между демоном алгебры и ангелом геометрии. Но в целом вопрос о наглядности возвращает нас к вопросу об изучении объекта математической реальности, выражаемого и понятием, и образом.
Эффективным средством, помогающим в достижении наглядности, в том числе являются краткие электронные конспекты. Приведём пример такого конспекта, дотошность которого в чём-то превосходит краткость.
Функция - это зависимость, связывающая значения двух переменных числовых величин. Любая функция - это описание некоторого процесса изменения. При этом функция - абстрактное (без лишних деталей) описание некоторого процесса. При таком описании мы можем узнать о процессе только то, возрастает функция, убывает или возрастание сменяется убыванием (либо наоборот).
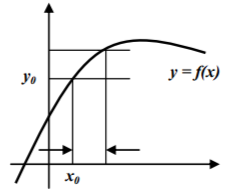
Пусть задана функция y = f(x). Считая аргумент аналогом времени, рассмотрим значения функции в момент х0 и в близкий к нему момент х. Функция принимает в эти моменты значения y0 = f(x0) и y = f(x). Основная характеристика изменения числовой величины – разность между старым и новым значениями функции, которая называется приращением функции ∆у = у – у0. Её смысл таков: было значение у0, стало значение у. Произошедшее изменение – разность значений ∆у. Одно и то же изменение может произойти за разное время. Характеристика длительности изменения – разность значений аргумента, которая называется приращением аргумента. Она равна ∆х = х – х0. Её смысл таков – время, за которое произошло изменение равно ∆х.
Скорость изменения функции – это изменение, которое происходит за единицу времени, т. е. отношение ∆у к ∆х. Однако отношение ∆y/∆x - это всего лишь средняя скорость изменения значения функции за время ∆х.
Для вычисления мгновенной скорости нужно уменьшить длительность времени изменения ∆х, приближая (устремляя) значение х к значению х0. Процесс вычисления отношения ∆y/∆x при таком уменьшения называется вычислением предела. Этот предел и называется производной, которая обозначается через у’. Производная - это предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Символически вычисление производной записывается следующим образом ![]()
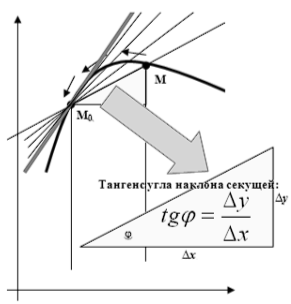
Очень важен геометрический смысл производной. Он выясняется при попытке решения задачи о проведении через точку М0 (х0; у0) касательной к графику функции y = f(x). Решение задачи состоит в том, что сначала проводят секущую, через точки М (х; у) и М0, лежащие на графике. Приближение точки М к точке М0 превращает секущую в касательную, поскольку она отсекает всё меньшую дугу. «Отсечение точки» и есть касание.
Тангенс угла наклона секущей равен отношению приращения функции к приращению аргумента. При слиянии точек М и М0 этот тангенс переходит в тангенс угла наклона касательной. Итак, тангенс угла наклона касательной к графику функции равен производной функции в этой точке.
Касательная указывает направление изменения функции. Если касательная направлена вниз, то функция убывает, если касательная направлена вверх - функция возрастает. Но касательная направлена вниз, если тангенс угла наклона касательной отрицателен (y'< 0). Вверх она направлена, если тангенс угла наклона касательной положителен (y' > 0).
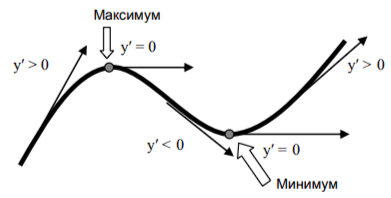
При смене знака производной функция достигает наивысшей или наоборот низшей точки, называемой экстремумом.
Если знак производной меняется с плюса на минус, функция имеет максимум. Если знак производной меняется с минуса на плюс, функция имеет минимум. На практике для поиска экстремумов нужно приравнять производную к нулю. Таким образом, можно изучать поведение функций с помощью производных.
Хочется отметить следующее обстоятельство. При освоении понятия производной необходимо пояснять студентам, что в формуле ![]() отношение ∆у/∆x является и средней скоростью изменения значений функции, и тангенсом угла наклона секущей. Подобные напоминания никогда не являются лишними. Без них помнят, что получается в пределе, но забывают предел какого выражения вычисляется.
отношение ∆у/∆x является и средней скоростью изменения значений функции, и тангенсом угла наклона секущей. Подобные напоминания никогда не являются лишними. Без них помнят, что получается в пределе, но забывают предел какого выражения вычисляется.
Естественно, что кроме выявления пробелов в подготовке студентов необходимо определять уровень способностей каждого, его мотивацию, и даже личную ситуацию. Дело в том, что в наше время мы имеем дело с поколением молодых людей с ослабленным здоровьем. Увы, иногда немолодой преподаватель, проводящий занятия, является самым здоровым человеком в аудитории. Часто студенты испытывают финансовые сложности. Всё это нужно учитывать преподавателям, работающим в эпоху Кали-юги (согласно индуистским учениям Кали-юга - век раздора, за которым следует махапралая - уничтожение мира). Однако проблемы скорой гибели мироздания выходят за рамки методической работы. Их упоминание уместно лишь как некое юмористическое отступление, возможно, немного темноватого оттенка.
Что же касается выявления творческой активности студентов и уровня их способностей, то на первых порах (до того момента, когда студент может обратиться к решению, пусть и несложных, чисто математических вопросов), полезно использование развивающих задач. Размышление над этими задачами с одной стороны не требуют предварительного освоения новых понятий, а с другой - предполагает наличие самого настоящего творчества. Особенно важно то, что решение задач, подобного типа, заинтересовывает студента.
Выбор задач, конечно, должен соответствовать личным приоритетам преподавателя. Отбор задач при этом требует только ознакомления с содержанием большого числа прекрасных сборников старинных задач, задач олимпиадного характера и книг таких замечательных авторов как, например, Мартин Гарднер.
Я приведу одну задачу, которая в годы моей юности была опубликована в журнале «Наука и жизнь». Встречаются две женщины. Одна из них говорит другой: «Я знаю, что у тебя три сына, но не знаю их возрастов». - «Произведение их возрастов равно 36». - «Данных недостаточно». - «Сумма их возрастов равна числу окон в доме, около которого мы стоим». - «Данных недостаточно». - «У моего старшего сына рыжие волосы». - «Этого достаточно». Определите возраст всех троих мальчиков.
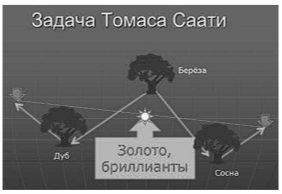
Иногда занимательная задача может соответствовать изучаемому предмету. И, конечно, это особенно ценно. Например, преподавая предмет «Исследование операций», я давал вводную задачу, принадлежащую Томасу Саати. Суть задачи такова. Кладоискатель узнаёт, что на некой поляне находится клад. Чтобы его найти, нужно встать спиной к берёзе, отсчитать число шагов до дуба, повернуть под прямым углом направо и сделать ещё столько же шагов. В данной точке следует забить колышек. Затем, вернувшись к берёзе и ту же процедуру проделать относительно сосны с тем отличием, что поворот делается налево. Клад находится в середине отрезка, соединяющего колышки. Беда в том, что, прибыв на поляну, кладоискатель обнаруживает дуб и сосну, но никаких следов берёзы не нашёл. Как отыскать клад в этой ситуации?
Следует также иметь ввиду, что существует целый класс задач, простых по формулировке, но важных для математики. Среди них следует выделить диофантовы уравнения. Их место в математике хорошо известно (имеется ввиду десятая проблема Гильберта). Не менее знамениты и сложности, возникающие при решении этих уравнений. Однако диофантово уравнение x2 + y2 = z2, связанное с теоремой Пифагора решается весьма просто, причём многими поучительными методами. И это при том, что самые первые размышления об этом уравнении немедленно приводят к вопросам, связанным с великой теоремой Ферма. Прив е- дём в высшей степени наглядное, но частное решение уравнения Пифагора с помощью гномонов, пришедших к нам аж из Древней Греции.
Задача. В мешочке лежат камешки. Мы можем их вынимать оттуда и раскладывать на земле. Можем ли мы, не считая камешки, узнать, чётное или нечётное их количество лежало в мешочке?
Ответ. Можем, раскладывая камешки в 2 ряда один под другим.

Задача. В мешочке лежат камешки. Мы можем их вынимать оттуда и раскладывать на земле. Можем ли мы, не считая камешки, узнать, является ли квадратом общее число камешков, лежавших в мешочке?
Ответ. Можем, раскладывая камешки в виде квадрата. При этом камешки следует подкладывать к уже выложенному квадрату углами (по- гречески - гномонами).

Задача. Докажите, что сумма первых n нечётных чисел равна n2.
Задача. Найдите какие-нибудь три натуральных числа x, y и z, связанных соотношением x2 + y2 = z2.
Указание. Приложив гномон к одному квадрату, мы получим другой. Если число камешков в самом гномоне также является квадратом, то мы как раз и получим соотношение x2 + y2 = z2.
Задача. Найдите формулу для нахождения бесконечного количества решений неопределённого уравнения x2 + y2 = z2.
Далее можно заинтересованных студентов подвести к получению общего решения уравнения Пифагора. В частности, это можно сделать с помощью тригонометрических формул, выражающих синус и косинус через тангенс половинного угла. Это позволяет установить связь диофантовых уравнений с процедурой интегрирования, что может помочь в дальнейшем при разъяснении причин существования «неберущихся» интегралов типа эллиптических. Далее возможно ознакомление с уравнениями Пелля и Маркова. Это открывает путь к более глубокому изучению проблематики теории чисел. Но всё это делается в рамках индивидуальной работы со студентом.
5. ВОПРОСЫ ПОСТРОЕНИЯ СОВОКУПНОСТИ МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН КАК ЕДИНОГО ЦЕЛОГО
Очень важным является вопрос об общем построении курса математики как единого целого. В значительной степени это и методический вопрос. Здесь тоже необходим единый взгляд на курс в целом. Целью же является выделение «скелета» курса, а также избранных (центральных) вопросов курса. При этом необходимо включить в корпус математических дисциплин и разделы элементарной математики, не только являющейся мостиком к математике высшей, но и выступающей в качестве совершенно необходимого инструмента, без которого нельзя решать более сложные проблемы.
Ниже автор перечислит разделы математики, о которых в дальнейшем и пойдёт речь. Из списка по различным причинам исключены
-
теория чисел, как область наиболее далёкая от прикладной математики;
-
высшая геометрия и топология, поскольку все необходимые вопросы рассматриваются в рамках других предметов;
-
комплексный анализ, функциональный анализ и уравнения математической физики. Эти разделы слишком усложнили бы обсуждение методических проблем. Вопросы, связанные с использованием комплексных чисел в аналитической геометрии, линейной алгебре и теории дифференциальных уравнений и т. д., можно рассмотреть в курсе общей алгебры и при изучении рядов Тейлора (вывод формулы Эйлера);
-
исследование операций (предмет который автор неизменно преподавал на факультете ИТ), поскольку основные вопросы можно рассмотреть в курсах линейной алгебры и теории вероятностей;
-
вычислительная математика, поскольку основные вопросы можно рассмотреть в курсах линейной алгебры и математического анализа.
В итоге корпус рассматриваемых ниже разделов математики включены
-
Элементарная математика.
-
Аналитическая геометрия.
-
Общая алгебра.
-
Линейная алгебра.
-
Математический анализ функций одной переменной.
-
Математический анализ функций нескольких переменных.
-
Теория дифференциальных уравнений.
-
Теория вероятностей.
Приступим к рассмотрению соответствующих разделов математики. При этом нашей целью является выделение центральных вопросов каждого курса, а не перечисление всех изучаемых в курсе тем. По возможности причины нашего выбора будут мотивироваться или хотя бы кратко комментироваться. В отношении некоторых вопросов будет просто-напросто отмечена их важность и то, что на них необходимо сделать акцент в процессе преподавания.
Кроме того, целый ряд центральных вопросов будет рассмотрен особо, причём это будет сделано достаточно подробно. Примером может послужить изучение показательной функции и введение числа е. Речь идёт именно о тех вопросах, где автор что -то придумал сам, хотя повторим, что никаких притязаний на методические открытия мы не имеем. В дальнейшем отсылки к разделам, где обсуждаются подобные вопросы, будут для краткости даваться в форме: см. Тему № такой-то. Все указанные темы рассматриваются в следующем разделе.
Итак, начинаем с элементарной математики, хотя делаем это с некоторой опаской, так как боимся услышать: «Повторять такие вещи в высшем учебном заведении? Нонсенс». И тем не менее...
Элементарная математика. Отметим, что повторение некоторых вопросов, связанных с элементарной математикой может быть превращено в пропедевтику, нацеленную на достаточно сложные вопросы, которые будут изучаться в дальнейшем.
Работа с дробями. Необходимая в наше время проверка навыков работы с дробями может быть проведена при изучении числовой прямой.
Геометрическая прогрессия. Формулы суммы членов конечной и особенно бесконечной геометрической прогрессии используются и в математическом анализе, и в теории вероятностей. По этой причине их можно повторить в тот момент, когда они потребуются. Следует довести до студента тот факт, что формулы сокращённого умножения связанные с разностью квадратов, а также разностью и суммой кубов являются частным случаем формулы суммы членов конечной геометрической прогрессии: 1-qn+1 = (1-q)(1 + q + q2 +... + qn). Это обстоятельство может быть использовано при вычислении производной степенной функции с натуральным показателем. Рассмотрение формулы суммы бесконечной геометрической прогрессии с определённой точки зрения может стать пропедевтикой перед изучением рядов Тейлора, поскольку формулу суммы бесконечной геометрической прогрессии 1/(1-x) = 1 + x + x2 +... + xn +... можно рассматривать как разложение функции в ряд Тейлора. На сравнении с геометрической прогрессией основаны и признаки сходимости числовых рядов.
Теорема Пифагора является основой для вычисления расстояний в рамках аналитической геометрии и линейной алгебры. По этой причине разговор о ней должен вестись в соответствующих местах курса.
Связь между вычислением площади прямоугольника и перемножением скобок имеет, с нашей точки зрения, большое значение (см. Тему 1). Это может быть подтверждено результатами Леонарда Эйлера, которому ясное понимание того, как перемножаются скобки, позволило создать аналитическую теорию чисел. В нашем случае речь при обсуждении темы 1 будет идти в основном о вопросах теории вероятностей.
Число пи, радианная мера, тригонометрия. Как уже говорилось выше в школьном курсе градусная мера в известном смысле подавляет радианную. Кроме того, в курсе математического анализа необходимо провести чёткое описание тригонометрических функций произвольного угла (см. Тему 2).
Квадратный трёхчлен, выделение полного квадрата, разложение на множители. Квадратные уравнения выпускники школы решают довольно прилично, но, как правило, затрудняются с ответом на вопрос, как возникла формула решения квадратного уравнения. По этой причине желательно вспомнить, как производится выделение полного квадрата. Поскольку квадратичная функция и квадратные уравнения обязательно появляется в момент изучения производной, можно давать в контрольных работах задачи, которые предлагают найти экстремум функции и с помощью выделения полного квадрата, и с помощью производной. Вопрос о разложении квадратного многочлена на множители возникает и при вычислении пределов, и при интегрировании, и, конечно, в рамках курса общей алгебры. Так что для повторения этого вопроса можно где-нибудь найти несколько минут. Поскольку работа с комплексными числами обычно вызывает затруднения, желательно предложить студентам решить квадратное уравнение с комплексными коэффициентами. Не следует забывать и тот факт, что при решении линейных дифференциальных уравнений с постоянными коэффициентами квадратные уравнения играют заметную роль.
Доведём до сведения читателей и один довольно забавный эпизод, который показывает, что квадратные уравнения могут фигурировать и в высоконаучных дискуссиях. Мой друг со студенческой скамьи Виктор Иванович Буслаев получил следующий важный результат.
О гипотезе Бейкера-Гаммеля-Уиллса в теории аппроксимаций Паде.
Известная Паде-гипотеза, высказанная в 1961 году Г. Бейкером, Д. Гаммелем и Д. Уиллсом, утверждает, что для всякой мероморфной в единичном круге D функции f найдется бесконечная подпоследовательность ее диагональных аппроксимаций Паде, сходящаяся к f равномерно на компактах, лежащих в D и не содержащих полюсов f. В 2001 году Д. Любин- ски указал мероморфную в D функцию, опровергающую Паде-гипотезу. В. И. Буслаевым найдена функция, опровергающая голоморфный вариант Паде-гипотезы [Сайт Математического института].
Поскольку мероморфная функция имеет полюса, а голоморфная их не имеет, ясно, что результат Буслаева, полученный фактически через несколько месяцев после результата Любински, полностью перекрыл последний. При личной встрече с Буслаевым Любински проверял все составляющие доказательства Виктора Ивановича. К его огорчению не было обнаружено никаких ошибок. А поскольку результат зависел от значения корней некого квадратного уравнения, Любински не удержался и спросил: «А квадратное уравнение Вы правильно решили?»
Что касается рассмотрения вопросов высшей математики, то, на наш взгляд, желательно использование элементарных методов рассуждений там, где это возможно. Примером может послужить математический анализ многочленов и рациональных функций.
С другой стороны, полезно демонстрировать получение элементарных результатов методами высшей математики. Например, базовые для тригонометрии формулы синуса и косинуса суммы и разности выводятся в школе достаточно сложными путями. По этой причине они запоминаются с трудом. В то же время их можно вывести при помощи скалярного произведения очень просто.
Два единичных радиус-вектора, образующие с осью абсцисс углы а и ß, имеют координаты (cos а; sin а) и (cos ß; sin ß). Угол между ними равен ß - а. Таким образом, скалярное произведение этих векторов в геометрической форме равно cos (ß-а), а в координатной форме равно cos а•cos ß + sin а-sin ß, из чего и вытекает формула для косинуса разности: cos (ß- а) = cos а•cos ß + sin а-sin ß.
Здесь особенно важна возможность самостоятельного восстановления результата, что вообще может рассматриваться как одна из особых целей обучения.
Аналитическая геометрия лежит в основе линейной алгебры и математического анализа. Напомним, что нашей главной задачей является выделение центральных вопросов курса аналитической геометрии. О формировании понятия числовой прямой мы уже говорили выше. Важный вопрос о вычислении расстояний связан с повторением теоремы Пифагора.
Возможны различные варианты построения курса аналитической геометрии. Наиболее интересным вариантом, на наш взгляд является использование векторной алгебры. При этом, рассматривая операции над векторами, следует использовать физическую пропедевтику (см. Тему 3). Важнейшие темы курса, связанные с различной формой уравнения прямых и с линейными преобразованиями можно определённым образом соединить (см. Тему 4). Знакомство с кривыми второго порядка в значительной мере помогает студенту подготовиться к встрече с рядом понятий математического анализа. Речь идёт о неявном и параметрическом задании функций и о методах построения касательных (см. Тему 5).
Несомненно, что для некоторых математиков курс аналитической геометрии является архаикой, поскольку его полностью перекрывает курс линейной алгебры. Однако, если можно так выразиться, плоская (двумерная) математика является полигоном, работа на котором развивает интуицию учащегося. Сошлюсь на [И. М. Глазман, 1969]. Один из авторов этой книги не дожил до её выхода в свет. Вот что пишет о нём его соавтор, неявно обосновывая необходимость изучения курса «архаичной» аналитической геометрии.
«30 мая 1968 года, когда эта книга была в наборе, не стало Израиля Марковича Глаз- мана, которому всецело принадлежит основной замысел книги - конечномерное «моделирование» функционального анализа. Когда кто-нибудь рассказывал ему о сложных бесконечномерных построениях, он обычно спрашивал: «А как это выглядит в двумерном случае?» - и нередко этот шокирующий вопрос помогал лучше понять суть дела. Вся математическая деятельность этого яркого таланта была направлена на то, чтобы увидеть простую основу сложных вещей».
Увидеть простую основу сложных вещей - это суть настоящей методики. По этой причине автор статьи всегда планировал написать учебник по «двумерной математике». Поскольку автор много лет занимается компьютерной геометрией [6,7] он начал реализовывать соответствующую программу в своей неопубликованной многотомной работе «Компьютерная геометрия». Однако автор должен признать, что интереса к его работе не проявило ни одно издательство. Видимо, нужна хотя бы «трёхмерная математика».
Анализ. Мы уже затрагивали вопрос о формах введения понятия функции и понятия переменной. Очень важной частью курса является полноценное освоение основных элементарных функций (см. Тему 6). Одно из основополагающих понятий анализа - понятие предела (см. Тему 7). Очевидно, что понятие производной является важнейшим в курсе анализа, поскольку на нём основываются и такие понятия как интеграл, и такие методы, как разложение функций в ряды, и теория дифференциальных уравнений (См. Тему 8). Наконец, затронем некоторые аспекты, связанные с понятием интеграла (см. Тему 9).
Анализ функций нескольких переменных. При изучении функций нескольких переменных следует поставить во главу угла тему «Неявные функции и их дифференцирование». Это связано с тем, что именно эта тема завершает изучение функций одной переменной.
Алгебра. Особое внимание при изучении многочленов над полем действительных чисел следует уделить связи основной теоремы алгебры и теоремы Безу. При обсуждении вопросов деления с остатком одного многочлена на другой полезно использовать аналогию с делением чисел в позиционных системах счисления. Необходимо акцентировать внимание на способах нахождения целых корней. В частности, студенту необходимо научиться для уравнений третьей степени, имеющих целый корень, находить и остальные корни. Следует детально рассмотреть работу с комплексными числами в тригонометрической форме с акцентом на извлечение корней из единицы. Вся эта тематика активно используется и в линейной алгебре, и в теории обыкновенных дифференциальных уравнений.
Обыкновенные дифференциальные уравнения. Пропедевтика дифференциальных уравнений с разделяющимися переменными с помощью дифференциальных уравнений вида y ' = f ( y ) (см. Тему 10). Образное описание уравнений первого порядка (см. Тему 11). Аналогия между множеством решений уравнения второго порядка и множеством прямых на плоскости (см. Тему 12).
Линейная алгебра. Вопрос об определителе как объёме (см. Тему 13). Геометрическое истолкование правила Крамера (см. Тему 14).
Теория вероятности. Все рассматриваемые нами вопросы, связанные с теорией вероятности, а именно, комбинаторика, геометрические вероятности, независимые события, аксиоматическое определение независимости и вывод геометрического характера независимости из алгебраического определения, вынесены в Тему 1.
Преподавание математики в наше время не может обойтись без использования вычислительной техники. Преподавателем могут быть использованы и такие программы общего назначения как Excel, и многочисленные программы, изначально имеющие математическую направленность. Автор статьи использует подобные программы, но его особой благосклонностью пользуется язык программирования Small Basic. Написание простых, но основанных на математических идеях, программ в известном смысле помогает своеобразной материализации математических понятий.
Отметим, что выбранные темы, как правило, не являются «финальными». Предпочтение отдавалось «промежуточным» темам, затрагивающим те вопросы, которые ещё появится в процессе обучения.
6. МЕТОДИЧЕСКИЕ РАЗРАБОТКИ, ОТНОСЯЩИЕСЯ К КОНКРЕТНЫМ ТЕМАМ
Рассказ о соответствующих разработках уместно предварить известнейшим, но и остроумнейшим анекдотом, связанным с важными особенностями процесса обучения. Учитель сетует на бестолковость ученика: «Ну, такая бестолочь, что сил нет. Объяснял ему, объяснял, сам понял, а он не понимает». В анекдоте точно схвачена определённая особенность преподавательской работы. Годами объясняя одни и те же темы, учитель порой начинает видеть их несколько иначе. Оказывается, что в на первый взгляд простом и не таящем никаких сложностей материале, вскрываются неожиданные внутренние связи. И тот, кто вдруг начинает их видеть, может гордо заявить: «Сам понял». Так что далее читатель имеет возможность ознакомится с некоторыми простыми математическими вопросами, которые понял автор статьи.
Тема 1. Связь между вычислением площади прямоугольника и перемножением скобок. Данная тема восходит к геометрической алгебре, возникшей в Древней Греции, когда числа понимались как длины отрезков, а произведение двух чисел интерпретировалось как площадь прямоугольника.
Для умножения действуют законы коммутативности и ассоциативности, выражаемые равенствами a х b = b х a и (a х b) х с = a х (b х с).
Для обоснования этих правил следует использовать геометрическое истолкование умножения. При многократном сложении (b раз) нескольких равных куч (по a предметов), можно заменить каждую кучу полосой из a единичных квадратов и сложить b полос одну под другой. В итоге получится прямоугольник a на b, площадь которого равна a х b. Его можно повернуть на 90° и представить, что он сложен из a горизонтальных полос, содержащих по b единичных квадратов. Площадь его не изменилась, следовательно, a х b = b х a.

При рассмотрении произведения трёх чисел a х b х с предметы можно заменить единичными кубами и сложить из них параллелепипед. Его можно сложить из с горизонтальных пластин размером a на b, или же из а вертикальных пластин размером b на с. Произведение a х b х с равно объёму параллелепипеда, а, значит, (a х b) х с = a х (b х с). Так же как и в случае сложения, закон ассоциативности позволяет использовать запись произведения нескольких сомножителей вообще без скобок.
a = 6, b = 3, c = 3
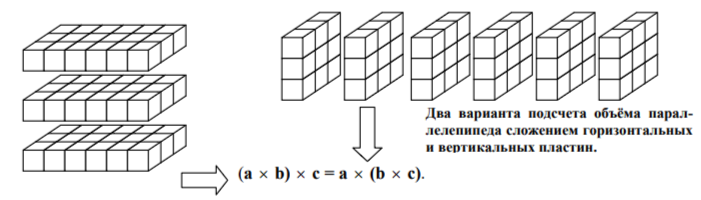
Геометрическое истолкование умножения позволяет понять смысл закона, связывающего операции сложения и умножения. Речь идёт о законе дистрибутивности.
Произведение чисел a и d можно рассматривать как выражение для площади прямоугольника со сторонами a и d. Разобьём сторону длиной d на две части, длины которых обозначим через b и c (таким образом, d = b + c). Исходный прямоугольник будет разбит на две части, сумма площадей которых как раз и равна площади исходного прямоугольника. Символически это обстоятельство можно записать в виде равенства a • (b + c) = a • b + a • c, которое выражает закон дистрибутивности.
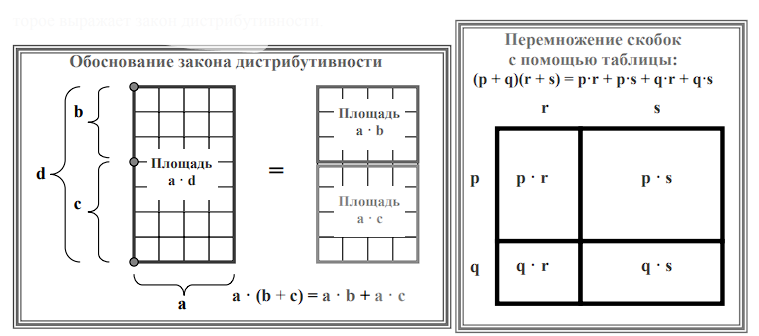
Закон дистрибутивности позволяет перемножать скобки, содержащие любое количество слагаемых. При этом могут использоваться два подхода. Первый состоит в том, что исходное выражение преобразуется по законам коммутативности, ассоциативности и дистрибутивности. В этом состоит основной принцип алгебраических вычислений, приводящий к выводу новых формул. Приведём пример перемножения двух скобок, содержащих по два слагаемых:
(p + q) • (r + s) = (p + q) • r + (p + q) • s = r • (p + q) + s • (p + q) = r • p + r • q + s • p + s • q
Второй подход основан на геометрическом истолковании умножения. Одну сторону прямоугольника разбивают на отрезки, число которых равно числу слагаемых в первой скобке, и возле каждого отрезка записывают одно из этих слагаемых. Со второй стороной прямоугольника поступают аналогично, применительно ко второй скобке. Проводя через точки деления вертикальные и горизонтальные линии, разбивают исходный прямоугольник на малые прямоугольники, в каждый из которых вписывают его площадь, равную произведению длин его сторон. Можно сказать, что исходный прямоугольник превратится в таблицу, клетками которой являются малые прямоугольники. Площадь большого прямоугольника одновременно равна произведению скобок и сумме малых прямоугольников. В итоге можно сформулировать правило: произведение скобок равно сумме всех попарных произведений каждого слагаемого из первой скобки на каждое слагаемое второй скобки.
Итак, при подобном подходе возникает своеобразная триада: перемножаемые скобки, прямоугольная таблица и прямоугольник, разбитый на части вертикальными и горизонтальными линиями. Пока речь шла только о том, как надёжно перемножить две скобки с большим числом слагаемых - с помощью таблице. Однако указанная триада тесно связана с некоторыми вопросами теории вероятностей.
Кроме статистической и классической интерпретаций понятия вероятности можно дать этому понятию геометрическое истолкование. С помощью достаточно простой геометрической модели можно успешно решать некоторые задачи вероятностей, имеющие заведомо негеометрическое содержание. Более того, эта модель позволяет разъяснить важнейшее понятие теории вероятности - понятие независимых событий.
Задача о стрелках. Предположим, что навыки стрелка обеспечивают вероятность поражения цели с вероятностью р. Таким образом, вероятность промаха стрелка равна q = 1 - p. Естественно, что этим обеспечивается выполнение стандартного условия: p + q = 1. Геометрической моделью процесса стрельбы сделаем процесс бросания точки на отрезок единичной длины. При этом отрезок должен быть разбит на две части длиной p и q. Если точка попадает в первый отрезок, то событие соответствует попаданию стрелка в мишень (с вероятность p), соответственно, попадание точки в отрезок q соответствует промаху стрелка (с вероятностью q). Модель полностью соответствует бытовой интуитивной установке: вероятность найти упавшую монету на некотором участке пропорциональна длине этого участка. Сразу отметим, что числа p и q могут быть иррациональными и несоизмеримыми. Это означает, что задача не может быть сведена к классической вероятности.
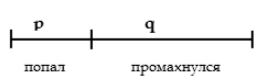
Теперь рассмотрим стрельбу двух стрелков. Первый из них попадает с вероятностью р1 и промахивается с вероятность q1 = 1 - p1, а второй с вероятностями р2 и q2 = 1 - p2.
Решим вопрос о том, какова вероятность различных исходов стрельбы двух стрелков. Совместный выстрел можно рассматривать как бросание двух точек на стороны единичного квадрата. Однако можно рассматривать брошенные на стороны квадрата точки как проекции третьей точки, случайным образом брошенной в квадрат.
Квадрат можно рассматривать как комнату, пол которой полностью покрыт четырьмя прямоугольными коврами. Каждый ковёр соответствует одному из четырёх возможных событий:
А - попали оба стрелка;
Б - первый попал, второй промазал;
В - первый промазал, второй попал;
Г - оба промазали.
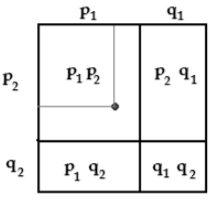
Геометрическая модель в полном соответствии с бытовой интуицией показывает, что исходы стрельбы двух стрелков ковров, то есть произведениями вероятностей попаданий и промахов обеих стрелков:
Событие А (оба попали) наступает с вероятностью р1*р2;
Событие Б (первый попал, второй промазал) - с вероятностью р1*q2;
Событие В (первый промазал, второй попал) - с вероятностью p2*q1;
Событие Г (оба промазали) - с вероятностью q1*q2.
Задача об исходе стрельбы двух стрелков решена.
Теперь можно немного поговорить о понятии независимости событий. С одной стороны, независимость интуитивно понимается как, отсутствия влияния одного события на другое. С другой стороны, в теории вероятностей события называются независимыми, если вероятность совместного наступления двух событий равна произведению вероятностей этих событий. Геометрическая модель хотя бы отчасти демонстрирует, почему используются столь разные определения независимости.
Когда совместное событие конструируется с помощью прямого произведения, как квадрат из двух отрезков, возникает независимость событий.

Если стреляют два стрелка, событий четыре. Они перечислены выше. Если же стреляют три стрелка, то есть к двум добавляется третий, то каждое событие для двух стрелков превращается в два: два стрелка стреляли именно так, при этом третий либо попал, либо не попал. Значит, для трёх стрелков событий 8. Легко понять, что для n стрелков событий 2n.
![]() Для трёх стрелков события таковы: все трое попали, не попал только первый, не попал только второй, не попал только третий, попал только первый, попал только второй, попал только третий, все трое не попали. (Куб разрезан на 8 частей).
Для трёх стрелков события таковы: все трое попали, не попал только первый, не попал только второй, не попал только третий, попал только первый, попал только второй, попал только третий, все трое не попали. (Куб разрезан на 8 частей).
Чтобы получить полное решение задачи о трёх стрелках, то есть для роятностей всех восьми событий, нужно перемножить три скобки (найти объём каждой из восьми составляющих куб частей):
(p1 + q1) (p2 + q2) (p3 + q3) = p1p2p3 + q1p2p3 + p1q2p3 + p1p2q3 + p1q2q3 + q1p2q3 + q1q2p3 + q1q2q3.
Часто требуется найти вероятности объединённых событий, например, событие «попал только один стрелок» складывается из трёх событий «попал только первый», «попал только второй», «попал только третий». Его вероятность равна p1q2q3 + q1p2q3 + q1q2p3.
Аналогичным способом, перемножая скобки, можно решить задачу о нескольких стрелках. Одним из вариантов задачи о многих стрелках является задача об одном стрелке, который стреляет несколько раз. Здесь вероятности попаданий (р) и промахов (q) одинаковы в каждой скобке. Для перемножения скобок можно использовать бином Ньютона.
Наиболее естественный вопрос в данном случае, какова вероятность того, что цель при n выстрелах поражена 0 раз, 1 раз, ... n раз. Каждое из этих событий можно рассматривать как объединение событий более простых событий.
Например, событие «стрелок попал один раз» состоит из событий типа «стрелок попал первым выстрелом, остальными промахнулся», «стрелок попал вторым выстрелом, остальными промахнулся» и т. д.
Итак, упомянутая выше триада действует в элементарной теории вероятностей. Она работает там, где события независимы. Перемножение скобок и таблица позволяют определиться с возможными исходами и их вероятностями. Прямоугольник даёт задаче геометрическую интерпретацию. При этом независимость событий увязывается с прямым произведением единичных отрезков.
Следующим этапом изучения является схема испытаний Бернулли. При этом триада продолжает иметь столь же большое значение. В том числе и при выводе формулы бинома Ньютона
Бином Ньютона - это формула для возведения двучлена p + q в n-ю степень. При перемножении n скобок из каждой скобки выбирают либо слагаемое р, либо слагаемое q. Любое произведение слагаемых имеет вид pkqn-k Поскольку мы вынимаем из каждой скобки или р, или q, возникает вопрос: сколько членов вида pkqn-k будет получено для каждого конкретного значения k?
Мы приходим к следующей задаче. Дано n коробок, в каждой из которых лежат один белый (р) и один чёрный (q) шар. Из каждой коробки наугад вынимают один шар. Каково количество вариантов, при которых будет вынуто ровно k белых шаров?
По смыслу сочетаний таких вариантов будет Cnk. Следовательно, произведение pkqn-k войдёт в окончательный результат с коэффициентом Cnk . Из этого и следует формула бинома:
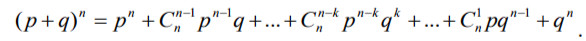
Схема испытаний Бернулли. Задача о стрелках и комбинаторика соединяется в теории, созданной Якобом Бернулли, старшим в семье великих математиков Бернулли. В схеме испытаний Бернулли многократно выполняются однотипные опыты, приводящие к наступлению (с вероятностью р) или ненаступлению (с вероятностью q = 1 - р) одного и того же события А. Например, такая ситуация возникает при многократных выстрелах по цели одного и того же стрелка.
Опыты предполагаются независимыми. По этой причине вероятности событий перемножаются как выше в задаче о стрелках. Только в этом случае стрелок один и стреляет последовательно. Для двух выстрелов вероятность двух попаданий равна р2. Вероятность двух промахов равна q2. Наконец, вероятность одного попадания складывается из вероятностей двух несовместных событий - (попадание, промах) и (промах, попадание), то есть эта вероятность равна 2pq.
Легко понять, что указанные вероятности равны слагаемым бинома Ньютона: (p + q)2 = p2 + 2pq + q2. Можно понять, что при многочисленных испытаниях возникнет сходная ситуация.
Пусть проведено n испытаний Бернулли. Обозначим через P(n, k) вероятность того, что в n испытаниях благоприятное событие А наступило ровно k раз. Тогда на основе того, что вероятности совместного наступления независимых событий перемножаются и с помощью бинома, получим формулу: P(n, k)=Cnkpkqn-k.
Итак, вероятность того, что число успехов при n испытаниях равно m такова:
Pm=Cnmpmqn-m. Если рассмотреть все вероятности событий от нуля до n успехов будет получено так называемое биномиальное распределение вероятностей.
Наконец, приведём ещё одно рассмотрение в том же ключе.
О понятии независимости. Очевидно, что для возникновения зависимости необходимо наличие хотя бы двух персонажей. Рассмотрим систему из двух субъектов А и В. Пусть субъект А в отсутствии субъекта В может по собственному произволу переходить в одно из состояний (а1; а2; ... ап). Соответственно, субъект В в отсутствии субъекта А может по собственному произволу переходить в одно из состояний (b1; b2; ... bm).
При совместной деятельности обоих субъектов каждый из них может ограничивать свободу другого. Это выражается, например, в том, что субъект В не может попадать в состояние b1, когда субъект А находится в состоянии а1. Таким образом, независимость субъектов друг от друга состоит в том, что при любом состоянии субъекта А субъект В также может принимать любое доступное ему в одиночестве состояние. И наоборот, при любом состоянии субъекта В субъект А также может принимать любое доступное ему состояние.
При описании совместных действий субъектов А и В в качестве состояния системы следует указывать пару (состояние А; состояние В). Итак, состояния системы можно полностью описать двумерной таблицей или, иными словами, матрицей <ai, bj>:
|
(a1, b1) |
(a2, b1) |
... |
(an, b1) |
|
(a1, b2) |
(a2, b2) |
... |
(an, b2) |
|
... |
... |
... |
... |
|
(a1, bm) |
(a2, bm) |
... |
(an, bm) |
Легко понять, что в случае, когда состояния системы, состоящей из двух субъектов, описываются полной матрицей, приведённой выше, субъекты А и В независимы. Если же некоторые состояния запретить, вычеркнув из клеток матрицы, соответствующие элементы, между субъектами возникает зависимость.
Состояние зависимости описать порой нелегко. Зато независимость описать достаточно просто. Для этой цели следует использовать важное математическое понятие - прямое произведение, созданное Рене Декартом при разработке метода координат. Прямым произведением Х*У двух непустых множеств Х и У называется множество всех упорядоченных пар вида (х, у), где х ∈ Х и у ∈ У.
Множества Х и У могут быть и конечными и бесконечными. Если оба множества конечны, то прямое произведение можно представить, как матрицу, что мы уже и сделали. Наиболее известным примером прямого произведения бесконечных множеств является декартова плоскость.
Можно рассматривать прямое произведение множества на себя. Поскольку множество действительных чисел можно отождествить с точками прямой, то декартова плоскость может рассматриваться и как множество пар действительных чисел (алгебраическая точка зрения), и как евклидова плоскость (геометрическая точка зрения). Произведение R*R* ,, ,*R = Rn является множеством упорядоченных n-ок действительных чисел и называется n-мерным пространством.
Теперь обратимся к аксиоматическому определению независимости событий, которое даётся в алгебраической форме и сводит независимость к ситуации, когда вероятность одновременного наступления событий А и В равна произведению вероятностей этих событий.
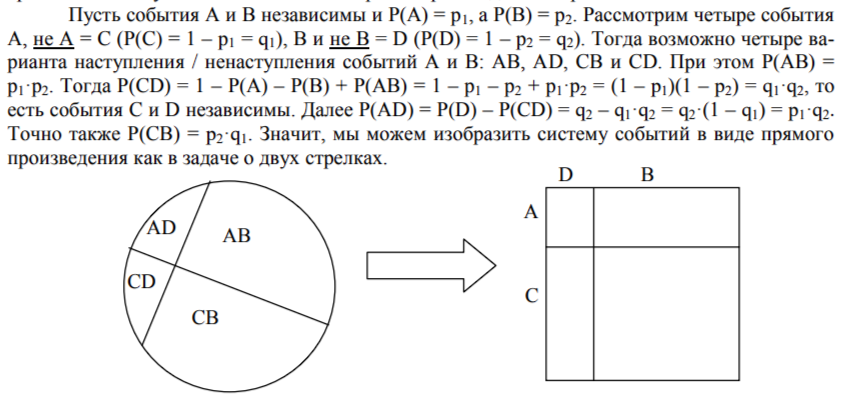
То есть даже чисто алгебраическое определение независимости событий приводит к геометрическому образу, связанному с прямым произведением, а, следовательно, к осмысленному восприятию независимости в реальном мире.
Отметим ещё, что понятие независимости является необходимым и при освоении программирования. Речь идёт о выборе простого (переменные зависимы) или вложенного цикла (переменные независимы).
Тема 2. Число п, радианная мера, тригонометрия.
Личное знакомство с числом п. Число п является важнейшим математическим объектом. Но о его значении учащимся просто сообщают. Желательно, чтобы они сами осуществили хоть какое-то действие в этом направлении, хотя бы и примитивное. Для этого можно раздать студентам (конечно, лучше было начать со школьников) распечатанные заранее чертежи с четвертью круга, покрытой сеткой из единичных квадратов. Далее производится приближённый, и в чём-то субъективный, подсчёт площади круга, что в итоге позволяет, используя формулу площади круга, вычислить приближённое значение числа п. Если Рамануджан был лично знаком с каждым натуральным числом, то студенту полезно лично познакомиться хотя бы с одним иррациональным.
Приведём чертёж и пример вычисления (операция умножения обозначена по-программистски - звёздочкой). Сначала вычисляется площадь сектора, потом площадь круга и, наконец, число п с помощью деления площади на квадрат радиуса (r = 25). Sсектора=18*18+2*(16+15+14+12+10+7+2) +2*(0,9+0,8+0,5+0,5+0,2+0,9+0,5+0,2+0,5+0,2+0,5+0,2+0,5+0,5 +0,5)=490,8 4*490,8 : 625 = 3,14112 ~ п.
Площадь сектора состоит из площади квадрата, из числа незакрашенных клеток двух полусегментов и из субъективно оцененных площадей разрезанных окружностью клеток.
Радианная мера углов. Тот факт, что все окружности подобны друг другу, лежит в основе формулы для вычисления длины окружности: c = 2пг. А эта формула в свою очередь положена в основание радианной меры углов. Прежде всего, надо отметить, что понятие угла не является таким уж простым и однозначным. Существует, по крайней мере, три точки зрения на углы.
-
Угол - это фигура, составленная двумя лучами, исходящими из одной точки. Эта точка называется вершиной угла, а лучи - сторонами угла.
-
Угол - это фаза вращения луча вокруг его начала. При этом фиксируется как начальное, так и конечное положение луча, т. е. угол в первом смысле, но и количество проделанных лучом оборотов. Обычно вращение против часовой стрелки считается положительным, а по часовой стрелке - отрицательным.
-
Угол - это мера угла второго типа. Естественной мерой углов является количество оборотов, которое проделал луч при вращении. Это количество может быть не только целым или дробным, но и любым действительным числом со знаком. Мерой угла первого типа обычно считают количество оборотов со знаком плюс, получаемое при вращении одной стороны угла до совпадения с другой по кратчайшему пути.
Итак, исходной мерой для измерения углов, являются обороты (и их доли). Всякая другая мера получается из оборотов с помощью умножения на избранный по каким-то соображениям коэффициент. Например, градусы - это обороты, умноженные на 360. В данном случае коэффициент выбран для астрономических нужд (он близок к количеству дней в году и делится на многие «удобные» числа: 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180).
Важнейшей для математики мерой углов является радианная мера (от слова «радиус», указывающего на участие окружности). Рассмотрим угол второго типа. Из центра вращения опишем окружность единичного радиуса. Теперь вращение луча сопровождается движением по окружности точки (это точка пересечения окружности с лучом). Теперь при вращении луча сам луч отмеряет угол, а точка на окружности - дугу. После полного оборота точка пробежит по окружности расстояние равное двум п. Если выбрать коэффициентом для меры угла 2п, то мера угла будет совпадать с длинной дуги, пройденной точкой по окружности. Именно эта мера и называется радианной.
Если вместо единичной окружности использовать окружность радиуса r, то при полном обороте луча точка пройдёт по окружности расстояние 2пг, т. е. радианы умножаются на радиус. Легко понять, что если луч заметёт угол ф, то точка пройдёт по дуге расстояние, равное фг. Установление простой связи между мерой угла и длиной дуги и определяет важность радианной меры углов.
Поясним, почему в математическом анализе используется именно радианная мера углов. При вычислении производной синуса используется замечательный предел ![]() . Для доказательства того факта, что данный предел равен единице, используются неравенства, снизу и сверху оценивающие площадь сектора единичной окружности, соответствующего углу ф. Эта площадь заключена между sinx/2 и tgx/2. Площадь окружности единичного радиуса равна пr2 = п. Она соответствует сектору в 2п радиан. Тогда сектору с углом ф соответствует площадь, равная ф/2п*п*r2=ф/2. Отсюда следует, что для радианной меры величина угла заключена между синусом и тангенсом, а любая другая мера нарушает эти неравенства. Замечательный предел в случае другой меры углов не равнялся бы единице.
. Для доказательства того факта, что данный предел равен единице, используются неравенства, снизу и сверху оценивающие площадь сектора единичной окружности, соответствующего углу ф. Эта площадь заключена между sinx/2 и tgx/2. Площадь окружности единичного радиуса равна пr2 = п. Она соответствует сектору в 2п радиан. Тогда сектору с углом ф соответствует площадь, равная ф/2п*п*r2=ф/2. Отсюда следует, что для радианной меры величина угла заключена между синусом и тангенсом, а любая другая мера нарушает эти неравенства. Замечательный предел в случае другой меры углов не равнялся бы единице.
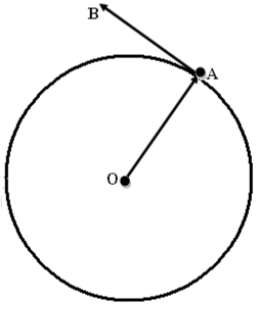
Тригонометрия. О повторении тригонометрических формул мы уже говорили. Теперь поговорим о вычислении производных синуса и косинуса с помощью соображений, относящихся к кинематике. Возможно, уместнее было бы разместить это рассуждение в рамках темы 8, однако, как верно сказано в «Повести о Ходже Насреддине», таньга не превращается в динар, если переложить её из правого кармана в левый. Отметим, что обращение при изучении математики к кинематическим, механическим и физическим аналогиям бывает довольно продуктивным (см. например [М. Е. Степанов, 2007]).
После того, как дано общее определение синуса и косинуса как абсциссы и ординаты конца единичного радиус-вектора, исходящего из начала координат, можно сразу определить вертикальную и горизонтальную составляющие скорости конца единичного радиус-вектора, то есть производные синуса и косинуса.
Рассмотрим единичный радиус-вектор ОА (созф; зтф), вращающийся против часовой стрелки с единичной угловой скоростью. Поскольку величина угла ф задаётся радианной мерой, вектор скорости АВ точки А перпендикулярен ОА. Кроме того, в силу согласованности радианной меры и длины дуги скорость точки А равна единице. Из этого следует, что вектор АВ имеет координаты (-sinф; соsф). А это и означает, что производной синуса является косинус, а производной косинуса - минус синус.
Тема 3. Векторная трактовка аналитической геометрии.
Вектор как смещение. Геометрическое определение вектора на плоскости как направленного отрезка АВ я предпочитаю заменить определением вектора как сдвига или смещения из точки А в точку В. Кто-то скажет, что разница невелика. Однако для такой замены всё же есть основание. Оно состоит в следующем. Хорошо развитое понимание работы с векторами не только на плоскости, но и в многомерном евклидовом пространстве, основывается на аксиоматике Вейля, которая связывает точки и вектора.
В то же время студенты часто воспринимают точки и вектора порознь. Восприятие вектора как сдвига позволяет донести до студента смысл точечно-векторного равенства типа В = А + АВ. Далее приведём фрагмент из электронного конспекта.
Главным понятием векторной алгебры является вектор. На данном этапе рассматриваются только вектора на плоскости. Вектор одновременно может рассматриваться и с геометрической точки зрения, и с точки зрения алгебраической. В геометрическом смысле понятие вектора совпадает с понятием сдвига или перемещения из точки в точку. Сдвиг из точки А в точку В можно изобразить направленным отрезком АВ. Каждый сдвиг можно разбить на два последовательных - горизонтальный сдвиг на расстояние х и вертикальный сдвиг на расстояние у. Вектор АВ алгебраически записывают в виде пары координат (х; у). При этом координаты точки А (хА; уА) и точки В (хВ; уВ) связаны соотношениями хВ = хА + х и уВ = уА + у.
Пусть на плоскости заданы точки А (хА; уА) и В (хВ; уВ). Их координаты называются абсолютными. Координаты вектора АВ (х; у) называются относительными координатами точки В относительно точки А, при этом х = хВ - хА и у = уВ - уА. Успешный расчёт координат точек требует использования абсолютных и относительных координат.
Поскольку смысл вектора состоит в сдвиге из точки в точку, сдвиг из точки А в точку В, а затем из В в точку С, приводит к сдвигу из точки А в точку С. Если заданы координаты двух векторов - АВ (х1; у1) и ВС (х2; у2), то вектор АС имеет координаты (х1 + х2; у1 + у2). Так определяется операция сложения векторов.
Ещё одной операцией, связанной с векторами является умножение вектора на число. Пусть задан вектор АВ (х; у) и любое действительное число λ, тогда λ*АВ = АС (λ*х; λ*у). Исключительная важность умножения вектора на число связана с тем, что концы векторов вида λ*АВ заметают прямую АВ. Кроме того, операция умножения вектора на число позволяет делить отрезок на равные части. Наконец, умножение вектора на число позволяет выполнять гомотетию на плоскости.
Смысл гомотетии лучше всего передаётся процессом фотографирования и проектирования изображения на экран с помощью проектора.

Название «гомотетия» складывается из двух греческих корней: гомо - одинаковый и тетос - расположение, т. е. гомотетия - это одинаковое расположение одинаковых по форме (но не по размеру) фигур или тел. С гомотетией связано важнейшее геометрическое понятие подобие. Любые две подобных фигуры можно расположить так, чтобы они оказались гомотетичными.
Математически гомотетия описывается следующим образом. Пусть задана некоторая фигура Ф1, точка О, называемая центром гомотетии, и число k, называемое коэффициентом гомотетии. Фигура Ф2 гомотетичная фигуре Ф1 с центром О и коэффициентом гомотетии k строится так:
-
возьмём любую точку М1 фигуры Ф1;
-
получим вектор ОМ2, умножив вектор ОМ1 на число k (ОМ2 = k*0М1);
-
точка М2 - конец полученного вектора ОМ2, является точкой гомотетичной фигуры Ф2, соответствующей точке М1;
-
пусть точки О, М1, М2 имеют координаты (х0, у0), (х1, у1), (х2, у2) соответственно. Тогда, используя координатную запись операции умножения вектора на число, получим следующие результаты: ОМ1 = (х1 - х0; у1 - у0), ОМ2 = k*OМ1 = (k*(х1 - х0); k*(у 1 - у0)). Наконец, координаты точки М2 вычисляются по формулам х2 = х0 + k*(x1 - x0) и y2 = y0 + k*(y1 - y0).
Подвергнув все точки фигуры Ф1 этой операции, получим фигуру Ф2.
Ортогональность векторов. Рассмотрим элементарный (без использования скалярного произведения) способ поворота вектора на четверть полного оборота. Этот вопрос так
или иначе рассматривается в курсе аналитической геометрии, например, при написании уравнения прямой, перпендикулярной данной.
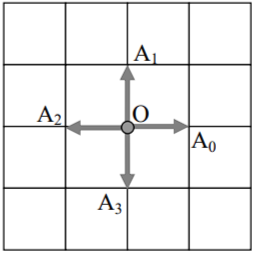
Рассмотрим операцию поворота вектора на 90° (или на — радиан). Займёмся детальным изучением этой процедуры. 2
Начнём с вектора ОА0 (1; 0). Будем последовательно поворачивать его на 90° против часовой стрелки, получая его новые положения ОА1 (0; 1), ОА2 (-1; 0), ОА3 (0; -1). Изначально горизонтальный вектор становится вертикальным. Таким образом, первая и вторая координаты вектора ОА0 переставляются и становятся координатами вектора ОА1.
При следующем повороте вектор снова становится горизонтальным, но имеет теперь противоположное направление. Чтобы получить вектор ОА2, координаты вектора ОА1 переставляются, и дополнительно первая координата меняет знак. На самом деле точно также можно было поступить и при переходе от вектора ОА0 к ОА1, поскольку смена знака нуля ничего не меняет. Таким же образом осуществляется переход от вектора ОА2 к вектору ОА3 и от вектора ОА3 к вектору ОА0.
Задание. Сформулировать правило поворота вектора на 90° против часовой стрелки и обосновать, что оно действует и для произвольных векторов, то есть для тех, которые имеют обе ненулевые координаты.
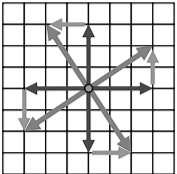
Правило поворота вектора на 90° против часовой стрелки: при повороте вектора на 90° против часовой стрелки переставляются его первая и вторая координаты, новая первая координата при этом меняет знак.
Произвольный вектор может быть разложен на горизонтальную и вертикальную составляющие. При вращении вектора эти составляющие также вращаются и, для них выполняется это правило. Из этого следует, что правило выполняется и в общем случае. Теперь легко сформулировать ещё одно правило.
Правило поворота вектора на 90° по часовой стрелке: при повороте вектора на 90° по часовой стрелке переставляются его первая и вторая координаты, а новая вторая координата меняет знак.
Скалярное произведение. Приведём небольшой электронный конспект, посвящённый этому важному понятию с физической мотивировкой.
Введём операцию скалярного умножения векторов. Она кардинально отличается от операции сложения векторов и операции умножения вектора на число. И в том, и в другом случае результатом являются вектора. Результатом же скалярного перемножения двух векторов является число.
Чтобы разобраться с причинами возникновения этой необычной операции, надо отметить, что векторы имеют прямую связь с физикой, поскольку в физических теориях часто встречаются направленные величины: скорости, ускорения, силы. По этой причине введение алгебраической операции, называемой скалярным произведением двух векторов, можно мотивировать с помощью физической аналогии.

Пусть мы перемещаем тело по горизонтали, прилагая к нему силу F, направленную к этой горизонтали под углом а. Примером такой ситуации в быту является перемещение санок, которые любитель кататься тянет за верёвочку, или перемещение повозки, которую тянет лошадь. Разложим силу, приложенную к повозке, на её вертикальную и горизонтальную составляющие. Тогда в перемещении тела будет участвовать только активная горизонтальная составляющая силы. Она равна F •cos а, то есть длине проекции силы F на горизонталь.

Это и есть формула для получения скалярного произведения в координатах. Выпишем её ещё раз без промежуточных вычислений: (a, b) = xa*xb + ya*yb.
Тема 4. Уравнения прямых и кинематическая форма линейных преобразований. Пропедевтика некоторых вопросов линейной алгебры.
В аналитической геометрии используются различные формы уравнений, описывающих прямые, но основными являются два вида. Первый вид - линейное уравнение с двумя неизвестными, которое выводится с помощью скалярного произведения. Второй вид - параметрическое уравнение, которое выводится с помощью операции умножения направляющего вектора на число-параметр.
Параметрические уравнения можно вывести и с помощью кинематических соображений. При этом уравнения принимают специфическую форму, поскольку эти уравнения будут содержать координаты двух точек, через которые проходит соответствующая прямая. Выведем эти уравнения.

Аффинная геометрия изучает свойства фигур на плоскости, в трёхмерном пространстве, а также в многомерных пространствах, задаваемых точечно-векторной аксиоматикой. При произвольных аффинных преобразованиях, сохраняются отношение длин параллельных отрезков, параллельность прямых, свойство фигуры быть прямой линией или плоскостью. Аффинное преобразование плоскости переводит сеть, состоящую из единичных квадратов, в сеть, состоящую из равных параллелограммов. Соответственно, аффинное преобразование многомерного пространства переводит укладку, состоящую из единичных многомерных кубов, в сеть, состоящую из равных многомерных параллелепипедов. Используя это обстоятельство, получим сначала формулы для аффинных отображений одной плоскости на другую в кинематической форме, а затем обобщим их на многомерный случай.
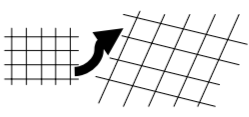
Рассмотрим две плоскости, на каждой из которых задана декартова система координат: (t1, t2) и (х, у). Кроме того, на второй плоскости задан параллелограмм ABCD. Его положение задаётся координатами трёх его вершин А (х0, у0), В (х1, у1) и D (х2, у2). Отметим, что упомянутые системы координат могут быть определены и на одной плоскости. Наша задача состоит в том, чтобы отобразить точки единичного квадрата, расположенного на первой плоскости, на параллелограмм, лежащий на второй плоскости. Сделаем это с помощью следующей кинематической модели.
Возьмём два секундомера и начнём перемещаться по первой плоскости из начала координат в точку (t1, t2). Включим первый секундомер и будем двигаться по горизонтали, согласуя показания секундомера и абсциссу движущейся точки. В момент t1 отключим первый секундомер, включим второй и будем двигаться вертикально, согласуя показания второго секундомера и ординату движущейся точки. В момент t2 остановимся.
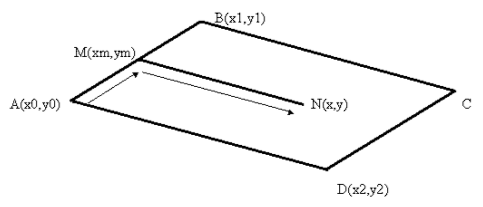
На второй плоскости организуем синхронное движение второй точки, которая является аффинным образом первой точки. Пусть эта точка движется, ориентируясь на направление сторон параллелограмма AbCD следующим образом. Сначала движение происходит по стороне АВ с такой скоростью, что за единицу времени, она переместилась бы в точку В. Однако остановка происходит в момент времени t1. Обозначим точку, которой мы достигли через М, и обозначим её координаты через xm и ym. Затем будет начато движение точки параллельно стороне AD в течение времени t2. Во второй фазе движения скорость её такова, что путь от А до D она также прошла бы за единицу времени. Точка N, которая будет достигнута в итоге, и есть аффинный образ точки (t1, t2). Наша задача состоит в том, чтобы определить координаты х и у точки N. Это легко сделать, используя параметрические уравнения прямой АВ и прямой MN, параллельной к AD.


Тема 5. Секущие кривых второго порядка и метод построения касательных с помощью параллельных секущих. Пучки прямых и кривых.
Кривые второго порядка открывают большие возможности пропедевтики идей математического анализа, в частности связанных с проведением касательных. Одним с способов работы с касательными предоставляет аппарат квадратных уравнений. Очень эффектными и эффективными являются и методы Роберваля, связанные с разложением скоростей точки, двигающейся по кривой, на две составляющие [Е. Н. Берёзкин, 1974]. Мы же опишем применяемый нами метод построения касательных с помощью параллельных секущих, который будет развит в Теме 8. Этот метод позволяет обойти явное применение пределов.
Метод построения касательных с помощью параллельных секущих. Поясним эффективность работы с секущими на трёх примерах. Рассмотрим функцию у = х2. Секущая, проходящая через точки х1 и х2 имеет уравнение у = (х1 + х2)*х - х1 х2. Допустим, что (х1 + х2)= 2х0, где х0 постоянное число. Тогда всевозможные секущие вида у = (х1 + х2)*х + b параллельны друг другу. Если точки х0 и х1 сольются, то секущая превратится в касательную. Её уравнение примет вид y=2х0 - х02. Тем самым получено не только уравнение касательной, но и вычислена производная соответствующей функции.

Пучки прямых и кривых. Рассмотрение пучков прямых, окружностей и кривых второго порядка может быть проведён без особых проблем, например, следуя [П. С. Александров, 1968]. Нам представляется, что это очень полезно, поскольку готовит студента к восприятию таких принципиально связанных с семействами функций разделами математики как теория дифференциальных уравнений.
Тема 6. Линейная функция, элементарные функции (показательная функция), число е.
Линейная функция и арифметическая прогрессия. Графики функций являются непрерывными кривыми, но, рассматривая только целые значения х, из функций можно получать последовательности. Поведение последовательностей иногда легче себе представить, чем поведение функций.
Задача. Какая последовательность порождается линейной функцией?
Решение. Линейная функция описывается формулой у = кх + b. Взяв вместо х натуральные числа n = 1, 2, 3, ... , и, использовав вместо у для обозначения членов последовательности символ an, получим формулу an = k*n + b. Это формула арифметической прогрессии с разностью равной k.
Иногда наоборот следует переходить от последовательности к функции. Взяв за основу арифметическую прогрессию, можно определить любые её члены с натуральными и даже целыми индексами. Затем можно «уплотнить» прогрессию введя индексы вида (2n+1)/2. Такому индексу соответствует значение, равное среднему арифметическому an и an+1. В результате такого уплотнения можно от последовательности чисел прийти к линейной функции (см. [М. Е. Степанов, 2009]).

В [Г. М. Фихтенгольц, 1962] доказывается, что последовательность (1 + 1/n)n является монотонно возрастающей и ограниченной. Из этого следует, что указанный предел, названный в честь Эйлера числом е, действительно существует. Доказательство ведётся с использованием бинома Ньютона. При этом выкладки студенту могут показаться довольно сложными, как и вообще любые вычисления, основанные исключительно на загадочной для новичка технике преобразований. Ему неясно, почему делается именно так, и как можно было именно это преобразование придумать.
Далее в курсе анализа устанавливается, что показательная функция, с основанием равным е, обладает замечательным свойством. Её производная равна самой этой функции, т. е. (ex )' = ех. Однако не совсем понятна причина этого обстоятельства: сначала вводится какой-то замысловатый предел, а его введение почему-то даёт такой удачный результат. Мы хотим показать, что объяснить причины, по которым такая «хитрая» последовательность приводит к хорошему результату, довольно легко без сложных вычислений. Сделаем это по пунктам.

Теперь связь между двумя определениями числа е становится понятной.
Нам остаётся получить результат, связанный с дифференцированием функции y = ex. Пока мы знаем, что её производная в нуле равна единице, то есть ![]() . Но теперь мы можем найти производную в любой точке:
. Но теперь мы можем найти производную в любой точке:
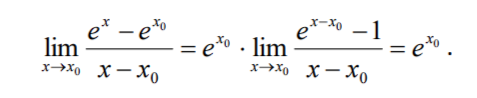


Построение касательных методами кинематики (см. также [М. Е. Степанов], [М. Е. Степанов, 2016]). Покажем эффективность кинематических методов на примере кардиоиды. Если закрепить окружность и катить по ней равную ей окружность с пером на ободе, будет построена одна из бесконечного числа улиток Паскаля, за сходство с сердцем названная кардиоидой. Кардиоида, как и прочие улитки Паскаля, является благодарным предметом для исследователя. Все доказательства её свойств основаны на простейших теоремах элементарной геометрии.
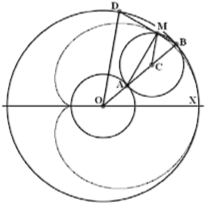
Теорема. Пусть точки В и D движутся по окружности радиуса 3r с постоянными скоростями, причём скорость точки D в два раза больше скорости точки В. Точка М, которая отсекает треть хорды BD (ВМ = 1/3 BD) описывает кардиоиду, а любая хорда BD является касательной к этой кардиоиде.
Доказательство. Кардиоида построена с помощью неподвижной окружности радиуса r с центром О и катящейся окружности радиуса r с центром С. Пусть ∠ ВОХ = u. Выберем точку D так, чтобы ∠ BoD = u
Соприкоснувшиеся при качении дуги обеих окружностей имеют длину ru. Из исходного положения Х перо переместилось в точку М. При этом горизонтальная линия ОХ перешла в линию ОВ, а перо же за счёт качения отклонилось от этой линии на угол u, то есть ∠ ВСМ = u. Треугольники OBD и СВМ являются равнобедренными и имеют углы при вершинах равные u. Значит у них равны и углы при основании, то есть ∠ СВМ = ∠ OBD = (п-u)/2. Из этого следует, что точка М лежит на хорде BD. Из подобия названных треугольников следует, что ВМ = 1/3 BD.
Далее ∠ ВАМ = u/2, как вписанный в окружность и опирающийся на дугу, соответствующую центральному углу u. Таким образом, треугольник МАВ является прямоугольным, то есть хорда BD перпендикулярна отрезку АМ, исходящему из неподвижный в данный момент точки А. Как указано выше, это означает, что хорда BD является касательной к этой кардиоиде в точке М. Теорема доказана.
Теорема позволяет без всяких проблем получить параметрические уравнения кардиоиды. Точка В имеет координаты (3r*cos u; 3г sin u), а точка D - координаты (3r*cos 2u; 3г*sin 2u). Из теоремы следует, что отрезки с концами, имеющими соответствующие координаты, являются огибающими кардиоиды. Координаты точки М вычисляются по формулам, которые и являются нужными уравнениями:

Отметим, что фактически рассматривались вопросы, относящиеся к дифференциальной геометрии, но методы использовались элементарные.
О связи производной и интеграла. Как известно, в курсе математического анализа принято выявлять механический и геометрический смыслы производной. При введении интеграла полезно каким-то образом обосновать связь между производной и интегралом. При этом слова Барроу о том, что задача проведения касательных является обратной к задаче вычисления площадей, могут только озадачить студентов. Иное дело, когда мы говорим, что дифференцированию соответствует задача отыскания скорости в случае, когда известна зависимость пройденного пути от времени, а интегрированию соответствует задача отыскания пути в случае, когда известна зависимость скорости движения от времени. Здесь очевидным образом проявляется тот факт, что задачи дифференцирования и интегрирования являются обратными друг к другу. Таким образом, связь между производной и интегралом должна объясняться через механический смысл производной.
Тема 9. Определение интеграла и простейшее дифференциальное уравнение вида y' = f(x). Пропедевтика дифференциальных уравнений первого порядка. Приёмы использования интеграла как суммы с опорой на символику Лейбница.
Определение интеграла. Определённые сложности при введении интеграла возникают из-за того, что сразу появляется несколько понятий таких, как первообразная, неопределённый интеграл, определённый интеграл. К тому же определение первообразной не является слишком кратким и удобным.
Возможно, наиболее удобно определять первообразную и неопределённый интеграл как решение дифференциального уравнение вида y' = f(x), а самоё это уравнение следует назвать простейшим дифференциальным уравнением. Это позволяет сразу же готовить студентов к восприятию дифференциальных уравнений, к тому, что существует бесконечное множество решений, каждое из которых является функцией. А единственное решение можно выбрать, указав на плоскости точку, через которую проходит кривая, соответствующая единственному решению. Полезно также сразу изобразить векторное поле, соответствующее простейшему дифференциальному уравнению.
Приёмы использования интеграла как суммы с опорой на символику Лейбница . Для вычисления площадей криволинейных трапеций вводится понятие определенного интеграла. Интуитивно он является пределом суммы бесконечно малых величин f(x)dx. Согласно обозначениям Лейбница интеграл записывается следующим образом:
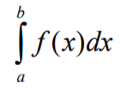
Смысл этого обозначения прост: знак ∫ - стилизованная буква S символизирует сумму. Буквы a и b указывают отрезок, на котором задана величина f(x). Они называются пределами интегрирования. Произведение f(x)dx выражает бесконечно малые суммируемые порции вычисляемой величины - длины, площади, объёма и т.д.
Для решения задач, состоящих в вычислении некоторой величины, с помощью определённого интеграла нужно представить эту величину, как сумму произведений вида f(x)dx. При этом не имеет значения, являются ли слагаемые площадями, длинами, объёмами, массами, зарядами и т. д. Далее рассматриваются примеры вычисления величин различного характера.
Тема 10. Пропедевтика дифференциальных уравнений с разделяющимися переменными с помощью дифференциальных уравнений вида y ' = f (y) .

Тема 11. Образное описание дифференциальных уравнений первого порядка.
Уравнения первого порядка вида y' = f(x, y) задаёт на плоскости векторное поле. Можно сравнить ситуацию либо с устоявшимися ветрами над озером, либо с устоявшимися течениями в водах того же озера. Решением же этого уравнения является траектория парусного кораблика или лодочки, движущихся под влиянием ветров, либо под влиянием течений. Ясно, что траектория существенным образом зависит от начального положения судёнышка, то есть от того, где оно опущено на воду.
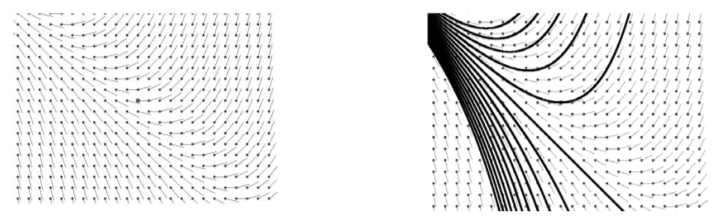
Тема 12. Аналогия между множеством решений дифференциального уравнения второго порядка и множеством прямых на плоскости.
Поскольку обыкновенное дифференциальное уравнение первого порядка имеет множество решений, зависящих от одного параметра, студенту легко представить совокупность всех решений по аналогии с решениями простейшего дифференциального уравнения y' = f(x). Множество решений дифференциального уравнения второго порядка характеризуется тем, что через каждую точку плоскости проходит решение имеющее своё направление (мы не рассматриваем случаи существования особых точек). По этой причине можно сказать, что структурно множество решений дифференциального Уравнения второго порядка напоминает множество прямых на плоскости. С каждой точкой связан своеобразный пучок решений.

Что касается множества решений дифференциального уравнения третьего порядка, то с каждой точкой плоскости и с каждым направлением связано семейство решений отличающихся друг от друга кривизной. Наглядной моделью здесь может послужить пучок касающихся друг от друга окружностей.
Тема 13. Вопрос об определителе как объёме.
Очень важным для математики вообще является то обстоятельство, что определитель квадратной матрицы равен объёмУ параллелепипеда, натянУтого на вектора, соответствУющие столбцам (строкам) этой матрицы. Этот факт доказывается в рамкаХ аналитической геометрии при рассмотрении смешанного произведения. Однако для матриц всеХ остальныХ размерностей, включая и матрицУ 2 на 2 об этом факте едва ли не Умалчивают. Возможно, я ошибаюсь, но, например, в такиХ прекрасныХ книгаХ как [А. Г. Курош, 1962] и [И. М. Гельфанд, 1966] об этом не говорится, по крайней мере, специально.
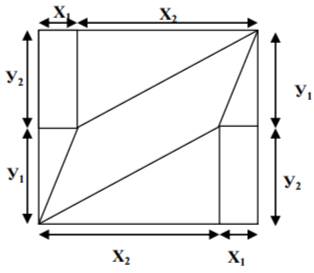
По этой причине желательно уделить данному вопросу особое внимание. Для этой цели нужно акцентировать внимание студентов на этом вопросе и хотя бы для матрицы 2 на 2 получить указанный результат, что не представляет труда:
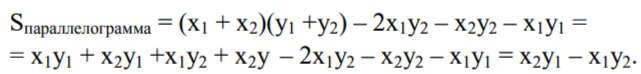


7. ЗАКЛЮЧЕНИЕ
В статье рассмотрены некоторые вопросы методики преподавания высшей математики. Многие из обсуждаемых автором методических проблем связаны с современной ситуацией, возникшей в школьном и вузовском образовании.
Рассматриваются и конкретные вопросы методики. Прежде всего, речь идёт о математическом анализе и линейной алгебре. Например, в статье показано, что определение числа е через предел известной числовой последовательности является следствием определения числа е как основания степенной функции, имеющей в нуле производную равную единице. Приведён также метод построения касательных с помощью параллельных секущих, как и многие другие методические результаты. Рассмотрение этого и других вопросов ведётся с позиции геометрической наглядности
Литература
- Ю. Л. Ершов. Алгебра и логика: старые и новые связи. В Библиографическом указателе работ Ершова. Новосибирск, Изд. Института математики, 2015.
- А. Б. Сосинский. Умер ли Никола Бурбаки? Ega-math.narod.ru.
- А. Пуанкаре, Л. Кутюра. Математика и логика. М., Изд. ЛКИ, 2010.
- Сайт Математического института им. В. А. Стеклова РАН. Наиболее важные результаты научных исследований (mi.ras.ru).
- И. М. Глазман, Ю. И. Любич. Конечномерный линейный анализ в задачах. М., Наука, 1969.
- М. Е. Степанов. Метод сложных движений в компьютерной геометрии. Моделирование и анализ данных. Научный журнал. – Вып. 1, 2011.
- М. Е. Степанов. Метод криволинейных координат в компьютерной геометрии. Моделирование и анализ данных. Научный журнал. – Вып. 3, 2013.
- М. Е. Степанов. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных. Труды факультета информационных технологий. – Вып. 3, 2007.
- Е. Н. Берёзкин. Курс теоретической механики, М., Изд. МГУ, 1974.
- П. С. Александров. Лекции по аналитической геометрии. М., Наука, 1968.
- М. Е. Степанов. Об одном классе непрерывных функций. Моделирование и анализ данных. Труды факультета информационных технологий. – Вып. 4, 2009.
- Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. М., Физматгиз, 1962.
- Б. Гелбаум, Дж. Олмстед. Контрпримеры в анализы. М., Мир, 1967.
- М. Е. Степанов. Эрлангенская программа Клейна и геометрия треугольника (часть первая). Моделирование и анализ данных. Научный журнал. – Вып. 1, 2015
- М. Е. Степанов. Эрлангенская программа Клейна и геометрия треугольника (часть вторая). Моделирование и анализ данных. Научный журнал. – Вып. 1, 2016.
- А. Г. Курош. Курс высшей алгебры. М., Физматгиз, 1962.
- И. М. Гельфанд. Лекции по линейной алгебре. М., Наука, 1966.
Информация об авторах
Метрики
Просмотров
Всего: 859
В прошлом месяце: 18
В текущем месяце: 2
Скачиваний
Всего: 560
В прошлом месяце: 3
В текущем месяце: 0