Экспериментальная психология
2025. Том 18. № 1. С. 54–69
doi:10.17759/exppsy.2025180104
ISSN: 2072-7593 / 2311-7036 (online)
Роль внимания в преодолении ограничений пространственного статистического научения
Аннотация
Контекст и актуальность. Визуальное пространственное статистическое научение — способность непреднамеренно усваивать закономерности, связанные с расположением предметов относительно друг друга. Если закономерность касается некоторого множества объектов, то усваиваться может информация о целом множестве или о некоторых его подмножествах, например попарных связях между элементами. Согласно выводам проведенных ранее исследований, при усвоении глобальной информации происходит блокировка информации о подмножествах и, наоборот, усвоение информации о подструктуре приводит к блокировке информации о целом множестве. Цель. Нас интересовала ситуация, когда внимание направляется на одни элементы множества чаще, чем на другие. В эксперименте проверялось, сохранится ли в данном случае информация обо всем множестве элементов или усвоится только то подмножество, на которое чаще направлялось внимание. Методы и материалы. Испытуемые (N = 104) выполняли задачу поиска целевого элемента конфигурации. Частота направления внимания на разные элементы стимулов, составленных по определенной схеме, варьировалась с помощью инструкции. Результаты. Было обнаружено, что полные стимулы и стимулы, состоящие из подмножества элементов, на которые чаще направлялось внимание, представляются более знакомыми, чем стимулы с нарушением закономерности. Выводы. В представленном эксперименте продемонстрирована возможность одновременного усвоения пространственной информации как о глобальной закономерности, так и о ее подструктуре. Результаты обсуждаются с точки зрения существования двух типов статистического научения — требующего и не требующего участия внимания.
Общая информация
Ключевые слова: научение, имплицитное научение, зрительное внимание, закономерности обучения/научения
Рубрика издания: Когнитивная психология
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2025180104
Получена: 03.03.2024
Принята в печать:
Для цитаты: Деева Т.М., Козлов Д.Д. Роль внимания в преодолении ограничений пространственного статистического научения // Экспериментальная психология. 2025. Том 18. № 1. С. 54–69. DOI: 10.17759/exppsy.2025180104
Полный текст
Введение
При взаимодействии с окружающей средой человек способен неосознанно выделять и выучивать существующие в ней закономерности. Это явление называют статистическим научением (Conway, 2020; Turk-Browne, 2012). На усвоение закономерностей могут уходить годы или минуты (Turk-Browne, 2012). Выучиваться могут визуальные (Fiser, Aslin, 2001) аудиальные (Saffran, Aslin, Newport, 1996; Saffran et al., 1999) или даже кинестетические (Conway, 2005) паттерны. Статистическое научение происходит непреднамеренно, способность к нему проявляется уже в младенческом возрасте (Saffran, Aslin, Newport, 1996) и c незначительными изменениями сохраняется на протяжении всей жизни (Cox, Aimola Davies, 2022; Herff et al., 2020), но проявляется у разных людей в разной степени (Kidd et al., 2023; Siegelman, Bogaerts, Frost, 2017).
В ходе научения вычисляются условные вероятности одновременного или последовательного появления элементов паттерна (Endress, Mehler, 2009; Saffran, Aslin, Newport, 1996) и происходит фрагментирование входящей информации — чанкинг (Lengyel, Nagy, Fiser, 2021; Orbán et al., 2008; Perruchet, Pacton, 2006; Servan-Schreiber, Anderson, 1990). При выучивании одной и той же закономерности эти процессы могут протекать совместно и взаимодействовать (Franco, Destrebecqz, 2012; Rutar et al., 2022). Во многих ситуациях модулирующим фактором для статистического научения является внимание (Conway, 2020). Однако существуют и формы научения, не требующие внимания (Hendricks, Conway, Kellogg, 2013). Статистическое научение, происходящее при участии внимания, называют эксплицитным, а не требующее участия внимания — имплицитным. В современной литературе по статистическому научению общепринятым считается двусистемный подход, предполагающий, что данные типы научения обеспечиваются работой двух параллельных познавательных систем (Batterink et al., 2015; Conway, 2020; Dale R., Duran N., Morehead, 2012; Hendricks, Conway, Kellogg, 2013). Подключение той или иной системы может определяться сложностью и структурой паттерна (de Diego-Balaguer, Martinez-Alvarez, Pons, 2016), его одно- или мультимодальным характером (Keele et al., 2003). Возможно также, что имплицитная система активируется «по умолчанию», а эксплицитная подключается «опционально» в более сложных ситуациях научения (Batterink et al., 2015; Conway, 2020).
Статистическое научение происходит непреднамеренно, в процессе выполнения каких-либо других задач, не требующих знания о существовании закономерности. В экспериментальных условиях задача, выполняемая во время обучения, называется «задачей-прикрытием» (cover task) и подбирается так, чтобы затруднить экспликацию существующей закономерности и в то же время обеспечить обработку информации, содержащей эту закономерность. В визуальной модальности это может быть, например, задача зрительного поиска (Chun, Jiang, 1998; Goujon, Didierjean, Thorpe, 2015), детекция движения (Turk-Browne et al., 2009), задача категоризации изображений (Turk-Browne et al., 2010) или пассивное наблюдение (Fiser, Aslin, 2001; Fiser, Aslin, 2002). В ряде исследований продемонстрирована зависимость статистического научения от задачи-прикрытия (Himberger, Finn, Honey, 2022; Vickery et al., 2018; Zhao et al., 2011): одна и та же закономерность во время выполнения одних задач выучивается лучше, чем при выполнении других. Пока до конца не ясно, какими характеристиками должна обладать задача-прикрытие, чтобы научение происходило успешно или, наоборот, затруднялось.
Когнитивные процессы, задействованные при решении задачи, определяются, прежде всего, стимульным материалом и целью, задаваемой в инструкции. Основные характеристики стимульного материала, влияющие на эффективность научения — это сложность существующего паттерна (Remillard, 2008), структура отдельных элементов паттерна (Deroost, Soetens, 2006), неоднородность стимульного материала, приводящая к эффекту выскакивания (Деева, Козлов, 2022; Geyer, Zehetleitner, Müller, 2010). Если для одного и того же стимульного ряда в инструкциях ставятся разные задачи, то эффективность научения также оказывается различной (Himberger, Finn, Honey, 2022). Варьирование инструкций позволяет исследовать научение в условиях различной направленности и распределения внимания (Lleras, Von Mühlenen, 2004; Zhao et al., 2011). Для статистического научения одним из важнейших свойств внимания является селективность: визуальный паттерн усваивается лучше, если он содержится в релевантных задаче, а не в игнорируемых стимулах. Этот эффект был продемонстрирован при решении в процессе обучения задачи зрительного поиска (Jiang, Leung, 2005) и при одновременном предъявлении нескольких потоков визуальной информации (Turk-Browne, Jungé, Scholl, 2005). Похожий эффект наблюдался и при использовании задачи классификации стимулов: усвоение закономерности происходило только в том случае, если она была связана с характеристикой стимулов, служившей основанием для классификации; при классификации по другому основанию эффект научения исчезал (Vickery et al., 2018). Таким образом, статистическое научение модулируется вниманием, но при этом происходит непреднамеренно и не осознается, что приводит к двойственным выводам об автоматичности данного процесса (Himberger, Finn, Honey, 2022; Turk-Browne, Jungé, Scholl, 2005).
Еще одна общая проблема статистического научения связана с выбором меры научения. В экспериментах по статистическому научению могут применяться прямые или непрямые меры научения. В качестве прямой меры чаще всего используется тест на знакомость: после обучающей части испытуемым предъявляются пары стимулов, и в каждой паре требуется выбрать стимул, который кажется более знакомым. При выборе прямых мер научения необходимо учитывать, что знание о закономерности, полученное при решении каких-либо задач, не всегда проявляется при решении задач другого типа (Bays, Turk-Browne, Seitz, 2015). Непрямые меры научения предполагают измерение времени реакции или доли правильных ответов при продолжении решения той же задачи, что и в период обучения. Во многих случаях научение удается зафиксировать только с помощью прямых или только с помощью непрямых мер, в связи с чем хорошей практикой представляется использование в экспериментах мер научения разных типов (Himberger, Finn, Honey, 2022; Siegelman et al., 2018).
Наше исследование посвящено визуальному пространственному статистическому научению, т. е. усвоению закономерностей, определяемых пространственными отношениями между элементами сложного стимула. Это один из наименее изученных типов статистического научения. Выучивание пространственных закономерностей происходит в условиях обработки информации о множестве одновременно предъявляемых объектов. И механизмы статистического научения, и механизмы обработки зрительных массивов связаны с работой внимания. При статистическом научении уже после нескольких проб внимание сдвигается и/или распределяется с учетом существующего паттерна (Turk-Browne, 2012). Таким образом, статистическое научение оказывает влияние на «карту приоритетов», определяющую распределение и направление внимания при обработке сложных зрительных сцен (Theeuwes, Bogaerts, van Moorselaar, 2022). Как указывает Ян Тиус, на выбор объектов зрительного пространственного внимания влияют: входящая сенсорная информация, задаваемая стимулами (восходящее влияние); цель, определяемая текущей задачей (нисходящее влияние); и история решения таких задач, т. е. статистическое научение (Theeuwes, 2019; Theeuwes, Bogaerts, van Moorselaar, 2022). Данные факторы могут оказывать влияние на выполнение задачи независимо друг от друга (Gao, Theeuwes, 2020).
В экспериментальных условиях восходящее влияние визуальной информации легко минимизировать за счет использования однородного стимульного материала, что и осуществляется в стандартных экспериментах по визуальному пространственному статистическому научению (Fiser, Aslin, 2001; Fiser, Aslin, 2005; Zhao et al., 2011). Таким образом, при обработке визуального массива, состоящего из однородных элементов, в расположении которых имеется закономерность, «карта приоритетов» составляется под влиянием двух факторов — выполняемой задачи и выучиваемого паттерна. В парадигме усвоения контекстной подсказки при зрительном поиске было продемонстрировано, что не все элементы паттерна усваиваются одинаково: лучше усваиваются объекты, релевантные задаче или пространственно близкие к цели (Brady, Chun, 2007; Jiang, Leung, 2005; Zang et al., 2021). Однако, если поисковый массив предъявляется на очень короткое время (300 мс), картина меняется и происходит усвоение информации о полном множестве элементов, но не о релевантном подмножестве (Zang et al., 2021). Обсуждая полученные результаты, авторы противопоставляют селективное внимание глобальному, соответствующему восприятию множества как единого целого. Согласно их положению, при длительном времени предъявления происходит выделение релевантной информации с помощью селективного внимания, а глобальное внимание при этом блокируется, так как способствует получению нерелевантной информации.
Если же задача отсутствует и испытуемым предлагается пассивно смотреть на предъявляемые стимулы, то релевантность элементов паттерна оказывается выровненной, а знание — имплицитным, т.е. полученным без участия внимания. В этом случае статистическое научение также происходит, причем выучиваться могут как двухэлементные паттерны (Fiser, Aslin, 2001), так и более сложные структуры — паттерны из трех или четырех элементов (Fiser, Aslin, 2005). Для структур, содержащих более двух элементов, был продемонстрирован феномен, названный авторами ограничением встраиваемости статистического научения (embeddedness constraint of statistical learning): двухэлементные подструктуры, встроенные в более сложный паттерн, усваивались значительно хуже, чем аналогичные самостоятельные двухэлементные паттерны. Другими словами, пространственные структуры из трех или четырех элементов выучиваются только как целое, без знания о более мелких подструктурах этих множеств.
Как можно заметить, феномен ограничения встраиваемости (Fiser, Aslin, 2005) и идея блокировки глобального внимания (Zang et al., 2021) опираются на общий принцип оптимизации обработки информации, но описывают противоположные явления. В описанном ниже эксперименте мы проверяли возможность усвоения как целого множества, так и его подструктуры. Будет ли наблюдаться феномен ограничения встраиваемости, если при решении задачи-прикрытия внимание чаще направляется на одни элементы множества, чем на другие? Сохранится ли информация обо всем множестве элементов или усвоится только то подмножество, на которое чаще направлялось внимание?
Метод
Выборка и отбор испытуемых
Эксперимент проводился онлайн с помощью платформы PsyToolkit v. 3.4.4. (Stoet, 2010, 2017). В исследовании приняли участие студенты НИУ ВШЭ. За участие предусматривалось вознаграждение в виде дополнительных зачетных баллов. Исходная выборка составила 125 человек. Данные испытуемых исключались из анализа, если выполнялось хотя бы одно из условий:
- общее время прохождения эксперимента превышало 45 мин.;
- было больше 15 ошибок (10%) в основной части;
- было больше 3-х пропусков или долгих (больше 10 с) реакций в основной части.
После исключения 21 испытуемых итоговая выборка составила 104 человека от 18 до 21 года (М = 18,3; SD = 0,7), среди которых 16 мужчин.
Стимульный материал
Стимульный материал представлял собой наборы из пяти фигур черного цвета, одинаковых по форме, но различающихся размером, расположенных в фиксированных вершинах правильного пятиугольника (рис. 1а). Расстояние между центрами соседних фигур составляло 3,6 см, таким образом, угловой размер каждого стимула составлял около 13º. Порядок расположения фигур во всех стимулах соответствовал правилу, проиллюстрированному на рис. 1б. Всего использовалось 15 различных форм. Каждая форма использовалась в пяти стимулах, различающихся позицией начального (наименьшего) элемента, т.е. дающих все возможные «повороты» конфигурации. Таким образом, всего было составлено 75 стимулов.
В тестовой части эксперимента использовались также «неправильные» стимулы, расположение фигур в которых не соответствовало схеме, представленной на рис. 1б, и неполные стимулы, содержащие только 1, 2, 3-й или 3, 4, 5-й элементы. Неполные стимулы также могли быть «правильными» и «неправильными». Примеры стимульного материала для тестовой части представлены на рис. 2.
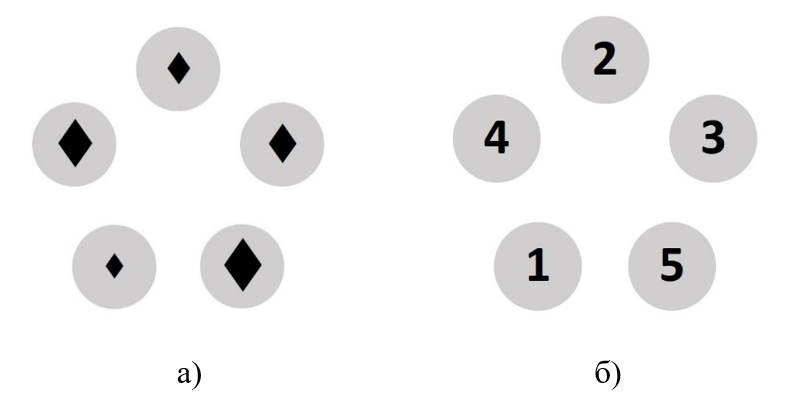
Рис. 1. Стимулы для обучающей части:
а) пример стимула; б) правило расположения фигур. Числа от 1 до 5 соответствуют рангу размера фигуры, где 1 — наименьшая фигура. Наименьшая фигура может занимать любую из пяти возможных позиций, в результате чего происходит «поворот» конфигурации на 36º, 72º, 98º или 144º
Fig. 1. Stimuli for the training part:
a) an example of a stimulus; b) a rule for the arrangement of figures. The numbers from 1 to 5 correspond to the figure size rank, where 1 is the smallest figure. The smallest figure can occupy any of the five possible positions, resulting in a “rotation” of the configuration by 36º, 72º, 98º, or 144º
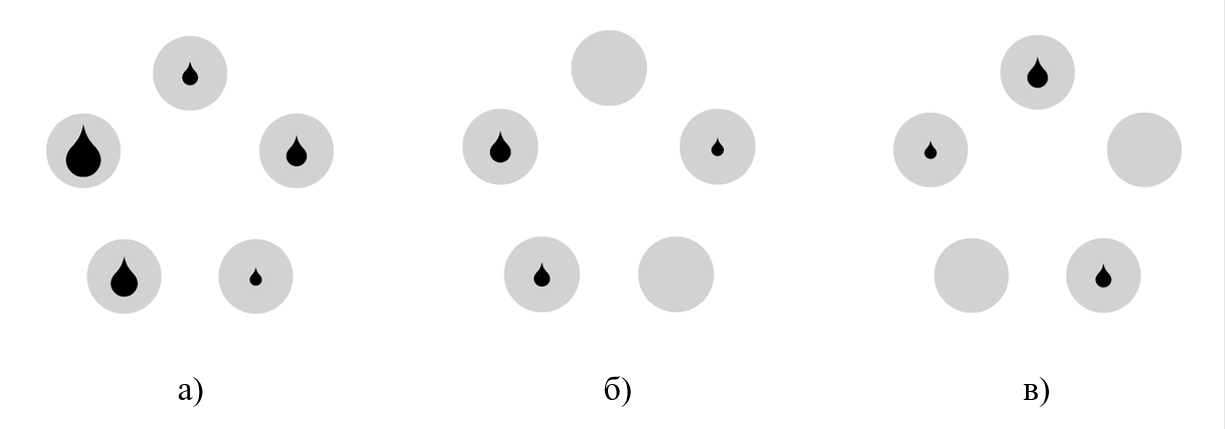
Рис. 2. Примеры дополнительных стимулов для тестовой части:
а) неправильный полный стимул; б) неполный правильный стимул с элементами 1, 2, 3; в) неполный неправильный стимул с элементами 1, 2, 3
Fig. 2. Examples of additional stimuli for the test part:
a) incorrect complete stimulus; b) incomplete correct stimulus with elements 1, 2, 3; c) incomplete incorrect stimulus with elements 1, 2, 3
Для указания целевых элементов в обучающей части и для обозначения типа стимулов в тестовой части использовались шкалы, представленные на рис. 3.

Рис. 3. Шкалы для указания целевых стимулов и типов стимульных пар:
а) пример шкалы для указания целевого элемента в обучающей части; в данном случае требуется указать позицию второй по величине фигуры; б, в, г) шкалы для тестовой части, соответствующие: б) полным стимулам; в) неполным «частым» стимулам из элементов 1, 2, 3; г) неполным «редким» стимулам из элементов 3, 4, 5
Fig. 3. Scales for specifying target stimuli and for the types of stimulus pairs:
a) an example of a scale for indicating the target element in the training part; in this case it is required to indicate the position of the second largest figure;
b, c, d) scales for the test part corresponding to: b) complete stimuli; c) incomplete “frequent” stimuli with only elements 1, 2, 3; d) incomplete “rare” stimuli with only elements 3, 4, 5
Ход эксперимента
Эксперимент состоял из двух частей — обучающей и тестовой. В каждой пробе обучающей части задача испытуемых состояла в указании позиции целевого элемента стимула, т. е. 1-й, 2-й, 3-й, 4-й или 5-й по величине фигуры. Позиции указывались нажатием одной из клавиш “Y”, “J”, “N”, “B”, “G”, расположение которых на клавиатуре примерно повторяет расположение вершин стимульного пятиугольника. Целевой элемент задавался с помощью специальной шкалы (см. образец на рис. 3а). Шкала предъявлялась в начале пробы в нижней части экрана и оставалась видимой до конца пробы. Через 700 мс после предъявления шкалы в центре экрана на 30 с или до реакции испытуемого предъявлялся стимул. Интервал между пробами составлял 600 мс.
Для выучивания соответствия клавиш и ознакомления с задачей перед началом эксперимента проводилась небольшая тренировка.
Обучающая часть эксперимента состояла из 150 проб, разбитых на два блока, с перерывом между блоками 30 с. Каждый из 75 стимулов предъявлялся дважды, по одному разу в первом и втором блоках, но целевые элементы для этих предъявлений не совпадали. Задачи, решаемые в ходе обучающей части, делились на частые и редкие. К частым задачам относился поиск 1-й (30 проб), 2-й (49 проб) или 3-й (50 проб) по величине фигуры; редкие задачи подразумевали поиск 4-й (10 проб) или 5-й (11 проб) фигуры. Частота нахождения целевого элемента в каждой из позиций была одной и той же. Фиксировались правильность и время ответа.
Сразу после завершения обучающей части следовала тестовая часть. В каждой пробе испытуемые решали задачу принудительного бинарного выбора: из двух стимулов предлагалось выбрать тот, который кажется более знакомым. Стимулы в каждой паре могли содержать пять фигур, как было раньше, или быть неполными — содержать только три из пяти фигур. Всего использовалось три типа тестовых пар:
- полные стимулы, содержащие 5 фигур;
- неполные «частые», содержащие только три меньшие фигуры (1, 2, 3-я по рангу);
- неполные «редкие», содержащие только три большие фигуры (3, 4, 5-я по рангу).
При этом только один стимул в каждой паре был «правильным», т. е. соответствовал схеме составления стимулов обучающей части. Всего в случайном порядке предъявлялось 30 стимульных пар — по 10 каждого типа.
В начале пробы на экране появлялась шкала, соответствующая типу предъявляемой в этой пробе пары (см. рис.3 б, в, г). Шкала оставалась на экране до окончания пробы. Через 1 с после предъявления шкалы в центре экрана последовательно с перерывом в 1 с предъявлялись два стимула, на 3 с каждый. Затем предлагалось выбрать более знакомый с помощью нажатия клавиш «1» или «2». Перерыв между пробами составлял 1,5 с. В каждой пробе фиксировалась правильность ответа.
Экспериментальные гипотезы
Нашей целью было сравнить выучивание подструктуры стимула, определяемой 1, 2 и 3-м элементами (далее «подструктуры 1-2-3»), на элементы которой чаще направлялось внимание, и выучивание полной структуры стимула. В качестве непрямой меры научения мы использовали время нахождения целевого элемента. Уменьшение времени поиска 2-й и 3-й фигур от начала к концу эксперимента рассматривалось как показатель научения1. Прямой мерой научения выступало количество правильных выборов на основании чувства знакомости в тестовой части. Результаты тестовой части могли соответствовать одному из четырех вариантов, представленных в табл. 1. Кроме того, мы планировали исследовать, насколько согласованными являются показатели научения, полученные с использованием прямой и непрямой мер. Если научение в тестовой части обнаружится главным образом у испытуемых, продемонстрировавших научение в обучающей части, то такая ситуация будет согласовываться с предположениями о постоянной активности имплицитной системы и «опциональном» подключении эксплицитной.
Таблица 1 / Table 1
Объяснения возможных результатов тестовой части
Explanations of possible results of the test part
|
Результаты тестовой части |
Возможные теоретические объяснения |
|
Усвоится только полный паттерн |
Фактор ограничения встраиваемости является довольно «сильным» и может помешать выучиванию подструктуры, на которую часто направляется внимание |
|
Усвоится только релевантная задаче подструктура 1-2-3 |
Внимание оказывает детерминирующее влияние на статистическое научение, а ограничение встраиваемости представляется «слабым» фактором, проявляющимся только при отсутствии задачи. Происходит блокировка знания о целостной структуре |
|
Усвоятся и полный паттерн, и подструктура 1-2-3 |
Процессы статистического научения, требующие и не требующие участия внимания, происходят параллельно и не интерферируют. Механизмы, осуществляющие ограничение встраиваемости и блокировку глобального внимания, требуют более тщательного исследования |
|
Не усвоятся ни паттерн, ни подструктура 1-2-3 |
Интерференция процессов статистического научения, требующих и не требующих участия внимания, может блокировать научение |
Анализ данных и результаты
Обучающая часть
В первую очередь мы проверяли наличие научения с помощью непрямой меры — времени решения. Для этого использовалась линейная модель со смешанными эффектами, где зависимой переменной было время поиска 1-го, 2-го и 3-го элементов конфигурации, независимыми переменными — номер пробы (численная) и ранг целевого элемента (фактор с тремя значениями), а случайными факторами — испытуемый и стимул. Значимыми оказались все коэффициенты регрессии (табл. 2). На протяжении всей обучающей части поиск 1-го элемента осуществлялся быстрее, а поиск 3-го элемента медленнее, чем поиск 2-го. От начала к концу обучающей части время поиска 2-го и 3-го элементов уменьшалось примерно одинаково, ускорение для этих задач оказалось больше, чем для поиска 1-го элемента. Наглядно динамика изменения среднего времени поиска элементов представлена на рис. 4.
Таблица 2 / Table 2
Смешанная линейная регрессия для времени поиска «частых» элементов
Mixed linear regression for the search time of “frequent items”
|
Предикторы |
Коэффициент |
Ст. ошибка |
df |
t |
p |
|
Интерсепт |
1870,07 |
65,89 |
249,93 |
28,382 |
< 0,001 |
|
Проба |
–3,75 |
0,48 |
1044,93 |
–7,815 |
< 0,001 |
|
2-й элемент |
968,28 |
55,13 |
629,11 |
17,564 |
< 0,001 |
|
3-й элемент |
1327,71 |
54,91 |
700,37 |
24,182 |
< 0,001 |
|
Проба: 2-й элемент |
–2,51 |
0,63 |
722,72 |
–3,970 |
< 0,001 |
|
Проба: 3-й элемент |
–2,56 |
0,63 |
728,64 |
04,070 |
< 0,001 |
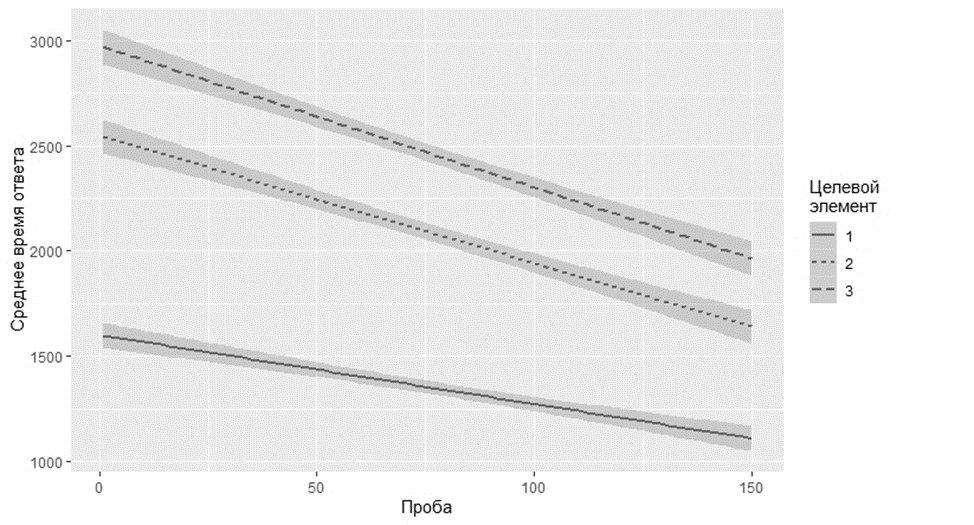
Рис. 4. Динамика изменения медианного времени поиска для «частых» задач
Fig. 4. Dynamics of change in median search time for “frequent” tasks
Далее мы провели индивидуальный анализ. Для каждого испытуемого строились две линейные модели зависимости времени решения от номера пробы. Одна модель для задачи поиска 2-го, а другая — для поиска 3-го по величине элемента конфигурации. Значимое уменьшение времени поиска хотя бы для одного из этих элементов рассматривалось как условный показатель научения. По этому критерию научение продемонстрировали 61 человек.
Тестовая часть
Для анализа выбора стимулов в тестовой части была построена логистическая регрессионная модель со смешанными эффектами, где зависимой переменной выступал выбор стимула, соответствующего или не соответствующего схеме, независимой переменной выступал тип стимульной пары (полный стимул, «частые» или «редкие» тройки элементов), а случайными факторами — испытуемый и стимульная пара. Данные логистической регрессии представлены в табл. 3. Условимся для краткости называть стимулы, соответствующие схеме, правильными. Правильным также будем называть выбор таких стимулов в пробах тестовой части. Вероятность выбора правильного полного стимула составила 0,54; правильные неполные «частые» стимулы выбирались с такой же вероятностью, а правильные «редкие» неполные стимулы — с вероятностью 0,49. Разница между вероятностью правильного выбора «редких» и «частых» неполных стимулов обнаружила значимость на уровне тенденции (р = 0,08). Согласно этим результатам, испытуемые чаще совершали правильный выбор на основании чувства знакомости, встречаясь с полными и «частыми» неполными стимулами, чем при встрече с «редкими» неполными. Наглядно оценка вероятности правильного выбора для стимулов каждого типа представлена на рис. 5.
Таблица 3 / Table 3
Смешанная логистическая регрессия для правильности выбора в тестовой части
Mixed logistic regression for correctness of choice in the test part
|
Предикторы |
Коэффициент |
Ст. ошибка |
Вероятность верного ответа |
z |
p |
|
«Частые» неполные стимулы |
0,15 |
0,08 |
0,54 |
1,80 |
0,07 |
|
«Редкие» неполные стимулы |
–0,21 |
0,12 |
0,49 |
–1,73 |
0,08 |
|
Полные стимулы |
0,01 |
0,12 |
0,54 |
0,12 |
0,90 |

Рис. 5. Вероятность правильного выбора в тестовой части по всей выборке. Пунктирная линия соответствует случайному выбору
Fig. 5. Probability of correct choice in the test part over the whole sample. The dotted line corresponds to a random choice
Аналогичный анализ, проведенный только для испытуемых, продемонстрировавших научение в обучающей части (61 чел.), показал, что в этой группе указанная выше тенденция усиливалась. Правильные «частые» неполные стимулы выбирались как более знакомые чаще случайного (р = 0,029) и чаще, чем неполные «редкие» стимулы (р = 0,044). Различия в частоте выбора правильных стимулов для разных типов стимулов у испытуемых, не продемонстрировавших научение, отсутствовали (для всех коэффициентов р > 0,42). Вероятность правильного выбора с учетом наличия или отсутствия показателей научения в обучающей части наглядно представлена на рис. 6. Мы также вводили фактор «научение» в логистическую регрессионную модель для всей выборки, описанную выше. Коэффициент при соответствующем предикторе оказался незначимым. Таким образом, мы оцениваем взаимосвязь между научением в обучающей части и правильными выборами в тестовой части как весьма слабую и недостаточно достоверную.
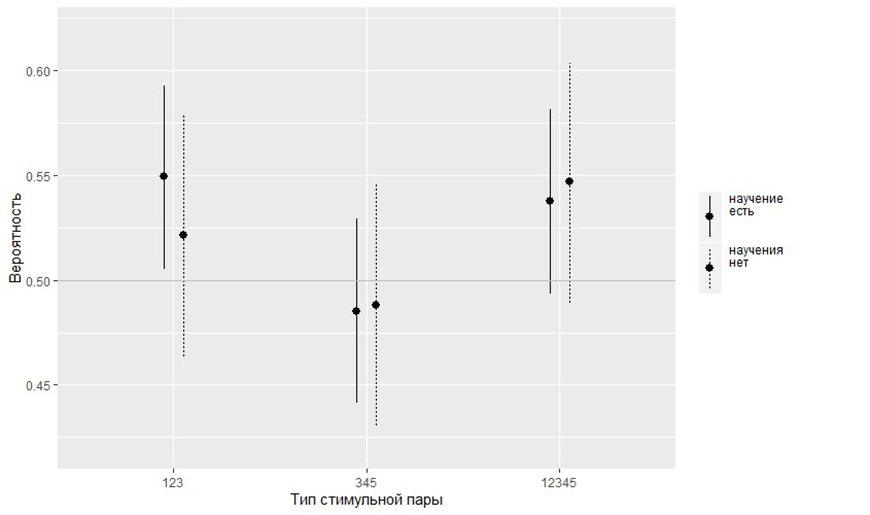
Рис. 6. Вероятность правильного выбора у испытуемых, продемонстрировавших и не продемонстрировавших научение в обучающей части. Серая линия соответствует случайному выбору
Fig. 6. Probability of correct choice in subjects who did and did not demonstrate learning in the training part. The gray line corresponds to a random choice
Обсуждение
Формально результаты анализа времени поиска в обучающей части могут служить лишь косвенным показателем научения из-за отсутствия контрольной группы, но, опираясь на полученные ранее результаты, мы склонны трактовать их в пользу существования научения. Согласно результатам нашего предыдущего исследования (Деева, Козлов, 2022, эксперимент 1), при отсутствии постоянной схемы составления стимулов уменьшение времени поиска также происходит, но в меньшей степени, чем при наличии постоянной схемы. В представленном в настоящей работе эксперименте мы не ставили цель репликации предыдущего исследования и полагали, что увеличение числа проб в обучающей части может лишь усилить, но не ослабить обнаруженный ранее эффект научения. Как было указано выше, уменьшение времени поиска 1-го элемента наблюдается независимо от наличия схемы составления стимула и, следовательно, объясняется причинами, не связанными с усвоением схемы, например ускорением моторной реакции или выучиванием размера элемента. В любом случае все эти причины ускорения ответа оказываются актуальны и для поиска других фигур, что, при отсутствии дополнительных факторов, позволяет ожидать той же динамики изменения времени ответа и для задач поиска 2-й и 3-й фигур. Однако при оценке для 2-й и 3-й фигур ускорение возрастает (см. рис. 4). Большее ускорение в задачах поиска 2-го и 3-го элементов происходит, скорее всего, за счет некоторого дополнительного фактора, не влияющего на скорость поиска наименьшей фигуры. Таким фактором нам представляется именно усвоение схемы расположения элементов в стимуле. Следовательно, можно говорить об обнаружении эффекта научения с помощью непрямой меры — динамики изменения времени ответа.
Наибольший интерес представляют результаты тестовой части эксперимента, в которой научение было обнаружено одновременно для полных стимулов и «частых» подструктур. Полученные результаты не демонстрируют ни блокировку глобального внимания (Zang et al., 2021), ни феномен ограничения встраиваемости (Fiser, Aslin, 2005). В условиях нашего эксперимента оба типа предполагаемых ограничений обработки информации оказались преодолены. На наш взгляд, такая ситуация полностью соответствует положению о задействовании в визуальном статистическом научении двух параллельных систем — эксплицитной и имплицитной. Эксплицитная система обеспечивала выучивание «частой» подструктуры 1-2-3, на элементы которой внимание направлялось в большинстве проб. А полная структура стимулов выучивалась за счет работы имплицитной системы, без участия внимания, аналогично тому, как это происходило в ранних экспериментах Файзера и Аслина (Fiser, Aslin, 2001; Fiser, Aslin, 2005) при отсутствии задачи-прикрытия. Таким образом, блокировка глобального внимания, скорее всего, может быть преодолена не только ограничением времени обработки стимула, как это было продемонстрировано в оригинальной работе (Zang et al., 2021), но и направлением внимания на разные элементы стимула или в разные области стимульной сцены. Что касается феномена ограничения встраиваемости, то он был зафиксирован только в условиях отсутствия задачи-прикрытия (Fiser, Aslin, 2005) и, согласно нашим результатам, не наблюдается при выполнении в процессе научения выполнению задачи, требующей фокусировки внимания на отдельных элементах стимула.
Альтернативное объяснение правильных выборов для полных и неполных «частых» стимулов может быть связано с тем, что либо часть стимула кажется знакомой благодаря знанию о целом стимуле, либо опознание полного стимула происходит за счет знакомости его части. Первый вариант представляется маловероятным, так как в этом случае знакомыми оказывались бы не только «частые», но и «редкие» неполные правильные стимулы. Возникновение ощущения знакомости для полного стимула на основании знания о его «частой» подструктуре более вероятно. Однако эта версия противоречит результатам экспериментов с контекстной подсказкой, где имплицитное выучивание части паттерна не приводит к опознанию целой конфигурации как более знакомой. При этом мы отдаем себе отчет в невозможности непосредственного перенесения результатов на наш случай хотя бы потому, что в парадигме контекстной подсказки, в отличие от нашего эксперимента, не предлагалось опознавать отдельные фрагменты паттерна. Вопрос о содержании знания, полученного в результате статистического научения, несомненно требует дальнейшего, более тщательного изучения.
Раздельный анализ для испытуемых, продемонстрировавших и не продемонстрировавших научение в обучающей части, показал противоречивые результаты. Мы не можем сделать однозначный вывод о связи уменьшения времени поиска в обучающей части и правильности выбора в тестовой части. Тем не менее тенденция к демонстрации научения в обеих частях эксперимента соответствует положению об индивидуальных различиях в способностях к статистическому научению (Kidd et al., 2023; Siegelman, Bogaerts, Frost, 2017) и может говорить об одновременном проявлении этих способностей для имплицитного и эксплицитного научения. Однако и здесь существует альтернативное объяснение, основанное на возникновении корреляции за счет использованных нами мер научения. Более точные выводы станут возможны только после исследования соответствия типов и способов измерения статистического научения.
Заключение
В целом, результаты проведенного нами эксперимента еще раз подчеркивают ведущую роль внимания в статистическом научении. Распределение и направление внимания в процессе научения являются ключевыми факторами, регулирующими содержание знания о закономерности и влияющими на эффективность научения. При этом полученные результаты соответствуют положению двусистемного подхода в статистическом научении, предполагающему усвоение части знания без участия внимания. Вопросы взаимодействия эксплицитной и имплицитной систем, обеспечивающих статистическое научение, заслуживают дальнейшего более подробного исследования.
1 Уменьшение времени поиска наименьшего элемента происходит независимо от наличия повторяющейся структуры и поэтому не рассматривается в качестве критерия научения (Деева, Козлов, 2022).
Литература
- Деева, Т.М., Козлов, Д.Д. (2022). Знак или форма? Имплицитное усвоение пространственной закономерности при сравнении величин чисел и фигур [Электронный ресурс]. Психологические исследования, 15(82), 4. https://doi.org/10.54359/ps.v15i82.1089
Deeva, T.M., Kozlov, D.D. (2022). A sign or a shape? Implicit learning of spatial regularity in size comparison tasks using numbers or geometrical figures. Psychological Studies, 15(82), 4. (In Russ.). https://doi.org/10.54359/ps.v15i82.1089 - Batterink, L.J., Reber, P.J., Neville, H.J., Paller, K.A. (2015). Implicit and explicit contributions to statistical learning. Journal of memory and language, 83, 62—78. https://doi.org/10.1016/j.jml.2015.04.004
- Bays, B.C., Turk-Browne, N.B., Seitz, A.R. (2015). Dissociable behavioral outcomes of visual statistical learning. Visual Cognition, 23(9—10), 1072—1097. https://doi.org/10.1080/13506285.2016.1139647
- Brady, T.F., Chun, M.M. (2007). Spatial constraints on learning in visual search: modeling contextual cuing. Journal of experimental psychology. Human perception and performance, 33(4), 798—815. https://doi.org/10.1037/0096-1523.33.4.798
- Chun, M.M., Jiang, Y. (1998). Contextual cueing: implicit learning and memory of visual context guides spatial attention. Cognitive psychology, 36(1), 28—71. https://doi.org/10.1006/cogp.1998.0681
- Conway, C.M. (2020). How does the brain learn environmental structure? Ten core principles for under-standing the neurocognitive mechanisms of statistical learning. Neuroscience and Biobehavioral Reviews, 112, 279—299. https://doi.org/10.1016/j.neubiorev.2020.01.032
- Conway, C.M., Christiansen, M.H. (2005). Modality-constrained statistical learning of tactile, visual, and auditory sequences. Journal of Experimental Psychology: Learning, Memory, and Cognition, 31, 24—39. https://doi.org/10.1037/0278-7393.31.1.24
- Cox, J.A., Aimola Davies, A.M. (2022). Age differences in visual statistical learning: Investigating the effects of selective attention and stimulus category. Psychology and Aging, 37(6), 698—714. https://doi.org/pag0000697
- Dale, R., Duran, N., Morehead R. (2012). Prediction during statistical learning, and implications for the implicit/explicit divide. Advances in cognitive psychology, 8(2), 196—209. https://doi.org/10.5709/acp-0115-z
- de Diego-Balaguer, R., Martinez-Alvarez, A., Pons, F. (2016). Temporal attention as a scaffold for language development. Frontiers in psychology, 7, 44. https://doi.org/10.3389/fpsyg.2016.00044
- Deroost, N., Soetens, E. (2006). Spatial processing and perceptual sequence learning in SRT tasks. Experimental Psychology, 53(1), 16—30. https://doi.org/10.1027/1618-3169.53.1.16
- Endress, A.D., Mehler, J. (2009). The surprising power of statistical learning: when fragment knowledge leads to false memories of unheard words. Journal of Memory and Language, 60(3), 351—367. https://doi.org/10.1016/j.jml.2008.10.003
- Fiser, J., Aslin, R.N. (2005). Encoding multielement scenes: statistical learning of visual feature hierarchies. Journal of Experimental Psychology: General, 134(4), 521. https://doi.org/10.1037/0096-3445.134.4.521
- Fiser, J., Aslin, R.N. (2002). Statistical learning of higher-order temporal structure from visual shape sequences. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(3), 458—467. https://doi.org/10.1037/0278-7393.28.3.458
- Fiser J., Aslin R.N. (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychological Science, 12, 499—504. https://doi.org/10.1111/1467-9280.00392
- Franco, A., Destrebecqz, A. (2012). Chunking or not chunking? How do we find words in artificial language learning? Advances in Cognitive Psychology, 8(2), 144—154. https://doi.org/10.5709/acp-0111-3
- Gao, Y., Theeuwes, J. (2020). Independent effects of statistical learning and top-down attention. Attention, perception & psychophysics, 82(8), 3895—3906. https://doi.org/10.3758/s13414-020-02115-x
- Geyer, T., Zehetleitner, M., Müller, H.J. (2010). Contextual cueing of pop-out visual search: When context guides the deployment of attention. Journal of Vision, 10(5), 20. https://doi.org/10.1167/10.5.20
- Goujon, A., Didierjean, A., Thorpe, S. (2015). Investigating implicit statistical learning mechanisms through contextual cueing. Trends in Cognitive Sciences, 19(9), 524—533. https://doi.org/10.1016/j.tics.2015.07.009
- Hendricks, M.A., Conway, C.M., Kellogg, R.T. (2013). Using dual-task methodology to dissociate automatic from nonautomatic processes involved in artificial grammar learning. Journal of Experimental Psychology. Learning, Memory, Cognition, 39(5), 1491—1500. https://doi.org/10.1037/a0032974
- Herff, S.A., Zhen, S., Yu, R., Agres, K.R. (2020). Age-dependent statistical learning trajectories reveal differences in information weighting. Psychology and Aging, 35(8), 1090. https://doi.org/10.1037/pag0000567
- Himberger, K.D., Finn, A.S., Honey, C.J. (2022). On the automaticity of visual statistical learning. bioRxiv, 07. https://doi.org/10.1101/2022.07.04.498716
- Jiang, Y., Leung, A.W. (2005). Implicit learning of ignored visual context. Psychonomic Bulletin and Review, 12, 100—106. https://doi.org/10.3758/BF03196353
- Keele, S.W., Ivry, R., Mayr, U., Hazeltine, E., Heuer, H. (2003). The cognitive and neural architecture of sequence representation. Psychological review, 110(2), 316—339. https://doi.org/10.1037/0033-295X.110.2.316
- Kidd, E., Arciuli, J., Christiansen, M.H., Smithson, M. (2023). The sources and consequences of individual differences in statistical learning for language development. Cognitive Development, 66, 101335. https://doi.org/10.1016/j.cogdev.2023.101335
- Lengyel, G., Nagy, M., Fiser, J. (2021). Statistically defined visual chunks engage object-based attention. Nature communications, 12(1), 1—12. https://doi.org/10.1038/s41467-020-20589-z
- Lleras, A., Von Mühlenen, A. (2004). Spatial context and top-down strategies in visual search. Spatial vision, 17(4—5), 465—482. https://doi.org/10.1163/1568568041920113
- Orbán, G., Fiser, J., Aslin, R.N., Lengyel, M. (2008). Bayesian learning of visual chunks by human observers. Proceedings of the National Academy of Sciences, 105(7), 2745—2750. https://doi.org/10.1073/pnas.0708424105
- Perruchet, P., Pacton, S. (2006). Implicit learning and statistical learning: One phenomenon, two approaches. Trends in Cognitive Sciences, 10, 233—238. https://doi.org/10.1016/j.tics.2006.03.006
- Remillard, G. (2008). Implicit learning of second-, third-, and fourth-order adjacent and nonadjacent sequential dependencies. Quarterly journal of experimental psychology, 61(3), 400—424. https://doi.org/10.1080/17470210701210999
- Rutar, D., de Wolff, E., Kwisthout, J., Hunnius, S. (2022). Statistical learning mechanisms are flexible and can adapt to structural input properties. Available at SSRN 4027230. https://doi.org/10.21203/rs.3.rs-2402303/v1
- Saffran, J.R., Aslin, R.N., Newport, E.L. (1996). Statistical learning by 8-month-old infants. Science, 274, 1926—1928. https://doi.org/10.1126/science.274.5294.1926
- Saffran, J.R., Johnson, E.K., Aslin, R.N., Newport, E.L. (1999). Statistical learning of tone sequences by human infants and adults. Cognition, 70(1), 27—52. https://doi.org/10.1016/S0010-0277(98)00075-4
- Servan-Schreiber, E., Anderson, J.R. (1990). Learning artificial grammars with competitive chunking. Journal of Experimental Psychology: Learning, Memory, and Cognition, 16(4), 592. https://doi.org/10.1037/0278-7393.16.4.592
- Siegelman, N., Bogaerts, L., Frost, R. (2017). Measuring individual differences in statistical learning: Current pitfalls and possible solutions. Behavior research methods, 49, 418—432. https://doi.org/10.3758/s13428-016-0719-z
- Siegelman, N., Bogaerts, L., Kronenfeld, O., Frost, R. (2018). Redefining “Learning” in Statistical Learning: What Does an Online Measure Reveal About the Assimilation of Visual Regularities? Cognitive Science, 42, 692—727. https://doi.org/10.1111/cogs.12556
- Stoet, G. (2010). PsyToolkit - A software package for programming psychological experiments using Linux. Behavior Research Methods, 42(4), 1096—1104.
- Stoet, G. (2017). PsyToolkit: A novel web-based method for running online questionnaires and reaction-time experiments. Teaching of Psychology, 44(1), 24—31.
- Theeuwes, J. (2019). Goal-driven, stimulus-driven, and history-driven selection. Current opinion in psychology, 29, 97—101. https://doi.org/10.1016/j.copsyc.2018.12.024
- Theeuwes, J., Bogaerts, L., van Moorselaar, D. (2022). What to expect where and when: how statistical learn-ing drives visual selection. Trends in Cognitive Sciences, 26(10), 860—872. https://doi.org/10.1016/j.tics.2022.06.001
- Turk-Browne, N.B. (2012). Statistical learning and its consequences. The influence of attention, learning, and motivation on visual search. Springer, New York, NY, 117—146. https://doi.org/10.1007/978-1-4614-4794-8_6
- Turk-Browne, N.B., Jungé, J.A., Scholl, B.J. (2005). The automaticity of visual statistical learning. Journal of experimental psychology. General, 134(4), 552—564. https://doi.org/10.1037/0096-3445.134.4.552
- Turk-Browne, N.B., Scholl, B.J., Chun, M.M., Johnson, M.K. (2009). Neural evidence of statistical learning: Efficient detection of visual regularities without awareness. Journal of cognitive neuroscience, 21(10), 1934—1945. https://doi.org/10.1162/jocn.2009.21131
- Turk-Browne, N.B., Scholl, B.J., Johnson, M.K., Chun, M.M. (2010). Implicit perceptual anticipation triggered by statistical learning. Journal of neuroscience, 30(33), 11177—11187. https://doi.org/10.1523/JNEUROSCI.0858-10.2010
- Vickery, T.J., Park, S.H., Gupta, J., Berryhill, M.E. (2018). Tasks determine what is learned in visual statistical learning. Psychonomic Bulletin and Review, 25(5), 1847—1854. https://doi.org/10.3758/s13423-017-1405-6
- Zang, X., Assumpção, L., Wu, J., Xie, X., Zinchenko, A. (2021). Task-Irrelevant Context Learned Under Rapid Display Presentation: Selective Attention in Associative Blocking. Frontiers in Psychology, 12, 675848. https://doi.org/10.3389/fpsyg.2021.675848
- Zhao, J., Ngo, N., McKendrick, R., Turk-Browne, N.B. (2011). Mutual interference between statistical summary perception and statistical learning. Psychological Science, 22(9), 1212—1219. https://doi.org/10.1177/0956797611419304
Информация об авторах
Метрики
Просмотров web
За все время: 17
В прошлом месяце: 0
В текущем месяце: 17
Скачиваний PDF
За все время: 7
В прошлом месяце: 0
В текущем месяце: 7
Всего
За все время: 24
В прошлом месяце: 0
В текущем месяце: 24