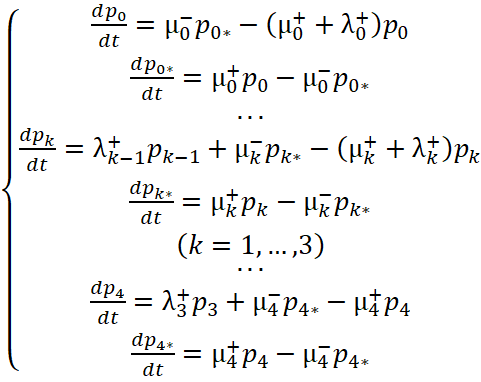Экспериментальная психология
2023. Том 16. № 2. С. 178–202
doi:10.17759/exppsy.2023160211
ISSN: 2072-7593 / 2311-7036 (online)
Построение систем психологической диагностики на основе новых математических представлений
Аннотация
Разработан новый подход к созданию адаптивных систем психологической диагностики, которые могут рассматриваться как средства искусственного интеллекта для оценки деятельности испытуемых. Его применение опирается на свёртку прикладных марковских процессов, представляющих диагностическую процедуру, в квантовые представления, что позволяет выявить структуру исследуемых процессов с помощью квантового спектрального анализа. В случае ограниченного объема эмпирических данных, используемых для настройки диагностического инструментария, рассмотренные квантовые оценки имеют значимые преимущества, как перед оценками правдоподобия и байесовскими оценками, построенными с помощью представлений диагностических процедур в форме марковских процессов, так и более простыми оценками, полученными с помощью нейронных сетей.
Общая информация
Ключевые слова: психологическая диагностика, квантовые представления, марковские процессы, квантовая фильтрация
Рубрика издания: Психодиагностика
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2023160211
Финансирование. Государственное задание Министерства просвещения Российской Федерации № 073-00038-23-02 от 13.02.2023 г.
Получена: 01.04.2023
Принята в печать:
Для цитаты: Куравский Л.С., Юрьев Г.А., Юрьева Н.Е., Николаев И.А., Несимова А.О., Поляков Б.Ю., Козырев А.Д. Построение систем психологической диагностики на основе новых математических представлений // Экспериментальная психология. 2023. Том 16. № 2. С. 178–202. DOI: 10.17759/exppsy.2023160211
Полный текст
Введение
В последние годы возросла популярность различных форм психологической диагностики, использующих практически все формы и способы получения информации с помощью информационных и коммуникационных технологий. Применяемые подходы имеют как известные преимущества, так и недостатки, наиболее значимые из которых обусловлены отсутствием эффективной адаптации диагностического процесса к индивидуальным особенностям и возможностям его участников. Проблемы, связанные с адаптацией такого рода, сложны для решения и наиболее актуальны при оценке неформализуемых умений и навыков. Существующие средства автоматизации обходят рассматриваемую проблему, решая более доступные задачи. Причина этого заключается, в первую очередь, в трудностях формализации и отсутствии подходящего математического аппарата.
Задача практической реализации систем адаптивной психологической диагностики к настоящему времени не имеет удовлетворительного решения. В частности, существенными с точки зрения практического применения недостатками современной теории тестирования (Item Response Theory — IRT), которая является одним из наиболее известных инструментов, являются:
- «статичность» оценок: игнорирование усталости и других факторов, которые могут существенно изменяться со временем;
- невозможность учета времени, затрачиваемого на решение тестовых задач, при построении расчетных оценок;
- необходимость выполнения достаточно большого числа заданий для получения оценок с приемлемой точностью;
- сложность оценки распределения вероятностей различных исходов теста для заданного результата его прохождения;
- сравнительно сложная для практической реализации процедура оценки точности результата, связанная с применением метода максимального правдоподобия и расчетом доверительных интервалов.
Кроме того, одной из основных нерешенных проблем адаптивного подбора заданий, опирающегося на оценки IRT, является выбор заданий с приблизительным равенством вероятностей правильного и неправильного выполнения, что делает результаты тестирования зависимыми в основном от посторонних случайных факторов, не связанных с измеряемыми конструктами.
Подходы на основе обучаемых структур (нейронных сетей, идентифицируемых марковских процессов и др.) создают свои проблемы, включая необходимость получения большого объема эмпирических данных для их настройки.
Применение технологий искусственного интеллекта в психологической диагностике целесообразно при реализации генерации тестовых заданий и автоматизации подбора заданий оптимального уровня сложности. Достаточно гибкий процесс адаптации содержания заданий под индивидуальный уровень способностей обеспечивает более точную оценку диагностируемых характеристик.
Указанные проблемы сделали актуальной разработку новых подходов. В 2010-2012 гг.был разработан метод адаптивного тестирования [2—4], построенный на применении идентифицируемых марковских моделей с непрерывным временем и байесовской классификации. Как развитие этого результата, в 2017 г. предложен новый вариант марковской модели адаптивного тестирования с дискретным временем [Куравский, 2017], предполагающий оценки конструктов с использованием предельных распределений вероятностей пребывания в состояниях, вычисленных с помощью матриц вероятностей переходов.
Различные возможности марковских процессов для решения диагностических, прогностических и других задач подробно рассмотрены в работах [2—6; 9; 10; 14—15], где представлены многочисленные решения, реализованные в различных областях, включая анализ психологических данных, системы поддержки принятия решений, адаптивное тестирование и обучение, управление прикладными мультиагентными системами. Однако диагностика на основе процессов такого типа обычно требует достаточно подробной информации о наблюдаемых переходах между многочисленными состояниями и поэтому нуждается в большом объеме эмпирических данных, которые часто недоступны [подходящие примеры можно найти в: 6]. Эти причины формируют запрос на разработку более эффективных математических представлений в рассматриваемой прикладной области.
Применение квантовых представлений, аналогичных тем, что были в работах [2—4], для моделирования поведения марковских процессов при решении диагностических задач может дать требуемое решение благодаря тому, что квантовые структуры являются обобщением традиционных вероятностных конструкций (поэтому они лучше отвечают имеющимся результатам наблюдений), а число необходимых кубитов обычно намного меньше, чем число состояний соответствующей марковской модели. Следуя субъективной интерпретации вероятности вместо частотной, данный подход дает новую гибкую форму представления поведения прикладных вероятностных систем, что существенно расширяет возможности их анализа.
Следует отметить, что рассмотренные квантовые представления являются чисто теоретическими построениями и не требуют для своей реализации специальных вычислительных инструментов, обеспечивающих квантовые вычисления в привычном понимании. Допустимость этого подхода обосновывается, опираясь на теорему Готтесмана—Книлла [Nielsen, 2010].
Предложенная в работе [Kuravsky, 2023] квантовая фильтрация является новым вариантом применения квантовых представлений для решения прикладных задач и может рассматриваться как развитие результатов, представленных в работах [16—18]. Целесообразность применения квантовой фильтрации обусловлена необходимостью очистки результатов вычислений от случайного «шума», обусловленного ошибками выборочного наблюдения.
В этой работе представлен новый фундаментальный подход к созданию систем психологической диагностики, которые могут рассматриваться как средства искусственного интеллекта для оценки компонентов деятельности испытуемых, проявляющихся при выполнении специализированных форм заданий. Предложенные в рамках этого подхода математические модели и методы обеспечивают возможность для разработки и программной реализации средств адаптивной диагностики. В частности, рассмотрен новый подход к решению задач диагностики путем свертки прикладных марковских моделей в квантовые представления, что позволяет выявлять структуру процесса выполнения заданий с помощью квантового спектрального анализа.
Перспективность использования квантовых представлений в качестве компонентов математического аппарата при создании систем искусственного интеллекта для решения диагностических задач обусловлена дефицитом эмпирических данных для идентификации диагностического инструментария, который, как правило, имеет место в реальных условиях практического применения. В частности, доступных данных обычно совершенно недостаточно для обучения нейронных сетей, особенно в случае наиболее популярных разновидностей этих структур (свёрточные сети, LSTM-сети, многослойные персептроны).
Решения, принимаемые на основе эмпирических данных, допустимы, однако они часто приводят к ошибкам, обусловленным достаточно грубыми выборочными оценками матриц вероятностей переходов и интенсивностей переходов между состояниями процедур тестирования в случае, если применяется диагностика на основе оценок правдоподобия и байесовских оценок, построенных с помощью представлений диагностических процедур в форме марковских процессов. Используя особенности кубитов, свёртка марковских процессов в квантовые представления позволяет извлечь максимум полезной информации из доступных эмпирически данных и обеспечить создание эффективных диагностических инструментов, параметры которых идентифицируются по выборкам экспериментальных данных ограниченного объема (так называемых «малых» выборках).
В случае ограниченного объема эмпирических данных, используемых для настройки диагностического инструментария (именно такие данные, как правило, доступны в реальных условиях практического применения), квантовые оценки имеют значимые преимущества, как перед оценками правдоподобия и байесовскими оценками, построенными с помощью представлений диагностических процедур в форме марковских процессов, так и более простыми оценками, полученными с помощью нейронных сетей.
Рассмотренный в этой работе пример практического применения проиллюстрировал, что построение квантовых представлений для анализа динамики марковских процессов в сочетании с квантовой фильтрацией существенно улучшает результаты диагностики при ограниченном объеме эмпирических данных, превращая их из ненадежных в достаточно надежные.
В целом, анализ литературы по тематике проведенных исследований позволяет утверждать, что представленные далее результаты обладают значительной новизной и имеют существенные преимущества по сравнению с современными зарубежными и отечественными аналогами. Это подтверждается сравнениями эффективности предложенных методов и подходов, традиционных для данной области междисциплинарных исследований [Ермаков, 2023].
1. Марковский процесс как математическая модель диагностической процедуры
Для реализации диагностических процедур применяется марковский процесс с дискретными состояниями и непрерывным временем [Марковские модели в, 2017; Овчаров, 1969], для которого известны начальные распределения вероятностей и наблюдаемые частоты нахождения в состояниях процесса ![]() в контрольные моменты времени
в контрольные моменты времени![]() , где
, где![]() — индекс состояния,
— индекс состояния,![]() — число моментов времени, для которых известны частоты
— число моментов времени, для которых известны частоты![]()
![]() , —конечный момент времени. Интенсивности переходов между состояниями являются идентифицируемыми параметрами рассматриваемых моделей.
, —конечный момент времени. Интенсивности переходов между состояниями являются идентифицируемыми параметрами рассматриваемых моделей.
Полагается, что каждый испытуемый имеет одну из заданных оценок диагностического уровня с индексами![]() . Вероятности пребывания в состояниях процесса, как функции времени, определяются следующей системой обыкновенных дифференциальных уравнений Колмогорова в матричной форме:
. Вероятности пребывания в состояниях процесса, как функции времени, определяются следующей системой обыкновенных дифференциальных уравнений Колмогорова в матричной форме:
![]()
где![]() ,
,![]() — матрица размера
— матрица размера ![]() ,
, ![]() — упорядоченное множество интенсивностей переходов между состояниями процесса для уровня подготовки испытуемого , представляет вероятности пребывания в состояниях марковского процесса {xi}i=0,…,n и,{xi*}i=0,…,n, для определенного уровня подготовки испытуемого
— упорядоченное множество интенсивностей переходов между состояниями процесса для уровня подготовки испытуемого , представляет вероятности пребывания в состояниях марковского процесса {xi}i=0,…,n и,{xi*}i=0,…,n, для определенного уровня подготовки испытуемого ![]()
![]()
![]() , .
, .
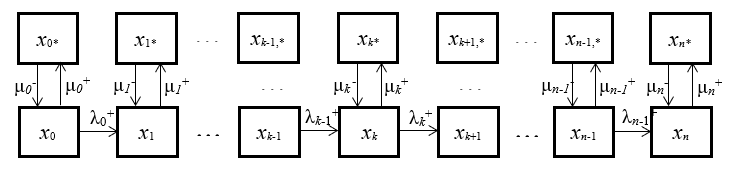
Для определения того, как вероятности пребывания в состояниях изменяются со временем, используется марковский процесс, представляющий собой конечную цепь из 2n+2 состояний (рис. 1). Состояния xk и xk* соответствуют фрагментам заданий, представляющим kые содержательные уровни процесса оценки. Для каждого k может быть определен свой собственный адаптирующийся к возможностям испытуемого набор заданий с релевантным содержанием.
Рис. 1. Марковский процесс с дискретными состояниями и непрерывным временем, представляющий динамику оценки: {xi}i=0,…,nи {xi*}i=0,…,n — состояния процесса,![]() — упорядоченное множество интенсивностей переходов между состояниями для уровня подготовки испытуемого
— упорядоченное множество интенсивностей переходов между состояниями для уровня подготовки испытуемого
Когда испытуемый находится в состоянии xk, назначенное для выполнения тестовое задание адаптивно выбирается из множества возможных вариантов, соответствующих данному состоянию. Каждое задание имеет свои ограничения, в том числе по времени выполнения.
Переходы между состояниями определяются следующими правилами, обеспечивающими для испытуемого адаптивность диагностической процедуры:
- если испытуемый, пребывая в состоянии xk, выполняет соответствующее задание правильно и не нарушает временные или другие ограничения, связанные с этим заданием, выполняется переход в состояние xk+1 ;
- если испытуемый, пребывая в состоянии xk, выполняет соответствующее задание неправильно и не нарушает временные или другие ограничения, связанные с этим заданием, пребывание в состоянии xk продолжается;
- если испытуемый, пребывая в состоянии xk, выполняет соответствующее задание правильно, но нарушает временные или другие ограничения, связанные с этим заданием, выполняется переход в состояние xk*;
- если испытуемый, пребывая в состоянии xk*, при выполнении задания нарушает временные или другие ограничения, связанные с этим заданием, либо выполняет соответствующее задание неправильно и не нарушает временные или другие ограничения, связанные с этим заданием, пребывание в состоянии xk* продолжается;
- если испытуемый, пребывая в состоянии xk*, выполняет соответствующее задание правильно и не нарушает временные или другие ограничения, связанные с этим заданием, выполняется возвращение в состояние xk.
Полагается, что в начальный момент времени испытуемый находится в состоянии x0. Функционально состояния xk* выполняют роль своего рода «ловушек» для тех испытуемых, которым не удается уложиться в заданные лимиты времени или другие ограничения при выполнении заданий.
Зная состояние процесса, в котором испытуемый в определенный момент времени оказывается после выполнения текущего задания, а также соответствующие прогнозируемые вероятности пребывания в состояниях процесса, которые можно рассчитать с помощью уравнений Колмогорова для каждого диагностического уровня, с помощью формулы Байеса оцениваются апостериорные вероятности диагностических уровней подготовки экипажа:
![]()
где ![]() — событие, состоящее в том, что испытуемый обладает lой оценкой диагностического уровня (
— событие, состоящее в том, что испытуемый обладает lой оценкой диагностического уровня (![]() );
);![]() — событие, состоящее в том, что испытуемый находится в указанном состоянии процесса в указанный момент времени;
— событие, состоящее в том, что испытуемый находится в указанном состоянии процесса в указанный момент времени;![]() — априорная вероятность того, что испытуемый обладает lой оценкой диагностического уровня;
— априорная вероятность того, что испытуемый обладает lой оценкой диагностического уровня;![]() — вероятность пребывания в указанном состоянии процесса в указанный момент времени при условии, что испытуемый обладает lой оценкой диагностического уровня; — вероятность того, что lая оценка диагностического уровня соответствует испытуемому, который находится в указанном состоянии процесса в указанный момент времени.
— вероятность пребывания в указанном состоянии процесса в указанный момент времени при условии, что испытуемый обладает lой оценкой диагностического уровня; — вероятность того, что lая оценка диагностического уровня соответствует испытуемому, который находится в указанном состоянии процесса в указанный момент времени.
Оценка диагностического уровня, при которой достигается наибольшее значение условной апостериорной вероятности
![]()
является искомой.
Процесс обхода состояний рассматриваемых марковских процессов прерывается, если указанное выше наибольшее значение условной апостериорной![]() вероятности превысит все оставшиеся значения апостериорных вероятностей не менее чем на установленное критическое значение
вероятности превысит все оставшиеся значения апостериорных вероятностей не менее чем на установленное критическое значение ![]() . После этого адаптивная оценка диагностического уровня устанавливается по текущему результату.
. После этого адаптивная оценка диагностического уровня устанавливается по текущему результату.
Параметры марковского процесса
![]()
![]()
идентифицируются по наблюдаемым и прогнозируемым гистограммам, представляющим распределения частот пребывания в состояниях процесса. Вычисляются оценки этих параметров, обеспечивающие наибольшее согласование между наблюдаемыми и прогнозируемыми частотами пребывания в контрольных состояниях процесса в заданные моменты времени, а именно: определяется множество интенсивностей переходов между состояниями , которым соответствует наименьшее значение статистики Пирсона:
![]()
где ![]() ;
; ![]() — наблюдаемые частоты пребывания в состояниях процесса в моменты времени
— наблюдаемые частоты пребывания в состояниях процесса в моменты времени ![]() . Эта статистика используется для проверки статистической гипотезы о том, что набор прогнозируемых частот попадания в состояния значимо не отличается от соответствующего набора наблюдаемых частот [Куравский, 2011; Марковские модели в, 2017; Kuravsky, 2010] и представляет собой меру согласования применяемой математической модели с наблюдениями.
. Эта статистика используется для проверки статистической гипотезы о том, что набор прогнозируемых частот попадания в состояния значимо не отличается от соответствующего набора наблюдаемых частот [Куравский, 2011; Марковские модели в, 2017; Kuravsky, 2010] и представляет собой меру согласования применяемой математической модели с наблюдениями.
Для решения данной задачи идентификации разработан специальный численный метод [Kuravsky, 2015]. При ограниченном объеме эмпирических данных интенсивности переходов между состояниями могут приближенно оцениваться как обратные величины к средним интервалам времени между двумя смежными переходами в соответствующем направлении [71], что является наиболее практичным решением в случае эмпирических данных ограниченного объема.
Работа с эмпирическими данными показала, что использование для построения байесовских оценок диагностического уровня вероятностей пребывания в парах состояний « » (т.е. состояний вместе с соответствующими им состояниями-«ловушками») ![]()
![]() обеспечивает существенно более высокий уровень дискриминации между оцениваемыми уровнями, чем в случае использования вероятностей пребывания в состояниях, вычисленных раздельно.
обеспечивает существенно более высокий уровень дискриминации между оцениваемыми уровнями, чем в случае использования вероятностей пребывания в состояниях, вычисленных раздельно.
2. Построение квантовых представлений для анализа динамики марковских процессов
Применение квантовых представлений для анализа марковских процессов при решении диагностических задач обеспечивает необходимое решение благодаря тому, что такие квантовые структуры являются обобщениями традиционных вероятностных конструкций (поэтому они лучше отвечают имеющимся результатам наблюдений). Следуя субъективной интерпретации вероятностной конструкции вместо частотной, этот подход дает новую гибкую форму представления поведения прикладных вероятностных систем, что существенно расширяет возможности их анализа.
Для исходного представления динамики поведения исследуемой системы в рассматриваемом контексте удобны марковские процессы с дискретными состояниями и дискретным временем (марковские цепи), при этом вероятности перехода из состояния в состояние являются параметрами модели. Переход от рассмотренных выше марковских процессов с непрерывным временем к соответствующим процессам с дискретным временем обеспечивается путем фиксации пребывания в заданных состояниях процесса в моменты, взятые с постоянным временным шагом.
Динамика вероятностей пребывания в состояниях марковского процесса определяется матричным уравнением:
![]() ,
,
где значения индекса![]() соответствуют дискретным моментам времени в основной шкале; вероятности пребывания в состояниях в момент времени
соответствуют дискретным моментам времени в основной шкале; вероятности пребывания в состояниях в момент времени![]() представляются как
представляются как![]() ; — количество состояний марковского процесса;
; — количество состояний марковского процесса;![]() — стохастическая матрица вероятностей перехода между состояниями размера
— стохастическая матрица вероятностей перехода между состояниями размера ![]() , в которой
, в которой ![]() — вероятность перехода из состояния в состояние .
— вероятность перехода из состояния в состояние .
Преобразование марковских моделей в квантовые представления позволяет выявить структуру исследуемых процессов с помощью квантового спектрального анализа [Kuravsky, 2021; Kuravsky, 2022]. Результаты этого анализа, подобно анализу функций с помощью преобразования Фурье, выражают внутреннюю структуру случайного наблюдаемого процесса в частотной области. Они, в свою очередь, могут быть использованы для последующего углубленного анализа поведения квантовой системы. Накопленный эмпирический опыт показывает, что такой подход существенно увеличивает количество полезной и значимой информации о поведении исследуемой системы по сравнению с марковскими процессами.
Чтобы представить прикладной марковский процесс данного типа для решения диагностической задачи, используется набор![]() кубитов
кубитов![]() , размер и величина которого определяются количеством распознаваемых состояний. Полученное представление кубитов отражает переходы между кластерами состояний, число которых значительно меньше числа состояний исходной марковской модели. Кластеры распознаваемых состояний определяются на основе эмпирических данных, содержащихся в матрице вероятностей переходов между состояниями марковской модели, преобразуемой посредством процедуры многомерного шкалирования.
, размер и величина которого определяются количеством распознаваемых состояний. Полученное представление кубитов отражает переходы между кластерами состояний, число которых значительно меньше числа состояний исходной марковской модели. Кластеры распознаваемых состояний определяются на основе эмпирических данных, содержащихся в матрице вероятностей переходов между состояниями марковской модели, преобразуемой посредством процедуры многомерного шкалирования.
Таким образом, этапами свертки марковского процесса в систему кубитов являются как многомерное шкалирование [Borg, 2005; Cox, 2001; Lloyd, 1984; Morrison, 1976] для получения определенного представления состояний марковской модели в пространстве шкалирования, так и последующий кластерный анализ [Lloyd, 1984; Morrison, 1976] для формирования кластеров объединенных состояний этой модели. Пары состояний марковской модели, имеющие большие вероятности взаимных переходов, в результате выполнения указанной процедуры располагаются в пространстве шкалирования ближе друг к другу.
По сравнению с исходным марковским процессом, рассмотренное представление имеет преимущества благодаря уменьшению размерности задачи (число кубитов определяется числом кластеров и поэтому в несколько раз меньше числа состояний в исходном марковском процессе) и использованию более обобщенного и гибкого квантового представления вероятности [Kuravsky, 2021; Kuravsky, 2022]. Каждое квантовое представление соответствует одному из кластеров, выявленных в результате проведенного кластерного анализа. Оптимальное количество кластеров определяется с использованием информации об эффективности решения рассматриваемой прикладной задачи. Благодаря кластеризации для принятия диагностического решения используется только существенная информация.
Для рассматриваемых квантовых систем наблюдаемой величиной является пребывание марковского процесса в заданном кластере состояний. Поэтому ее «измеряемые» значения могут быть представлены биполярными константами типа либо 1 (марковский процесс находится внутри набора заданных состояний), либо –1 (марковский процесс без этого набора состояний).
Исследуемые марковские процессы могут быть выражены с помощью квантовых представлений пребывания в соответствующих кластерах состояний, а именно: вероятностная структура, представляемая кубитами, описывает динамику пребывания в нескольких кластерах состояний, причем рассматриваемый процесс в любой момент времени находится в одном и только одном из M рассматриваемых кластеров.
Пребывание процесса в кластере состояний ![]() (
(![]() ) представляется кубитом =
) представляется кубитом = ![]()
![]() , где — время;
, где — время;![]() и
и ![]() образуют базис, элементы которого становятся результатами наблюдений за системой кубитов;
образуют базис, элементы которого становятся результатами наблюдений за системой кубитов; ![]() ,
, ![]() ( );
( );![]() , где согласно правилу Борна рассматривается как вероятность пребывания в кластере состояний
, где согласно правилу Борна рассматривается как вероятность пребывания в кластере состояний ![]() ; где
; где ![]() согласно правилу Борна рассматривается как вероятность отсутствия в кластере состояний
согласно правилу Борна рассматривается как вероятность отсутствия в кластере состояний ![]() (т.е. пребывания в любом другом доступном кластере системы
(т.е. пребывания в любом другом доступном кластере системы![]() , который не совпадает с кластером
, который не совпадает с кластером![]() ).
).
Векторы![]() и
и![]() получаются в результате наблюдений за системой кубитов, а именно: каждое такое наблюдение («измерение») дает или
получаются в результате наблюдений за системой кубитов, а именно: каждое такое наблюдение («измерение») дает или![]() или
или![]() с двумя очевидными условиями нормализации, следующими из приведенных выше определений
с двумя очевидными условиями нормализации, следующими из приведенных выше определений ![]() и
и![]() :
:
![]() ,
, ![]() .
.
Опираясь на подход фон Неймана к интерпретации измерений [Марковские модели в, 2017], отличия от обычных квантовых систем можно выразить с помощью следующих преобразований нормализации![]() , обеспечивающих выполнение при «измерении» заданных условий для
, обеспечивающих выполнение при «измерении» заданных условий для ![]() и
и ![]() (
( ![]() ):
):![]()
Как отмечено в [Kuravsky, 2021; Kuravsky, 2022], указанные преобразования нормализации делают представленные кубиты запутанными измерениями (entangled by measuring — EM). Вся совокупность представленных кубитов, запутанных измерениями, называется далее EM-квантовой системой. Нормализация, о которой идет речь, формирует ограничение, накладываемое прикладными задачами. Фактически рассматриваемые кубиты используются как зонды, которые получают информацию о состоянии системы и формируют фон для диагностических выводов.
Каждый кубит![]() рассматривается как формальная квантовая структура, эволюция которой в закрытом режиме описывается некоторым унитарным оператором эволюции
рассматривается как формальная квантовая структура, эволюция которой в закрытом режиме описывается некоторым унитарным оператором эволюции![]() -й квантовой системы:
-й квантовой системы:
![]() =
= ![]() ,
,
где ![]() — текущее состояние исследуемой замкнутой системы в момент времени
— текущее состояние исследуемой замкнутой системы в момент времени![]() ;
; ![]() — последующее состояние той же замкнутой системы в момент времени
— последующее состояние той же замкнутой системы в момент времени![]() .
.
Оператор![]() унитарной эволюции, который отвечает за эволюцию системы в течение малого промежутка времени ∆t (от
унитарной эволюции, который отвечает за эволюцию системы в течение малого промежутка времени ∆t (от ![]() в момент времени до
в момент времени до ![]() в момент времени
в момент времени ![]() ) можно выразить как
) можно выразить как![]() , где
, где![]() — оператор Гамильтона (гамильтониан) k-й квантовой системы; — тождественный оператор. Это выражение вытекает из непрерывности оператора
— оператор Гамильтона (гамильтониан) k-й квантовой системы; — тождественный оператор. Это выражение вытекает из непрерывности оператора ![]() , причем является его главной линейной частью приращения.
, причем является его главной линейной частью приращения.
Если гамильтониан ![]() установлен, то полное поведение k-го рассматриваемого кубита определяется решением уравнения Шрёдингера, записанного для оператора :
установлен, то полное поведение k-го рассматриваемого кубита определяется решением уравнения Шрёдингера, записанного для оператора :
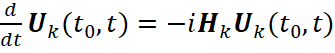 .
.
Эта форма уравнения легко выводится из условий непрерывности и унитарности оператора эволюции. Очевидно, что гамильтониан полностью определяет поведение EM-квантовой системы. Экспериментально наблюдаются («измеряются») значения, определяемые этим оператором.
Применяемая вероятностная модель квантовых представлений подтверждена известными физическими экспериментами [Holevo, 2011; Nielsen, 2010].
Согласно одному из основных постулатов квантовой механики, каждой экспериментально наблюдаемой величине соответствует определенный эрмитов оператор в гильбертовом пространстве, причем собственные числа этого оператора являются ее измеряемыми значениями. Поскольку исследуемые системы не являются физическими, в качестве экспериментальных результатов можно рассматривать биполярные константы -1 и 1 со следующей интерпретацией: -1 — система не находится в данном кластере состояний; 1 — система находится в данном кластере состояний.
Решение уравнения Шрёдингера имеет вид:![]() . Так как используемый гамильтониан является эрмитовым оператором, операторы
. Так как используемый гамильтониан является эрмитовым оператором, операторы![]() определяются измеренными биполярными собственными значениями (-1 или 1). Начальные условия для решения уравнения могут быть представлены в любой приемлемой форме, поскольку начальный момент времени можно располагать в любой точке временной оси.
определяются измеренными биполярными собственными значениями (-1 или 1). Начальные условия для решения уравнения могут быть представлены в любой приемлемой форме, поскольку начальный момент времени можно располагать в любой точке временной оси.
В качестве решения уравнения Шрёдингера допустим хорошо известный оператор вращения, который использовался в работах [16—18] для описания поведения квантовой системы, а именно:
![]()
Скорость эволюции различных кубитов может различаться. Однако все кубиты, работающие в одной и той же EM-квантовой системе, должны эволюционировать в одном и том же масштабе времени. Поэтому для каждого кубита должен быть определен частотный параметр . В этом случае приведенный выше оператор вращения принимает вид:
![]() ,
,
где t — общее время;![]() — частота вращения кубита, которую необходимо определить. Эволюция, представленная таким образом, выражает скрытую периодичность нахождения в заданных кластерах состояний в течение периода наблюдения.
— частота вращения кубита, которую необходимо определить. Эволюция, представленная таким образом, выражает скрытую периодичность нахождения в заданных кластерах состояний в течение периода наблюдения.
Идентификация параметров представлений кубитов, выполняемая отдельно для каждого из исследуемых процессов, а также сопутствующие проблемы представлены в работах [Kuravsky, 2021; Kuravsky, 2022]. Моделируя динамику марковской цепи в соответствии с вероятностями перехода между состояниями соответствующих матриц, генерируются выборки траекторий прохождения кластеров состояний для каждого распознаваемого класса объектов. Эти выборки, а также выявленные параметры представлений кубитов используются для вычисления элементов матриц взаимных расстояний в определенной далее спектральной метрике.
Важно, что использование матриц вероятностей переходов дает возможность получать траектории обхода кластеров состояний марковских процессов произвольной длины, не проводя для этого трудоемкие эксперименты, связанные с содержательной реализацией обхода этих состояний.
Для каждой исследуемой ЕМ-квантовой системы в качестве соответствующего спектра анализируемого процесса рассматриваются как значения частоты ![]() , так и наблюдаемые числа
, так и наблюдаемые числа ![]() попаданий в кластеры состояний
попаданий в кластеры состояний![]() , в моменты времени
, в моменты времени ![]() , которые называются амплитудами
, которые называются амплитудами ![]() . При анализе поведения ЕМ-квантовой системы определяются скрытые периодичности попаданий в эти кластеры в течение периода наблюдений. Спектральная метрика [Kuravsky, 2021; Kuravsky, 2022] оказалась наиболее эффективной для сравнения спектров процессов для пары вариантов поведения системы:
. При анализе поведения ЕМ-квантовой системы определяются скрытые периодичности попаданий в эти кластеры в течение периода наблюдений. Спектральная метрика [Kuravsky, 2021; Kuravsky, 2022] оказалась наиболее эффективной для сравнения спектров процессов для пары вариантов поведения системы:
![]()
где![]() и
и![]() — пара индексов сравниваемых Zпроцессов;
— пара индексов сравниваемых Zпроцессов;![]() — расстояние между процессами
— расстояние между процессами![]() и
и![]() ;
; ![]() — количество совпадающих частот
— количество совпадающих частот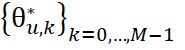 и
и 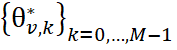 с одинаковыми индексами для сравниваемых процессов и (частоты
с одинаковыми индексами для сравниваемых процессов и (частоты ![]() и
и ![]() с одинаковым индексом k считаются совпадающими, если модуль их разности меньше заданной общей точности
с одинаковым индексом k считаются совпадающими, если модуль их разности меньше заданной общей точности ![]() , т.е.
, т.е.![]() );
); ![]() и
и ![]() — амплитуды k-го кубита для процессов и соответственно; — определенный эмпирический коэффициент. Очевидно, что указанный экспоненциальный коэффициент принимает наибольшее значение, если для всех
— амплитуды k-го кубита для процессов и соответственно; — определенный эмпирический коэффициент. Очевидно, что указанный экспоненциальный коэффициент принимает наибольшее значение, если для всех![]() ,
,![]() при этом расстояние принимает наименьшее значение.
при этом расстояние принимает наименьшее значение.
Для решения диагностической задачи для исследуемого испытуемого, представленного определенной траекторией прохождения кластеров состояний, необходимо включить соответствующую ему траекторию в выборку других допустимых траекторий. Используя вычисленную матрицу взаимных расстояний в качестве входных данных, многомерное шкалирование позволяет получить представление рассматриваемых траекторий прохождения кластеров состояний (включая траекторию, соответствующую исследуемому объекту) в виде точек в пространстве шкалирования заданной размерности. Основываясь на информации о принадлежности к заданным классификационным классам, дискриминантный анализ того или иного типа может выявить класс траектории, соответствующей исследуемому объекту. Преимущества представленного подхода рассмотрены в работах [Kuravsky, 2020; Lloyd, 1984].
-
Распознавание типов испытуемых на основе квантовой фильтрации: описание процедуры
Эффективность диагностической процедуры может быть существенно повышена путем свертки прикладных марковских моделей в квантовые представления с использованием методов, рассмотренные в работах [Kuravsky, 2021; Kuravsky, 2023].
В качестве одного из этапов анализа, эта свёртка предполагает генерацию выборки траекторий прохождения кластеров состояний, формирующих квантовые представления, в соответствии с элементами матриц вероятностей переходов марковских процессов, описывающих динамику обхода состояний марковской цепи с использованием имитационного моделирования. Для элементов таких выборок, вычисленных для пар рассматриваемых траекторий прохождения кластеров состояний, далее вычисляются матрицы взаимных расстояний в специально построенной спектральной метрике, после чего многомерное шкалирование позволяет представить эти траектории в виде точек в пространстве шкалирования заданной размерности.
Полученные пары множеств точек в пространстве шкалирования, в свою очередь, позволяют вычислить попарные статистики Уилкса, или Λ-статистики. Эти статистики Уилкса используются для количественной оценки качества дискриминации между указанными парами множеств точек. Их значения лежат в интервале от 0 до 1, причем значения, близкие к нулю, указывают на хорошую дискриминацию, а близкие к единице — на фактическое отсутствие дискриминации.
Статистики Уилкса для пар траекторий прохождения кластеров состояний и вычисляются следующим образом:
![]() ,
,
где ![]() — матрица внутригрупповых ковариаций;
— матрица внутригрупповых ковариаций;![]() — общая матрица ковариаций;
— общая матрица ковариаций;![]() ;
;![]() , — значение переменной
, — значение переменной ![]() для -й сгенерированной траектории -го варианта; — среднее значение переменной по всем вариантам траекторий; и — средние значения переменных и по всем сгенерированным траекториям -го варианта;
для -й сгенерированной траектории -го варианта; — среднее значение переменной по всем вариантам траекторий; и — средние значения переменных и по всем сгенерированным траекториям -го варианта;![]() и — координаты точек, представляющих сгенерированные траектории в пространстве шкалирования; — число сгенерированных траекторий, относящихся к -му варианту; — число вариантов траекторий. В рассматриваемом случае .
и — координаты точек, представляющих сгенерированные траектории в пространстве шкалирования; — число сгенерированных траекторий, относящихся к -му варианту; — число вариантов траекторий. В рассматриваемом случае .
Попарные статистики Уилкса далее используются как оценки близости между траекторией прохождения кластеров состояний, соответствующей исследуемому испытуемому, и паттернами таких траекторий для распознаваемых типов испытуемых. Эти оценки «отфильтрованы» от искажений, обусловленных ошибками в выборочных оценках элементов матриц вероятностей переходов между состояниями исходной марковской цепи.
Эффект, приводящий к фильтрации указанных искажений, объясняется:
- использованием дополнительной скрытой информации о поведении испытуемых, выявляемой с помощью квантового спектрального анализа [см.: 17; 18]), а также
- эффектом, обусловленным тем, что разнонаправленные сдвиги точек в пространстве шкалирования, вызванные искажениями элементов рассматриваемых матриц вероятностей переходов, при вычислении статистик Уилкса для рассмотренных выше пар выборок траекторий прохождения кластеров состояний взаимно компенсируются, что приводит к существенному уменьшению уровня случайного «шума», обусловленного ошибками выборочного наблюдения (в результате выявляется «тенденция», отфильтрованная от «шума»).
Таким образом, последовательное выполнение:
- свертки марковских процессов, описывающих динамику обхода состояний марковской цепи, представляющих результат прохождения диагностической процедуры, в квантовые представления (каждому рассматриваемому типу испытуемых при этом ставится в соответствие свое квантовое представление);
- генерации выборок траекторий прохождения кластеров состояний, формирующих указанные квантовые представления, в соответствии с матрицами вероятностей переходов марковских процессов, описывающих динамику обхода состояний марковской цепи (каждому типу испытуемых соответствует свое множество траекторий прохождения кластеров состояний фиксированного объема);
- вычисления элементов матриц взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике с выполнением следующих условий:
- каждой паре рассматриваемых типов испытуемых соответствует своя пара указанных сгенерированных множеств;
- эти матрицы вычисляются для одного и того же разбиения на кластеры, полученного, используя матрицу вероятностей переходов первого типа пары, для всех траекторий, входящих в указанную пару множеств;
- представления указанных в п. 3 траекторий в виде точек в пространстве заданной размерности с помощью процедуры многомерного шкалирования;
- вычисления статистик Уилкса для указанных в п. 4 сгенерированных пар множеств точек в пространстве шкалирования, представляющих рассматриваемые пары типов траекторий;
- вычисления для траекторий прохождения кластеров состояний, соответствующих исследуемым испытуемым, ближайших паттернов прохождения кластеров состояний, соответствующих их распознаваемымтипам и определяющих этим искомый результат классификации, используя в качестве меры близости указанные в п. 5 попарные статистики Уилкса, —
повышает эффективность распознавания типов испытуемых по сравнению с методом, опирающимся на байесовские оценки. Сложность данной вычислительной процедуры, далее называемой квантовой фильтрацией, компенсируется качеством получаемого результата.
Представленные выше шаги квантовой фильтрации можно содержательно интерпретировать следующим образом:
- шаг 1 упрощает представление анализируемого процесса, выделяя его существенную часть с точки зрения возможности получения полезных выводов;
- шаг 2 обеспечивает представление вариативности возможных траекторий обхода кластеров состояний для каждого из возможных типов испытуемых;
- шаг 3 обеспечивает попарные сравнения в новой метрике, отражающей существенные особенности анализируемых процессов в квантовом представлении;
- шаг 4 переводит представление исследуемых диагностических процедур в форму, удобную для последующего анализа;
- шаг 5 выявляет «тенденции» в расположении точек, представляющих исследуемые диагностические процедуры, «отфильтрованные» от случайного шума, обусловленного ошибками выборочных наблюдений;
- шаг 6 обеспечивает решение задачи классификации на основе результатов квантовой фильтрации.
-
Распознавание типов испытуемых на основе квантовой фильтрации: иллюстрация практического применения
Для иллюстрации эффективности практического применения представленного подхода рассматриваются оценки интеллектуальных способностей относительно небольшой выборки, состоящей из 21 испытуемого, полученные с помощью адаптивной версии теста «Матрицы Равена» [Равен, 2012]. Определялась принадлежность испытуемых к трем типам, условно называемым «Сильный», «Средний» и «Слабый». Эталонное распределение по типам для последующих сравнений было выявлено с помощью экспертных оценок. Марковский процесс (рис. 1), использованный для представления диагностической процедуры, включал 5 пар состояний. Объем имеющейся выборки испытуемых позволяет говорить о решении задачи классификации на малой выборке эмпирических данных.
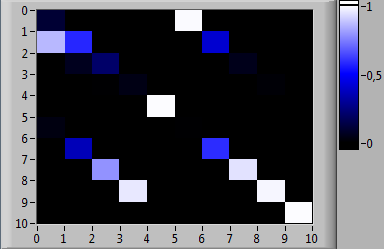
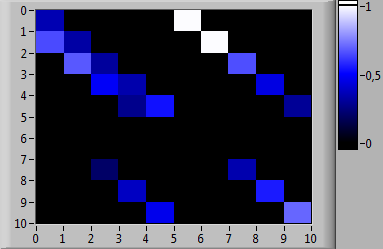
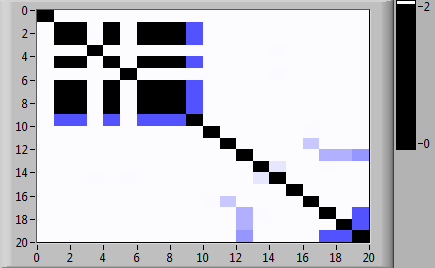
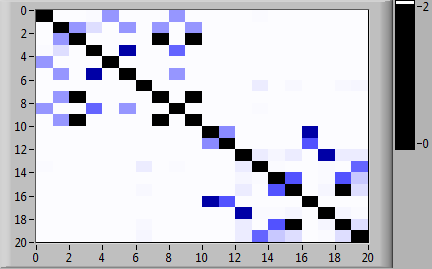
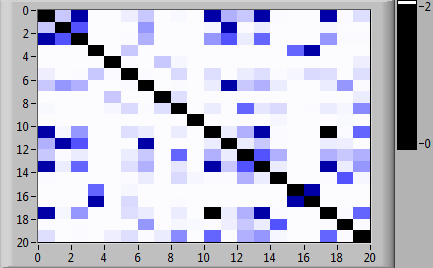
Матрицы вероятностей переходов между состояниями марковских цепей, соответствующих рассматриваемым типам, представлены на рис. 2. На рис. 3 представлена матрица вероятностей переходов для исследуемого испытуемого. На рис. 4 показаны матрицы взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике.
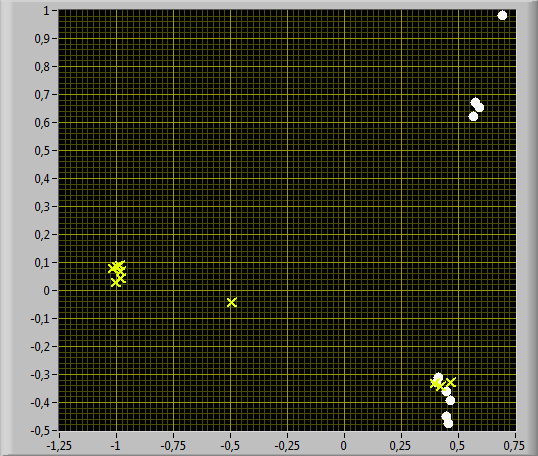
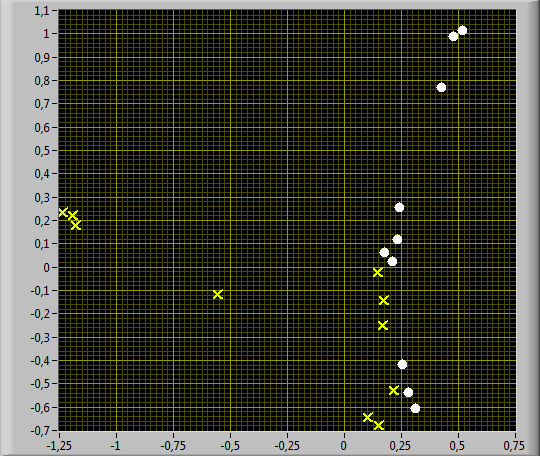
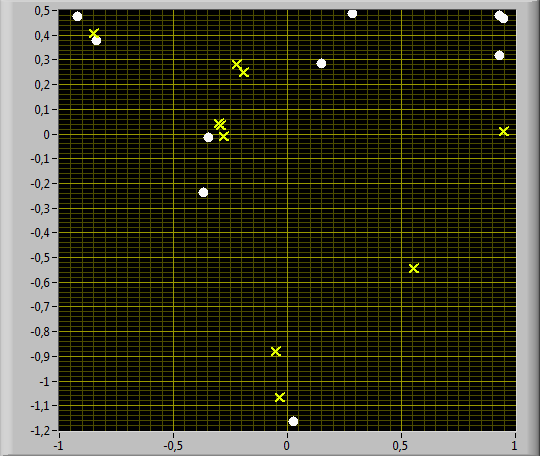
На рис. 5 приведены диаграммы рассеяния для сгенерированных траекторий прохождения кластеров состояний марковской цепи. Указанные траектории получены посредством имитационного моделирования и показаны в виде пар множеств точек в пространстве шкалирования размерности 2. Для генерации траекторий использовались матрицы вероятностей переходов, описывающие динамику переходов между состояниями. Как для каждого рассматриваемого типа, так и для заданного испытуемого генерировались 10 траекторий обхода кластеров.
На рис. 6 представлены значения попарных статистик Уилкса для исследуемого испытуемого и трех рассматриваемых типов.
Вычисления выполнялись с помощью Интеллектуальной системы квантового моделирования («Intelligent System for Quantum Modeling», ISQM) [Kuravsky, 2022]. Проведенные вычислительные эксперименты выявили на заданной выборке только одну ошибку классификации (4,8% выборки).
(а)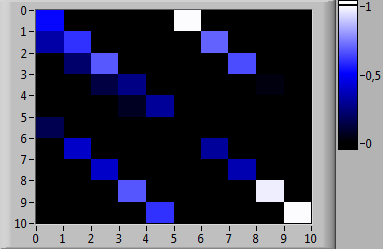
(в)
Рис. 2. Матрицы вероятностей переходов между состояниями марковских цепей, соответствующие типам испытуемых (а) «Сильный», (б) «Средний» и (в) «Слабый», в цветовой шкале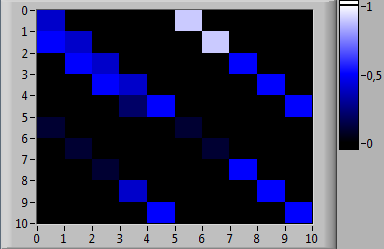
Рис. 3. Матрица вероятностей переходов между состояниями марковской цепи, соответствующая исследуемому испытуемому, в цветовой шкале
(в)
Рис. 4. Матрица взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике: (а) «Слабый» тип испытуемых против исследуемого испытуемого; (б) «Средний» тип испытуемых против исследуемого испытуемого; (в) «Сильный» тип испытуемых против исследуемого испытуемого (по 10 траекторий для каждого варианта)
(б)
(в)
Рис. 5. Диаграммы рассеяния для сгенерированных траекторий прохождения кластеров состояний марковской цепи: указанные траектории получены посредством имитационного моделирования и показаны на диаграммах в виде пар множеств точек в пространстве шкалирования размерности 2 для следующих вариантов: (а) «Слабый» тип испытуемых против исследуемого испытуемого; (б) «Средний» тип испытуемых против исследуемого испытуемого; (в) «Сильный» тип испытуемых против исследуемого испытуемого (по 10 траекторий для каждого варианта)
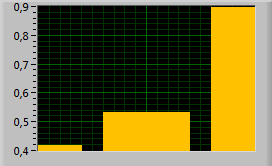
Рис. 6. Попарные статистики Уилкса (0,42; 0,53; 0,9) для исследуемого испытуемого и трех рассматриваемых типов испытуемых («Слабый», «Средний» и «Сильный»)
Полученный результат может быть сопоставлен с рассмотренными в разделе 2 байесовскими диагностическими оценками, опираясь на представление диагностических процедур с помощью марковских процессов с дискретными состояниями и непрерывным временем. Учитывая, что в модели используется 5 пар состояний, соответствующих заданным уровням сложности заданий теста «Матрицы Равена», приведенная выше в матричной форме система обыкновенных дифференциальных уравнений Колмогорова, определяющая динамику пребывания в состояниях марковского процесса, приобретает следующий вид:
(обозначения см. в разделе 2).
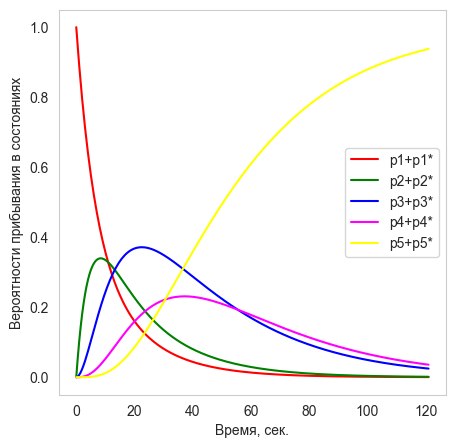
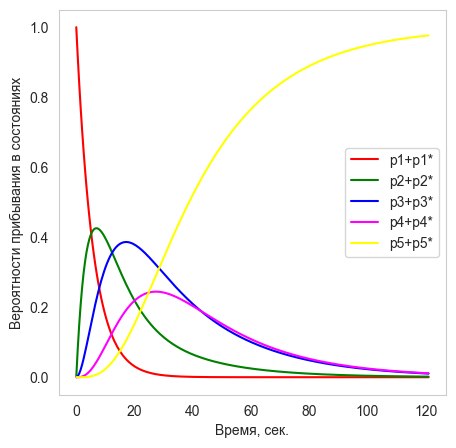
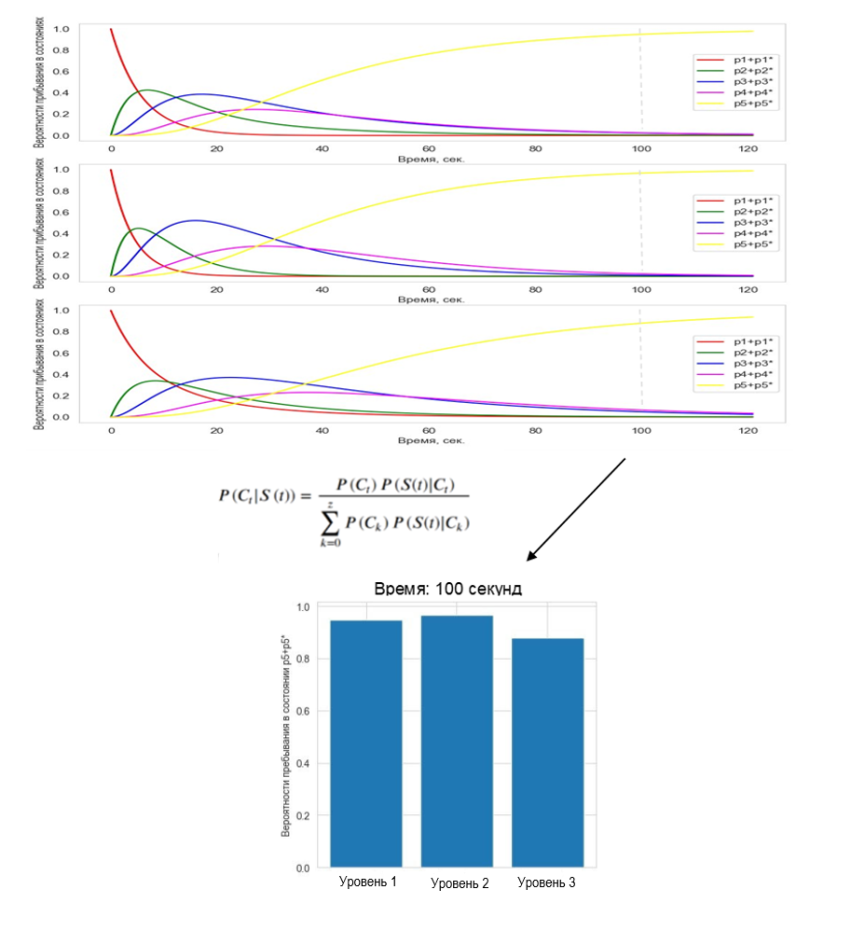
Идентификация параметров этих уравнений [Марковские модели в, 2017] для трех заданных вариантов диагностической оценки, с использованием имеющейся малой выборки эмпирических данных, привела к временной динамике вероятностей пребывания в состояниях марковского процесса, представленной на рис. 7.
(а)
(в)
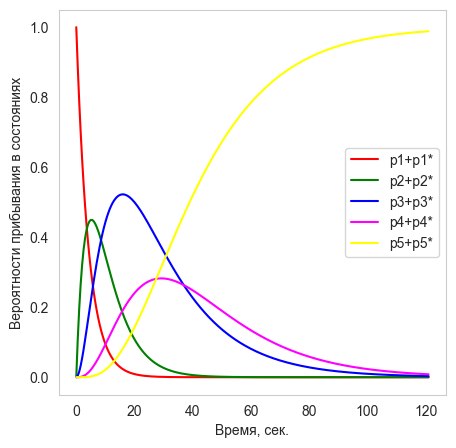
Рис. 7. Временная динамика вероятностей пребывания в сдвоенных состояниях марковского процесса в случае испытуемых, соответствующих диагностическим уровням: (а) «Слабый», (б) «Средний» и (в) «Сильный»
Построение диагностической оценки проиллюстрировано на рис. 8 с помощью расчетной диаграммы для сдвоенных состояний. Приведенная оценка вычислялась для состояния процесса , в котором испытуемый находился в контрольный момент времени (100-я секунда выполнения теста). Для повышения качества дискриминации, использовались вероятности пребывания в паре состояний « ». Текущая оценка, соответствующая контрольному моменту времени, — уровень 2(«Сильный»).
Рис. 8. Построение байесовской диагностической оценки на 100-й секунде выполнения тестовых заданий с помощью графиков вероятностей пребывания в состояниях соответствующего марковского процесса
Проведенные вычислительные эксперименты выявили на заданной выборке 8 ошибок классификации (38,1% выборки).
С целью получения более полного представления об эффективности применения квантовых представлений можно провести сопоставление с классическими оценками правдоподобия, полученными с помощью марковских цепей. Дискретизация временной шкалы выполняется по моментам завершения испытуемыми работы над тестовыми заданиями. Результат выполнения испытуемым диагностической процедуры представляется траекторией (последовательностью) пройденных состояний марковской цепи . Правдоподобие траектории по отношению к диагностическому уровню ![]() ( ), представленному соответствующей матрицей вероятностей переходов между состояниями марковских цепей , может быть представлено как условная вероятность , которая вычисляется по последовательности пройденных состояний для матрицы :
( ), представленному соответствующей матрицей вероятностей переходов между состояниями марковских цепей , может быть представлено как условная вероятность , которая вычисляется по последовательности пройденных состояний для матрицы :
![]()
Величина есть оценка правдоподобия соответствия диагностической процедуры диагностическому уровню . Выбор подходящего диагностического уровня определяется наибольшим значением указанной оценки правдоподобия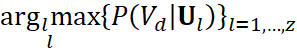 .
.
Для вычисления значений величин использовались выборочные оценки матриц , что при имеющемся малом объеме эмпирических данных привелок8 ошибкам классификации (38,1% выборки).
Гипотеза об однородности распределения корректных и некорректных результатов диагностической процедуры в случае 8 ошибок классификации и имеющегося объема выборки не может быть отвергнута по критерию хи-квадрат Пирсона (p>0,2 при χ2=1,19 и df=1), что свидетельствует о статистически незначимом преобладании корректных результатов.
Таким образом, построение квантовых представлений для анализа динамики марковских процессов в сочетании с квантовой фильтрацией существенно улучшает в данном примере результаты диагностики, превращая их из ненадежных в достаточно надежные. Гипотеза о незначимости различий в распределениях корректных и некорректных результатов диагностической процедуры в случае применения, представленного выше и применявшихся ранее классических подходов с высокой степенью статистической достоверности отвергается по критерию хи-квадрат Пирсона (p<0,001 при χ2=9,89 и df=1), что свидетельствует о значимом улучшении результатов диагностики при использовании квантовых представлений.
Применение обучаемых нейронных сетей для решения данной задачи на доступном объеме эмпирических данных (21 испытуемый, 3 распознаваемых типа) корректные результаты не обеспечивает.
Основные результаты и выводы
- Разработан новый подход к созданию систем психологической диагностики, которые могут рассматриваться как средства искусственного интеллекта для оценки компонентов деятельности испытуемых, проявляющихся при выполнении специализированных заданий. Предложенные в его рамках математические модели и методы обеспечивают возможность для разработки и программной реализации средств адаптивной диагностики.
- Применение разработанного подхода опирается на свёртку прикладных марковских процессов в квантовые представления. Эти представления подразумевают: запутывание путем измерения, количественную оценку соответствия между замкнутой системой кубитов и наблюдениями для определения параметров кубитов, а также специализированную спектральную метрику для сравнения траекторий обхода кластеров состояний.
- Очевидным преимуществом представленного подхода является то, что число кубитов определяется числом кластеров и поэтому в несколько раз меньше числа состояний в исходном марковском процессе. Благодаря этому при формировании диагностического решения используется только существенная информация.
- Преобразование марковских моделей в квантовые представления позволяет выявить структуру исследуемых процессов с помощью квантового спектрального анализа. Результаты этого анализа, подобно анализу функций с помощью преобразования Фурье, выражают внутреннюю структуру случайного наблюдаемого процесса в частотной области. Они, в свою очередь, могут быть использованы для последующего углубленного анализа поведения квантовой системы. Накопленный эмпирический опыт показывает, что такой подход существенно увеличивает количество полезной и значимой информации о поведении исследуемой системы по сравнению с марковскими процессами.
- На основе квантовых представлений построена процедура квантовой фильтрации, реализуемая последовательным выполнением:
- свёртки марковских процессов, описывающих динамику обхода состояний марковской цепи, представляющих результат прохождения диагностической процедуры, в квантовые представления;
- генерации выборок траекторий прохождения кластеров состояний, формирующих указанные квантовые представления, в соответствии с матрицами вероятностей переходов марковских процессов, описывающих динамику обхода состояний марковской цепи;
- вычисления элементов матриц взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике с выполнением следующих условий: каждой паре рассматриваемых типов испытуемых соответствует своя пара указанных сгенерированных множеств; эти матрицы вычисляются для одного и того же разбиения на полученные кластеры, с использованием матрицы вероятностей переходов первого типа пары, для всех траекторий, входящих в указанную пару множеств;
- представления указанных траекторий в виде точек в пространстве заданной размерности с помощью процедуры многомерного шкалирования;
- вычисления статистик Уилкса для сгенерированных пар множеств точек в пространстве шкалирования, представляющих рассматриваемые пары типов траекторий;
- вычисления для траекторий прохождения кластеров состояний, соответствующих исследуемым испытуемым, ближайших паттернов прохождения кластеров состояний, соответствующих их распознаваемым типам и определяющих этим искомый результат классификации с использованием в качестве меры близости попарные статистики Уилкса.
- Квантовая фильтрация существенно повышает эффективность распознавания типов испытуемых по сравнению с методами, опирающимся на байесовские оценки и оценки правдоподобия. Эффективность этой процедуры обусловлена использованием дополнительной скрытой информации, выявляемой с помощью квантового спектрального анализа, а также взаимной компенсацией разнонаправленных сдвигов точек в пространстве шкалирования, представляющих выборки траекторий прохождения кластеров состояний при вычислении статистик Уилкса.
- В случае ограниченного объема эмпирических данных, используемых для настройки диагностического инструментария (так называемых «малых выборок»), рассмотренные квантовые оценки имеют значимые преимущества, как перед оценками правдоподобия и байесовскими оценками, построенными с помощью представлений диагностических процедур в форме марковских процессов, так и более простыми оценками, полученными с помощью нейронных сетей.
Литература
- Ермаков С.С., Шепелева Е.А., Савенков Е.А. Анализ возможностей метода компьютеризированного адаптивного подхода к задачам психологической диагностики и обучения // Экспериментальная психология. 2023. (В печати).
- Куравский Л.С., Юрьев Г.А. Адаптивное тестирование как марковский процесс: модели и их идентификация // Нейрокомпьютеры: разработка и применение. 2011. № 2. С. 21—29.
- Куравский Л.С., Юрьев Г.А. Вероятностный метод фильтрации
артефактов при адаптивном тестировании // Экспериментальная психология. 2012. № 1(5). С. 119—131. - Куравский Л.С., Юрьев Г.А. Об одном подходе к адаптивному тестированию и устранению его артефактов // Нейрокомпьютеры: разработка и применение. 2012. № 1. С. 54—66.
- Куравский Л.С., Артеменков С.Л., Юрьев Г.А., Григоренко Е.Л. Новый подход к компьютеризированному адаптивному тестированию // Экспериментальная психология. 2017. Том 10. № 3. С. 33—45. DOI:10.17759/exppsy.2017100303
- Марковские модели в задачах диагностики и прогнозирования: учеб. пособие / Под ред. Л.С. Куравского. 2-е изд., доп. М.: Изд-во МГППУ, 2017. 197 с.
- Овчаров Л.А. Прикладные задачи теории массового обслуживания. М.: Машиностроение, 1969. 324 с.
- Равен Дж., Равен Дж.К., Корт Дж.Х. Руководство к Прогрессивным Матрицам Равена и Словарным Шкалам. Раздел 3. Стандартные Прогреccивные Матрицы (включая Параллельные и Плюс версии). М.: Когито-Центр, 2012.
- Amosov G.G. On Markovian Cocycle Perturbations in Classical and Quantum Probability // Int. J. Math. & Math. Sci. № 54. P. 3443—3467.
- Amosov G.G. On Markovian Perturbations of the Group of Unitary Operators Associated with a Stochastic Process with Stationary Increments // Theory Prob. & its Applications. 2005. № 49(1). P. 123—132.
- Borg I., Groenen P.J.F. Modern Multidimensional Scaling Theory and Applications. New York: Springer, 2005.
- Cox T.F., Cox M.A.A. Multidimensional Scaling, 2nd ed. New York: Chapman and Hall/CRC, 2001.
- Holevo S. Probabilistic and Statistical Aspects of Quantum Theory, 2nd ed. Edizioni della Normale, Pisa, 2011.
- Kuravsky L.S., Margolis A.A., Marmalyuk P.A., Panfilova A.S., Yuryev G.A., Dumin P.N. A Probabilistic Model of Adaptive Training // Applied Math. Sciences. 2016. 10. № 48. P. 2369—2380.
- Kuravsky L.S., Marmalyuk P.A., Yuryev G.A., Dumin P.N. A Numerical Technique for the Identification of Discrete-State Continuous-Time Markov Models // Applied Mathematical Sciences. 2015. Vol. 9. № 8. P. 379—391. DOI:10.12988/ams.2015.410882
- Kuravsky L.S. Discriminant analysis based on the approaches of quantum computing // Lobachevskii J. Math. 2020. 41. № 12. P. 2338—2344.
- Kuravsky L.S. Modeling Dynamical Behavior of Stochastic Systems: Spectral Analysis of Qubit Representations vs the Mutual Markovian Model Likelihood Estimations // Lobachevskii J. Math. 2021. 42. № 10. P. 2364—2376.
- Kuravsky L.S. Simplification of Solving Diagnostics Problems by Convolution of Applied Markovian Models into the Quantum Representations // Lobachevskii J. Math. 2022. 43. № 7. P. 1669—1682.
- Kuravsky L.S., Greshnikov I.I., Zlatomrezhev V.I., Yuryev G.A. Synthesis of Civil Aircraft Control using Empirical Data and Quantum Filtering // Lobachevskii J. Math. 2023. 44. (In print).
- Kuravsky L.S., Baranov S.N., Yuryev G.A. Synthesis and Identification of Hidden Markov Models Based on a Novel Statistical Technique in Condition Monitoring. In: Proc. 7th Int. Conf. on Condition Monitoring & Machinery Failure Prevention Technologies. Stratford-upon-Avon, England, 2010.
- Lloyd E. Handbook of Applicable Mathematics, Vol. 6: Statistics / Ed. by W. Ledermann. Hoboken: Wiley, 1984.
- Morrison D.F. Multivariate Statistical Methods, 2nd ed. New York: McGraw-Hill, 1976.
- Nielsen M.A., Chuang I.L. Quantum Computation and Quantum Information. Cambridge University Press, 2010.
- von Neumann J. Mathematical Foundations of Quantum Mechanics. Princeton: Princeton Univ. Press, 1955.
Информация об авторах
Метрики
Просмотров web
За все время: 517
В прошлом месяце: 33
В текущем месяце: 19
Скачиваний PDF
За все время: 151
В прошлом месяце: 9
В текущем месяце: 2
Всего
За все время: 668
В прошлом месяце: 42
В текущем месяце: 21