Культурно-историческая психология
2016. Том 12. № 1. С. 35–45
doi:10.17759/chp.2016120104
ISSN: 1816-5435 / 2224-8935 (online)
Использование рисунков как культурных средств при установлении сходства между решениями алгебраических задач
Аннотация
Общая информация
Ключевые слова: алгебраические задачи, решение , репрезентация, символизация, культурные средства
Рубрика издания: Эмпирические исследования
Тип материала: научная статья
DOI: https://doi.org/10.17759/chp.2016120104
Для цитаты: Котов А.А., Котова Т.Н. Использование рисунков как культурных средств при установлении сходства между решениями алгебраических задач // Культурно-историческая психология. 2016. Том 12. № 1. С. 35–45. DOI: 10.17759/chp.2016120104
Полный текст
Решение текстовых алгебраических задач требует от учащихся нахождения в тексте важных математических переменных и перенесения их в уравнение. Многие учащиеся по рекомендации учителя или спонтанно составляют при решении рисунки, используя их в качестве средств понимания математической структуры задачи. В эксперименте мы исследовали, какие свойства рисунков наиболее важны для учащихся в подборе способа решения из опыта. Мы составили набор рисунков, которые различались по параметрам аналоговости и полноты отношений между элементами. Испытуемые оценивали степень полезности решения исходной задачи (представленной рисунком) для решения целевой. Оказалось, что испытуемые были более склонны при вынесении суждения опираться на параметр полноты отношений, чем на аналоговость рисунка. Эта зависимость также была сильнее выражена у опытных решателей по сравнению с неопытными. Результаты исследования интерпретируются в контексте развития культурных средств при переходе от житейских понятий к научным в обучении.
Решение математических задач интересует многих исследователей, поскольку оно проявляет общие свойства мышления, необходимые для решения любых задач, как, например, нахождение неизвестной информации, формирование релевантной репрезентации, обобщение и перенос способа решения. С другой стороны, математические задачи невозможно решать без усвоения большого количества культурных средств, таких как числовая система и приемы составления уравнения. Изучение их решения показывает, как эти культурные знаковые системы осваиваются в ходе специально организованного обучения. Алгебраические задачи являются частью математических задач и осваиваются учащимися после арифметических задач, решению которых детей учат в начальных классах школы. В отличие от последних, алгебраические или текстовые задачи интересны для психологических исследований прежде всего тем, что несмотря на их явную отнесенность к определенному разделу математики, не существует общепринятого способа их решения [Спиридонов, 2006]. Как правило, в школе учащихся знакомят с несколькими распространенными приемами решения на примере типовых задач. Потом эти приемы становятся индивидуальными правилами, которые ученики самостоятельно переносят на новые задачи, если они кажутся им похожими на те, что они успешно решали ранее [Rehder, 1999]. Каким образом учащиеся развивают навык переноса решения алгебраических задач? Ответ на этот вопрос зависит от того, чем различаются между собой алгебраические задачи, и как учащиеся понимают эти различия.
Роль внутренней формы репрезентации в обучении решению алгебраических задач
В школьной практике объяснение различий между задачами сводится или к их тематическому содержанию (задачи на работу, на движение и т. д.), или к способу решения (уравнение или система уравнений). Это различие невозможно использовать для объяснения учащимся, с какой задачей они столкнулись в текущий момент и как именно следует начинать ее решение, поскольку как у достаточно непохожих по содержанию задач может быть общий тип уравнения для решения, так и наоборот, задачи со сходным содержанием могут решаться разными уравнениями [Charles A W]. Более удобным способом для объяснения различий между задачами может быть отделение в процессе решения двух этапов: ориентировочном — понимание структуры задачи (чтение текста, выделение релевантных и нерелевантных переменных, определение соответствия условий и вопроса) и исполнительском — выполнение самого решения (составление уравнения, его упрощение, проверка правильности вычислений через соотнесение с текстом задачи).
Цель первого этапа можно обозначить как создание репрезентации, максимально подходящей для будущего решения. В репрезентации традиционно выделяют, с одной стороны, внутреннюю форму — мысленные представления о релевантных для решения переменных, а с другой стороны, — внешнюю — записи, рисунки, схемы, диаграммы, которые представляют собой еще не само решение, а лишь отображение частей задачи и связи между ними, необходимые для более полного осознания решающим структуры задачи [Gallistel, 2001]. Внимание к ориентировочной части действия сопровождает формирование любой новой формы поведения [Гальперин, 2010], однако наличие для этой части действия символической и конвенциональной формы особенно заметно в случае школьных задач. Насколько важен процесс создания репрезентации для учащихся, и каковы особенности каждой из ее форм?
В ответе на вопрос о роли внутренней формы репрезентации в обучении ряд исследователей использовали специфические задания, требующие от испытуемых не решения алгебраических задач, а определения перед решением, является ли задача решаемой (содержит все необходимые переменные и их значения) или нерешаемой (часть переменных и их значений может быть пропущена). Оказалось, что даже опытные решатели, в том случае, если их не предупреждали о возможном появлении нерешаемой задачи, испытывали большие сложности, пытаясь ее решать как решаемую [Rehder, 1999]. Этот результат говорит о том, что решение задачи в отдельных случаях требует предварительных действий по анализу ее структуры, и эти действия не происходят спонтанно, а требуют сознательного контроля. Такая же закономерность действует и в случае переноса решения с одной задачи на другую: намек на сходство решенной и нерешенной задачи резко увеличивает успешность переноса [Seifert, 1986] Другие данные показывают, что способность к обнаружению нерешаемости задачи связана практически со многими математическими способностями [Крутецкий, 1968], а обучение специальному навыку по обнаружению ошибок в условии задаче и в ее решении способствует формированию более гибкой схемы решения новых задач [Ohlsson, 1996]. Таким образом, процедуры, которые выполняют учащиеся до самого решения — на первом этапе, крайне важны для обучения решению задач.
Если при создании подходящей репрезентации задачи учащиеся тратят отдельные усилия на поиск и анализ важных переменных задачи, то насколько связано внимание к этим переменным с самим решением? На каком этапе решения — ориентировочном или исполнительском — решатель находит те компоненты, по которым потом будет сравнивать новые задачи с уже решенными? Этими компонентами являются, скорее, условия задачи или детали готового уравнения?
У. Кинч [Kintsch, 1992] предположил, что при оценке сходства одной алгебраической задачи с другой решатель в наименьшей степени ориентируется на сходство конечных уравнений, составленных для этих задач, поскольку одну и ту же задачу часто можно решить разными уравнениями. Значительно более важным является сходство по типу неизвестной переменной — относительной (скорость) или неотносительной (время или расстояние). Например, по схеме на рис. 1 видно, что в текстовой задаче слева неизвестное значение переменной приходится на относительную переменную, скорость. В задаче справа неизвестное значение приходится на неотносительную переменную — время. Эти задачи также можно преобразовать в схему (в нижней части рисунка), по которой будет видна их структура, уже независимая от предметного содержания.

Для проверки своего предположения У. Кинч использовал процедуру сравнения задач, различающихся по форме уравнения и по типу переменных в разных сочетаниях: одинаковые уравнения и разные переменные, одинаковые уравнения и одинаковые переменные, разные уравнения и разные переменные, разные уравнения и одинаковые переменные. На основе суждений испытуемых о том, насколько первая задача (с готовым уравнением) помогла бы решению второй (без уравнения), он обнаружил, что испытуемые оценивают как более похожие задачи со сходным типом переменных, а не со сходным уравнением. Эти результаты хорошо согласуются с выводами теоретических работ по психологии мышления, утверждающими, что в любой задаче, и тем более в естественно-научной, испытуемый работает не с отдельными понятиями (время, сила, ускорение, гипотенуза), а с их зависимостью друг от друга в отношении к вопросу задачи [Брушлинский, 1996].
Роль внешней формы репрезентации в обучении решению алгебраических задач
В соответствии с приведенным выше описанием процесса решения алгебраической задачи, построение успешной репрезентации должно помочь соединить оба этапа решения задачи (ориентировочный и исполнительский). Косвенно такой переход можно заметить по тому, что практически все люди при чтении текста задачи, и особенно в случае затруднений в начале решения, составляют рисунки к тексту задачи перед самим решением и говорят, что рисунки помогают им понять задачу.
Так, Л. Новик в своем исследовании показала, что функция рисунков, которые составляют сами решатели при решении различных задач, заключается не столько в том, что они помогают понять решение актуальной задачи, сколько в том, что они, выделяя структуру переменных задачи, помогают найти в собственном опыте как можно более похожую из уже решенных задач и использовать ее для решения настоящей задачи [Novick, 1994]. Кроме того, сопровождение решения творческих задач рисунками значительно ускоряет обобщение способа решения похожих задач [12, наряду с этим; есть данные о модально-неспецифических подсказках при решении творческих задач, 3].
Если обнаружение решаемости задачи, сосредоточение на важных переменных — это в большей степени внутренние когнитивные процессы, связанные с индивидуальным опытом решения, то создание рисунков к задаче можно считать частью внешнего процесса, зависимого от культурной практики решения тех или иных задач. Однако, в отличие от многих культурных практик, используемых в школьном обучении, составление рисунков не является целью обучения. Чаще всего рисунок — это индивидуальный прием решателя, необходимый ему для компенсации недостатка внимания к переменным, слабого осознания их связи, трудностей с определением всех неизвестных значений и пр. В рамках так называемых «формирующих» экспериментов эта проблема активно изучается: искусственное введение дополнительных средств символизации предметного содержания понятий часто приводит как к последующему улучшению действий с этими понятиями, так и к их большему осознанию [Давыдов, 1981; Веракса, 2015].
Для проверки предположения о рисунке как индивидуальном приеме решения в пилотажном исследовании мы предложили группе испытуемых (студенты 19—20 лет, N=15) решить две алгебраические текстовые задачи. Если они считали нужным, они могли рисовать любые схемы, рисунки или пометки к условиям задач, до или в процессе их решения. Мы обнаружили, что испытуемые, практически не отличавшиеся по успешности решения задач, значительно отличались друг от друга по рисункам, которые они составляли. Например, испытуемые делились на тех, кто после составления первоначального рисунка далее по ходу решения не вносил в него никаких изменений, и тех, кто делал это на всем протяжении решения; тех, кто включал в рисунок изображения предметов (поезда, коробки с печеньем и т. д.), и тех, кто предпочитал символьные обозначения (стрелки, области и т. д.); тех, кто соединял части изображений связями и пояснениями их значений, и тех, чьи рисунки выглядели как изображение группы несвязанных между собой переменных. По этим результатам мы выделили два параметра, удобные для различения рисунков, используемых при решении задач. Первый параметр мы назвали аналоговостью/схематично- стью изображения. Аналоговыми изображениями можно считать те рисунки, которые включают изображения реальных предметов (поезда, катера, воду). Также аналоговыми можно назвать и те изображения, где скорость или время, которые непосредственно выразить нельзя, изображают через другое измерение, наример, соотношение времени движения передается соотношением длин изображенных линий. Соответственно, неаналоговыми, или схематическими, можно назвать те рисунки, в которых вместо изображения реальных предметов используются их условные заменители: в случае движения используется стрелочка для передачи информации о направлении, а такие переменные, как скорость и время, обозначаются символами t, V, отношение же между переменными одного типа (например, V1 u V2) передается с помощью специальных символов — «<, >, =».
Второй параметр рисунков мы обозначили как полнота отношений между его элементами. Ключевой особенностью рисунков с полным составом отношений является такая группировка переменных одного типа (например, скорости движения разных объектов), при которой их изображения располагаются близко друг с другом. На рисунках же с неполным составом отношений изображения переменных одного типа разнесены по разным областям рисунка или сгруппированы вокруг объектов, к которым они относятся (например, скорость и время изображены вокруг поезда, движение которого они характеризуют). Такая группировка наблюдается как в схематических, так и в аналоговых рисунках. Аналоговые рисунки могут, например, содержать линии, соединяющие отдельные группы условий друг с другом, для обозначения равенства пройденных двумя объектами расстояний. Группировка переменных по типу, характерная для рисунков с полным составом отношений, по-видимому, является удобной формой для перенесения переменных в уравнение.
Рисунки каждого испытуемого, как правило, было сложно однозначно отнести к одному из указанных типов: в одном и том же рисунке могли встречаться детали аналогового и схематического типа, часть переменных могла быть сгруппирована по типу, а часть — нет.
Однако смысловая связь данных параметров с процессом решения задачи позволяет использовать их в изучении этого процесса.
В нашем исследовании мы решили определить, насколько при сравнении двух задач эти параметры изображений используются решателями и какой из них более важен. В эксперименте мы создали набор изображений, которые должны были помочь испытуемым понять основные переменные задачи и ее требования. Эти изображения сопровождали текст первой, или исходной, задачи. От испытуемого требовалось оценить по тексту и рисунку, насколько решение этой задачи, если бы оно состоялось, помогло бы для решения второй, или целевой, задачи. Такая форма вопроса позволяет косвенно оценить, кажутся ли две задачи испытуемому похожими. Как было показано в нескольких исследованиях мышления по аналогии, если испытуемые воспринимают две задачи как сходные, то продвижение в решении одной задачи они считают полезным для решения другой [Gick, 1980]. Кроме того, перенос решения улучшается, если просить решателя самостоятельно придумать похожую задачу [Bernardo, 2001]. Таким образом, далее мы будем рассматривать ответы испытуемых как оценку ими сходства задач.
Мы намеренно не давали испытуемым решать исходную задачу, чтобы определить, действительно ли внешняя форма репрезентации влияет на обнаружение сходства между задачами. Важным ограничением нашего исследования было также и то, что предлагаемые задачи имели одинаковый уровень сложности: все они могли быть решены одним уравнением, а не их системой. В настоящее время, как мы уже писали выше, нет классификации алгебраических задач, используемой, например, для создания последовательности в обучения их решению. То есть алгоритмически определить, может ли решение исходной задачи помочь в решении целевой, нельзя. Однако в исследовании мы проверяли другую гипотезу: какие свойства рисунков влияют на субъективную оценку решателем сходства между способами решения задач.
Метод
Испытуемые. В исследовании приняли участие 100 испытуемых в возрасте от 17 до 26 лет, из них 47 мужчин и 53 женщины. Все участники эксперимента были студентами первого и второго курса двух гуманитарных вузов нематематических специальностей.
Материал. Материал эксперимента состоял из набора алгебраических задач и рисунков к ним. Мы использовали 8 алгебраических текстовых задач на движение из стандартного курса математики для средней школы. Все задачи были разделены на две группы по типу переменной, на которую приходится неизвестное значение. Напомним, по аналогии с описанным выше экспериментом У. Кинча [Kintsch, 1992], мы выделяли относительные и неотносительные переменные. В каждой группе было четыре задачи, чтобы каждый испытуемый мог сравнить пары с одинаковым типом неизвестных и пары с различным типом неизвестных.
В каждой паре в сюжете одной задачи фигурирует движение по суше, а в сюжете второй — движение по воде. Половина испытуемых получали их в одном сочетании: исходная задача — на движение по суше, целевая — по воде. Вторая половина получали задачи в обратном сочетании. По всему набору из восьми задач мы составили 28 пар возможных сочетаний в двух вариантах для контроля эффекта сюжета задачи.
К каждой из задач нами были подготовлены по четыре рисунка, варьировавшиеся по двум параметрам: аналоговость/схематичность и полнота отношений, которые и представляли собой независимые переменные в данном эксперименте (2 х 2) (рис. 2).
В рисунках аналогового типа мы помещали изображения объектов из условия задачи, например, велосипед и поезд. Равенство в значениях переменных, например, расстояния или скорости, задавалось пунктирной линией или линиями разной длины, поделенными на секции. В рисунках схематичного типа объекты были заменены на условные изображения — одинаковые стрелки и символьные обозначения переменных. Равенство значений переменных обозначалось знаком «=» между линиями или математическими выражениями со знаками сравнения («<», «>»).
В рисунках с полным составом отношений известные значения были сгруппированы относительно типа переменных. Группировка значений расстояния выражалась в том, что линии, их обозначавшие, изображались без смещения друг относительно друга и равными (если по условию они были равны). В рисунках с неполным составом отношений известные значения группировались вокруг объектов, а линии, обозначавшие расстояния, изображались со смещением.

Процедура. Испытуемых в случайном порядке разделили на пять групп по 20 участников в каждой. В каждой из четырех экспериментальных групп испытуемым предъявляли рисунки одного из типов на протяжении всех проб, поскольку использование рисунков разного типа могло их запутать. Пятая, контрольная, группа оценивала сходство задач без опоры на рисунок. По результатам выполнения задания в этой группе можно было оценить в целом эффект действия рисунка на оценку сходства.
Испытуемые принимали участие в исследовании группами по 5—6 человек. Перед началом работы каждый участник получал стопку из 28 карточек. На каждой карточке были написаны: инструкция, тексты задач, рисунок к исходной задаче (в четырех группах) и 20-балльная шкала с обозначенными крайними значениями (полностью бесполезна, полностью полезна).
Испытуемых просили прочитать текст первой, исходной, задачи и представить себе, как бы они ее решали. После этого им нужно было оценить по 20-балльной шкале, насколько это решение было бы полезно для решения второй, целевой, задачи. Целевая задача всегда предъявлялась без рисунка, в противном случае испытуемые могут формировать суждение о сходстве задач по содержанию рисунков, а не самих задач.
После оценки карточку нужно было переместить вниз стопки и больше к ней не возвращаться. Испытуемого также предупреждали, что всего будет восемь задач для оценивания, но они будут даны в разных комбинациях. Время на этапе оценивания не ограничивалось и в среднем вся процедура занимала 40 мин.
Сразу после выполнения всех заданий испытуемого просили решить две задачи из числа тех, которые он оценивал. Соответственно, каждый испытуемый был оценен по 3-балльной шкале: 0 — не решил ни одну задачу, 1 — решил одну из двух задач, 2 — решил обе задачи. Время на решение задач также не ограничивалось.
Единственной зависимой переменной в исследовании была оценка степени полезности решения исходной задачи с рисунком для решения целевой задачи. Независимыми переменными были параметры рисунка: аналоговость элементов и полнота отношений переменных в рисунке. Также в экспериментальных целях мы варьировали особенности алгебраических задач: тип переменной с неизвестным значением (тип неизвестного) и сюжет задачи. Уровень эксперт- ности решателя был субъектным фактором, чье влияние на зависимую переменную мы также оценивали.
Для определения влияния каждого фактора на зависимую переменную мы использовали дисперсионный анализ (ANOVA), в котором факторы ана- логовость рисунка, полнота отношений в рисунке, наличие рисунка и уровень экспертности решателя были межсубъектными, а факторы сюжет задачи и тип неизвестного — внутрисубъектными.
Результаты и обсуждение
Для пар задач с одинаковым типом неизвестных и пар с разным типом неизвестных были вычислены средние оценки сходства задач. Мы не обнаружили влияния фактора типа неизвестного на оценку сходства, t(2798)=0,15; p>0,1. Испытуемые не считали, что решение исходной задачи, где неизвестным является переменная того же типа, что и в целевой задаче, мо
жет быть более полезно, чем решение задачи с другим типом неизвестного. Наши данные отличаются от результатов эксперимента У. Кинча [Kintsch, 1992], но в его эксперименте испытуемые выносили суждения о сходстве задач на основе уравнений, сопровождающих текст исходной задачи, а не на основе рисунков. Возможно, влияние сходства переменных задачи проявляется в решении позже, ближе к заключительным этапам решения, например, при составлении уравнения.
Также не было обнаружено и влияние сюжета задачи, варьирование которого мы использовали для контроля эффекта материала , t(2798)=0,87; p>0,1.
При этом, как мы и ожидали, тип рисунка в целом значимо влиял на оценку сходства задач, F(4)=99,05; p<0,001. Средние оценки степени полезности исходной задачи для решения целевой приведены ниже.
Как видно по диаграмме (рис. 3), можно выделить две группы оценок, если сравнивать их с уровнем контрольной группы, т. е. оценки без использования рисунка. Во-первых, выделяется группа оценок с опорой на аналоговые и схематичные рисунки с полным составом отношений, средние значения которых были наиболее высокими. Средние оценки сходства в этих группах, оцененные post hoc тестом по методу Шеффе, не различались между собой, p=0,43. Испытуемые в этих условиях присваивают сходству задач значимо более высокие оценки, чем в условии без рисунка, p<0,001 (в обоих случаях). Во-вторых, выделяется группа оценок с опорой на аналоговые и схематичные рисунки с неполным составом отношений, в которых испытуемые присваивают сходству задач значительно более низкие оценки, чем в условии без рисунка, p<0,001 (в обоих случаях). Между собой оценки в этих условиях, однако, различаются. Оценки сходства задач при опоре на схематические рисунки с неполным составом отношений были ниже, чем в условии с аналоговыми рисунками с неполным составом отношений, p<0,001. Мы отдельно оценили влияние фактора полноты отношений и фактора аналоговости/схематичности с помощью двухфакторного дисперсионного анализа (ANOVA). Влияние обоих факторов на оценку сходства задач было значимым, F=359,66; p<0,001; np2=0,14 и F=15,61; p<0,001; np2=0;007, соответственно. Но сила эффекта гораздо выше у фактора полноты отношений, по сравнению с фактором аналоговости/схематичности.
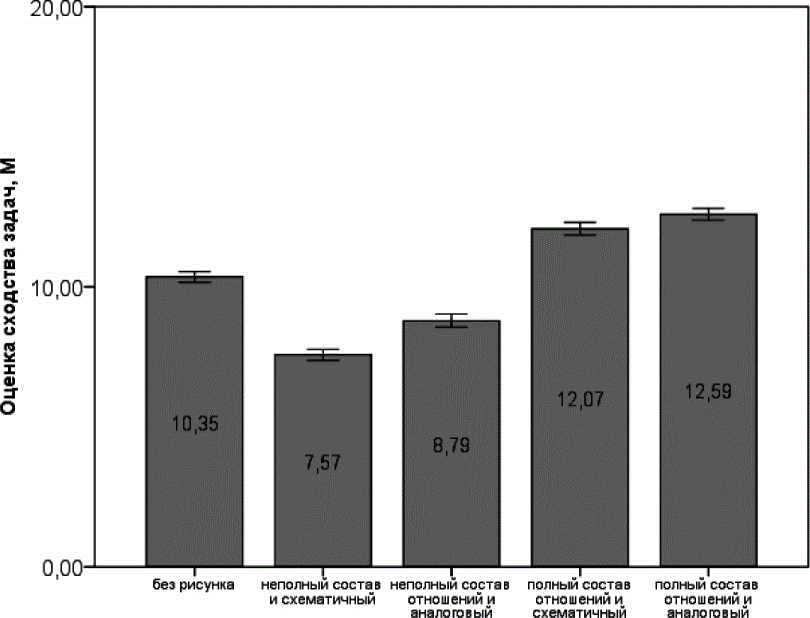
|
Таким образом, степень полноты отношений в элементах рисунка более важна для оценки сходства задач, чем наличие в нем аналоговых компонентов. Если использовать результаты условия без рисунка как контрольный уровень, то получается, что полнота отношений в элементах рисунках повышает уверенность испытуемых в том, что исходная задача может быть полезна для решения целевой задачи. Как мы упоминали выше, рисунки с полным набором отношений между элементами условий выглядят как отображение задачи, полностью подготовленное для составления уравнения, т. е. для решения задачи. Благодаря этому, на наш взгляд, испытуемые и воспринимают эту задачу как полезную для решения других задач.
Насколько уровень экспертности испытуемых в решении задач повлиял на оценку сходства их решения? Все испытуемые были оценены по трехбалльной шкале на основе их успешности в решении двух задач. Количество испытуемых каждой группы было следующим: не решили ни одной задачи 30 испытуемых (30,9%) , решили одну задачу 41 испытуемый (42,3%), решили обе 26 испытуемых (26,8%). Мы оценили общий вклад фактора успешности решателя в оценку сходства задач. Влияние этого фактора оказалось незначимым, F(2)=0,54; p=0,58. Испытуемые с разным уровнем экспертности в решении задач в целом не различались в оценке сходства задач. Однако мы обнаружили значимое взаимодействие фактора типа рисунка с фактором успешности решателя, F(8)=5,16; p<0,001. Содержание этого взаимодействия трудно однозначно интерпретировать, в частности, из-за большой разницы в количестве данных внутри отдельных условий.
Если оценить общую картину в распределении оценок (табл. 1), то видно, что испытуемые, решившие одну или две задачи, демонстрируют схожие результаты. На их оценки сильно влияет фактор полноты отношений между элементами рисунка. Результаты же группы испытуемых, не решивших ни одну задачу, иные. В этой группе при использовании рисунков с аналоговыми элементами оценки сходства по рисункам с полным составом отношений и с неполным практически не различаются между собой и равны оценкам в условии без рисунка. Однако их оценки сильно различаются при использовании схематичных рисунков: в этом случае задачи кажутся гораздо более похожими, если используется рисунок с полным составом отношений и наоборот — с неполным. Результаты можно интерпретировать таким образом, что аналоговость рисунка в группе неуспешных решателей «зашумляет» нахождение основных переменных задачи. Также можно предположить, что с возрастанием уровня экспертности учащиеся, по- видимому, приобретают умение абстрагироваться от материала, из которого состоит рисунок, и сосредотачиваться лишь на тех отношениях, которые он отражает в задаче.
Кроме взаимодействия уровня экспертности решателя с фактором типа рисунка, мы также обнаружили его слабое значимое взаимодействие с фактором сходства задач по типу неизвестного, F(2)=3,21; p=0,04. Напомним, что общего эффекта влияния типа неизвестного в сравниваемых задачах на оценку их сходства мы не обнаружили. Однако если проанализировать оценки сходства в зависимости от уровня эксперт- ности решателя, то видно, что чем выше уровень экс- пертности, тем более сходными кажутся испытуемым задачи, содержащие переменные одного типа (табл. 2).
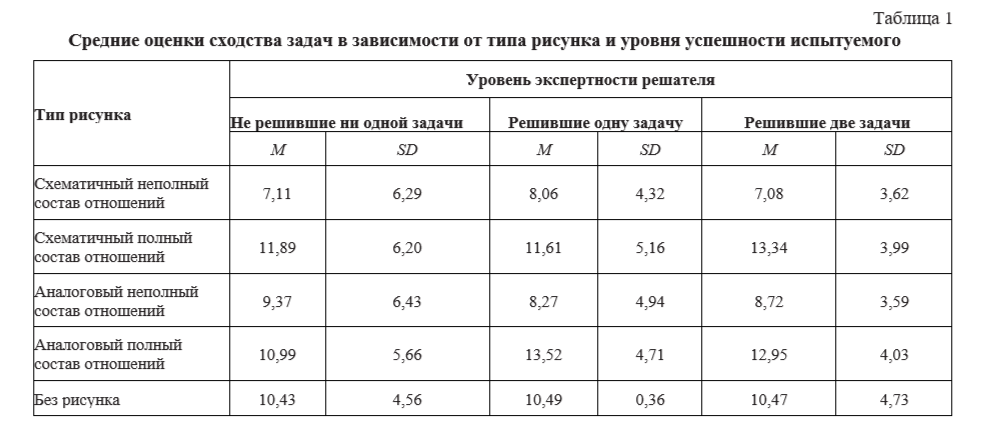

Выводы
В ходе исследования мы показали, что студенты гуманитарных специальностей используют рисунки как культурные средства при формировании суждения о переносе способа решения исходной задачи на целевую. Поскольку исходная задача в эксперименте ими не решалась, то испытуемые в большей степени были вынуждены сосредоточиваться на анализе структуры задачи и подготовке к предполагаемому решению. Именно в этом, на наш взгляд, могут заключаться культурные функции рисунков как средств, помогающих построению правильной репрезентации задачи в ходе обучения.
При наблюдении за составлением рисунков в свободном процессе решения мы обнаружили, что рисунки сильно различаются по количеству и форме элементов. Однако в ходе эксперимента, мы уточнили, что параметр полноты отношений элементов рисунка имеет большее значение для решателя при суждении о переносе способа решения, чем параметр схематичности/аналоговости. Также с возрастанием опыта решения подобных задач эта зависимость усиливается и к ней добавляется еще и фактор сходства переменных в исходной и целевой задачах. То есть, опытные решатели принимают решение о сходстве двух задач на основании как рисунков, отражающих определенным образом части условий, так и переменных, из которых эти условия состоят.
Почему такой параметр, как полнота отношений между элементами рисунка, более важен, чем параметр аналоговость/схематичность? Ряд исследований решения творческих задач по аналогии показывают, что сходство элементов задач влияет на воспоминание решателя, что он уже решал похожую задачу, но только сходство в отношениях между элементами влияет на перенос опыта прошлого решения на текущее [Holyoak, 1987].
С другой стороны, известно, что на ранних этапах онтогенеза, в возрасте 3 лет, дети значительно успешнее находят спрятанный в комнате предмет на основе условного рисунка-карты, чем трехмерной модели комнаты [DeLoache, 1991]. Одно из обобщений этого факта таково, что для выполнения поисковой задачи удобнее использовать средство, материал которого отличается от материала самой задачи. В противном случае на ранних этапах научения затруднительно осуществлять переходы от задачи к репрезентации и обратно. На похожую зависимость указывал Л.С. Выготский, говоря об отношениях между обучением и развитием как переходе от внешних, доступных для произвольного внимания и обсуждения, форм представления во внутренние — индивидуальные и автоматические [Выготский, 1996]. Сходным образом в нашем эксперименте для студентов с низкой успешностью аналоговость рисунка «зашумляла» отношения между элементами задачи.
Однако студенты, решившие хотя бы одну из предложенных нами задач, могли, по-видимому, игнорировать аналоговость рисунка и опирались на полноту отношений в рисунке. Дело в том, что при решении алгебраических задач учащиеся уже имеют дело с другим типом заданий. В отличие от поиска предметов в пространстве, текст задачи содержит не столько описание предметных отношений объектами задачи (поезда и их перемещение в пространстве), сколько описание математической зависимости между абстрактными переменными. Именно связь между частями знания, системный характер их зависимости друг от друга характеризуют отличие научных понятий от житейских [Выготский, 2012]. В этом, как нам кажется, и состоит причина доминирования параметра полноты отношений между элементами рисунка над параметром аналоговости/схематичности. Рисунок к алгебраической задаче является таким же культурным средством, что и рисунок при поиске предмета или запоминании его местоположения, однако в ходе обучения области научного знания он помогает выполнению другого типа мыслительных операций.
Нам впервые удалось показать, что рисунки, сопровождающие процесс решения алгебраических задач, оказывают влияние на суждения о переносе способа решения. Дальнейшее направление исследований может быть связано с вопросами обучающего характера. Можно ли обучать учащихся более эффективно переносить освоенное решение на новые задачи, если при этом решении использовать рисунки нужного типа, например, с группировкой всех переменных относительно друг друга? Некоторые эксперименты с обучением испытуемых решению новых задач показывают, что предварительное сравнение задач значительно ускоряет это обучение [Catrambone, 1989]. В совокупности с нашими результатами мы можем предположить, что более опосредованное сравнение — с использованием схем — позволит не только быстро усваивать новые понятия, но и приведет к более высокому уровню осознания отношений между ними.
При этом важно учитывать и то, что трудности в решении математических задач отражают, наряду с собственно обучением понятиям, и индивидуальные особенности формирования высших психических функций. Например, при решении арифметических задач в начальной школе для одних текстовых задач (инвертированных, или косвенных) требуется определенная развитость действий программирования и контроля, а для других, содержащих сложные логико-грамматические конструкции («на сколько больше, чем...»), требуется понимание отдельных понятий и развитость пространственных представлений [Ахутина, 2001].
Могут ли учащиеся более эффективно распознавать, решаема ли задача, если обучать их отдельному действию по отображению в рисунке элементов условия и отношений между ними? Исследования материала заданий по переносу решения задач с опорой на рисунок показывают, что при возрастании нагрузки на рабочую память испытуемые переходят от переноса по сходству отношений между частями изображения к переносу по сходству отдельных элементы [Waltz, 2000]. Такие исследования необходимы для более полного понимания участия культурных средств символизации реальности в обучении.
Литература
- Ахутина Т.В., Обухова Л.Ф., Обухова О.Б. Трудности усвоения начального курса математики в форме ква- зиисследовательской деятельности // Психологическая наука и образование. 2001. № 1. С. 65—78.
- Брушлинский А.В. Субъект: мышление, учение, воображение. М. «Институт практической психологии», 1996. 392 с.
- Валуева Е., Лаптева Е. Использование подсказок при решении задач: модальная специфичность или универ- сальная способность // Российский журнал когнитивной науки. 2015. № 2 (2—3). С. 53—65.
- Веракса А.Н., Якупова В.А., Мартыненко М.Н. Сим- волизация в структуре способностей детей дошкольного и школьного возраста // Культурно-историческая психоло- гия. 2015. Т. 11. № 2. С. 48—56.
- Выготский Л.С. Мышление и речь. M.: Лабиринт, 2012. 352 c.
- Выготский Л.С. Проблема обучения и умственного развития в школьном возрасте // Психологическая наука и образование. 1996. № 4. С. 5—18.
- Гальперин П.Я. О формировании умственных дей- ствий и понятий // Культурно-историческая психология. 2010. № 3. С. 111—114.
- Давыдов В.В., Маркова А.К. Концепция учебной дея- тельности школьников // Вопросы психологии. 1981. № 6. С. 13—26.
- Крутецкий В.А. Психология математических спо- собностей школьников. М.: Просвещение, 1968. 431 с.
- Спиридонов В.Ф. Психологические механизмы ре- шения текстовых задач по математике. Вестник РГГУ. 2006. № 1. C. 156—173.
- Bernardo A.B. Analogical problem construction and transfer in mathematical problem solving // Educational Psy- chology. 2001. Vol. 21. №2. P. 137—150.
- Beveridge M., Parkins E. Visual representation in ana- logical problem solving // Memory & Cognition. 1987. Vol. 15. № 3. P. 230—237.
- Catrambone R., Holyoak K.J. Overcoming contextual limitations on problem-solving transfer // Journal of Experimental Psychology: Learning, Memory and Cognition. 1989. Vol. 15. № 6. P. 1147.
- Charles A W., Kintsch W. Enhancing students’ compre- hension of the conceptual structure of algebra word problems // Journal of Educational Psychology. 1992. Vol. 84. № 4. P. 419—428.
- DeLoache J.S. Symbolic functioning in very young chil- dren: Understanding of pictures and models // Child Develop- ment. 1991. Vol. 62. P. 736—752.
- Gallistel C.R. Mental representations, psychology of // Encylopedia of the Behavioral and Social Sciences. N.Y.: Else- vier, 2001. P. 9691—9695.
- Gick M.L., Holyoak K.J. Analogical problem solving // Cognitive Psychology. 1980. Vol. 12. № 3. P. 306—355.
- Holyoak K.J., Koh K. Surface and structural similarity in analogical transfer // Memory & Cognition. 1987. Vol. 15. № 4. P. 332—340.
- Kintsch W., Weaver C. A. Enhancing students’ com- prehension of the conceptual structure of algebra word prob- lems // Journal of Educational Psychology. 1992. Vol. 84. P. 419—428.
- Novick L.R. Transferring symbolic representations across nonisomorphic problems // Journal of Experimental Psychology: Learning, Memory and Cognition. 1994. Vol. 20. P. 1296—1321.
- Ohlsson S. Learning from performance errors // Psy- chological Review. 1996. Vol. 103. № 2. P. 241—262.
- Reed D.K., Dempster A., Ettinger M. Usefulness of analo- gous solutions for solving algebra word problems // Journal of Experimental Psychology: Learning, Memory and Cognition. 1985. Vol. 11. P. 106—125.
- Rehder B. Detecting unsolvable algebra word prob- lems // Journal of Educational Psychology. 1999. Vol. 91. № 4. P. 669—683.
- Seifert C.M., McKoon G., Abelson R.P., Ratcliff R. Memory connections between thematically similar episodes // Journal of Experimental Psychology: Learning, Memory and Cognition. 1986. Vol. 12. № 2. P. 220.
- Waltz J.A., Lau A., Grewal S.K., Holyoak K.J. The role of working memory in analogical mapping // Memory & Cogni- tion. 2000. Vol. 28. № 7. P. 1205—1212.
Информация об авторах
Метрики
Просмотров web
За все время: 2446
В прошлом месяце: 21
В текущем месяце: 16
Скачиваний PDF
За все время: 661
В прошлом месяце: 5
В текущем месяце: 1
Всего
За все время: 3107
В прошлом месяце: 26
В текущем месяце: 17