Психолого-педагогические исследования
2016. Том 8. № 4. С. 174–184
doi:10.17759/psyedu.2016080417
ISSN: 2587-6139 (online)
Опыт диагностики метапредметных компетенций учащихся основной школы (на математическом материале)
Аннотация
Общая информация
Ключевые слова: метапредметные компетенции, предметная диагностика, обучение математике, диагностика компетенций
Рубрика издания: Психологический инструментарий
Тип материала: научная статья
DOI: https://doi.org/10.17759/psyedu.2016080417
Для цитаты: Соколов В.Л., Фомин А.А. Опыт диагностики метапредметных компетенций учащихся основной школы (на математическом материале) [Электронный ресурс] // Психологическая наука и образование psyedu.ru. 2016. Том 8. № 4. С. 174–184. DOI: 10.17759/psyedu.2016080417
Полный текст
Статья посвящена проблеме диагностики метапредметных компетенций в свете введения новых образовательных стандартов основного общего образования. Рассмотрен опыт проведения диагностики компетенций у учащихся V–VII классов в возрасте от 10 до 15 лет. Приводятся примеры заданий, построенных на математическом содержании. Предлагаются модели построения диагностических заданий, подробные комментарии к каждому из них.
Анализируются результаты апробации на 340 испытуемых (учащихся различных образовательных организаций). Авторы констатируют разброс результатов выполнения заданий, обосновывают гипотезу о возможности использования диагностических материалов для учащихся различных классов основной школы. Статья будет интересна педагогам и психологам, решающим задачу организации диагностики метапредметных компетенций учащихся основной школы.
Введение в 2015/2016 учебном году Федерального государственного образовательного стандарта основного общего образования в V классах всех школ России устанавливает требования к метапредметным результатам освоения образовательной программы, в том числе способность использовать универсальные учебные действия в учебной, познавательной и социальной практике [Федеральный государственный образовательный]. Таким образом встает вопрос о формировании содержательно-критериальной основы для оценки результатов освоения обучающимися основной образовательной программы основного общего образования. Интересным представляется подход к диагностике, построенный не на внеучебном материале, а на содержании изучаемых в школе предметов. Имеется опыт разработки данной проблемы для начальной ступени образования, в частности, описаны диагностические задания на математическом материале [Гуружапов, 2012; Гуружапов, 2013].
Ниже представлены результаты апробации заданий на математическом содержании, которые позволяют, согласно нашей гипотезе, проследить за развитием некоторых метапредметных компетенций у учащихся основной школы на всем периоде обучения.
Программа исследования
Предложенные учащимся задания были разработаны в рамках действия временного научно-исследовательского коллектива МГППУ. Одна часть заданий предполагала выбор одного правильного ответа из предложенных, другая часть – запись ответа в числовом виде.
В исследовании участвовали 340 учащихся из четырех школ Москвы и Московской области, среди них 120 пятиклассников, 122 шестиклассника и 98 семиклассников. Школы также отличались по своим видам: один кадетский корпус, расположенный в сельской местности, одна гимназия, одна городская школа и одна поселковая. Апробация заданий проводилась во время уроков. Детям раздавались задания на бланках, давалась стандартная инструкция по участию в эксперименте.
Всего в бланки было включено восемь заданий. В данной статье мы подробно рассмотрим результаты апробации пяти заданий. Время на выполнение всех заданий ограничивалось одним уроком. Задания размещались на четырех стандартных листах. Ниже мы представляем результаты констатирующего эксперимента.
Предполагается, что выполнение предлагаемых заданий потребует проявления следующих умений, обозначенных в ФГОС: умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; умение устанавливать причинно-следственные связи, строить логическое рассуждение и делать выводы [Федеральный государственный образовательный].
При проектировании предлагаемых заданий учитывался опыт проведения диагностики в международном исследовании PISA [Международное исследование PISA]. Использование заданий, построенных по аналогии с заданиями из PISA, представляется правомерным, так как в данном исследовании заявлено, что наряду с формированием предметных знаний и умений школа должна обеспечивать развитие у учащихся умения использовать свои математические знания для разрешения разнообразных ситуаций, близких к реальным. В дальнейшем это умение будет способствовать активному участию выпускника школы в жизни современного общества. Как отмечает К.Н. Поливанова, идеология исследования PISA, связанная с пониманием знания как средства решения реальных жизненных задач, в той или иной мере выступала в качестве основания для описания планируемых образовательных результатов в ФГОС основного общего образования [Поливанова, 2015].
Особенностью всех заданий является возможность их использования в течение всего периода обучения в основной школе с V по IX класс. Такая возможность сможет обеспечить отслеживание динамики формирования метапредметных компетенций в процессе обучения.
К каждому заданию мы приводим комментарий, в котором описаны возможные способы рассуждения для решения задания. Мы предполагаем, что нахождение верного способа решения требует от испытуемого проявления заявленных метапредметных компетенций. Само описание метапредметных компетенций дается в ФГОС в интегрированном виде. При решении конкретных заданий то или иное умение, обеспечивающее метапредметную компетенцию, будет задействовано в большей или меньшей степени. Качество метапредметной компетенции и уровень ее сформированности невозможно оценить при решении какого-то одного задания. Именно поэтому подобран ряд заданий с разными предметными основаниями и с разными сюжетами.
Таким образом, об уровне сформированности компетенции можно будет судить по количеству решенных заданий. Другими словами, если у испытуемого компетенция развита, то он сможет найти способ использовать свои умения в разнообразных ситуациях. Если компетенция развита недостаточно, то увидеть возможности использования своих умений испытуемый сможет только в ограниченном круге ситуаций.
Рассмотрим каждое из заданий.
Задание 1.
В примере на вычитание две цифры заменили буквами. Определи, что больше: К или Р и на сколько. 
Комментарий к заданию 1.
Идея использования задания такого вида для диагностики метапредметных компетенций описана в работах В.А. Гуружапова [Гуружапов, 2000]. Методы предметной диагностики должны в равной мере опираться как на традиции исследования мышления с использованием «задач на соображение», так и на достижения в области проектирования квазиисследовательской деятельности учащихся на конкретных предметах. Для этого тестовые задания должны быть аналогом учебной задачи на обобщение пройденного материала, а по форме – «задачами на соображение», содержащими тонкие различия существенных и несущественных признаков объекта. Условием задачи на обобщение пройденного материала должны являться способы преобразования объекта, которые ученик осваивал в учебной деятельности на уроках по определенной теме. Задание должно заключаться в определении типа практической предметной задачи, которая допускает эти преобразования.
Провокационным моментом в задании выступает ориентация на то, что при вычитании чисел разность меньше уменьшаемого. В примере из К вычитают 8. Казалось бы Р будет меньше, чем К. Но это верно только для случая, когда не происходит перехода через разряд. В данном случае при вычитании из 4-х десятков 3-х десятков получилось 0 десятков, значит, при вычитании единиц был переход через разряд. Следовательно, цифра К должна быть меньше 8, но при этом Р окажется большим, чем К. Чтобы установить, насколько именно Р больше К, достаточно провести несколько испытаний с конкретными цифрами. В действительности окажется, что Р больше К на 2.
Задание 2.
Маша и Петя живут на одинаковом расстоянии от школы и на расстоянии 8 км друг от друга. Каким может быть расстояние от дома Маши до школы?
Ответы:
не менее 4 км; не более 4 км; не менее 8 км; не более 8 км.
Комментарий к заданию 2.
Задание является модифицированным вариантом задачи из исследования PISA [Международное исследование PISA].
Успешность решения данного задания должна быть обеспечена переводом условия реальной ситуации на язык математической модели. Можно рассмотреть равнобедренный треугольник с основанием 8 км и неизвестными боковыми сторонами. В соответствии с неравенством треугольника длины боковых сторон не могут оказаться меньше, чем 4 км. Для учащихся, не знакомых с неравенством треугольника, решение задания доступно в виде исследовательской ситуации.
Комментарий к заданию 3.
Для успешного решения задания потребуется установить связи между данными из условия.
При этом уровень сложности возрастает от первой подзадачи к третьей. В первом случае возможен и будет правильным любой из способов решения. Например, всего в листе бумаги 6х12 будет 72 клетки. Один квадрат 3х3 содержит 9 клеток. Следовательно, всего получится 72 : 9 = 8 квадратов. Также возможен непосредственный предметный способ решения, при котором учащийся разобьет данный лист на квадраты 3х3 и посчитает количество получившихся квадратов.
Однако во второй подзадаче наступает ограничение в применении арифметического способа решения. В условии содержится требование, что квадраты склеивать нельзя, поэтому нужно рассчитать, сколько квадратов 3х3 уместится по длине и ширине данного листа. 10 : 3 = 3 (ост. 1); 26 : 3 = 8 (ост. 2). Таким образом получится 3 х 8 = 24 квадрата.
При решении третьей подзадачи возникает ограничение в применении только что описанного способа, поскольку вырезают не квадраты, а прямоугольники. Следовательно, нужно учитывать, что прямоугольники можно по-разному располагать на листе бумаги. Оптимальным в данном случае оказывается следующий способ рассуждения. Всего клеток в листе 10х26 будет 260. Площадь вырезаемого прямоугольника 3х4 будет равна 12. Наибольшее возможное количество прямоугольников: 260 : 12 = 21 (ост. 8). Однако нужно еще проверить, можно ли расположить на данном листе 21 такой прямоугольник. Это возможно. Таким образом, правильный ответ – 21.
Задание 4.
Офисы российской компании находятся в Москве, Красноярске и Владивостоке. Когда в Красноярске полночь, в Москве – 8 часов вечера, а во Владивостоке – 3 часа ночи.
В таблице указаны обязательные часы присутствия в офисе сотрудников компании по местному времени. В какой промежуток по красноярскому времени возможно проведение совещания, чтобы в нем могли участвовать, сотрудники компании, находящиеся в Москве, Красноярске и Владивостоке?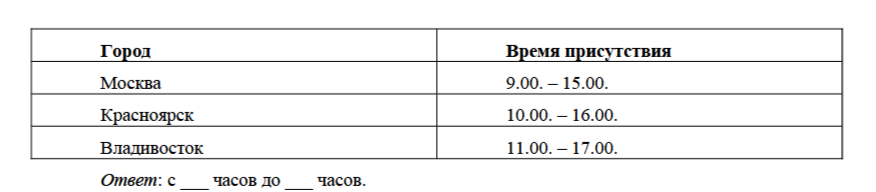
Комментарий к заданию 4.
Задание является модифицированным вариантом задачи из исследования PISA [Международное исследование PISA].
Установить связь между данными этого задания можно разными способами. Например, отложить на числовой прямой временные отрезки, соответствующие рабочему времени сотрудников с учетом часовых поясов. Тогда решение задачи сводится к нахождению пересечения трех множеств. Возможен перевод рабочего времени на красноярское и непосредственное получение верного ответа: с 13 до 14 часов. В любом случае для того чтобы построить логическое рассуждение и сделать вывод, учащийся может использовать любые средства, помогающие организовать поиск решения: таблицу, график, числовую прямую, схему, чертеж. Такое использование средств организации мышления и будет проявлением метапредметной компетенции, позволяющей эффективно решить поставленную проблему.
Задание 5.1.
Сайт МН РЕЙТИНГ проводит оценку квартир в новых домах. Была проведена экспертная оценка квартир по нескольким критериям по пятибалльной шкале в четырех новых домах.
Результаты представлены в таблице.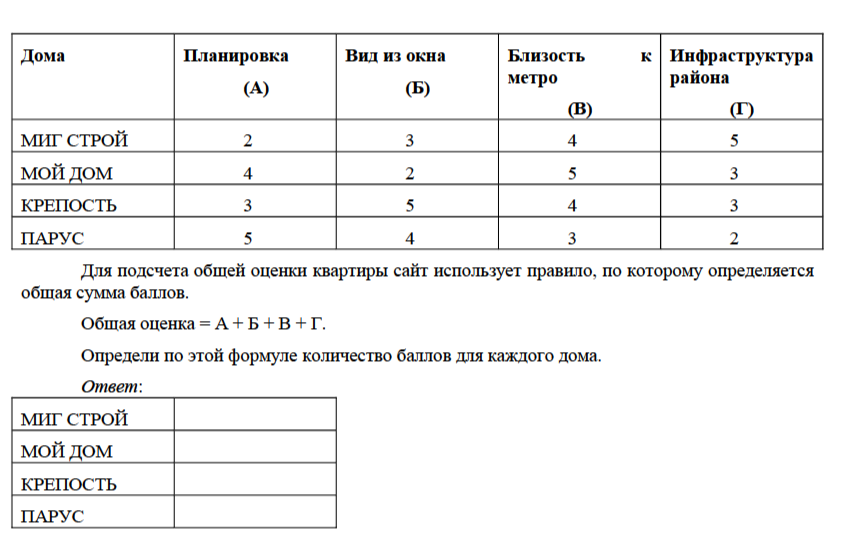
Задание 5.2.
Ниже приведены другие формулы для подсчета общей оценки. Какой формулой нужно воспользоваться, чтобы лучшими были признаны квартиры «МОЙ ДОМ»?
Ответы:
1) общая оценка = 2 ∙ А + Б + В + Г; 2) общая оценка = А + 2 ∙ Б + В + Г; 3) общая оценка = А + Б + 3 ∙ В + Г; 4) общая оценка = А + Б + В + 2 ∙ Г.
Задание 5.3.
Какой формулой нужно воспользоваться, чтобы лучшими были признаны квартиры «МИГ СТРОЙ»?
Ответы:
1) общая оценка = 2 ∙ А + Б + В + Г; 2) общая оценка = А + 2 ∙ Б + В + Г; 3) общая оценка = А + Б + 3 ∙ В + Г; 4) общая оценка = А + Б + В + 2 ∙ Г.
Комментарий к заданию 5.
Задание основано на способе диагностики анализа как компонента теоретического мышления. Особенностью этого задания является возможность двух различных способов его решения. Для диагностики анализа принято использовать задания, допускающие как возможность независимого эмпирического решения всех отдельных задач, так и нахождение общего способа их решения. Анализ рассматривается как логическое действие, позволяющее выделить отдельные элементы из целого, как действие, противоположное синтезу, – объединению частей в целое.
Кроме того, В.В. Давыдов говорит о содержательном анализе, позволяющем обнаружить существенные признаки в постигаемом объекте. Примером проявления содержательного анализа может быть задание, где требуется обнаружить внутреннюю связь между отдельными его элементами [Давыдов, 1996].
Решение задания 5.1. не представляет никакой трудности и призвано подготовить учащегося к решению второй части задания. Предполагается, что, выполняя сложение чисел из таблицы, учащийся обратит внимание на большой разброс в оценках домов по разным критериям.
В этом случае при решении второй части задания возможно использование способа, исключающего непосредственные вычисления по каждой из четырех формул, представленных в ответе. Такое непосредственное вычисление, конечно, тоже приведет к нахождению верного ответа, однако потребует значительно больше времени. Именно поэтому данное задание поставлено последним, чтобы повысить вероятность обнаружения тех учащихся, которые решат его на основе анализа данных и формул и смогут обнаружить существенное свойство. Понятно, что для признания квартир фирмы «Мой дом» лучшими нужно усилить удельный вес лучшего показателя. Таковым является критерий «В». Следовательно, формула: Общая оценка = А + Б + 3 ∙ В + Г должна обеспечить первое место. Но необходимо выполнить проверку, что при использовании данной формулы другие дома окажутся в худшем положении. Таким образом, оптимальным будет решение, когда расчет нужно произвести по одной формуле для четырех домов, а не по четырем формулам для четырех домов. Аналогичные рассуждения в задании 5.3. приводят к верному ответу: Общая оценка = А + Б + В + 2 ∙ Г. Задание 5 мы оценивали как верно выполненное, если испытуемый давал верные ответы ко всем трем подзадачам: 5.1., 5.2. и 5.3.
Результаты и их интерпретация
Максимально возможный результат за выполнение всех указанных заданий составляет 7 баллов. В результате проведенной диагностики мы получили следующие средние арифметические баллы в классах: V класс – 2,0 балла; VI класс – 2,5 балла; VII класс – 3,3 баллов. Среди учащихся V классов 39 % детей выполнили три и более заданий. В VI классе три и более заданий выполнили 47 % учащихся. Среди VII классов 51 % учащихся выполнили три и более заданий.
Обратимся к различиям в полученных результатах относительно образовательных учреждений. Средний результат в классах кадетского корпуса составил 2,3 балла; в поселковой школе – 2,3 балла; в городской школе – 3,0 балла; в гимназии – 2,9 баллов. Более подробно полученные результаты отображены на рис. 1. Из полученных данных можно сделать вывод о том, что уровень развития метапредметных компетенций учащихся зависит от особенностей школы и ее образовательной среды.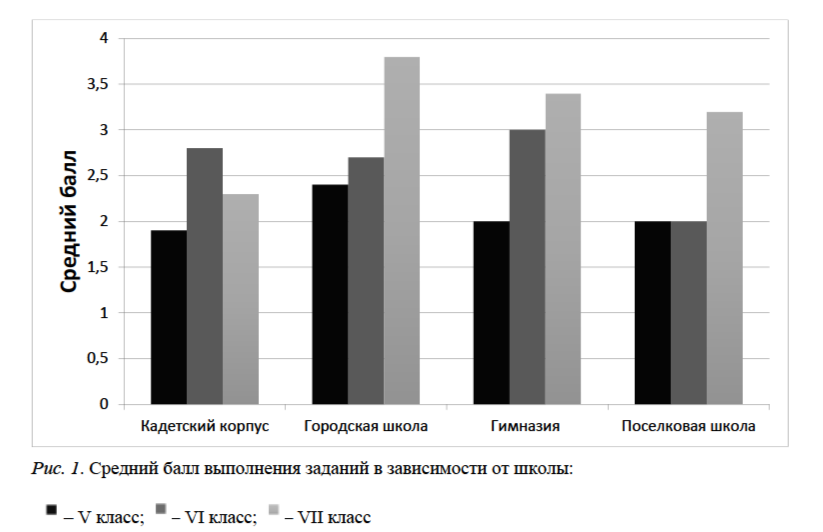
Обратимся к анализу самих диагностических заданий. Средний процент выполнения по каждому заданию представлен на рис. 2.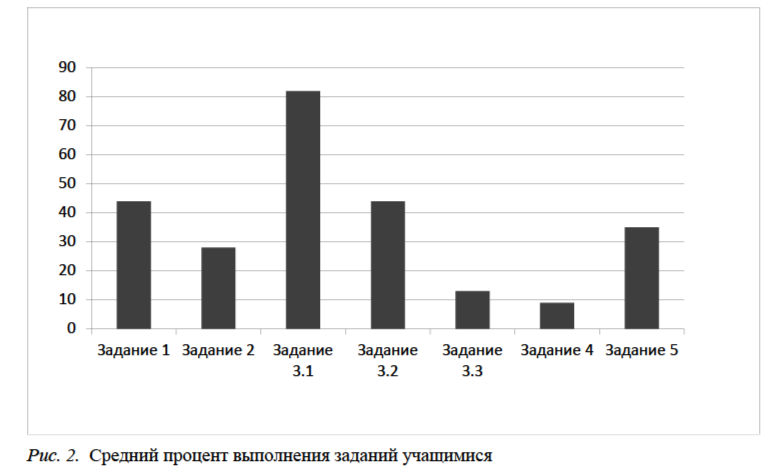
Самым трудным оказалось задание 4 – его верно выполнили 8 % учащихся из всей выборки.
Результаты выполнения заданий по классам представлены в таблице.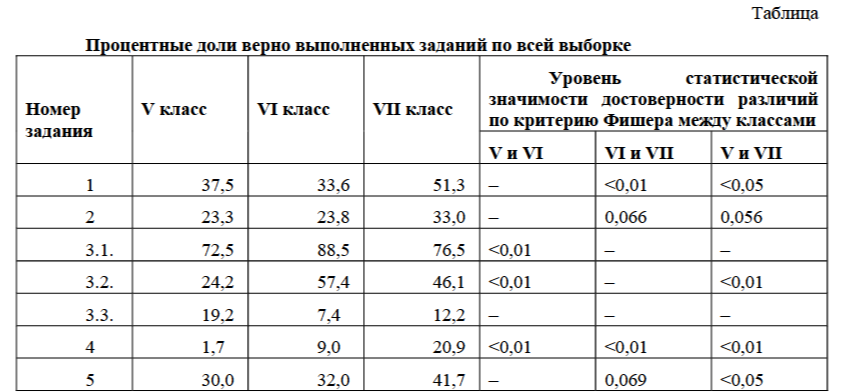
При анализе результатов констатирующего эксперимента на выборке, состоящей из учащихся общеобразовательных организаций разных видов и имеющих разную образовательную среду, нас интересовала динамика успешности выполнения заданий от V к VII классу. Для статистического анализа был использован критерий φ* – угловое преобразование Фишера. Можно констатировать, что наблюдается достоверная положительная динамика от V к VII классу при выполнении заданий 1, 3.2., 4 и 5. На уровне тенденции есть положительная динамика по заданию 2. Самым неудачным оказалось задание 3.3. Поскольку эксперимент носил констатирующий характер, те или иные колебания в динамике могут быть обусловлены наличием в выборке более сильных и слабых классов.
Выводы
1. Имеются резервы в развитии метапредметных компетенций у учащихся основной школы. Об этом свидетельствуют невысокие результаты выполнения отдельных заданий и разброс результатов как между классами, так и между учащимися одного класса, что в свою очередь характеризует дифференцирующие возможности диагностических заданий. 2. На данном этапе исследования можно сделать предположение, что, в целом, рассмотренные диагностические задания могут использоваться в качестве инструмента измерения метапредметных компетенций у учащихся основной школы. Подтверждение данной гипотезы возможно при продолжении исследования в экспериментальных группах. Низкий уровень выполнения задания 4 свидетельствует о необходимости его модернизации для учащихся V класса. 3. Полученные данные позволяют утверждать, что уровень развития выделенных метапредметных компетенций тем выше, чем старше класс. 4. Дальнейшее накопление эмпирических данных по результатам апробации заданий позволит провести содержательный анализ качества представляемых заданий, возрастных возможностей учащихся, зависимости результатов от вида школы и получить для практического использования диагностический инструментарий определения уровня развития метапредметных компетенций у учащихся основной школы
Литература
- Гуружапов В.А. К вопросу о соотношении психологической диагностики и коррекции учебной деятельности на уроках математики // Психологическая наука и образование. 2000. № 2. С. 79–85.
- Гуружапов В.А. К проблеме оценки метапредметной компетентности испытуемых [Электронный ресурс] // Психологическая наука и образование PSYEDU.ru. 2012. №1. URL: https://psyjournals.ru/psyedu_ru/2012/n1/50747.shtml (дата обращения: 14.07.2015).
- Гуружапов В.А., Шиленкова Л.Н. Умение анализировать условие задачи как метапредметный результат обучения [Электронный ресурс] // Психологическая наука и образование PSYEDU.ru. 2013. №5. URL: https://psyjournals.ru/psyedu_ru/2013/n5/Gurugapov_Schilenkova.shtml (дата обращения: 14.07.2015).
- Давыдов В.В. Теория развивающего обучения. М.: ИНТОР, 1996. 544 с.
- Международное исследование PISA. Примеры заданий по математике[Электронный ресурс] //URL: http://www.centeroko.ru/public.htm#pisa_pub (дата обращения 14.07.2015).
- Поливанова К.Н. Образовательные результаты основной школы в контексте международных исследований // Психологическая наука и образование. 2015. Т. 20. № 4. C.19–30. doi: 10.17759/pse.2015200402.
- Федеральный государственный образовательный стандарт основного общего образования[Электронный ресурс]// URL:http://минобрнауки.рф/документы/543/файл/749/приказ%20Об%20утверждении%201897.rtf(дата обращения 14.07.2015).
Информация об авторах
Метрики
Просмотров web
За все время: 2458
В прошлом месяце: 34
В текущем месяце: 12
Скачиваний PDF
За все время: 980
В прошлом месяце: 7
В текущем месяце: 1
Всего
За все время: 3438
В прошлом месяце: 41
В текущем месяце: 13