Моделирование и анализ данных
2022. Том 12. № 4. С. 5–24
doi:10.17759/mda.2022120401
ISSN: 2219-3758 / 2311-9454 (online)
Онтологический и эпистемологический аспекты моделирования: модельное отношение и адиафорные системы
Аннотация
На основе рассмотрения модельного отношения, предложенного Р. Розеном, в статье представлены онтологические и эпистемологические аспекты моделирования каузальных системных процессов. Модельное отношение позволяет осуществлять сравнение систем и их моделей, а также дает возможность перейти к определению и известной формализации процессов измерений. Рассмотренный онтологический аспект моделирования включает представление о сложных системах и в случае импредикативных систем позволяет говорить о выделении качественно более сложного класса сверхсложных систем. В эпистемологическом плане на основе положений трансцендентальной психологии дано определение порождающих (формопорождающих) систем, как адиафорных систем, чьи механизмы, как правило, не проявляют себя в порождаемых формах и продуктах. Адиафорность исследуемых процессов прямо не зависит от онтологической сложности моделируемой системы и означает, что система порождает новые структуры и формы независимо от каких-либо проявляемых свойств или производимых частей и продуктов. Адиафорные системы могут иметь место при рассмотрении процессов перехода между системообразующими формопорождающими структурами, изучаемыми разными иерархически взаимосвязанными науками.
Общая информация
Ключевые слова: система, модель, отношение, формопорождение, сложная система, трансцендентальная психология
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2022120401
Получена: 22.09.2022
Принята в печать:
Для цитаты: Артеменков С.Л. Онтологический и эпистемологический аспекты моделирования: модельное отношение и адиафорные системы // Моделирование и анализ данных. 2022. Том 12. № 4. С. 5–24. DOI: 10.17759/mda.2022120401
Полный текст
1. Введение
Моделирование является особым направлением развития современной науки, которое вместе с тем является искусством, отражающим важное качество жизни, поскольку наличие внутренней модели мира является важной характеристикой телесности живых организмов [Князева, 2015]. Тот факт, что моделирование во многом представляет собой искусство, связан, с одной стороны, с онтологическим аспектом собственной сложности устройства рассматриваемой части мира, а с другой стороны, с эпистемологическим и гносеологическим аспектами трудности познания качеств и механизмов тех процессов, которые подлежат моделированию и не поддаются автоматической формализации.
В отношении первого аспекта, сложность мира выступает для ученого в качестве такого устройства мира, которое фиксируется в понятии сложные системы. При этом известно, что для понятия сложности не существует однозначного определения. Ученые расходятся в определениях системной «сложности». Однако общее пересечение всех характеристик «сложности» содержит как минимум необходимое возникновение явлений из множества взаимодействий, при том, что количество этих взаимодействий не обязательно является большим. Сложная система часто влечет за собой появление новых явлений, вещи удивительные, неожиданные и явно непредсказуемые. Простая (т.е. несложная) система как правило не порождает таких непредсказуемых или эмерджентных вещей [3, 42].
В отношении второго гносеологического аспекта, можно утверждать, что трудность познания процессов, которые подлежат моделированию и не поддаются автоматической формализации, может быть также охарактеризована степенью сложности проникновения в исследуемые процессы и дальнейшего создания их соответствующих моделей. При этом моделирование сложных систем, по-видимому, должно быть связано с дополнительными трудностями. Вместе с тем существующие здесь познавательные сложности не связаны только со сложностью и онтологией рассматриваемых систем и, в частности, определяются наличными возможностями теоретического постижения и вывода естественных законов.
Выводимость закономерностей тех или иных процессов при достаточной степени установления их существования и характера проявления, в первую очередь, может быть обусловлена различными обстоятельствами доступности этих процессов для соответствующего исследования. Если адекватные средства проникновения в существо некоторого процесса недоступны по тем или иным причинам, то установление закономерностей и должное моделирование этого процесса будет затруднительным делом. Например, в психологии с такого рода трудностями наука встречается постоянно, поскольку многие из наличных здесь процессов имеют частично скрытый или полностью бессознательный характер.
Современные конструктивный, информационный и другие подходы к анализу процессов часто позволяют обойти представленные трудности на основе известных свойств продуктов соответствующих процессов в предположении, что механизмы этих процессов могут быть основаны на свойствах этих продуктов. Такой подход может быть назван продуктным подходом [Миракян, 1990]. Он хорошо работает в научно-технической сфере. При наличии знаний о деталях какой-либо машины и самой машины в целом, по-видимому, так или иначе можно будет понять и построить процесс создания этой машины без наличия чертежей или посещения завода ее производства.
Понятно, что такой способ реконструкции процесса (по его продуктам) не всегда возможен. Например, секрет приготовления сыра пармезан не содержится ни в самом сыре, ни в молоке как основном продукте, из которого он сделан, т.е., фактически, эти продукты и их свойства не дают никакой информации о процессе создания (созревания) сыра. Метафорически можно сказать, что процесс создания сыра пармезан является адиафорным процессом, в том смысле, что его механизмы «неразличимы» в его продуктах или «безразличны» (индифферентны) к получаемому результату [Artemenkov, 2021].
Целью настоящей работы является рассмотрение онтологии и эпистемологии системного моделирования каузальных процессов, в частности, для определения выделенного класса адиафорных систем на основе анализа, так называемого, модельного отношения [40, 44-46].
2. Модельное отношение
Моделирование так или иначе связано с представлением одной вещи или системы с помощью другой. Телеологическое представление одной системы в другой представляет собой древнейшее человеческое предприятие: человек находит закономерности и всегда теоретизирует, осуществляя даже метамоделирование самого моделирования, что включает методологическое изучение моделирования как процесса, а не просто создание самих моделей различных систем [Louie, 2019].
Генрих Герц во введении к своему посмертно опубликованному труду «Принципы механики, изложенные в новой связи» раскрывает метод моделирования в постановке задачи нахождения возможности предвидения будущего опыта, что позволяет регулировать наши действия в настоящем [Герц, 1959]. Основой для решения этой задачи служит предшествующий опыт и следующий метод: «мы создаем себе внутренние образы или символы внешних предметов, причем мы создаем их такими, чтобы логически необходимые следствия этих представлений в свою очередь были образами естественно необходимых следствий отображенных предметов. Чтобы это требование вообще было выполнимым, должно существовать некоторое соответствие между природой и нашим умом. Опыт учит нас, что это требование выполнимо и что такое соответствие существует с действительности. Если нам удалось создать из накопленного до сих пор опыта представление требуемого характера, то мы можем в короткое время вывести из них, как из моделей, следствия, которые сами по себе проявились бы во внешнем мире только через продолжительное время или же были результатом нашего вмешательства» [Герц, 1959, с. 13]. Таким образом, моделирование позволяет нам предвидеть факты и координировать принятые нами решения в соответствии с разработанными моделями соответствующих вещей (явлений или процессов). Здесь модель-образ выступает как мысленный образ внешнего объекта с определенным соответствием между природой этого объекта и мыслью. При этом, как замечает Г. Герц, модели-образы «находятся с вещами лишь в одном существенном соответствии» и, «отнюдь не необходимо, чтобы они, кроме того, были в каком-либо другом соответствии с вещами» [Герц, 1959, с. 14].
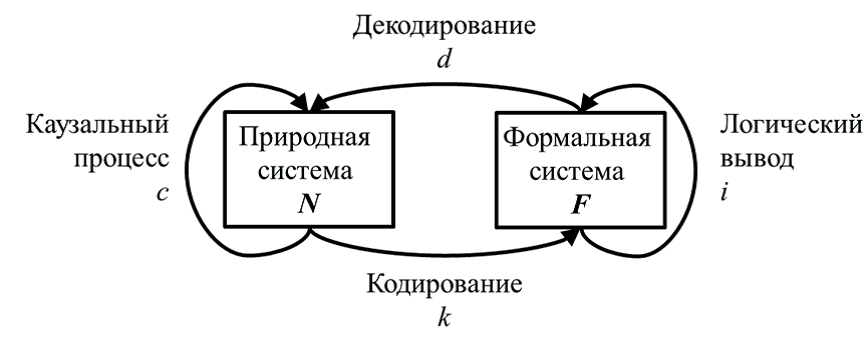
Характерным примером дальнейшего метамоделирования может служить функциональное представление модели в виде диаграммы модельного отношения Р. Розена [44-46]. Модельное отношение – это коммутативное функциональное отношение между естественной (природной) системой N и формальной системой F, определенное отображениями кодирования и декодирования между ними (Рис. 1).
Рис. 1. Прототипическое модельное отношение.
Процессы, происходящие в системах N и F, определяются как каузальные. Каузальный процесс c представляет собой проявление Аристотелевской действующей причины в природной системе, и, процесс логического вывода i соответствует проявлению Аристотелевской действующей причины в формальной системе. Кодирование k отображает естественную систему N и ее каузальный процесс c в формальную систему F и ее внутренний процесс i. Декодирование d осуществляет обратное отображение. Выводы здесь удовлетворяют условию коммутативности, согласно которому прослеживание по стрелке c — это то же самое, что последовательное прослеживание трех стрелок k, i, d.
c = k ∘ i ∘ d (1)
Иными словами, при наличии модельного отношения можно получить один и тот же ответ, если наблюдать за разворачивающейся последовательностью событий c в естественной системе N, или проследить как происходит кодирование k некоторых свойств естественной системы в формализм F, используется импликативная структура формальной системы для вывода теорем, а затем d декодирует эти теоремы в предложения (предсказания) о самой системе N. Когда выполняется коммутативность (1), то устанавливается соответствие между (некоторыми) каузальными свойствами естественной системы и импликативной структурой формальной системы. До определенной степени мы тогда может узнать об одной системе, смотря на другую. Отношение между N и F выражает модельное отношение, F является моделью N, а N является реализацией F.
С формальной точки зрения диаграмма модельного отношения полностью симметрична и запись (1) можно заменить на обратную.
i = d ∘ c ∘ k (2)
В принципе мы можем, как интересоваться совокупностью моделей, которые могут заместить природную систему с помощью некоторого формального языка, так и равным образом рассматривать совокупность таких объектных систем, которые могут быть закодированы в некоторый формализм или декодированы из данного формального языка [Rosen, 1999].
Однако, как отмечает A.H. Louie [Louie, 2019], в общее модельное соотношение на рисунке 1 встроена «полярность». Хотя кодирование k и декодирование d являются функторами, их операции (а также роли систем N и F) не взаимозаменяемы, даже для моделирования. Одна из причин заключается в том, что коммутативность c = k ∘ i ∘ d уравнения (1) не влечет за собой (2): i = d ∘ c ∘ k. Это, в первую очередь, связано с тем, что причинно-следственные процессы в F обычно не могут соответствовать всей возможной коллекции действующих причин в N. Вопрос о том, когда первое подразумевает второе, как правило, является предметом специального исследования [Louie, 2017].
Частным случаем модельного отношения при условии, что динамический процесс в системе N заменяется на статические отношения внутри изучаемого явления или вещи, а F представляет символьную или числовую системы, является отношение измерения. Согласно современному определению измерения по Супесу и Зинесу его можно представить как гомоморфизм (в лучшем случае изоморфизм) f = (k,d) между состояниями измеряемой системой A = N и числовым множеством R = F, с учетом наличия определенной группы отношений G, определяющей тип шкалы [Суппес, 1967]. Сведенные к общему морфизму кодирование k и декодирование d во многих случаях могут быть успешно формализованы, что обусловливает возможность автоматизации многих процессов измерения.
3. Сравнение систем между собой
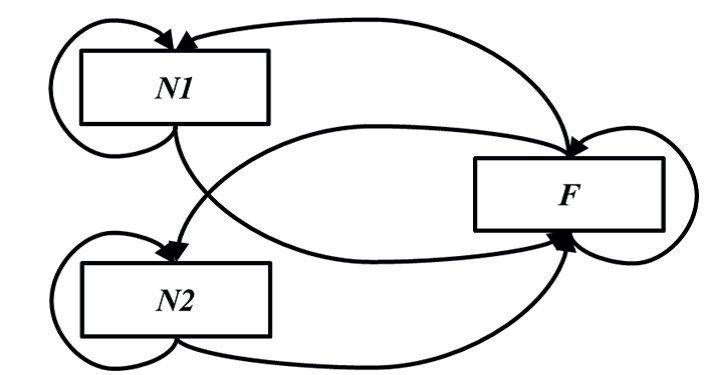
Диаграмму модельного отношения удобно использовать для сравнения разных систем между собой. Частный случай конгруэнтности между двумя различными природными системами N1 и N2 возникает, когда они обладают одной и той же формальной моделью F (или, альтернативно, они составляют различные реализации F), как показано на рисунке 2 [Rosen, 1991]. Используя систему F, можно «закодировать» признаки N1 в соответствующие признаки N2 и, наоборот, таким образом, чтобы две структуры следования в двух системах N1 и N2 были приведены в соответствие. Этому отвечает коммутативная диаграмма (показанная на рис. 3) взаимного моделирующего отношения между двумя естественными системами.
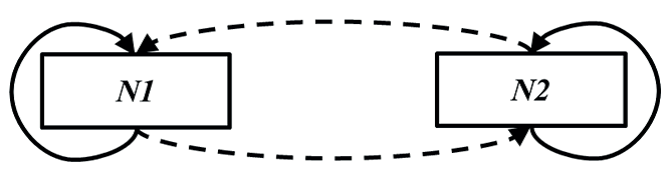
В этом случае, изображенные на рисунках 2 и 3, природные системы N1 и N2 являются аналогами. Аналогичные системы позволяют нам узнать об одной из них, наблюдая за другой. Отношения аналогии лежат в основе эффективности «масштабных моделей» в технике, а также всех различных «принципов эквивалентности» в физике.
Рис. 2. Общая модель F для двух аналогичных систем N1 и N2.
Но отношение аналогии имеет гораздо более глубокие последствия. Естественные системы самого разного рода (например, организмы, общества, экономические системы и политические системы) могут быть аналогичными. В частности, известно, что биологические и социально-экономические системы являются аналогичными антиципативными системами. Здесь аналогия — это отношение между системами, возникающее на основании моделей их причинных следствий, а не непосредственно из их материальных или иных структур. Таким образом, такая аналогия и родственные ей предлагают наиболее мощную и физически обоснованную альтернативу редукционизму (а именно, «имеют общую модель» и, следовательно, «аналогичны», а не «одно охватывает другое») [Louie, 2019].
Рис. 3. Аналогия.
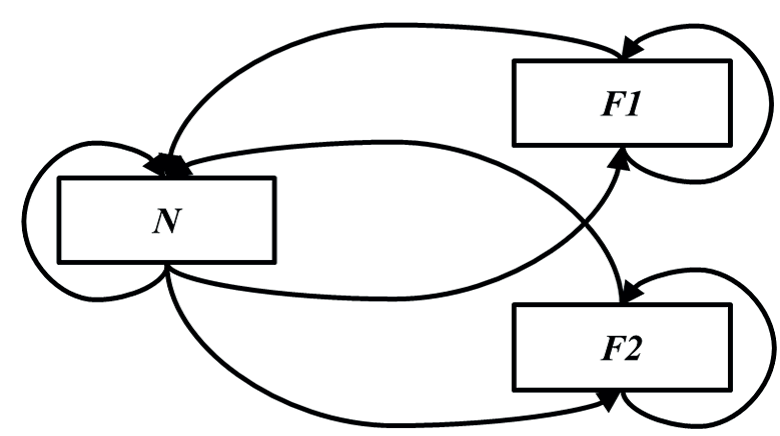
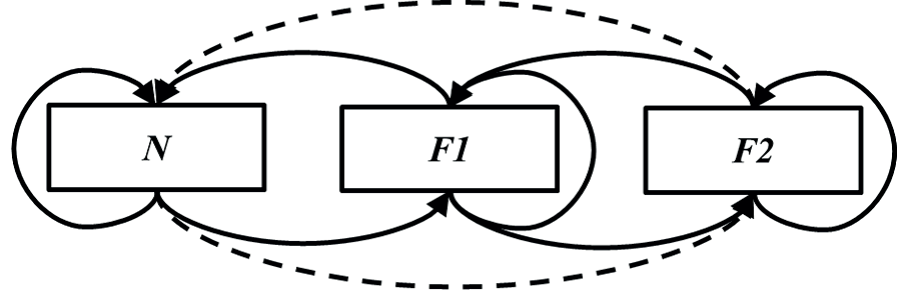
Диаграмма, дополнительная к рис. 2, показана на рис. 4. Здесь единая естественная система N моделируется двумя различными возможно альтернативными формализмами: F1 и F2 [Rosen, 1991]. Вопрос об отношении между формализмами F1 и F2 в этом случае не так прост, как раньше, и зависит от степени перекрытия N двумя кодировками в F1 и в F2. В некоторых случаях можно эффективно построить по крайней мере некоторые стрелки кодирования и декодирования между двумя формализмами. В качестве одного из примеров можно рассмотреть формулировку теории преобразований Дирака в квантовой механике, которая объединяет матричную механику Гейзенберга и волновую механику Шредингера. Другим примером может быть взаимосвязь между термодинамической и статистико-механической моделями жидкостей [Louie, 2019].
В остальных случаях формальной связи между F1 и F2 не существует. Тогда возникает ситуация, когда N одновременно реализует два различных и независимых формализма. Примерами являются различные дополнительности Бора для микрофизических явлений [Louie, 2019].
Рис. 4. Альтернативные формальные модели.
Модели можно формировать также итеративно: функторы кодирования и декодирования двух моделей могут быть составлены согласно второй конфигурации (Рис. 5), в которой естественная система N связана с двумя формальными системами F1 и F2 последовательно.
Рис. 5. Машинная модель.
Предположим, что формальная система F1 является моделью естественной системы N, причем прототипическое модельное отношение представляет собой переход из области науки в область математики. Если выделить только предикативные процессы F1, можно построить чисто синтаксическую «машинную» модель F2, как на рисунке 5.
Тогда можно рассматривать только две внешние системы N и F2 и забыть об исходной модели F1. Формальная система F2 является машинной моделью естественной системы N и отражает чисто синтаксические аспекты последней. Сами стрелки кодирования и декодирования (штриховые стрелки на рисунке 5) между N и F2 нельзя назвать эффективными в каком-либо формальном смысле, но они составляют исключительно входные и выходные цепочки машин Тьюринга в F2, и эти композиции можно сразу отождествить с эффективными процессами в N. Независимо от того, исчерпывают ли они импликативные ресурсы системы N или нет, такая модель системы N сама по себе служит для различения предикативных и непредикативных систем [Louie, 2019а].
Последовательное образование модельных отношений в случае, когда систему N можно считать относительно стабильной системой с внутренними отношениями, часто встречается при проведении измерений в общественных науках. В частности, схема процесса психологического измерения процедурно может включать большое количество множеств, связанных различными морфизмами: Y -> S -> P -> M -> U, где физическая шкала Y представляет собой концептуальную переменную, S – соответствует набору стимулов измеряемой переменной, P – представляет результаты психологического отражения, M - является формальным множеством и U – психологической числовой шкалой [Зароченцев, 2005, с. 110]. Каждый из таких морфизмов так или иначе включает операции кодирования и декодирования соответствующих модельных отношений.
Рассмотренное модельное отношение позволяет воплотить природный закон и тесно связано с возможностями теоретического объяснения и предсказания, что является одними из основных целей научного исследования. Будущее оказывается определено настоящим настолько хорошо, насколько конгруэнтной является используемая модель. При этом часто правильное предсказание может быть действием прямого декодирования из формализма (даже без использования кодирования).
Такое декодирование без кодирования является сутью метафоры, и наука ими переполнена: метафора химеры, машинная метафора Декарта и др. Метафора хотя и предоставляет возможность для объяснения и предсказания недостаточна и по сути не научна. Наука требует обеспечить экспериментальные возможности проверки предсказаний, что невозможно без обеспечения адекватного кодирования.
4. Порождающие системы и их механизмы
На практике во многих случаях представить адекватную формальную модель трудно или это не представляется возможным. В особенной мере это относится к таким процессам, которые обозначают появление чего-то нового не совсем понятным образом, что в разных науках и, в частности, в психологии часто обозначается термином «порождение». Например, в психолингвистике используется термин «порождения речи» и, в частности, объясняется, что: «В начале построения высказывания лежит мотив. Мотивация порождает речевую интенцию. На этом этапе говорящий имеет образ результата, но еще не имеет плана действия, которое он должен произвести, чтобы этот результат получить» [Вержбицкая, 2009, с. 33]. Таким образом, порождение осуществляет некоторое действие образования нового, не имеющее собственного плана или алгоритма. Этот алгоритм может в принципе отсутствовать или быть только не известным исследователю.
В программировании порождением может называться многократное применение правил: от начального символа к предложению (содержащему только терминальные символы). В результате язык программирования «допускает порождение эффективного кода «хорошо» написанных программ» [Городняя, 2015, с. 70].
Исследования природы психики указывают на наличие порождения действительной формы существования психики, будь то процессы порождения образа объекта или процессы порождения деятельности [17, 18, 28]. В частности, в психологии восприятия была разработана особая концепция «порождающего процесса восприятия» [25-27, 29]. Непосредственно-чувственное восприятие здесь представляется в виде общеприродного формопорождающего процесса. При этом «необходимым условием возникновения порождающего процесса восприятия является анизотропность отражающей системы, которая, расчленяя принимаемое воздействие на различающиеся относительно друг друга дискретные части, создает возможность для образования между ними анизотропного отношения» [Панов, 1998, с. 87].
На основе этой концепции восприятия А.И. Миракяном был предложен новый подход трансцендентальной психологии, в котором сделана попытка философско-теоретического осмысления и формализации возможностей осуществления формопорождения на основе ряда фундаментальных принципов и положений трансцендентального подхода [1, 2, 6, 9, 10, 22-24, 30, 31, 35]. Результирующие характеристики трех современных парадигм психологии восприятия представлены в таблице ниже [Артеменков, 2020].
Таблица. Характеристики трех парадигм психологии восприятия.
|
№ |
Элементы парадигмы |
Парадигмальная область психологии восприятия |
||
|
Гносеологическая |
Онтологическая |
Трансцендентальная |
||
|
1 |
Основание знаний |
Свойства продуктов восприятия |
Среда и ситуация восприятия |
Общие природные принципы |
|
2 |
Методо-логический подход |
Феноменально-систематизиру-ющий |
Событийный |
Аксиоматический |
|
3 |
Предмет изучения восприятия |
Функциональное поведение и явления восприятия |
Перцептивное событие как процесс |
Трансцендентальные процессуальные механизмы |
|
4 |
Позиция иссследова-теля |
Внешний наблюдатель преобразований |
Внешний наблюдатель событий |
Внутренний соучастник процесса |
|
5 |
Модель системы |
Основана на свойствах продуктов (образов) |
Основана на структурах событий |
Основана на формопорождении |
|
6 |
Описание структуры системы |
Функциональная гетерогенность |
Структурная гетерогенность |
Анизотропная однородность |
|
7 |
Внутренний процесс |
Детекция свойств |
Формирование структур |
Образование отношений |
|
8 |
Описание процесса восприятия |
Выделение и объединение свойств |
Выделение и структуриро-вание событий |
Процесс формопорождения |
|
9 |
Уровень свойств образов |
Отдельные свойства |
Событийные свойства |
Сопредставленные свойства |
Моделирование процессов формопорождения в восприятии на основе принципов трансцендентальной психологии позволило выявить ряд структурных особенностей процесса восприятия [2, 6-11, 26, 36]. Представленные в теории процессы кодирования форм в те или иные их имена обусловливают некоторые необходимые механизмы, но не обладают достаточной универсальностью для адекватного моделирования процессов непосредственно-чувственного восприятия в целом. Общие результаты проведенных исследований представлены в работах [30, 31].
Попытки раскрытия специфики процессов порождения делаются и в современном системном анализе, в котором системное целое в его определенной организованности обычно фиксируется посредством относительно устойчивой схемы связей и отношений между элементами системы. Порождающие системы рассматриваются при этом как системы с поведением или с изменяющимися состояниями. Состояние некоторых переменных модели порождаются при изменении их параметров и выборе граничных условий на основе заданных правил, законов и формул. Порождение в этом случае начинается с исходных данных, соответствующих базовым свойствам моделируемой системы, и значений, отвечающих параметрам этих свойств. В этой системной ситуации, четко определенной ограниченным набором формальных операций, модельная система осуществляет порождение информации о поведении или структуре моделируемого объекта с изменяющимся состоянием.
Этот подход удобен для компьютерной реализации и структурированные системы тогда выражают отношения между рядом построенных моделей, а метасистемы могут отражать отношения между построенными отношениями между моделями. Данная технология предполагает также возможности учета решения разных проблем и задач моделирования различными авторами и возможности упрощения для оптимизации работы пользователя [12, 19, 34].
Важно отметить, что предлагаемый подход моделирования порождения, фактически, расширяет контекст модельного отношения, поскольку отчасти позволяет формально описать те интеллектуальные действия, которые в модельном отношении на рисунке 1 скрыты за операциями кодирования и декодирования (в общем случае эти операции остаются не формализуемыми и, естественно, могут по-разному осуществляться различными авторами). При этом в систему данных и порождающих правил формальной модели могут быть включены определенные семантические и прагматические компоненты, характеризующие возможности субъектов. Это позволяет говорить об онтологиях интеллектуального моделирования [Валькман, 2016].
В целом можно сказать, что определение моделируемых процессов как порождающих, остается важной основой для указания на их сложную и непознанную природу, что, в частности, имеет место для психологических процессов генерации речи, восприятия, деятельности и поведения. При этом решающим фактором возможности моделировать порождение является сложность реализуемой системы. Однако, сложность нельзя использовать в качестве объяснительного принципа, поскольку «сложность» и «проявление» оказываются связаны с действием общего причинного источника, требующего расшифровки его механизмов в том числе с помощью метода моделирования. Традиционные способы моделирования с помощью систем, включающих фиксированные наборы состояний вместе с соответствующими динамическими законами, фактически ограничиваются только подклассом относительно простых естественных систем. При таком рассмотрении «простота» и «сложность» не имеют какого-либо существенного качественного различия.
Если полагать, что физика вооружает нас универсальными законами, которые охватывают все (природные) системы, тогда существует только один вид «системы» (а именно, подмножество вселенной), где «простые» и «сложные» системы отличаются только степенью простоты или сложности. Типичным сторонником этого взгляда являлся фон Нейман, который утверждал, что «сложность» — это измеримое (или даже вычислимое) количество систем, которое может быть использовано для их полного упорядочения, т.е. сложность – это что-то вроде таксономического индекса для ранжирования систем [фон Нейман, 1960]. Кроме того, он предположил, что существует критическое значение или порог сложности. Ниже этого порога находились простые системы, которые ведут себя в своих обычных механических режимах, а выше порога мы имеем сложные системы, способные проявлять новые, нелогичные, непредвиденные модели поведения [Louie, 2019а].
Существенно отличное представление о сложности было развито в реляционной биологии [44, 45], где проводится качественное различие между классом простых систем и классом сложных систем, что требует абсолютного разделения вселенной систем на два взаимодополняющих множества. Во множестве естественных систем U набор P простых систем определяется все те системы, которые удовлетворяют свойству предикативности (p). С другой стороны, как его дополнение, определяют набор сложных (импредикативных) систем - множество Pi всех естественных систем, не удовлетворяющих свойству p; эквивалентно, все те системы, которые удовлетворяют свойству (не p) [Louie, 2019а].
Разделение между P и Pi представляет собой «непроницаемую» границу: система либо проста, либо сложна (но не то, и другое одновременно), и две категории простых систем и сложных систем исключают друг друга. С самого начала устанавливается дихотомия: сложная система определяется как система, которая не является простой, и наоборот. Поскольку в языке термин «сложность» так или иначе предполагает различие в степени простоты или сложности и многие вполне предикативные системы часто называются сложными, то импредикативные системы имеет смысл именовать сверхсложными системами. Различие в сложности здесь абсолютно: не существует «более сложных» сравнений по степени между системами.
Разница в степени между простым и сложным сродни классификации размера множеств на «маленькие» и «большие». Инстинктивно множество, содержащее несколько элементов, мало, а множество, содержащее, скажем, 10 в сотой степени элементов (гугол), велико; но переход от малого к большому нечеткий и зависит от контекста. Различие между сложными и сверхсложными системами аналогично различию между конечными и бесконечными множествами. Разделение между конечными множествами и бесконечными множествами непроницаемо. Бесконечное — это не «большое конечное»: внутри конечного царства конечное (хотя и большое) число повторений механистических операций, таких как «добавление одного элемента», не сделает конечное множество бесконечным.
С гносеологической точки зрения, можно утверждать, что трудность познания процессов, которые подлежат моделированию и не поддаются автоматической формализации, также может быть охарактеризована степенью сложности создания соответствующих моделей. При этом моделирование сложных и сверхсложных систем, по-видимому, должно быть связано с дополнительными гносеологическими трудностями. Существующая здесь познавательная сложность также может быть качественно разной, что при этом может быть прямо не связано с рассмотренной выше онтологической сложностью рассматриваемых систем.
Традиционно в физике теории считались связными сетями естественных законов. Законы должны были быть универсальными, общими и необходимыми. Однако даже для физики эта картина законов как применимых ко всей вселенной, без исключений и со следствиями, которые можно вывести из причин, подвергалась сомнению [Cartwright, 1983]. В биологии многие философы высказывали сомнения в существовании законов в физическом смысле. Биологические законы, если они существуют, по-видимому, подвержены пространственным ограничениям, никогда не бывают без исключений и чаще всего имеют невыводимые причинно-следственные связи [Boogerd, 2007]. В этом отношении социальные и социально-психологические закономерности не уступают биологическим процессам в своей неопределенности и невыводимости, что обусловливает и трудности в их моделировании.
5. Адиафорные системы
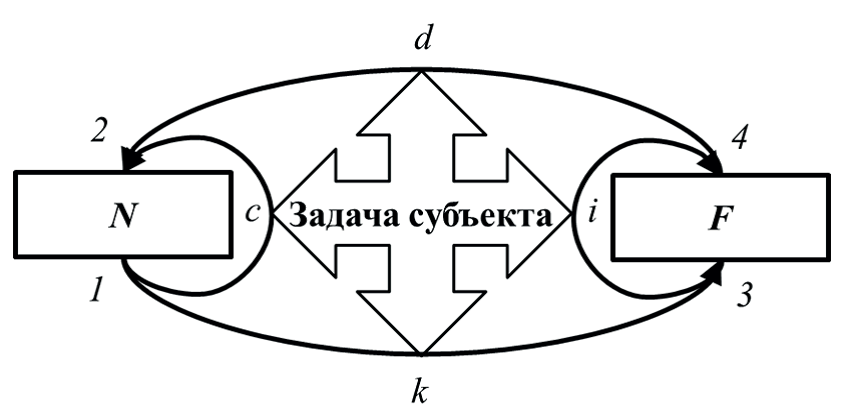
Эпистемологическую трудность выявления механизмов процессов можно пояснить на основе рассмотрения того же модельного отношения. На рисунке 6 показана инфраструктура задачи субъекта по моделированию системы N с помощью модели F. Задача уподобления процесса i процессу c без возможности проникновения в процесс c заключается в определении базовых свойств, характеризующих систему N как на ее входе 1, так и на выходе 2. Эти свойства и определяют продукты процесса N. Преобразование 1 в 3, затем 3 в 4 и 4 в 2 представляет собой другой путь получения продуктов 2. Иными словами моделирование позволяет обеспечить идентификацию конечных продуктов, получаемых двумя различными путями. Это представлено в равенстве (3), которое является другим видом равенства (1).
1->2 = 1->3 + 3->4 + 4->1 (3)
Рис. 6. Инфраструктура задачи моделирования.
Как было отмечено ранее, знание о механизме i может быть получено на основе свойств продуктов 1 и 2, т.е. без какого-либо проникновения в процесс c. Такой подход вполне можно назвать продуктным подходом к поиску системных механизмов. Например, проблема механизма зрения может быть представлена задачей «построения символического описания сцены с использованием информации, содержащейся во входном визуальном образе» [Frisby, 1979, с. 26]. В психологии восприятия этот подход был объяснен образованием «в сознании исследователей эмпирического постулата отождествления характеристик процесса психического отражения с его предметно-содержательным результатом» [Миракян, 1990, с. 185]. Как отмечает А.И. Миракян [Миракян, 1990], этот результат был всегда ближе к «сознанию практически действующего человека» [Миракян, 1990, с. 186]. Адекватность соотношения объекта отражения и продукта отражения всегда имела большое функционально-практическое значение для успешной деятельности человека, в то время как непосредственно процессуальная сторона отражения такого значения для сознательной деятельности человека не имела.
Памятуя о значимости процессуальных продуктов, порождающими можно назвать такие процессы, механизмы которых (в независимости от их сложности) не определяются свойствами своих продуктов и не зависят от них. Эти механизмы являются своеобразными адиафорами по отношению к своим продуктам. Адиафора в философском смысле является термином для фиксации индифферентного, представляющего собой нечто непосредственно безразличное по отношению к значимому (моральному благу или злу).
Поэтому системы с такими порождающими механизмами можно назвать адиафорными системами. Например, перцептивные процессы возможно являются адиафорными в том смысле, что они, по-видимому, специфически порождают новые структуры и формы с помощью механизмов, которые безразличны к участвующим в них продуктам и их свойствам. В результате, эти свойства тогда не содержит никакой адекватной информации для познания соответствующих механизмов. Собственно говоря, разработка трансцендентальной психологии восприятия [22-24] потребовалась А.И. Миракяну в связи с тем, что на основании проведенных им исследований восприятия он был вынужден постулировать такой адиафорный непродуктный характер механизмов непосредственно-чувственного восприятия и обозначить эти процессы как формопорождающие [Психология восприятия: трансцендентальный, 2020].
В целом эти перцептивные процессы адиафорны в том смысле, что они специфически порождают новые структуры и формы, безразличные к этим продуктам процессов и характеристикам продуктов. Это также означает, что собственная перцептивная система не манифестирует свои механизмы феноменологически в нормальных условиях ее функционирования. В этом случае экспериментальные исследования должны отказаться от традиционной экологической валидности, которая относится к способности обобщать результаты исследований в искусственных условиях на реальные условия. Проявления внутренних механизмов не могут в этом случае естественно возникать в пределах функционального диапазона восприятия. Чтобы увидеть явления, связанные с этими механизмами, необходимо вывести систему из ее естественного функционального диапазона. Таким образом, исследование адиафорных систем, по-видимому, требует нового типа экспериментирования, направленного на выявление работы гипотетических модельных принципов в особых условиях [Артеменков, 2016б].
Следует отметить, что свойством адифорности, по-видимому, обладают и другие психологические процессы. Более того ситуацию можно обобщить, поскольку процессы, носящие особый структурно-порождающий характер, обычно характеризуют переходы между системообразующими структурами, изучаемыми разными иерархически взаимосвязанными науками [21, 43]. Процессуальные механизмы здесь также не зависят от явленных свойств их частей или продуктов.
Например, рассмотрим гипотетический процесс образования поваренной соли (хлористого натрия) из натрия и хлора. Можно утверждать, что знание химических молекулярных свойств хлористого натрия или его ингредиентов не позволит понять, как получить из двух этих ингредиентов поваленную соль. Реальный механизм этой реакции лежит на физическом уровне и требует знания устройства соответствующих атомов.
Таким образом, идея формопорождения, выдвинутая при изучении психических процессов восприятия, важна и методологически с точки зрения ее более широких обобщений и выделения в системологии отдельного класса адиафорных структурно-порождающих процессов. Механизмы этих процессов не зависят от явленных особенностей их частей или продуктов и специфичны для процесса перехода между системообразующими структурами, изучаемыми разными иерархически взаимосвязанными науками [4, 21, 36].
6. Заключение
На основе рассмотрения модельного отношения [44, 45] рассмотрены онтологический и эпистемологический (гносеологический) аспекты моделирования сложных систем.
Модельное отношение позволяет осуществлять сравнение систем и их моделей, а также переходить к отношениям измерения в случае, когда каузальные процессы заменяются относительно стабильными отношениями между частями (свойствами) внутри исходной системы.
Онтологический аспект моделирования связан со сложностью моделируемой системы. Качественное увеличение этой сложности в импредикативных системах позволяет говорить о них как о сверхсложных системах [Louie, 2019а].
В эпистемологическом плане на основе подхода трансцендентальной психологии восприятия [1, 2, 22-24] дано определение порождающих (формопорождающих) систем, как адиафорных систем, чьи механизмы, как правило, не проявляют себя в порождаемых формах, структурах и продуктах. Адиафорность исследуемых процессов прямо не зависит от онтологической сложности моделируемой системы и означает, что эти системы порождают новые структуры и формы независимо от каких-либо свойств, представленных в них, или производимых ими частей и продуктов. Представляется, что адиафорные системы могут иметь место при рассмотрении процессов перехода между системообразующими формопорождающими структурами, изучаемыми разными иерархически взаимосвязанными науками.
Представленные в статье результаты имеют методологическое значение для системологии и практики разработки системных моделей и подходов к исследованию сложных и сверхсложных систем и, в частности, порождающих или формопорождающих систем.
Литература
- Артеменков С.Л. Проблематика формопорождения в психологии восприятия: анализ с позиций трансцендентальной парадигмы исследования восприятия. Психология восприятия: трансцендентальный вектор развития: Коллективная монография / под ред. Г. В. Шуковой. М. ; СПб. : Нестор-История, 2020. С. 113-150.
- Артеменков С.Л. Трансцендентальная психология и проблемы исследования формопорождаюших процессов // Психология восприятия: Трансцендентальная перспектива. Ереван: Наири, 2017. С. 27-52.
- Артеменков С.Л. Аспекты моделирования и особые свойства сложных систем // Моделирование и анализ данных. 2016. № 1. С. 47–59. doi:10.17759/mda.04.
- Артеменков С.Л. Реализация методологического принципа научного обобщения Выготского в современной трансцендентальной психологии // В сборнике: Научная школа Л. С. Выготского: традиции и инновации. материалы международного симпозиума. 2016. С. 154-157.
- Артеменков С.Л. Экспериментальное исследование зрительных процессов на основе конфликтной ситуации в восприятии // Социальный мир человека. Вып. 7. Вопросы конфликтологии и медиации / под ред. Н. И. Леонова. Электрон. текстовые дан. Ижевск: ERGO, 2016. С. 64–69.
- Артеменков С.Л. Модель сопредставленности для оценки вероятности объединения событий // Моделирование и анализ данных. 2014. №1. С. 43–54.
- Артеменков С.Л. Иерархия процессов опознания в «перцептроне» Миракяна // Информационные технологии. 2013. №3. С. 56 – 61.
- Артеменков С.Л. Реконструкция модели «перцептрона» Миракяна // Моделирование и анализ данных. 2013. №1. С. 49–60.
- Артеменков С.Л. Трансцендентальная психология как изменение образа мышления. А. И. Миракян и современная психология восприятия. М.: УРАО «Психологический институт»; Обнинск: ИТ-СОЦИН, 2010. С. 324-358.
- Артеменков С.Л. Методология трансцендентальной психологии и проблемы моделирования и экспериментального исследования порождающих процессов // Труды ФИТ (выпуск 2). Москва. РУСАВИА, 2005. С. 37-57.
- Афанасьев И.А., Артеменков С.Л. Компьютерное моделирование «перцептрона» Миракяна для кодопорождения форм объектов // Экспериментальный метод в структуре психологического знания. М.: «Институт психологии РАН», 2012. С. 157-161.
- Валькман Ю.Р., Степашко П.В. Об онтологии интеллектуального моделирования / Открытые семантические технологии проектирования интеллектуальных систем = Open Semantic Technologies for Intelligent Systems (OSTIS-2016) : материалы VI междунар. науч.-техн. конф. (Минск, 18-20 февраля 2016 года)/ редкол. : В. В. Голенков (отв. ред.) [и др.]. Минск : БГУИР, 2016. С. 165-170.
- Вержбицкая Т.Н., Алексина Л.И. Психолингвистика: Учебное пособие. Мн.: БГПУ, 2009. 188 с.
- Герц Г.Р. Принципы механики, изложенные в новой связи / Г. Р. Герц ; ред. И. И. Артоболевский ; пер. В. Ф. Котов, А. В. Сулимо-Самуйло. Москва : Изд-во Акад. наук СССР, 1959. 383 с.
- Городняя Л.В. Парадигма программирования : курс лекций / Л. В. Городняя ; Новосиб. гос. ун-т. Новосибирск : РИЦ НГУ, 2015. 206 с.
- Зароченцев Л.Д., Худяков А.И. Экспериментальная психология: учеб. М. : ТК Велби, Изд-во Проспект, 2005. 208 с.
- Иванников В.А. Порождение деятельности и проблема мотивации // Вестник Московского университета. Серия 14. Психология: Научный журнал. 2015. № 2. С.15–22.
- Иванников В.А. О природе и происхождении психики // Национальный психологический журнал. 2015. № 3(19). С. 15-23.
- Клир Дж. Системология. Автоматизация решений системных задач / Дж. Клир. М.: Радио и связь, 1990. 540 с.
- Князева Е.Н. Понятие «Umwelt» Якоба фон Икскюля и его значимость для современной эпистемологии // Вопросы Философии. 2015. № 5. С. 30-44.
- Магаршак Ю. Структура эмпирической реальности // Независимая Газета от 10.10.2007. – URL: http://www.ng.ru/science/2007-10-10/14_structure.html
- Миракян А.И. Контуры трансцендентальной психологии. Книга 2. М.: ИП РАН, 2004. 384 с.
- Миракян А.И. Контуры трансцендентальной психологии. Книга 1. М.: ИП РАН, 1999. 208 с.
- Миракян А.И. Начала трансцендентальной психологии восприятия // Философ. исслед. 1995. № 2. С. 77–94.
- Миракян А.И. Константность и полифункциональность восприятия. М.: Изд-во ВНИИ ПК ССК, 1992. 216 с.
- Миракян А.И. Афизикальные принципы психического отражения и их моделирование // Принципы порождающего процесса восприятия / Под ред. А. И. Миракяна. М.: Изд-во НИИ СО и УК АПН, 1992. С. 9-48.
- Миракян А.И. Психология пространственного восприятия. Ереван: Айастан, 1990. 206 с.
- Панов В.И. Парадоксы изучения психики и возможность их преодоления // Национальный психологический журнал. 2011. № 1 (5). С. 50–54.
- Панов В.И. Непосредственно-чувственный уровень восприятия движения и стабильности объектов. Вопросы психологии. 1998. № 2. С. 82-107.
- Психология восприятия: трансцендентальный вектор развития: Коллективная монография / под ред. Г. В. Шуковой. М. ; СПб. : Нестор-История, 2020. 384 с.
- Психология восприятия: Трансцендентальная перспектива. Ереван: Наири, 2017. 344 с.
- Суппес П., Зинес Дж. // Льюс Р., Галантер Е. Психологические измерения: Основы теории измерений (Суппес П., Зинес Дж.). Психофизические шкалы (Льюс Р., Галантер Е.): Пер. с англ. 1967. 196 с.
- фон Нейман Дж. Общая и логическая теория автоматов. Пер. и примечания Ю.В. Данилова. В книге: Тьюринг А. Может ли машина мыслить? ГИФМЛ; М.; 1960. С. 39-65.
- Швецова Н.А., Синельникова Т.И. Методы системологии в системе поддержки принятия решений // Международный журнал экспериментального образования. 2015. № 11-1. С. 136-137.
- Шукова Г.В. Парадигмальные изменения в современной психологии восприятия: от психического отражения к порождению психической реальности // Гуманитарный вектор. Серия Психология и Педагогика, 2013. 1(33). С. 124–131.
- Artemenkov S.L. Metaphysics and Fundamentals of Transcendental Psychology Approach. Open Journal of Philosophy, 2021, 11, 125-147.
- Boogerd F.C., Bruggeman F.J., Hofmeyr J-HS., & Westerhoff H.V. (Eds.) Systems Biology - Philosophical Foundations. Elsevier. 2007. 360 p.
- Cartwright N. How the laws of physics lie. Oxford University Press, 1983. 232 p.
- Frisby J. Seeing: Illusion, Brain and Mind. Oxford: Oxford University Press. 1979. 160 p.
- Louie A.H. Mathematical Foundations of Anticipatory Systems. In Handbook of Anticipation. Poli R. (ed.), Springer, New York. 2019. 937-964.
- Louie A.H. Intangible life: Functorial connections in relational biology. Anticipation Science, Vol. 2. New York: Springer. 2017. 264 p.
- Louie A.H. & Poli R. Complex Systems. In Handbook of Anticipation. Poli R. (ed.), Springer, New York. 2019. 17-35.
- Magarshak Y. On the Issue of Completeness of the Modern Conception of Atomic and Molecular Structure. Universal Journal of Physics and Application, 2008, 5, 535-540.
- Rosen R. Essays on life itself. Columbia University Press, 1999, 361 p.
- Rosen R. Life itself: A comprehensive inquiry into the nature, origin and fabrication of life. Columbia University Press, 1991, 285 p.
- Rosen R. Ergodic approximations and specificity. Mathematical Modelling, 1980, 1, 91–97.
Информация об авторах
Метрики
Просмотров
Всего: 250
В прошлом месяце: 22
В текущем месяце: 12
Скачиваний
Всего: 64
В прошлом месяце: 4
В текущем месяце: 1