Моделирование и анализ данных
2022. Том 12. № 2. С. 5–19
doi:10.17759/mda.2022120201
ISSN: 2219-3758 / 2311-9454 (online)
Анализ больших данных в задачах многокритериального выбора
Аннотация
Общая информация
Ключевые слова: принятие решений, критерий качества, анализ данных, матрица предпочтений, ранжирование альтернатив
Рубрика издания: Анализ данных
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2022120201
Получена: 25.04.2022
Принята в печать:
Для цитаты: Иванов А.А., Яшина Н.П. Анализ больших данных в задачах многокритериального выбора // Моделирование и анализ данных. 2022. Том 12. № 2. С. 5–19. DOI: 10.17759/mda.2022120201
Полный текст
Введение
До недавнего времени считалось, что проблема выбора из предложенных альтернатив лежит в области психологии, напрямую зависит от индивидуальных способностей человека. В последние годы возможность получения и необходимость обработки большого объема исходной информации не позволяют осуществить выбор, основываясь только на интуиции лица, принимающего решения (ЛПР). Появилась потребность в разработке математически обоснованных методов и алгоритмов, позволяющих доверить процесс выбора оптимальных вариантов программной системе.
При принятии решений большинство задач обычно являются многокритериальными: рассматриваемые альтернативы оцениваются по критериям качества. Методы выбора и упорядочения альтернатив в таких задачах в значительной степени зависят от шкал критериев. Традиционные алгоритмы выбора оптимальных вариантов решений основываются на задании информации в количественных шкалах, т.е. численными оценками альтернатив по критериям качества, при этом обычно требуется, чтобы шкалы критериев были однородными. Но, практические задачи с однородными шкалами встречаются крайне редко, поэтому приходится использовать дополнительные процедуры приведения оценок по критериям к единой шкале [Петровский].
Данная статья основывается на алгоритмах, не требующих предварительного приведения шкал критериев к однородным [2,3]. Все алгоритмы имеют полиномиальную вычислительную сложность, что позволяет анализировать большие объемы исходной информации.
В разработанную программную систему данные от ЛПР поступают через Excel таблицы. Это простой и удобный способ ввода информации для обычных пользователей в случае больших данных [Shikhman, 2021]. Информация хранится на удаленном сервере, что позволяет зарегистрированному пользователю всегда иметь доступ для её корректировки, причем с различных устройств. Работа программной системы продемонстрирована на примере выбора наиболее предпочтительных для ЛПР моделей дронов.
Математическая модель задачи многокритериального выбора
Для решения задачи необходимо сформировать математическую модель, полностью отражающую разнообразие информации и методов принятия решений. Будем рассматривать математическую модель многокритериального выбора, содержащую следующие элементы:
![]() ,
,
где t – постановка задачи (ранжирование, выбор наилучших альтернатив);
![]() – множество рассматриваемых альтернатив;
– множество рассматриваемых альтернатив;
![]() – множество критериев;
– множество критериев;
![]() – множество шкал критериев;
– множество шкал критериев;
![]() – предпочтения по шкалам критериев;
– предпочтения по шкалам критериев;
![]() отображение
отображение ![]()
![]() – информация о важности критериев;
– информация о важности критериев;
![]() – решающее правило (последовательность алгоритмов
непротиворечивого агрегирования предпочтений).
– решающее правило (последовательность алгоритмов
непротиворечивого агрегирования предпочтений).
В зависимости от содержательной постановки задачи t
требуется построить агрегированное отношение предпочтения на множестве
альтернатив ![]() ,
провести ранжирование альтернатив и\или осуществить выбор наилучших вариантов
альтернатив. Множество альтернатив
,
провести ранжирование альтернатив и\или осуществить выбор наилучших вариантов
альтернатив. Множество альтернатив ![]() задается ЛПР. Альтернативы оцениваются по
критериям качества
задается ЛПР. Альтернативы оцениваются по
критериям качества ![]() с порядковыми или числовыми шкалами
с порядковыми или числовыми шкалами
![]() . Таким
образом, каждой альтернативе ставится в соответствие векторная оценка из
множества
. Таким
образом, каждой альтернативе ставится в соответствие векторная оценка из
множества ![]() .
Значения оценок по числовым шкалам критериев минимизируются или
максимизируются. Так стоимость альтернативы обычно минимизируется, а скорость –
максимизируется. Существуют шкалы, у которых наилучшие и худшие оценки зависят
от предпочтений ЛПР, например, месторасположение альтернативы. Предпочтения по
шкалам критериев
.
Значения оценок по числовым шкалам критериев минимизируются или
максимизируются. Так стоимость альтернативы обычно минимизируется, а скорость –
максимизируется. Существуют шкалы, у которых наилучшие и худшие оценки зависят
от предпочтений ЛПР, например, месторасположение альтернативы. Предпочтения по
шкалам критериев ![]() могут быть заданы численными оценками альтернатив по
данному критерию, попарным сравнением (в частности ранжированием альтернатив),
т.е. отношениями предпочтения
могут быть заданы численными оценками альтернатив по
данному критерию, попарным сравнением (в частности ранжированием альтернатив),
т.е. отношениями предпочтения ![]() , выбором множества наилучших альтернатив, вербальными оценками.
В случае задания предпочтений бинарными отношениями оценок альтернатив по
шкалам критериев не существует.
, выбором множества наилучших альтернатив, вербальными оценками.
В случае задания предпочтений бинарными отношениями оценок альтернатив по
шкалам критериев не существует.
Информация ![]() о важности критериев
о важности критериев ![]() может быть задана отношением предпочтения на
множестве критериев (относительная важность критериев) или весовыми
коэффициентами
может быть задана отношением предпочтения на
множестве критериев (относительная важность критериев) или весовыми
коэффициентами ![]() , численно выражающими важность критериев. Относительная важность
критериев может быть дополнена информацией о том, во сколько раз один критерий
лучше другого. Коэффициенты важности могут быть заданы ЛПР или вычислены в
результате работы одной из специально разработанных процедур. Если критерии
обладают одинаковой важностью, то все весовые коэффициенты равны единице.
, численно выражающими важность критериев. Относительная важность
критериев может быть дополнена информацией о том, во сколько раз один критерий
лучше другого. Коэффициенты важности могут быть заданы ЛПР или вычислены в
результате работы одной из специально разработанных процедур. Если критерии
обладают одинаковой важностью, то все весовые коэффициенты равны единице.
Под решающим правилом ![]() понимается последовательность алгоритмов,
приводящая к решению задачи. В первую очередь решающее правило содержит
алгоритмы многокритериального выбора, а также вспомогательные алгоритмы
обработки информации. При формировании решающего правила
понимается последовательность алгоритмов,
приводящая к решению задачи. В первую очередь решающее правило содержит
алгоритмы многокритериального выбора, а также вспомогательные алгоритмы
обработки информации. При формировании решающего правила
![]() учитывается тип входной информации и требования ЛПР к
выходной информации. В связи с этим требуются процедуры, позволяющие выявить и
формализовать в удобном для работы основных алгоритмов виде входную информацию.
В ряде методов могут потребоваться дополнительные процедуры приведение шкал
критериев к единой шкале, а на заключительном этапе решения задачи алгоритмы
для упорядочения альтернатив и выбора наилучших из них. Решающее правило также
может содержать алгоритмы нахождения коэффициентов важности критериев.
учитывается тип входной информации и требования ЛПР к
выходной информации. В связи с этим требуются процедуры, позволяющие выявить и
формализовать в удобном для работы основных алгоритмов виде входную информацию.
В ряде методов могут потребоваться дополнительные процедуры приведение шкал
критериев к единой шкале, а на заключительном этапе решения задачи алгоритмы
для упорядочения альтернатив и выбора наилучших из них. Решающее правило также
может содержать алгоритмы нахождения коэффициентов важности критериев.
В данной статье предлагаются алгоритмы многокритериального выбора, основанные на задании численных оценок альтернатив по критериям, но не требующие приведения шкал критериев к однородным. Все алгоритмы полиномиальные, что позволяет анализировать большое число альтернатив.
Пусть альтернативы из множества
![]() оцениваются по критериям качества
оцениваются по критериям качества
![]() с
числовыми шкалами отношений
с
числовыми шкалами отношений ![]() . Каждой альтернативе из множества
. Каждой альтернативе из множества
![]() ставится
в соответствие вектор оценок по критериям. Требуется ранжировать альтернативы,
т.е. упорядочить их по предпочтению.
ставится
в соответствие вектор оценок по критериям. Требуется ранжировать альтернативы,
т.е. упорядочить их по предпочтению.
Каждому критерию ![]() поставим в соответствие вектор оценок
альтернатив
поставим в соответствие вектор оценок
альтернатив ![]() ,
,
![]() .
.
Определение 1. Матрицей предпочтений
![]() называется квадратная матрица порядка
называется квадратная матрица порядка
![]() (
(![]() – число альтернатив,
– число альтернатив, ![]() ) с элементами
) с элементами
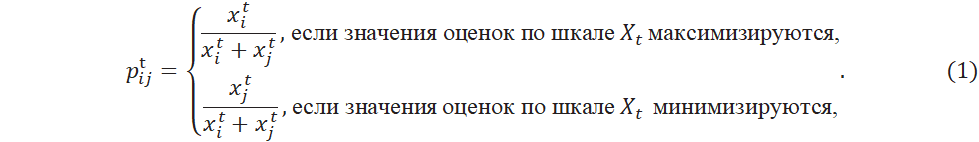
Элемент матрицы ![]() показывает, что по критерию
показывает, что по критерию
![]() альтернатива
альтернатива ![]() более предпочтительна, чем
более предпочтительна, чем
![]() в
в
![]() раз.
раз.
Для элементов матрицы предпочтений
![]() выполняется:
выполняется:
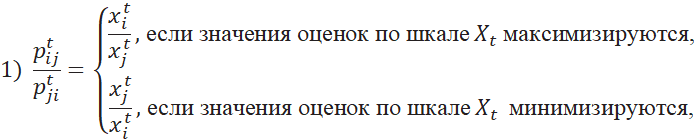
– сохраняется информация о том, во сколько раз альтернатива
![]() предпочтительнее альтернативы
предпочтительнее альтернативы
![]() ;
;
![]()
Эти свойства фактически позволяют заменить процедуру приведения шкал критериев к однородным.
Таким образом, на входе алгоритма, позволяющего построить
агрегированное предпочтение, должны быть заданы матрицы предпочтений по
критериям![]() .
.
При нахождения агрегированного отношения предпочтения в зависимости от пожеланий ЛПР можно использовать алгоритмы, основывающиеся на суммировании матриц исходных предпочтений. Можно также построить агрегированное отношение, минимально удаленное от исходных. Опишем подробно алгоритмы, рассматриваемые в данной статье.
Алгоритм построения агрегированного ранжирования альтернатив для двух критериев
Рассмотрим случай, когда оценка альтернатив проводится по двум критериям качества, имеющим равную важность.
Просуммировав матрицы предпочтений по критериям, получим
матрицу суммарных предпочтений ![]() .
.
Утверждение 1. Для альтернатив, оцениваемых по двум критериям качества, оценки по которым являются положительными и максимизируются, предпочтительнее альтернатива с большим произведением компонент векторной оценки.
Доказательство утверждения 1. Пусть оценки по шкалам
критериев ![]() и
и ![]() максимизируются. Альтернатива
максимизируются. Альтернатива
![]() имеет
векторную оценку по критериям
имеет
векторную оценку по критериям ![]() , а альтернатива
, а альтернатива ![]() –
– ![]() (
(![]() ). Тогда матрицы предпочтений по критериям
). Тогда матрицы предпочтений по критериям
![]() и
и
![]() имеют
вид:
имеют
вид:
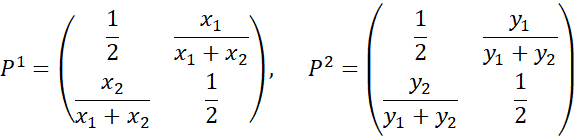
Найдем матрицу суммарных предпочтений:
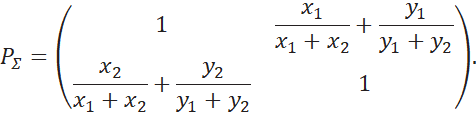
Сравним числа:
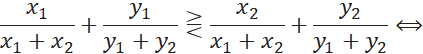
(так как все оценки положительные)
![]()
Получаем, для двух критериев лучшей будет векторная оценка с большим значением произведения ее компонент.
Утверждение 2. Для альтернатив, оцениваемых по двум критериям качества, оценки по которым являются положительными и минимизируются, предпочтительнее альтернатива с меньшим произведением компонент векторной оценки.
Доказательство утверждения 2. Пусть оценки по шкалам
критериев ![]() и
и ![]() минимизируются. Альтернатива
минимизируются. Альтернатива
![]() имеет
векторную оценку по критериям
имеет
векторную оценку по критериям ![]() , а альтернатива
, а альтернатива ![]() –
– ![]() (
(![]() ). Тогда матрицы предпочтений по критериям
). Тогда матрицы предпочтений по критериям
![]() и
и
![]() имеют
вид:
имеют
вид:
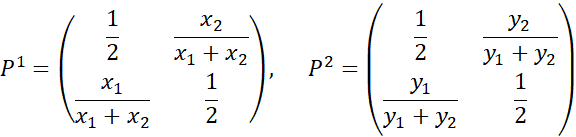
Найдем матрицу суммарных предпочтений:
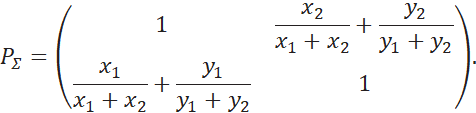
Сравним числа:
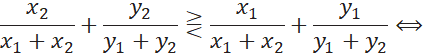
![]()
Получаем, для двух критериев, для которых оценки по шкалам минимизируются, лучшей будет векторная оценка с меньшим значением произведения ее компонент.
Утверждение 3. Пусть для альтернатив, оцениваемых по
двум критериям качества с положительными шкалами, оценки по критерию
![]() максимизируются, а по
максимизируются, а по ![]() , минимизируются. Тогда предпочтительнее альтернатива
с большим отношением оценки по критерию
, минимизируются. Тогда предпочтительнее альтернатива
с большим отношением оценки по критерию ![]() к оценке по критерию
к оценке по критерию
![]() .
.
Доказательство утверждения
3. Пусть альтернатива ![]() имеет вектор оценок по критериям
имеет вектор оценок по критериям
![]() , а
альтернатива
, а
альтернатива ![]() –
– ![]() (
(![]() ). Найдем матрицы предпочтений по критериям
). Найдем матрицы предпочтений по критериям
![]() и
и
![]() .
.
По шкале критерия ![]() оценки максимизируются, следовательно,
оценки максимизируются, следовательно,
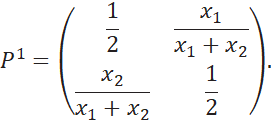
По шкале критерия
![]() оценки
минимизируются, следовательно,
оценки
минимизируются, следовательно,
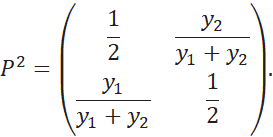
Матрица суммарных предпочтений имеет вид:
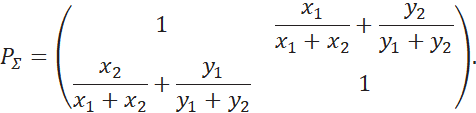
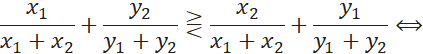
![]()
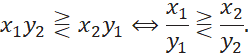
Получаем: предпочтительнее альтернатива, у векторной оценки которой большее значение отношения первой компоненты (оценки максимизируются) ко второй (оценки максимизируются). Что и требовалось доказать.
Теорема 1. При сравнении векторных оценок альтернатив по двум критериям качества с положительными шкалами получим ранжирование альтернатив, т. е. все альтернативы попарно сравнимы.
Доказательство теоремы 1 следует из утверждений 1-3, в которых векторным оценкам ставится в соответствие число, что позволяет сравнить все альтернативы по предпочтительности. Заметим, что в случае равенства чисел альтернативы имеют равную предпочтительность.
Пример 1. Пусть множество альтернатив
![]() оценивается по двум критериям качества
оценивается по двум критериям качества
![]() . Численные
оценки альтернатив приведены в таблице.
. Численные
оценки альтернатив приведены в таблице.
|
|
|
|
Произведение оценок |
Отношение оценок |
|
|
3 |
6 |
18 |
|
|
|
4 |
5 |
20 |
|
|
|
2 |
7 |
14 |
|
|
|
7 |
3 |
21 |
|
Если значения оценок по шкалам критериев максимизируются, то
по утверждению 1 наилучшая альтернатива ![]() .
.
Если значения оценок по шкалам критериев минимизируются, то
по утверждению 2 наилучшая альтернатива ![]() .
.
Если значения оценок по шкале критерия
![]() максимизируются, а по шкале критерия
максимизируются, а по шкале критерия ![]() минимизируются, то по утверждению 3 наилучшая
альтернатива
минимизируются, то по утверждению 3 наилучшая
альтернатива ![]() .
■
.
■
Алгоритмы построения агрегированного ранжирования альтернатив для произвольного числа критериев
Опишем алгоритмы построения агрегированного отношения предпочтения для произвольного числа альтернатив, основывающиеся на суммировании матриц исходных предпочтений.
Алгоритм ранжирования альтернатив на основе орграфа суммарного предпочтения.
1. Формирование матриц предпочтения
![]() по
критериям по формулам
по
критериям по формулам ![]() .
.
2. Построение матрицы суммарных предпочтений.
3. ![]()
4. Ранжирование альтернатив.
Предложенный алгоритм допускает введение весовых
коэффициентов ![]() ,
характеризующих компетентность экспертов или важность критериев качества. В
этом случае матрица суммарных предпочтений будет вычисляться по формуле:
,
характеризующих компетентность экспертов или важность критериев качества. В
этом случае матрица суммарных предпочтений будет вычисляться по формуле:
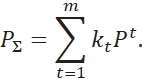
Ранжирование альтернатив по одному критерию качества осуществляет Excel таблица. Алгоритмы ранжирования в случае задания двух критериев описаны в предыдущем параграфе. Для ранжирования альтернатив при большем числе критериев воспользуемся алгоритмами, основанными на индексирования альтернатив [Нефедов, 2018].
Опишем алгоритмы нахождения индексов альтернатив. Будем рассматривать следующие процедуры.
1. Процедура разности весов: каждой альтернативе
![]() ставится в
соответствие индекс, равный разности суммы элементов строки матрицы суммарных
предпочтений
ставится в
соответствие индекс, равный разности суммы элементов строки матрицы суммарных
предпочтений ![]() и элементов столбца этой матрицы.
и элементов столбца этой матрицы.
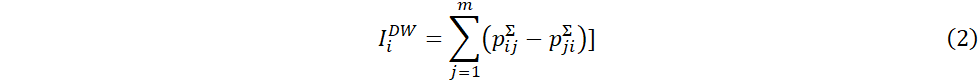
2. Процедура отношения весов: каждой
альтернативе ![]() ставится в соответствие индекс, равный отношению суммы
элементов строки матрицы суммарных предпочтений
ставится в соответствие индекс, равный отношению суммы
элементов строки матрицы суммарных предпочтений
![]() и
элементов столбца этой матрицы.
и
элементов столбца этой матрицы.
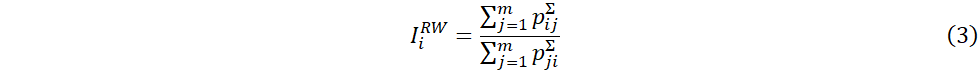
Если знаменатель дроби равен нулю, то
![]() . При
программной реализации знак бесконечности заменяется числом, заведомо большим
индексов всех альтернатив, индекс которых не равен бесконечности. В
случае, когда числитель и знаменатель равен нулю можно рекомендовать поставить
альтернативу
. При
программной реализации знак бесконечности заменяется числом, заведомо большим
индексов всех альтернатив, индекс которых не равен бесконечности. В
случае, когда числитель и знаменатель равен нулю можно рекомендовать поставить
альтернативу ![]() в ранжировании на последнее место, т.к. информация о
сравнении ее с другими альтернативами отсутствует. Мы будем решать задачи с
полной информацией об альтернативах.
в ранжировании на последнее место, т.к. информация о
сравнении ее с другими альтернативами отсутствует. Мы будем решать задачи с
полной информацией об альтернативах.
Преобразуем формулу (2) с учетом особенностей матриц
предпочтений по критериям и матрицы суммарных предпочтений в рассматриваемом
случае. По определению для матрицы предпочтений по критерию
![]() выполняется:
выполняется: ![]() . Следовательно, для элементов матрицы суммарных
предпочтений справедливы равенства
. Следовательно, для элементов матрицы суммарных
предпочтений справедливы равенства ![]() . Тогда
. Тогда
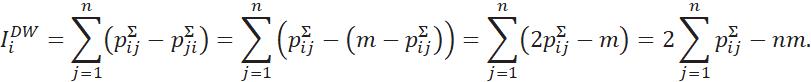
Таким образом, при ранжировании индекс альтернативы
![]() можно
определять суммой элементов
можно
определять суммой элементов ![]() ой строки матрицы суммарных предпочтений.
ой строки матрицы суммарных предпочтений.
Проведем аналогичные преобразования для формулы (3).
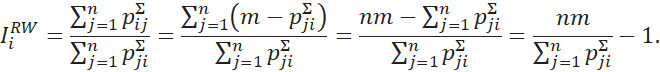
Таким образом, при ранжировании индекс альтернативы
![]() можно
определять величиной, обратной к сумме элементов
можно
определять величиной, обратной к сумме элементов
![]() го столбца
матрицы суммарных предпочтений.
го столбца
матрицы суммарных предпочтений.
Вместо элементов столбца можно подставить элементы строки:
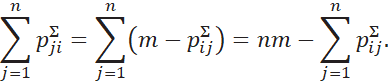
Заметим, что полученные формулы справедливы только при
выполнении соотношений ![]() . Но предложенную методику формирования матриц предпочтений можно
распространить на весьма частую ситуацию, когда не для каждой альтернативы
известны все оценки по критериям. В этом случае при сравнении
альтернатив, информация о которых отсутствует по некоторому
. Но предложенную методику формирования матриц предпочтений можно
распространить на весьма частую ситуацию, когда не для каждой альтернативы
известны все оценки по критериям. В этом случае при сравнении
альтернатив, информация о которых отсутствует по некоторому
![]() ому критерию
(
ому критерию
(![]() ,
целесообразно положить
,
целесообразно положить ![]() , а не
, а не ![]() , уменьшив их значимость в матрице суммарных предпочтений.
, уменьшив их значимость в матрице суммарных предпочтений.
Пример 2. Пусть множество альтернатив
![]() оценивается по трем критериям качества
оценивается по трем критериям качества
![]() . Численные
оценки альтернатив приведены в таблице (значения по шкалам оценок
максимизируются).
. Численные
оценки альтернатив приведены в таблице (значения по шкалам оценок
максимизируются).
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
3 |
4 |
2 |
|
|
2 |
4 |
4 |
|
|
3 |
3 |
2 |
Матрицы предпочтений альтернатив для каждого критерия соответственно имеют вид:

Вычислим матрицу суммарных предпочтений
![]() :
:

Применив процедуру разности весов
![]() , получим вектор
индексов
, получим вектор
индексов
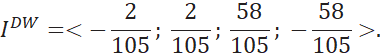
Получим ранжирование альтернатив
![]() .
.
Убедимся, что ранжирование не изменится при суммировании элементов строк. Поскольку диагональные элементы равны будем суммировать без них. Получим вектор
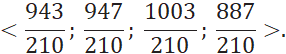
Применив процедуру отношения весов
![]() , получим вектор
индексов (приближенно)
, получим вектор
индексов (приближенно)
![]()
Ранжирования альтернатив
![]() не
изменилось.
не
изменилось.
Если полученные разными методами агрегированные ранжирования различны, то выбрать ранжирование наиболее согласованное с ранжированиями по критериям можно следующим способом.
1. Зададим отношение предпочтения,
соответствующее полученному ранжированию бинарной матрицей
![]() c
элементами
c
элементами
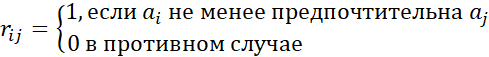
2. Проранжируем альтернативы по критериям и
зададим соответствующие отношения предпочтения бинарными матрицами
![]() .
.
3. Найдем суммарное расстояние от матрицы
![]() до
до
![]() по
формуле
по
формуле
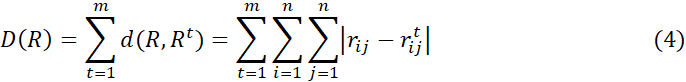
Расстояние между матрицами зададим, как расстояние Хэмминга.
Пример 3. На основе оценок по критериям из примера 2
построим бинарные матрицы ![]() .
.
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
3 |
4 |
2 |
|
|
2 |
4 |
4 |
|
|
3 |
3 |
2 |
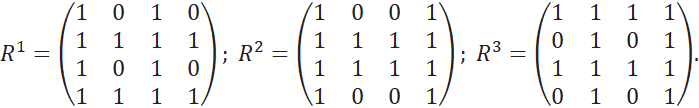
Для ранжирования ![]() бинарная матрица
бинарная матрица
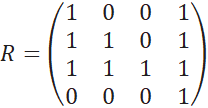
Суммарное расстояние найдем по формуле (4)
![]()
■
Если мы получим различные агрегированные ранжирования, решая задачу разным методами, то их можно сравнить по суммарному расстоянию до предпочтений по критериям. Наиболее согласованным с ранжированиями по критериям является агрегированное ранжирование с наименьшим суммарным расстоянием.
Организация работы с большими данными в программной системе многокритериального выбора
При решении задач с большим объемом исходных данных у разработчика программной системы возникает проблема выбора наиболее удобного способа хранения информации и для ввода ЛПР, и для считывания программой. Необходимо учесть, что в задачах принятия решений информация может постоянно обновляться в связи с поступлением новых вариантов альтернатив.
В разработанной программной системе выбран наиболее простой и удобный для ЛПР способ ввода данных через Excel таблицы. Программа загружает Excel таблицу в систему, считывает и создаёт свои таблицы, удобные для работы алгоритмов многокритериального выбора. База данных программной системы содержит следующую информацию.
1. Таблица с наименованиями альтернатив и их числовые характеристиками.
2. Информация по критериям: тип шкалы, максимизируются или минимизируются оценки по шкале, весовые коэффициенты важности критериев.
Программная система организована так, что исходные данные хранятся на удаленном сервере, т. о. зарегистрированный пользователь всегда имеет доступ для их корректировки, причем с различных устройств.
Рассмотрим работу программы на примере ранжирования дронов с целью приобретения для наблюдения за местностью, сьемки местности и передачи информации оператору. В настоящее время разработано сотни различных моделей дронов даже в рамках данного предназначения. ЛПР обращается на специальный сайт по продажам дронов, например в интернет-магазин, где ему предоставляется огромный список моделей. Сайт предлагает ЛПР помощь в выборе наиболее предпочтительных вариантов дронов. Разработчики сайта хранят список моделей дронов с их характеристиками по критериям качества в Excel таблице. В таблице также присутствует информация о том максимизируются или минимизируются оценки по критериям.
Будем оценивать модели дронов по следующим критериям:
![]() стоимость
(в рублях, min);
стоимость
(в рублях, min); ![]() вес (в кг, min);
вес (в кг, min); ![]() максимальная длительность полета (в часах или
мин., max);
максимальная длительность полета (в часах или
мин., max); ![]() максимальная высота полета (в метрах, max);
максимальная высота полета (в метрах, max);
![]() обслуживание (в баллах, max);
обслуживание (в баллах, max);
![]() защита от
столкновений и погодных явлений (в баллах, max).
защита от
столкновений и погодных явлений (в баллах, max).
Основные этапы работы программной системы ранжирования альтернатив в диалоговом режиме с ЛПР
1. ЛПР (лицо, принимающее решения) вводит интервалы-ограничения для каждого критерия (например, ограничения по стоимости). Таблица может сама упорядочивать модели по одному критерию, и мы легко отсекаем дроны вне заданного интервала.
2. ЛПР выбирает критерии из заданного перечня, по которым хочет ранжировать дроны. Дополнительно, по желанию ЛПР, можно ввести весовые коэффициенты важности критериев.
3. Программа ранжирует дроны и выдает на экран 5 (или более) наилучших аппаратов.
ЛПР имеет возможность изменять наборы критериев и повторно осуществлять выбор наиболее предпочтительных моделей дронов.
ЛПР выбирает одну или несколько понравившихся ему моделей и оставляет на сайте заказ.
Заключение
Предложены и обоснованы алгоритмы многокритериального выбора, не требующие приведения шкал критериев к однородным. Все алгоритмы имеют полиномиальную вычислительную сложность, что позволяет работать с большими массивами исходной информации. Разработана программная система, предназначенная для решения задач многокритериального принятия решений, а также для проведения практических и лабораторных работ в вузах по дисциплине «Математическая теория принятие решений».
Литература
- Петровский А.Б. Теория принятия решений. М.: Академия. 2009
- Smerchinskaya S.O., Yashina N.P. On an algorithm for pairwise comparison of alternatives in multi-criteria problems // International Journal of Modeling, Simulation, and Scientific Computing. 2018. Vol. 9, Issue 1. DOI: 10.1142/S179396231850006X.
- Смерчинская C.О., Яшина Н.П. Агрегирование предпочтений в многокритериальных задачах // Вестник Московского авиационного института. 2013. № 2, том 20. С. 219-225.
- Shikhman V., Müller D. Mathematical Foundations of Big Data Analytics. 2021. DOI: 10.1007/978-3-662-62521-7. ISBN: 978-3-662-62520-0
- Нефедов В.Н., Смерчинская С.О., Яшина Н.П. Построение агрегированного отношения, минимально удаленного от экспертных предпочтений. Прикладная дискретная математика. 2018. № 42. C. 120–132. DOI: 10.17223/20710410/42/9
Информация об авторах
Метрики
Просмотров web
За все время: 527
В прошлом месяце: 23
В текущем месяце: 20
Скачиваний PDF
За все время: 168
В прошлом месяце: 3
В текущем месяце: 4
Всего
За все время: 695
В прошлом месяце: 26
В текущем месяце: 24